Abstract
Nowadays, the Oil and Gas (O&G) industry faces significant challenges due to the relentless pressure for rationalization of project expenditure and cost reduction, the demand for greener and renewable energy solutions and the recent outbreak of the pandemic and geopolitical crises. Despite these barriers, the O&G industry still remains a key sector in the growth of world economy, requiring huge capital investments on critical megaprojects. On the other hand, the O&G projects, traditionally, experience cost overruns and delays with damaging consequences to both industry stakeholders and policy-makers. Regarding this, there is an urgent necessity for the adoption of innovative project management methods and tools facilitating the timely delivery of projects with high quality standards complying with budgetary restrictions. Certainly, the success of a project is intrinsically associated with the ability of the decision-makers to estimate, in a compelling way, the monetary resources required throughout the project’s life cycle, an activity that involves various sources of uncertainty. In this study, we focus on the critical management task of evaluating project cost performance through the development of a framework aiming at handling the inherent uncertainty of the estimation process based on well-established data-driven concepts, tools and performance metrics. The proposed framework is demonstrated through a benchmark experiment on a publicly available dataset containing information related to the construction cost of natural gas pipeline projects. The findings derived from the benchmark study showed that the applied algorithm and the adoption of a different feature scaling mechanism presented an interaction effect on the distribution of loss functions, when used as point and interval estimators of the actual cost. Regarding the evaluation of point estimators, Support Vector Regression with different feature scaling mechanisms achieved superior performances in terms of both accuracy and bias, whereas both K-Nearest Neighbors and Classification and Regression Trees variants indicated noteworthy prediction capabilities for producing narrow interval estimates that contain the actual cost value. Finally, the evaluation of the agreement between the performance rankings for the set of candidate models, when used as point and interval estimators revealed a moderate agreement ().
1. Introduction
The Oil and Gas (O&G) industry is considered as one of the largest and most important pillars in the world economy [1] dealing with the delivery of megaprojects that are complex ventures characterized by large-scale capital investments and exceedingly long life-cycles for their completion [2]. Similar to capital projects in other industries, the success of O&G projects is strongly associated with three types of constraints which are cost, time, and scope, known as the iron triangle model [3].
In order to keep track of all three constraints, there is an imperative need to accurately evaluate O&G project performance via specific metrics, thus contributing to wise decision-making that supports achievement of project objectives [3]. Regarding this, Rui et al. [4] conduct a literature review with the aim of identifying key factors that affect the performance of O&G projects. Based on the empirical evidence synthesized from the collected studies and the results from an expert opinion survey, they propose a taxonomy classifying performance metrics into five distinct categories (cost, schedule, safety, quantity, and production). Among these five categories, cost performance metrics are considered of high practical importance, since they are the main output of the cost estimation task, which is, in turn, a vital activity of Project Cost Management (PCM) and, generally, energy project management [3].
Although the evaluation of project performance via specific metrics is a crucial PCM activity in other industries, the cost performance of O&G projects was seemingly neglected until historical oil price collapses [5]. In addition, historical records from completed O&G projects related to a variety of scopes, e.g., exploration, drilling and production, transportation, refining and marketing [3] indicate significant cost and time overruns with delivered projects of low-quality standards [5]. Due to this fact, a rapidly increased interest has been noted from both research community and industry leaders to understand the causes of this unwelcome phenomenon [4,5,6,7,8,9,10,11,12]. A few interesting remarks are extracted from the study of Rui et al. [5], in which the authors investigate the cost performance of two hundred public O&G projects with the aim of identifying key drivers contributing to cost overruns. The authors conclude that the most important drivers are (a) the size of the project with large O&G projects facing higher cost overruns, (b) the geographical variations and the unique factors of regions, where the projects are going to be developed, (c) the number of partners participating in joint venture projects, (d) the diversity in terms of size and type of companies undertaking the delivery of a project and (e) the diversity of projects in terms of their functions.
Apart from these factors related to the unique characteristics and the complexity of O&G projects, a significant source for cost overruns, as in any other industrial sector, lies in the fact that, in practice, the estimation process is usually accomplished with a primary focus on the approximation of the most likely value of cost, or in other words, on the assessment of a single “point estimate” [13]. Although the strategy of inferring about forthcoming projects utilizing a point estimator (POE) mechanism may be a valuable PCM tool for achieving specific managerial goals, i.e., the bidding of a project and the signing of a contract [14] or the establishment of practices related to resource allocation tasks [3]; it may lead to erroneous managerial decisions and project failures [3,13]. Having in mind that the prediction of a future event is a probabilistic activity, there is inherent uncertainty which has to be taken into consideration for decision-making purposes [15]. Moreover, the empirical evidence shows that project teams usually underestimate or ignore the risks associated with projects due to a lack of experience [5] and the availability of theoretical methodologies and tools that are able to guide the cost estimation process in terms of uncertainty [16].
One practical remedy for handling probabilistic uncertainty associated with the estimation process is the utilization of interval estimates or prediction intervals [3,13,15]. A Prediction Interval (PI) is defined as a range of values bounded by two estimates representing the “best-case” and the “worst-case” scenarios [3,13] or, in other words, the optimistic and the pessimistic evaluation of the cost under a predefined probability [13]. Although prediction interval estimators (PIEs) provide invaluable information concerning the uncertainty for probabilistic future events, while, at the same time, being the sole practical tool for exploring risk management strategies [3] and what-if analysis under alternative scenarios [14], the practitioners in many industries base PCM activities on point estimates of cost [15].
A possible reason may be the fact that decision-makers seem to have doubts about the merits of producing interval estimates or they believe that these types of estimates do not add value to the PCM life-cycle [17,18]. Another reason for the limited usage of interval estimates is due to the lack of built-in methodologies and approaches for the construction of PIs for the majority of cost estimation techniques [16,19]. Last but not least, although the evaluation of project cost performance has been the subject of debate among researchers and practitioners in the O&G sector during the last decade, to the best of our knowledge, the attention has been mainly focused on the development and adaption of performance metrics fulfilling the goal of evaluating prediction systems that provide point estimates [4]. In contrast, the assessment of project cost performance based on an interval estimation strategy is, certainly, a more complicated project exercise, due to the limited availability of appropriate analytical tools for accomplishing this type of task [20].
Based on the previous considerations, the motivation behind the current study is the exploration of practices and methodologies that will serve as a unified tool for the evaluation of O&G project cost performance through the quantification of the expected amount of uncertainty in the cost estimation process. Regarding this, the general goal of this study, by adopting the Goal–Question–Metric (GQM) approach that is used in software engineering metrics to measure and improve the software quality [21], is “to analyze the cost estimates of projects for the purpose of investigating, validating, and comparing the quality of alternative data-driven prediction systems with respect to their produced interval estimates from the point of view of researchers and practitioners in the context of O&G project cost management”. Moreover, the sheer number of ML algorithms and their variants put a heavy burden on decision-makers, since there is not a decisively optimal solution and thus there is a need to conduct benchmark experiments on the available datasets. At this point, we have to emphasize that, although there is a wide variety of traditional cost estimation techniques (i.e., expert judgement, Delphi method, bottom-up/top-down strategies, etc.) [3], this study focuses on the investigation of data-driven solutions utilizing historical records of completed projects for the development of a prediction model that provides an expectation of actual cost.
To meet our objectives, we propose a framework composed of advanced statistical and Machine Learning (ML) approaches that have been proved beneficial in other scientific domains and industries. More specifically, the framework is based on a two-step process aiming at (a) the construction of cost interval estimates (i.e., PIs) and (b) the adoption of efficient metrics and inferential procedures for evaluating competing PIEs through the prism of uncertainty. Regarding the former direction, the core methodology is a simulation resampling technique, namely the non-parametric bootstrap [22], that generates a large number of independent samples drawn with replacement from the original sample in order to infer about an unknown parameter of interest. The bootstrap resampling technique has been already applied for different scopes in the O&G sector (see indicatively [23,24,25,26,27,28,29]), while it has been also used for managing uncertainty into a similar industry context dealing with the estimation of effort needed for the completion of software engineering projects [19]. Hence, the effective deployment of this specific class of simulation resampling techniques into a wide range of O&G scopes and the idea of transferring well-established practices from other industries were the main motives for exploring its usage for PCM purposes into the O&G sector. As far as the second direction is concerned, the framework synthesizes knowledge extracted from the adoption of appropriate performance metrics and statistical inferential procedures in order to evaluate the quality of competing prediction systems (PS) guiding, in turn, the process of identifying the most appropriate one(s) for future interval estimates of cost.
To provide straightforward directions and guidelines to both researchers, project managers and decision-makers who are actively engaged in PCM activities, the proposed framework is demonstrated through the conduction of a benchmark experiment on a publicly available dataset containing information about the cost and the associated drivers of the U.S. natural gas pipeline network. Although the proposed approach is illustrated on a representative case study comprising projects for a specific scope, the framework is generic and thus it can be easily adapted to both dimensions of O&G project (hierarchical structure and phases) [4], assuming that there are available data from past projects. We believe that the proposed framework can contribute to the extension of the body of knowledge related to O&G PCM by providing a systematic way to analyze project cost estimates based on data-driven mechanisms that have been successfully, applied in other similar industry contexts. In addition, the empirical results of our benchmark study shed light on the challenges involved in the estimation process and the practical requirements for the establishment of structured frameworks that will provide useful guidance to both researchers and practitioners that are willing to integrate data-driven project cost management solutions following the current trends of the new digitalized O&G 4.0 era. In this regard, the current study can also be of high value for the identification of the statistical and ML competencies and skills that are required for supporting the transformation of traditional project management activities into digitalized decision-making processes.
The rest of the paper is organized as follows: In Section 2, we present the background information related to the proposed framework. Section 3 summarizes the main components of the framework and the posed research questions of the study. In Section 4, we present the experimental setup of the study, while, in Section 5, we showcase the results derived from the conduction of the benchmark experiment. Threats to validity are presented in Section 6, whereas, in Section 7, we conclude by discussing the results and providing directions to both researchers and practitioners.
2. Background Information
In this section, we present background information necessary for facilitating the understanding of the proposed framework and its main components.
2.1. Prediction System and Probabilistic Uncertainty
Formulated mathematically, the goal of any PS is to build a function of the form that describes in an efficient way the relationship between the dependent variable () (e.g., the cost) and a set of independent variables or predictors (e.g., cost drivers ()), where the error term ε is usually assumed to be normally distributed with mean zero and constant variance () [30]. In other words, a PS is an approximate realization of the cost function based on the available past projects for a given dataset [31].
The practical implications related to the accurate prediction of unobserved phenomena have led to a significant research activity for many decades with a plethora of methods appearing so far varying from statistical models to ML algorithms. A common characteristic of these data-driven approaches is the fact that they produce point estimates of the dependent variable without providing any further information about uncertainty, which arises in many forms [32]. Regarding this, many researchers point out potential sources of uncertainty and their associated error types (see indicatively, [14,15,16,33,34]). Firstly, uncertainty may arise from erroneous model fit (model error), since a PS provides only an approximation of the true relationship between the response variable and a set of predictors [33,34]. In addition, the quality of the dataset used into the fitting phase plays a significant role, since measurement errors and noise may exist in the data affecting, in turn, the quality of the derived estimates [15]. Finally, there is also a type of error, namely the scope error, that is incurred, when the model is applied in a way that deviates from the intended scope or the data may not be representative of the intended scope [14].
Taking into account the above considerations, the estimation process of future events should be accompanied by appropriate mechanisms able to provide uncertainty assessment in a diligent and efficient manner [3,13,15]. Typically, the quantification of probabilistic uncertainty involved in PCM is accomplished through the computation of a PI approximating a lower (optimistic) and an upper (pessimistic) expectation (or prediction bounds) of the future unknown value given a prescribed probability or confidence level [15,16]:
In Equation (1), represents the prescribed probability level (usually 0.05), provides the confidence level of the PI, while and are the expectations of the lower and upper bounds corresponding to the -th and the -th percentiles of the distribution of estimates, respectively.
At this point, we have to clarify that there is a distinction between the terms PI and confidence interval (CI), which may be inappropriately used in an interchangeable manner [15]. The term PI is associated with the estimate of an unknown future value of a random variable with a prescribed confidence level [16,35], which, in our case, is the cost of a forthcoming project. In contrast, a CI provides information about an unknown population parameter, e.g., the expected mean value of a dependent variable, with a prescribed confidence level [16,35]. Hence, these two types of intervals should be used with caution, since they are both valuable inferential tools but for entirely different managerial purposes. In cases where the objective is the evaluation of uncertainty associated with the cost estimation process for a new project, or in other words, predicting what is more likely to happen in the future, the construction of a PI instructs project managers that they should feel, for example, 95% confident that the predicted cost will lie within the estimated range of values [30]. In contrast, CIs capture relevant information about what happened in the past and thus, they constitute a valuable PCM tool for inferring about uncertainty associated with the true population parameter of interest [30]—for example, the mean cost value of completed projects.
2.2. Non-Parametric Booststrap Resampling
Based on the above considerations, the assessment of one of the most common sources of uncertainty, i.e., inaccurate cost estimates [3], is a key part of project management, since it is directly associated with the identification, quantification and prioritization of risks that can potentially threaten the success of a project [3,13,14,33]. As we have already mentioned, the evidence from historical past O&G projects reveals significant cost overruns [3,4,36] that may, among other reasons, have a detrimental effect on wrong managerial decisions based solely on point estimates of cost [3,13]. A possible explanation for this erroneous management practice stems from the fact that, despite the overabundance of algorithmic approaches producing point estimates of the dependent variable of interest, there is a gap regarding the theoretical guidance for the construction of PIs [16]. An exception to this general rule is the class of the statistical parametric linear regression models that encompasses analytical formulae for the evaluation of PIs along with the derived point estimate [19]. On the other hand, in real-life contexts, the strong assumptions of this type of regression techniques may not stand, due to the existence of highly-skewed distributions rendering the produced PIs too wide and are thus rendered impractical or unrealistic for usage into risk management activities [19].
The lack of analytical tools for quantifying the uncertainty in ML algorithms has forced researchers into the adoption of empirically-based, simulation and resampling techniques [14,15,16] in order to compute PIs for a future value, e.g., the cost of a new project. The non-parametric bootstrap [22], belonging to the broad class of resampling techniques, is a generic method that has attracted the researchers’ interest, due to its applicability in several ML contexts [30]. Generally speaking, the bootstrap is a distribution-free method based on the reconstruction of the empirical distribution without making any assumption about the shape of its theoretical distribution, whereas the rationale behind the approach is the generation of a large number of independent samples drawn with the replacement from the original random sample [30]. In statistical terms, the general aim is to infer about an unknown population parameter based on a random sample , whereas denotes the sample statistic of the parameter . The basic principles of the method can be summarized into the following steps [30]:
- Obtain a large number of equal-sized samples drawn randomly with replacement from the original random sample .
- For each bootstrap sample , , evaluate an estimate for the unknown parameter of interest .
- The bootstrap estimates form an approximation of the empirical distribution of .
The empirical bootstrap distribution can be used, in turn, to compute several statistical measures for , e.g., mean, bias, variance, standard error, etc. [30].
The simplicity of the method and its distribution-free nature have rendered bootstrap resampling a popular approach among researchers for providing practical solutions to a wide range of problems. This is also the case for the O&G industry, in which the related literature reveals a significant body of research attempts focusing on the deployment of bootstrap resampling in many application domains, such as reserves estimation [23,24], evaluation of natural gas and oil production [27], economic analysis of stock prices [25,26,28,29], and evaluation tasks in drilling operations [37,38]. Certainly, these are only indicative examples of bootstrap applications in the O&G sector, since the extensive review of the literature is outside of the scope of the current study. Moreover, bootstrap resampling has been successfully introduced in the software engineering industry in order to facilitate PCM activities and handling of uncertainty [14,19,39,40,41,42].
The latter was the main reason motivating us to explore the possibilities of utilizing bootstrap resampling in the context of PCM in the O&G sector. In the proposed framework, the non-parametric bootstrap resampling is the main component responsible for estimating PIs for the set of projects comprised in a dataset . Regarding this, the generic steps of the methodology presented above should be adapted to fulfil the intended goal. In addition, apart from the utilization of the bootstrap resampling technique, the evaluation of project cost performance should be empirically accomplished through the investigation of the capabilities for a given PS to provide accurate estimates for unseen future projects. In order to resemble such a real-life application scenario, we make use of the leave-one-out cross-validation (LOOCV) validation scheme. The following steps summarizes the methodology followed in our study for producing interval estimates of cost:
- 1.
- For project
- i.
- Partition the dataset into training and test sets (LOOCV).
- a.
- For each iteration , where denotes a large number of iterations:
- From the set of the projects of the training set , draw randomly with replacement of a set of indices of size .
- Evaluate the cost of the project belonging to the test set, based on the model fitted on the training set.
- b.
- Construct the bootstrap empirical distribution through the estimated values of the project.
- ii.
- Evaluate the PI of the project through the following formula:
- 2.
- Repeat steps (1-i)–(1-ii) for the total number of projects .
In Equation (2), represents the prescribed probability level, whereas and are the lower and upper bounds corresponding to the -th and the -th percentiles of the bootstrap distribution for project under consideration, respectively (Figure 1).
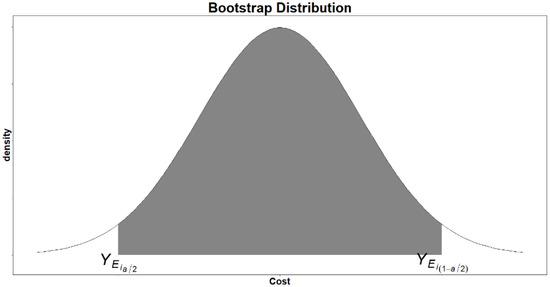
Figure 1.
Bootstrap distribution with % empirical prediction interval.
2.3. Performance Evaluation and Model Selection
2.3.1. Cost Performance Metrics for Prediction Interval Estimators
The building of a data-driven model (PS) on a given dataset results in a sample of predictions for the variable of interest (in our case, the cost response). Based on a set of predictions, the next critical issue concerns the quality assessment of the derived solution, since it offers a straightforward way to evaluate the extent to which a PS estimates the actual response value efficiently [30,43]. Furthermore, in industrial settings, the performance evaluation is the main empirical tool that can be used for guiding a wide range of managerial decisions including project risk analysis [3,13]. On the other hand, the nature of the extracted solution poses significant challenges, since the two variants of estimates (point estimates and interval estimates) demand the evaluation of completely different performance metrics in order to provide an overview of the quality of the two estimator types (POEs and PIEs) [20].
Regarding the quality assessment of POEs, there are plenty of loss functions evaluating the performance through an expression of the divergence (or error) between the actual () and the estimated (or predicted) () values [44]. The sample of error measurements computed by the total number of projects are used, in turn, for the evaluation of an overall performance indicator through the computation of a central tendency measure, such as the mean or the median in cases of highly-skewed error distributions [32]. The overabundance of the proposed performance metrics has triggered an extended debate among researchers and practitioners concerning the most appropriate indicator that should be used in the evaluation phase, since each criterion may present desired properties, but, at the same time, significant flaws or limitations [45]. From a statistical point of view, the alternative loss functions quantify different aspects of performance such as accuracy, bias and variance of POEs, and thus the practitioners should base their choice on the most appropriate indicator satisfying their assessment goals. For example, the absolute error (AE), the bias error (BE) and squared error (SE) are well-known loss functions that can be used for evaluating the accuracy, bias and the variance of a POE, respectively [46]. Apart from the usage of loss functions for the assessment phase of alternative POEs and the investigation of their capabilities in several aspects of performance, these metrics are also examined from an industrial point of view. For example, Rui et al. [5] point out that the relative error to the estimate and other relative cost ratio metrics are widely used in many industries for evaluating the cost growth of individual projects in order to identify high levels of cost growth affecting, in turn, the economies of firms.
In parallel to the evaluation of the above loss functions, visualization techniques can also be applied for extracting valuable information regarding specific aspects of prediction capabilities. Regarding this, the construction of the Regression Receiver Operating Curves (RROC) space [47] provides evidence about the proneness of a POE to systematically under- or over-estimate the actual cost value. More specifically, the performance of a POE is graphically displayed on a two-dimensional plot, namely the RROC space, where the horizontal and the vertical axes represent the sum of overestimation ( = ) and the sum of underestimation ( = ), respectively, for a given set of projects [47].
Although the findings extracted from both literature and empirical evidence reveal a significant body of knowledge concerning the evaluation of project cost performance for the case of POEs, the assessment phase for PIEs is, undoubtedly, a more challenging process, since the cost estimate is expressed via a range of probabilistic outcomes (lower and upper bounds) for which there are no actual values that can be used for measuring discrepancies from the derived solution [15]. Usually, the quality of PIEs is assessed via two performance indicators that are the coverage probability (CP) [48] and indices aggregating the mean (or median values) of the derived widths (Equation (5)) for a given set of prediction intervals [20].
Regarding the former performance metric, CP is computed by the following formula:
where is defined as
The indicator variable denotes whether the actual cost value of a project lies within the bounds of the constructed PI, and it can be perceived as a measure of containment [49], while CP (Equation (3)), usually expressed as a percentage, quantifies the reliability of PIEs [48,50]. Generally, a PIE is considered to perform well when CP (or empirical coverage) approximates the nominal coverage probability (NCP) (or confidence level) [51]. On the other hand, the findings from experimental studies indicate that this rule of thumb is rarely satisfied in practice, since PIEs usually result in CP values that are lower than the NCP [52]:
Although coverage is a widely used performance metric for assessing the ability of PIEs to contain the actual response, the final decision regarding the superiority of a model against comparative ones should not be based only on the computation of CP, since there is a trade-off between CP and width performance indicators for a given set of prediction intervals [49]. For example, a PS may provide prediction bounds encompassing the actual value for all projects but to a high cost of extremely wide PIs. In this case, the project manager should feel confident that the actual value of cost for a new project will lie into the derived PI, but the wide range may render the derived PI impractical and/or useless for decision-making purposes [53]. Generally, larger CP values are more likely to be associated with wider PIs and vice versa [54]. Hence, the ability of a PS to provide efficient interval estimates in terms of CP should be assessed in conjunction with the width of the estimated PI.
To overcome the above barriers during the assessment phase, a specific composite loss function, namely the Winkler Score (WS) [55], taking into account both the width and the containment of the actual value into the derived interval estimate, can be proved to be beneficial. For a given project , WS is computed via the following equation:
where indicates the prescribed probability level, and and are the lower and upper bounds corresponding to the -th and the -th percentiles of the bootstrap distribution, respectively, for project under consideration. The above loss function has an intuitive interpretation, since it penalizes PIEs producing generally wide intervals, while, at the same time, it assigns an extra penalty to PIEs [51] that are unable to provide bounds containing the actual value of cost in our case.
2.3.2. Model Selection
The loss functions and aggregated indicators presented in the previous section are valuable PCM tools for performance evaluation given a set of POE and PIE candidates. Despite the fact that these metrics are informative for assessing the performance of competing PSs, they can only be used for exploratory purposes. In contrast, the identification of the most capable PS cannot be guided from a naïve approach that bases the inferential process on a single comparison of performance metrics, since this policy may lead to unstable results and erroneous decision-making. This is because an aggregated indicator, computed from a finite set of errors through the utilization of a specific loss function, is just a statistical measure of central tendency (i.e., mean, median, etc.) containing significant variability [43].
Based on the previous considerations, the task of comparing a set of PSs in order to decide upon the superiority of a specific PS among competing ones plays a predominant role in benchmark experiments and thus appropriate inferential procedures should be engaged in the process [43]. Regarding this, the findings from related literature designate a wide range of statistical methodologies that can be used for inferring about whether the observed divergences in prediction performances for a set of competing PSs can be generalized to the population of cases (e.g., projects) with similar characteristics [40,43,56,57,58,59]. Certainly, the choice of the most appropriate statistical inferential mechanism is a critical decision that depends solely on the elements of the experimental design (or design of experiment-DOE) synthesizing a benchmark study [43] and the type of the response for which a practitioner wishes to derive conclusions.
Following the terminology proposed by Hothorn et al. [43], the benchmark experiment, in our context, consists of a set of candidate SPs, with the aim of inferring about their prediction capabilities and selecting the candidate outperforming the rest in terms of two predefined sets of indicators , and , used for assessing the quality of the derived solutions taking into consideration their two-fold nature (point and interval estimates). Regarding the elements of DOE, the experimental unit of the analysis is the project being estimated, whereas the response, or in simple words, the variable of interest that deserves a thorough investigation, is the error measurements computed by alternative competing PSs. Having in mind that the benchmark experiment involves the examination of more than two PSs, we have to deploy an inferential mechanism taking into consideration that each experimental unit is measured repeatedly under different experimental conditions.
In order to extract meaningful and statistically valid conclusions, we make use of Mixed Effects Models (MEMs) [60], a branch of advanced methodologies able to deal with two types of effects that are (a) the fixed and (b) the random effects [61]. In brief, fixed effects are parameters associated with certain levels of experimental factors that may affect the mean value of the response, while random effects are associated with the individual experimental units drawn at random from an unknown population and thus they may affect the variance of the response. In addition, random effects provide a straightforward way to deal with pseudo-replication caused by the multiple measures of each experimental unit [62].
In summary, two specific classes of MEMs are adopted, namely (a) the Linear Mixed Effects Models (LMEMs) and (b) the Generalized Linear Mixed Models (GLMMs). LMEMs are used for modeling the effects (both fixed and random) on loss functions resulting in error samples of continuous measurements. On the other hand, the examination of the effects on the distribution indicating whether an interval estimate produced by a PIE contains the actual value of cost () is conducted via GLMMs.
A typical LMEM [61] is described by the following general form:
where is a column vector, the variable of interest (or response variable); is a matrix of the fixed effects; is a column vector of the fixed effects coefficients; is a design matrix for the random effects; is a vector of the random effects and is a column vector of the residuals.
On the other hand, a GLMM, the generalization of LMEMs, does not model the response variable directly [60], but rather, it applies a link function specifying the link between the response variable to a linear predictor of the form
Thus, the conditional expectation of the response variable is given by the following equation:
which can be written as
where is the inverse link function. In our case, the response () is a dichotomous variable, so a reasonable option is the utilization of the logit link function , where is the probability of success, i.e., the actual cost lies within the interval estimate.
Generally, MEMs are useful statistical inferential procedures, since they allow the simultaneous investigation of several fixed factors on the response in complex DOEs. In the context of benchmark experimental studies, this is a typical real-life scenario, since the quality of a PS may be strongly affected by decisions related to the choice of the algorithm and the Feature Scaling Mechanism (FSM) (or pre-processing transformation) applied on the input variables [63]. More interestingly, except from the examination of the main fixed effects, an interaction effect occurring when two or more variables interact to affect the response is of great practical importance, allowing a decision-maker to gain a deeper insight into the superiority of a specific combination of algorithm and FSM.
Based on the previous considerations, we made use of a predefined strategy proposed by Zuur et al. [64] in order to decide upon the main and interaction effects that will be finally inserted in the inferential process. Initially, a model incorporating the main fixed effects of interest and their interactions is tested against a second model without the interaction term through the Likelihood Ratio (LR) test. In case of a non-significant difference between the two examined models, the simpler model (without the interaction term) against the more complex model (with the interaction term) is preferred satisfying the principle of parsimony [64], while the comparison of the two models is conducted via the Akaike Information Criterion (AIC) and the model with the lowest AIC value is finally chosen for inferential purposes.
3. Research Objectives and Research Questions
As mentioned in Section 1, the current study is a research attempt towards the adoption of data-driven project management solutions through the synthesis, into a unified framework, of well-established statistical and ML approaches that have been proved valuable to researchers and practitioners involved into PCM activities in other industries. Figure 2 summarizes, through a graphical overview, the methodological framework along with the challenges faced in PCM, the definition of the problem under examination and the main components of the proposed solution discussed in Section 2. Additionally, in Table 1, we present the mapping of the state-of-the-art approaches to the corresponding components of the framework along with a short description of their intended scopes.
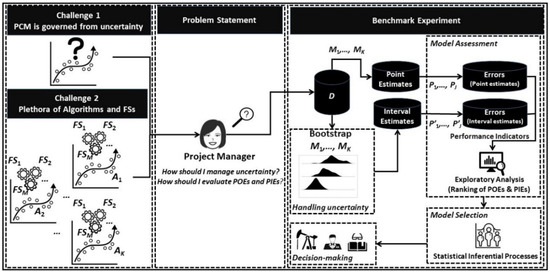
Figure 2.
Methodological framework of the study.

Table 1.
List of adopted approaches and associated components/scopes in the proposed framework.
To illustrate the practical implications of the framework, we conducted a benchmark experiment on a publicly available dataset comprising information about the cost and characteristics of completed natural gas transportation pipelines. To provide guidelines to researchers and practitioners regarding the deployment of the proposed framework, we formulate the following indicative research questions (RQs):
[RQ1]
Does the performance of an algorithm providing point estimates depend on the type of the applied FSM?
Motivation: In ML literature, it is well-known that the performance of an algorithm may be affected by the magnitudes, units and range of the predictors (or features), while other algorithms are immune to feature scaling [63]. By answering RQ1, we aim to investigate whether specific types of FSMs present a statistically significant effect on the performances of the examined algorithms, when used as POEs.
[RQ2]
Is there a candidate model(combination of algorithm and FSM) outperforming the rest in terms of point estimates?
Motivation: RQ2 focuses on the main objective of any benchmark experiment which is the quality assessment of alternative candidate models through the usage of appropriate performance metrics and the identification of the “best” candidate model [43]. In particular, based on the findings derived from RQ1, we seek for a model, i.e., a combination of a specific algorithm and FSM that is able to provide accurate point estimates of cost.
[RQ3]
Does the performance of an algorithm providing interval estimates depend on the type of the applied FSM?
Motivation: Although the performance of an algorithm producing point estimates may be significantly affected by the application of specific FSMs, this claim may not be true for the case of models that construct interval estimates. RQ3 aims at the examination of the effect of FSMs on the performances of algorithms, when used as PIEs.
[RQ4]
Is there a candidate model(combination of algorithm and FSM) outperforming the rest in terms of interval estimates? Does the performance evaluation in terms of point and interval estimates result in a consistent ranking of candidate models?
Motivation: Similar to RQ2, the first part of RQ4 deals with the task of identifying the best PIE among a set of competing ones. This question can be considered as a critical one in PCM, since a model may result in, generally, accurate point estimates, but at the same time, it may be proven to be a poor candidate in handling probabilistic uncertainty producing, generally, wide PIs that are impractical for decision-making purposes or PIs that do not comprise the actual cost value. The second part of RQ4 sheds light on the ranking consistency of candidates by examining whether a practitioner should feel confident that a set of candidates will present similar performances, when used as point and interval estimators of the cost variable.
4. Experimental Study Design
This section presents details regarding the experimental setup followed in this benchmark study. More specifically, we present the set of the examined candidate models (combination of algorithms and FSMs) and the dataset used for demonstrating the applicability of the proposed framework.
4.1. Candidate Models
The literature of the statistical and ML approaches for the learning task of a mapping function between a continuous response and a set of predictors is vast, and for this reason, we decided to explore only a specific subset of algorithms based on two criteria that are (a) their popularity, i.e., they should have been widely used in other scientific domains and related benchmark studies and (b) their complexity, i.e., the number of their tuning parameters should be relatively small. Based on these criteria and the fact that it was infeasible to investigate the whole range of possible regressors, we ended up including six candidate algorithms in our experimental setup. A brief description of the idea behind each selected algorithm and its associated tuning parameters are summarized into the following paragraphs.
Multivariate Linear Regression (MLR) belongs to the general class of the statistical parametric approaches assuming that the function can be approximated by a linear expression of the predictors via a vector of unknown parameters called, the regression coefficients [31]. In the statistical literature, various techniques for the estimation of the regression coefficients have been proposed, but the ordinary least squares regression, minimizing the overall sum of squared errors, is certainly the most popular one. Despite its applicability in a wide range of problems and contexts, the linear model makes a series of assumptions (e.g., the linearity assumption between the set of the predictors and the dependent variable, the homoscedasticity assumption of residuals (zero mean and constant variance), etc.) that must be satisfied in order to build an accurate and valid model [31].
Classification and Regression Trees (CART) is an ML approach resulting in a decision tree-based structure for estimating the value of the dependent variable by recursively partitioning the predictor space according to splitting rules [65]. The algorithm invokes the optimization of a cost complexity parameter (cp) that provides a strategy for selecting a sub-tree yielding the lowest error [30].
K-Nearest Neighbors (KNN) belongs to the general class of the non-parametric statistical learning algorithms [66]. The methodology, an alternative to the traditional parametric regression, provides an estimate of the dependent variable without making any assumption about the underlying structural relationship between the response and the set of predictors. The basic idea is the identification of similar cases (neighbors) to the one that has to be estimated according to a predefined criterion (a distance metric) and the evaluation of the dependent variable through a weighted scheme (usually the mean) [30]. An important parameter of KNN is the number of the nearest neighbors (nn) that one has to combine for evaluating the response value for a new case.
Principal Component Regression (PCR) is a two-step regression methodology based on the dimensional reduction of highly-correlated predictors [67]. At the first step, Principal Component Analysis (PCA) is applied on the set of predictors with the aim of extracting a small number of principal components that are able to explain a high amount of the observed variability. At the second step, based on the projections of the observations into the extracted orthogonal components, PCR evaluates the regression coefficients through the Ordinary Least Squares (OLS) algorithm [67].
Partial Least Squares Regression (PLSR) is a variant of PCR sharing common characteristics, i.e., they both construct orthogonal components through linear combinations of the initial predictors [67]. The main difference is because PLSR extracts the set of components explaining the highest possible variation in a dataset taking into account the values of the response. The optimal number of components (nc) for both PCR and PLRS algorithms has to be determined during the tuning phase of the model.
Support Vector Regression (SVR) is a kernel machine learning method that is based on the principle of structural risk minimization [68]. Regarding the kernel method, in the current study, the linear kernel is used, minimizing the epsilon intensive loss function and the cost of constraints violation for the regularization term in the Lagrange formulation.
Although the selection of the algorithm may present a significant effect on the quality of the derived solutions, we have already mentioned that a key factor that may affect the performance of a PS is the pre-processing mechanism (or FSM) applied on the input variables during the fitting phase [63]. In this study, three FSMs are examined that are briefly described below.
None. This is the trivial situation, in which the fitting process is conducted on the initial (raw) measurements of the predictors (features) given a dataset.
Normalization (Norm) or Min-Max Scaling. The value for each predictor is normalized into the range through the formula .
Standardization (Stand). The value for each predictor is standardized using the formula , where and represent the sample mean and standard deviation, respectively.
At this point, we have to note that the fitting process of MLR was based on the logarithmic transformation of raw measurements for both the response and the set of predictors, since all the continuous variables presented highly-skewed distributions (see Section 4.2). In addition, in order to provide a fair comparison for the set of the examined algorithms, the same transformation was applied on all regression-based approaches (PCR, PLSR and SVR), since preliminary experimentation on data revealed their strong dependency on the shape of the distributions. In contrast, CART and KNN did not present significant divergences after the deployment of the logarithmic transformation and thus the raw measurements were finally used. Regarding the application of FSMs, Norm and Stand pre-processors were not applied on the MLR algorithm, since the parametric regression model is immune to the pre-processing of the raw measurements.
The tuning of each model and the determination of the best parameters were based on a grid-search strategy following the repeated k-fold cross-validation schema. In each iteration of the process, the dataset was partitioned into ten folds (10-fold cross-validation), and each fold was left out during the training phase of the model. The excluded fold was used as a test set for evaluating the prediction capabilities of each model on unseen cases. The prediction performance was computed via the aggregated mean value of the error incurred in the ten testing folds, in terms of the Root Mean Squared Error (RMSE). The above process was repeated thirty (30) times after shuffling the dataset, which resulted in different splits of the sample (training/test sets), and the overall performance indicator error was computed on the results of the thirty repetitions in order to decide upon the best tuning parameters of each model (Table 2). For our experimentation, we made use of the train function implemented in the caret library [69] of the R language [70].

Table 2.
List of examined models, values of grid and best value for tuning parameters, R function/packages.
4.2. Dataset
The dataset used for experimentation contains information related to natural gas pipeline projects reported by the U.S. Energy Information Administration [71] with 874 completed projects covering the 1996–2017 period. Previous versions of this dataset have been used in other studies investigating the pipeline construction cost [6,7,9,10]. Regarding the number of projects and the variables of the dataset, certain pre-processing steps were conducted to obtain a set of appropriate cases that were used for fitting and evaluation purposes. Initially, uninformative features, e.g., project name, pipeline operator name, etc., were removed. As far as the treatment of missing values is concerned, we decided to follow a listwise deletion strategy by omitting projects presenting at least one missing value for a specific variable, since there was no available information about the mechanism related to this missingness (missing at random, missing completely at random, missing not at random, etc.). After these pre-processing steps, a set of 544 completed projects with six input features (predictors) and one dependent cost variable was the basis of our experimental setup (Table 3). We also have to note that projects belonging to Reversal, Conversion and Upgrade levels for factor Project Type were also excluded, since there was a limited number of observations for these categories that might, in turn, affect the performances of the models. The descriptive statistics for each variable are presented in Table 4, whereas Figure 3 presents the frequency distribution for the discrete variable year.

Table 3.
Variables of the dataset.

Table 4.
Descriptive statistics of variables.
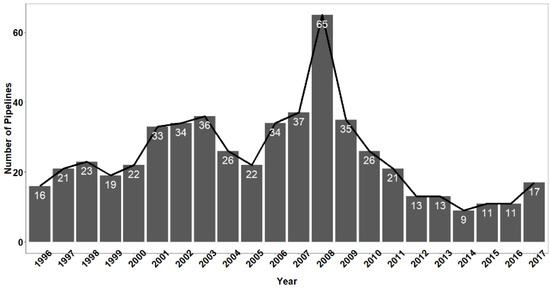
Figure 3.
Frequency distribution for year of completion/put in service.
The examination of the descriptive statistics for both the dependent variable Cost and the predictors shows that the continuous variables are highly-skewed with non-normal distributions, a common characteristic of real-life cost datasets. This fact results in the violation of important assumptions of parametric regression-based models, which can lead to invalid models and misleading findings. The problem that has arisen can be effectively addressed by the deployment of an appropriate transformation on the raw measurements of the continuous variables. In Figure 4, we indicatively present the form of the relationship between Cost and Mileage after the application of the logarithmic transformation on both variables, where different colors represent the levels of Project Type. The inspection of the graph confirms the findings of past studies [6,7] pointing out that the size of projects (log-transformed) is a significant driver of cost (log-transformed) and this relationship can be adequately expressed via a linear model. Moreover, the type of project seems to also be a significant cost factor [6], since New Pipeline projects are usually larger in terms of size and cost compared to both Lateral and Expansion projects.
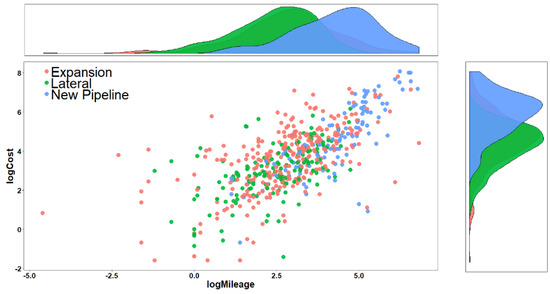
Figure 4.
Scatter plot of Mileage (log-transformed) and Cost (log-transformed) across the categories of Project Type.
5. Results
This section presents the results of the benchmark experiment based on the proposed framework aiming at answering the RQs stated in Section 3.
5.1. [RQ1] Does the Performance of an Algorithm Providing Point Estimates Depend on the Type of the Applied FSM?
Table 5 summarizes the overall performance indicators for the set of candidate models (combination of Algorithm and FSM) evaluated via the appropriate loss function presented in Section 2.3.1. Regarding the model assessment phase of POEs, we made use of the widely applied AE loss function, since it is related to the aspect of accuracy for a given model [46]. The examination of the performance indicators based on the AE distributions reveals a high divergence between the aggregated results computed by the two central tendency measures that are the mean (MAE) and the median (MdAE) values of AE. This is in accordance with previous findings in other experimental studies designating that error distributions may present asymmetry that should be taken into account during the assessment phase. To mitigate the risk of erroneous decision-making concerning the superiority of a specific model, performance indicators based on robust statistical measures (e.g., median) of error distributions should be preferred for exploratory purposes [43,72,73].

Table 5.
Performance evaluation of the examined models (combination of algorithm and FSM).
The comparison of MdAEs shows that there is a subset of POEs outperforming the rest in terms of accuracy. For example, MLR and the variants of SVR algorithm seem to provide accurate point estimates of cost. In addition, the investigation of the overall indicators reveals that, although the majority of POEs are immune to the choice of FSM, this is not the case for the entire set of candidate models. Indeed, the visual inspection of error distributions through boxplots (Figure 5) demonstrates that the deployment of alternative FSMs seems to affect the performance of PCR with a specific model (PCR (Stand)) outperforming the competing ones (PCR with None and Norm pre-processing options). We have to note that the -axis is logarithmically transformed to enhance the readability of the plot, since the initial error measurements presented heavily-skewed distributions.
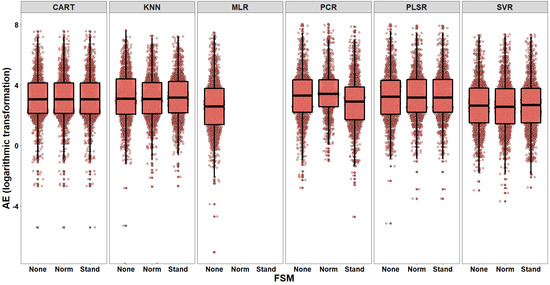
Figure 5.
Boxplots of AE distributions (log-transformed scale) for each model (combination of algorithm and FSM).
In order to infer about the presence of an interaction effect of the Algorithm and FSM factors on the accuracy of POEs expressed by the AE error measurements, it is vital to statistically examine, whether the finding (observed differences) can be generalized to the population of error distributions. Table 6 presents the results of the statistical inferential process (LMEM) after the application of the protocol for the model selection phase described in Section 2.3.2. To provide guidelines to both researchers and practitioners on how they should apply it on their decision-making process, we, indicatively, demonstrate its sequential steps for the case of the AE loss function.

Table 6.
Results of mixed effects models on performance metrics.
In the first step, an LMEM model (LMEM A, Table 6) is defined, incorporating the main fixed effects of Algorithm and FSM and their two-way interaction term (Algorithm FSM). In the second step, this model (LMEM A) is tested against the model (LMEM B) without the two-way interaction term. The conduction of the hypothesis test through the LR test revealed a statistically significant difference between LMEM A and LMEM B, and thus the model with the interaction term (LMEM A) was finally selected, since it presented lower AIC value compared to LMEM B. We also have to note that all LMEMs were fitted on the logarithmic transformations of the raw measurements of sample errors, since their distributions did not satisfy the normality assumption. The final LMEM includes a statistically significant interaction term, Algorithm FSM, and statistically significant main effects for both Algorithm, and FSM, .
Lessons Learned: The performance of an algorithm providing point estimates may be significantly affected by the choice of the applied feature scaling mechanism, but this effect may vary across the set of the examined algorithms.
5.2. [RQ2] Is There a Candidate Model (Combination of Algorithm and FSM) Outperforming the Rest in Terms of Point Estimates?
Having addressed RQ1, the next critical step is to investigate whether there is a specific candidate (or a subset of candidates) outperforming the rest. In other words, we are interested in the determination of homogenous groups of POEs in terms of their performances and the identification of candidates belonging to the group of superior models. Again, the inferential strategy should be settled on formal statistical mechanisms bringing insights to the final decision.
The fitting of the LMEM (RQ1) provides a straightforward manner to detect whether there are statistically significant differences on the performances of competing models, through the conduction of post-hoc analysis. The statistically significant interaction term (Algorithm FSM) identified in RQ1 poses an additional challenge into the process, since the practitioner should adjust the interaction effect during the consecutive pairwise comparisons of the candidate models. In order to perform simultaneous multiple comparisons for all possible pairwise levels of the two experimental factors (Algorithm and FSM) and their interaction (Algorithm FSM), we decided to utilize the Least Squares Means (LSMEANS) approach [74] executing hypothesis tests on the predicted mean values for levels that are adjusted for means of other factors in a fitted LMEM (or GLMM).
Table 7 and Figure 6 summarize the results of the post-hoc analysis derived from the estimated LSMEANS after controlling the familywise Type I error [75] through the Tukey’s adjustment. In this table, the set of models are ranked starting from the best to the worst, whereas models that did not present a statistically significant pairwise difference in terms of AE values are categorized into homogenous groups denoted by the same letter. The post-hoc analysis signifies four homogenous groups (A–D) of POEs with similar performances in terms of accuracy. In addition, there are models that are classified into overlapping groups, e.g., SVR (None/Stand) belongs to both group A and group B.

Table 7.
Homogenous groups of models after post-hoc analysis.
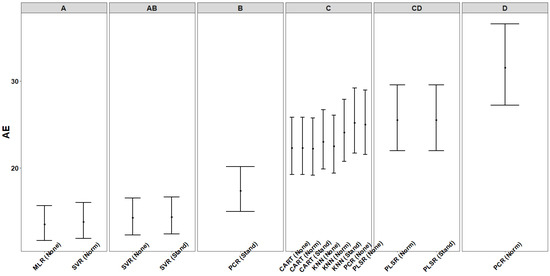
Figure 6.
Post-hoc analysis for AE distributions (LMEM on performances of point estimators).
Interpreting the results, two specific models (MLR (None) and SVR (Norm)) seem to be the best choices, when used as POEs. This finding reinforces the results extracted from the graphical exploration presented in Section 4.2, indicating that the relationship between the response and the set of cost drivers can be adequately captured by a linear relationship after some transformations of the initial measurements. Another interesting remark is that, although most of the dimensional reduction models (PCR and PLSR) do not provide accurate estimates of cost, there is a specific combination, namely the PCR algorithm with Stand feature scaling mechanism, that can be considered as a second alternative (group B) for predicting the cost of a future project.
Apart from the aspect of accuracy, the RROC space (Figure 7) is constructed for investigating whether the subset of superior POEs exhibits acceptable behavior in terms of bias, which is another important aspect of prediction performance. Described briefly, in the RROC space, an ideal POE would be represented by a point very close to the origin on the upper left corner of the plot () [47]. In addition, the diagonal reference line can be used for the identification of POEs providing generally unbiased estimations of the actual response value [47]. Finally, points below (or above) the diagonal line indicate POEs that systematically under- (or over-) estimate the actual cost [47]. In our case, the inspection of the RROC space (Figure 7) illustrates that there is a subset of POEs (PLSR and PCR variants) presenting a high tendency for under-estimation. In contrast, the CART and KNN variants seem to be the least biased choices followed by the SVR variants. Taking into consideration the findings extracted from the post-hoc analysis conducted on the AE distributions and the RROC space, the SVR variants present satisfactory performances in terms of both accuracy and bias.
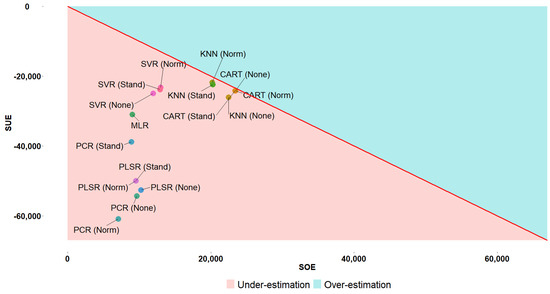
Figure 7.
RROC space for the set of candidate models (combination of algorithm and FSM).
Lessons Learned: The performance evaluation of alternative prediction mechanisms producing point estimates of cost may result in the identification of a subset of candidates that statistically outperform the competing models. The data-driven benchmarking and identification of the “best” set of candidates can facilitate the prioritization and selection of cost estimation techniques when the objectives are (a) the accurate approximation of the most likely cost value for a forthcoming project and (b) the assessment of the prediction capabilities for a new ML candidate. In our case, the formulated benchmark encompasses mainly support vector regression variants.
5.3. [RQ3] Does the Performance of an Algorithm Providing Interval Estimates Depend on the Type of the Applied FSM?
Despite the fact that the performance evaluation of POEs unveils significant insights facilitating specific PCM activities (Section 1), it does not provide any guidance related to the uncertainty of the estimation process. Regarding this, we have already emphasized the imperative need for the establishment of well-defined practices contributing to the quantification and investigation of uncertainty for a given set of candidate models.
Indeed, the results derived from the experimentation on the set of candidate models using the non-parametric bootstrap as the core mechanism for producing interval estimates (PIs) of cost for each project showcase the complicated reality caused by the trade-off between the two widely-used indicators (Coverage and Width) (Table 5). More specifically, a ranking instability problem is noted, complicating the task of promoting a PIE against the set of competing ones. For example, CART variants can be considered as a reasonable choice for managing uncertainty, since they generally succeed at containing the actual cost of projects, a fact that is highlighted by the satisfactory CP values (Table 5). At the same time, the corresponding PIs of CART variants are, generally, too wide, constituting them as the worst candidate models.
Despite this fact, the findings from the examination of factors (Algorithm and FSM) affecting the distributions of indicator variable and width through the fitting of GLMM and LMEM procedures, respectively (Table 6), bring to light differences concerning the fixed effects on each performance metric. As far as the ability of models to contain the actual cost value into the derived PIs is concerned, the comparison of GLMMs (Table 6) demonstrates that the performance of the examined algorithms is not affected by the type of the applied FSM (GLMM A vs. GLMM B). In addition, the investigation of the main effects (Algorithm and FSM) did not reveal a statistically significant main effect of FMS on the response. The final GLMM (GLMM C) provides evidence only for a statistically significant main effect of the factor algorithm on the distributions of the indicator variable , .
The inferential process becomes even more complicated, since the examination of the fixed effects of Algorithm and FSM on the distributions of the second performance metric (width) used for assessing the capabilities of PIEs implies quite different results. In this case, the fitting of the LMEMs designates that the performance of candidates is strongly affected by both the applied FSM () and the type of algorithm () but, more importantly, a significant interaction effect is noted ().
Summing up, the empirical evidence indicates that the evaluation of PIEs is certainly not a trivial task due to significant challenges arising from the fact that the most known performance metrics do not provide straightforward directions that could guide, in turn, the decision-making process. Having in mind that it is misguided to base the evaluation process on the comparison of width distributions derived from a set of PIEs presenting different CP values, a possible solution is to the inferential process on the WS loss function.
The graphical exploration of the distributions in terms of the WS error measurements obtained for the set of PIEs displays a few interesting topics of discussion regarding the ability of competing models to produce acceptable interval estimates balancing the trade-off between coverage and widths. A first noteworthy finding concerns the identification of the merits of the KNN variants in producing generally satisfactory PIs, despite the fact that these types of estimators were characterized as middle-ranked models in terms of point estimates. Additionally, while MLR is identified as the candidate model belonging to the best group of POEs, in terms of accuracy, it seems to present high variability, when used for extracting interval estimates of cost. Finally, the boxplots indicate different performances for specific combinations of levels for the two examined factors (Algorithm and FSM).
The latter claim is statistically confirmed by the inferential process (Table 6), which designates the existence of a statistically significant interaction term between Algorithm and FSM (Algorithm FSM), and statistically significant main effects for both factors, Algorithm, and FSM, on the WS distributions.
Lessons Learned: The performance evaluation of alternative prediction mechanisms producing interval estimates is a demanding and complicated task, since widely-used performance metrics assessing the quality of these estimators may present a significant trade-off. The utilization of appropriate metrics quantifying into a unified way, multifaceted aspects of prediction performance in terms of uncertainty can be valuable for decision-making goals. Moreover, the performance of an algorithm providing interval estimates may be also affected by the choice of the applied feature scaling mechanism, a conclusion that is in accordance with the derived findings for the case of point estimators.
5.4. [RQ4] Is there a Candidate Model (Combination of Algorithm and FSM) Outperforming the Rest in Terms of Interval Estimates? Does the Performance Evaluation in Terms of Point and Interval Estimates Result in a Consistent Ranking of Candidate Models?
Similarly to the model selection phase of POEs, this RQ aims at the identification of a benchmark set of PIEs that can be used as a reference basis for handling uncertainty. Figure 8 displays the WS distributions for the set of the candidate models, whereas Table 7 and Figure 9 present the results from the post-hoc analysis conducted on the fitted LMEM (WS distributions). The findings validate the results obtained from the graphical investigation of boxplots (Figure 8) showing that MLR (None) and SVR (Norm) do not belong to the best group of PIE candidates. In contrast, KNN (Norm) is the top-ranked model for managing uncertainty, since it produces interval estimates that sufficiently balance the trade-off between coverage and width. Finally, the other two variants of KNN algorithm (Stand and None) and all the CART variants constitute an alternative option for estimating PIs of cost.
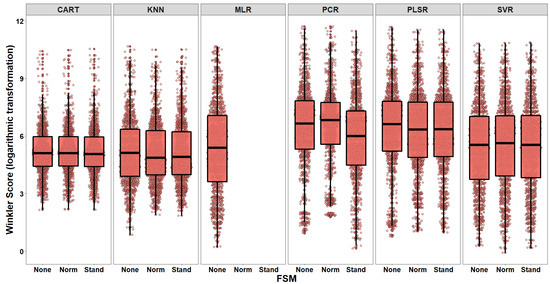
Figure 8.
Boxplots of WS distributions (log-transformed scale) for each model (combination of algorithm and FSM).
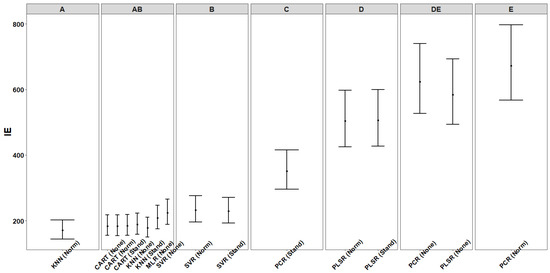
Figure 9.
Post-hoc analysis for WS distributions (LMEM on performances of interval estimators).
In summary, the statistical inferential process that was conducted on the error samples computed via the WS loss function points out ranking instabilities of candidate models, when they are used as point and interval estimators of cost. To assess the degree of agreement between the rankings of POEs and PIEs, we made use of the Krippendorff’s alpha coefficient [76]. In brief, the identified groups were transformed into rankings, whereas, for models belonging to two overlapping groups, we assigned a ranking value of X.5. The computation of the alpha coefficient () indicates a moderate agreement between the rankings extracted from the two setups of the experimentation.
Lessons Learned: The performance evaluation of alternative prediction mechanisms producing interval estimates of cost may result in the identification of a subset of candidates that statistically outperform the rest. On the other hand, the quality of the two types of estimates (point and interval) should be assessed independently, since the rankings of candidate models may be divergent, signifying the necessity to inspect, which estimation technique can be thought of as a reasonable choice for handling probabilistic uncertainty in PCM.
6. Threats to Validity
This section presents potential threats to the validity of the study that can be categorized into four types that are internal validity, construct validity, conclusion validity and external validity [77]. Calder et al. [77] defines internal validity as threats related to the causal relationships examined in a study. Regarding this, we made use of appropriate statistical methods (descriptive statistics, exploratory analysis, and ML approaches) for building models between the response and the set of predictors based on empirical evidence from past studies indicating significant factors affecting the cost of projects.
Construct validity refers to the agreement between a theoretical concept and a specific measurement [77]. Having in mind that the main objective of the current study is the performance evaluation of models producing point and interval estimates of cost, we made use of appropriate loss functions that have been proposed and widely used for fulfilling these different goals. Furthermore, we discussed, in detail, the limitations of performance metrics quantifying quality aspects of prediction interval estimators. To this end, we based the inferential process on a specific loss function that is able to evaluate the capabilities of candidates mitigating the threats related to other well-known metrics.
Conclusion validity deals with the degree to which the conclusions about the underlying phenomena are reasonable and correct [77]. In this paper, we made use of advanced statistical methodologies (i.e., mixed effects models) taking into account both the fixed and the random effects that may affect the variables of interest (i.e., the prediction performance of candidates).
Concerning the external validity, we have to note that the basis of our experimental setup was a publicly available dataset containing information related to completed natural gas pipeline projects. Despite the high number of the examined projects, the execution of a benchmark experiment on other datasets with different cost drivers or projects from different O&G scopes may affect the extracted findings. On the other hand, we believe that this is not a major threat, since our objective was not to lay emphasis on a specific type of algorithm but, rather, to propose a generic framework with structured guidelines, describing how researchers and practitioners should conduct experiments based on well-established concepts, methods and practices from the statistical and ML scientific domains. Regarding this, we have already mentioned that the statistical and ML literature encompasses a wide variety of proposed methodologies that can be used in the demanding task of building an accurate prediction model, so it was impossible to take into consideration the entire range of possible candidates. Instead, we decided to select algorithms satisfying two specific criteria, which were the popularity and the complexity of the algorithms. The latter one could also bring certain threats, since a complex algorithm requiring the tuning of a high number of parameters could also raise threats regarding the basis for a fair comparison. Moreover, a critical aspect that may affect the performance of an algorithm is the feature scaling mechanism. In this study, we thoroughly investigated the effect of scaling mechanisms on the prediction performances evaluated from the set of competitive algorithms. In addition, we also utilized the logarithmic transformation for regression-based techniques to assess normality, which is an important assumption for the building of a valid model. Regarding the validation method, we chose the leave-one-out cross-validation procedure, since this schema is related to lower bias in the estimation process [31]. On the other hand, leave-one-out cross-validation may be related to high variability for small samples, but this is not a limitation for our experimental setup, since the examined dataset contains a high number of projects. More importantly, the utilization of leave-one-out cross-validation enables the reproducibility of our experimental setup and thus the extension of the study incorporating alternative algorithms, feature selection mechanisms, loss functions, etc.
7. Discussion
In this section, we discuss the main findings of this study and present certain directions and implications to both researchers and practitioners. Motivated by the fact that megaprojects in the O&G industry are complex and dynamic, there is an imperative need for establishing well-defined project management methodologies, practices and tools to alleviate challenges and problems commonly faced by decision-makers during the life-cycle of a new project. Moreover, the rapid advances in information and communication technologies and the accumulation of huge amounts of data offer a great opportunity to accelerate the transition of the O&G sector into the new O&G 4.0 era. Certainly, the establishment of a data-driven project management culture should become a strategic priority for industry stakeholders, since, among other application domains in the O&G sector, the adoption of data analytics approaches can unveil significant hidden knowledge that can be proved, in turn, to be beneficial for project managers and decision-makers.
Driven by the above considerations and similar research related to project management practices followed in other industries, we proposed a data-driven framework augmented with statistical and ML methodologies focusing on the critical challenge of managing uncertainty in project cost management. The framework consists of a series of phases and related tasks that facilitate practitioners to cope with the inherent uncertainty of the cost estimation process. Despite the fact that the proposed approach is illustrated through a benchmark study on projects from a specific scope, the framework can be applied to a variety of project management activities and scopes.
Regarding the main findings derived from the utilization of the framework on the representative case study, below we present a few interesting conclusions, so as to provide guidelines to both researchers and practitioners that are willing to adopt data-driven project cost management solutions and decide upon the quality of alternative prediction mechanisms. Firstly, the non-parametric bootstrap resampling approach provides an effective way to manage probabilistic uncertainty of statistical and ML models through the construction of prediction intervals for the cost response. Based on a relatively simple idea that is the generation of a large number of samples drawn with replacement from the original one, this resampling technique constitutes a straightforward way for the practitioners in the O&G sector to overcome the limitation for the majority of ML approaches to associate the derived point estimations with an approximation of the optimistic and pessimistic expectation of cost. The successful application of the bootstrap resampling method to similar project cost management tasks in other industrial sectors and the findings of the current study suggest the need for an in-depth investigation of the benefits for its adoption in the O&G industry.
Secondly, different feature scaling mechanisms may have a significant but different impact on the quality of statistical and ML algorithms and thus this effect should be examined, independently, by the practitioners, when building prediction mechanisms concerning point and interval estimates of cost. In our benchmark study, there was noted a statistically significant interaction effect between algorithms and feature scaling mechanisms on the absolute error distributions of models, when used as point estimators of the cost function, . This was also the case for the width () and Winkler score () loss functions, when the candidate models were evaluated in terms of their ability to produce accurate interval estimates. In contrast, the generalized linear mixed models indicated that the ability of the models to provide interval estimates containing the actual cost value was only affected by the type of the applied algorithm, .
Thirdly, the two common performance metrics (coverage and width) that are used for the quality assessment of statistical and ML models in terms of uncertainty may not be informative for decision-making purposes. For example, the CART (Norm) model presented the highest coverage probability percentage () but with a cost of extremely wide intervals as expressed by the highest median width value (). Thus, composite loss functions (e.g., the Winkler score) combining information about the ability of a model to incorporate the actual cost value within a practical range of bounds should be used by the practitioners in order to derive meaningful conclusions regarding the performances of interval estimators.
Fourthly, the model assessment of statistical and ML models may not result in stable rankings, when used as point and interval estimators. A model that is able to provide accurate point estimates of cost may be inappropriate for handling probabilistic uncertainty. Regarding this, the utilization of the Krippendorff’s alpha coefficient signified a moderate agreement between the candidate set of models, when used as point and interval estimators (). Thus, practitioners should base their selection on the empirical assessment of models’ performances and consider employing different prediction strategies guided by their intended scopes, i.e., expectation of the most likely value or estimation of the optimistic and pessimistic scenarios.
Finally, the model selection phase should be based on formal statistical procedures that are able to keep control of all possible factors that may affect the inferential process. Mixed effects modeling techniques constitute a branch of advanced and robust methodologies that efficiently address limitations of other traditional statistical hypothesis testing procedures. Indeed, the fitting of the two types of mixed effects models identified different factors that affected the performances of the candidate set of models, when used as point and interval estimators of the cost function.
An interesting direction for future work concerns the fitting of alternative ML algorithms and the assessment of their prediction capabilities in terms of point and interval estimates. Certainly, the recent advances in the ML field offer an overabundant pool of techniques that can be deployed for evaluating O&G project performance that would potentially result in a different subset of superior benchmark models. Apart from the investigation of single models, another interesting topic for further research would be the investigation of ensemble methods that exploit the merits of several single models in order to improve the prediction performances of base ML algorithms. Furthermore, in the current study, the focus of our interest was the evaluation of single-project data-driven solutions assuming that a project is undertaken by a specific O&G firm independently of other projects. On the other hand, an O&G organization may be involved in multiple projects at the same time and thus there is a need for feeding the framework with this extra source of variation [14]. Finally, our research team is working towards the development of an open-source web-based platform that will implement the proposed approach in a fully automated manner serving, in turn, to the extensibility and further exploitation of the framework.
Author Contributions
Conceptualization of the study, N.M. and A.M.; methodology, N.M. and A.M.; data curation, N.M.; writing—original draft preparation, N.M.; writing—review and editing, N.M. and A.M.; supervision, N.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The publicly archived dataset analyzed can be found at https://www.eia.gov/naturalgas/data.php (accessed on 27 April 2018).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Green, J.; Hadden, J.; Hale, T.; Mahdavi, P. Transition, hedge, or resist? Understanding political and economic behavior toward decarbonization in the oil and gas industry. Rev. Int. Polit. Econ. 2021, 1–28. [Google Scholar] [CrossRef]
- Altawell, N. Project management in oil and gas. In Rural Electrification; Altawell, N., Ed.; Academic Press: Cambridge, MA, USA, 2021; pp. 91–107. [Google Scholar]
- Badiru, A.; Osisanya, S. Project Management for the Oil and Gas Industry: A World System Approach; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Rui, Z.; Li, C.; Peng, F.; Ling, K.; Chen, G.; Zhou, X.; Chang, H. Development of industry performance metrics for offshore oil and gas project. J. Nat. Gas. Sci. Eng. 2017, 39, 44–53. [Google Scholar] [CrossRef]
- Rui, Z.; Peng, F.; Ling, K.; Chang, H.; Chen, G.; Zhou, X. Investigation into the performance of oil and gas projects. J. Nat. Gas Sci. Eng. 2017, 38, 12–20. [Google Scholar] [CrossRef]
- Rui, Z.; Metz, P.; Reynolds, D.; Chen, G.; Zhou, X. Historical pipeline construction cost analysis. Int. J. Oil Gas Coal Technol. 2011, 4, 244–263. [Google Scholar] [CrossRef]
- Rui, Z.; Metz, P.; Reynolds, D.; Chen, G.; Zhou, X. Regression models estimate pipeline construction costs. Oil Gas J. 2011, 109, 120. [Google Scholar]
- Merrow, E. Oil and gas industry megaprojects: Our recent track record. Oil Gas Facil. 2012, 1, 38–42. [Google Scholar] [CrossRef]
- Rui, Z.; Metz, P.; Chen, G. An analysis of inaccuracy in pipeline construction cost estimation. Int. J. Oil Gas. Coal Technol. 2012, 5, 29–46. [Google Scholar] [CrossRef]
- Rui, Z.; Metz, P.; Chen, G.; Zhou, X.; Wang, X. Regressions allow development of compressor cost estimation models. Oil Gas J. 2012, 110, 110–115. [Google Scholar]
- Rui, Z.; Metz, P.; Wang, X.; Chen, G.; Zhou, X.; Reynolds, D. Inaccuracy in pipeline compressor station construction cost estimation. Oil Gas Facil. 2013, 2, 71–79. [Google Scholar] [CrossRef]
- Rui, Z.; Cui, K.; Wang, X.; Chun, J.H.; Li, Y.; Zhang, Z.; Lu, J.; Chen, G.; Zhou, X.; Patil, S. A comprehensive investigation on performance of oil and gas development in Nigeria: Technical and non-technical analyses. Energy 2018, 158, 666–680. [Google Scholar] [CrossRef]
- Garvin, J. A Guide to Project Management Body of Knowledge; Project Management Institute: Newton Square, PA, USA, 2000. [Google Scholar]
- Stamelos, I.; Angelis, L. Managing uncertainty in project portfolio cost estimation. Inf. Softw. Technol. 2001, 43, 759–768. [Google Scholar] [CrossRef]
- Trendowicz, A.; Jeffery, R. Software Project Effort Estimation. Foundations and Best Practice Guidelines for Success; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Chatfield, C. Calculating interval forecasts. J. Bus. Econ. Stat. 1993, 11, 121–135. [Google Scholar]
- Klassen, R.D.; Flores, B.E. Forecasting practices of Canadian firms: Survey results and comparisons. Int. J. Prod. Econ. 2001, 70, 163–174. [Google Scholar] [CrossRef]
- Goodwin, P.; Önkal, D.; Thomson, M. Do forecasts expressed as prediction intervals improve production planning decisions? Eur. J. Oper. Res. 2010, 205, 195–201. [Google Scholar] [CrossRef]
- Angelis, L.; Stamelos, I. A simulation tool for efficient analogy based cost estimation. Empir. Softw. Eng. 2000, 5, 35–68. [Google Scholar] [CrossRef]
- Christoffersen, P.F. Evaluating interval forecasts. Int. Econ. Rev. 1998, 39, 841–862. [Google Scholar] [CrossRef]
- Solingen, V.R.; Basili, V.; Caldiera, G.; Rombach, H. Goal question metric (GQM) approach. In Encyclopedia of Software Engineering; John and Wiley and Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Efron, B.; Tibshirani, R. An Introduction to the Bootstrap; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Jochen, V.A.; Spivey, J.P. Probabilistic reserves estimation using decline curve analysis with the bootstrap method. In SPE Annual Technical Conference and Exhibition; OnePetro: Richardson, TX, USA, 1996. [Google Scholar]
- Attanasi, E.D.; Coburn, T.C. A bootstrap approach to computing uncertainty in inferred oil and gas reserve estimates. Nat. Resour. Res. 2004, 13, 45–52. [Google Scholar] [CrossRef]
- Chang, T.; Chen, W.Y.; Gupta, R.; Nguyen, D.K. Are stock prices related to the political uncertainty index in OECD countries? Evidence from the bootstrap panel causality test. Econ. Syst. 2015, 39, 288–300. [Google Scholar] [CrossRef] [Green Version]
- Li, X.L.; Balcilar, M.; Gupta, R.; Chang, T. The causal relationship between economic policy uncertainty and stock returns in China and India: Evidence from a bootstrap rolling window approach. Emerg. Mark. Financ. Trade 2016, 52, 674–689. [Google Scholar] [CrossRef] [Green Version]
- Kondash, A.J.; Albright, E.; Vengosh, A. Quantity of flowback and produced waters from unconventional oil and gas exploration. Sci. Total Environ. 2017, 574, 314–321. [Google Scholar] [CrossRef] [Green Version]
- Kang, W.; De Gracia, F.P.; Ratti, R.A. Oil price shocks, policy uncertainty, and stock returns of oil and gas corporations. J. Int. Money Financ. 2017, 70, 344–359. [Google Scholar] [CrossRef]
- Abumunshar, M.; Aga, M.; Samour, A. Oil price, energy consumption, and CO2 emissions in Turkey. New evidence from a bootstrap ARDL test. Energies 2020, 13, 5588. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112, p. 18. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining Inference and Prediction; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Murphy, K. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Kitchenham, B.; Linkman, S. Estimates, uncertainty, and risk. IEEE Softw. 1997, 14, 69–74. [Google Scholar] [CrossRef]
- Kläs, M.; Vollmer, A.M. Uncertainty in machine learning applications: A practice-driven classification of uncertainty. In International Conference on Computer Safety, Reliability, and Security; Springer: Berlin/Heidelberg, Germany, 2018; pp. 431–438. [Google Scholar]
- Ross, S.M. Introduction to Probability and Statistics for Engineers and Scientists; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Jawad, S.; Ledwith, A. Analyzing enablers and barriers to successfully project control system implementation in petroleum and chemical projects. Int. J. Energy Sect. Manag. 2020, 15, 789–819. [Google Scholar] [CrossRef]
- Hegde, C.M.; Wallace, S.P.; Gray, K.E. Use of regression and bootstrapping in drilling inference and prediction. In SPE Middle East Intelligent Oil and Gas Conference and Exhibition; OnePetro: Richardson, TX, USA, 2015. [Google Scholar]
- Liu, K.; Zhang, Y.; Wang, X. Applications of bootstrap method for drilling site noise analysis and evaluation. J. Pet. Sci. Eng. 2019, 180, 96–104. [Google Scholar] [CrossRef]
- Mittas, N.; Angelis, L. Bootstrap prediction intervals for a semi-parametric software cost estimation model. In Proceedings of the 2009 35th Euromicro Conference on Software Engineering and Advanced Applications, Patras, Greece, 27–29 August 2009; pp. 293–299. [Google Scholar]
- Mittas, N.; Angelis, L. Comparing cost prediction models by resampling techniques. J. Syst. Softw. 2008, 81, 616–632. [Google Scholar] [CrossRef]
- Mittas, N.; Athanasiades, M.; Angelis, L. Improving analogy-based software cost estimation by a resampling method. Inf. Softw. Technol. 2008, 50, 221–230. [Google Scholar] [CrossRef]
- Song, L.; Minku, L.L.; Yao, X. Software effort interval prediction via Bayesian inference and synthetic bootstrap resampling. ACM Trans. Softw. Eng. Methodol. 2019, 28, 1–46. [Google Scholar] [CrossRef]
- Hothorn, T.; Leisch, F.; Zeileis, A.; Hornik, K. The design and analysis of benchmark experiments. J. Comput. Graph. Stat. 2005, 14, 675–699. [Google Scholar] [CrossRef] [Green Version]
- Botchkarev, A. A new typology design of performance metrics to measure errors in machine learning regression algorithms. Interdiscip. J. Inf. Knowl. Manag. 2019, 14, 45. [Google Scholar] [CrossRef] [Green Version]
- Foss, T.; Stensrud, E.; Kitchenham, B.; Myrtveit, I. A simulation study of the model evaluation criterion MMRE. IEEE Trans. Softw. Eng. 2003, 29, 985–995. [Google Scholar] [CrossRef] [Green Version]
- Pal, R. Validation methodologies. In Predictive Modeling of Drug Sensitivity; Academic Press: Cambridge, MA, USA, 2017; pp. 83–107. [Google Scholar]
- Hernández-Orallo, J. ROC curves for regression. Pattern Recognit. 2013, 46, 3395–3411. [Google Scholar] [CrossRef] [Green Version]
- Tripathy, D.; Prusty, R. Forecasting of renewable generation for applications in smart grid power systems. In Advances in Smart Grid Power System; Academic Press: Cambridge, MA, USA, 2021; pp. 265–298. [Google Scholar]
- Casella, G.; Hwang, J. Evaluating confidence sets using loss functions. Stat. Sin. 1991, 1, 159–173. [Google Scholar]
- Troccoli, A.; Harrison, M.; Anderson, D.L.; Mason, S.J. Seasonal Climate: Forecasting and Managing Risk; Springer: Berlin/Heidelberg, Germany, 2008; Volume 82. [Google Scholar]
- Gneiting, T.; Raftery, A. Strictly proper scoring rules, prediction, and estimation. J. Am. Stat. Assoc. 2007, 102, 359–378. [Google Scholar] [CrossRef]
- Wang, H. Closed form prediction intervals applied for disease counts. Am. Stat. 2010, 64, 250–256. [Google Scholar] [CrossRef] [Green Version]
- Khosravi, A.; Nahavandi, S.; Creighton, D. Construction of optimal prediction intervals for load forecasting problems. IEEE Trans. Power Syst. 2010, 25, 1496–1503. [Google Scholar] [CrossRef] [Green Version]
- Landon, J.; Singpurwalla, N.D. Choosing a coverage probability for prediction intervals. Am. Stat. 2008, 62, 120–124. [Google Scholar] [CrossRef]
- Winkler, R.L. A decision-theoretic approach to interval estimation. J. Am. Stat. Assoc. 1972, 67, 187–191. [Google Scholar] [CrossRef]
- Dietterich, T. Approximate statistical tests for comparing supervised classification learning algorithms. Neural Comp. 1998, 10, 1895–1923. [Google Scholar] [CrossRef] [Green Version]
- Demšar, J. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- Garcia, S.; Herrera, F. An extension on “statistical comparisons of classifiers over multiple data sets” for all pairwise comparisons. J. Mach. Learn. Res. 2008, 9, 2677–2694. [Google Scholar]
- Mittas, N.; Angelis, L. Ranking and clustering software cost estimation models through a multiple comparisons algorithm. IEEE Trans. Softw. Eng. 2013, 39, 537–551. [Google Scholar] [CrossRef]
- Jiang, J. Linear and Generalized Linear Mixed Models and Their Applications; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Pinheiro, J.; Bates, D. Mixed-Effects Models in S and S-PLUS; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Millar, R.B.; Anderson, M.J. Remedies for pseudoreplication. Fish. Res. 2004, 70, 397–407. [Google Scholar] [CrossRef]
- Guyon, I.; Gunn, S.; Nikravesh, M.; Zadeh, L. Feature Extraction: Foundations and Applications; Springer: Berlin/Heidelberg, Germany, 2008; Volume 207. [Google Scholar]
- Zuur, A.; Ieno, E.; Walker, N.; Saveliev, A.; Smith, G. Mixed Effects Models and Extensions in Ecology with R; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Breiman, L.; Friedman, J.; Stone, C.; Olshen, R.A. Classification and Regression Trees; Taylor & Francis: Abingdon, UK, 1984. [Google Scholar]
- Härdle, W. Applied Non-Parametric Regression; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Jolliffe, I. Principal Component Analysis; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Vapnik, V.; Golowich, S.; Smola, A. Support vector method for function approximation, regression estimation and signal processing. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1997; pp. 281–287. [Google Scholar]
- Kuhn, M. Building predictive models in R using the caret package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef] [Green Version]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014. [Google Scholar]
- International Energy Agency. World Energy Investment, Executive Summary; International Energy Agency: Paris, France, 2018. [Google Scholar]
- García, S.; Fernández, A.; Luengo, J.; Herrera, F. Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: Experimental analysis of power. Inf. Sci. 2010, 180, 2044–2064. [Google Scholar] [CrossRef]
- Hornik, K.; Meyer, D. Deriving consensus rankings from benchmarking experiments. In Advances in Data Analysis; Springer: Berlin/Heidelberg, Germany, 2007; pp. 163–170. [Google Scholar]
- Lenth, R. Using lsmeans. J. Stat. Softw. 2017, 9, 1–33. [Google Scholar]
- Sheskin, D. Handbook of Parametric and Nonparametric Statistical Procedures; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Krippendorff, K. Estimating the reliability, systematic error and random error of interval data. Educ. Psychol. Meas. 1970, 30, 61–70. [Google Scholar] [CrossRef]
- Calder, B.; Phillips, L.; Tybout, A. The concept of external validity. J. Consum. Res. 1982, 9, 240–244. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).