Parallelization of Runge–Kutta Methods for Hardware Implementation
Abstract
1. Introduction
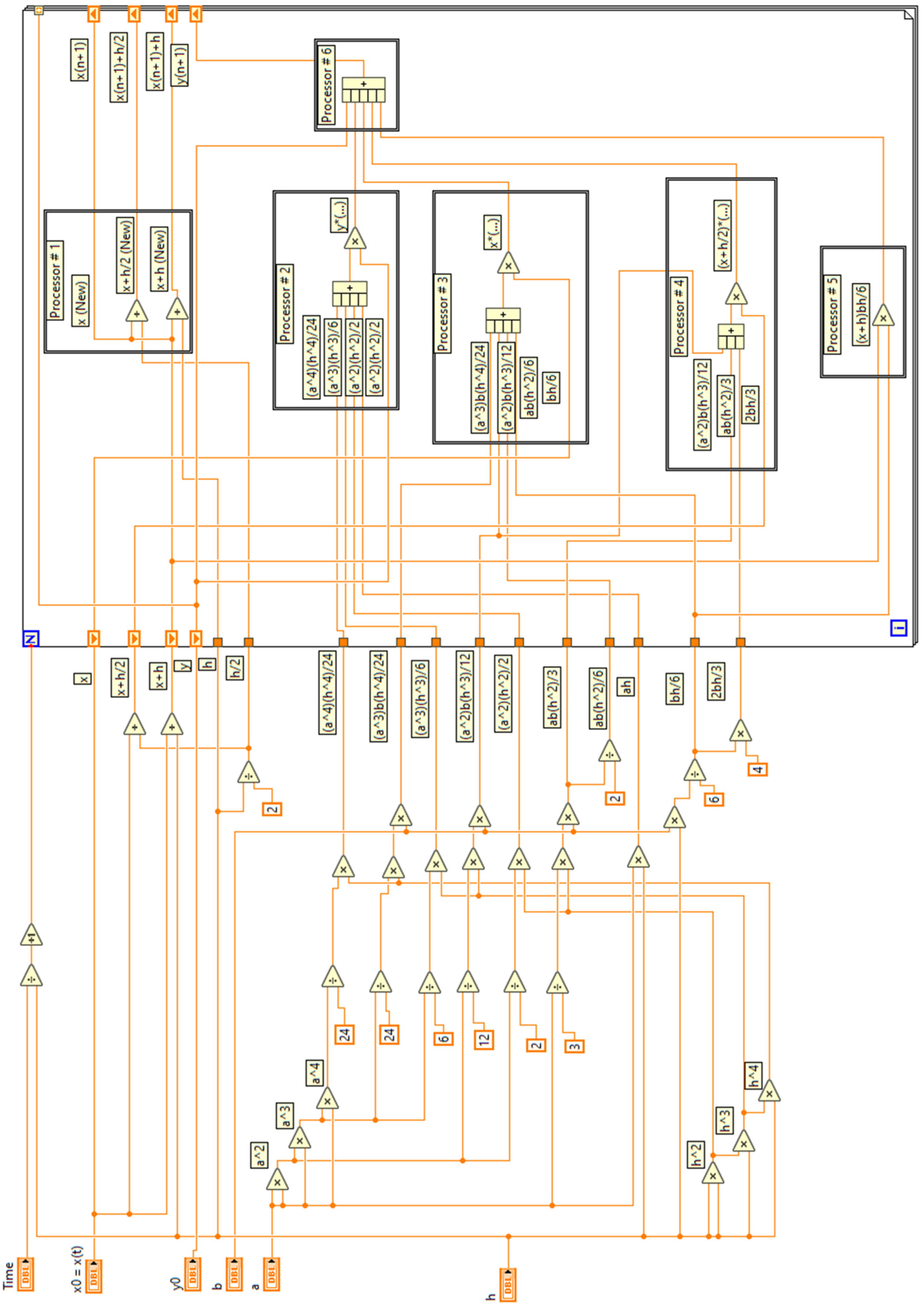
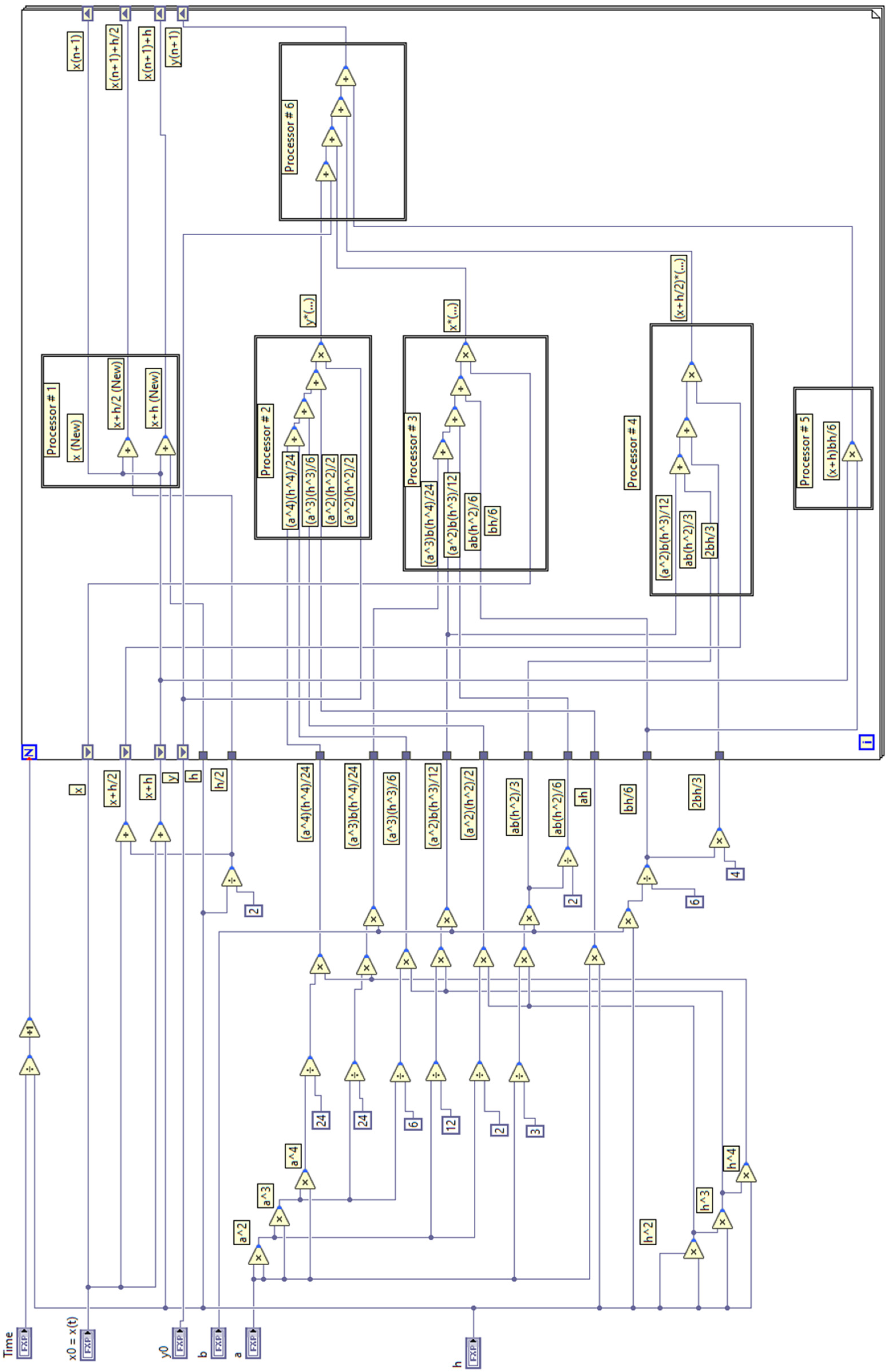
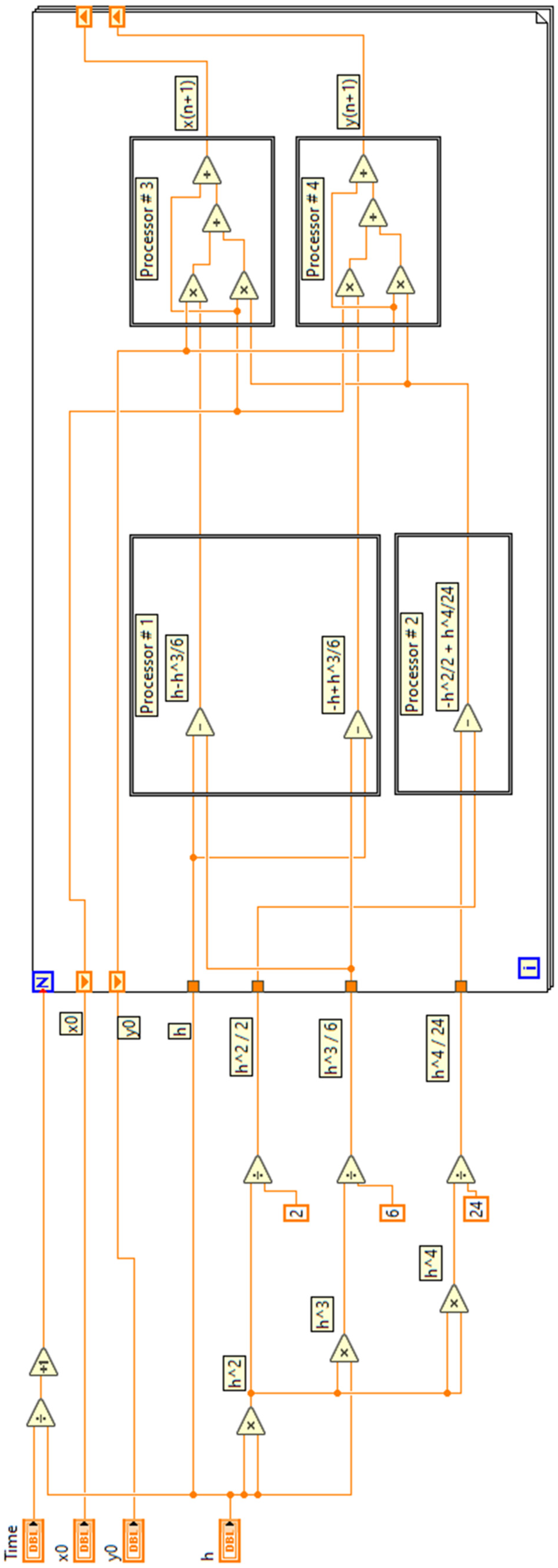
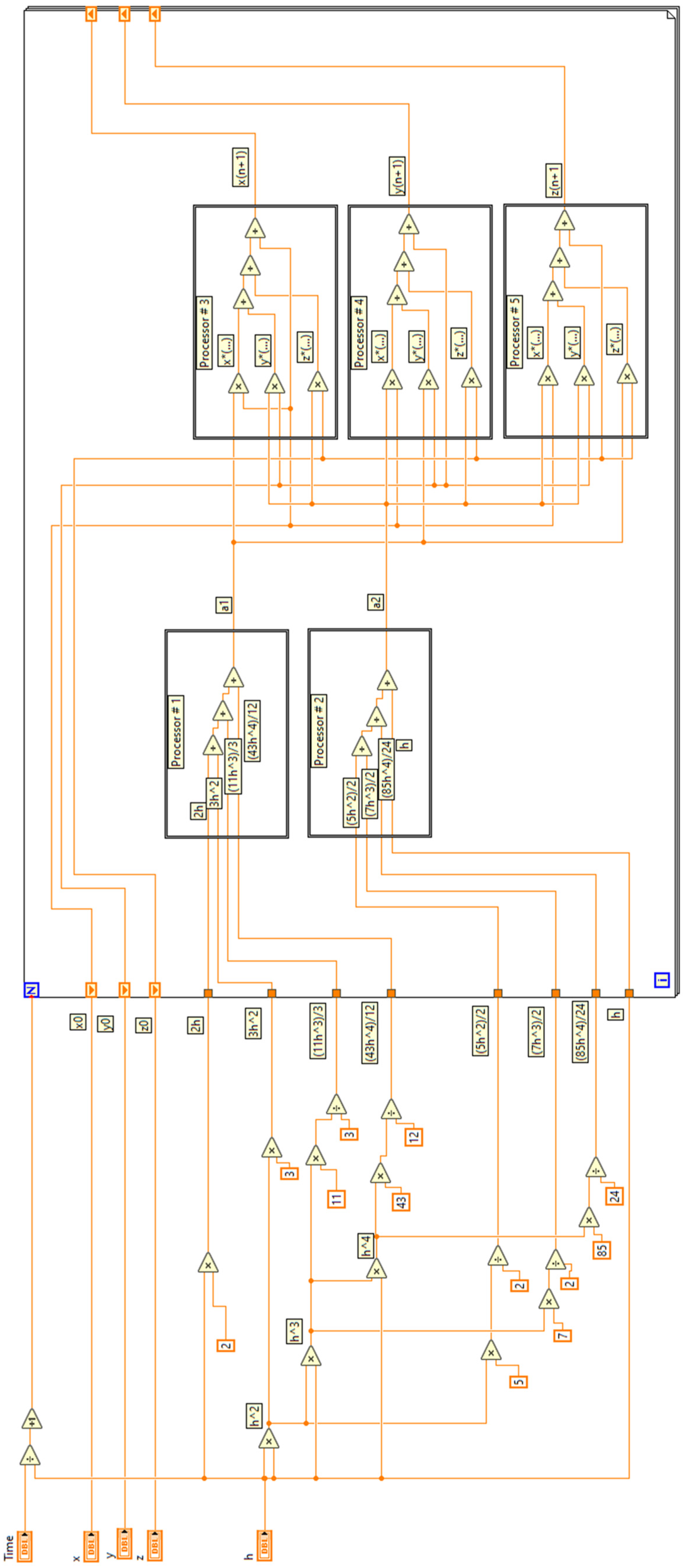
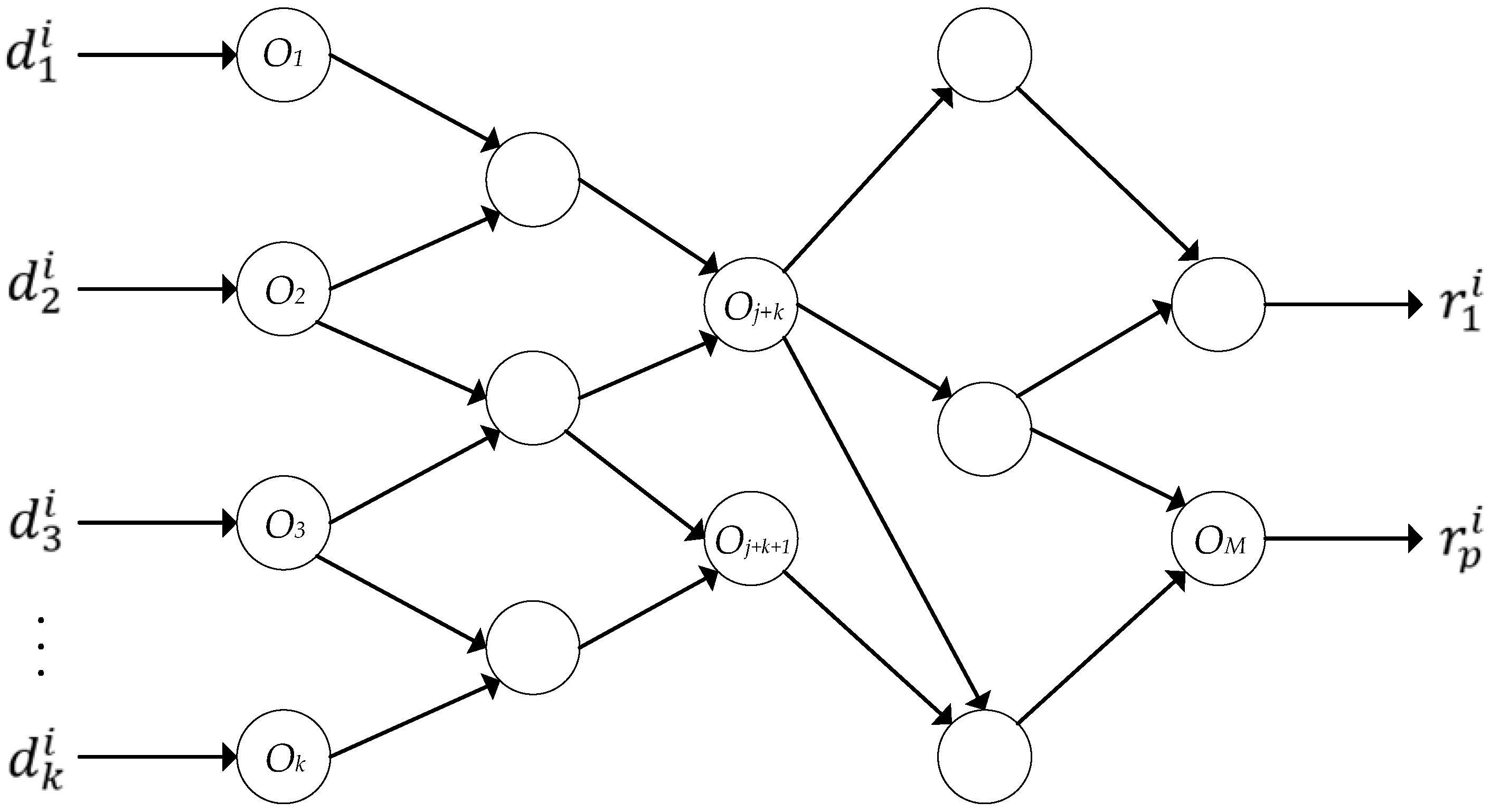
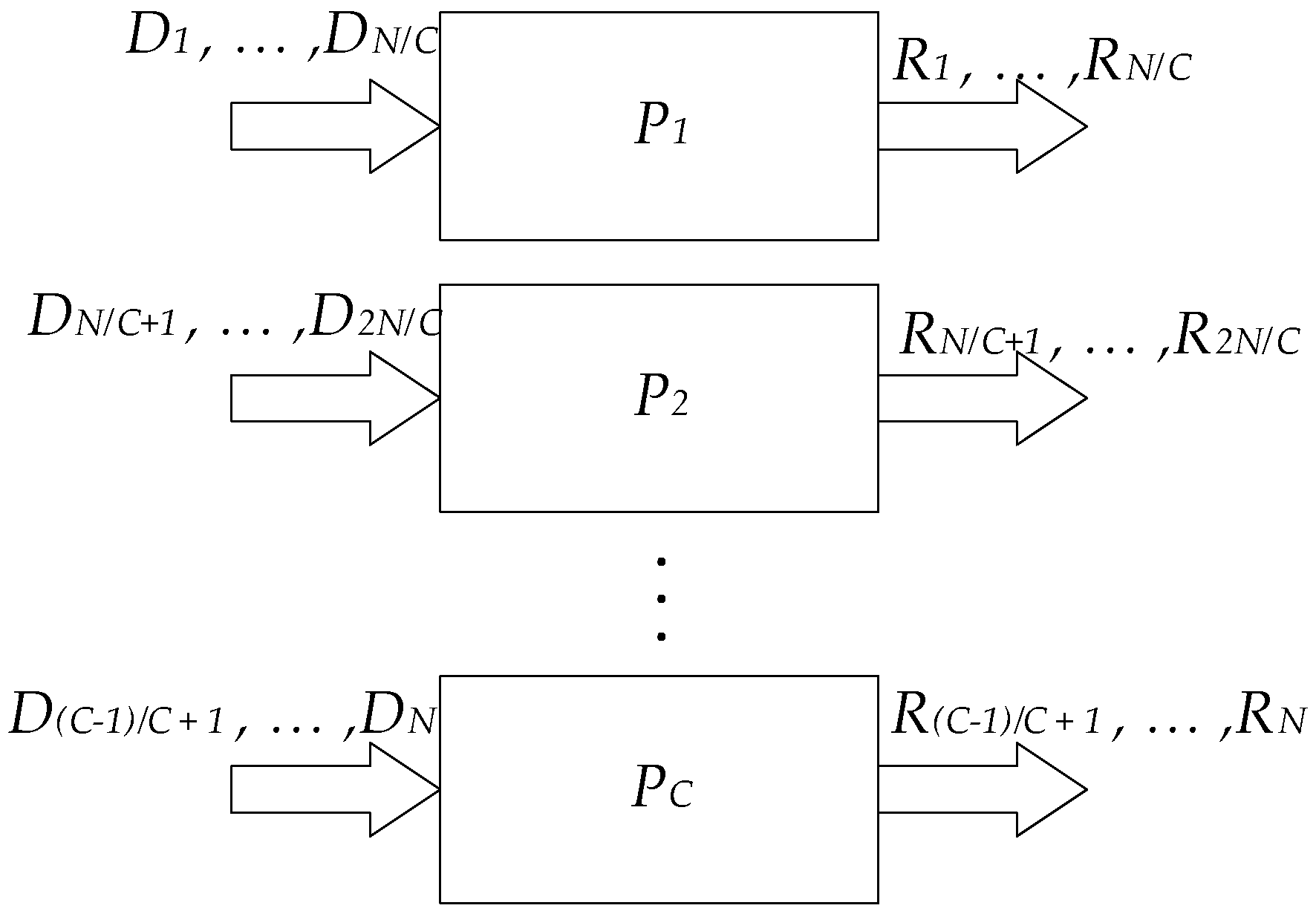
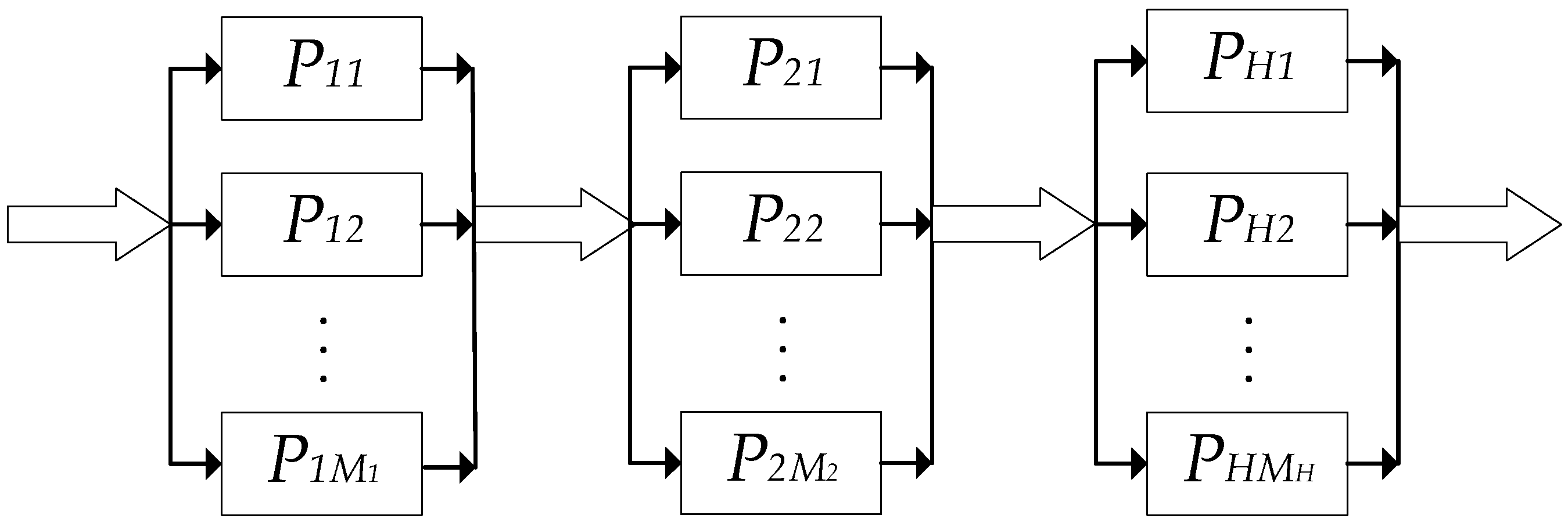
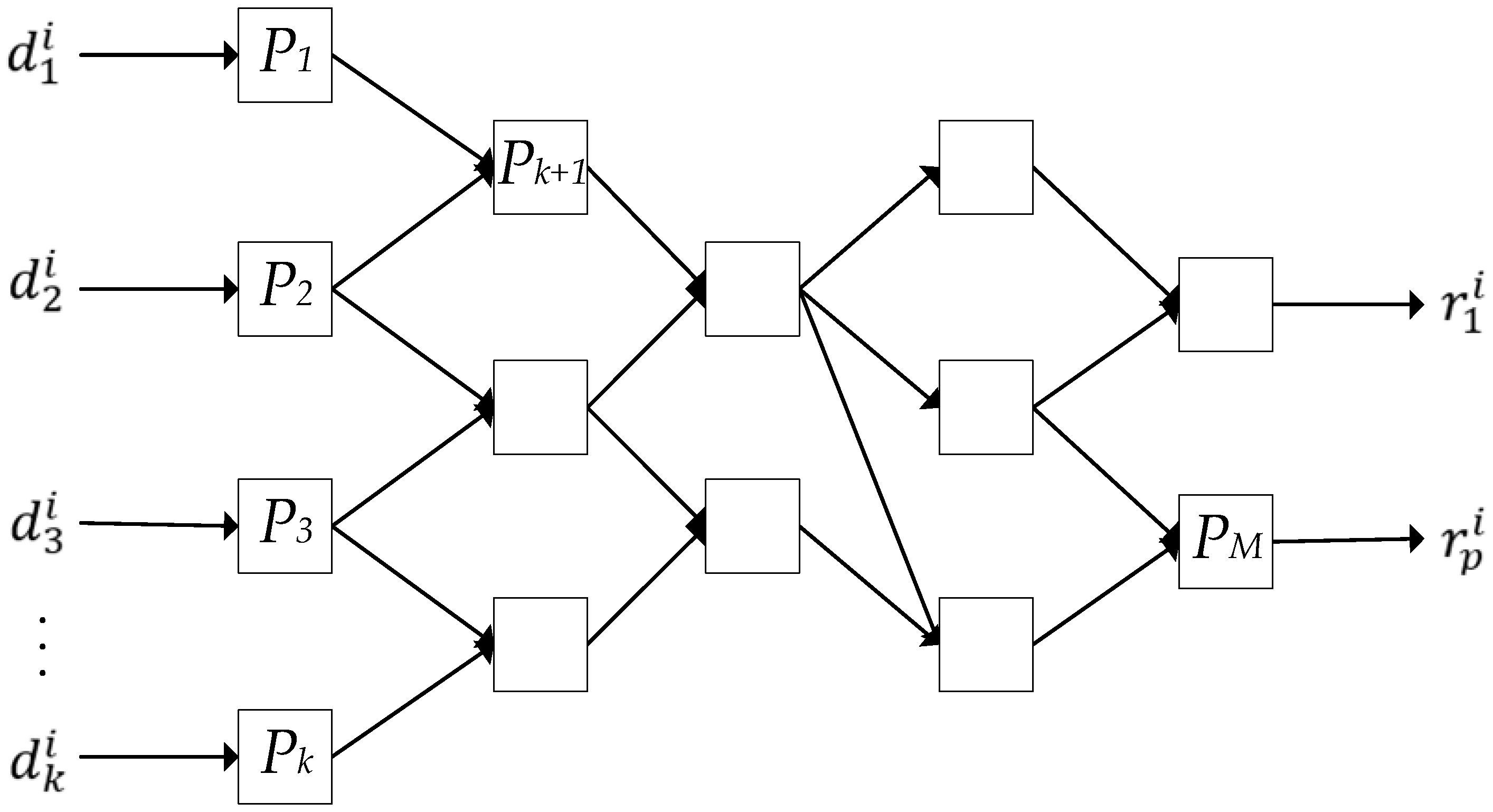
2. Materials and Methods
3. Results
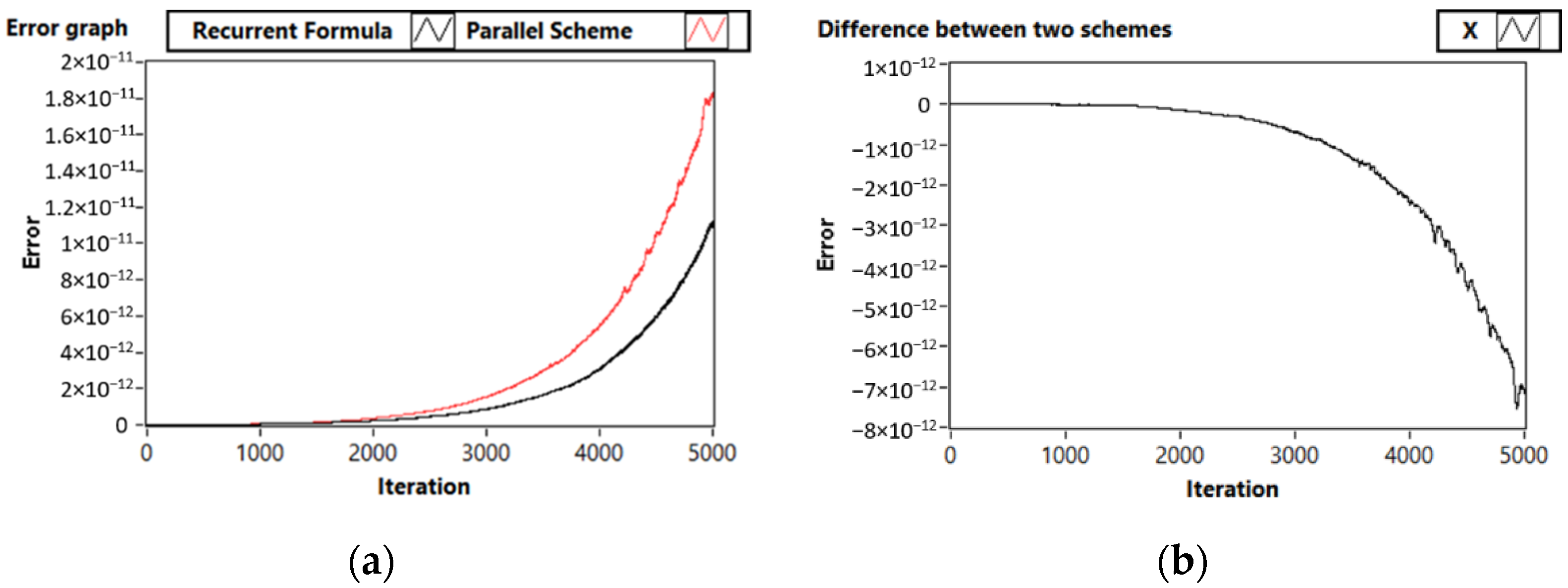
3.1. Test Problem 1: A Simple Linear System
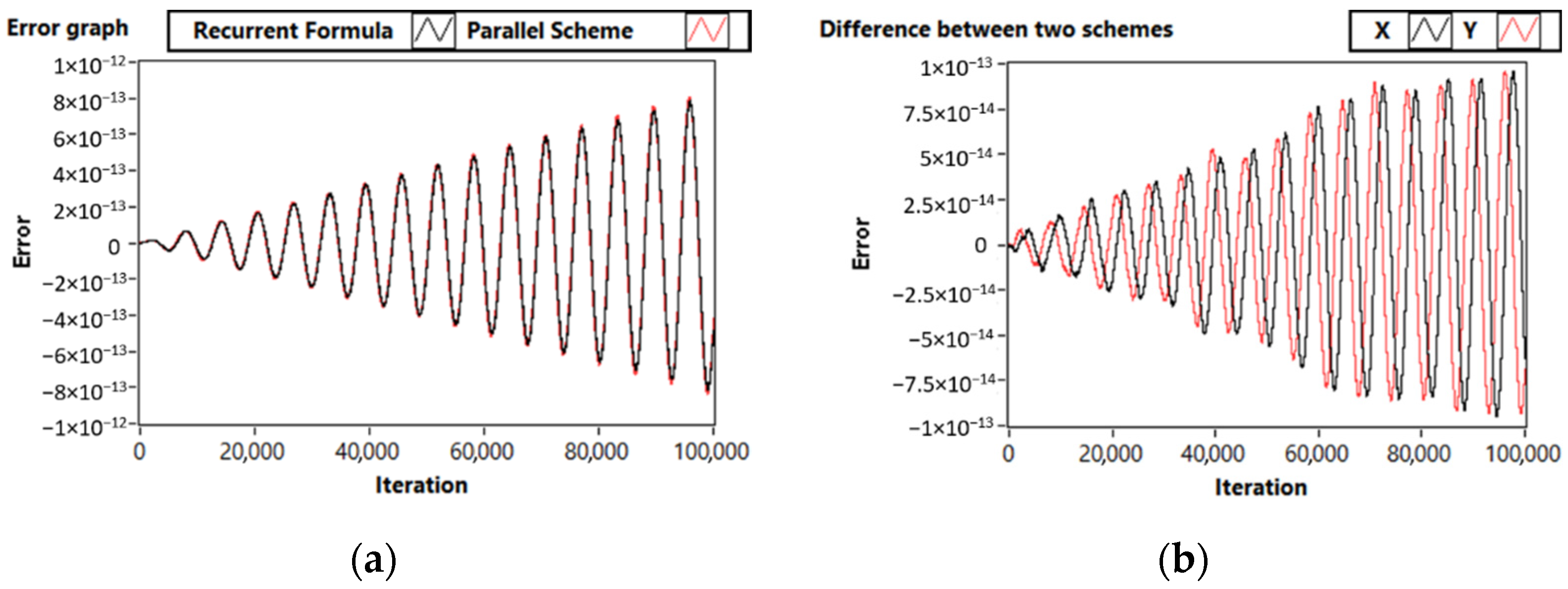
3.2. Test Problem 2: System with Periodic Solution
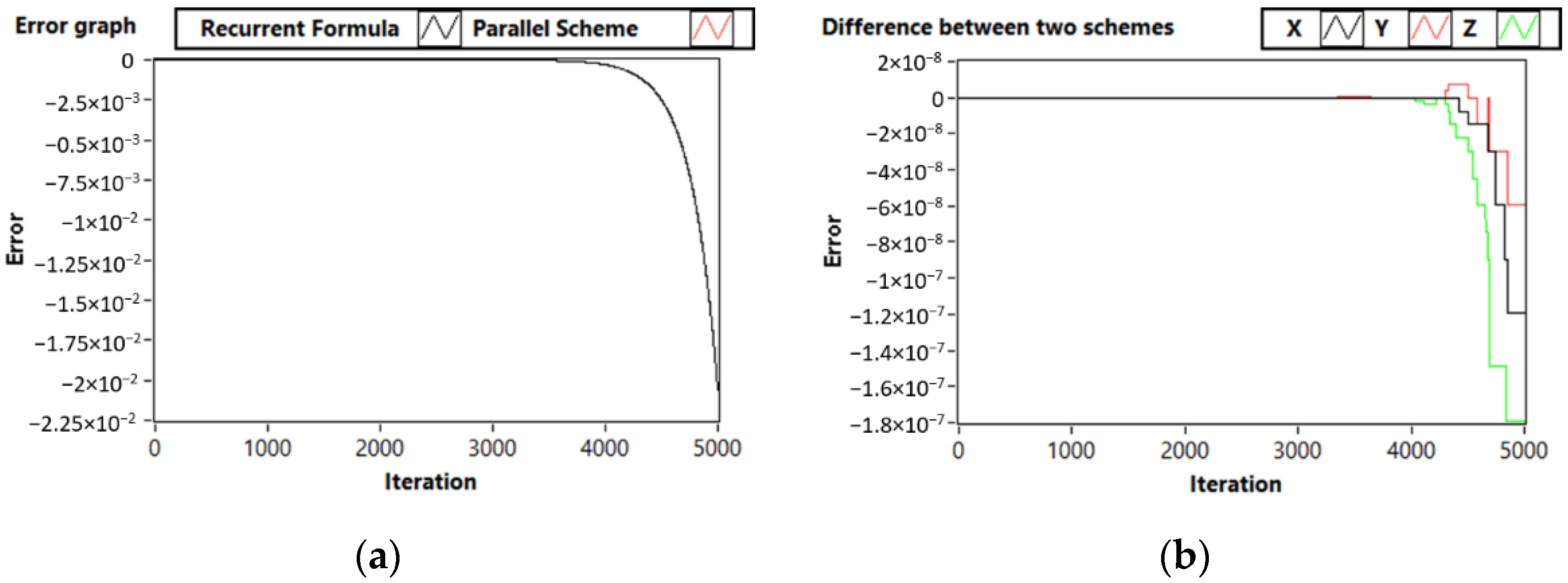
3.3. Test Problem 3: Third-Order System
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
Appendix A
References
- Rahaman, H.; Hasan, M.K.; Ali, A.; Alam, M.S. Implicit Methods for Numerical Solution of Singular Initial Value Problems. Appl. Math. Nonlinear Sci. 2021, 6, 1–8. [Google Scholar] [CrossRef]
- Liu, D.; He, W. Numerical Simulation Analysis Mathematics of Fluid Mechanics for Semiconductor Circuit Breaker. Appl. Math. Nonlinear Sci. 2021, 7, 331–342. [Google Scholar] [CrossRef]
- Wang, Y. Application of numerical method of functional differential equations in fair value of financial accounting. Appl. Math. Nonlinear Sci. 2022, 7, 533–540. [Google Scholar]
- Xu, L.; Aouad, M. Application of Lane-Emden differential equation numerical method in fair value analysis of financial accounting. Appl. Math. Nonlinear Sci. 2021, 7, 669–676. [Google Scholar] [CrossRef]
- Hairer, E.; Nørsett, S.P.; Wanner, G. Solving Ordinary Differential Equations I: Nonstiff probleme; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C++." The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, UK, 2007; p. 1002. [Google Scholar]
- Butusov, D.N.; Karimov, A.I.; Tutueva, A.V. Hardware-targeted semi-implicit extrapolation ODE solvers. In Proceedings of the 2016 International Siberian Conference on Control and Communications (SIBCON), Moscow, Russia, 12–14 May 2016. [Google Scholar]
- Butusov, D.N.; Ostrovskii, V.Y.; Tutueva, A.V. Simulation of dynamical systems based on parallel numerical integration methods. In Proceedings of the 2015 IEEE NW Russia Young Researchers in Electrical and Electronic Engineering Conference (EIConRusNW), St. Petersburg, Russia, 2–4 February 2015. [Google Scholar]
- Saralegui, R.; Sanchez, A.; Martinez-Garcia, M.S.; Novo, J.; de Castro, A. Comparison of numerical methods for hardware-in-the-loop simulation of switched-mode power supplies. In Proceedings of the 2018 IEEE 19th Workshop on Control and Modeling for Power Electronics (COMPEL), Padua, Italy, 25–28 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Farhani Baghlani, F.; Chamgordani, A.E.; Shalmani, A.N. HARDWARE IMPLEMENTATION OF NUMERICAL SOLUTION OF DIFFERENTIAL EQUATIONS ON FPGA. Sharif J. Mech. Eng. 2017, 33, 93–99. [Google Scholar]
- Liu, C.; Wu, H.; Feng, L.; Yang, A. Parallel fourth-order Runge-Kutta method to solve differential equations. In International Conference on Information Computing and Applications; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Ding, X.-H.; Geng, D.-H. The convergence theorem of parallel Runge-Kutta methods for delay differential equation. J. Nat. Sci. Heilongjiang Univ. 2004, 21, 17–22. [Google Scholar]
- Jinggao, F. A class of parallel runge-kutta methods for differential-algebraic systems of index 2. J. Syst. Eng. Electron. 1999, 10, 64–75. [Google Scholar]
- Bashashin, M.; Nechaevskiy, A.; Podgainy, D.; Rahmonov, I. Parallel algorithms for studying the system of long Josephson junctions. In Proceedings of the CEUR Workshop Proceedings, Stuttgart, Germany, 19 February 2019. [Google Scholar]
- Volokhova, A.V.; Zemlyanay, E.V.; Kachalov, V.V.; Rikhvitskiy, V.S. Simulation of the gas condensate reservoir depletion. Comput. Res. Model. 2020, 12, 1081–1095. [Google Scholar] [CrossRef]
- Tang, H.C. Parallelizing a Fourth-Order Runge-Kutta Method; US Department of Commerce, Technology Administration, Nation-al Institute of Standards and Technology: Gaithersburg, MD, USA, 1997. [Google Scholar]
- Jiang, W.; Yang, Y.-H.E.; Prasanna, V.K. Scalable multi-pipeline architecture for high performance multi-pattern string matching. In Proceedings of the 2010 IEEE International Symposium on Parallel & Distributed Processing (IPDPS), Atlanta, GA, USA, 19–23 April 2010. [Google Scholar]
- Runge, C. Über die numerische Auflösung von Differentialgleichungen. Math. Ann. 1895, 46, 167–178. [Google Scholar] [CrossRef]
- Kutta, W. Beitrag zur naherungsweisen integration totaler differentialgleichungen. Z. Math. Phys. 1901, 46, 435–453. [Google Scholar]
- Andreev, V.S.; Goryainov, S.V.; Krasilnikov, A.V.; Sarma, K.K. Scaling techniques for fixed-point chaos generators. In Proceedings of the 2017 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), St. Petersburg and Moscow, Russia, 1–3 February 2017. [Google Scholar]
- Andreev, V.; Ostrovskii, V.; Karimov, T.; Tutueva, A.; Doynikova, E.; Butusov, D. Synthesis and Analysis of the Fixed-Point Hodgkin–Huxley Neuron Model. Electronics 2020, 9, 434. [Google Scholar] [CrossRef]
- Amdahl, G.M. Validity of the single processor approach to achieving large scale computing capabilities, reprinted from the afips con-ference proceedings, vol. 30 (atlantic city, nj, apr. 18–20), afips press, reston, va., 1967, pp. 483–485, when dr. amdahl was at international business machines corporation, sunnyvale, california. IEEE Solid-State Circuits Soc. Newsl. 2007, 12, 19–20. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fedoseev, P.; Zhukov, K.; Kaplun, D.; Vybornov, N.; Andreev, V. Parallelization of Runge–Kutta Methods for Hardware Implementation. Computation 2022, 10, 215. https://doi.org/10.3390/computation10120215
Fedoseev P, Zhukov K, Kaplun D, Vybornov N, Andreev V. Parallelization of Runge–Kutta Methods for Hardware Implementation. Computation. 2022; 10(12):215. https://doi.org/10.3390/computation10120215
Chicago/Turabian StyleFedoseev, Petr, Konstantin Zhukov, Dmitry Kaplun, Nikita Vybornov, and Valery Andreev. 2022. "Parallelization of Runge–Kutta Methods for Hardware Implementation" Computation 10, no. 12: 215. https://doi.org/10.3390/computation10120215
APA StyleFedoseev, P., Zhukov, K., Kaplun, D., Vybornov, N., & Andreev, V. (2022). Parallelization of Runge–Kutta Methods for Hardware Implementation. Computation, 10(12), 215. https://doi.org/10.3390/computation10120215






