Development of a Computational Tool for the Estimation of Alveolar Bone Loss in Oral Radiographic Images
Abstract
1. Introduction
2. Materials and Methods
2.1. Collection of Study Samples
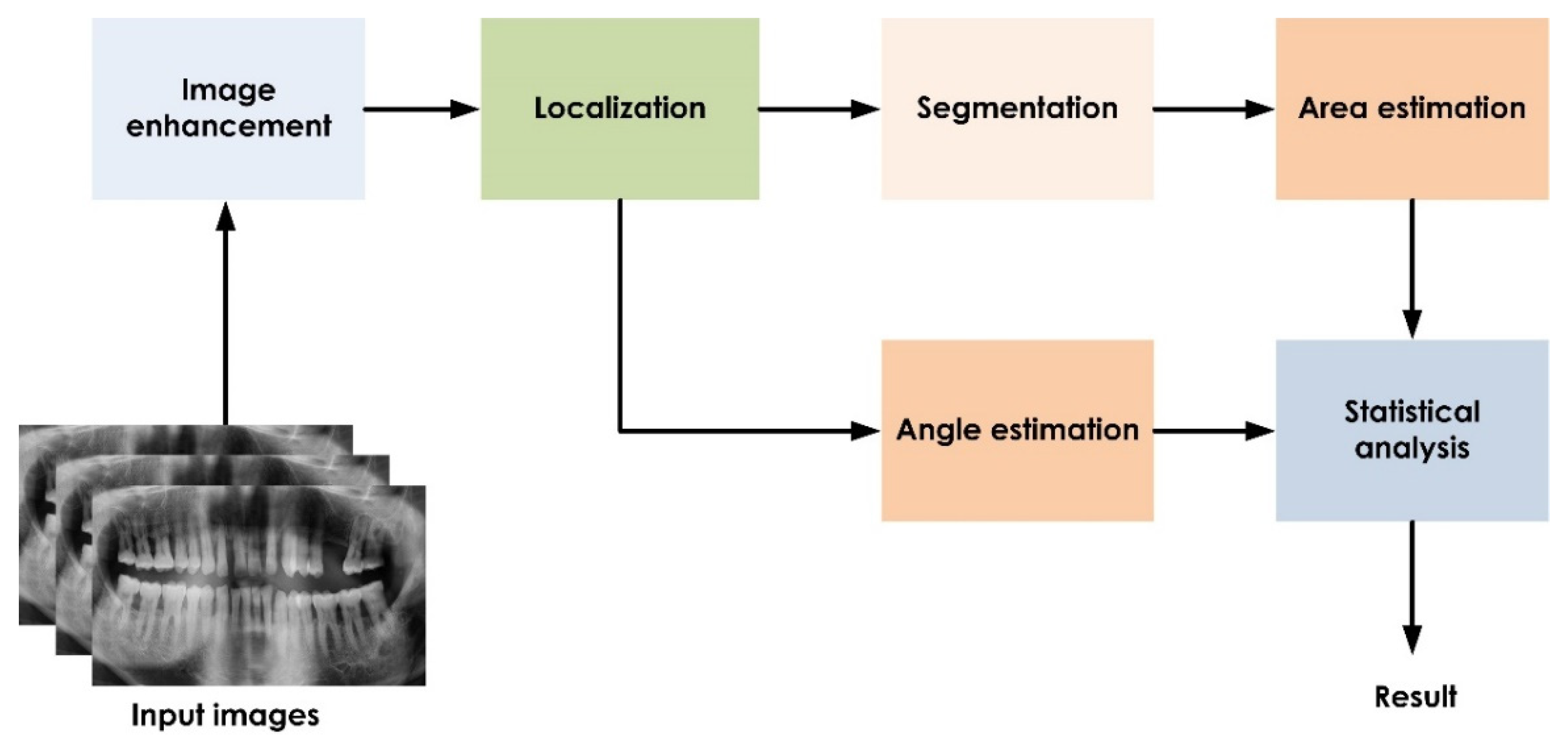
2.2. Computational Tool
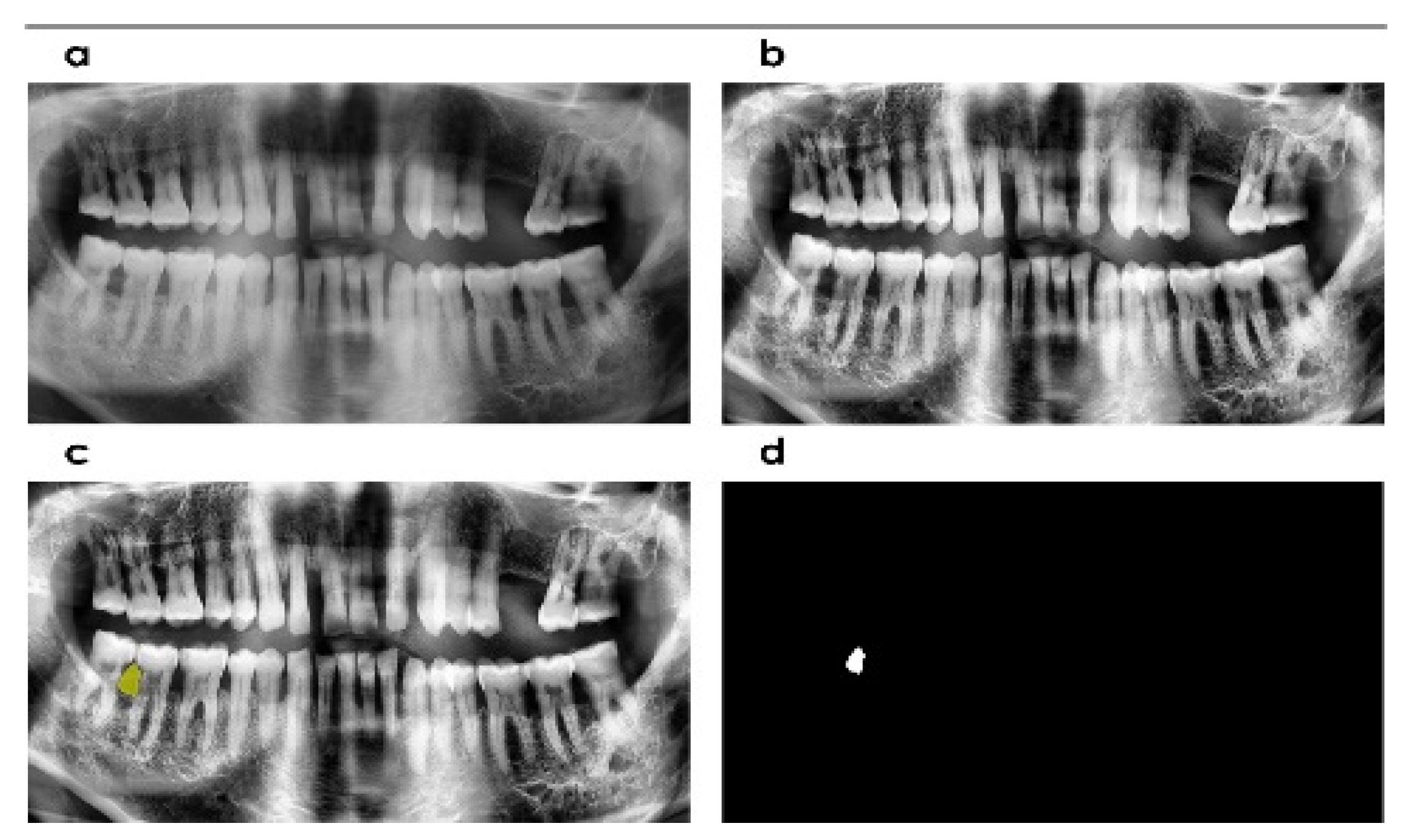
2.3. Image Enhancement
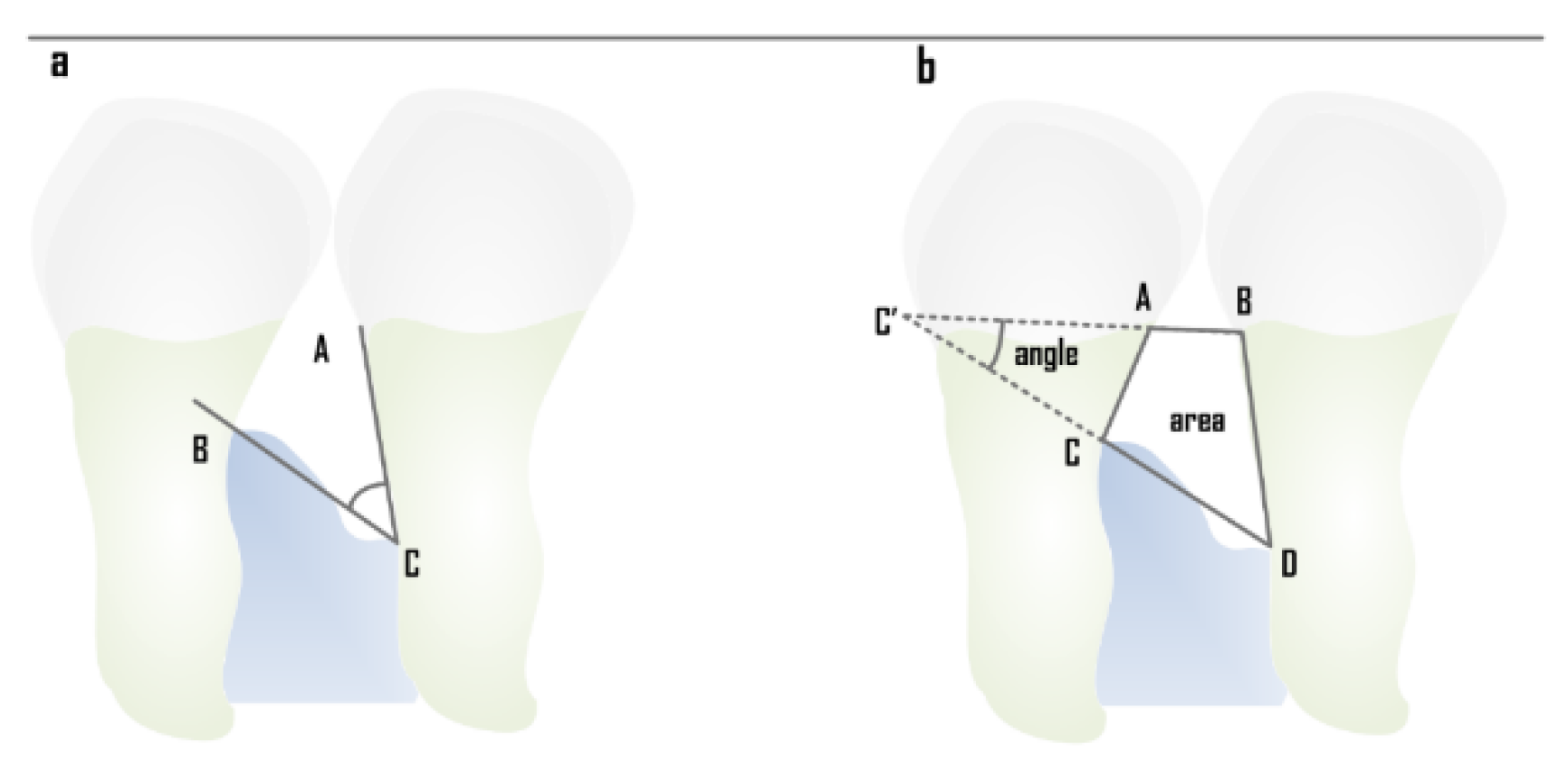
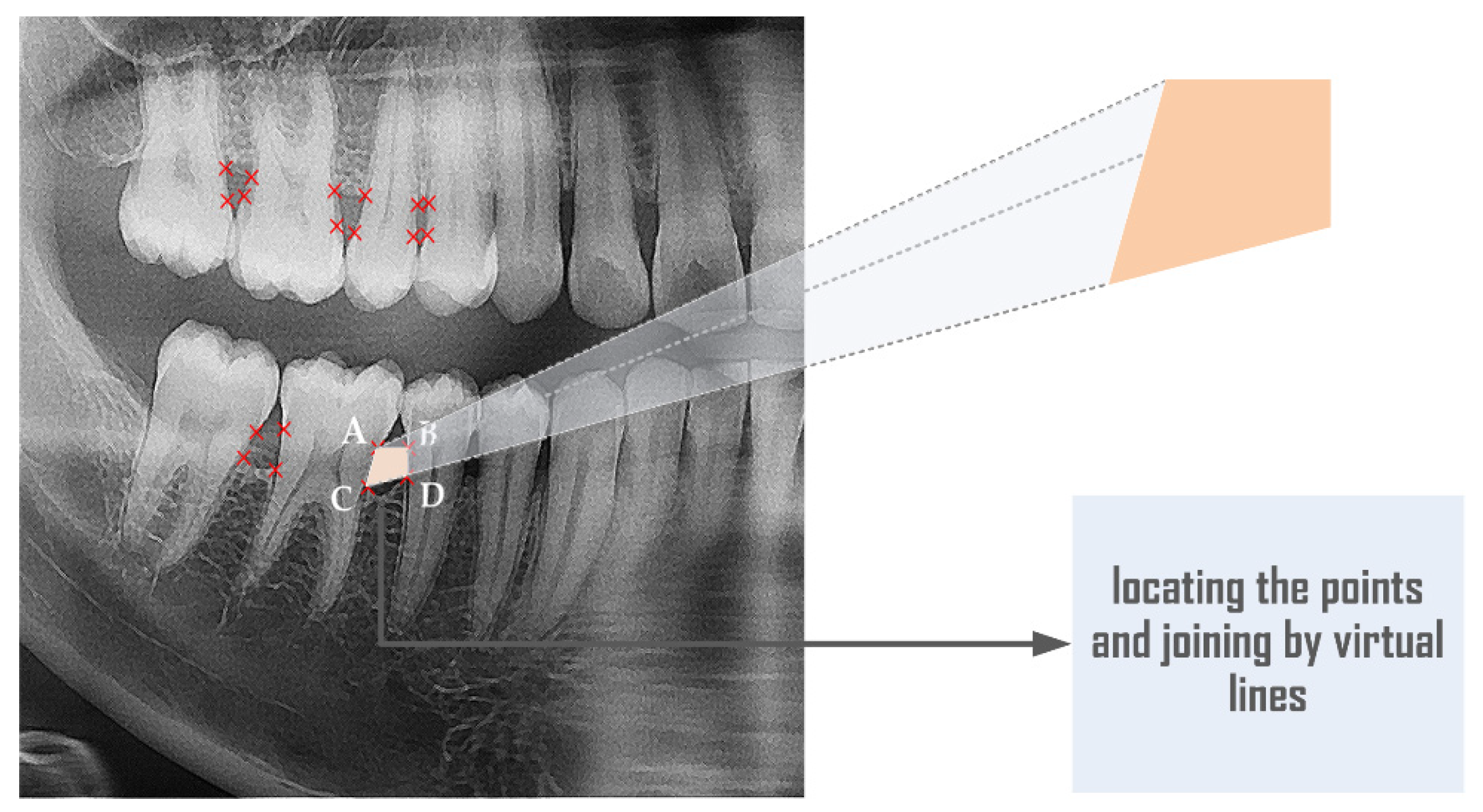
2.4. Localization and Angle Estimation
2.5. Segmentation
2.6. Manual Measurement (Ground Truth)
2.7. Statistical Analysis
3. Results
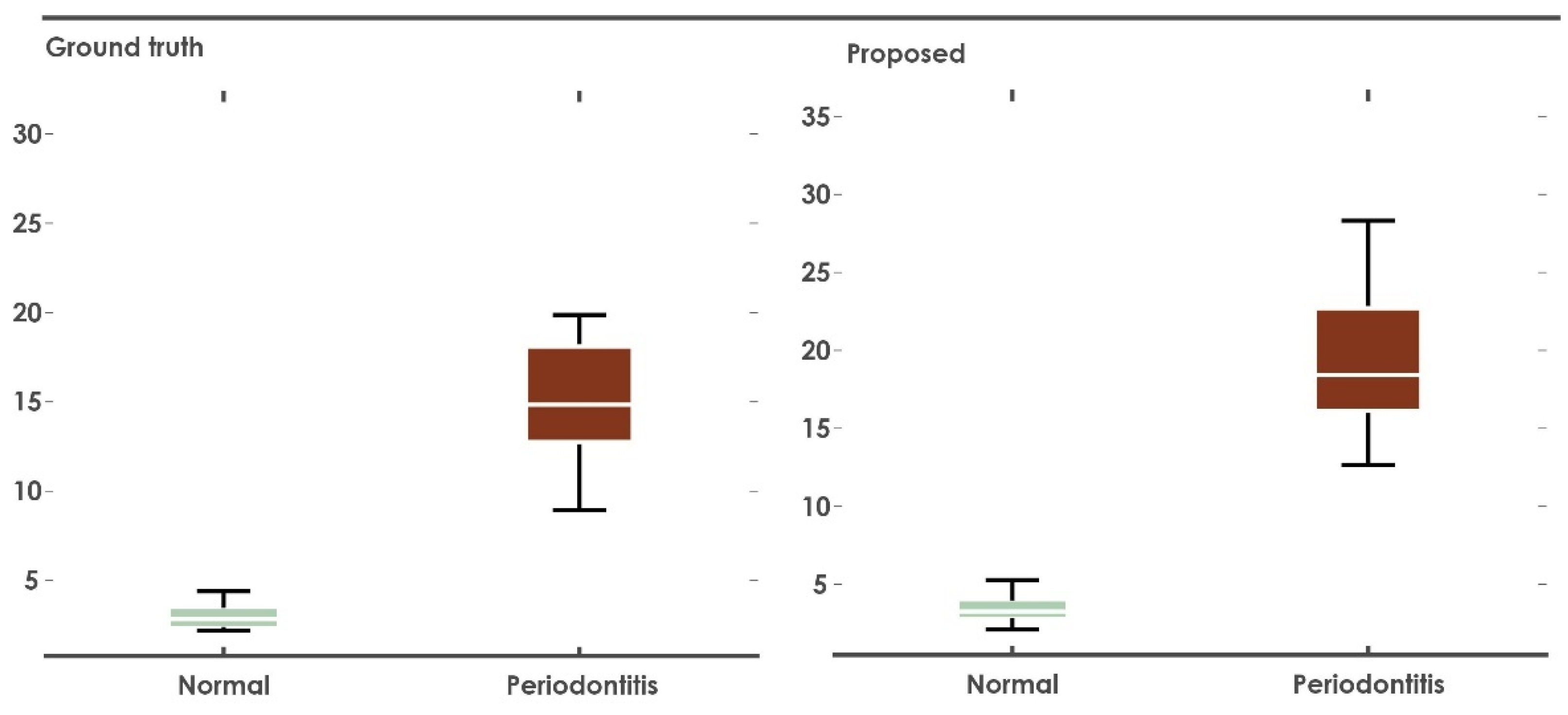
3.1. Alveolar Space Area
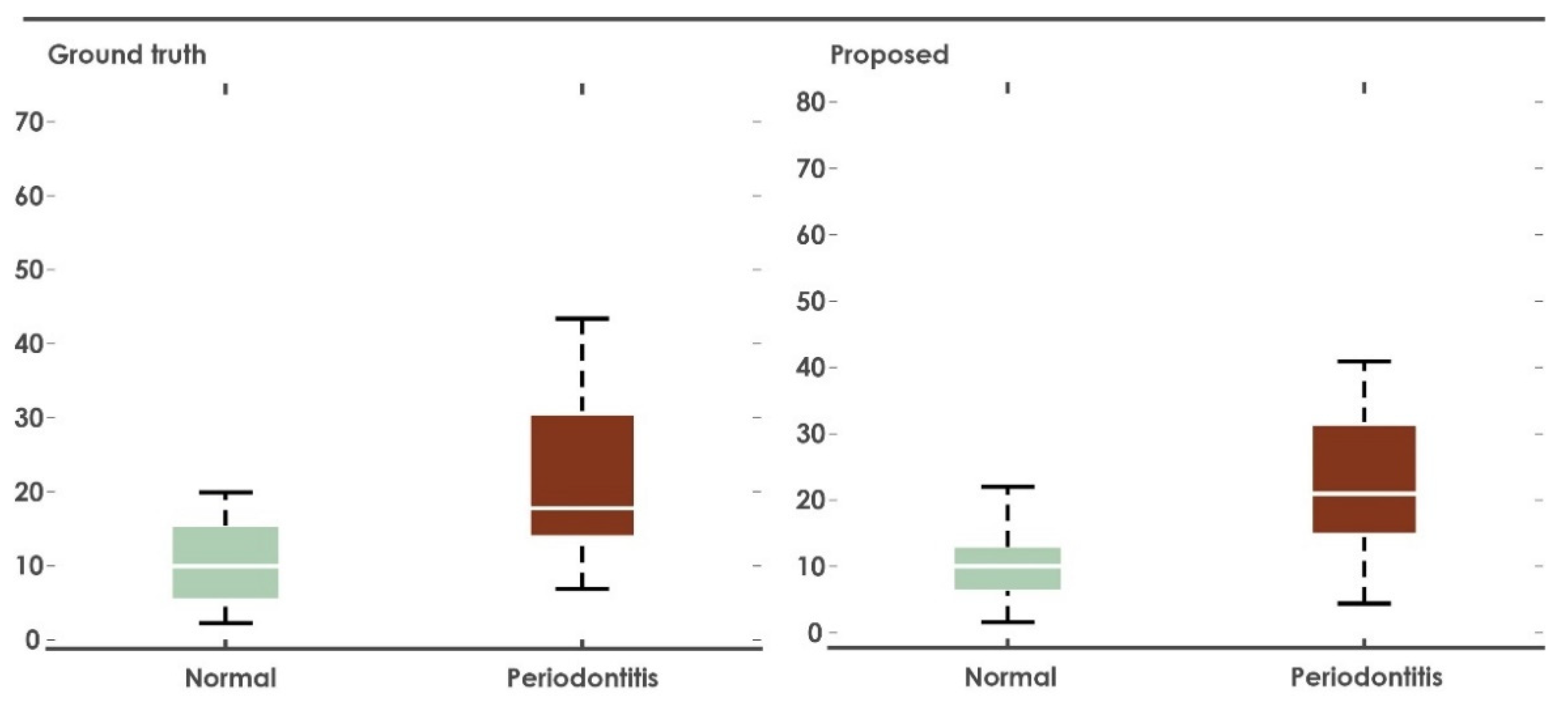
3.2. Alveolar Crest Angle
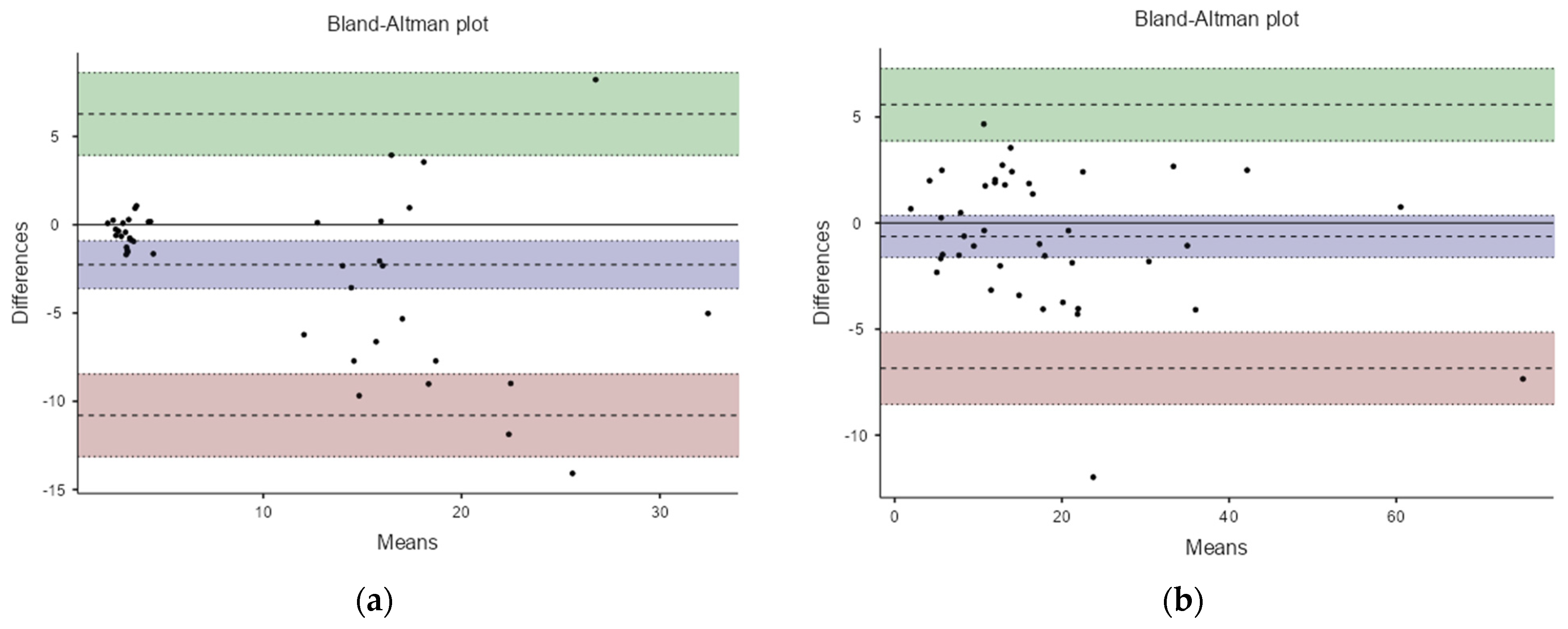
3.3. Analysis of Agreement
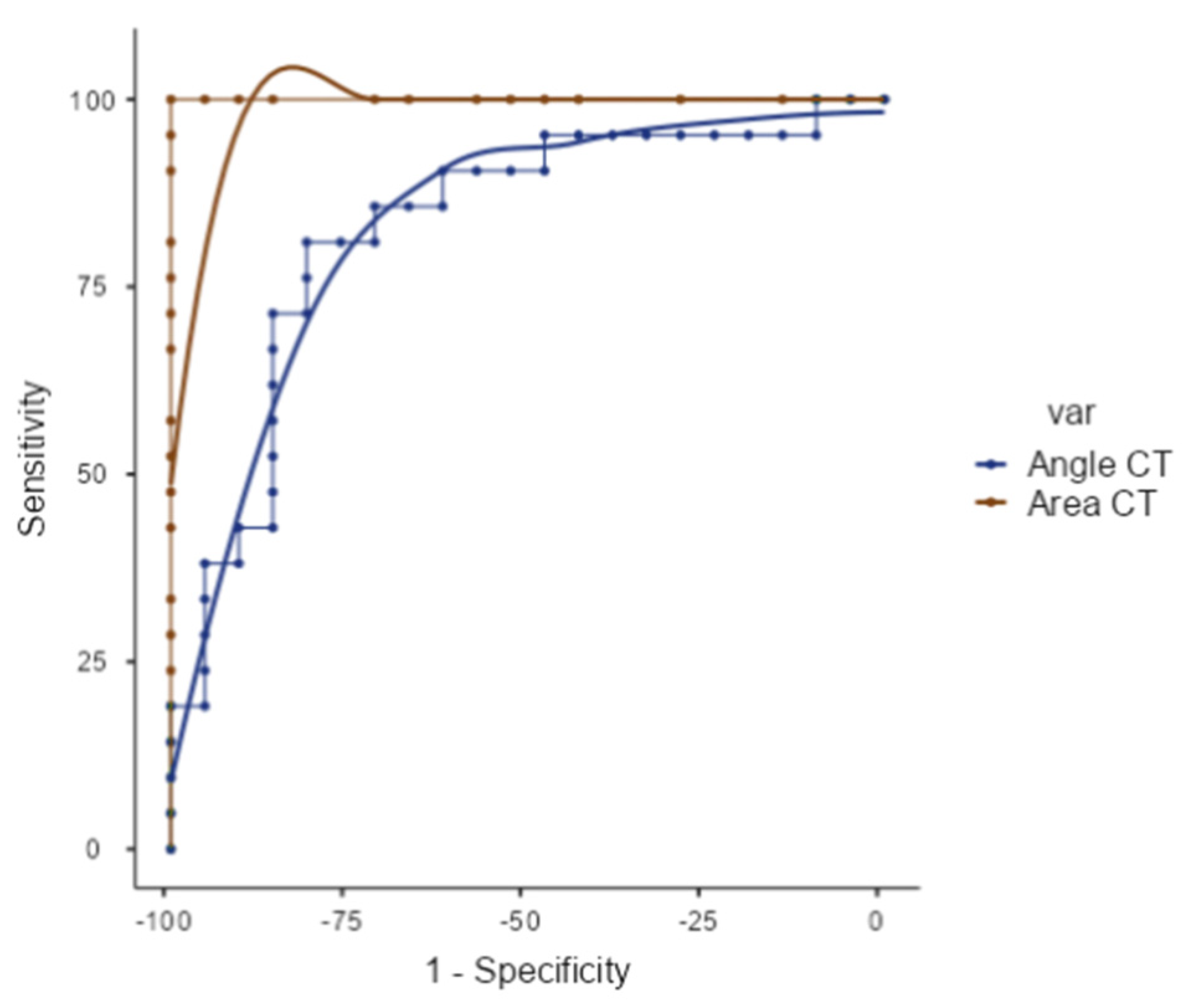
3.4. ROC Curve
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Greenstein, B.; Frantz, B.; Desai, R.; Proskin, H.; Campbell, J.; Caton, J. Stability of treated angular and horizontal bony defects: A retrospective radiographic evaluation in a private periodontal practice. J. Periodontol. 2009, 80, 228–233. [Google Scholar] [CrossRef]
- D’Ercole, S.; D’Addazio, G.; Di Lodovico, S.; Traini, T.; Di Giulio, M.; Sinjari, B. Porphyromonas Gingivalis Load is Balanced by 0.20% Chlorhexidine Gel. A Randomized, Double-Blind, Controlled, Microbiological and Immunohistochemical Human Study. J. Clin. Med. 2020, 9, 284. [Google Scholar] [CrossRef] [PubMed]
- Teeuw, W.; Coelho, L.; Silva, A.; Van Der Palen, C.; Lessmann, F.; Van der Velden, U.; Loos, B. Validation of a dental image analyzer tool to measure alveolar bone loss in periodontitis patients. J. Periodontal. Res. 2009, 44, 94–102. [Google Scholar] [CrossRef]
- Lin, P.-L.; Hsu, H.; Huang, P.-Y.; Huang, P.-W.; Chen, P. Alveolar bone-loss area localization in periapical radiographs by texture analysis based on fBm model and GLC matrix. In Proceedings of the 2014 IEEE International Symposium on Bioelectronics and Bioinformatics (IEEE ISBB 2014), Chung Li, Taiwan, 11–14 April 2014. [Google Scholar]
- Moutinho, R.; Coelho, L.; Silva, A.; Lobo Pereira, J.; Pinto, M.; Baptista, I. Validation of a dental image-analyzer tool to measure the radiographic defect angle of the intrabony defect in periodontitis patients. J. Periodontal. Res. 2012, 47, 695–700. [Google Scholar] [CrossRef]
- Lin, P.; Huang, P.; Huang, P. Automatic methods for alveolar bone loss degree measurement in periodontitis periapical radiographs. Comput. Methods Programs Biomed. 2017, 148, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Sinibaldi, R.; Conti, A.; Sinjari, B.; Spadone, S.; Pecci, R.; Palombo, M.; Komlev, V.S.; Ortore, M.G.; Tromba, G.; Capuani, S.; et al. Multimodal-3D imaging based on μMRI and μCT techniques bridges the gap with histology in visualization of the bone regeneration process. J. Tissue Eng. Reg. Med. 2018, 12, 750–761. [Google Scholar] [CrossRef]
- Krois, J.; Ekert, T.; Meinhold, L.; Golla, T.; Kharbot, B.; Wittemeier, A.; Dörfer, C.; Schwendicke, F. Deep Learning for the Radiographic Detection of Periodontal Bone Loss. Sci. Rep. 2019, 9, 1–6. [Google Scholar] [CrossRef]
- Lee, J.-H.; Kim, D.-H.; Jeong, S.-N.; Choi, S.-H. Diagnosis and prediction of periodontally compromised teeth using a deep learning-based convolutional neural network algorithm. J. Periodontal. Implant Sci. 2019, 48, 114–123. [Google Scholar] [CrossRef] [PubMed]
- Chang, H.J.; Lee, S.J.; Yong, T.H.; Shin, N.Y.; Jang, B.G.; Kim, J.E.; Huh, K.H.; Lee, S.S.; Heo, M.S.; Choi, S.C.; et al. Deep learning hybrid method to automatically diagnose periodontal bone loss and stage periodontitis. Sci. Rep. 2020, 10, 1–8. [Google Scholar]
- Woods, R.E.; Eddins, S.L.; Gonzalez, R.C. Digital Image Processing Using MATLAB; Institute of Geodesy and Photogrammetry, ETH: Zurich, Switzerland, 2009. [Google Scholar]
- Zaki, H.A.; Hoffmann, K.R.; Hausmann, E.; Scannapieco, F.A. Is radiologic assessment of alveolar crest height useful to monitor periodontal disease activity? Dent. Clin. 2015, 59, 859–872. [Google Scholar] [CrossRef]
- Shang, J.; Zheng, X.; Zhang, Y. A Teeth Identification Method Based on Fuzzy Recognition. In Proceedings of the 2010 Second International Conference on Intelligent Human-Machine Systems and Cybernetics, Nanjing, China, 26–28 August 2010; pp. 271–275. [Google Scholar]
- Al-Sherif, N.; Guo, G.; Ammar, H.H. A new approach to teeth segmentation. In Proceedings of the 2012 IEEE International Symposium on Multimedia, Irvine, CA, USA, 10–12 December 2012; pp. 145–148. [Google Scholar]
- Gan, Y.; Xia, Z.; Xiong, J.; Li, G.; Zhao, Q. Tooth and alveolar bone segmentation from dental computed tomography images. IEEE J. Biomed. Health Inf. 2018, 22, 196–204. [Google Scholar] [CrossRef]
- Winter, G.B. Ch. 7: Radiographic interpretation of the Ossistructure of the impacted mandibular third molar. In Principles of Exodontia as Applied to the Impacted Mandibular Third Molar: A Complete Treatise on the Operative Technic with Clinical Diagnoses and Radiographic Interpretations; American medical Book Company: St. Louis, MI, USA, 1926; p. 142. [Google Scholar]
- Zuiderveld, K. Chapter 5. Contrast limited adaptive histogram equalization. In Graphics Gems, 4th ed.; Heckbert, P.S., Ed.; Academic Press Professional Inc.: San Diego, CA, USA, 1994; pp. 474–485. [Google Scholar]
- Pizer, S.M.; Amburn, E.P.; Austin, J.D.; Cromartie, R.; Geselowitz, A.; Greer, T.; ter Haar Romeny, B.; Zimmerman, J.B.; Zuiderveld, K. Adaptive histogram equalization and its variations. Comput. Vis. Graph. Image Process. 1987, 39, 355–368. [Google Scholar] [CrossRef]
- The Jamovi Project. Jamovi. (Version 2.0) [Computer Software]. 2021. Available online: https://www.jamovi.org (accessed on 25 January 2020).
- Thiele, C. cutpointr: Determine and Evaluate Optimal Cutpoints in Binary Classification Tasks. [R package]. Available online: https://cran.r-project.org/package=cutpointr (accessed on 25 January 2020).
- Tran, T.-T.; Lee, P.-L.; Pham, V.-T.; Shyu, K.-K. MRI image segmentation based on fast global minimization of snake model. In Proceedings of the 2008 10th International Conference on Control, Automation, Robotics and Vision, Hanoi, Vietnam, 17–20 December 2008; pp. 1769–1772. [Google Scholar]
- Kass, M.; Witkin, A.; Terzopoulus, D. Snakes: Active Contour Models. Int. J. Comput. Vis. 1988, 1, 312–331. [Google Scholar] [CrossRef]
- Mundim, M.B.; Dias, D.R.; Costa, R.M.; Leles, C.R.; Azevedo-Marques, P.M.; Ribeiro-Rotta, R.F. Intraoral radiographs texture analysis for dental implant planning. Comput. Methods. Programs. Biomed. 2016, 136, 89–96. [Google Scholar] [CrossRef] [PubMed]
- Hausmann, E.; Allen, K.; Dunford, R.; Christersson, L. A reliable computerized method to determine the level of the radiographic alveolar crest. J. Periodontal Res. 1989, 24, 368–369. [Google Scholar] [CrossRef] [PubMed]
- Hausmann, E.; Allen, K.; Clerehugh, V. What alveolar crest level on a bite-wing radiograph represents bone loss? J. Periodontol. 1991, 62, 570–572. [Google Scholar] [CrossRef]
- Lin, P.; Huang, P.; Huang, P.; Hsu, H. Alveolar bone-loss area localization in periodontitis radiographs based on threshold segmentation with a hybrid feature fused of intensity and the H-value of fractional Brownian motion model. Comput. Methods Programs Biomed. 2015, 121, 117–126. [Google Scholar] [CrossRef]
- Khocht, A.; Janal, M.; Harasty, L.; Chang, K.-M. Comparison of direct digital and conventional intraoral radiographs in detecting alveolar bone loss. J. Am. Dent. Assoc. 2003, 134, 1468–1475. [Google Scholar] [CrossRef]
- Eickholz, P.; Kim, T.-S.; Benn, D.K.; Staehle, H.J. Validity of radiographic measurement of interproximal bone loss. Oral Surg. Oral Med. Oral Pathol. Oral Radiol. Endod. 1998, 85, 99–106. [Google Scholar] [CrossRef]
- Cha, J.-Y.; Yoon, H.-I.; Yeo, I.-S.; Huh, K.-H.; Han, J.-S. Peri-Implant Bone Loss Measurement Using a Region-Based Convolutional Neural Network on Dental Periapical Radiographs. J. Clin. Med. 2021, 10, 1009. [Google Scholar] [CrossRef]
- Sharma, H.; Dahiya, P.; Gupta, R.; Kumar, M.; Melwani, S.R.; Kachroo, L. Comparison of conventional and digital radiographic techniques for the assessment of alveolar bone in periodontal disease. Indian J. Dent. Sci. 2019, 11, 138. [Google Scholar] [CrossRef]
- Desai, S.R.; Shinde, H.H. Correlation of interdental and inter-radicular bone loss—Radiographic assessment. Bone 2008, 2, 35–37. Available online: https://www.semanticscholar.org/paper/bbba095076774bb4f7b477081655de818ea80fea (accessed on 10 December 2019).
- Talaiepour, A.R.; Panjnoush, M.; Soleimanishayeste, Y.; Abesi, F.; Sahba, S. A Survey on the Accuracy of Radiovisiography in the Assessment of Interproximal Intrabony Defects. Front. Dent. 2005, 2, 29–31. [Google Scholar]
| CT NP Area | CT P Area | GT NP Area | GT P Area | GT NP Angle | CT NP Angle | GT P Angle | CT P Angle | |
|---|---|---|---|---|---|---|---|---|
| N | 21 | 21 | 21 | 21 | 21 | 21 | 21 | 21 |
| Mean | 3.42 | 20.2 | 2.97 | 16.1 | 11.4 | 11.5 | 24.4 | 25.7 |
| Median | 3.26 | 18.4 | 2.84 | 14.8 | 9.95 | 10.0 | 17.8 | 21.0 |
| SD | 0.730 | 6.03 | 0.715 | 5.56 | 7.35 | 7.73 | 16.5 | 17.5 |
| Minimum | 2.11 | 12.7 | 2.19 | 8.94 | 2.26 | 1.59 | 6.88 | 4.40 |
| Maximum | 5.28 | 34.9 | 4.40 | 30.9 | 34.5 | 35.5 | 71.5 | 78.8 |
| Shapiro–Wilk W | 0.958 | 0.874 | 0.857 | 0.839 | 0.879 | 0.841 | 0.790 | 0.832 |
| Shapiro–Wilk p | 0.470 | 0.011 | 0.006 | 0.003 | 0.014 | 0.003 | < 0.001 | 0.002 |
| Cutpoint | Sensitivity (%) | Specificity (%) | AUC | Metric Score |
|---|---|---|---|---|
| 5.28 | 100% | 95.24% | 1.00 | 1.95 |
| 12.672 | 100% | 100% | 1.00 | 2.00 |
| 14.496 | 95.24% | 100% | 1.00 | 1.95 |
| Cutpoint | Sensitivity (%) | Specificity (%) | AUC | Metric Score |
|---|---|---|---|---|
| 12.2948 | 85.71% | 71.43% | 0.828 | 1.57 |
| 13.1061 | 80.95% | 76.19% | 0.828 | 1.57 |
| 13.627 | 80.95% | 80.95% | 0.828 | 1.57 |
| 15.1395 | 76.19% | 80.95% | 0.828 | 1.62 |
| 16.5873 | 71.43% | 85.71% | 0.828 | 1.57 |
| Scale: Area CT|Score: 12.672 | |||
| DECISION BASED ON MEASURE | |||
| Negative | Positive | ||
| CRITERION | Negative | 21 (TN) | 0 (FP) |
| Positive | 0 (FN) | 21 (TP) | |
| Scale: Angle CT|Score: 13.627 | |||
| DECISION BASED ON MEASURE | |||
| Negative | Positive | ||
| CRITERION | Negative | 17 (TN) | 4 (FP) |
| Positive | 4 (FN) | 17 (TP) | |
| Name | Study Design | Method | Results | Conclusions | |
|---|---|---|---|---|---|
| Cha, J-Y et al., 2021 [29] | 708 periapical dental radiographic images, 508—Training 100—validation, 100—test. | R-CNN vs. 2 dentists (1 Dental practitioner and another Oral and maxillofacial radiologist) The mean object Key-point similarity (OKS)—dentist vs. R-CNN. | Mean OKS Dentist—0.9012 Mean OKS Model—0.8885 Dentist vs. Model p-value 0.4095 | There is no difference between the dentist and the R-CNN in diagnosing and categorizing peri-implant bone loss. | |
| Krois et al., 2019 [8] | 350 panaromic dental radiographic Images, 1750 image segments; 350 for validation and 1400 for training | CNNs vs. 6 dental practitioners to detect periodontal bone loss (PBL) | Mean SD: 0.76 ± 0.06 t-test: p = 0.067. | Fleiss Kappa score of 0.52—moderate; No difference between dentist and the CNN P = 0.067. | |
| Sharma et al., 2019 [30] | 30 systemically healthy periodontitis patients with 100 interproximal sites. | Conventional (intraoral periapical [IOPA] radiographs) vs. digital radiographs (radiovisiography [RVG]) vs. intrasurgical (IS) | CEJ to the alveolar crest: Horizontal bone loss—4.38 ± 2.11, 4.26 ± 2.2, 4.67 ± 1.89 Vertical bone loss—8.23 ± 2.25, 8.25 ± 2.38, 7.79 ± 2.43 | Both radiographic methods (conventional and digital) showed statistically nonsignificant results in comparison to IS measurements. | |
| Lin et al., 2017 [6] | Automatic Alveolar bone loss measurement system and cementoenamel junction (CEJ) localization. | Local singularity and ABLifBM | 53% of the localization of the CEJ was within the 3-pixel deviation (appox. 0.15 mm) from GT and 90% have deviation within 9 pixels (approx. 0.44 mm) from GT | The method could automatically estimate the degree of alveolar bone loss and localize the cementoenamel junction. | |
| Jae-hong et al., 2018 [8] | Develop the computer assisted detection system based on deep convolution neural network (CNN) Algorithm | deep CNN architecture and self-trained network. | Accuracy: 81.0%—Premolars Accuracy: 76.7%—Molars | The algorithm used in this study gave the diagnosis and prognosis of the periodontitis tooth images. | |
| Lin et al., 2015 [26] | 31 periodontitis IOPA radiographic images | ABLIfBm vs. threshold segmentation. | True positive 92.5% False positive: 14% | ABLIfBm outperforms the threshold segmentation method, and it could localize the alveolar bone loss effectively. | |
| Moutinho et al., 2012 [5] | 60 teeth from 47 patients | Conventional vs. digital using DIA tool: measurement of the defect angle (BDA) | Interexaminer reliability: Intraclass Correlation Coefficient > 0.97 Intermethod reliability > 0.96. | There was no difference between the conventional method and the DIA tool for the radiographic measurement of intrabony defects. | |
| Popova et al., 2008 [31] | 49 patients with vertical and horizontal bitewing | Radiographic measurement and using the Williams periodontal probe | Interdental bone loss: 4.18 to 5.54 mm is associated with interradicular bone loss with values of 0.45 to 1.33 mm. | Interradicular bone loss was associated with the progression of bone destruction in multirooted teeth. | |
| Talaiepour et al., 2005 [32] | 32 radiographs of 56 periodontally diseased teeth | RVG (Radiovisiography) and intrasurgical method | RVG: CEJ to BD: 6.803±3.589 mm Intrasurgically (IS): CEJ to BD: 6.492 ± 3.492 mm (p < 0.000). | Radiographic measurement overestimated the bone loss. | |
| Khocht, et al., 2003 [27] | 25 Subjects 857 PA radiographs 315 Bitewing | Bone loss measurement in digital radiographs vs. conventional radiographs | Alveolar bone level differed in intraoral direct digital compared to conventional. (p < 0.02). | The digital radiographs showed a higher number of sites with bone loss than the conventional radiographs. | |
| Eickholz and Hausmann 2000 [2] | 34 interproximal bone loss in IOPAs | Linear measurement of intrabony defect vs. surgical measurement | Surgical: CEJ-BD—9.15 ± 2.09, AC-BD—5.15 ± 1.96, Radiographic Measurement: CEJ to BD—7.74 ± 2.11 AC-BD—3.97 ± 13.39 mm | The assessment of the bone loss was more accurate in surgical measurement than the radiographic measurement. | |
| Eickholz et al., 1998 [28] | 62 standardized radiographs taken presurgically of 35 patients suffering from advanced periodontal disease. | LMSRT (Computer assisted analysis system) vs. loupe | CEJ-AC: Loupe:0.86 ± 1.84 mm [p < 0.001] LMSRT 0.58 ±1.86 mm [p < 0.005] CEJ-BD: loupe: 1.22 ± 2.33 mm [p < 0.001] LMSRT: 0.80 ± 2.09 mm [p < 0.001] | LMSRT was better than loupes along with grid. Surgical method was the best. | |
| Hausmann et al., 1991 [25] | 134 sites in Bitewing radiographs from 68 adolescents 13–14 years of age. 18 months apart were included in the study | Mean radiographic distance from CEJ-to-crest distance (mm) | Distance: Baseline: 1.11 ± 0.37 mm After 18 Months 1.19 ± 0.34 mm | No crestal bone loss is consistent with a range of radiographic CEJ-to-crest distance between 0.4–1.9 mm. | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maithri, M.; Ballal, D.G.; Kumar, S.; Raghavendra, U.; Gudigar, A.; Chan, W.Y.; Macherla, S.; Vineetha, R.; Gopalkrishna, P.; Ciaccio, E.J.; et al. Development of a Computational Tool for the Estimation of Alveolar Bone Loss in Oral Radiographic Images. Computation 2022, 10, 8. https://doi.org/10.3390/computation10010008
Maithri M, Ballal DG, Kumar S, Raghavendra U, Gudigar A, Chan WY, Macherla S, Vineetha R, Gopalkrishna P, Ciaccio EJ, et al. Development of a Computational Tool for the Estimation of Alveolar Bone Loss in Oral Radiographic Images. Computation. 2022; 10(1):8. https://doi.org/10.3390/computation10010008
Chicago/Turabian StyleMaithri, M., Dhanush G. Ballal, Santhosh Kumar, U. Raghavendra, Anjan Gudigar, Wai Yee Chan, Shravya Macherla, Ravindranath Vineetha, Pratibha Gopalkrishna, Edward J. Ciaccio, and et al. 2022. "Development of a Computational Tool for the Estimation of Alveolar Bone Loss in Oral Radiographic Images" Computation 10, no. 1: 8. https://doi.org/10.3390/computation10010008
APA StyleMaithri, M., Ballal, D. G., Kumar, S., Raghavendra, U., Gudigar, A., Chan, W. Y., Macherla, S., Vineetha, R., Gopalkrishna, P., Ciaccio, E. J., & Acharya, U. R. (2022). Development of a Computational Tool for the Estimation of Alveolar Bone Loss in Oral Radiographic Images. Computation, 10(1), 8. https://doi.org/10.3390/computation10010008








