Abstract
Receiving a recommendation for a certain item or a place to visit is now a common experience. However, the issue of trustworthiness regarding the recommended items/places remains one of the main concerns. In this paper, we present an implementation of the Naive Bayes classifier, one of the most powerful classes of Machine Learning and Artificial Intelligence algorithms in existence, to improve the accuracy of the recommendation and raise the trustworthiness confidence of the users and items within a network. Our approach is proven as a feasible one, since it reached the prediction accuracy of 89%, with a confidence of approximately 0.89, when applied to an online dataset of a social network. Naive Bayes algorithms, in general, are widely used on recommender systems because they are fast and easy to implement. However, the requirement for predictors to be independent remains a challenge due to the fact that in real-life scenarios, the predictors are usually dependent. As such, in our approach we used a larger training dataset; hence, the response vector has a higher selection quantity, thus empowering a higher determining accuracy.
1. Introduction
The information used for the recommendation process can be derived from available content coming from articles and users, or it can be derived from explicit evaluations when users are asked to rate articles. Based on how the information is used, recommender systems are considered to be content-based, collaborative filtering, or hybrid (where both are used) recommender systems [1].
Social network analysis and ‘social mining’ can be very useful in the context where recommender systems can inherit adequate and useful information from social networks and vice versa, where network formation and evolution can be affected by recommendations.
There are cases where involvement of the neighborhood among items are important, as in cases where two items might be considered as neighbors, where there is more than one user that possibly rated these items somehow similarly [2], and in these cases, we have a matrix which contains a rating of items, and the ratings are populated either by the similarity between items or similarity of the users that are involved in the review process. In such cases, the most popular and used technique is Pearson correlation or cosine-based vector similarity calculations, as explained in [3].
Each recommender system intends to achieve an acceptable rate of recommendations that are accurate based on the predictions that are made, and the results of recommendation to be as closer as they can to what the predicted model estimated. Moreover, one RS should be able to keep the list of items that are seen as of particular interest to a certain user, and the RS must be always updated with eventual new items; hence, a user does not miss any new product/feature that he/she might be interested in. Following the evolvement of RS, it is obvious that the majority of recommendations and their rating approval are based on the friends/peers’ recommendations and thoughts, since people have a greater tendency to consider the opinions of the people they know from their social life, hence making a good relation and tie between RS and social network analysis. However, every RS should always take care of the people they involve in the recommendation process, due to a high number of malicious users/tools that seek to orient the recommendation toward a biased item.
In this rationale, in this paper, we have utilized Social Network Analysis (SNA) metrics, combined with trustworthiness metrics, to enhance the process of recommendations.
In our approach, we set the process in three phases, as depicted in Figure 1 below:
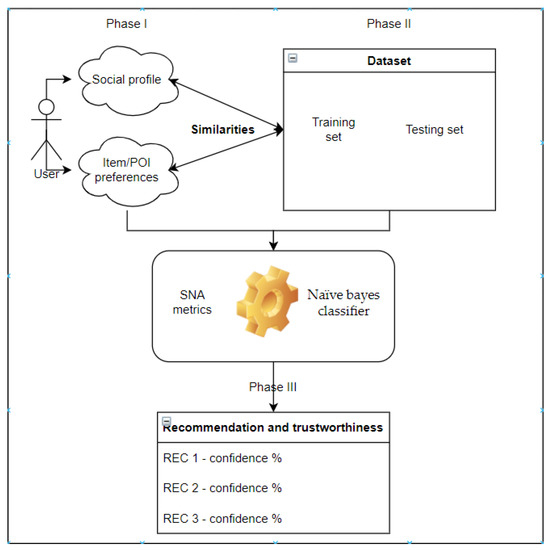
Figure 1.
Our Recommender System overview, with inclusion of SNA and trustworthiness metrics on evaluation process.
- In the first phase, we consider the social profile of a user, which includes social and personal information, such as gender, location, age, hobbies. Then, we considered the touristic preferences of a user, such as a category and a subcategory of a point of interest that a user prefers to visit.
- In the second phase, we used a dataset from [4] to distinguish certain points of interest that users selected and provided preferences for. From this dataset, we created a training and testing set to be further used in the next phase.
- In the third phase, we used the training set, to test the evaluation, and at this point, we used the Naive Bayes classifier as a classification and prediction model. Moreover, from this point, not only do we get the recommendation for a certain point of interest based on categories and subcategories users used at training set, where we used vector of dependent features, but we also calculated trustworthiness by considering the confidence of recommendations; hence, besides making the recommendation of a certain point of interest, we assured the user that the recommendation is coming from a trusted source.
2. Related Work
The main intention of each recommender system (RS) is to provide the most accurate and trusted recommendation to its users. For this purpose, there are common classification techniques among RS that are used today, as elaborated in [1]:
- Content-based recommendations: where the recommendation is based on users’ previous content evaluation.
- Collaborative recommendations: where recommendations are based exclusively on user and friend reviews, and among this class, there are two subgroups: memory- and model-based collaborative filtering.
- Hybrid approaches: combines the benefits of other two popular approaches (collaborative and content-based recommendations.
2.1. Similarity of External Information
In hybrid approaches, in cases where external social information of users, such as profession, location, nationality, age, etc., are taken into consideration, there were better recommendation results and satisfaction [5], even though exposing this personal information to an RS might expose one user to a privacy breach [6,7].
Among literature, another significant classification of recommender systems are content-based recommendations [8], where the algorithm calculates and recommends respectively, only based on the previous items that a user of a system previously evaluated. Among this classification technique, the term frequency—inverse document frequency (TF-IDF) measuring method—is mostly used [9], which calculated the frequency of the term t within a document d, among all documents that are used in experiment |D|, as follows:
Furthermore, in the literature there is a classification of combination methods, as follows:
- Combination of predictions from two RS methods—collaborative and content-based [10,11];
- the models of collaboration, where features of the content are taken into consideration [12,13,14];
- the addition applied to content-based techniques, where features of collaboration are added [15];
- the implementation of a unique model that not only combines, but also integrates into one solution the common features of collaborative recommendations and content-based recommendations [16,17,18], even though such an approach cannot be used in every domain of RS [19,20].
The process of labeling the systems that use collaborative filtering started since the arrival of Web 2.0 [21], and the extension is made toward applications and scenarios that are e-commerce-related [22,23]. Another enhancement of RS is the involvement of reviews and opinions of every user and respondent [24] by including here even negative reviews and thoughts [25,26], since even in cases where reviews and recommendations are with negative marks, it is important to find the correlation among items proposed and users involved [27]. Such approaches are used in many research works, such as [28,29].
In research groups, recommendations made by a friend or people we know are taken very much into consideration [30], and here social relations and relations among people from real life have significant importance [31,32]. All this leads to the empowerment of the role of social relations [33] and friendship [34] concerning recommender systems.
For recommendations not to be biased, hybrid methods are used in RS to overcome these issues [35,36], and therefore it also solves one of the main problems such as the cold start problem, thus diversifying the recommendation [37].
Among usage of linear mathematic calculations for hybrid methods defined in [10], Markov Monte Carlo methods [38] are being mostly applied today. Complex methods of forecasting combination are also in use to reduce errors with recommendations overall [39].
2.2. Trustworthiness
Trust as a concept is linked in social life and social sciences, but it also gained power in all fields of life and technology as well, by including Naïve bayes and probability techniques [40,41] in RS, and trust and semantic [42,43] as notations in RS. Even dealing with the economy and trades, trust is considered as the main factor to bring people together on trade [44], thus in many definitions trust is referred to as a belief [45].
In [46], trust is considered as a probability that is subjective and is dependent on certain actions that a person takes, while in [47], trustworthiness is considered and defined as subjective expectation, and meanwhile different cognitive models were studied [48], while in [49] is argued that trust/belief is very much related and dependent on others’ behavior, and the level of trust varies from the situation as well [50].
In [51], trust/reliability/belief is studied from the computer science perspective, where it is stated that “trust is a measurable level of risk through which one agent X assesses the likelihood another agent Y will successfully perform a particular action before X monitors such action and in the context in which it affects own actions.”
Besides belief and trust, disbelief and untrust [52,53] are also considered in other publications, and the inclusion of negative feedback is worth consideration in RS [54,55].
Furthermore, in [56] main computational characteristic of trust is summarized, such as asymmetry, dissemination—trusting the “friend-of-a-friend”, composition—when there is a need to consult the information that we receive from many sources, and nontransitivity, as argued in [57].
2.3. Trustworthiness Metrics
The process of trust calculation proved to be very difficult, and hence several approaches are considered today, based on the models and domains to which we must apply such calculations. In [58], trust is calculated based on its features using the ‘Fuzzy’ logic mathematical model. In another approach [59], the authors proposed a tool that can be used to change the belief accordingly (on the go) as the user reads the content, while the usage of ‘historical data’ of networks and its peer relation was argued as a feasible approach in [60]. Friend-of-a-Friend (FOAF) ontology and the relationship trust are used as an approach in [61], while in [62], reliability metrics are applied separately between local groups and bigger social groups.
Some of the main metrics used today are ‘Page Rank’ [63], which is a well-known metric to calculate the importance of a website, and ‘Eigen Trust’ [64], which is accepted as a global reliability metric for calculation the inter-personal relations among user in peer-to-peer networks.
2.4. ‘Trust-Aware’ Recommender Systems
Being in a situation when one is uncertain about its choices, it is normal to seek opinions and reviews from friends and people around you, and hence this is the overall intention of social networks itself.
In this relation, personal opinions are considered more trustworthy than different advertisements that can be made for a certain item, as argued in [65]. In [66], another approach is analyzed, where the information gathered from websites is no longer relevant, compared to information provided by peers and friends.
‘Filmtrust’, an RS proposed in [67], seeks to get direct trust values for certain movies by reviewers, while in [68], the author tended to calculate trustworthiness based on network trust.
‘Trust-aware’ recommendations were enhanced with ontologies to create indexed content for semantic websites [69]. In another approach, the ‘shuffled frog leaping’ algorithm was applied to group users of different social contexts [70]. As an overall outcome, the recommendations coming from RS that include trust in the evaluation process proved to be more accurate and raised the satisfaction factor of its users [71,72].
3. Bayesian Approach in Our Model
As elaborated in [73], in cases where we want to achieve recommendations that target the personalized recommendations, usually we have to consider groups with two factors. In our case, let us consider the user-object pair, where we depicted user classification and objects in the K user and K object classes, respectively. K user and K object values are parameters in the algorithm similar to K which was a Singular Value Decomposition (SVD) parameter. Assume that there is a simple Bayesian network—the simplest assumption is that riα depends only on the user class and the object class . Thus, the probability can then be written as:
It is obvious from this equation that in our case the Bayesian network corresponds to the simplest dependency structure linking ratings to user classes and objects.
Naive Bayes
In this work, we opted for a prediction model, that can give results based on the data that is observed. In this context, Naive Bayes (NB) fits our approach, mainly due to the following arguments:
- It is independent—that means that we can consider all properties as independent given the target Y.
- It is equal—an event where all attributes are considered as being with the same importance.
In this rationale, now we need to calculate the conditional probability, which is known as the Naive Bayes algorithm since it uses the Bayesian theorem, and thus calculates the probability of an event, based on the incidence of values in historical data. The following formula, shows the definition of the Bayesian Theorem:
where:
P(A|B) = (P(B|A) P(A))/(P(B))
A—represents the dependent event,
B—represents the preceding event, thus predictive attribute
P(A)—represents the probability of the event before it is observed.
P(A|B)—represents the probability of the event after the evidence is observed
While, “Naive” Assumption is defined as the evidence that is divided into pieces, that are meant and defined to be independent
where A1 and A2 are independent occurrences.
P(A) = (P(A1|B) P(A2|B)…P(An|B))/(P(B))
4. Evaluation and Preliminary Results
4.1. Naïve Bayes Classifier
Naive Bayes classifiers are a collection of classification algorithms based on the Bayesian theorem. It is defined as a family of algorithms where everyone shares a common principle, meaning each pair of characteristics that are classified is independent of each other.
To begin, let us look at a data set. We considered an imaginary and random data set describing one prediction and three conditional states, to make or not the certain recommendation. Given the prediction and conditions each pair classifies the conditions as suitable to make a recommendation (“Yes”) or unsuitable to make a recommendation (“No”). The following Table 1 depicts our data.

Table 1.
Our training dataset.
The data set is divided into two parts namely the properties matrix and the response vector.
- The properties matrix consists of the value of the dependent properties. In the above data set, the features are ‘Prediction’, ‘Condition#1′, ‘Condition#2′, and ‘Condition#3′.
- The response vector contains the value of the prediction or results of the property matrix. In the data set above, the class variable name is ‘Recommendation’.
At this point, we should consider the pairs of property matrices as totally independent. For example, condition#1 being ‘X’ has nothing to do with condition#2, or the ‘A’ in Prediction appearance does not affect condition#3.
For the data to be equally treated, each attribute has the same weight or relevance. For example, just knowing condition#1 and condition#2, one cannot predict the accuracy of the result. None of the attributes is unnecessary and we assume that they contribute equally to the result.
Now, with our data set we can apply the Bayesian theorem as follows:
where, y is a class variable and V is a vector of dependent properties (of size n) where:
P(X) = (P(X|y) P(y))/(P(X))
V = (v1, v2, v3, …vn)
To clarify, an example of a feature vector and the corresponding class variable could be:
V = (A, X, H, N) and y = No
So, P(y|X) means, the probability of “Do not recommend” given that the conditions are “Prediction A”, “condition#1 is X”, “ condition#2 is H” and “ condition#3 is S”.
4.2. Naïve Assumption
Now is the time to give a naive assumption to the Bayesian theorem which is independent among other properties. Now we divide the evidence into independent parts.
Since (v1,v2,v3,…,vn) are independent, now if either of the two events A and B are independent then,
P(A,B) = P(A) P(B)
Therefore, we reached the result:
Which is summarized as:
Now, while the denominator remains constant for a given input, we can remove that from the equation:
At his point, we have to define a classification model. To achieve this, we have to consider the maximum probability, which is calculated by having inputs for all values of Y:
And as a final step, we calculate P(y) and P (vi|y).
Where, P(y) is the class probability and P(vi|y) is the conditional probability.
4.3. Preliminary Results with the Initial Random Dataset
Let us try to manually apply the above formula to our dataset. For this, we need to make some calculations in our data community.
We find P (vi|yj) for each vi in V and yj in y. The following Figure 2 depict the calculation process.
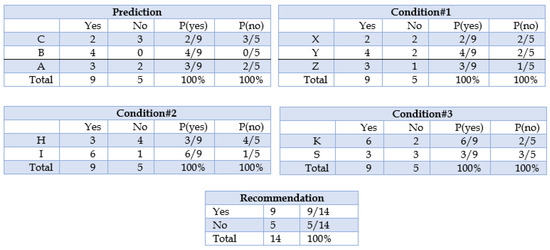
Figure 2.
Probabilities of dependent feature vector with size 4.
So, from the data in the Figure 2 above, we calculated P () for each in V and in y manually in Figure 2. For example, the probability of getting a recommendation since the condition#1 is Z, i.e., P(condition#1 = Z|recommendation = Yes) = 3/9.
Also, we need to find the probabilities of class (P(y)) which is calculated in Figure 2. For example, P(recommendation = Yes) = 9/14.
At this stage, the precalculations are completed, and the classifier is ready.
Now, we consider a new set of features (that we call today):
So, the probability of getting a recommendation is given by: today = (C, X, I, S)
and the probability of not playing golf is given by
Since P(today) is common to both probabilities, we can ignore P(today) and find the proportional probability as:
And,
Now, since
P (Yes|today) + P (No|today) = 1
These numbers can be converted to a probability by making the sum equal to 1 (normalization):
And,
Since,
So, the prediction that we are getting the recommendation is ‘Yes’.
4.4. Evaluation Results Based on Social Network Data
Considering the dataset that we used from [74], as a total there were 11,326 unique users, 2.2 million check-ins, 15 million venues, and more than 47 thousand social relations, while the check-ins are accessed through API in Foursquare application [75].
To adapt to our approach and model, we took into consideration a total of 724 users, who had more than one and less than 10 check-ins for distinct touristic points of interest.
In the next phase, we organized the data into two sets, where our training set consisted of 601 user inputs, while our testing set have 123 users, while the response vector contains exactly m = 75 values (distinct points of interest) of the class variable.
The following section will depict the calculation process, where we set a new feature, which we will call “Meal”:
meal = (Male, “Collierville, TN”, Food, “American Restaurant”)
We see that the vector of dependent features has the size n = 4.
By agreement let us call the partial probabilities, the probabilities of the feature vector dependent on the variable of the respective class, and denote them by:
respectively for k = 1, and let the random selection by the value of the variable of class “Wrigley Field”. So, the probability of eating at “Wrigley Field” is given by:
After the first iteration, let us go over the next 73 iterations which continue similarly. For k = m = 75.
Let the remaining selection be the class variable with value of the “Park Tavern”. So, the probability of eating in “Park Tavern” is given by:
Assuming that the sum of the probabilities of the response vector over meals is:
In the next step we normalize, and for:
Since,
So, the recommendation for the point of interest is “Park Tavern”.
After applying the algorithm on the training set, we reached an accuracy of recommendations of 89%, with a confidence of approximately 0.8943, which was our intention of this study, because except for recommendation, we wanted to raise the level of confidence and trustworthiness.
An expert of the results is given in the following Figure 3, where the focus should be on the last 2 columns. The POI—point of interest column shows if there is a certain POI recommendation for a user (identified with ID in the Figure 3), and the last column Confidence, empowers the potential recommendation by giving the confidence and trust that a user has for a recommendation made to him/her.
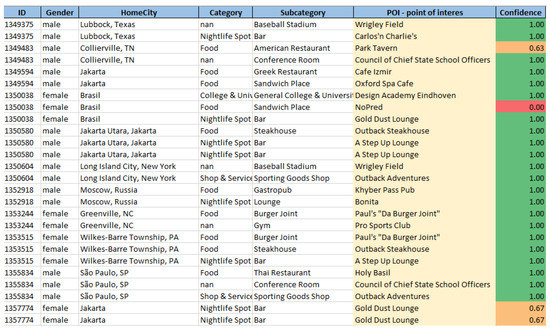
Figure 3.
An excerpt of evaluation results regarding recommendation and confidence.
The calculations for every dataset record are realized using Python—programming language, and an overview of the main parts of the algorithm where confidence and prediction are calculated is depicted in the Appendix A section.
The process starts with the calculation of similarities between training and testing set users, where initially the social profiles of tourists and reviewers are compared for similarities, and then the subcategories and categories of POI are compared. Therefore, whenever there is a match on these attributes (gender, home city, category, subcategory) the algorithm will recommend the POI to the new tourist. The process of calculating the probabilities for all potential POIs, as depicted in detail in Section 4.3, is realized using the findPropProb function that is defined and depicted in Appendix A, to further continue with the process of confidence calculation by using function predictAccurancy, that is depicted in the second part of Appendix A, where confidentiality is calculated as full (or 1), in cases where from a potential set of POIs, for example, 4 or 5 POI-s, the tourist is most satisfied with the recommended POI which is in a top list of a reviewer.
5. Conclusions
There are many studies that utilized Naive Bayes and probabilistic algorithms on a recommender system such as [9,40,41], as well as the inclusion of trust as a notion and semantic into recommender systems [42,43], including other studies that we mentioned in related work, of which the majority treated the approaches individually. In our work, we presented an approach where we correlate the usage of the Naive Bayes classifier and trustworthiness into social networks. By experiments conducted and evaluation results that we have, using our datasets, we agree that the Naive Bayes algorithm is very important in use for classifying data properties. Moreover, it is shown that the implementation of the Naive Bayes classifier is simple because it assumes that it only has the class node connected by a link to all the nodes of the other attributes. The preliminary results show our approach as a feasible one since it has reached the accuracy of recommendation of 89%, with a confidence of approximately 0.89.
We can conclude that the usage of a Bayesian classifier in a recommender system is known to greatly reduce errors and can involve a large set of training data. The Bayesian classifiers also need empirical mitigation, and the mitigation technique depends very much on each case. Bayesian classifiers are powerful, but lack of data or lack of access to proper data may be the first cause of incorrect implementation of classifiers.
Author Contributions
Conceptualization, K.R., L.A. and B.S.; methodology, K.R.; software, K.R.; validation, K.R., B.S. and L.A.; formal analysis, K.R.; investigation, K.R.; resources, K.R.; data curation, K.R.; writing—original draft preparation, K.R.; writing—review and editing, K.R., B.S.; supervision, B.S.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The following code is used to calculate calculating the probabilities for all potential POI-s with function findPropProb, and the process of confidence is calculated by using function predictAccurancy.

References
- Adomavicius, G.; Tuzhilin, A. Toward the Next Generation of Recommender Systems: A Survey of the State-of-the-Art and Possible Extensions; IEEE Transactions on Knowledge and Data Engineering: Los Angeles, CA, USA, 2005; Volume 17, pp. 734–749. [Google Scholar]
- Hu, Y.; Koren, Y.; Volinsky, C. Collaborative Filtering for Implicit Feedback Datasets. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 263–272. [Google Scholar]
- Koren, Y.; Sill, J. Ordrec: An ordinal model for predicting personalized item rating distributions. In Proceedings of the Fifth ACM Conference on Recommender Systems, Chicago, IL, USA, 23–27 October 2011; pp. 117–124. [Google Scholar]
- Gao, H.; Tang, J.; Hu, X.; Liu, H. Exploring temporal effects for location recommendation on location-based social networks. In Proceedings of the 7th ACM Conference on Recommender Systems, Hong Kong, 12–16 October 2013; pp. 93–100. [Google Scholar]
- Tso, K.H.; Schmidt-Thieme, L. Empirical Analysis of Attribute-Aware Recommendation Algorithms with Variable Synthetic Data, Data Science and Classification; Springer: Berlin/Heidelberg, Germany, 2006; pp. 271–278. [Google Scholar]
- Narayanan, A.; Shmatikov, V. Robust de-Anonymization of Large Sparse Datasets. IEEE Symposium on Security and Privacy. 2008, pp. 111–125. Available online: https://www.ieee-security.org/TC/SP2008/oakland08.html (accessed on 15 August 2021).
- Kobsa, A. Privacy-enhanced web personalization. In the Adaptive Web: Methods and Strategies of Web Personalization; Springer: Berlin/Heidelberg, Germany, 2007; pp. 628–670. [Google Scholar]
- Pazzani, M.J.; Billsus, D. Content-Based Recommendation Systems. In The Adaptive Web. Lecture Notes in Computer Science; Brusilovsky, P., Kobsa, A., Nejdl, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4321. [Google Scholar] [CrossRef] [Green Version]
- Salton, G.; McGill, M.J. Introduction to Modern Information Retrieval; McGraw-Hill: Auckland, New Zealand, 1983. [Google Scholar]
- Su, X.; Khoshgoftaar, T.M. A survey of collaborative filtering techniques. Adv. Artif. Intell. 2009, 2009, 421–425. [Google Scholar] [CrossRef]
- Claypool, M.; Gokhale, A.; Miranda, T.; Murnikov, P.; Netes, D.; Sartin, M. Combining content-based and collaborative filters in an online newspaper. In Proceedings of the ACM SIGIR ‘99 Workshop on Recommender Systems: Algorithms and Evaluation, Berkeley, CA, USA, 15–19 August 1999. [Google Scholar]
- Pazzani, M. A Framework for Collaborative, Content-Based, and Demographic Filtering. Artif. Intell. Rev. 1999, 13, 393–408. [Google Scholar] [CrossRef]
- Balabanović, M.; Shoham, Y. Fab: Content-based, collaborative recommendation. Commun. ACM 1997, 40, 66–72. [Google Scholar] [CrossRef]
- Melville, P.; Mooney, R.J.; Nagarajan, R. Content-boosted collaborative filtering for improved recommendations. In Proceedings of the 2002 National Conference on Artificial Intelligence, Edmonton, AB, Canada, 28 July–1 August 2002; pp. 187–192. [Google Scholar]
- Salter, J.; Antonopoulos, N. Cinemascreen Recommender Agent: Combining Collaborative nd Content-Based Filtering. IEEE Intell. Syst. 2006, 21, 35–41. [Google Scholar] [CrossRef]
- Soboroff, I.; Nicholas, C. Combining Content and Collaboration in Text Filtering. In Proceedings of the IJCAI Workshop on Machine Learning in Information Filtering, Stockholm, Sweden, 1 August 1999; pp. 86–91. [Google Scholar]
- Basu, C.; Hirsh, H.; Cohen, W. Recommendation as Classification: Using Social and Content-Based Information in Recommendation. In Proceedings of the 1998 National Conference on Artificial Intelligence, Madison, WI, USA, 26–30 July 1998; pp. 714–720. [Google Scholar]
- Popescul, A.; Ungar, L.H.; Pennock, D.M.; Lawrence, S. Probabilistic Models for Unified Collaborative and Content-Based Recommendation in Sparse-Data Environments. In Proceedings of the 17th Conference in Uncertainty in Artificial Intelligence, San Francisco, CA, USA, 2–5 August 2001; pp. 437–444. [Google Scholar]
- Schein, A.I.; Popescul, A.; Ungar, L.H.; Pennock, D.M. Methods and Metrics for Cold-Start Recommendations. In Proceedings of the 25th annual international ACM SIGIR conference on Research and development in information retrieval, Tampere, Finland, 11–15 August 2002; pp. 253–260. [Google Scholar]
- Yu, K.; Schwaighofer, A.; Tresp, V.; Ma, W.Y.; Zhang, H. Collaborative Ensemble Learning: Combining Collaborative and Content-Based Information Filtering. In Proceedings of the 19th Conference on Uncertainty in Artificial Intelligence, Acapulco, Mexico, 7–10 August 2003; pp. 616–623. [Google Scholar]
- Jin, X.; Zhou, Y.; Mobasher, B. A maximum entropy web recommendation system: Combining collaborative and content features. In Proceedings of the Eleventh ACM SIGKDD International Conference on Knowledge Discovery in Data Mining, Chicago, IL, USA, 21–24 August 2005; pp. 612–617. [Google Scholar]
- Zhang, Z.K.; Liu, C. A hypergraph model of social tagging networks. J. Stat. Mech. Theory Exp. 2010, 2010, P10005. [Google Scholar] [CrossRef] [Green Version]
- Linden, G.; Smith, B.; York, J. Amazon.com recommendations: Item-to-item collaborative filtering. IEEE Internet Comput. 2003, 7, 76–80. [Google Scholar] [CrossRef] [Green Version]
- Sarwar, B.; Karypis, G.; Konstan, J.; Riedl, J. Analysis of Recommendation Algorithms for E-Commerce. In Proceedings of the 2nd ACM Conference on Electronic Commerce, Minneapolis, MN, USA, 17–20 October 2000; pp. 158–167. [Google Scholar]
- Zeng, W.; Shang, M.S.; Zhang, Q.M.; Lü, L.; Zhou, T. Can Dissimilar Users Contribute to Accuracy and Diversity of Personalized Recommendation? Int. J. Mod. Phys. C 2010, 21, 1217–1227. [Google Scholar] [CrossRef]
- Zeng, W.; Zhu, Y.X.; Lü, L.; Zhou, T. Negative ratings play a positive role in information filtering. Physica A 2011, 390, 4486–4493. [Google Scholar] [CrossRef] [Green Version]
- Kong, J.S.; Teague, K.; Kessler, J. Just Count the Love-Hate Squares: A Rating Network-Based Method for Recommender System. In Proceedings of the KDD Cup Workshop at SIGKDD’11, The 13th ACM International Conference on Knowledge Discovery and Data Mining, San Jose, CA, USA, 12–15 August 2007. [Google Scholar]
- Shang, M.S.; Lü, L.; Zeng, W.; Zhang, Y.C.; Zhou, T. Relevance is more significant than correlation: Information filtering on sparse data. EPL 2009, 88, 68008. [Google Scholar] [CrossRef] [Green Version]
- Almazro, D.; Shahatah, G.; Albdulkarim, L.; Kherees, M.; Martinez, R.; Nzoukou, W. A survey paper on recommender systems. arXiv 2010, arXiv:1006.5278. [Google Scholar]
- Lü, L.; Zhou, T. Link Prediction in Complex Networks: A Survey. Physica A 2011, 390, 1150–1170. [Google Scholar] [CrossRef] [Green Version]
- Sinha, R.R.; Swearingen, K. Comparing recommendations made by online systems and friends. In Proceedings of the DELOS-NSF Workshop on Personalization and Recommender Systems in Digital Libraries, Dublin, Ireland, 18–20 June 2001. [Google Scholar]
- Salganik, M.J.; Dodds, P.S.; Watts, D.J. Experimental Study of Inequality and Unpredictability in an Artificial Cultural Market. Science 2006, 311, 854–856. [Google Scholar] [CrossRef] [Green Version]
- Bonhard, P.; Sasse, M.A. Knowing me, knowing you–Using profiles and social networking to improve recommender systems. BT Technol. J. 2006, 24, 84–98. [Google Scholar] [CrossRef]
- Hwang, S.Y.; Wei, C.P.; Liao, Y.F. Coauthorship networks and academic literature recommendation. Electron. Commer. Res. Appl. 2010, 9, 323–334. [Google Scholar] [CrossRef]
- Symeonidis, P.; Tiakas, E.; Manolopoulos, Y. Product Recommendation and Rating Prediction based on Multi-modal Social Networks. In Proceedings of the 5th ACM Conference on Recommender Systems, Chicago, IL, USA, 23–27 October 2011; pp. 61–68. [Google Scholar]
- Burke, R. Hybrid Recommender Systems: Survey and Experiments. User Model. User Modeling User-Adapt. Interact. 2002, 12, 331–370. [Google Scholar] [CrossRef]
- Burke, R. Hybrid web recommender systems. In The Adaptive Web: Methods and Strategies of Web Personalization; Brusilovsky, P., Kobsa, A., Nejdl, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 377–408. [Google Scholar]
- Zhou, T.; Kuscsik, Z.; Liu, J.G.; Medo, M.; Wakeling, J.R.; Zhang, Y.C. Solving the apparent diversity-accuracy dilemma of recommender systems. Proc. Natl. Acad. Sci. USA 2010, 107, 4511–4515. [Google Scholar] [CrossRef] [Green Version]
- Carlin, B.P. Bayes and Empirical Bayes Methods for Data Analysis; Chapman & Hall: London, UK, 1996. [Google Scholar]
- Jahrer, M.; Töscher, A.; Legenstein, R. Combining Predictions for Accurate Recommender Systems. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–28 July 2010; pp. 693–702. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Witten, I.H.; Frank, E. Data Mining: Practical Machine Learning Tools and Techniques, 3rd ed.; Morgan Kaufmann/Elsevier: Burlington, ON, Canada, 2011. [Google Scholar]
- Joly, A.; Maret, P.; Daigremont, J. Contextual recommendation of social updates, a tag-based framework. In Proceedings of the 6th International Conference, AMT 2010, Toronto, ON, Canada, 28–30 August 2010; Springer: Berlin/Heidelberg, Germany, 2010. Lecture Notes in Computer Science; Volume 6335. pp. 436–447. [Google Scholar]
- Stan, J.; Do, V.H.; Maret, P. Semantic user interaction profiles for better people recommendation. In Proceedings of the International Conference on Advances in Social Networks Analysis and Mining, ASONAM 2011, Kaohsiung, Taiwan, 25–27 July 2011; pp. 434–437. [Google Scholar]
- Harford, T. The Economics of Trust. Available online: https://www.forbes.com/2006/09/22/trust-economy-markets-tech_cx_th_06trust_0925harford.html?sh=161f9ebd2e13 (accessed on 15 August 2021).
- Adali, S. Modeling Trust Context in Networks, 1st ed.; Springer: New York, NY, USA, 2013; ISBN 978-1-4614-7030-4. [Google Scholar]
- Gambetta, D. Can We Trust Trust? In Trust: Making and Breaking Cooperative Relations; Electronic Edition; Gambetta, D., Ed.; Department of Sociology, University of Oxford: Oxford, UK, 2000; Chapter 13; pp. 213–237. [Google Scholar]
- Mui, L.; Mohtashemi, M.; Halberstadt, A. A Computational Model of Trust and Reputation for E-Businesses. In Proceedings of the 35th Annual Hawaii International Conference on System Sciences, Big Island, HI, USA, 7–10 January 2002. [Google Scholar]
- Castelfranchi, C.; Tan, Y.H. Trust and Deception in Virtual Societies; No. Social Trust: A Cognitive Approach; Kluwer: Norwell, MA, USA, 2001; pp. 55–90. [Google Scholar]
- McKnight, D.H.; Chervany, N.L. Trust and Distrust Definitions: One Bite at a Time. In Trust in Cyber-Societies. Lecture Notes in Computer Science; Falcone, R., Singh, M., Tan, Y.H., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; Volume 2246. [Google Scholar] [CrossRef]
- Jøsang, A.; Presti, S.L. Analyzing the Relationship between Risk and Trust. In Trust Management; Springer: Berlin/Heidelberg, Germany, 2004; Volume 2995, pp. 135–145. [Google Scholar]
- Marsh, S. Formalizing Trust as a Computational Concept. Ph.D. Thesis, University of Stirling, Stirling, UK, 1994. Available online: http://hdl.handle.net/1893/2010 (accessed on 25 September 2021).
- Victor, P.; Cornelis, C.; De Cock, M. Trust Networks for Recommender Systems; Atlantis Press: Paris, France, 2011; Volume 4. [Google Scholar]
- Lewicki, R.J.; McAllister, D.J.; Bies, R.J. Trust and Distrust: New Relationships and Realities. Acad. Manag. Rev. 1998, 23, 438–458. [Google Scholar] [CrossRef]
- Yuan, W.; Shu, L.; Chao, H.C.; Guan, D.; Lee, Y.K.; Lee, S. ITARS: Trust-aware recommender system using implicit trust networks. IET Commun. 2010, 4, 1709–1721. [Google Scholar] [CrossRef]
- O’Doherty, D.; Jouili, S.; Van Roy, P. Trust-Based Recommendation: An Empirical Analysis. In Sixth ACM Workshop on Social Network Mining and Analysis; SNA-KDD; 2012; Available online: https://www.researchgate.net/profile/Salim-Jouili/publication/266166376_Trust-Based_Recommendation_an_Empirical_Analysis/links/55dcba9408aeb41644aec9c0/Trust-Based-Recommendation-an-Empirical-Analysis.pdf (accessed on 15 August 2021).
- Golbeck, J. Computing and Applying Trust in Web-Based Social Networks; The University of Maryland: College Park, MD, USA, 2005. [Google Scholar]
- Sherchan, W.; Nepal, S.; Paris, C. A survey of trust in social networks. ACM Comput. Surv. 2013, 45, 47. [Google Scholar] [CrossRef]
- Falcone, R.; Pezzulo, G.; Castelfranchi, C. A Fuzzy Approach to a Belief-based Trust Computation; Springer: Berlin/Heidelberg, Germany, 2003; pp. 73–86. [Google Scholar]
- Hooijmaijers, D.; Stumptner, M. Trust Calculation. In Intelligent Information Processing III. IIP 2006. IFIP International Federation for Information Processing; Shi, Z., Shimohara, K., Feng, D., Eds.; Springer: Boston, MA, USA, 2006; Volume 228. [Google Scholar] [CrossRef] [Green Version]
- Selvaraj, C.; Anand, S. Peer profile-based trust model for P2P systems using a genetic algorithm. Peer Peer Netw. Appl. 2012, 5, 92–103. [Google Scholar] [CrossRef]
- Golbeck, J.; Parsia, B.; Hendler, J. Trust Networks on the Semantic Web. In Cooperative Information Agents VII; Klusch, M., Omicini, A., Ossowski, S., Laamanen, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2782, pp. 238–249. [Google Scholar] [CrossRef]
- Ziegler, C.N.; Lausen, G. Spreading Activation Models for Trust Propagation. In Proceedings of the 2004 IEEE International Conference on e-Technology, e-Commerce and e-Service (EEE’04) (EEE ‘04), Taipei, Taiwan, 28–31 March 2004; pp. 83–97. [Google Scholar]
- Brin, S.; Page, L. The anatomy of a large-scale hypertextual Web search engine. Comput. Netw. ISDN Syst. 1998, 30, 107–117. [Google Scholar] [CrossRef]
- Kamvar, S.D.; Schlosser, M.T.; Garcia-Molina, H. The Eigentrust algorithm for reputation management in p2p networks. In Proceedings of the 12th International Conference on World Wide Web, Budapest, Hungary, 20–24 May 2003; pp. 640–651. [Google Scholar] [CrossRef]
- Smith, D.; Menon, S.; Sivakumar, K. Online peer and editorial recommendations, trust, and choice in virtual markets. J. Interact. Mark. 2005, 19, 15–37. [Google Scholar] [CrossRef]
- O’Connor, P. User-Generated Content and Travel: A Case Study on Tripadvisor.Com. In Information and Communication Technologies in Tourism 2008; Springer: Singapore, 2008; pp. 47–58. [Google Scholar]
- Golbeck, J. Generating Predictive Movie Recommendations from Trust in Social Networks. In Lecture Notes in Computer Science; Stølen, K., Winsborough, W.H., Martinelli, F., Massacci, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3986, pp. 93–104. [Google Scholar] [CrossRef]
- Massa, P.; Avesani, P. Trust-aware recommender systems. In Proceedings of the 2007 ACM conference on Recommender systems-RecSys ’07, Minneapolis, MN, USA, 19–20 October 2007; pp. 17–24. [Google Scholar] [CrossRef]
- Bedi, P.; Kaur, H.; Marwaha, S. Trust-based recommender system for the semantic web. In Proceedings of the 20th International Joint Conference on Artificial Intelligence (IJCAI’07), Hyderabad, India, 6–12 January 2007; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2007; pp. 2677–2682. [Google Scholar]
- Mehta, S.; Banati, H. Trust aware social context filtering using Shuffled frog leaping algorithm. In Proceedings of the 2012 12th International Conference on Hybrid Intelligent Systems (HIS), Pune, India, 4–7 December 2012; pp. 342–347. [Google Scholar]
- Ray, S.; Mahanti, A. Improving Prediction Accuracy in Trust-Aware Recommender Systems. In Proceedings of the 2010 43rd Hawaii International Conference on System Sciences, Kauai, HI, USA, 5–8 January 2010; pp. 1–9. [Google Scholar]
- Lü, L.; Medo, M.; Yeung, C.H.; Zhang, Y.-C.; Zhang, Z.-K.; Zhou, T. Recommender systems. Phys. Rep. 2012, 519, 1–49. [Google Scholar] [CrossRef] [Green Version]
- Walter, F.E.; Battiston, S.; Schweitzer, F. A model of a trust-based recommendation system on a social network. Auton. Agents Multi-Agent Syst. 2007, 16, 57–74. [Google Scholar] [CrossRef] [Green Version]
- Gao, H.; Tang, J.; Liu, H. Modeling geo-social correlations for new check-ins on location-based social networks. In Proceedings of the 21st ACM International Conference on Information and Knowledge Management, Maui, HI, USA, 29 October–2 November 2012; pp. 1582–1586. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).