CryptoKnight: Generating and Modelling Compiled Cryptographic Primitives
Abstract
1. Introduction
- Our unique convolutional neural network architecture fits variable-length diagnostic data to map an application’s time-invariant cryptographic execution.
- Complimented by procedural synthesis, we address the issue of this task’s disproportionate latent feature space.
- The realised framework, CryptoKnight, has demonstrably faster results compared to that of previous methodologies, and is extensively re-usable.
2. Related Work
2.1. Heuristics
2.2. Data Flow Analysis
2.3. Machine Learning
2.4. Overview
- Procedural generation guides the synthesis of unique cryptographic binaries with variable obfuscation and alternate compilation.
- Assumptions of cryptographic code aid the discrimination of diagnostics from the dynamic analysis of synthetic or reference binaries, to build an ‘image’ of execution.
- A DCNN fits variable-length matrices for ease of training and the immediate classification of new samples.
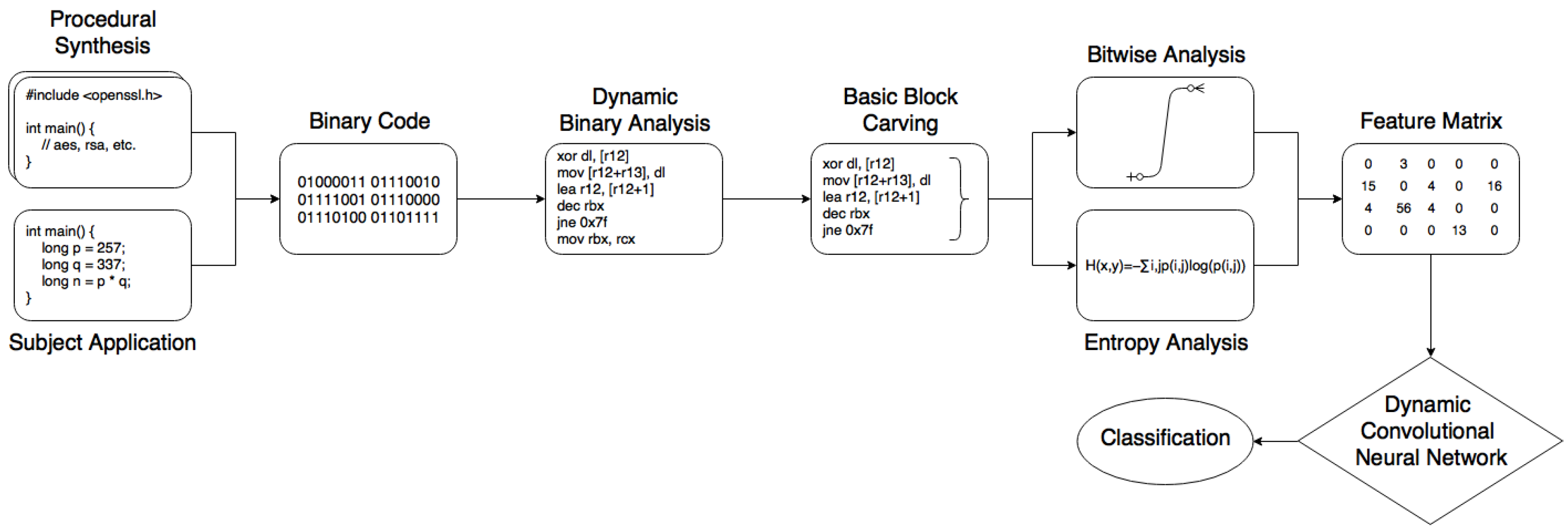
3. Methodology
3.1. Artefacts
3.2. Obfuscation
3.3. Interpretation
| Algorithm 1 Cryptographic Synthesis |
|
3.4. Feature Extraction
3.4.1. Basic Blocks and Loops
- unconditional or conditional branch—direct/indirect,
- return to caller.
| Algorithm 2 Instruction Sequencing, BBL Detection |
|
3.4.2. Instructions
3.4.3. Entropy
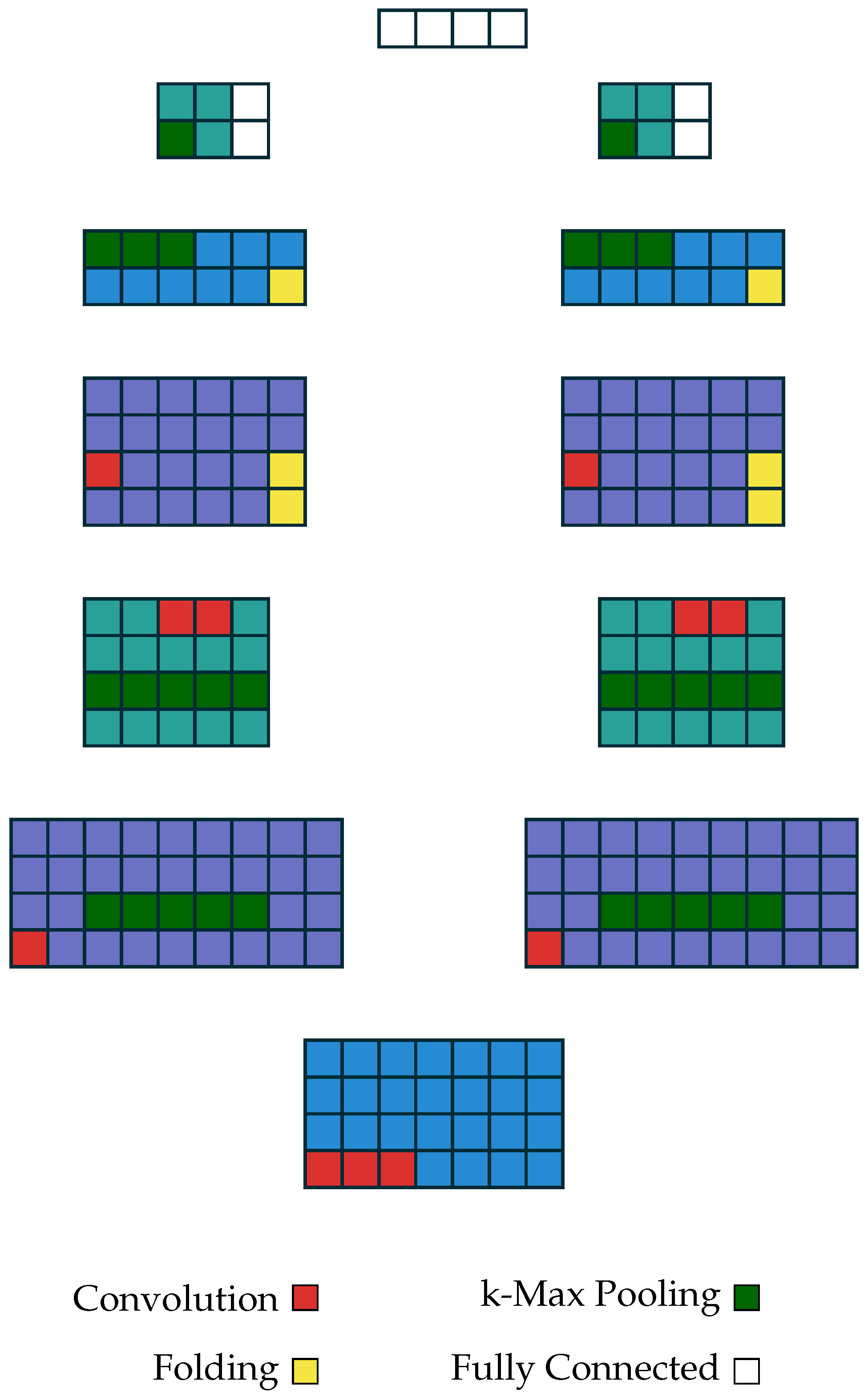
3.5. Model
3.6. Experimentation
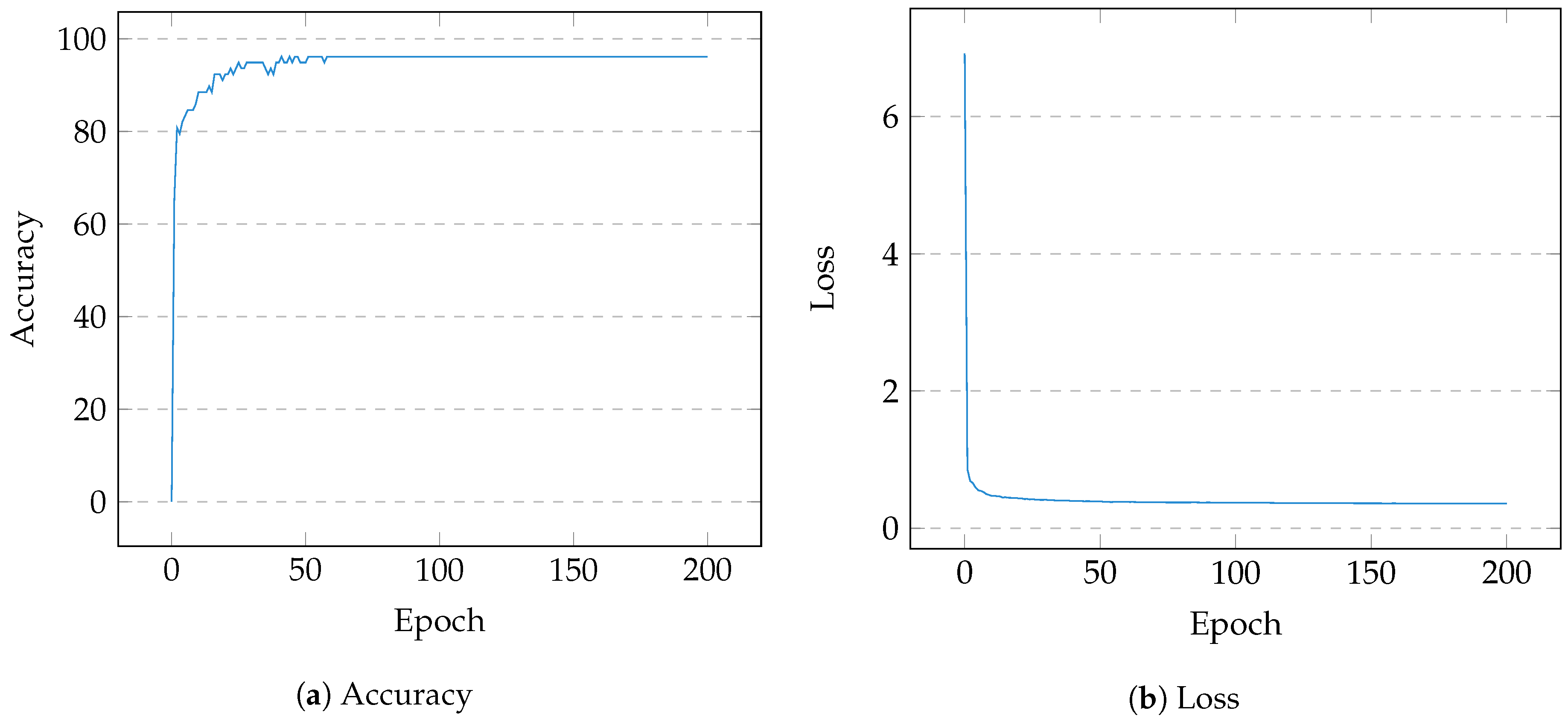
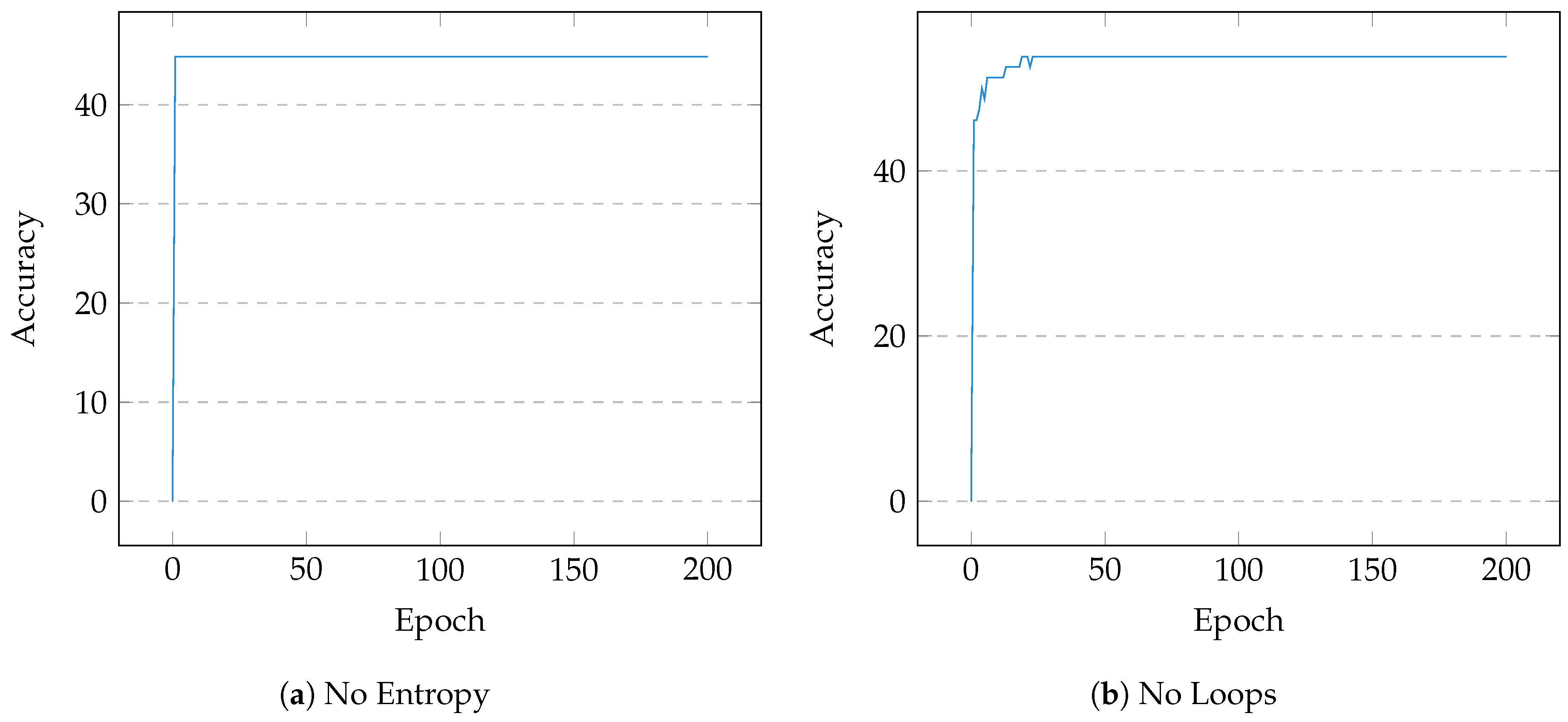
4. Evaluation
Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Young, A.; Yung, M. Cryptovirology: Extortion-based security threats and countermeasures. In Proceedings of the 1996 IEEE Symposium on Security and Privacy, Oakland, CA, USA, 6–8 May 1996; pp. 129–140. [Google Scholar]
- Snow, J. CryptXXX Ransomware, 2016. Available online: https://blog.kaspersky.com/cryptxxx-ransomware/11939/ (accessed on 10 September 2018).
- Chiu, A. Player 3 Has Entered the Game: Say Hello to ‘WannaCry’. Available online: https://www.cybrary.it/channelcontent/player-3-has-entered-the-game-say-hello-to-wannacry/ (accessed on 7 September 2018).
- Kharraz, A.; Robertson, W.; Balzarotti, D.; Bilge, L.; Kirda, E. Cutting the gordian knot: A look under the hood of ransomware attacks. In International Conference on Detection of Intrusions and Malware, and Vulnerability Assessment; Springer: Berlin, Germany, 2015; pp. 3–24. [Google Scholar]
- Scaife, N.; Carter, H.; Traynor, P.; Butler, K.R. Cryptolock (and drop it): Stopping ransomware attacks on user data. In Proceedings of the 2016 IEEE 36th International Conference on Distributed Computing Systems (ICDCS), Nara, Japan, 27–30 June 2016; pp. 303–312. [Google Scholar]
- Deane-McKenna, C. NHS Ransomware Cyber-Attack was Preventable; The Conversation, 13 May 2017. Available online: https://theconversation.com/nhs-ransomware-cyber-attack-was-preventable-77674 (accessed on 10 September 2018).
- Beek, C. McAfee Labs Threats Report; Intel Security: Santa Clara, CA, USA, 2016. [Google Scholar]
- Lutz, N. Towards Revealing Attackers’ Intent by Automatically Decrypting Network Traffic. Master’s Thesis, ETH Zürich, Zürich, Switzerland, August 2008. (A joint project between the ETH Zurich and Google, Inc.). [Google Scholar]
- Gröbert, F.; Willems, C.; Holz, T. Automated Identification of Cryptographic Primitives in Binary Programs. In Proceedings of the 14th International Symposium on Recent Advances in Intrusion Detection (RAID 2011), Menlo Park, CA, USA, 20–21 September 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 41–60. [Google Scholar]
- IBM. Bucbi Ransomware. Available online: https://exchange.xforce.ibmcloud.com/collection/Bucbi-Ransomware-16eef23d3b7ea484ed69ecd78b6c1232 (accessed on 7 September 2018).
- Lestringant, P.; Guihéry, F.; Fouque, P.A. Automated Identification of Cryptographic Primitives in Binary Code with Data Flow Graph Isomorphism. In Proceedings of the 10th ACM Symposium on Information, Computer and Communications Security, Singapore, 14–17 April 2015; ACM: New York, NY, USA, 2015; pp. 203–214. [Google Scholar]
- Moser, A.; Kruegel, C.; Kirda, E. Limits of static analysis for malware detection. In Proceedings of the Twenty-Third Annual Computer Security Applications Conference (ACSAC 2007), Miami Beach, FL, USA, 10–14 December 2007; pp. 421–430. [Google Scholar]
- Luk, C.K.; Cohn, R.; Muth, R.; Patil, H.; Klauser, A.; Lowney, G.; Wallace, S.; Reddi, V.J.; Hazelwood, K. Pin: Building customized program analysis tools with dynamic instrumentation. In Proceedings of the 2005 ACM SIGPLAN conference on Programming language design and implementation, Chicago, IL, USA, 12–15 June 2005; ACM: New York, NY, USA, 2005; Volume 40, pp. 190–200. [Google Scholar]
- Xu, D.; Ming, J.; Wu, D. Cryptographic function detection in obfuscated binaries via bit-precise symbolic loop mapping. In Proceedings of the 2017 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2017; pp. 921–937. [Google Scholar]
- Li, X.; Wang, X.; Chang, W. CipherXRay: Exposing cryptographic operations and transient secrets from monitored binary execution. IEEE Trans. Dependable Secur. Comput. 2014, 11, 101–114. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y. Generalization and network design strategies. In Connectionism in Perspective; Elsevier: New York, NY, USA, 1989; pp. 143–155. [Google Scholar]
- LeCun, Y.; Kavukcuoglu, K.; Farabet, C. Convolutional networks and applications in vision. In Proceedings of the 2010 IEEE International Symposium on Circuits and Systems (ISCAS), Paris, France, 30 May–2 June 2010; pp. 253–256. [Google Scholar]
- Hu, B.; Lu, Z.; Li, H.; Chen, Q. Convolutional neural network architectures for matching natural language sentences. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2014; pp. 2042–2050. [Google Scholar]
- Pearl, J. Heuristics: Intelligent Search Strategies for Computer Problem Solving; U.S. Department of Energy: Washington, DC, USA, 1984.
- Gröbert, F. Automatic Identification of Cryptographic Primitives in Software. In Proceedings of the 27th Chaos Communication Congress, Berlin, Germany, 27–30 December 2010. [Google Scholar]
- Matenaar, F.; Wichmann, A.; Leder, F.; Gerhards-Padilla, E. CIS: The Crypto Intelligence System for Automatic Detection and Localization of Cryptographic Functions in Current Malware. In Proceedings of the 2012 7th International Conference on Malicious and Unwanted Software, Fajardo, PR, USA, 16–18 October 2012. [Google Scholar]
- Zhang, P.; Wu, J.; Wang, X.; Wu, Z. Decrypted data detection algorithm based on dynamic dataflow analysis. In Proceedings of the 2014 International Conference on Computer, Information and Telecommunication Systems (CITS), Jeju, Korea, 7–9 July 2014; pp. 1–4. [Google Scholar]
- Zhao, R.; Gu, D.; Li, J.; Yu, R. Detection and Analysis of Cryptographic Data Inside Software. In Proceedings of the 14th International Conference on Information Security, Xi’an, China, 26–29 October 2011; Lai, X., Zhou, J., Li, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 182–196. [Google Scholar]
- Calvet, J.; Fernandez, J.M.; Marion, J.Y. Aligot: Cryptographic function identification in obfuscated binary programs. In Proceedings of the 2012 ACM Conference on Computer and Communications Security, Raleigh, NC, USA, 16–18 October 2012; ACM: New York, NY, USA, 2012; pp. 169–182. [Google Scholar]
- Hosfelt, D.D. Automated detection and classification of cryptographic algorithms in binary programs through machine learning. arXiv, 2015; arXiv:1503.01186. [Google Scholar]
- Baldwin, J.; Dehghantanha, A. Leveraging support vector machine for opcode density based detection of crypto-ransomware. In Cyber Threat Intelligence; Springer: Berlin, Germany, 2018; pp. 107–136. [Google Scholar]
- Sgandurra, D.; Muñoz-González, L.; Mohsen, R.; Lupu, E.C. Automated Dynamic Analysis of Ransomware: Benefits, Limitations and use for Detection. arXiv, 2016; arXiv:1609.03020. [Google Scholar]
- Drape, S. Intellectual Property Protection using Obfuscation. In Proceedings of the 2009 IEEE Sensors Applications Symposium, New Orleans, LA, USA, 17–19 February 2009. [Google Scholar]
- Tubella, J.; Gonzalez, A. Control speculation in multithreaded processors through dynamic loop detection. In Proceedings of the 1998 Fourth International Symposium on High-Performance Computer Architecture, Las Vegas, NV, USA, 1–4 February 1998; pp. 14–23. [Google Scholar]
- Moseley, T.; Grunwald, D.; Connors, D.A.; Ramanujam, R.; Tovinkere, V.; Peri, R. Loopprof: Dynamic techniques for loop detection and profiling. In Proceedings of the 2006 Workshop on Binary Instrumentation and Applications (WBIA), San Jose, CA, USA, 21–25 October 2006. [Google Scholar]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1961; pp. 547–561. [Google Scholar]
- Kalchbrenner, N.; Grefenstette, E.; Blunsom, P. A Convolutional Neural Network for Modelling Sentences. arXiv, 2014; arXiv:1404.2188. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving neural networks by preventing co-adaptation of feature detectors. arXiv, 2012; arXiv:1207.0580. [Google Scholar]
- Marinho, T. GonnaCry. 2018. Available online: https://github.com/tarcisio-marinho/GonnaCry (accessed on 7 September 2018).
- Akdemir, K.; Dixon, M.; Feghali, W.; Fay, P.; Gopal, V.; Guilford, J.; Ozturk, E.; Wolrich, G.; Zohar, R. Breakthrough AES Performance with Intel AES New Instructions; White Paper; Intel Corporatlon: Santa Clara, CA, USA, June 2010. [Google Scholar]
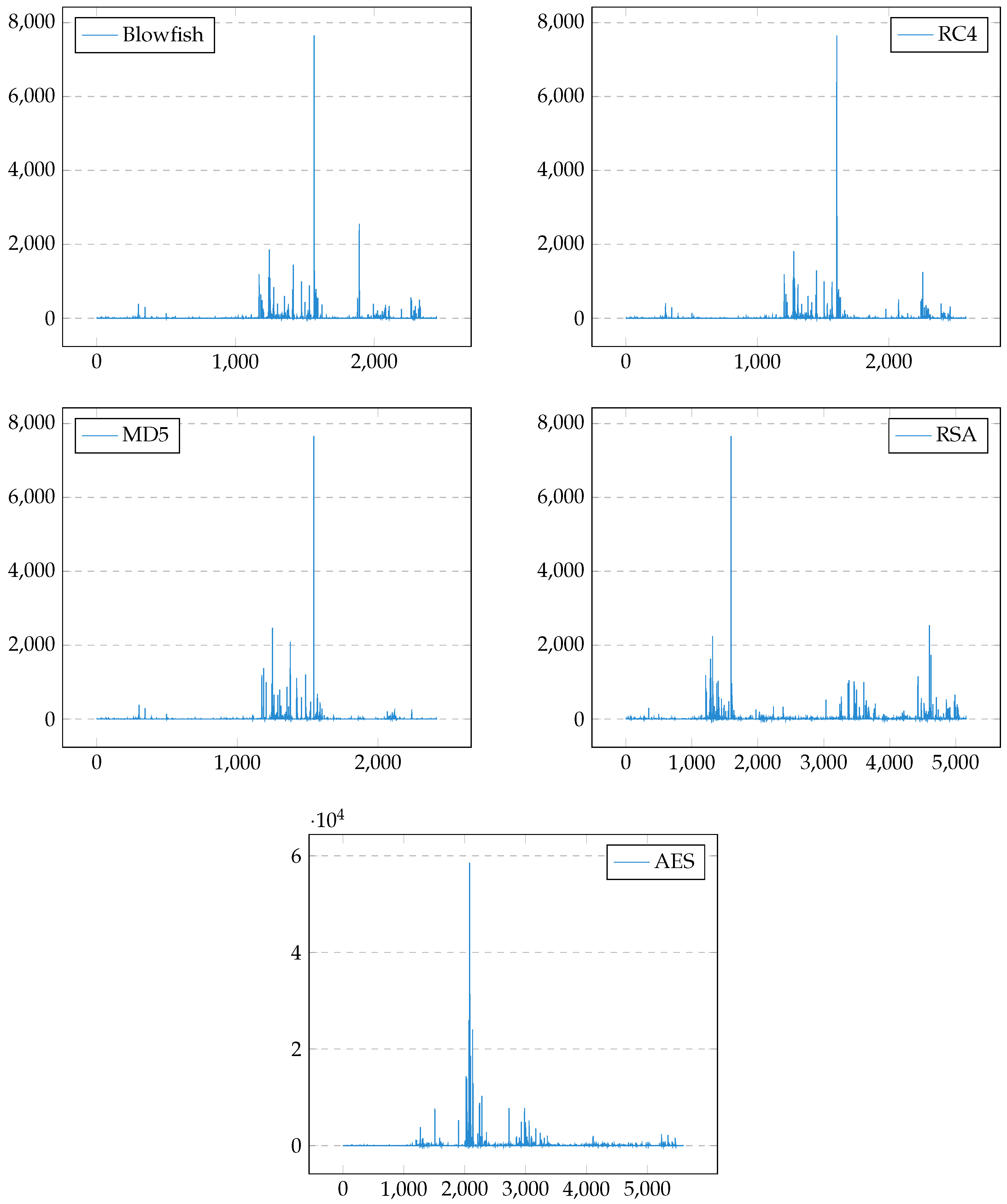
| Category | Algorithm |
|---|---|
| Symmetric | AES |
| RC4 | |
| Blowfish | |
| Asymmetric | RSA |
| Hashing | MD5 |
| AES | RC4 | BLF | MD5 | RSA | R/A | |
|---|---|---|---|---|---|---|
| AES | 13 | 0 | 0 | 0 | 0 | 0 |
| RC4 | 0 | 12 | 1 | 0 | 0 | 0 |
| BLF | 0 | 0 | 12 | 0 | 0 | 1 |
| MD5 | 0 | 1 | 0 | 12 | 0 | 0 |
| RSA | 0 | 0 | 0 | 0 | 13 | 0 |
| R/A | 0 | 0 | 0 | 0 | 0 | 13 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hill, G.; Bellekens, X. CryptoKnight: Generating and Modelling Compiled Cryptographic Primitives. Information 2018, 9, 231. https://doi.org/10.3390/info9090231
Hill G, Bellekens X. CryptoKnight: Generating and Modelling Compiled Cryptographic Primitives. Information. 2018; 9(9):231. https://doi.org/10.3390/info9090231
Chicago/Turabian StyleHill, Gregory, and Xavier Bellekens. 2018. "CryptoKnight: Generating and Modelling Compiled Cryptographic Primitives" Information 9, no. 9: 231. https://doi.org/10.3390/info9090231
APA StyleHill, G., & Bellekens, X. (2018). CryptoKnight: Generating and Modelling Compiled Cryptographic Primitives. Information, 9(9), 231. https://doi.org/10.3390/info9090231






