1. Introduction
Chaotic systems have great potential to be applied on the encryption of information. Crypto-systems are classified into branches: private-key and public-key [
1]. In chaos-based systems, a great deal of effort has been done in the private-key part in comparison with the public [
2]. One of the most important public-key chaos-based cryptosystem is presented in [
3] where Chebyshev maps are used to encrypt, but its efficiency is still lower than RSA [
4], a common weak point for this kind of crypto-proposal.
The logistic map is an excellent example of a chaotic system. Originally formulated to represent a simple demographic model to explain the increase of a population, the logistic map is a one-dimensional unimodal map and, as a result, its dynamics are quite limited [
5]. It can be expressed by using the equation:
where parameter
μ is in the interval 0 ≤
μ ≤ 4. The unimodal aspect of the logistic map makes it inadequate for cryptographic applications because the parameter
μ can be reconstructed from initial conditions, as in [
6], even though a reasonable number of applications have been created [
6]. A new relevant study [
7] has been conducted to improve the logistic map for cryptographic applications, but losing the mathematical simplicity of Equation (1).
A coupled map lattice (CML) is a dynamical system that models the behavior of non-linear systems. They are predominantly used to qualitatively study the chaotic dynamics of spatially-extended systems. This includes the dynamics of spatiotemporal chaos where the number of effective degrees of freedom diverges as the size of the system increases. CML incorporates a system of equations (coupled or uncoupled), a finite number of variables, a global or local coupling scheme, and the corresponding coupling terms [
8].
The logistic coupled map is one of the simplest CMLs, first considered as the simplest biologically realistic model that incorporates spatial effects, it is based on two coupled logistic maps by a linear coupling:
where
f(
x) is the logistic map of Equation (1) and
α is a coupling parameter. In the logistic map only two routes to chaos are observed (period doubling and intermittency), and the second dimension of the logistic coupled map allows the quasiperiodic route to occur [
9]. The non-symmetric case of the logistic coupled map [
10] occurs when, in Equations (2) and (3), we use a different parameter
μ for
f(
x), so the equations take the form:
where
f1(
x) means to use the logistic map of Equation (1) with
μ1 and
f2(
x) with
μ2. Multiple chaotic attractors are observed in this system improving the unimodal shortcoming of the simple logistic map [
8].
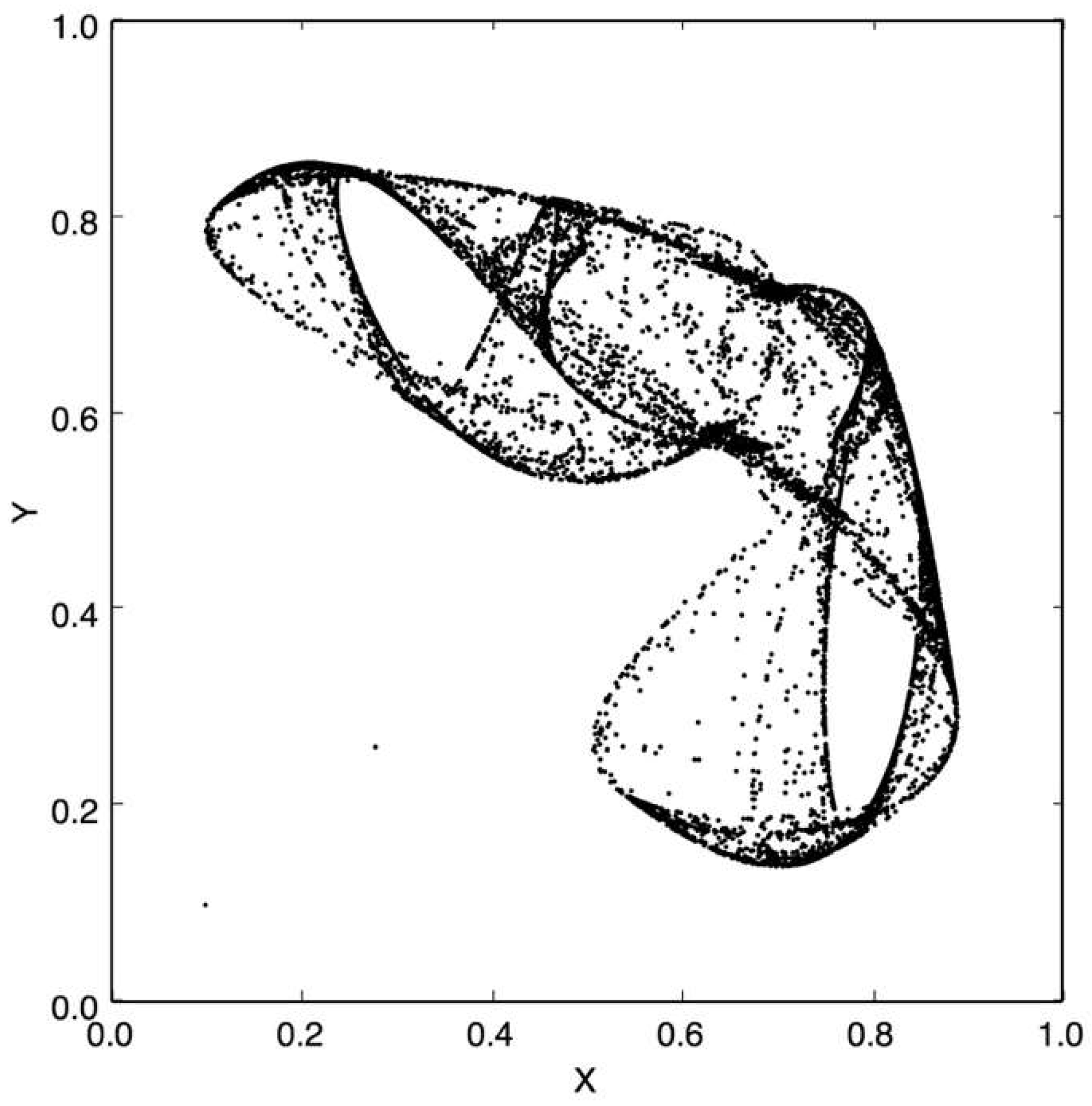
Figure 1 and
Figure 2 show examples of chaotic attractors for the non-symmetric logistic coupled map (NLCM). The NLCM has a well documented chaotic range for 3.63 ≤
μ ≤ 4 and 0 ≤
α ≤ 1 [
11].
A group from University of California San Diego (UCSD) introduced a theoretical scheme in [
12] for asymmetric encryption exploiting properties of nonlinear dynamical systems where a high-dimensional dissipative non-linear dynamical system is distributed between a transmitter and a receiver. Therefore, they call the method distributed dynamics encryption (DDE). The transmitter dynamics are public, and the receiver dynamics are private, and they are not shared in the channel. A message is encoded by modulation of the parameters of the transmitter, and this results in a shift of the overall system attractor. An unauthorized receiver does not know the hidden dynamics of the receiver and cannot decode the message [
12]. This proposal has been criticized due to its difficulties in the implementation and is categorized as non-practical [
13].
This work will take the proposal of DDE and adapt it for a low-dimensional system using the coupled logistic map. We will study the encryption, the decryption, and the common attack for this cryptographic system. This is important for DDE because it provides an implementation without loss of security with acceptable cost and speed, which is a relevant cryptographic requirement for chaos-based cryptosystems suggested by [
14]. It is our understanding that, at the time we wrote this work, this is the first fully functional computational implementation for encryption of DDE, besides the concept proof presented by the UCSD group. Even more, the work presented here is the missing example for DDE pointed out in the literature [
4].
4. Cryptanalysis
An unauthorized receiver may attempt several methods to attack DDE and decode the secret message
m(
n), but it has been demonstrated in [
15] that the only one where non-defense can be used it is the one analyzed in this section. As the security resides in the fact the signal traveling in the channel is chaotic, our implementation is still as defensible as the original DDE.
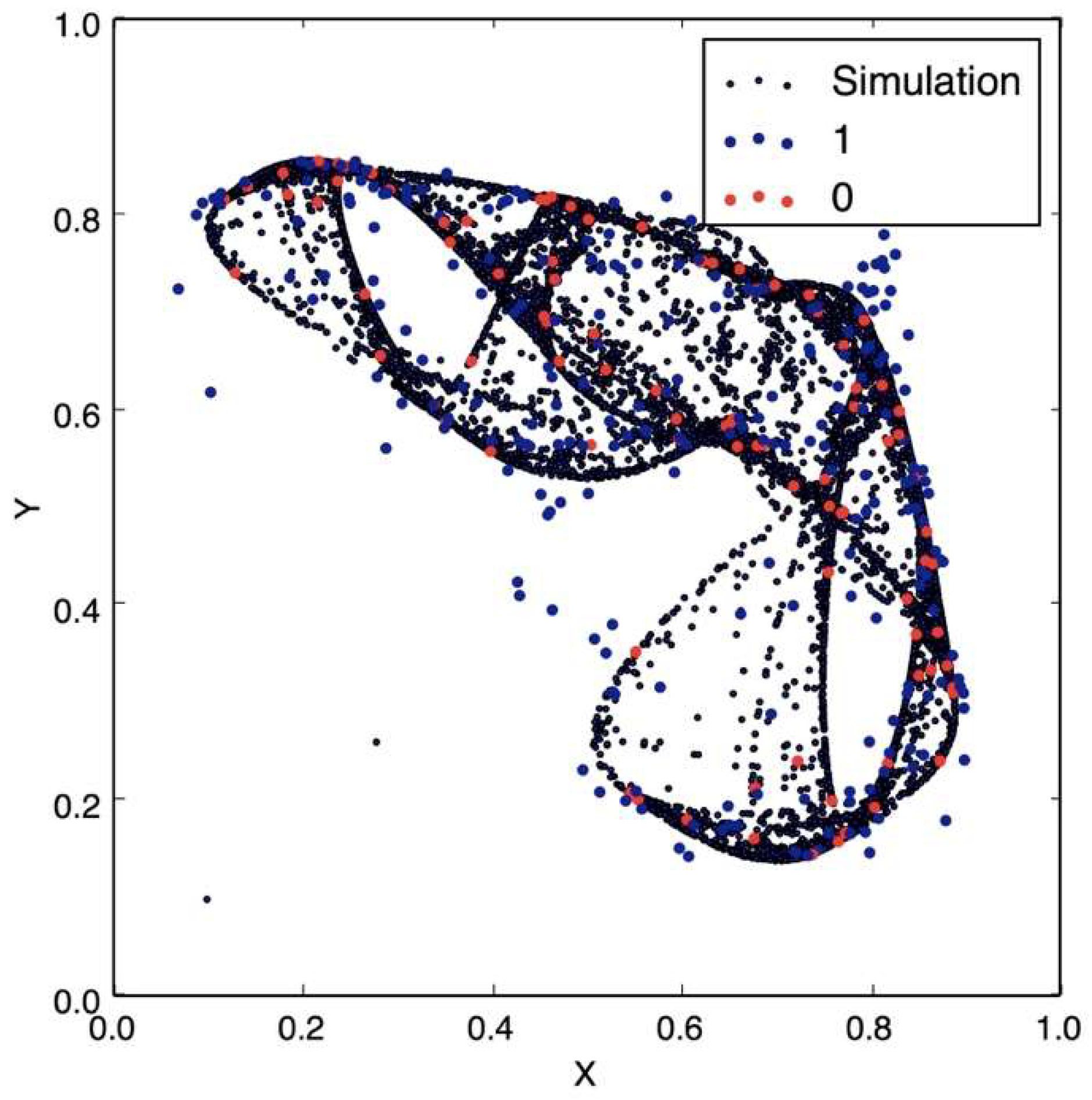
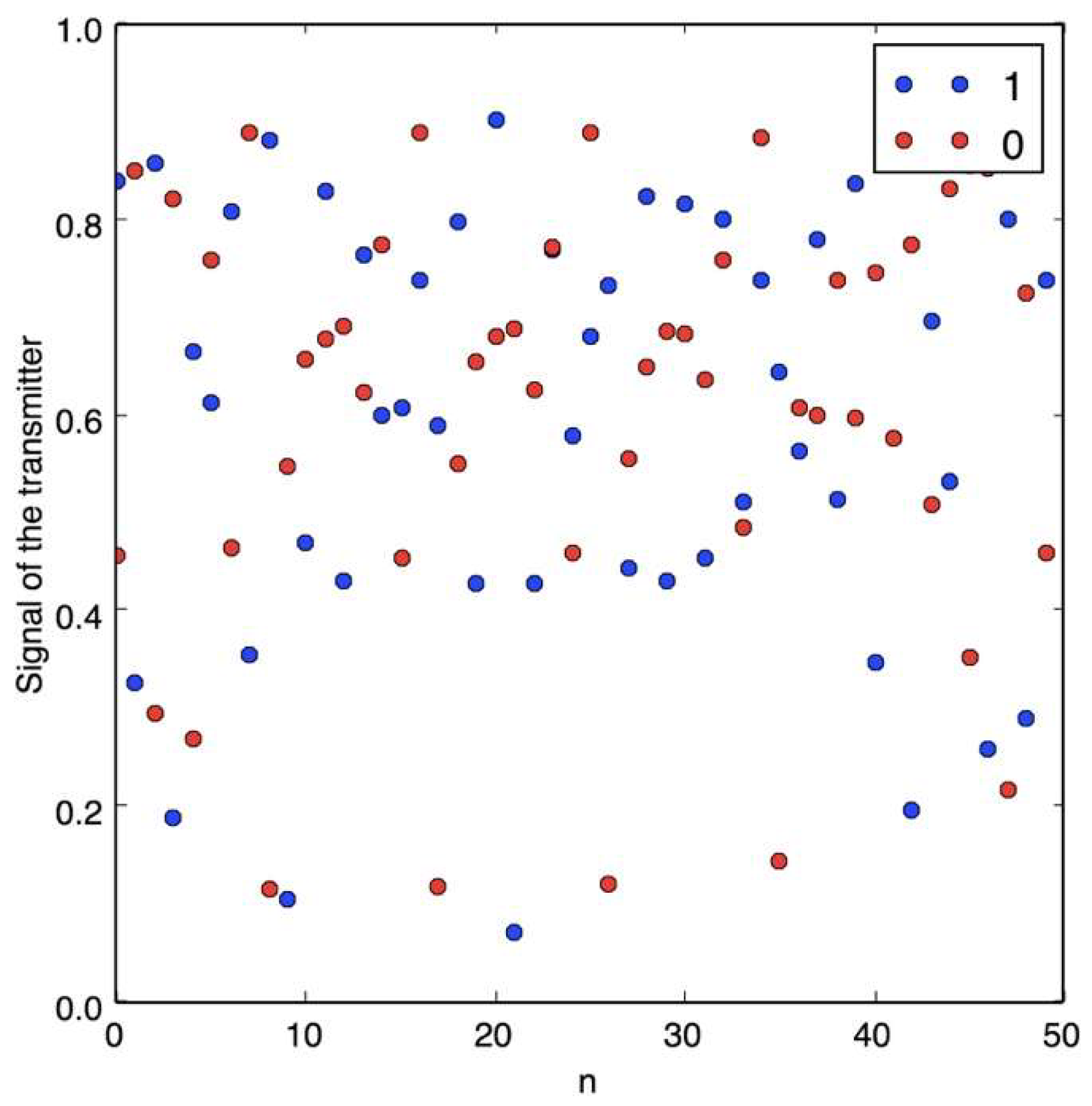
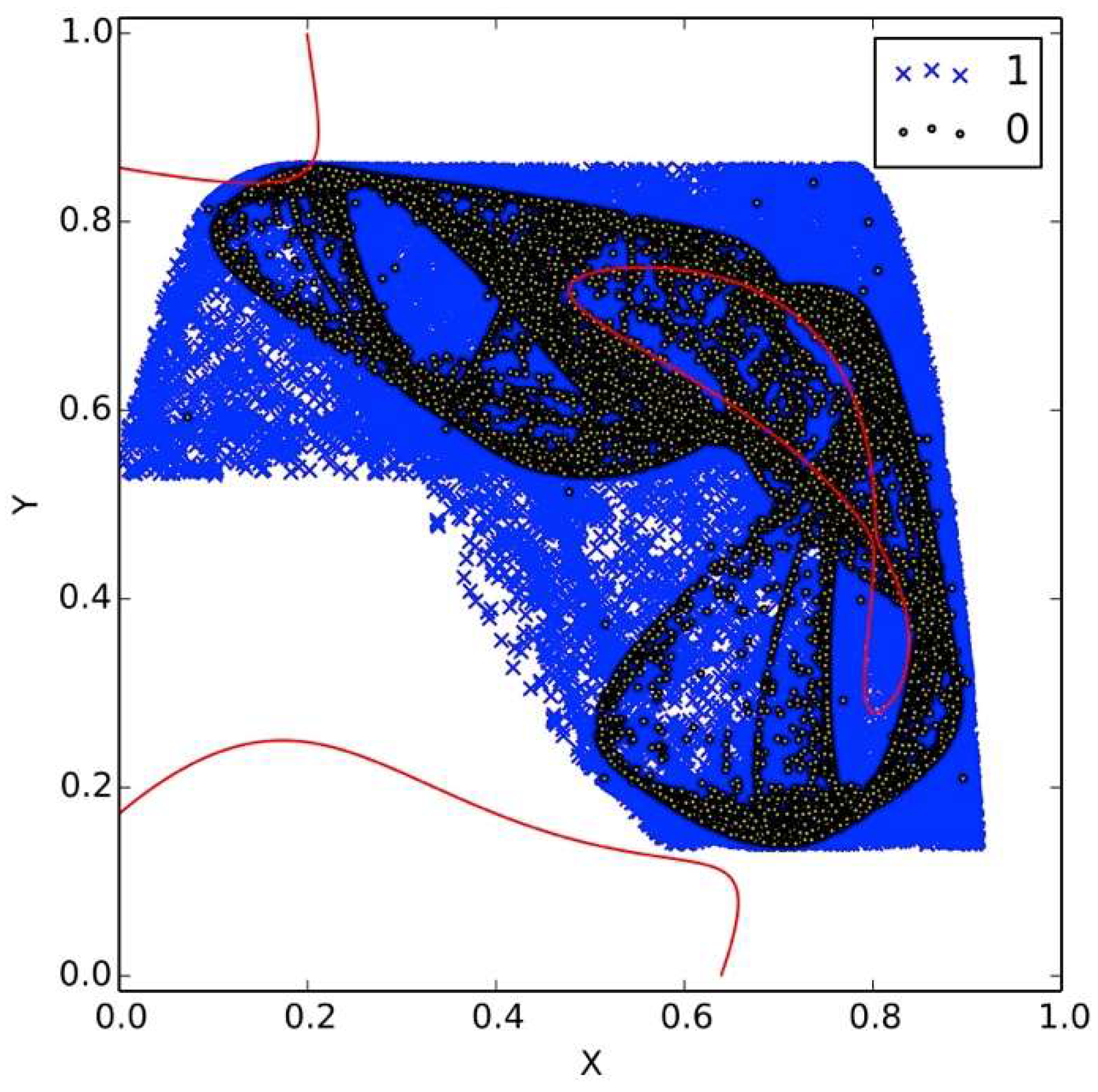
Figure 5 shows the data traveling through the communication channel, where an unauthorized receiver cannot easily resolve the message, and also due to topologically transitivity, as more data is transmitted in the channel, all the space will be occupied. On the other hand,
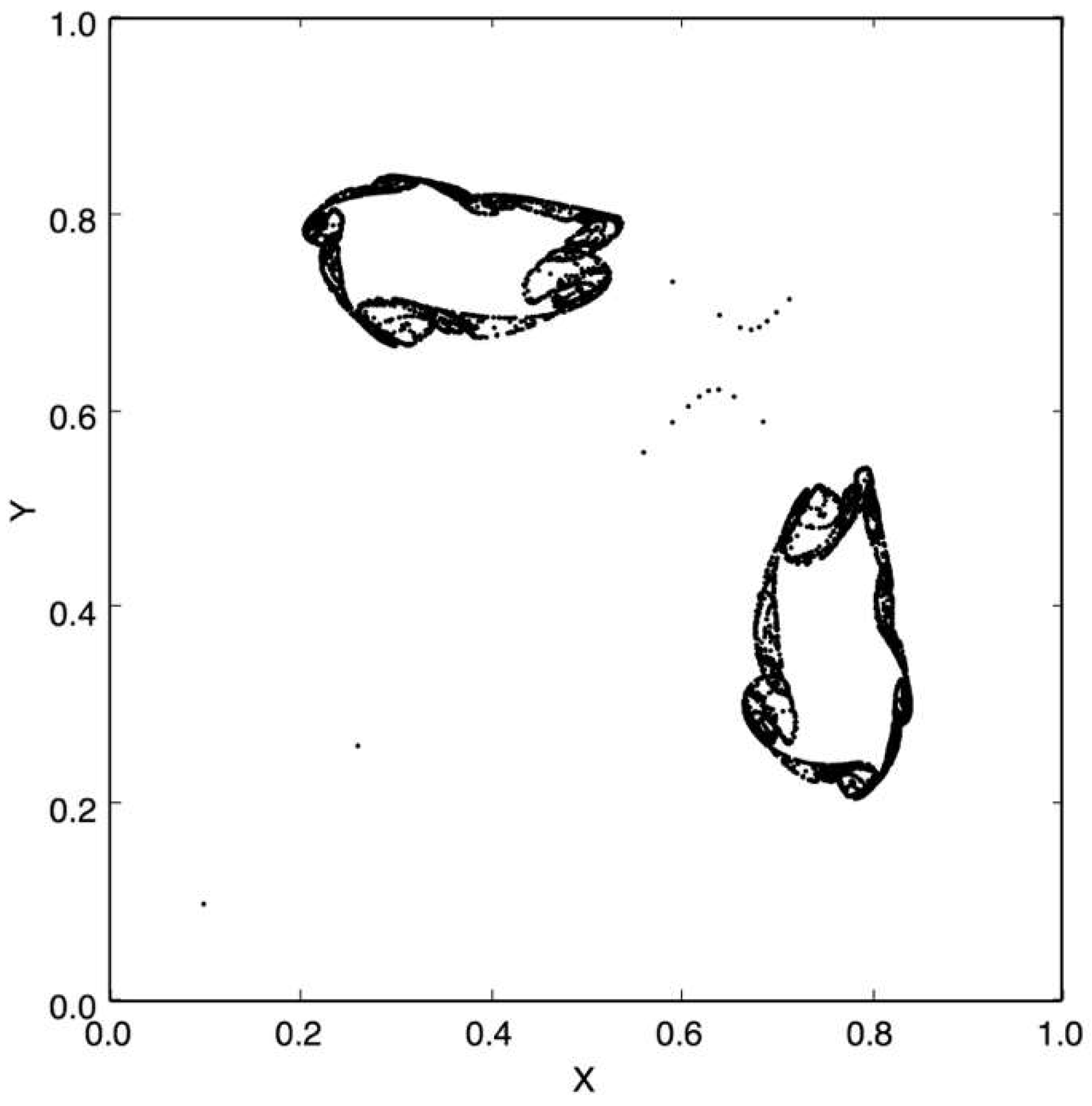
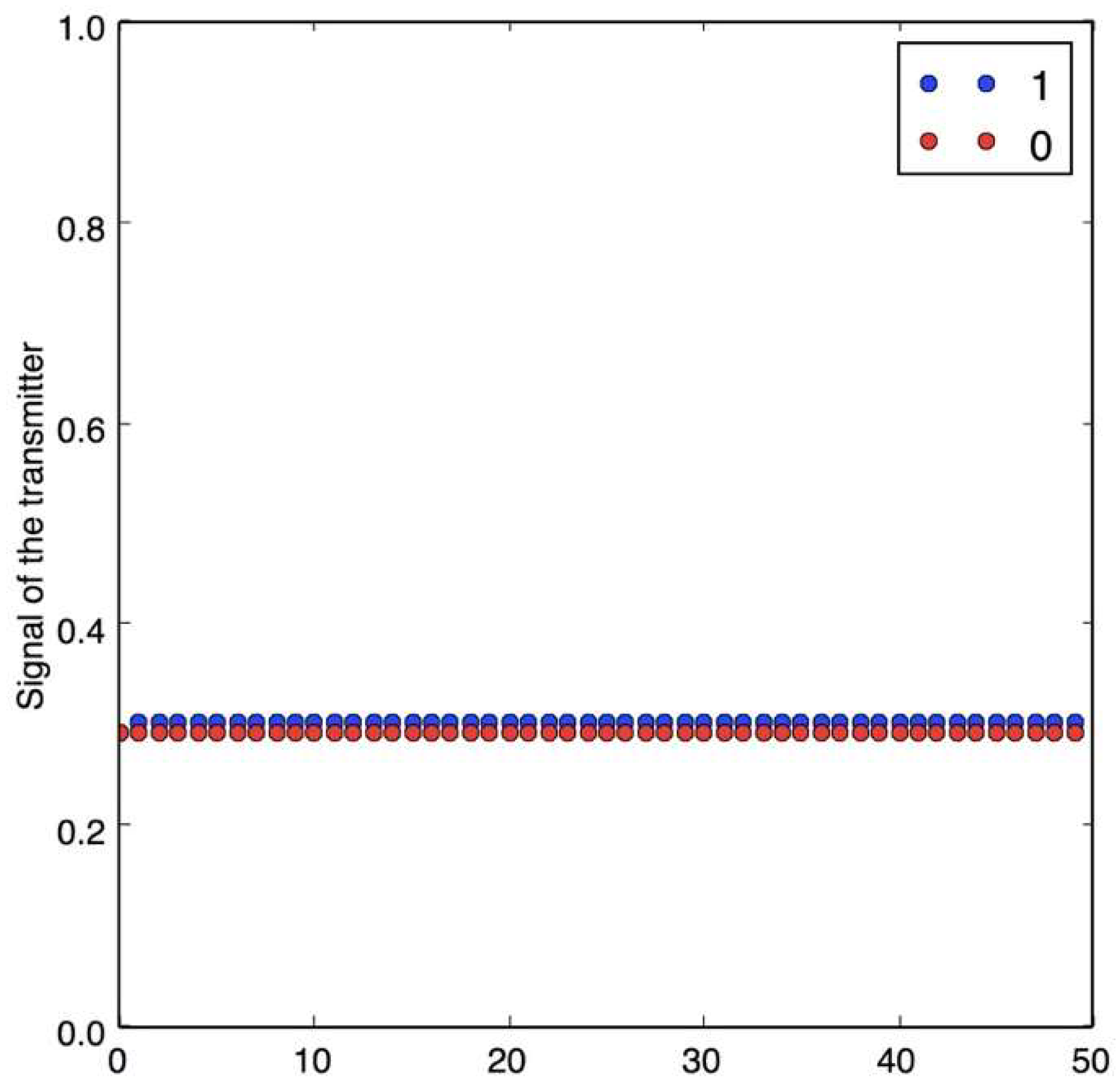
Figure 6 shows the case when the attractor is not chaotic: here, it is easy to identify the two states (0 or 1).
One such method is to reconstruct the positions of the attractors that correspond to the transmission of 0 and 1 by storing and clustering samples of many transmitted bits. Knowing the positions of the attractors would enable the unauthorized receiver to decode the message using the same method as the authorized receiver [
12].
The chaotic dynamics may contain channel and noise that make the dynamics stochastic. An unauthorized receiver may attempt to generate a hidden Markov model of the transmitter public dynamics for each possible value of the message m, and obtain a maximum likelihood (ML) estimation m’ of the message m. The decoded message will then be given by:
In order to generate the hidden Markov model, the unauthorized receiver will need to quantize the transmitter state in a time delay reconstructed embedding space, and to estimate the state transition probabilities, as well as the observation probabilities of the model [
15].
The attack proposed was implemented for our low-dimensional model.
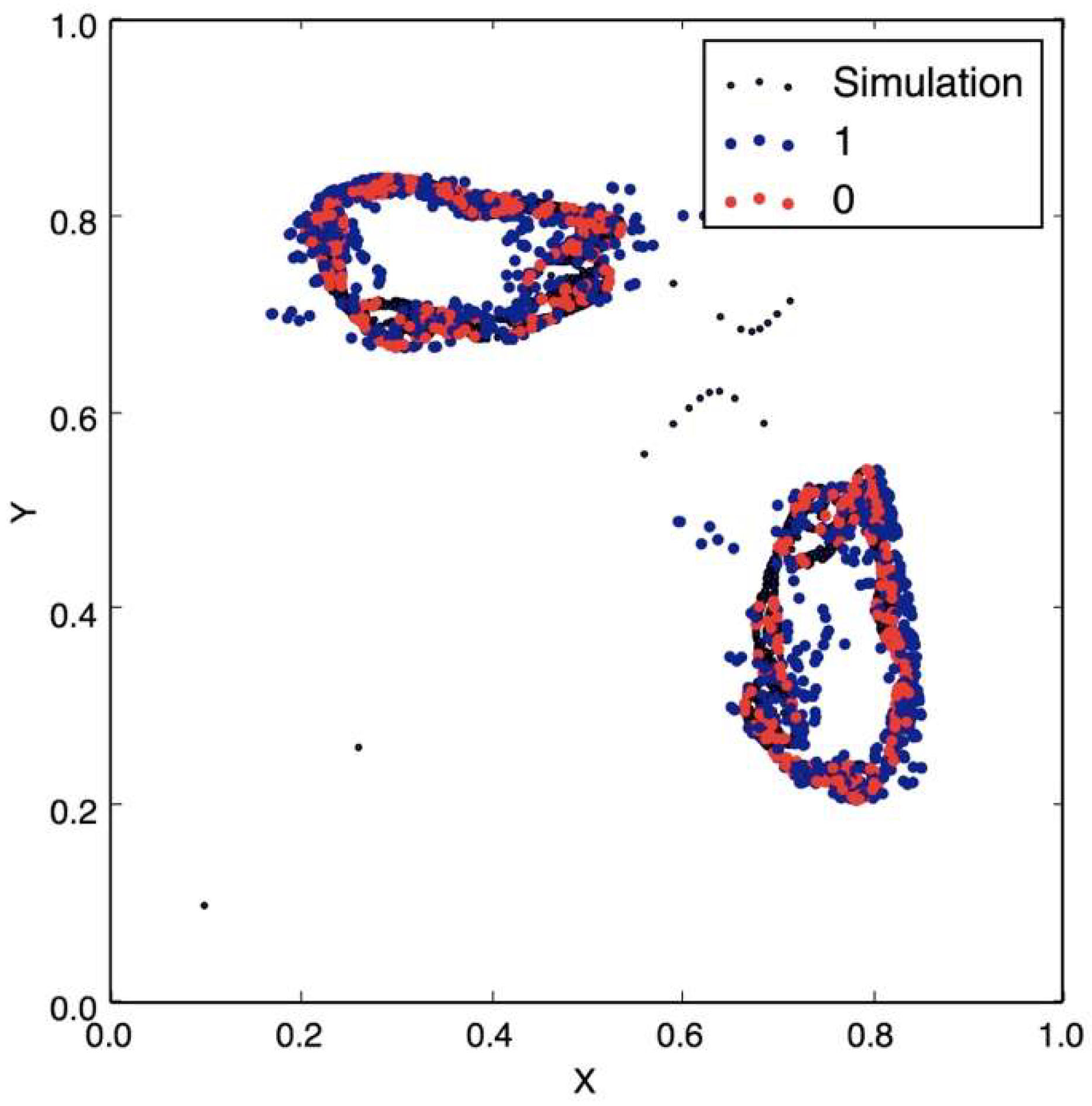
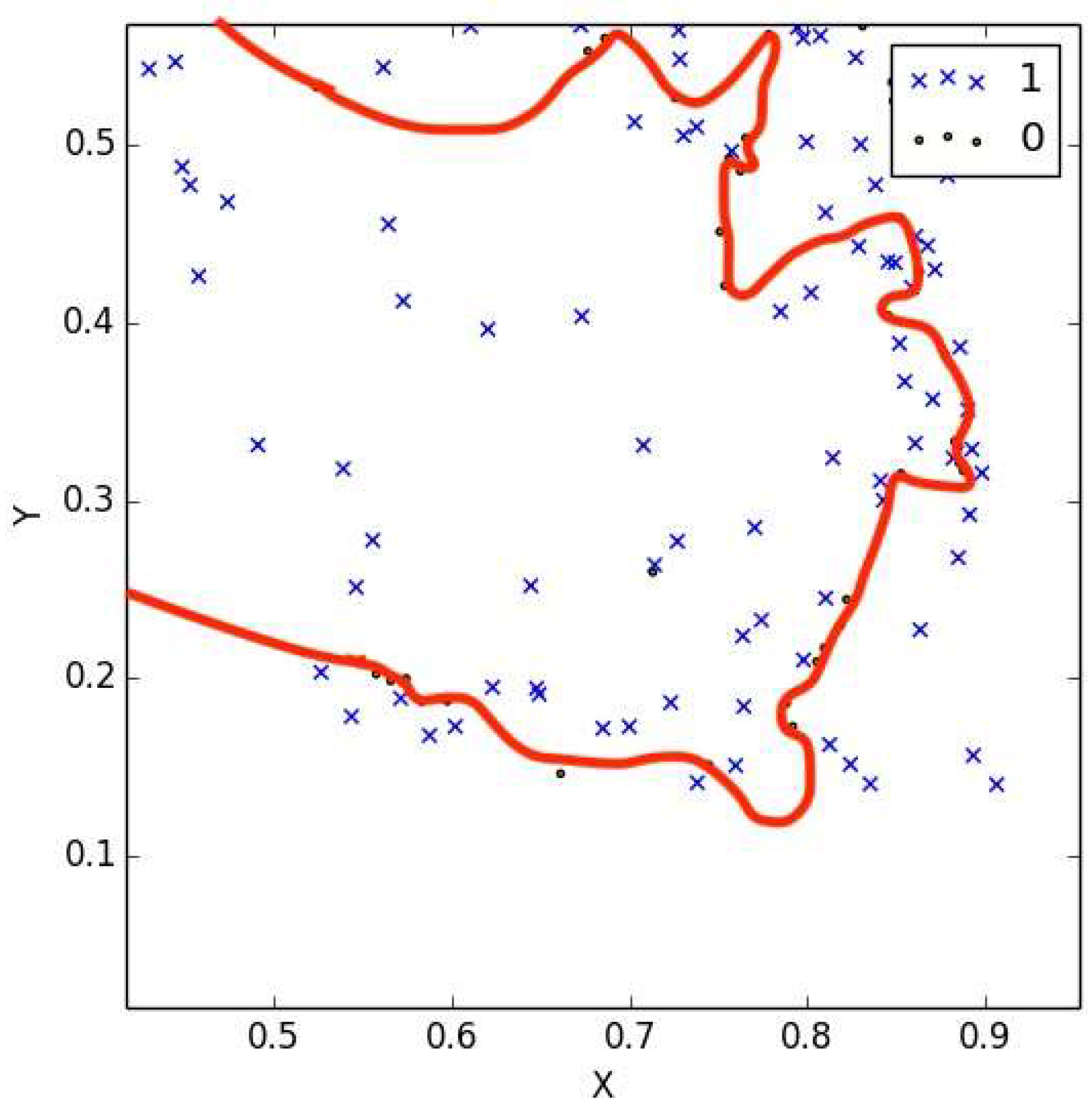
Figure 7 shows how the case of a message encrypted using a non-chaotic map where the training accuracy is 95%, which shows the effectiveness of the attack. When the number of bits is lower than that necessary to train the model, according to [
14], the accuracy reduces to lower than 40%, in which a probabilistic attack, as in [
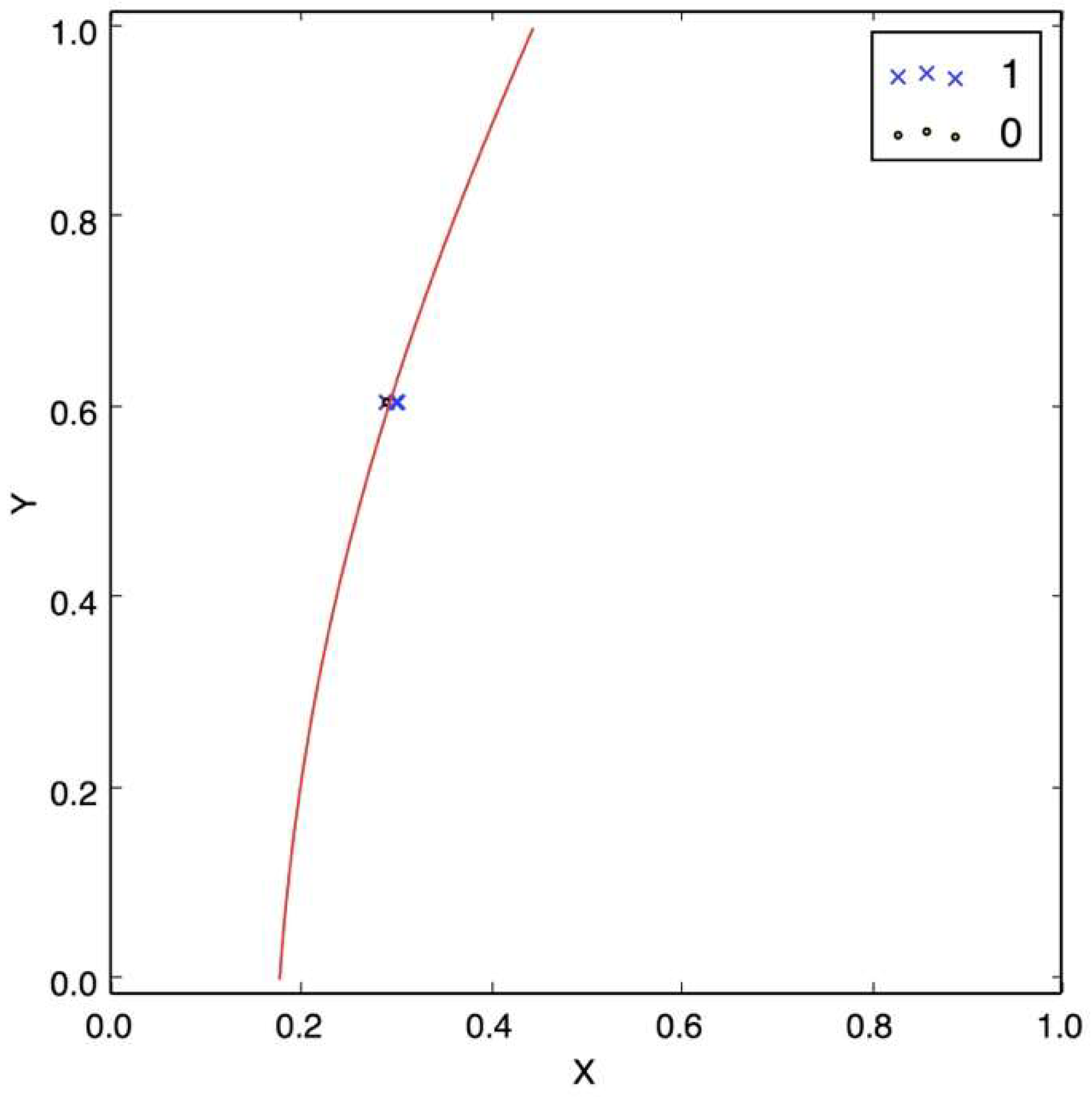
1], cannot help this particular attack. This case is shown in
Figure 8 where the red line is the decision boundary, which is far from being correct.
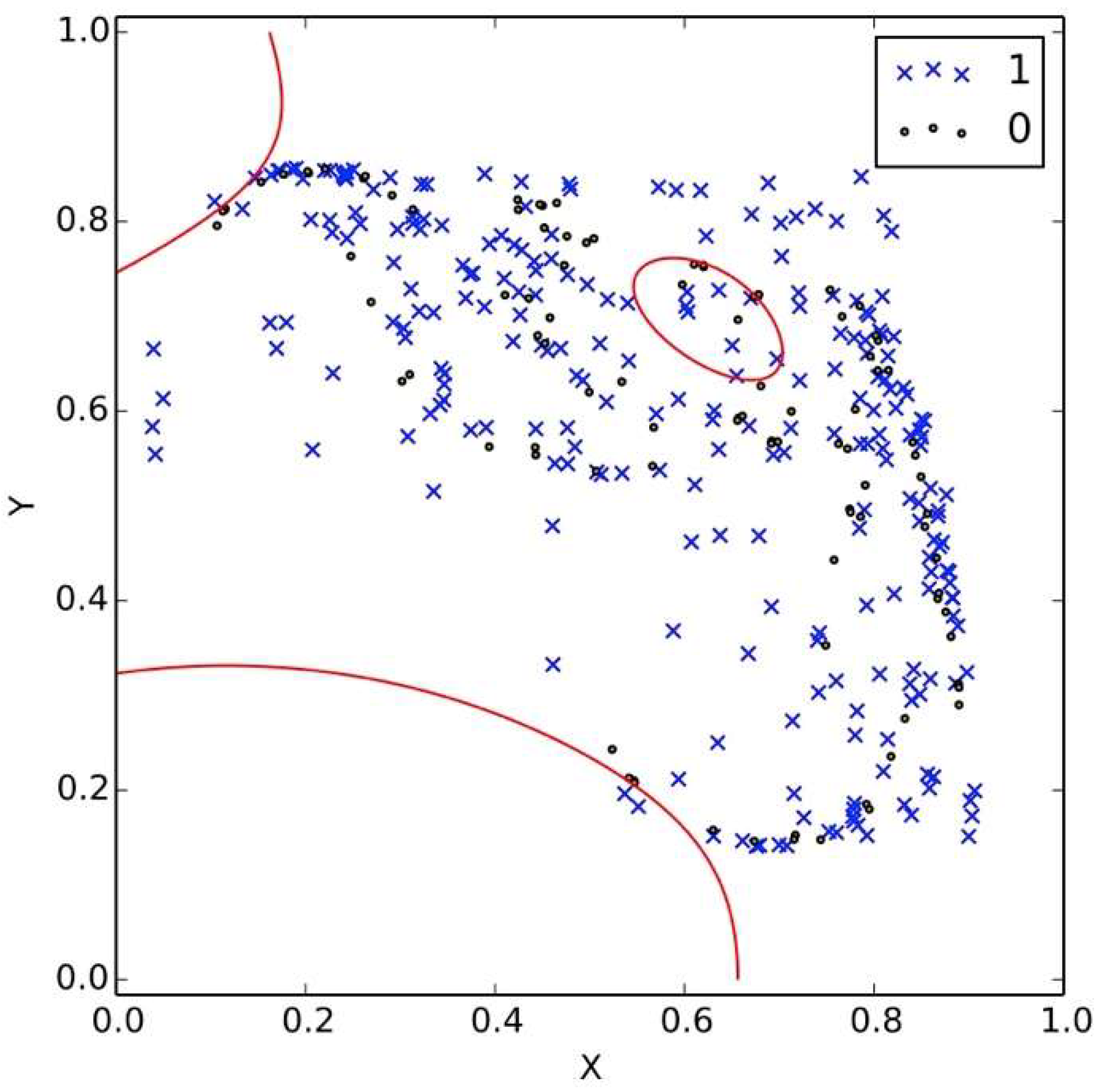
Figure 9 has a larger number of bits, 60,000, and the boundary is more visible, but it is not enough to recover the message.
Figure 10 shows the case where the number of bits is equal to that necessary to perform the attack: it is visible how the decision curve can resolve for 0 or 1-bits. Equation (9) from [
15] shows the number of states that can be transmitted before the decision curve can be resolved:
where
LT is the range of the data transmitted and
Lq is the quantization in the signal. Equation (11) is still useful in our case because it has been derived in general for any CML. For our implementation this number is around 4 × 10
7 which shows why
Figure 10 can resolve the decision curve and how the security of this implementation is of the same level as the original DDE proposal.
A relevant feature to point out is to see how a very small change in the dynamics of the receiver creates very different attractors. This can be observed in
Figure 1 and
Figure 2, where the only change between them is the value of
μ with just a 0.2 differential, and the produced dynamic is totally different. This is very useful because we do not need to change the public key to have a new crypto dynamic, representing a good option to protect from the attack described in this section.
The NLCM represents an improvement over the logistic map, but another map with our low-dimensional crypto scheme, like the piecewise linear map [
16], represents a new pair of crypto keys.
The chaos degradation is a well-known problem for chaos-based cryptosystems [
17]. In DDE, this problem is addressed by two means: (i) as the chaotic process is involved only in the simulation part, which happens off communication, algorithms of quality verification can be performed before using the data for the encryption; and (ii) also, as we are proposing when coupled maps from nature are used, there is information from the characterization of the phenomena that can indicate the degradation of the chaos, i.e., when the data is taken from an analog circuit.
5. Communication Scenario
In this section, we are going to provide the encryption and decryption algorithms for our proposal and give an example of the communication scenario between Alice and Bob.
Key selection. Alice should select μ1, μ2, and α. Additionally, Bob has his own private key: the parameter A, which is selected in the interval accepted by Alice.
Requirements. Alice, with the key selected, must compute the simulation with the help of Equations (8) and (9). This will generate a long list of (X,Y) points. Furthermore, she defines a tolerance which is related with the minimum value that she will accept for the parameter A.
Algorithm for encryption. To encrypt a message m, Bob should do the following:
- (a)
Obtain Alice’s authentic public key (Equation (8) and μ1).
- (b)
Represent the message as binary code.
- (c)
Obtain Alice’s first 50 X data.
- (d)
Compute 50 Y data for the first bit, using Equation (8), μ1, X data, and parameter A.
- (e)
Send Y data to Alice.
- (f)
Repeat for the next bits with a new 50 X data from Alice.
Algorithm for decryption. To recover the message Alice should do the following:
- (a)
Pair the first X data sent to Bob with the Y data received from Bob.
- (b)
Take just the last 12 pairs.
- (c)
For each pair calculate the Euclidian distance to each point of the long (X,Y) list of the simulation and preserve the minimum value of the distance.
- (d)
If the average of the 12 minimum pairs is greater than the tolerance, it is a 1-bit, otherwise it is a 0-bit.
- (e)
Repeat for the next 50 Y data from Bob.
Now for the example: Let us say that Alice wants to communicate with Bob, and he has a very important message to send her, the letter W. They want to use our crypto-proposal to transmit this letter by a secure channel. First Alice needs to choose the crypto-keys,
μ1,
μ2, and
α. Recall that they must lead to chaotic conditions (she could verify this with help of the Lyapunov exponent of NLCM from [
11]). Let us say she uses
μ1 = 3.1,
μ2 = 2.9, and
α = 0.3314, the same attractor from
Figure 1. She will announce publicly Equation (8) with
μ1 and
α from the previous selection and keep secret Equation (9) and
μ2. Bob will take this public information to transmit the message. Alice makes the simulation offline using Equations (8) and (9), and it will produce a long list of (X,Y) points. Equation (9), with its parameters, is the private key; it does not travel by channel. To start the communication from the long list that Alice has, she sends 50 X data to Bob. He will take his message and convert it to binary, he could use ASCII, so W will be 01010111, in eight bits. He takes the first bit, 0, and using Equation (8) recalculates a new pair Y for the fifty received from Alice and send back to her, in this Equation (8) it is the parameter A which Bob actually chooses, it is better if it is random, also to compute Equation he needs a Y
0 starting value which he selects also randomly. Eve the evil genius, who is listening in the channel from the data sent by Bob, cannot reconstruct the first bit from the 50 numbers thanks to the private keys of Bob and the fact that Equation (8) is in a chaotic state. Eve will need to wait until having enough data to use the attack described in the previous section. Alice receives the 50 Y numbers and using the last 12, pairs them with the last 12 of X that she sent and calculates the distance to every point in the long list from the simulation that she has and takes the minimum distances for the 12 pairs. If the average of the 12 minimum distances are lower than the tolerance (the minimum value that A can be) is a 0-bit, and if it is greater than the tolerance, it is a 1-bit. In this case, Alice will see a 0-bit. Now, the process is repeated for the next bits. Alice does not need to send adjacent X data to Bob for the transmission of the message.
Author Contributions
Conceptualization, H.S.-S.; Data curation, H.S.-S.; Formal analysis, H.S.-S.; Funding acquisition, E.G.B.; Investigation, H.S.-S. and E.G.B.; Methodology, H.S.-S.; Project administration, H.S.-S.; Supervision, E.G.B.; Validation, H.S.-S. and E.G.B.; Writing–original draft, H.S.-S.; Writing–review & editing, H.S.-S. and E.G.B.
Funding
This research was funded by MICITT and CONICIT grant number FI-0204-2012 and Universidad de Costa Rica’s Vicerrectoría de Investigación, grant number 834-B5-293.
Acknowledgments
We want to thank Manuel Ortega-Rodríguez for helpful discussions about non-linear physics and complexity.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Katz, J.; Menezes, A.J.; Van Oorschot, P.C.; Vanstone, S.A. Handbook of Applied Cryptography; CRC Press: Boca Raton, FL, USA, 1996; ISBN 9780849385230. [Google Scholar]
- Wang, X.; Gong, X.; Zhan, M.; Lai, C.H. Public-key encryption based on generalized synchronization of coupled map lattices. Chaos 2005, 15, 023109. [Google Scholar] [CrossRef] [PubMed]
- Kocarev, L.; Makraduli, J.; Amato, P. Public-key encryption based on Chebyshev polynomials. Circ. Syst. Signal Process. 2005, 24, 497–517. [Google Scholar] [CrossRef]
- Zhen, P.; Zhao, G.; Min, L.; Li, X. A survey of chaos-based cryptography. In Proceedings of the 2014 Ninth International Conference on P2P, Parallel, Grid, Cloud and Internet Computing, Guangdong, China, 8–10 November 2014; pp. 237–244. [Google Scholar]
- Devaney, R.L. An Introduction to Chaotic Dynamical Systems; CRC Press: Boca Raton, FL, USA, 1996; ISBN 9780201130461. [Google Scholar]
- Arroyo, D.; Amigo-Garcia, J.M.; Li, S.; Alvarez, G. On the Inadequacy of Unimodal Maps for Cryptographic Applications; RECSI: Tarragona, Spain, 2010; ISBN 9788469333044. [Google Scholar]
- Lawnik, M. Generalized logistic map and its application in chaos based cryptography. J. Phys. Conf. Ser. 2017, 936, 012017. [Google Scholar] [CrossRef]
- Kaneko, K. Theory and Applications of Coupled Map Lattices; Wiley: New York, NY, USA, 1993; Volume 159, ISBN 978-0471937418. [Google Scholar]
- Lloyd, A.L. The coupled logistic map: A simple model for the effects of spatial heterogeneity on population dynamics. J. Theor. Biol. 1995, 173, 217–230. [Google Scholar] [CrossRef]
- Schult, R.L.; Creamer, D.B.; Henyey, F.S.; Wright, J.A. Symmetric and nonsymmetric coupled logistic maps. Phys. Rev. A 1987, 35, 3115–3118. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Wang, X.Y. Spatiotemporal chaos in Arnold coupled logistic map lattice. Nonlinear Anal. Model. Control 2013, 18, 526–541. [Google Scholar]
- Tenny, R.; Tsimring, L.S.; Larson, L.; Abarbanel, H.D. Using distributed nonlinear dynamics for public key encryption. Phys. Rev. Lett. 2003, 90, 047903. [Google Scholar] [CrossRef] [PubMed]
- Xiao, D.; Liao, X.; Deng, S. A novel key agreement protocol based on chaotic maps. Inf. Sci. 2007, 177, 1136–1142. [Google Scholar] [CrossRef]
- Alvarez, G.; Li, S. Some Basic Cryptographic Requirements for Chaos-Based Cryptosystems. Int. J. Bifurc. Chaos 2006, 16, 2129–2151. [Google Scholar] [CrossRef]
- Tenny, R.; Tsimring, L.; Abarbanel, H.; Larson, L. Security of chaos-based communication and encryption. In Digital Communications Using Chaos and Nonlinear Dynamics; Larson, L., Tsimring, L., Liu, J.-M., Eds.; Institute for Nonlinear Science, Springer: New York, NY, USA, 2006; pp. 191–229. ISBN 978-0387297873. [Google Scholar]
- Elhadj, Z.; Sprott, J.C. Chaotifying 2-D piecewise-linear maps via a piecewise-linear controller function. Nonlinear Oscill. 2011, 13, 352–360. [Google Scholar] [CrossRef]
- Li, S.; Mou, X.; Cai, Y.; Ji, Z.; Zhang, J. On the security of a chaotic encryption scheme: Problems with computerized chaos in finite computing precision. Comput. Phys. Commun. 2003, 153, 52–58. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).