Using the Logistic Coupled Map for Public Key Cryptography under a Distributed Dynamics Encryption Scheme

Abstract

Nowadays, there is a high necessity to create new and robust cryptosystems. Dynamical systems have promised to develop crypto-systems due to the close relationship between them and the cryptographic requirements. Distributed dynamic encryption (DDE) represents the first mathematical method to generate a public-key cryptosystem based on chaotic dynamics. However, it has been described that the DDE proposal has a weak point in the decryption process related to efficiency and practicality. In this work, we adapted the DDE to a low-dimensional chaotic system to evaluate the weakness and security of the adaption in a realistic example. Specifically, we used a non-symmetric logistic coupled map, which is known to have multiple chaotic attractors improving the shortcomings related to the simple logistic map that manifests its inadequacy for cryptographic applications. We found a full implementation with acceptable computational cost and speed for DDE, which it is essential because it provides a key cryptographic requirement for chaos-based cryptosystems.

1. Introduction

Chaotic systems have great potential to be applied on the encryption of information. Crypto-systems are classified into branches: private-key and public-key [1]. In chaos-based systems, a great deal of effort has been done in the private-key part in comparison with the public [2]. One of the most important public-key chaos-based cryptosystem is presented in [3] where Chebyshev maps are used to encrypt, but its efficiency is still lower than RSA [4], a common weak point for this kind of crypto-proposal.

The logistic map is an excellent example of a chaotic system. Originally formulated to represent a simple demographic model to explain the increase of a population, the logistic map is a one-dimensional unimodal map and, as a result, its dynamics are quite limited [5]. It can be expressed by using the equation:

$$f\left(x\right)=\mu x\left(1-x\right)$$

(1)

where parameter μ is in the interval 0 ≤ μ ≤ 4. The unimodal aspect of the logistic map makes it inadequate for cryptographic applications because the parameter μ can be reconstructed from initial conditions, as in [6], even though a reasonable number of applications have been created [6]. A new relevant study [7] has been conducted to improve the logistic map for cryptographic applications, but losing the mathematical simplicity of Equation (1).

A coupled map lattice (CML) is a dynamical system that models the behavior of non-linear systems. They are predominantly used to qualitatively study the chaotic dynamics of spatially-extended systems. This includes the dynamics of spatiotemporal chaos where the number of effective degrees of freedom diverges as the size of the system increases. CML incorporates a system of equations (coupled or uncoupled), a finite number of variables, a global or local coupling scheme, and the corresponding coupling terms [8].

The logistic coupled map is one of the simplest CMLs, first considered as the simplest biologically realistic model that incorporates spatial effects, it is based on two coupled logistic maps by a linear coupling:

$$x_{n+1}=f\left(x_n\right)+\alpha \left(y_n-x_n\right)$$

(2)

$$y_{n+1}=f\left(y_n\right)-\alpha \left(y_n-x_n\right)$$

(3)

where f(x) is the logistic map of Equation (1) and α is a coupling parameter. In the logistic map only two routes to chaos are observed (period doubling and intermittency), and the second dimension of the logistic coupled map allows the quasiperiodic route to occur [9]. The non-symmetric case of the logistic coupled map [10] occurs when, in Equations (2) and (3), we use a different parameter μ for f(x), so the equations take the form:

$$x_{n+1}=f_1\left(x_n\right)+\alpha \left(y_n-x_n\right)$$

(4)

$$y_{n+1}=f_2\left(y_n\right)-\alpha \left(y_n-x_n\right)$$

(5)

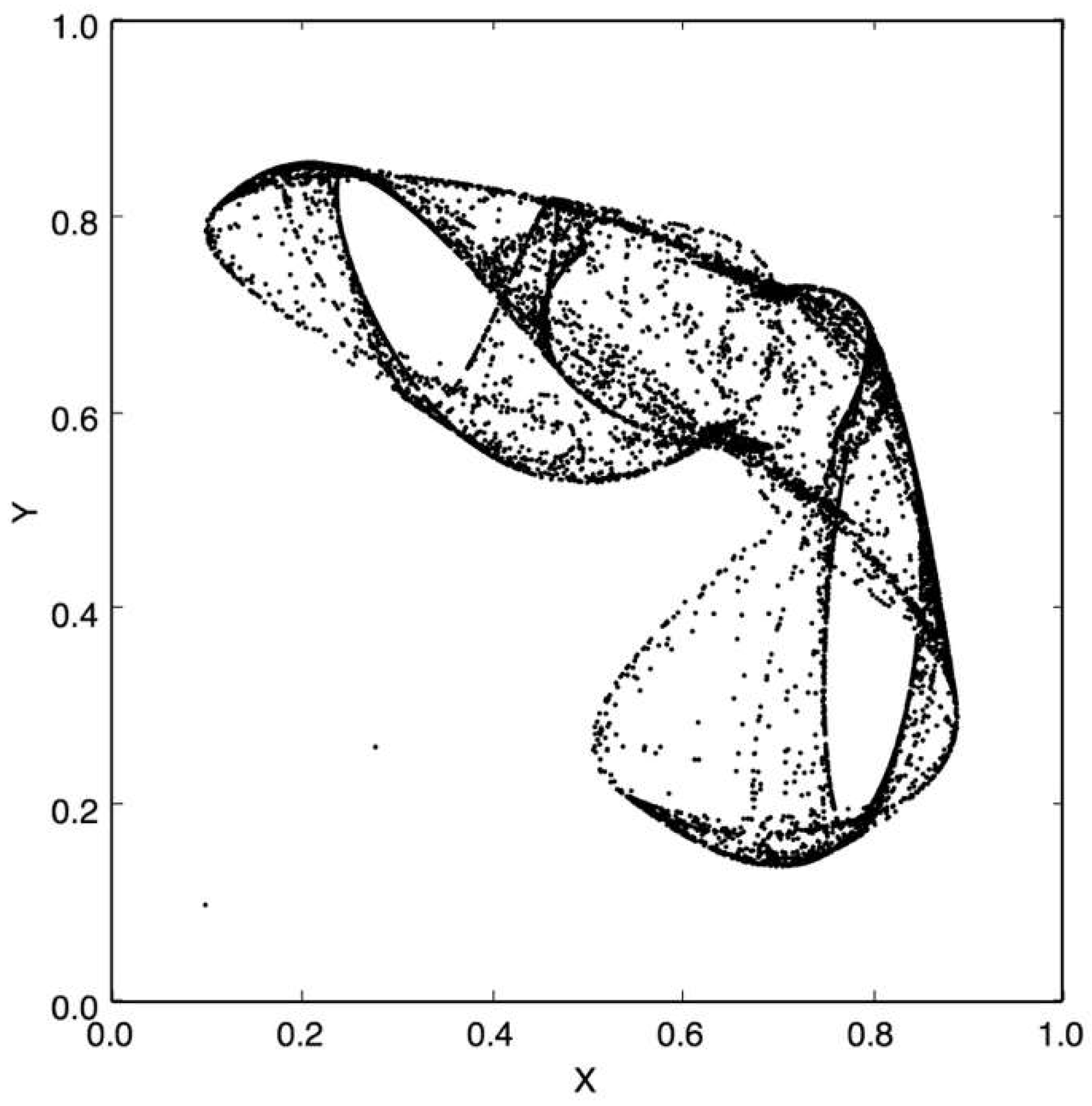
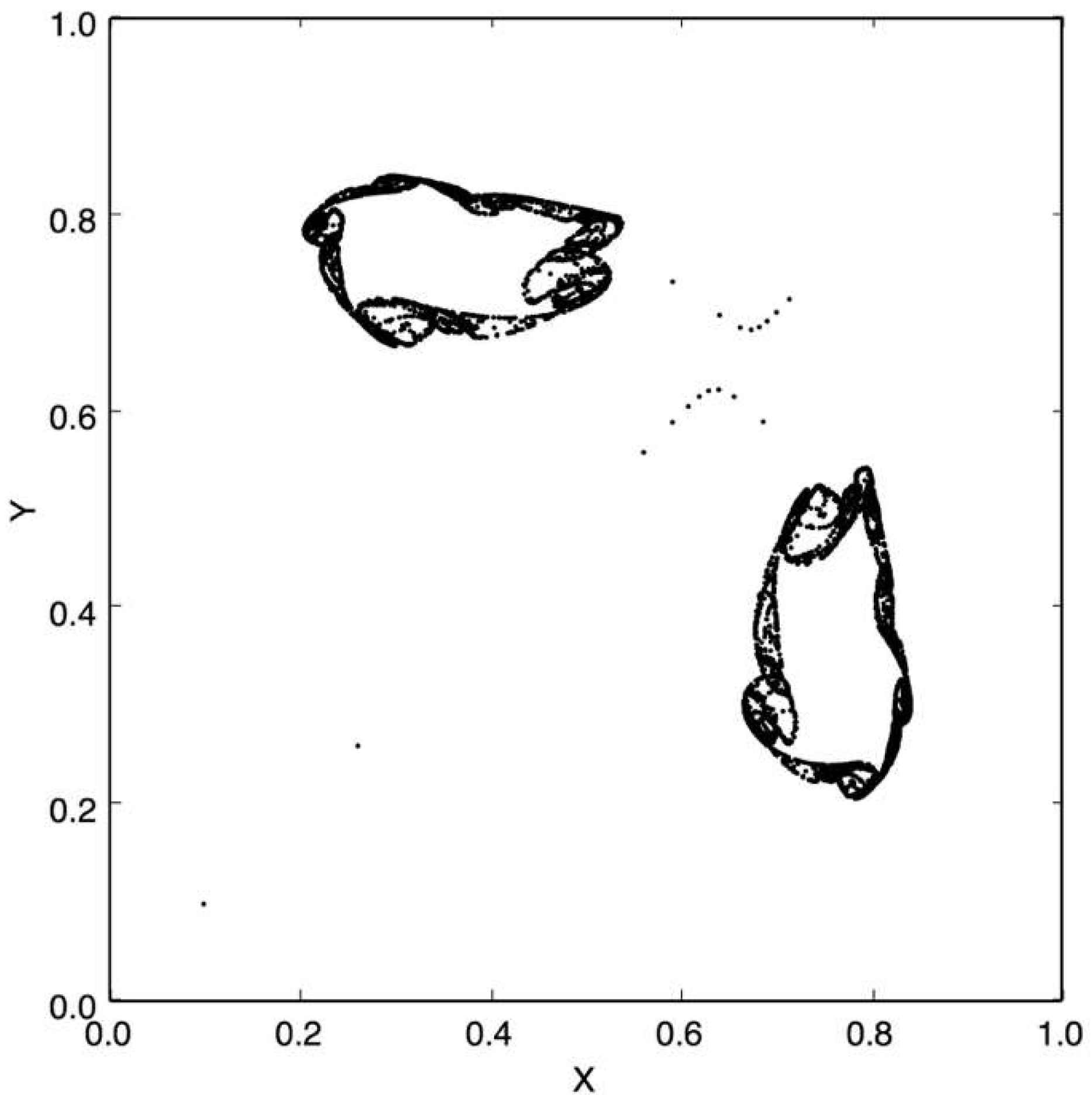
where f₁(x) means to use the logistic map of Equation (1) with μ₁ and f₂(x) with μ₂. Multiple chaotic attractors are observed in this system improving the unimodal shortcoming of the simple logistic map [8]. Figure 1 and Figure 2 show examples of chaotic attractors for the non-symmetric logistic coupled map (NLCM). The NLCM has a well documented chaotic range for 3.63 ≤ μ ≤ 4 and 0 ≤ α ≤ 1 [11].

A group from University of California San Diego (UCSD) introduced a theoretical scheme in [12] for asymmetric encryption exploiting properties of nonlinear dynamical systems where a high-dimensional dissipative non-linear dynamical system is distributed between a transmitter and a receiver. Therefore, they call the method distributed dynamics encryption (DDE). The transmitter dynamics are public, and the receiver dynamics are private, and they are not shared in the channel. A message is encoded by modulation of the parameters of the transmitter, and this results in a shift of the overall system attractor. An unauthorized receiver does not know the hidden dynamics of the receiver and cannot decode the message [12]. This proposal has been criticized due to its difficulties in the implementation and is categorized as non-practical [13].

This work will take the proposal of DDE and adapt it for a low-dimensional system using the coupled logistic map. We will study the encryption, the decryption, and the common attack for this cryptographic system. This is important for DDE because it provides an implementation without loss of security with acceptable cost and speed, which is a relevant cryptographic requirement for chaos-based cryptosystems suggested by [14]. It is our understanding that, at the time we wrote this work, this is the first fully functional computational implementation for encryption of DDE, besides the concept proof presented by the UCSD group. Even more, the work presented here is the missing example for DDE pointed out in the literature [4].

2. Encryption

The basic idea of distributed dynamics encryption (DDE) is to split a dynamical system of dimension D_T + D_R into two parts with D_T transmitter variables t(n) = [t₁(n); …; t_DT(n)], and D_R receiver variables r(n) = [r₁(n) ; …; r_DR(n)]. The receiver receives the scalar signal s_t(n) from the transmitter, and the transmitter receives the scalar signal s_r(n) from the receiver:

$$t\left(n+1\right)=F_T\left(t\left(n\right),s_r\left(n\right),m\left(n\right)\right)$$

(6)

$$r\left(n+1\right)=F_R\left(r\left(n\right),s_t\left(n\right)\right)$$

(7)

where m(n) is the message which we want to encrypt. We allow that m(n) only takes values 0 or 1; this requirement creates a binary message. The receiver must simulate the entire dynamics before she starts the communication; this will create a list of points necessary for encrypting and decrypting the message. To perform the simulation, she will select the parameters and equations that will serve as the public and private keys, which is explained below.

The encryption for our low-dimensional implementation comes from a relation between Equations (4)–(7), where x (Equation (4)) will be the dynamic split to the transmitter and y (Equation (5)) will be the receiver part:

$$x_{n+1}=f_1\left(x_n\right)+\alpha \left(y_n-x_n\right)+\mathrm{A}\ast \mathrm{m}$$

(8)

$$y_{n+1}=f_2\left(y_n\right)-\alpha \left(y_n-x_n\right)$$

(9)

where the parameter A is a modulation of the message. In our implementation A takes random values between 0.001 and 0.01 to provide additional security to the system. Figure 3 shows an eight-bit encrypted message (01010111, which, using the ASCII standard, is the letter, “W”). For an easy identification we differentiate the points which correspond to a 0 bit to those which correspond a 1 bit. The security of this implementation resides in the overlap and closeness of those points. Only if you have the previous simulation can you decrypt the message. Figure 4 shows a different attractor with a longer message of 32-bits (01010111 01101111 01110010 01110100, which, using the ASCII standard, is a four-letter message, “Wort”). In this scheme, a different chaotic attractor represents a different pair of cryptographic keys. Equation (8), with its corresponding parameters, is the public key and Equation (9) is the private key. Something relevant is that the receiver does not need to know the parameter A to decrypt the message: in this sense parameter A represents a private key of the transmitter, providing more security to the encrypted message. Parameter A is not used in the decryption process because we are using a chaotic attractor, which, after some iterations of the full dynamic, is only known by the receiver, and the signal sent by the transmitter will converge to the attractor or not.

3. Decryption

An authorized receiver knows all quantities, public and private, and can establish off-line the admissible attractors, or other dynamical aspects of the total system, for all allowed values of m(n). For decryption, it is necessary to previously know all the points of the simulation. The decrypting process corresponds to the calculation of the distance of each received point from the transmitter to the points of the simulations. It is necessary to compute this distance to every point of the simulation and select the minimum value. If this value is lower than a tolerance parameter, which is related to parameter A of Equation (8), it is a 0-bit, and if it is greater, it is a 1-bit.

Even though this decryption process seems to be easy when the full dynamic is known, it is computational expensive, an aspect covered in Section 6 of this paper.

4. Cryptanalysis

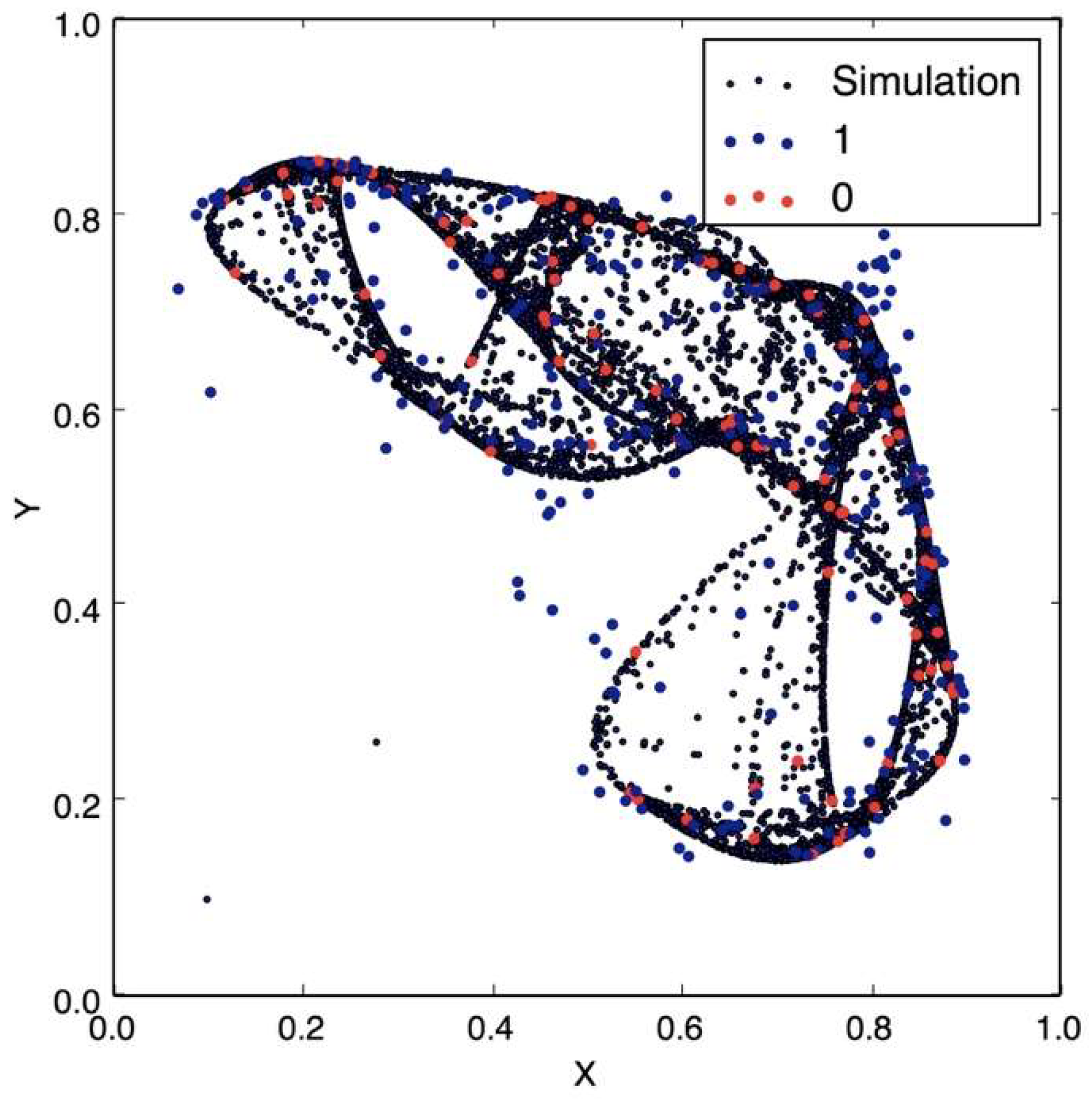
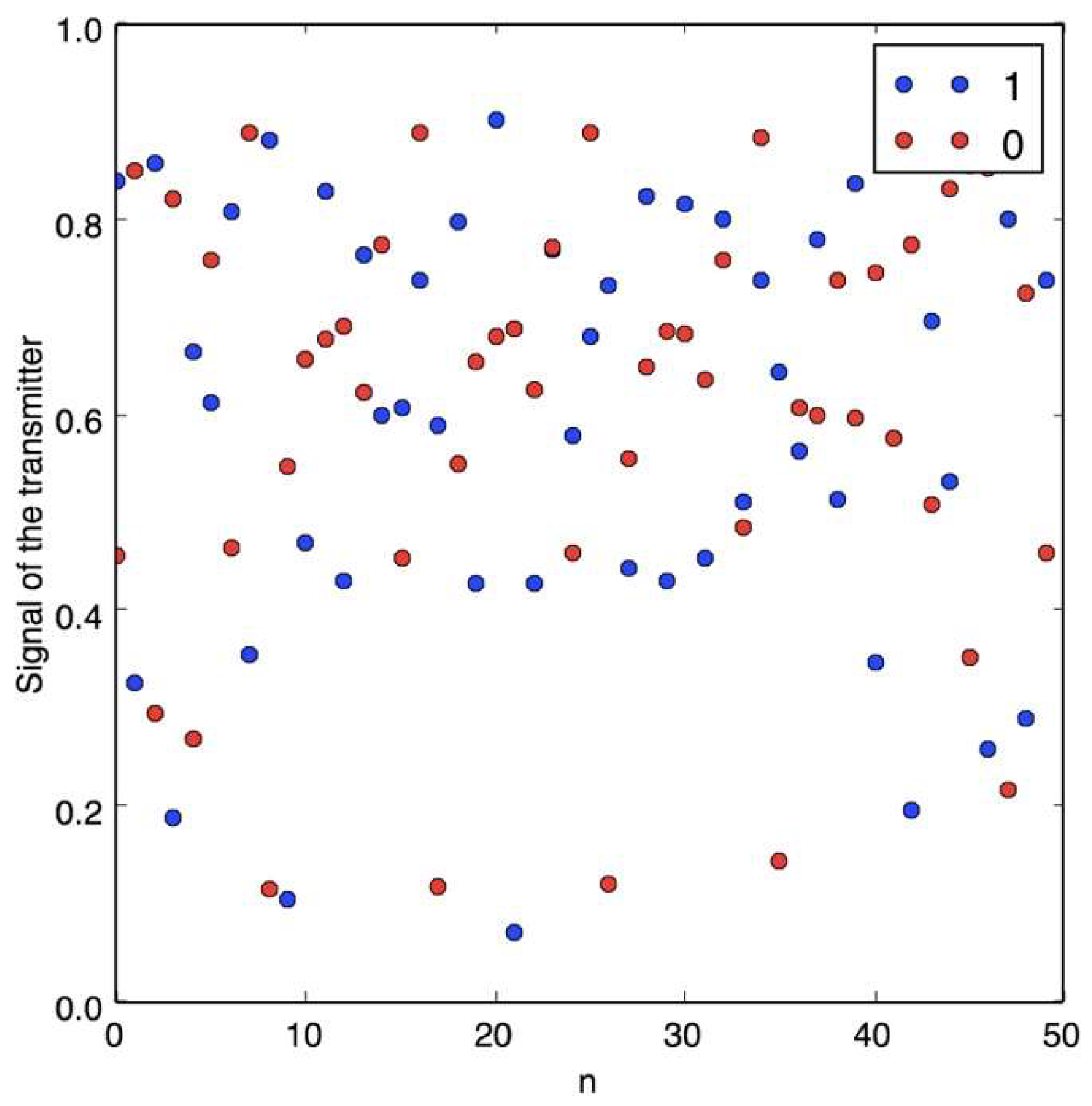
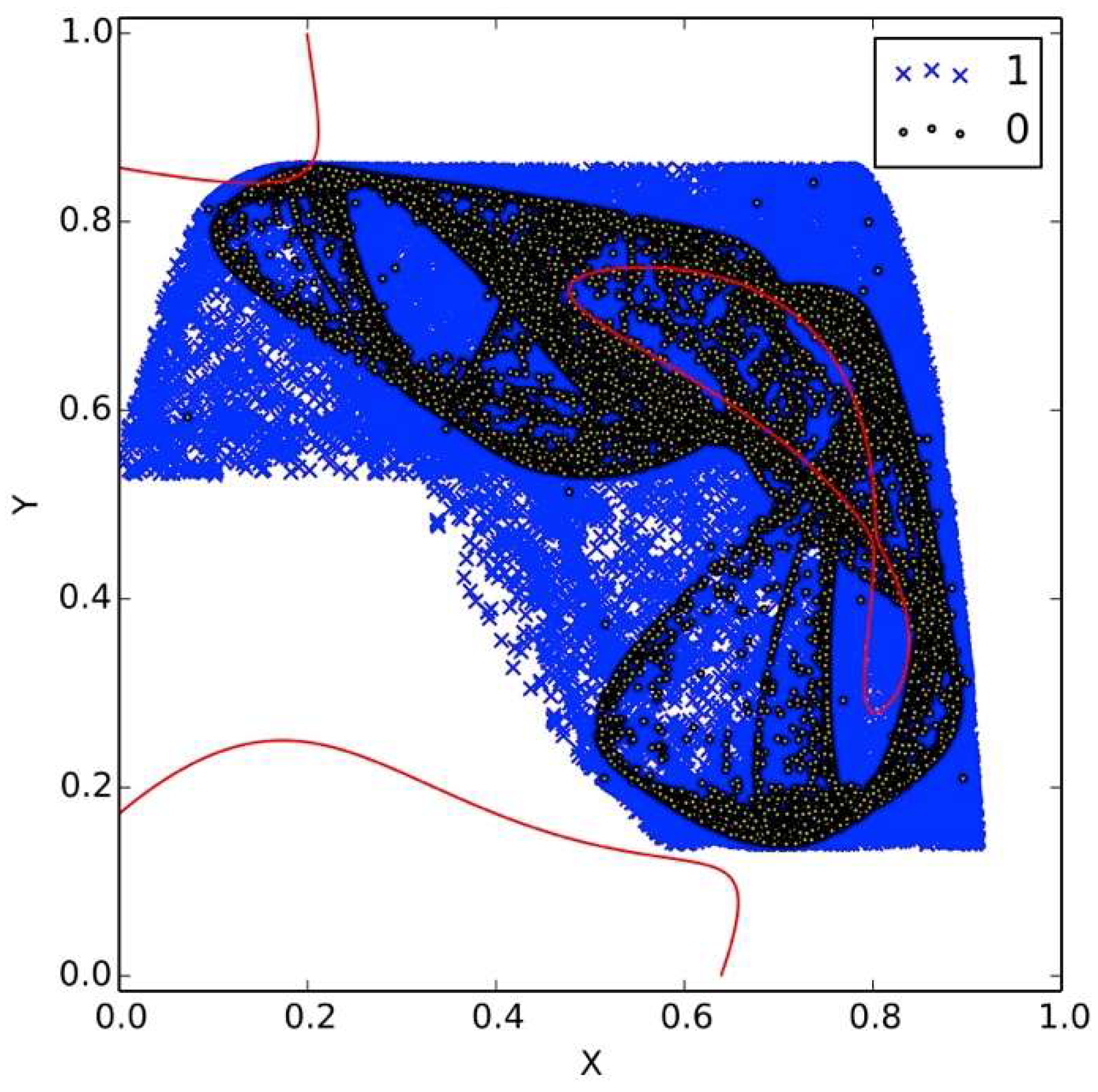
An unauthorized receiver may attempt several methods to attack DDE and decode the secret message m(n), but it has been demonstrated in [15] that the only one where non-defense can be used it is the one analyzed in this section. As the security resides in the fact the signal traveling in the channel is chaotic, our implementation is still as defensible as the original DDE. Figure 5 shows the data traveling through the communication channel, where an unauthorized receiver cannot easily resolve the message, and also due to topologically transitivity, as more data is transmitted in the channel, all the space will be occupied. 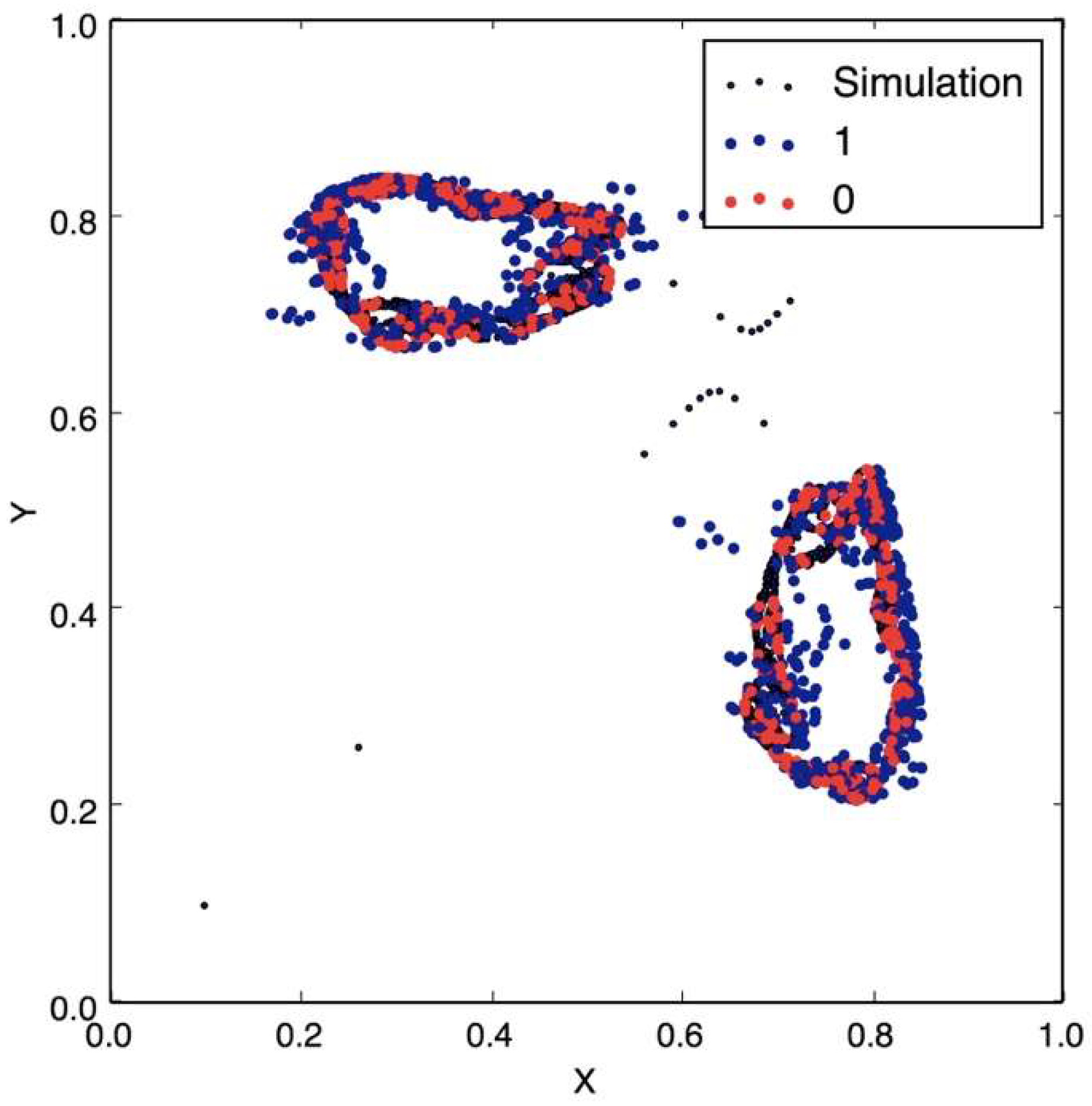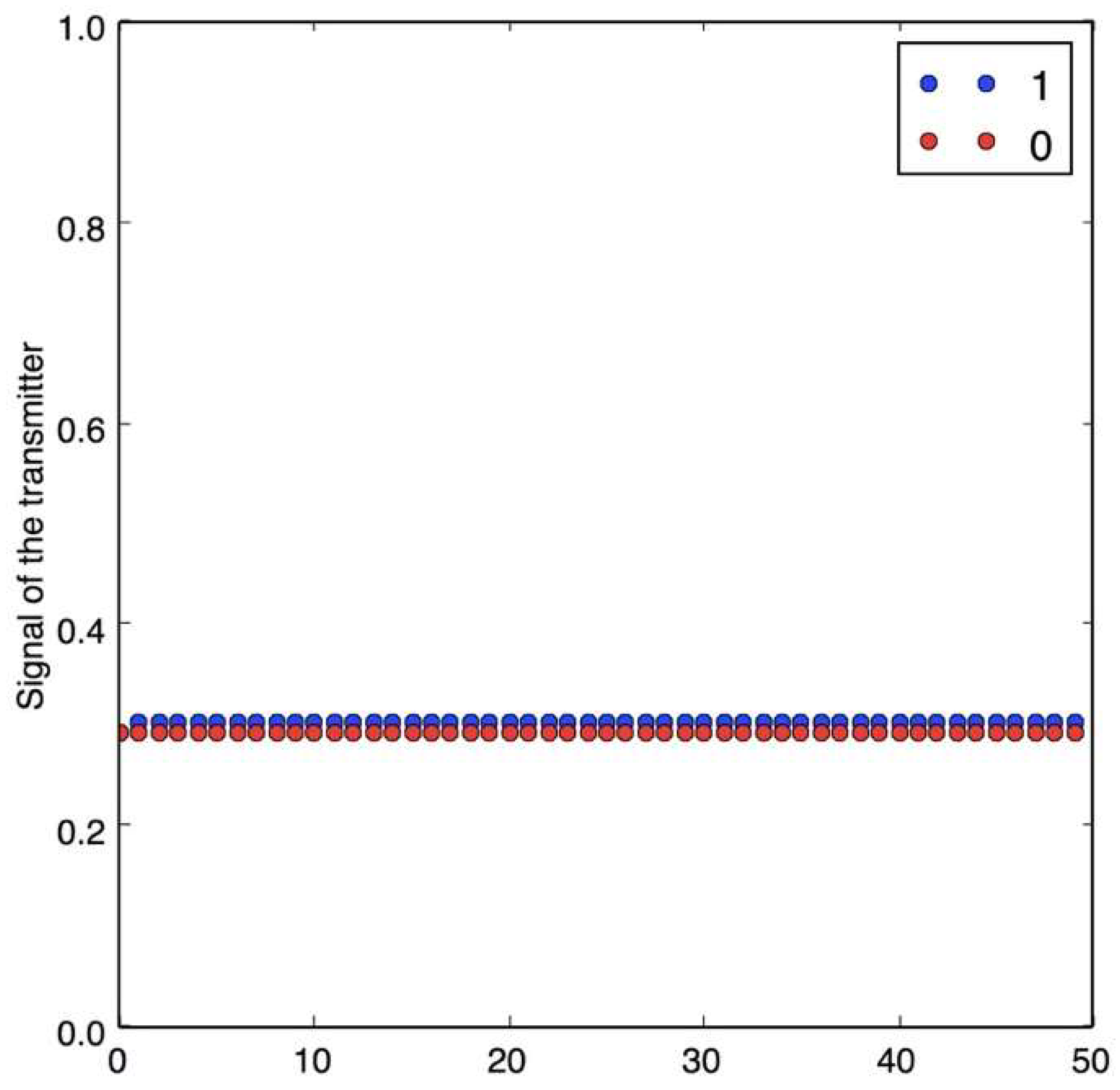On the other hand, Figure 6 shows the case when the attractor is not chaotic: here, it is easy to identify the two states (0 or 1).

One such method is to reconstruct the positions of the attractors that correspond to the transmission of 0 and 1 by storing and clustering samples of many transmitted bits. Knowing the positions of the attractors would enable the unauthorized receiver to decode the message using the same method as the authorized receiver [12].

The chaotic dynamics may contain channel and noise that make the dynamics stochastic. An unauthorized receiver may attempt to generate a hidden Markov model of the transmitter public dynamics for each possible value of the message m, and obtain a maximum likelihood (ML) estimation m’ of the message m. The decoded message will then be given by:

$$m^{\prime }=ma{x}_{m\in \left(0,1\right)}p\left(s_t\left(1\right),\dots ,s_t\left(D_T+1\right)|m\right)$$

(10)

In order to generate the hidden Markov model, the unauthorized receiver will need to quantize the transmitter state in a time delay reconstructed embedding space, and to estimate the state transition probabilities, as well as the observation probabilities of the model [15].

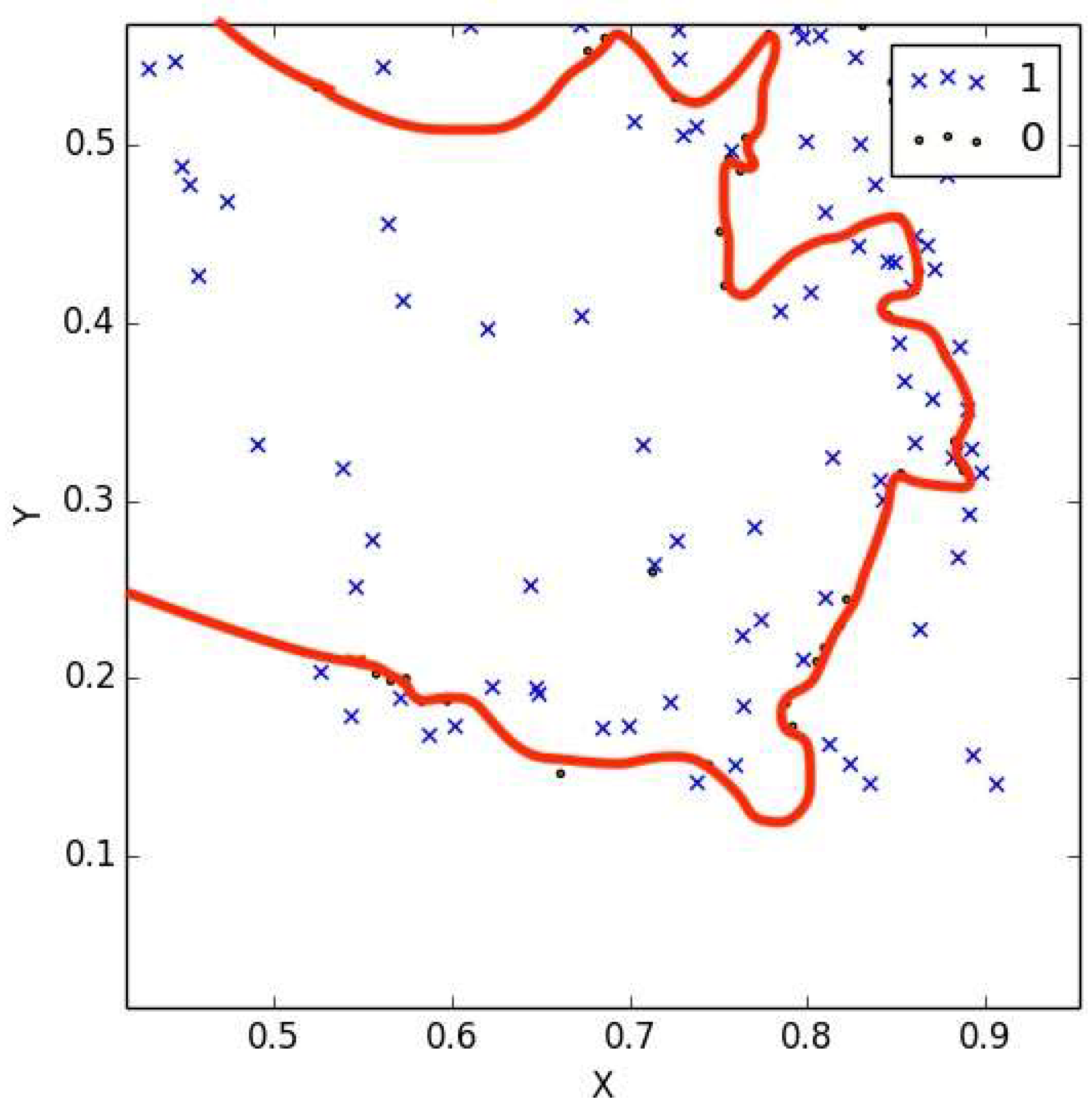
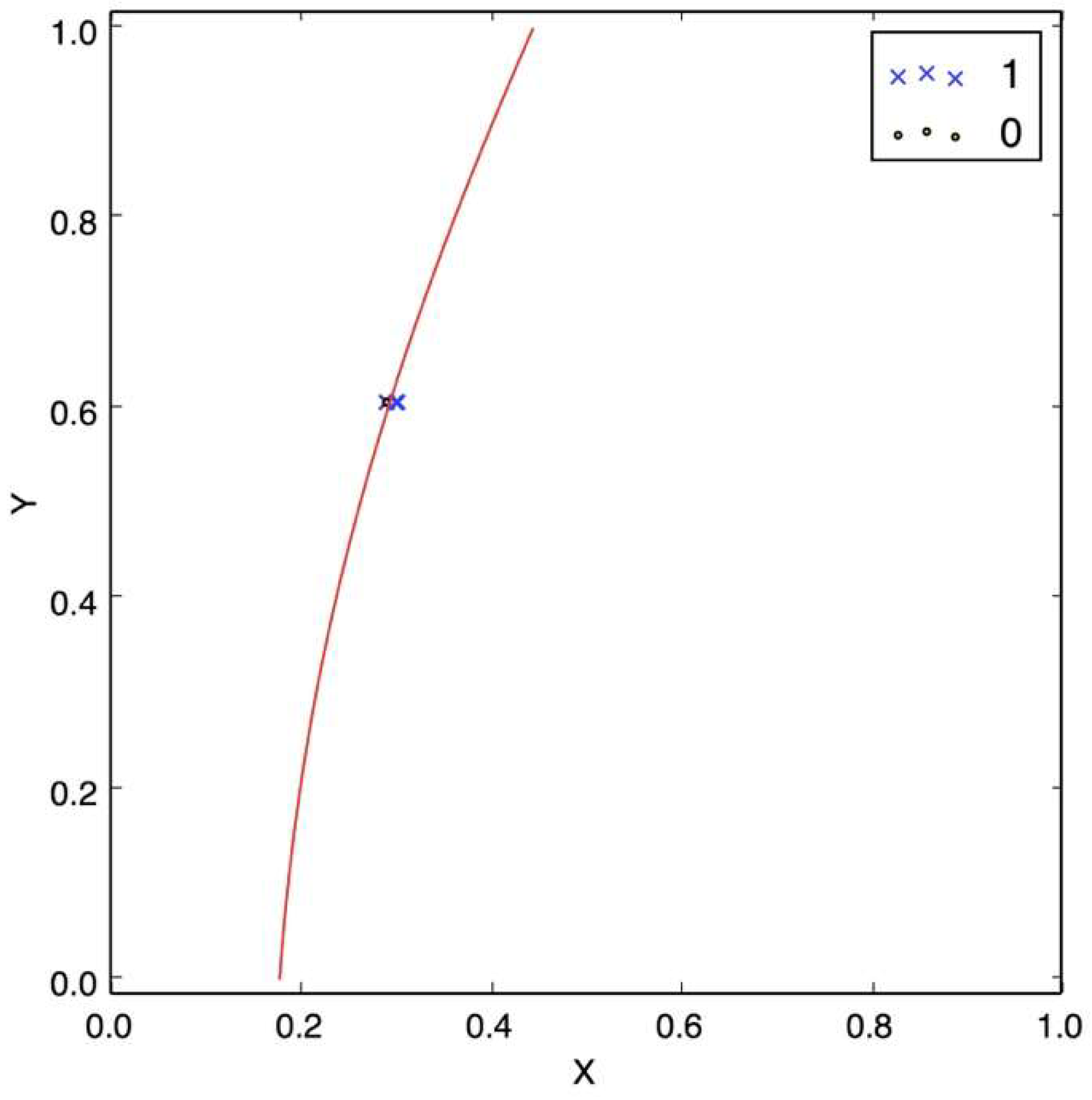
The attack proposed was implemented for our low-dimensional model. Figure 7 shows how the case of a message encrypted using a non-chaotic map where the training accuracy is 95%, which shows the effectiveness of the attack. When the number of bits is lower than that necessary to train the model, according to [14], the accuracy reduces to lower than 40%, in which a probabilistic attack, as in [1], cannot help this particular attack. This case is shown in Figure 8 where the red line is the decision boundary, which is far from being correct. 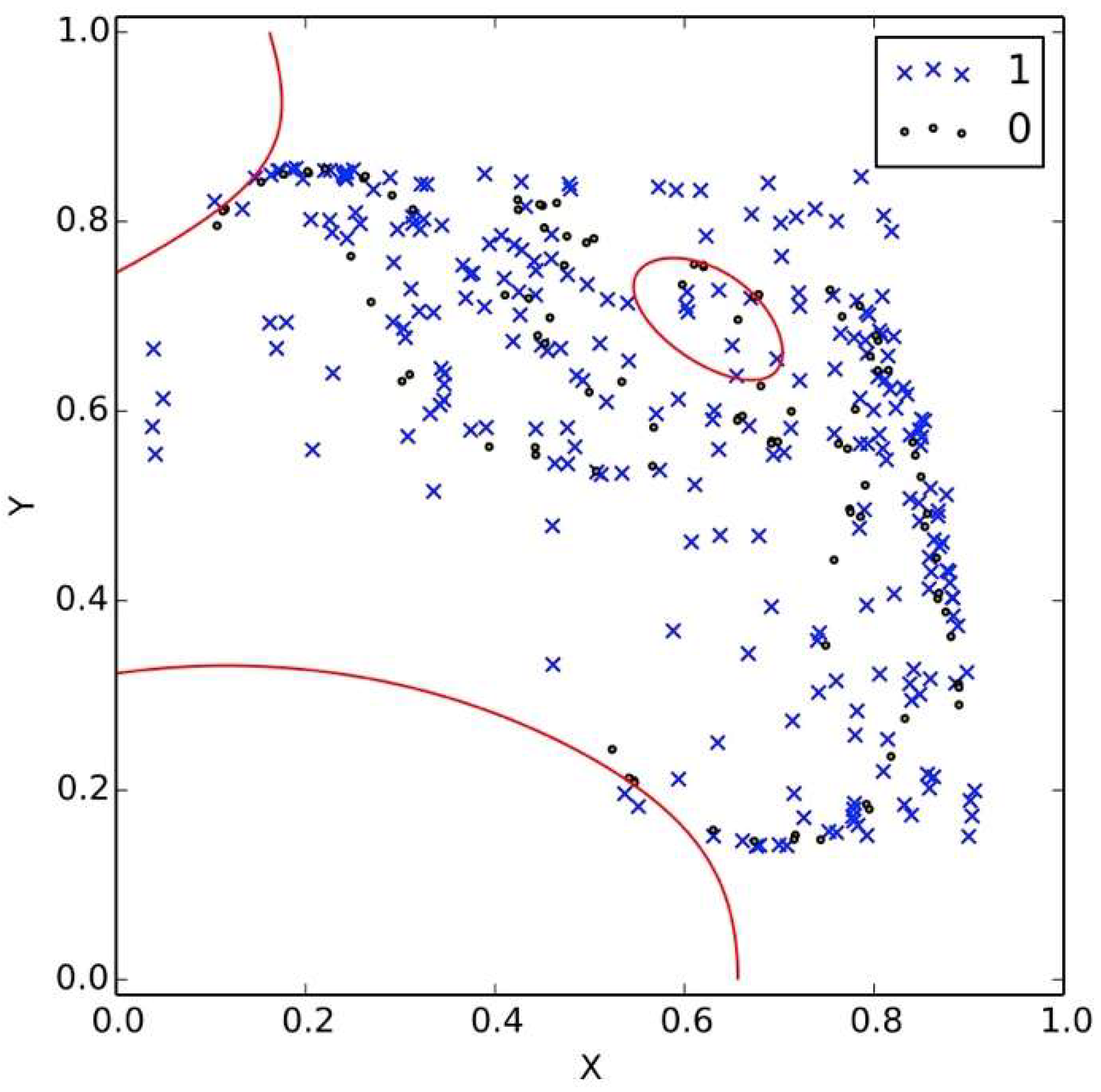Figure 9 has a larger number of bits, 60,000, and the boundary is more visible, but it is not enough to recover the message. Figure 10 shows the case where the number of bits is equal to that necessary to perform the attack: it is visible how the decision curve can resolve for 0 or 1-bits. Equation (9) from [15] shows the number of states that can be transmitted before the decision curve can be resolved:

$$Ns\approx {\left(\frac{L_T}{L_q}\right)}^{D_T}$$

(11)

where L_T is the range of the data transmitted and L_q is the quantization in the signal. Equation (11) is still useful in our case because it has been derived in general for any CML. For our implementation this number is around 4 × 10⁷ which shows why Figure 10 can resolve the decision curve and how the security of this implementation is of the same level as the original DDE proposal.

A relevant feature to point out is to see how a very small change in the dynamics of the receiver creates very different attractors. This can be observed in Figure 1 and Figure 2, where the only change between them is the value of μ with just a 0.2 differential, and the produced dynamic is totally different. This is very useful because we do not need to change the public key to have a new crypto dynamic, representing a good option to protect from the attack described in this section.

The NLCM represents an improvement over the logistic map, but another map with our low-dimensional crypto scheme, like the piecewise linear map [16], represents a new pair of crypto keys.

The chaos degradation is a well-known problem for chaos-based cryptosystems [17]. In DDE, this problem is addressed by two means: (i) as the chaotic process is involved only in the simulation part, which happens off communication, algorithms of quality verification can be performed before using the data for the encryption; and (ii) also, as we are proposing when coupled maps from nature are used, there is information from the characterization of the phenomena that can indicate the degradation of the chaos, i.e., when the data is taken from an analog circuit.

5. Communication Scenario

In this section, we are going to provide the encryption and decryption algorithms for our proposal and give an example of the communication scenario between Alice and Bob.

Key selection. Alice should select μ₁, μ₂, and α. Additionally, Bob has his own private key: the parameter A, which is selected in the interval accepted by Alice.

Requirements. Alice, with the key selected, must compute the simulation with the help of Equations (8) and (9). This will generate a long list of (X,Y) points. Furthermore, she defines a tolerance which is related with the minimum value that she will accept for the parameter A.

Algorithm for encryption. To encrypt a message m, Bob should do the following:

(a)

Obtain Alice’s authentic public key (Equation (8) and μ₁).

(b)

Represent the message as binary code.

(c)

Obtain Alice’s first 50 X data.

(d)

Compute 50 Y data for the first bit, using Equation (8), μ₁, X data, and parameter A.

(e)

Send Y data to Alice.

(f)

Repeat for the next bits with a new 50 X data from Alice.

Algorithm for decryption. To recover the message Alice should do the following:

(a)

Pair the first X data sent to Bob with the Y data received from Bob.

(b)

Take just the last 12 pairs.

(c)

For each pair calculate the Euclidian distance to each point of the long (X,Y) list of the simulation and preserve the minimum value of the distance.

(d)

If the average of the 12 minimum pairs is greater than the tolerance, it is a 1-bit, otherwise it is a 0-bit.

(e)

Repeat for the next 50 Y data from Bob.

Now for the example: Let us say that Alice wants to communicate with Bob, and he has a very important message to send her, the letter W. They want to use our crypto-proposal to transmit this letter by a secure channel. First Alice needs to choose the crypto-keys, μ₁, μ₂, and α. Recall that they must lead to chaotic conditions (she could verify this with help of the Lyapunov exponent of NLCM from [11]). Let us say she uses μ₁ = 3.1, μ₂ = 2.9, and α = 0.3314, the same attractor from Figure 1. She will announce publicly Equation (8) with μ₁ and α from the previous selection and keep secret Equation (9) and μ₂. Bob will take this public information to transmit the message. Alice makes the simulation offline using Equations (8) and (9), and it will produce a long list of (X,Y) points. Equation (9), with its parameters, is the private key; it does not travel by channel. To start the communication from the long list that Alice has, she sends 50 X data to Bob. He will take his message and convert it to binary, he could use ASCII, so W will be 01010111, in eight bits. He takes the first bit, 0, and using Equation (8) recalculates a new pair Y for the fifty received from Alice and send back to her, in this Equation (8) it is the parameter A which Bob actually chooses, it is better if it is random, also to compute Equation he needs a Y₀ starting value which he selects also randomly. Eve the evil genius, who is listening in the channel from the data sent by Bob, cannot reconstruct the first bit from the 50 numbers thanks to the private keys of Bob and the fact that Equation (8) is in a chaotic state. Eve will need to wait until having enough data to use the attack described in the previous section. Alice receives the 50 Y numbers and using the last 12, pairs them with the last 12 of X that she sent and calculates the distance to every point in the long list from the simulation that she has and takes the minimum distances for the 12 pairs. If the average of the 12 minimum distances are lower than the tolerance (the minimum value that A can be) is a 0-bit, and if it is greater than the tolerance, it is a 1-bit. In this case, Alice will see a 0-bit. Now, the process is repeated for the next bits. Alice does not need to send adjacent X data to Bob for the transmission of the message.

6. Computer Experiment

Our implementation has been made in Python with the help of packages Numpy for the data management and HMMlearn for the Markov chain used in the attack. The calculations were performed on a Linux system with a Core i7 2.6GHz PC with 16 GB of RAM. Figure 1, Figure 2, Figure 3 and Figure 4 were computed with one million points for the chaotic attractor with an average time of 33 s for the calculation. Figure 10 has the higher computation time; in this case, the Markov chain training took an average time of 72 h due to the 50 million bits needed for the training.

Table 1. Details of the encryption/decryption time.

No. Bits	Encryption Time (s)	Decryption Time (s)
8	0.045	141.1081
16	0.0997	293.1638
32	0.2017	600.4974
64	0.3199	1318.4119
128	0.5973	2567.0675
256	1.7431	5297.5988

shows the performance of the encryption and decryption algorithms where, as expected, the time of both increases as more bits are needed to be processed. It is remarkable how the encryption time is relatively small compared with the decryption time. This expensive decryption time is the weakness of DDE and opens additional research into this kind of crypto-system. However, we have shown how the DDE may be implemented.

7. Conclusions

In this paper, we have made a full implementation of DDE, where we have described both encryption and decryption processes, showing how the implementation of DDE is possible with a low-dimensional dynamical system. This is relevant to this research field because it provides a functional example for DDE with the same kind of security provided by the high-dimensional systems which it is a key cryptographic requirement for chaos-based cryptography. Further, this implementation opens the possibility to investigate better ways to enhance the efficiency of DDE.

Our low-dimensional DDE represents a platform to evaluate different coupled maps. Future research can be done in the comparison of the security of low-dimensional and high-dimensional DDE.