More Compact Orthogonal Drawings by Allowing Additional Bends †
Abstract
1. Introduction
2. State-of-the-Art
3. Notation and Preliminary Results
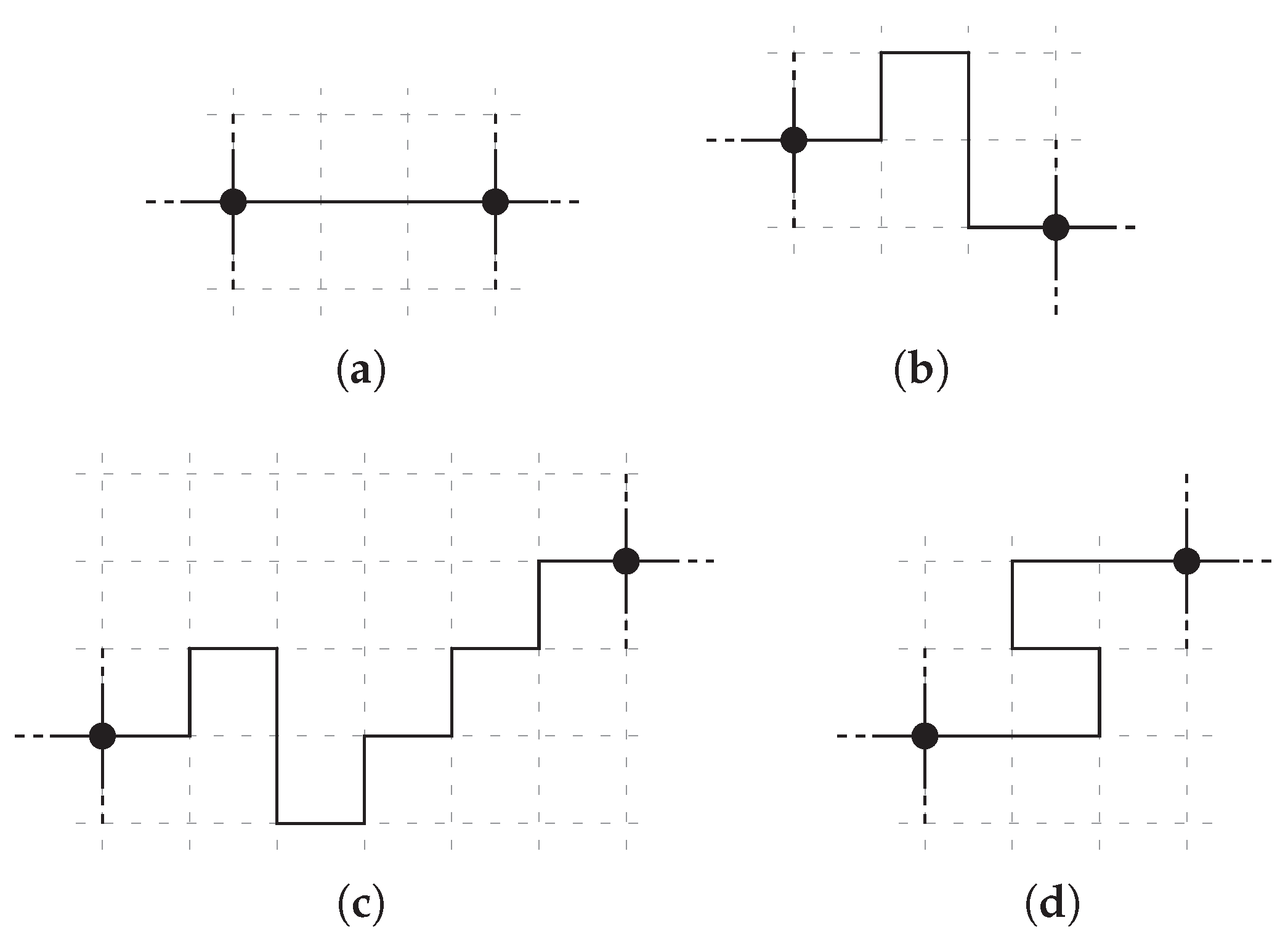
3.1. Orthogonal Graph Drawing
3.2. Compaction of Orthogonal Drawings
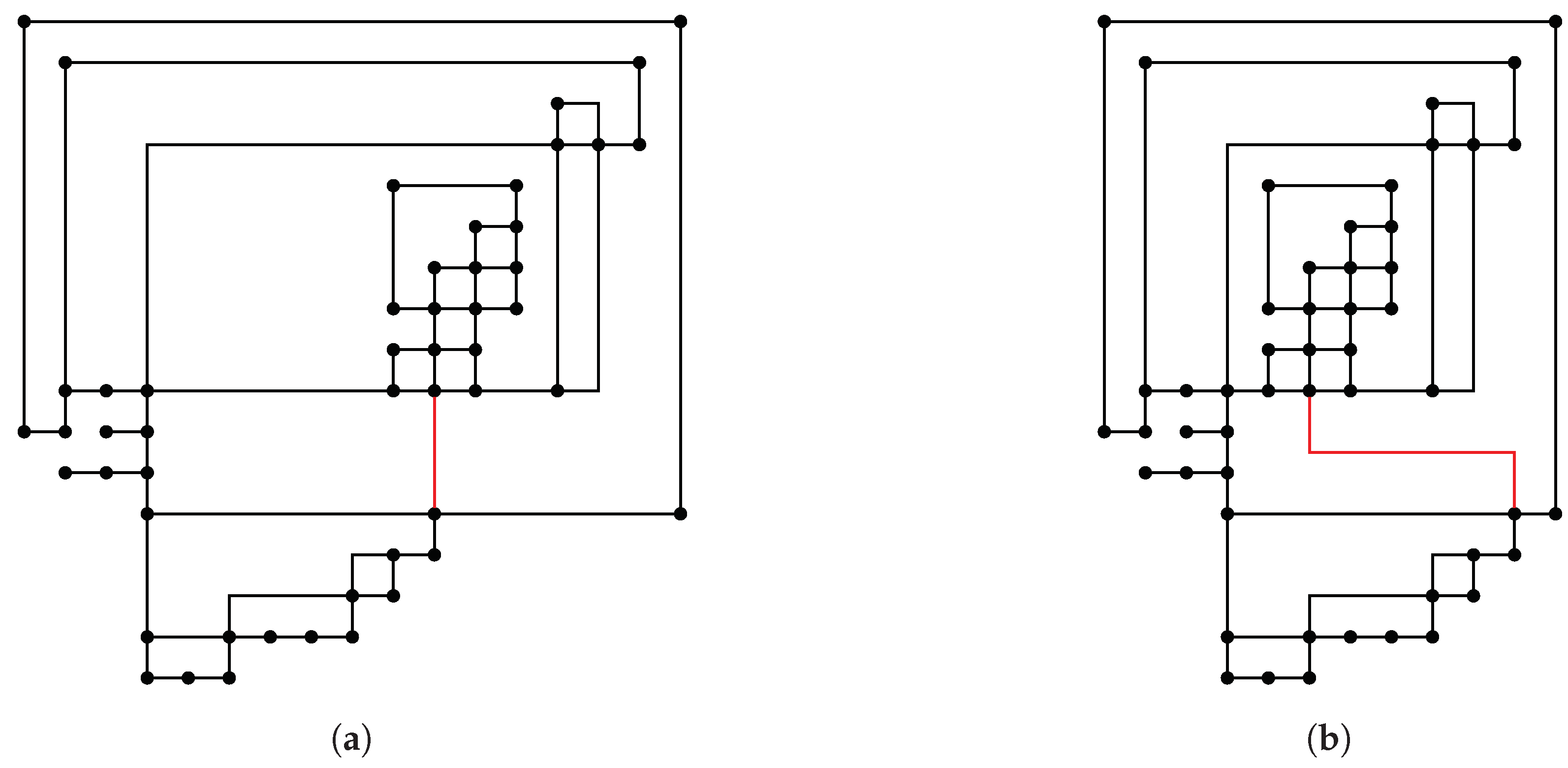
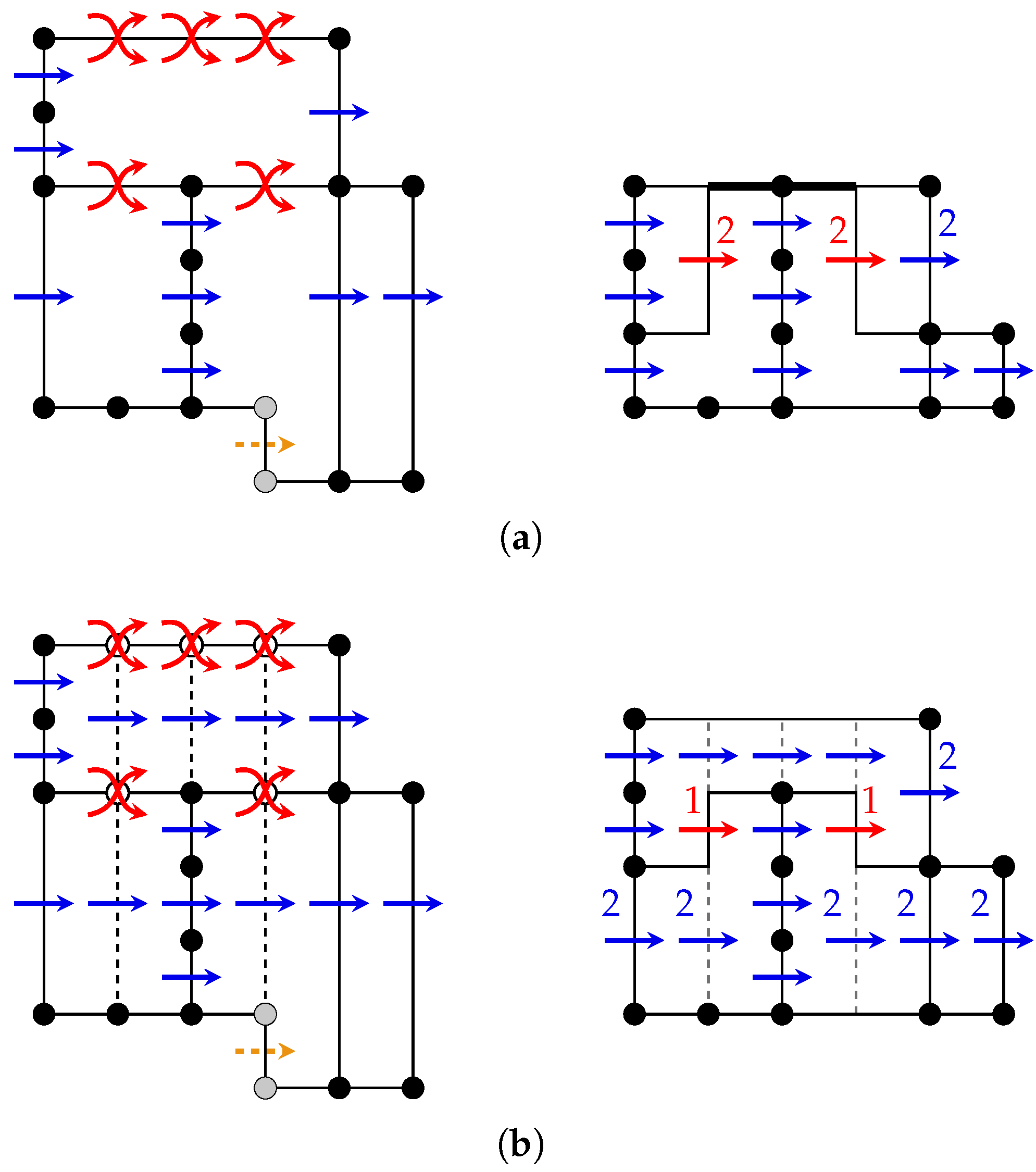
4. The Fled-Five Compaction Approach
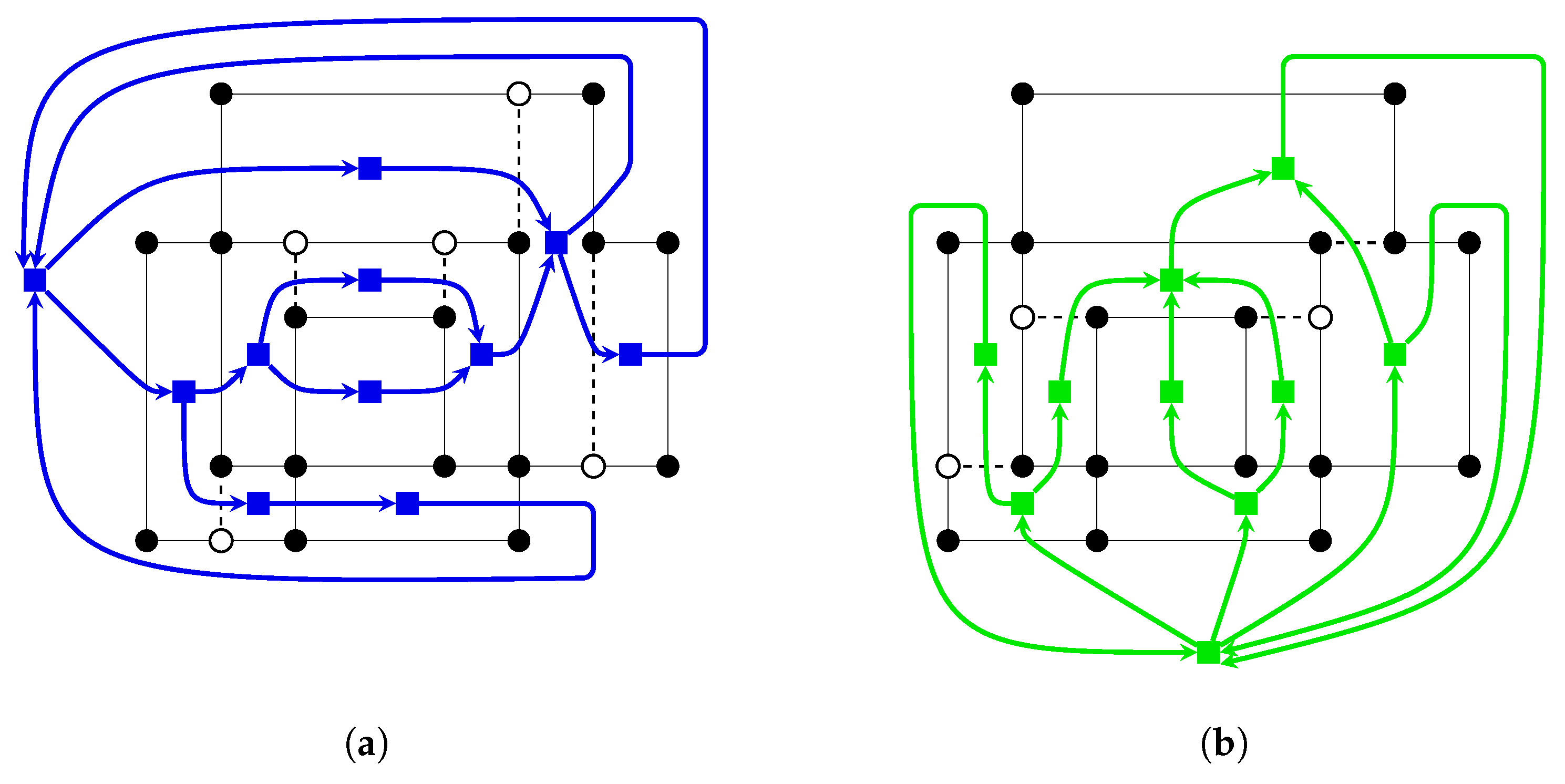
4.1. The Fled-Five Compaction Algorithm
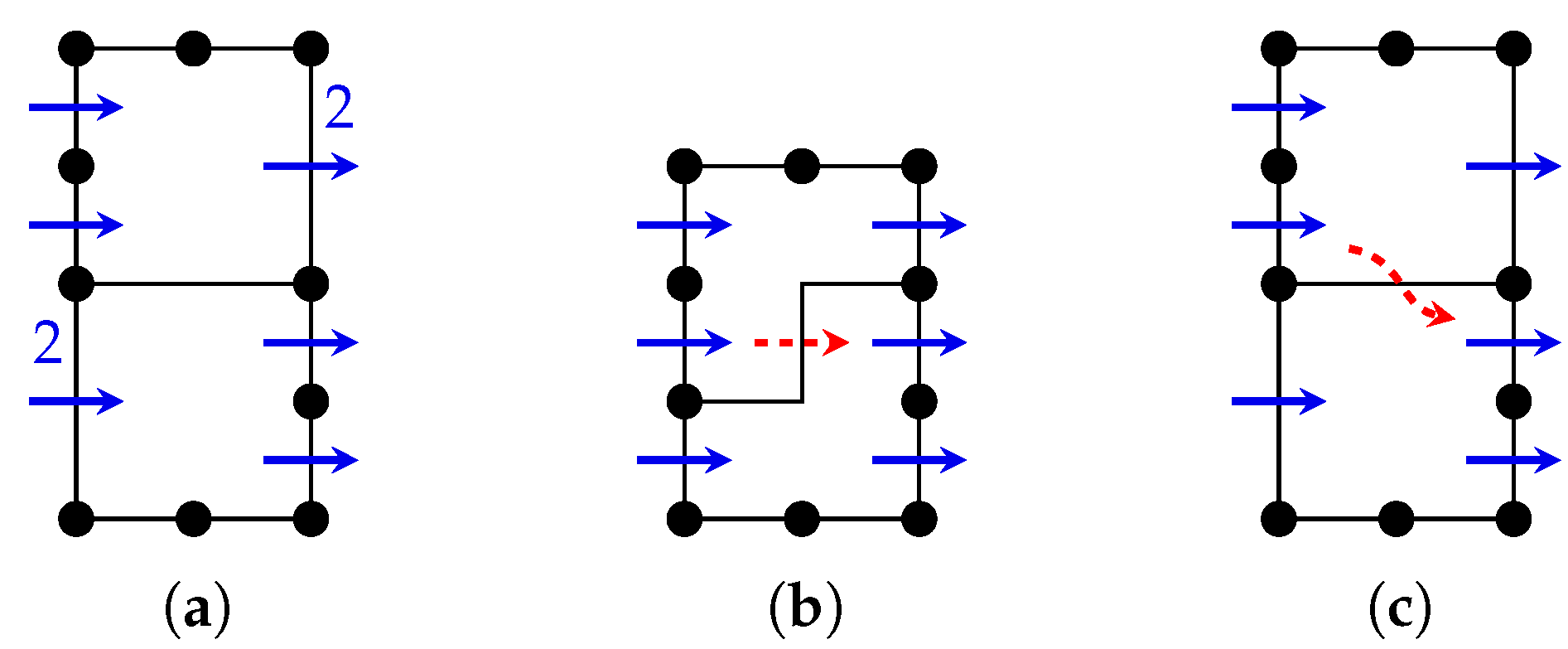
| Algorithm 1: verticalAugmentation |
 |
| Algorithm 2: verticalNetworkConstruction |
 |
| Algorithm 3: verticalLengthAssignment |
 |
| Algorithm 4: verticalFledFive |
| Input: orthogonal drawing Output: optimal solution to the Fled-Five compaction problem ← normalize(); ← verticalAugmentation(); N ← verticalNetworkConstruction(); x ← computeMinimumCostFlow(N); ← verticalLengthAssignment(, x); ← RemoveVisibilityEdges(); ← RemoveBendVertices(); |
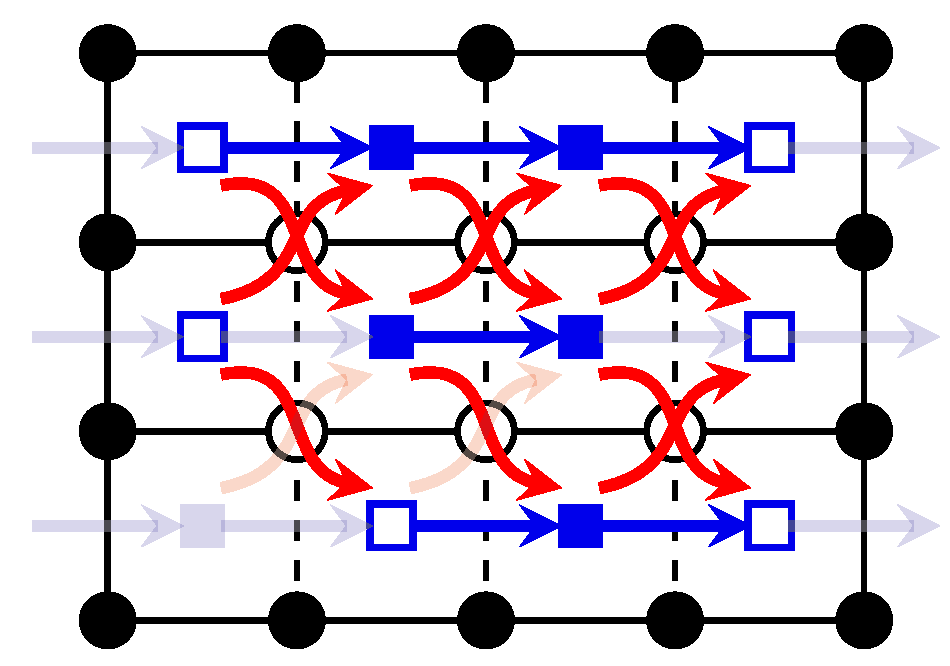
4.2. Remarks on the Running Time
4.3. Controlling the Number of New Bends
4.4. Extensions to Other Models
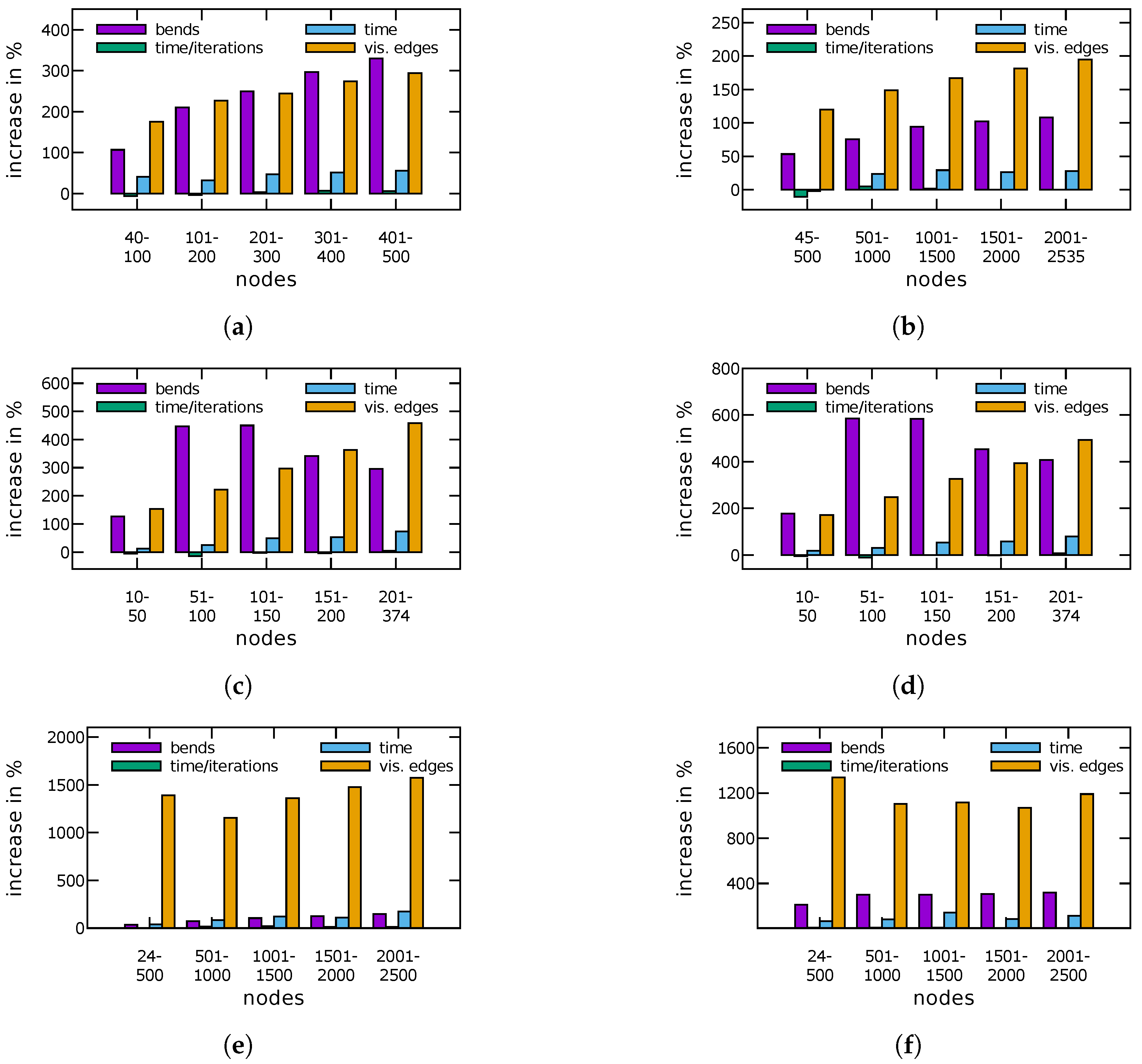
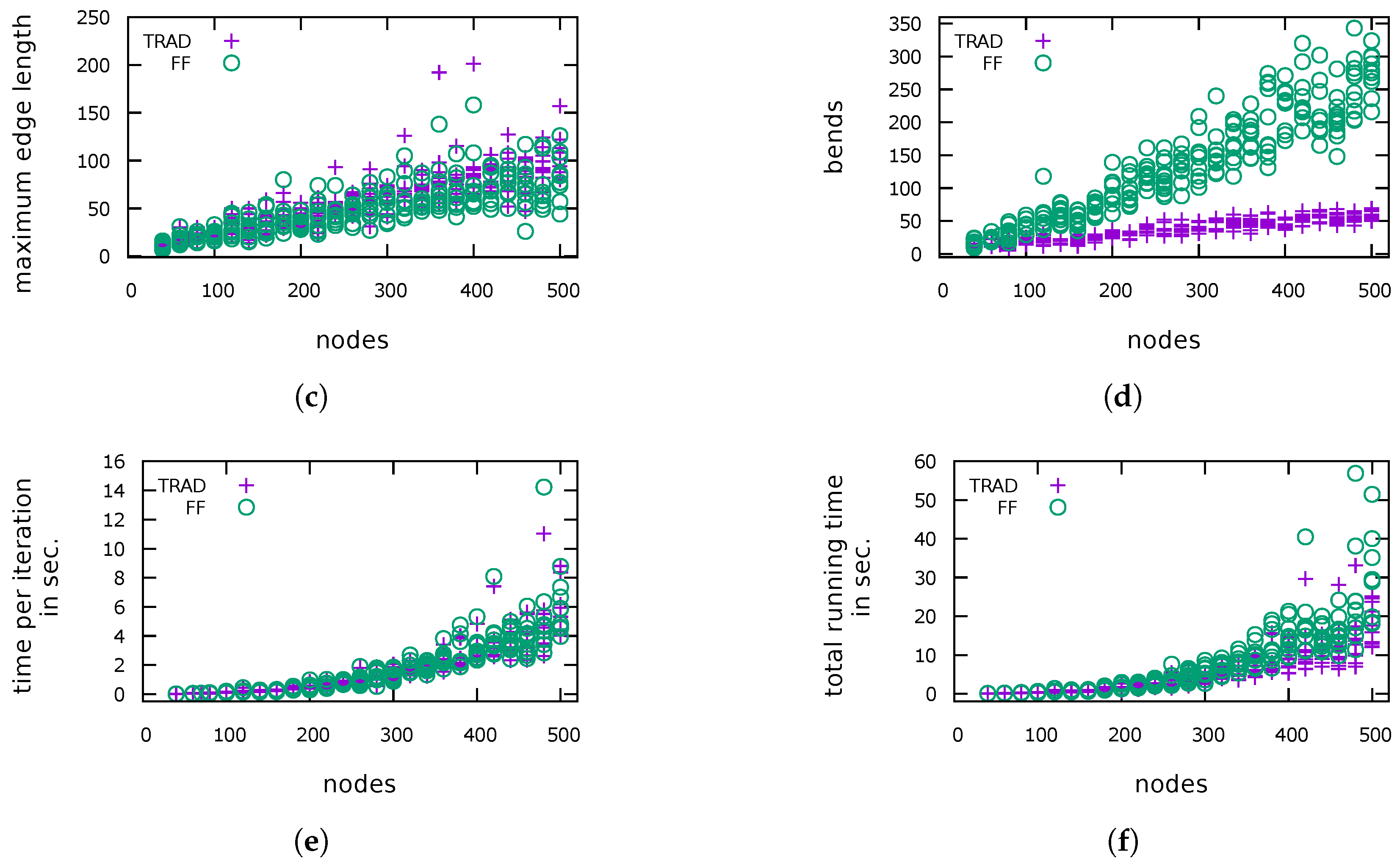
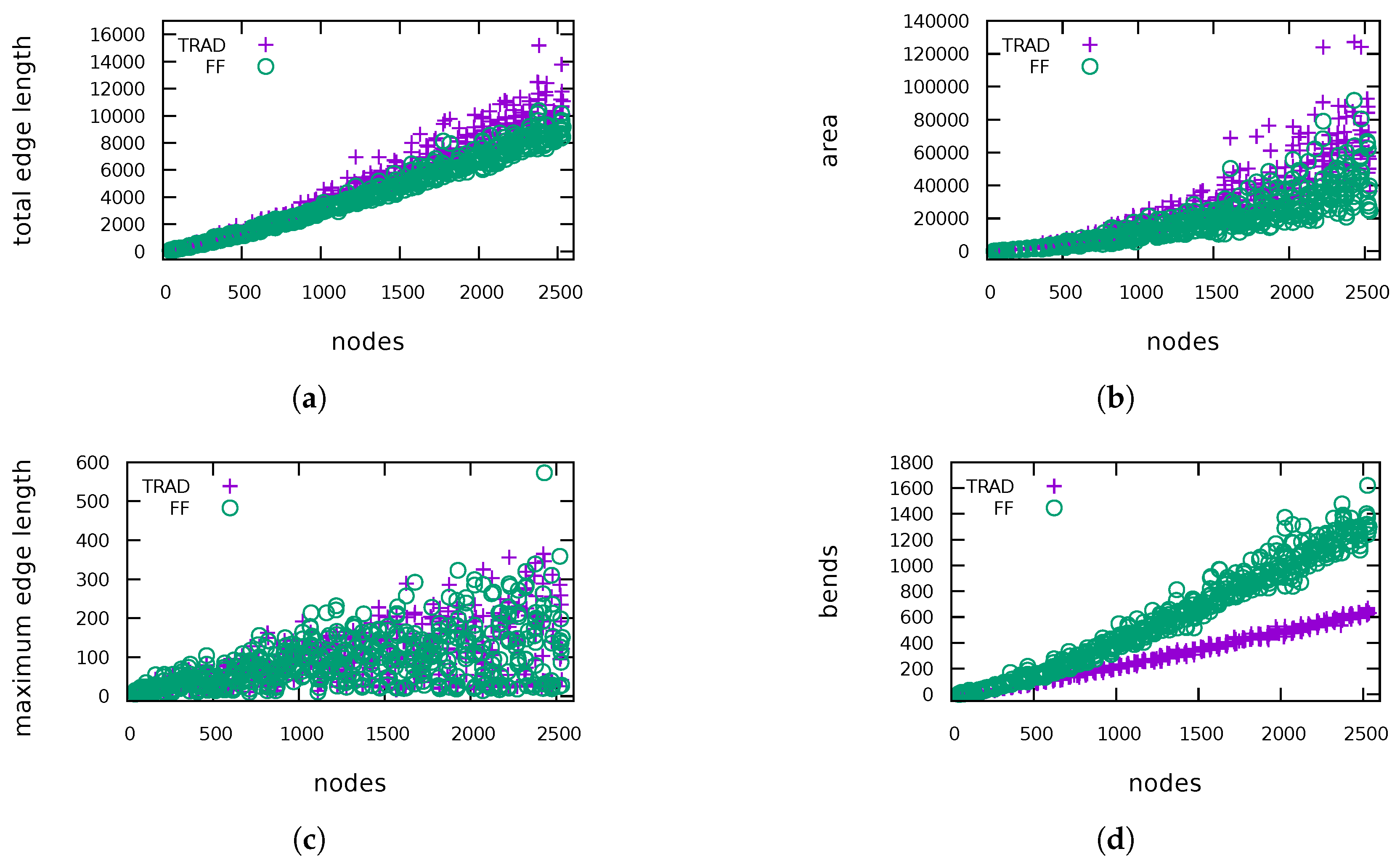
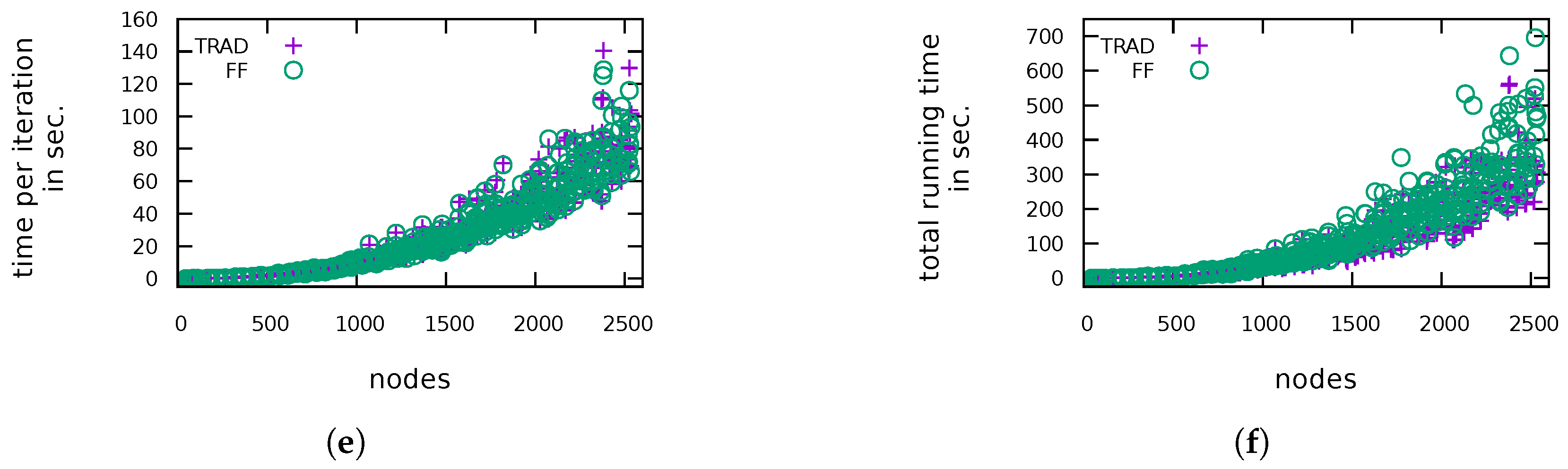
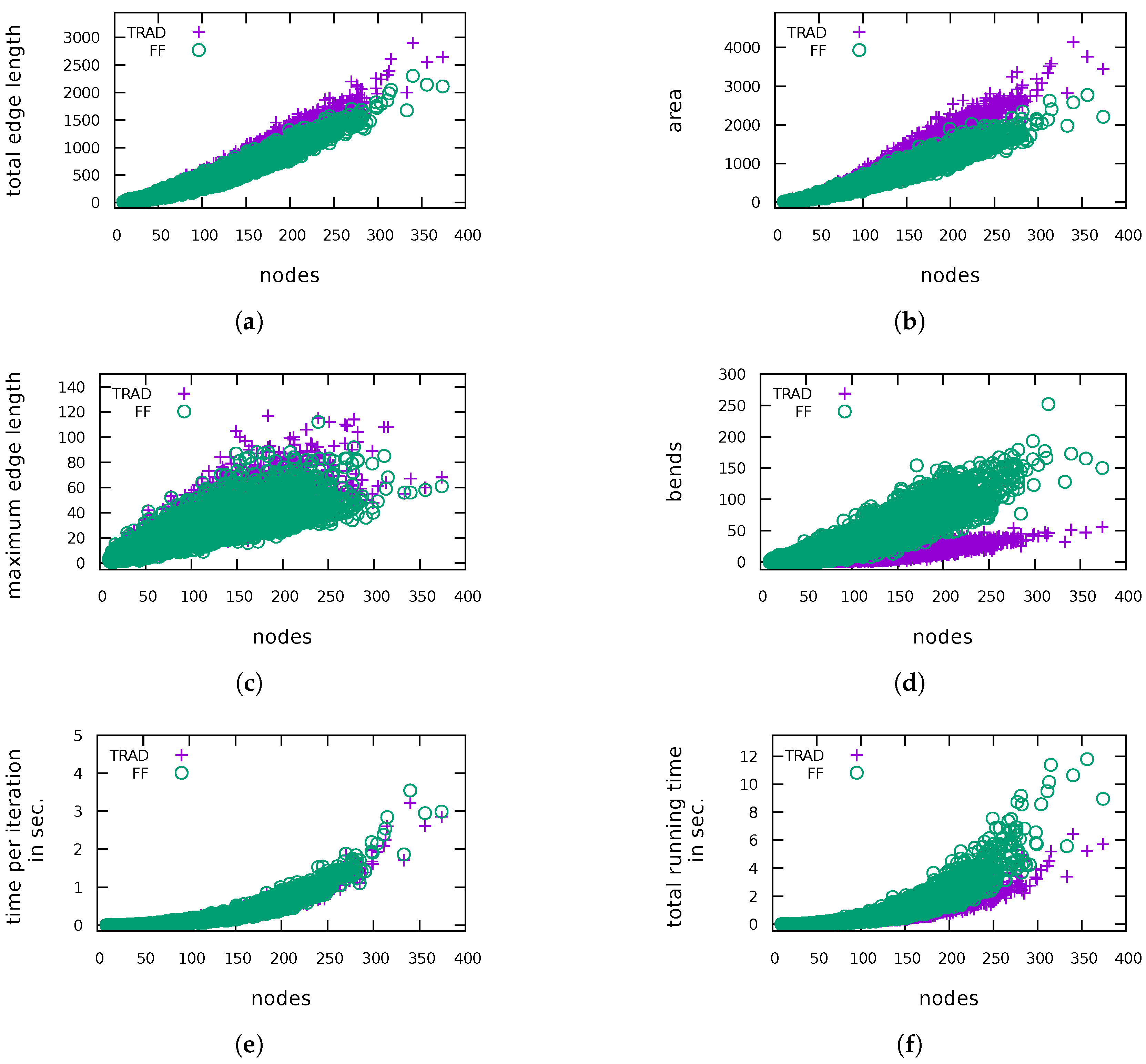
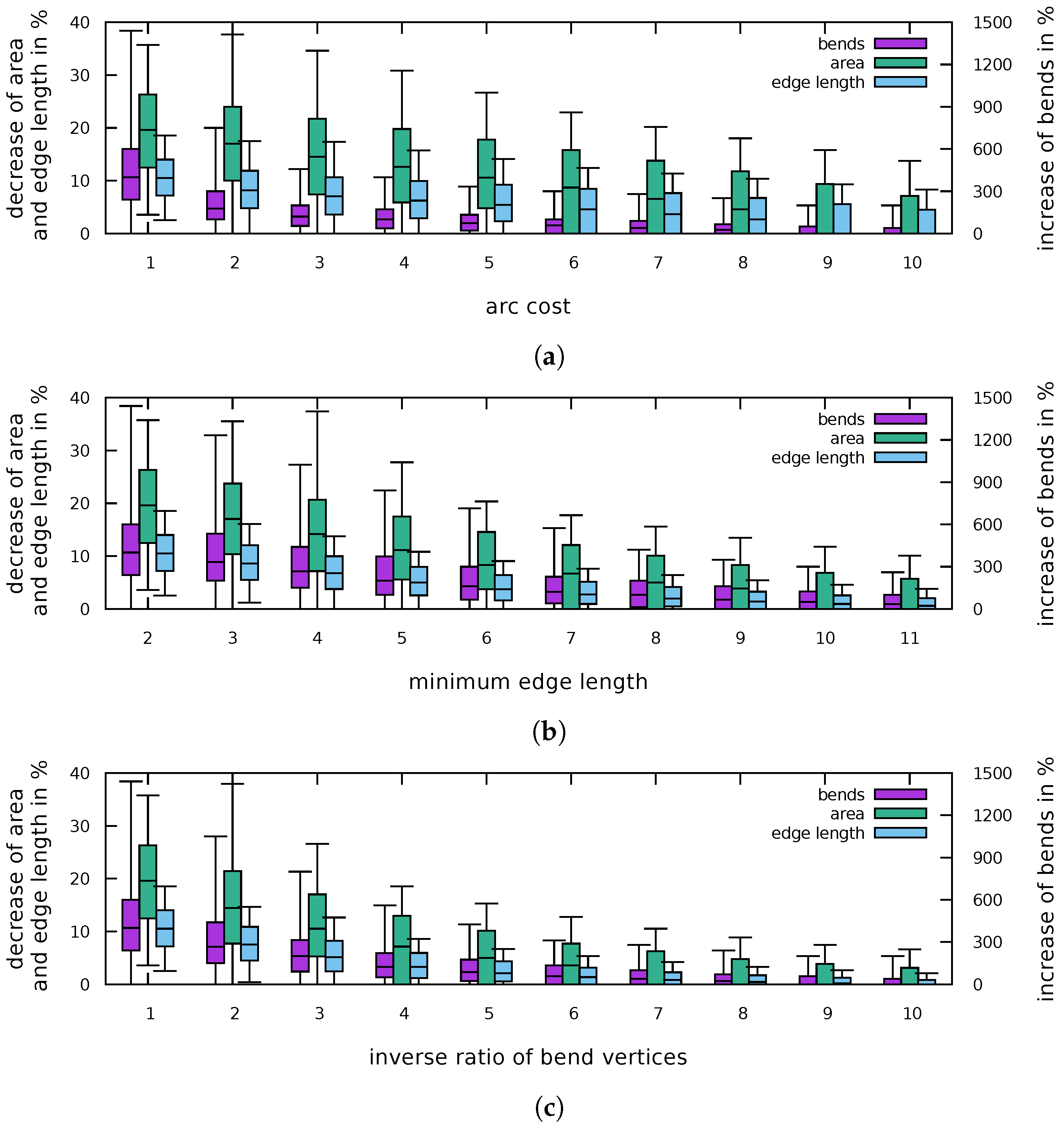
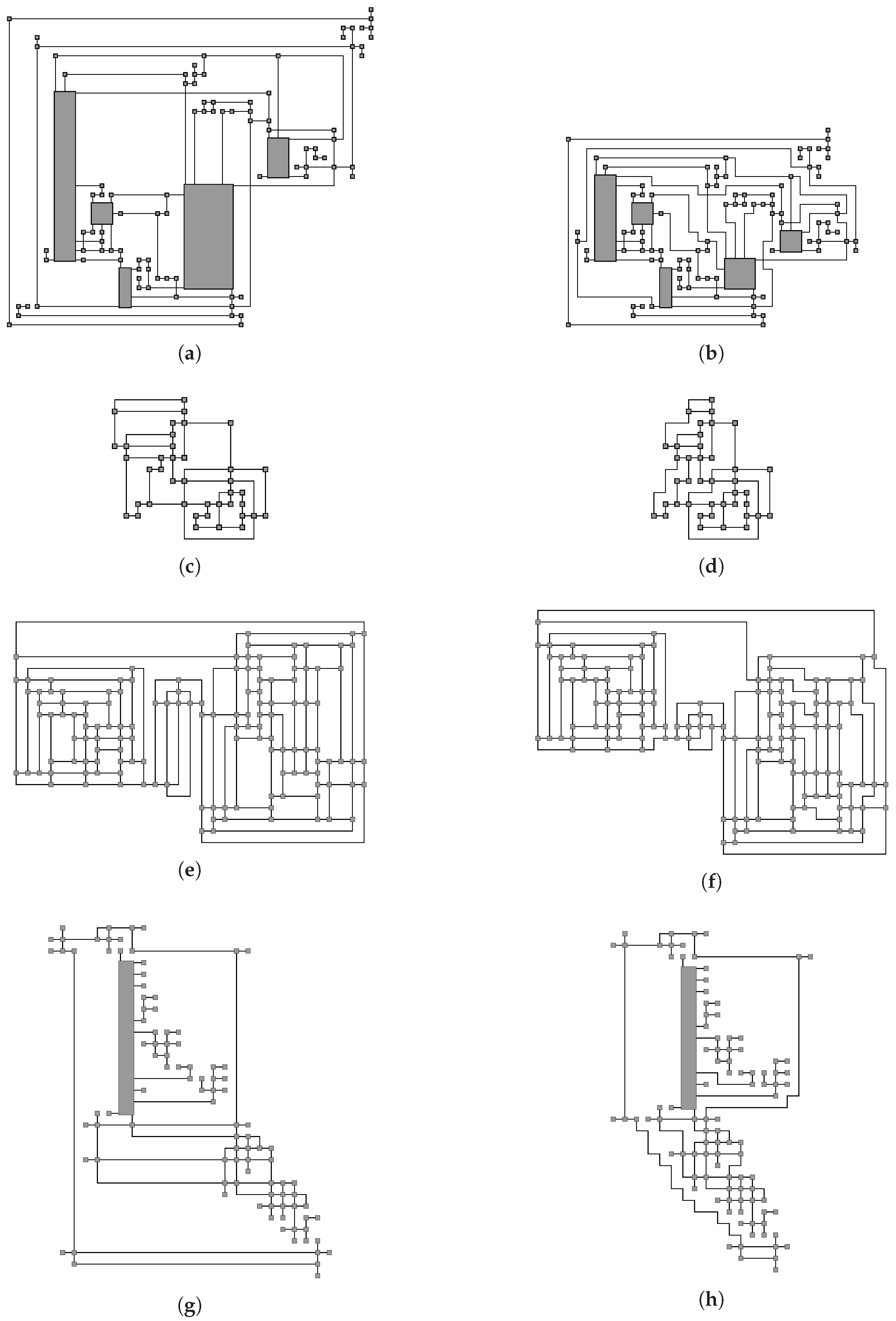
5. Experimental Evaluation
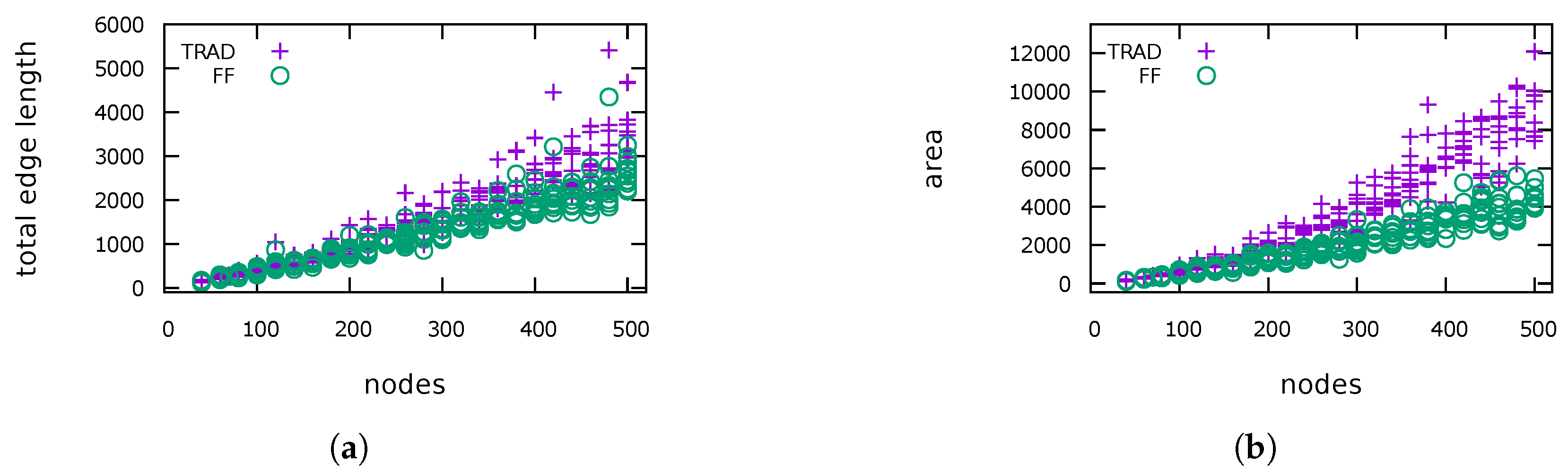
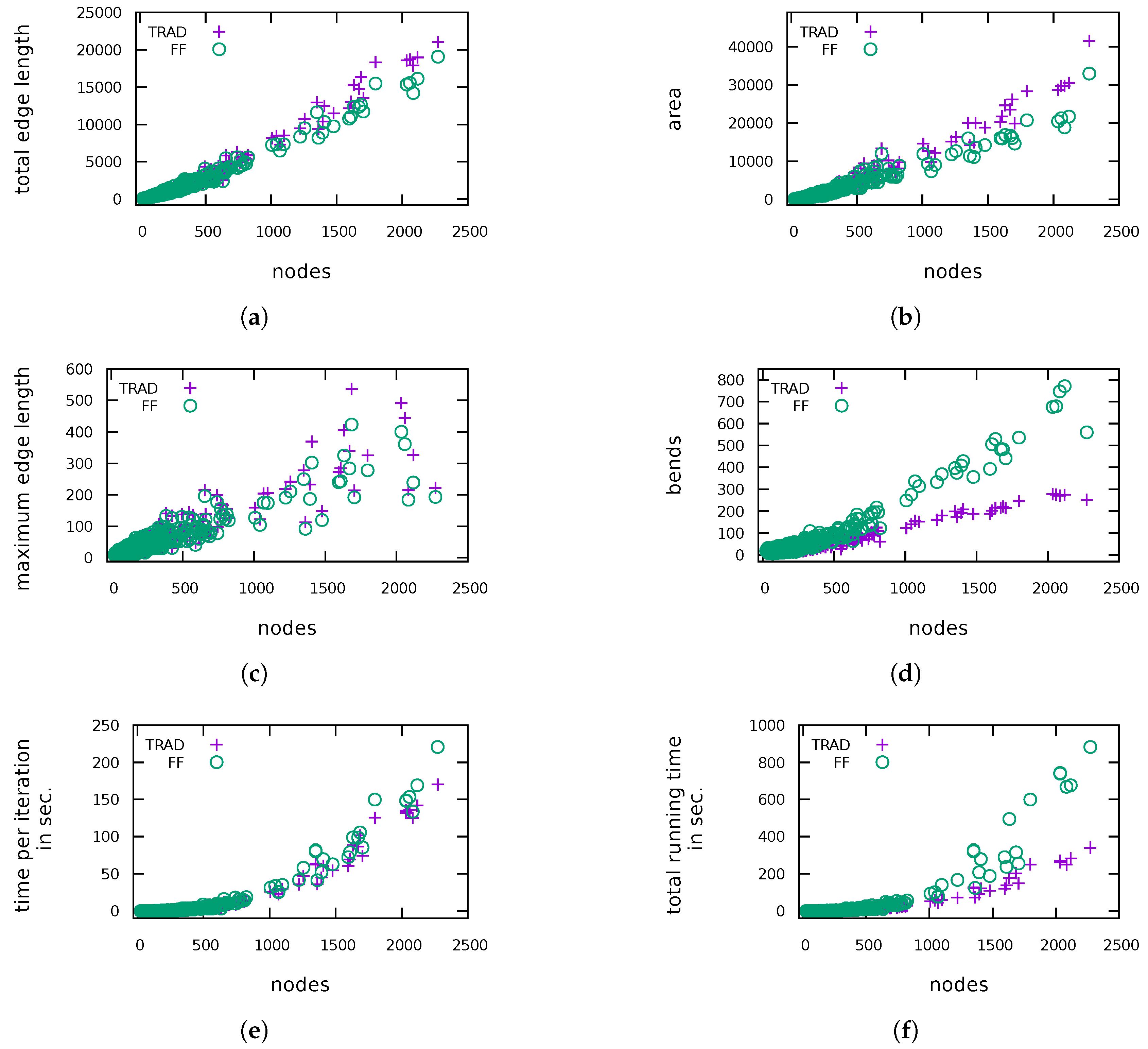
5.1. General Performance
| BICON | In total, 240 biconnected planar 4-graphs with 40–500 vertices, randomly generated with modified methods from OGDF. Starting with a triangle the graph is expanded by splitting edges or faces, maintaining 4-planarity. |
| QUASI | So-called quasi-trees which are known to be hard to compact optimally. They have already been used in the compaction literature (e.g., [14,30]). The set consists of 565 graphs with 40–2500 vertices. |
| ROME | The well-known Rome graphs introduced in [4] consists of about 11,000 real-world and real-world like graphs with 10–100 vertices. These graphs are widely used as benchmarks in various graph drawing experiments. |
| ROME4P | 4-planarized Rome graphs, i.e., we initially turned all Rome graphs into planar 4-graphs by planarizing them with methods from OGDF and replacing vertices with outgoing edges with faces of size k. This results in a graph size of up to 374 vertices. |
| IMDB | A movie collaboration data set of 1000 ego-networks of actors/actresses with 10–72 vertices [31]. |
| IMDB4P | A set of 4-planarized graphs of IMDB. Because the input graphs are very dense, we get graphs with over 10,000 vertices. Due to the very high running time for instances of this size, we selected a subset of 936 graphs that have at most 2500 vertices each. |
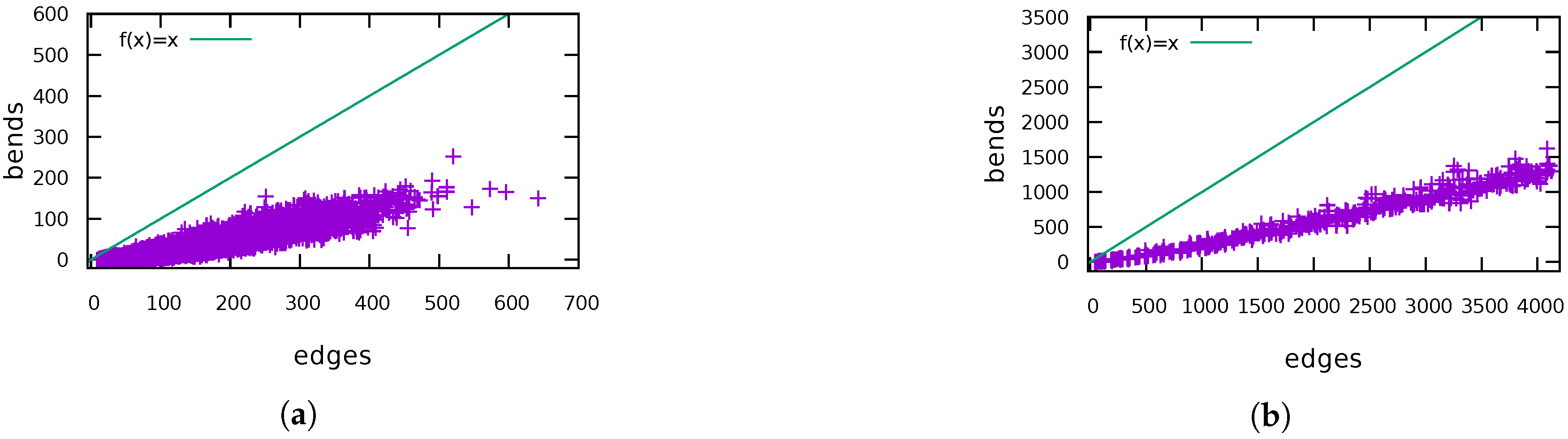
5.2. Reducing the Number of Additional Bends
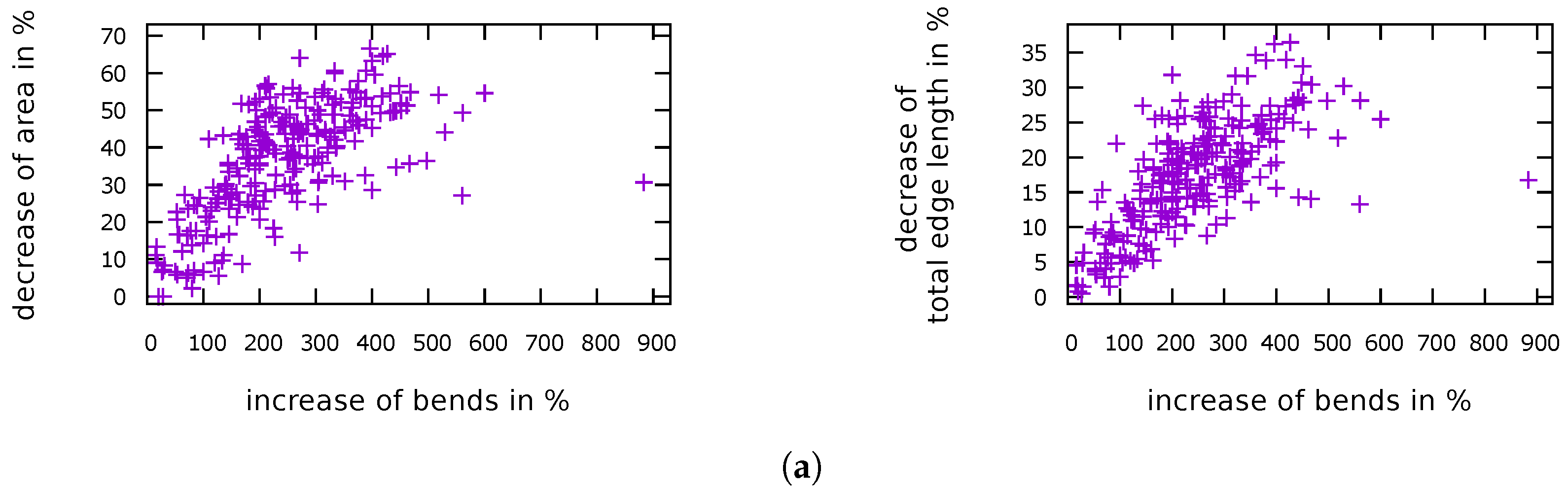
5.3. Increasing the Cost for New Bends
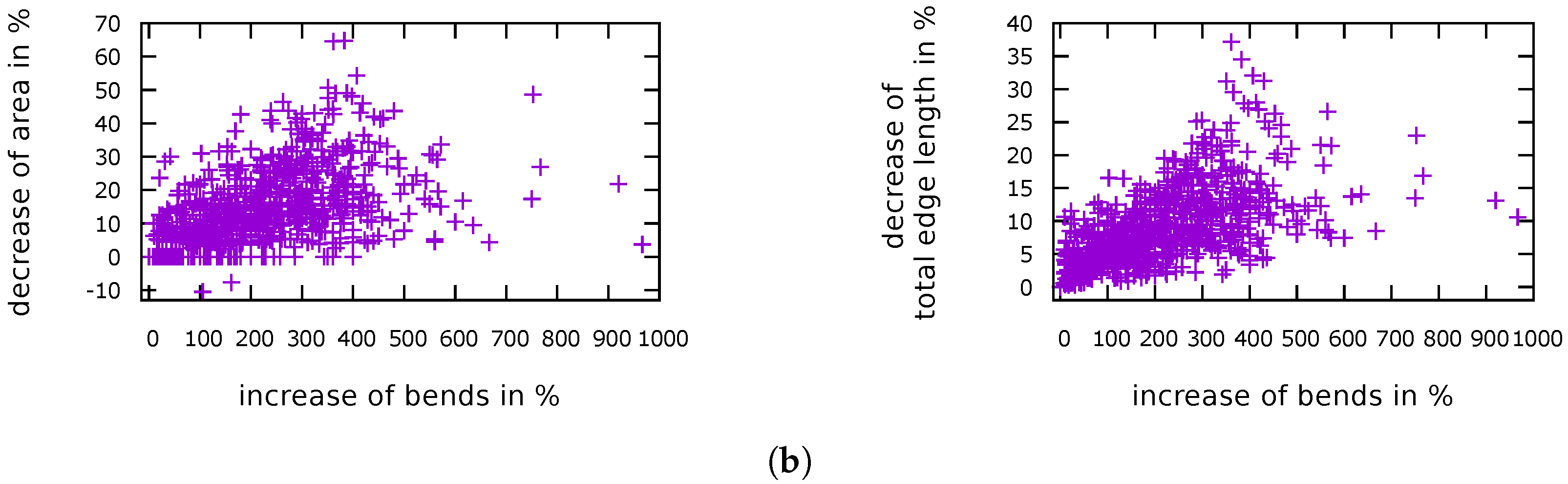
5.4. Increasing the Minimum Length of an Edge to Get Bends
5.5. Decreasing the Ratio of Number of Bends To Edge Length
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Batini, C.; Nardelli, E.; Tamassia, R. A layout algorithm for data flow diagrams. IEEE Trans. Softw. Eng. 1986, SE-12, 538–546. [Google Scholar] [CrossRef]
- Tamassia, R. On Embedding a Graph in the Grid with the Minimum Number of Bends. SIAM J. Comput. 1987, 16, 421–444. [Google Scholar] [CrossRef]
- Patrignani, M. On the Complexity of Orthogonal Compaction. In Algorithms and Data Structures, 6th International Workshop, WADS ’99; Springer: Berlin, Germany, 1999; Volume 1663, pp. 56–61. [Google Scholar] [CrossRef]
- Di Battista, G.; Garg, A.; Liotta, G.; Tamassia, R.; Tassinari, E.; Vargiu, F. An Experimental Comparison of Four Graph Drawing Algorithms. Comput. Geom. 1997, 7, 303–325. [Google Scholar] [CrossRef]
- Lengauer, T. Combinatorial Algorithms for Integrated Circuit Layout; John Wiley & Sons, Inc.: New York, NY, USA, 1990. [Google Scholar]
- Bannister, M.J.; Eppstein, D.; Simons, J.A. Inapproximability of Orthogonal Compaction. J. Graph Algorithms Appl. 2012, 16, 651–673. [Google Scholar] [CrossRef]
- Di Battista, G.; Eades, P.; Tamassia, R.; Tollis, I.G. Graph Drawing: Algorithms for the Visualization of Graphs; Prentice-Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Bridgeman, S.S.; Di Battista, G.; Didimo, W.; Liotta, G.; Tamassia, R.; Vismara, L. Turn-regularity and optimal area drawings of orthogonal representations. Comput. Geom. 2000, 16, 53–93. [Google Scholar] [CrossRef]
- Klau, G.W.; Mutzel, P. Optimal Compaction of Orthogonal Grid Drawings. In International Conference on Integer Programming and Combinatorial Optimization; Cornuéjols, G., Burkard, R.E., Woeginger, G.J., Eds.; Springer: Berlin, Germany, 1999; Volume 1610, pp. 304–319. [Google Scholar] [CrossRef]
- Kaufmann, M.; Wagner, D. (Eds.) Drawing Graphs, Methods and Models; Springer: Berlin, Germany, 2001; Volume 2025. [Google Scholar]
- Dai, W.; Kuh, E. Global spacing of building-block layout. In Proceedings of the IFIP TC 10/WG 10.5 International Conference on Very Large Scale Integration, Vancouver, BC, Canada, 10–12 August 1987; pp. 193–205. [Google Scholar]
- Eiglsperger, M.; Kaufmann, M. Fast Compaction for Orthogonal Drawings with Vertices of Prescribed Size. In Proceedings of the Graph Drawing, 9th International Symposium, GD 2001, Vienna, Austria, 23–26 September 2001; Revised Papers. pp. 124–138. [Google Scholar] [CrossRef]
- Hashemi, S.M.; Tahmasbi, M. A better heuristic for area-compaction of orthogonal representations. Appl. Math. Comput. 2006, 172, 1054–1066. [Google Scholar] [CrossRef]
- Klau, G.W.; Klein, K.; Mutzel, P. An Experimental Comparison of Orthogonal Compaction Algorithms. In International Symposium on Graph Drawing; Marks, J., Ed.; Springer: Berlin, Germany, 2001; Volume 1984, pp. 37–51. [Google Scholar] [CrossRef]
- Fößmeier, U.; Heß, C.; Kaufmann, M. On Improving Orthogonal Drawings: The 4M-Algorithm. In International Symposium on Graph Drawing; Whitesides, S., Ed.; Springer: Berlin, Germany, 1998; Volume 1547, pp. 125–137. [Google Scholar] [CrossRef]
- Six, J.M.; Kakoulis, K.G.; Tollis, I.G. Refinement of Orthogonal Graph Drawings. In International Symposium on Graph Drawing; Whitesides, S., Ed.; Springer: Berlin, Germany, 1998; Volume 1547, pp. 302–315. [Google Scholar] [CrossRef]
- Spönemann, M.; Fuhrmann, H.; von Hanxleden, R.; Mutzel, P. Port Constraints in Hierarchical Layout of Data Flow Diagrams. In International Symposium on Graph Drawing; Eppstein, D., Gansner, E.R., Eds.; Revised Papers; Springer: Berlin, Germany, 2010; Volume 5849, pp. 135–146. [Google Scholar] [CrossRef]
- De Mendonça Neta, B.M.; Araújo, G.H.D.; Guimarães, F.G.; Mesquita, R.C.; Ekel, P.Y. A fuzzy genetic algorithm for automatic orthogonal graph drawing. Appl. Soft Comput. 2012, 12, 1379–1389. [Google Scholar] [CrossRef]
- Freivalds, K.; Glagolevs, J. Graph Compact Orthogonal Layout Algorithm. In Proceedings of the Combinatorial Optimization—Third International Symposium, ISCO 2014, Lisbon, Portugal, 5–7 March 2014; Revised Selected Papers. pp. 255–266. [Google Scholar] [CrossRef]
- Tamassia, R. (Ed.) Handbook on Graph Drawing and Visualization; Chapman and Hall/CRC: Boca Raton, FL, USA, 2013. [Google Scholar]
- Ahuja, R.K.; Magnanti, T.L.; Orlin, J.B. Network Flows: Theory, Algorithms, and Applications; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Király, Z.; Kovács, P. Efficient implementations of minimum-cost flow algorithms. Acta Univ. Sapientiae Inform. 2012, 4, 67–118. [Google Scholar]
- Cornelsen, S.; Karrenbauer, A. Accelerated Bend Minimization. J. Graph Algorithms Appl. 2012, 16, 635–650. [Google Scholar] [CrossRef]
- Orlin, J.B. A Faster Strongly Polynominal Minimum Cost Flow Algorithm. In Proceedings of the 20th Annual ACM Symposium on Theory of Computing, Chicago, IL, USA, 2–4 May 1988; pp. 377–387. [Google Scholar] [CrossRef]
- Holzhauser, M.; Krumke, S.O.; Thielen, C. Budget-constrained minimum cost flows. J. Comb. Optim. 2016, 31, 1720–1745. [Google Scholar] [CrossRef]
- Fößmeier, U.; Kaufmann, M. Drawing High Degree Graphs with Low Bend Numbers. In International Symposium on Graph Drawing; Brandenburg, F., Ed.; Springer: Berlin, Germany, 1995; Volume 1027, pp. 254–266. [Google Scholar] [CrossRef]
- Tamassia, R.; Di Battista, G.; Batini, C. Automatic graph drawing and readability of diagrams. IEEE Trans. Syst. Man Cybern. 1988, 18, 61–79. [Google Scholar] [CrossRef]
- Jünger, M.; Klau, G.W.; Mutzel, P.; Weiskircher, R. AGD—A Library of Algorithms for Graph Drawing. In Graph Drawing Software; Springer: Berlin, Germany, 2004; pp. 149–172. [Google Scholar] [CrossRef]
- Chimani, M.; Gutwenger, C.; Jünger, M.; Klau, G.W.; Klein, K.; Mutzel, P. The Open Graph Drawing Framework (OGDF). In Handbook of Graph Drawing and Visualization; Tamassia, R., Ed.; CRC Press: Boca Raton, FL, USA, 2013; Chapter 17; pp. 543–569. [Google Scholar]
- Klau, G.W. A Combinatorial Approach to Orthogonal Placement Problems. Ph.D. Thesis, Saarland University, Saarbrücken, Germany, 2002. [Google Scholar] [CrossRef]
- Yanardag, P.; Vishwanathan, S.V.N. Deep Graph Kernels. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 1365–1374. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jünger, M.; Mutzel, P.; Spisla, C. More Compact Orthogonal Drawings by Allowing Additional Bends †. Information 2018, 9, 153. https://doi.org/10.3390/info9070153
Jünger M, Mutzel P, Spisla C. More Compact Orthogonal Drawings by Allowing Additional Bends †. Information. 2018; 9(7):153. https://doi.org/10.3390/info9070153
Chicago/Turabian StyleJünger, Michael, Petra Mutzel, and Christiane Spisla. 2018. "More Compact Orthogonal Drawings by Allowing Additional Bends †" Information 9, no. 7: 153. https://doi.org/10.3390/info9070153
APA StyleJünger, M., Mutzel, P., & Spisla, C. (2018). More Compact Orthogonal Drawings by Allowing Additional Bends †. Information, 9(7), 153. https://doi.org/10.3390/info9070153




