Fast Identification of High Utility Itemsets from Candidates
Abstract
:1. Introduction
1.1. Problem Definition
1.2. Previous Solutions
1.3. Contributions
- A basic algorithm for high utility itemset identification is formally presented.
- A novel structure called the candidate tree is proposed for storing candidate itemsets.
- A candidate tree-based algorithm is developed for the fast identification of high utility itemsets.
- Extensive experimental results that show the performance difference between the basic algorithm and the candidate tree-based algorithm are reported.
2. Basic Identification Algorithm
2.1. Pseudo-Code of the BIA
| Algorithm 1: Basic Identification Algorithm |
 |
2.2. Utility Computation
| Procedure 2: u(c, t) |
 |
3. Identifying HUIs by a Candidate-Tree
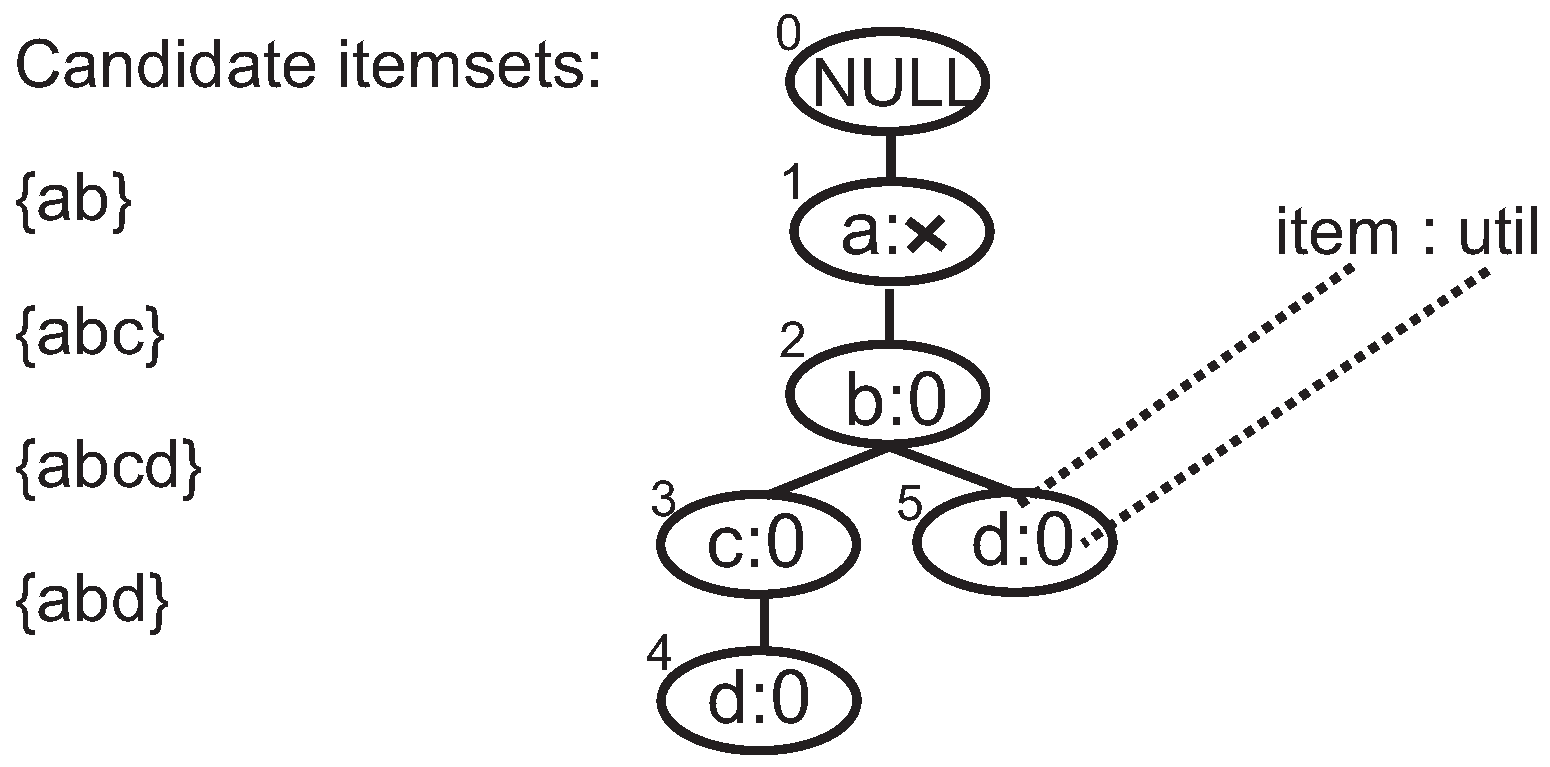
3.1. Candidate-Tree
3.2. Fast HUI Identification
| Algorithm 3: Fast Identification Algorithm |
 |
| Procedure 4: ComputeUtility(t, k, n, utility) |
 |
| Procedure 5: IdentifyHUI(n, X, minutil) |
 |
4. Complexity Analysis
5. Experiments
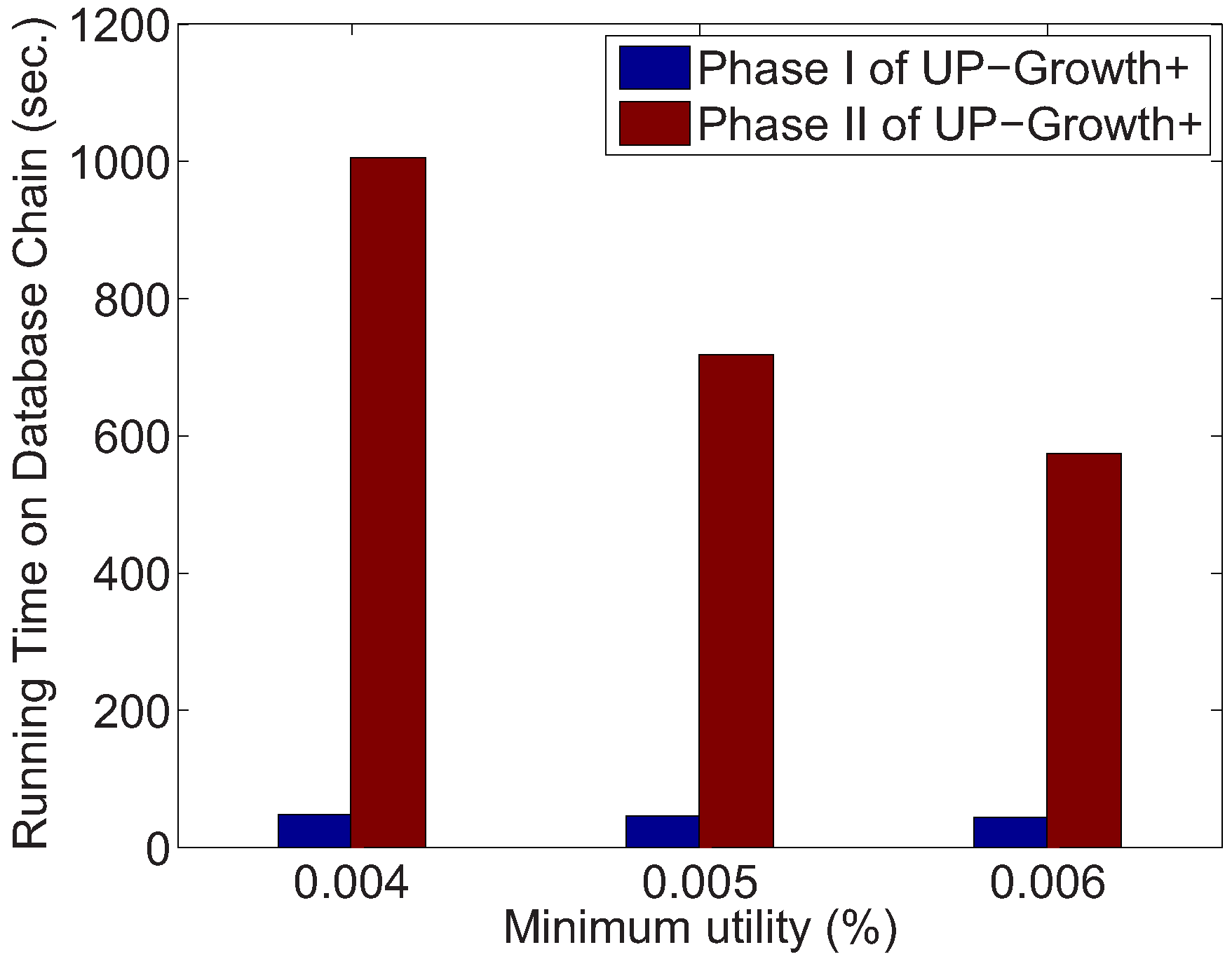
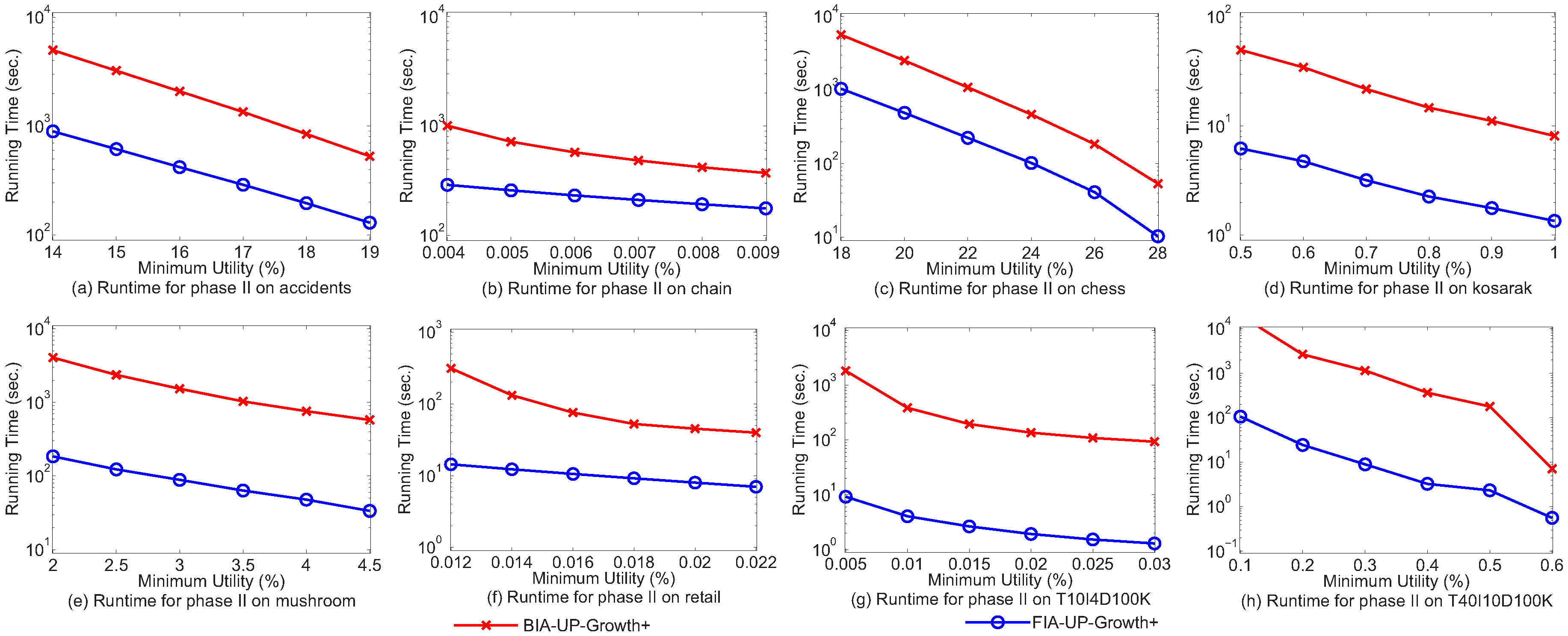
5.1. Running Time for Phase II
5.2. Running Time for Phase I
5.3. Memory Consumption
5.4. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yao, H.; Hamilton, H.J.; Butz, C.J. A Foundational Approach to Mining Itemset Utilities from Databases. In Proceedings of the Fourth SIAM International Conference on Data Mining, Lake Buena Vista, FL, USA, 22–24 April 2004. [Google Scholar]
- Agrawal, R.; Imieliński, T.; Swami, A. Mining association rules between sets of items in large databases. In Proceedings of the 1993 ACM SIGMOD International Conference on Management of Data, Washington, DC, USA, 25–28 May 1993; pp. 207–216. [Google Scholar]
- Krishnamoorthy, S. Efficient Mining of High Utility Itemsets with Multiple Minimum Utility Thresholds. Eng. Appl. Artif. Intell. 2018, 69, 112–126. [Google Scholar] [CrossRef]
- Zhang, L.; Fu, G.; Cheng, F.; Qiu, J.; Su, Y. A Multi-Objective Evolutionary Approach for Mining Frequent and High Utility Itemsets. Appl. Soft Comput. 2018, 62, 974–986. [Google Scholar] [CrossRef]
- Mai, T.; Vo, B.; Nguyen, L.T.T. A Lattice-Based Approach for Mining High Utility Association Rules. Inf. Sci. 2017, 399, 81–97. [Google Scholar] [CrossRef]
- Wu, J.M.-T.; Zhan, J.; Li, J.C.-W. An ACO-Based Approach to Mine High-Utility Itemsets. Knowl-Based Syst. 2017, 116, 102–113. [Google Scholar] [CrossRef]
- Guo, Z.; Yue, X.; Yang, H.; Liu, K.; Liu, X. Enhancing social emotional optimization algorithm using local search. Soft Comput. 2017, 21, 7393–7404. [Google Scholar] [CrossRef]
- Liu, Y.; Liao, W.; Choudhary, A.N. A Two-Phase Algorithm for Fast Discovery of High Utility Itemsets. In Proceedings of the 9th Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining, PAKDD 2005, Hanoi, Vietnam, 18–20 May 2005; pp. 689–695. [Google Scholar]
- Ahmed, C.F.; Tanbeer, S.K.; Jeong, B.; Lee, Y. Efficient tree structures for high utility pattern mining in incremental databases. IEEE Trans. Knowl. Data Eng. 2009, 21, 1708–1721. [Google Scholar] [CrossRef]
- Tseng, V.S.; Wu, C.-W.; Shie, B.-E.; Yu, P.S. Up growth: An efficient algorithm for high utility itemset mining. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 25–28 July 2010; pp. 253–262. [Google Scholar]
- Tseng, V.S.; Shie, B.-E.; Wu, C.-W.; Yu, P.S. Efficient algorithms for mining high utility itemsets from transactional databases. IEEE Trans. Knowl. Data Eng. 2012, 25, 1772–1786. [Google Scholar] [CrossRef]
- Li, Y.-C.; Yeh, J.-S.; Chang, C.-C. A fast algorithm for mining share-frequent itemsets. In Proceedings of the 7th Asia-Pacific Web Conference on Web Technologies Research and Development—APWeb 2005, Shanghai, China, 29 March–1 April 2005; pp. 417–428. [Google Scholar]
- Li, Y.-C.; Yeh, J.-S.; Chang, C.-C. Direct candidates generation: A novel algorithm for discovering complete share-frequent itemsets. In Proceedings of the International Conference on Fuzzy Systems and Knowledge Discovery, Changsha, China, 27–29 August 2005; pp. 551–560. [Google Scholar]
- Li, Y.-C.; Yeh, J.-S.; Chang, C.-C. Isolated Items Discarding Strategy for Discovering High Utility Itemsets. Data Knowl. Eng. 2008, 64, 198–217. [Google Scholar] [CrossRef]
- Han, J.; Pei, J.; Yin, Y.; Mao, R. Mining frequent patterns without candidate generation: A frequent-pattern tree approach. Data Min. Knowl. Discov. 2004, 8, 53–87. [Google Scholar] [CrossRef]
- NU-MineBench: A Data Mining Benchmark Suite. Available online: http://cucis.ece.northwestern.edu/projects/DMS/MineBench.html (accessed on 8 April 2018).
- Frequent Itemset Mining Dataset Repository. Available online: http://fimi.ua.ac.be/ (accessed on 8 April 2018).


| Item | a | b | c | d | e | f | g |
|---|---|---|---|---|---|---|---|
| Utility | 2 | 3 | 1 | 5 | 1 | 1 | 4 |
| Tid | Transaction | Count |
|---|---|---|
| T1 | {a, c, f} | {1, 1, 1} |
| T2 | {a, b, c, d} | {2, 1, 1, 3} |
| T3 | {b, c, d, e} | {1, 2, 1, 1} |
| T4 | {a, b, f} | {3, 1, 2} |
| T5 | {b, c} | {2, 2} |
| T6 | {a, b, d, e, g} | {2, 1, 1, 1, 1} |
| Algorithm (Year) | TP (2005) | FUM (2007) | UP-Growth (2010) | UP-Growth+ (2012) |
|---|---|---|---|---|
| #Candidates | 15,343 | 11,959 | 4485 | 4464 |
| Tid | Item | Util. | Item | Util. | Item | Util. | Item | Util. | Item | Util. |
|---|---|---|---|---|---|---|---|---|---|---|
| T1 | a | 2 | c | 1 | f | 1 | ||||
| T2 | a | 4 | b | 3 | c | 1 | d | 15 | ||
| T3 | b | 3 | c | 2 | d | 5 | e | 1 | ||
| T4 | a | 6 | b | 3 | f | 2 | ||||
| T5 | b | 6 | c | 2 | ||||||
| T6 | a | 4 | b | 3 | d | 5 | e | 1 | g | 4 |
| Comparison Number | Least | Most |
| BIA (contained) | = | |
| FIA (contained) | ||
| BIA (not contained) | ||
| FIA (not contained) | 1 | |
| Accumulation Number | Least | Most |
| BIA (contained) | ||
| FIA(contained) | ||
| BIA (not contained) | 0 | |
| = | ||
| FIA (not contained) | 0 | |
| = |
| Database | Size (MB) | #Trans | #Items | AvgLen | MaxLen |
|---|---|---|---|---|---|
| accidents | 56.89 | 340,183 | 468 | 33.8 | 51 |
| chain | 60.63 | 1,112,949 | 46,086 | 7.3 | 170 |
| chess | 0.56 | 3196 | 75 | 37 | 37 |
| kosarak | 47.55 | 990,002 | 41,270 | 8.1 | 2498 |
| mushroom | 0.92 | 8124 | 119 | 23 | 23 |
| retail | 5.79 | 88,162 | 16,470 | 10.3 | 76 |
| T10I4D100K | 5.86 | 100,000 | 870 | 10.1 | 29 |
| T40I10D100K | 22.69 | 100,000 | 942 | 39.6 | 77 |
| Database/Minutil | Algorithm | Phase I (s) | Phase II (s) | Memory (KB) | #Candidates | #HUIs |
|---|---|---|---|---|---|---|
| accidents/14% | Basic | 3.79 | 4981.55 | 8512 | 276,392 | 950 |
| Fast | 3.83 | 895.26 | 5440 | |||
| chain/0.004% | Basic | 48.03 | 1005.56 | 832 | 72,503 | 18,480 |
| Fast | 53.20 | 290.07 | 1440 | |||
| chess/18% | Basic | 13.32 | 5628.51 | 1,387,808 | 31,670,469 | 34,870 |
| Fast | 18.21 | 1042.78 | 623,008 | |||
| kosarak/0.5% | Basic | 10.91 | 49.76 | 64 | 3931 | 183 |
| Fast | 10.93 | 6.22 | 96 | |||
| mushroom/2% | Basic | 5.99 | 4065.73 | 675,328 | 16,681,768 | 3,583,596 |
| Fast | 8.24 | 185.00 | 331,552 | |||
| retail/0.012% | Basic | 0.83 | 313.11 | 4768 | 163,650 | 23,505 |
| Fast | 1.17 | 14.40 | 4000 | |||
| T10I4DX/0.005% | Basic | 1.51 | 1818.70 | 20,416 | 1,007,230 | 313,509 |
| Fast | 3.48 | 9.23 | 20,736 | |||
| T40I10DX/0.1% | Basic | 62.94 | 10,000 | 342,208 | 8,608,882 | 2,054,784 |
| Fast | 48.81 | 106.25 | 179,104 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, J.-F.; Liu, M.; Xin, C.; Wu, Z. Fast Identification of High Utility Itemsets from Candidates. Information 2018, 9, 119. https://doi.org/10.3390/info9050119
Qu J-F, Liu M, Xin C, Wu Z. Fast Identification of High Utility Itemsets from Candidates. Information. 2018; 9(5):119. https://doi.org/10.3390/info9050119
Chicago/Turabian StyleQu, Jun-Feng, Mengchi Liu, Chunsheng Xin, and Zhongbo Wu. 2018. "Fast Identification of High Utility Itemsets from Candidates" Information 9, no. 5: 119. https://doi.org/10.3390/info9050119
APA StyleQu, J.-F., Liu, M., Xin, C., & Wu, Z. (2018). Fast Identification of High Utility Itemsets from Candidates. Information, 9(5), 119. https://doi.org/10.3390/info9050119





