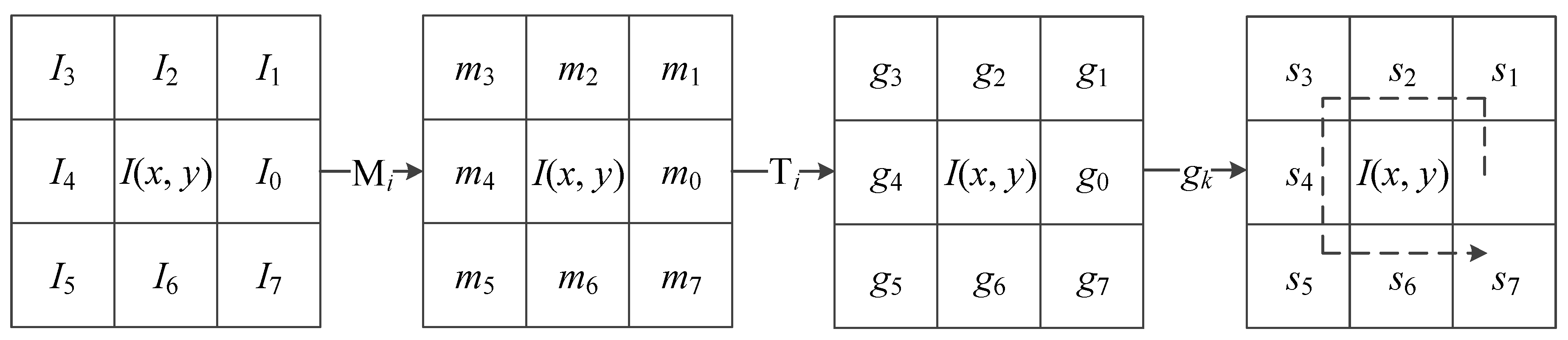
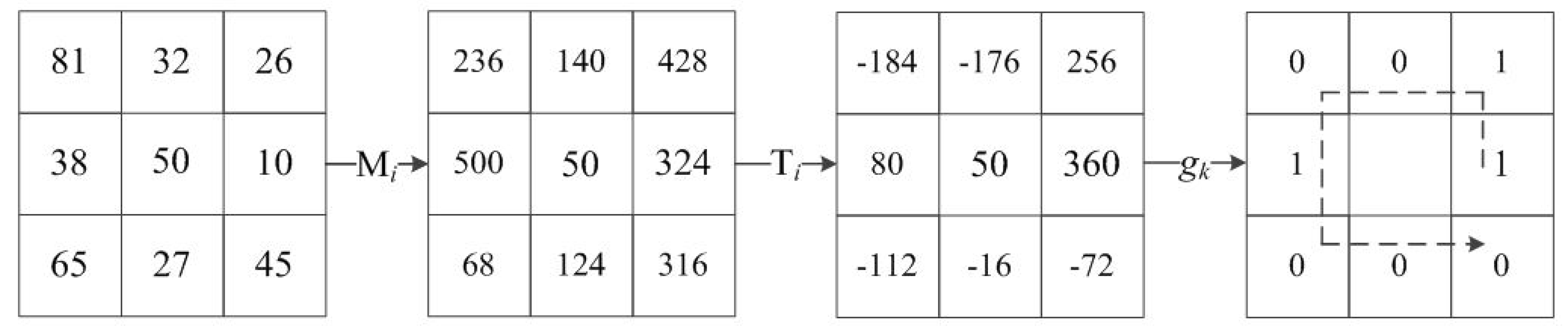
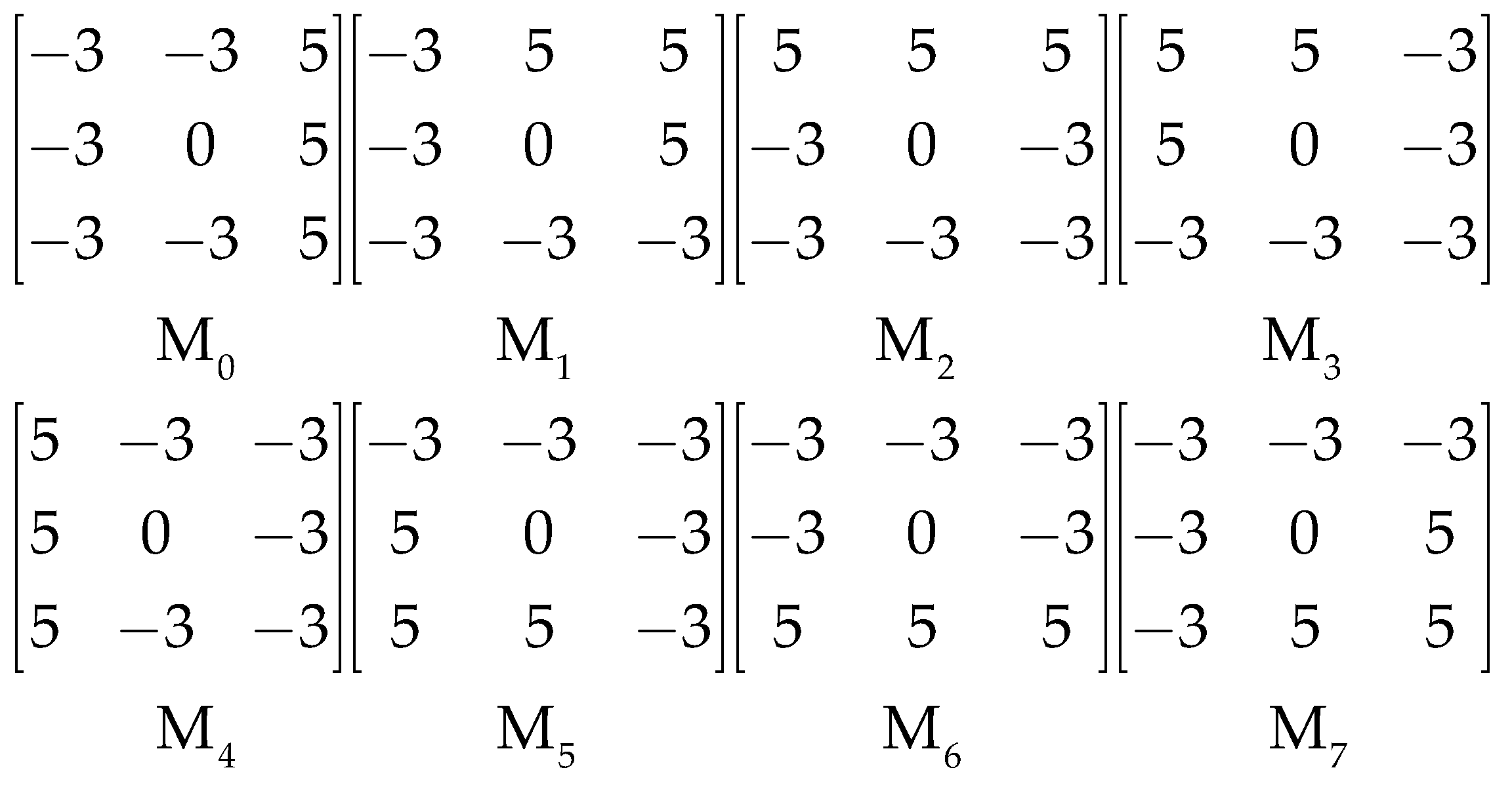1. Introduction
With the rapid development of technology and societal progress, efficient authentication is needed in many fields, e.g., surveillance, human–computer interaction, and biometric identification. The face, as a unique personal identity, has many advantages: it allows for good interaction and is stable, difficult to counterfeit, and cannot be lost, etc., has been widely used in authentication. In recent years, the improvement of 3D data acquisition on devices and computer processing capabilities make a rapid development of the 3D facial recognition technology. Compared with a 2D face, which is easily affected by external factors, such as facial expression, pose, illumination, and age variations, 3D data can express facial information more comprehensively and richly, and better reflect the geometric structure of the human face. Even though there is some loss of information caused by external conditions, it is still much smaller than with 2D data, so more and more researchers are focusing on the 3D field.
The existing 3D facial recognition techniques can be roughly classified into three categories: globally based, locally based, and multimodal hybrid methods. Global feature-based methods often extract statistical features from depth images [
1]. Thakare et al. [
2] used the principal component analysis (PCA) components of the normalized depth image and moment invariants on mesh images to implement an automatic 3D facial recognition system based on the fuzzy neural network (FNN). Independent component analysis (ICA) [
3], linear discriminant analysis (LDA) [
4], and sparse preserving projection (SPP) [
5] are also used to extract global facial features. The global features mainly describe the properties of the whole face, and have rotation invariance, simple calculation, and intuitive representation; however, they have high dimensional features, and cannot describe detailed changes of the face.
The local feature-based methods use stable local invariance features, such as facial curves, local descriptors, and curvature to match and identify faces, which can be applied to both the depth image and the 3D model. Li et al. [
6] extended the scale invariant feature transformation (SIFT)-like matching framework to mesh data, and used two curvature-based key point detectors to repeat the complementary position in the facial scan with high local curvature [
7]. Guo et al. [
8] represented the 3D face by a set of key points, and then used the relevant rotational projection statistics (RoPS) descriptor to expression variations. Lei et al. [
9] proposed a set of local key point-based multiple triangle statistics (KMTS), which is useful for partial facial data, large facial expressions, and pose variations. Tang et al. [
10] presented a 3D face method by using keypoint detection, description, and a matching framework based on three principle curvature measures. Yu et al. [
11] used the ridge and valley curve of the face to represent and match 3D surfaces, which are called 3D directional vertices (3D2V); using sparsely-distributed structure vertices, the structural information is transferred from its deleted neighboring points. Hariri et al. [
12] used geodesic distances on the manifold as the covariance metrics for 3D face matching and recognition. Emambakhsh et al. [
13] proposed a feature extraction algorithm, which is based on the normal surfaces of Gabor-wavelet-filtered depth images. With this method, a set of spherical patches and curves are positioned over the nasal region to provide the feature descriptors. Okuwobi et al. [
14] used the principal curvature direction and the normal surface vector to obtain directional discrimination, in order to improve the recognition performance. The local feature-based methods are robust for image transformations such as illumination, rotation, and viewpoint changes, and their feature descriptors have low dimensions and are easy to match quickly. However, the local features mainly describe the changes in details of the human face, and are inferior to the global features in describing the facial contour features.
The bimodal hybrid methods refer to the combination of 2D and 3D modes. The most common method is to combine the intensity map (2D mode) with the depth map (3D mode) for facial recognition. The depth map is equivalent to a projection of three-dimensional information in a two-dimensional plane, and contains the information of the face’s structure. The intensity map contains the texture information of the face, and the features extracted from these two kinds of images can be more complete and richer for representing the identity information of the face. The recognition rate is higher than in a single kind of image feature extraction. Kakadiaris et al. [
15] used a combination of 3D and 2D data for face alignment and the normalization of pose and illumination, and then constructed 3D deformable model with these data. This framework is more practical than 3D–3D and more accurate than 2D–2D. However, the recognition rate relies on the facial fitting in 2D mode. Elaiwat et al. [
16] proposed a fully automated, multimodal Curvelet-based approach, which uses a multimodal detector to repeatedly identify key points on textural and geometric local face surfaces. Zhang et al. [
17] proposed a cross-modal deep learning method, in which 2D and 2.5D facial features were extracted by two convolutional neural networks (CNN), both individually and fused on the matched face features. Ouamane et al. [
18] extracted multiple features, including multi-scale local binary patterns (MSLBP), statistical local features (SLF), Gabor wavelets, and scale invariant feature transformation (SIFT), and used combinations of these different features for 3D and 2D multimodal score-level fusion to get the best result. However, there are different kinds of feature combinations, so there is no guarantee that a given feature combination can achieve the best effect on different databases. Subsequently, Ouamane et al. [
19] proposed a high-order tensor encoded by 2D and 3D face images, and used different tensor representation as the basis for multimodal data fusion. This method needed to consider a large number of feature combinations and subspace combinations, which increased the time complexity. To overcome the uncontrolled environments in 3D facial recognition, Torkhani et al. [
20] used 3D-to-2D face mesh deformation to obtain the 2D mode, and then extracted facial features by combining edge maps with an extended Gabor curvature in the 2D projected face meshes. Bobulski [
21] presented the full ergodic two-dimensional Hide Markov model (2DHMM), which overcomes the drawback of information lost during the conversion to a one-dimensional features vector.
In addition, there are some 3D facial recognition methods based on the direct matching of airspace, without extracting features [
22]. The 3D point cloud data was used as the processing object, and the similarity calculation between input face and reference face models was performed directly, based on the iterative closest point (ICP). Some other methods, i.e., convolutional neural networks, are commonly used to process human face images for recognition [
23,
24,
25].
To extract facial information comprehensively and avoid a complex process of 3D point cloud data, this paper proposes a bimodal 3D facial recognition method, which can reduce the time cost and space complexity, as well as improving recognition efficiency. There are two kind of features extracted from the multiscale sub-block’s 3D mode depth map and 2D mode intensity map, which are the local gradient pattern (LGP) feature and the weighted histogram of gradient orientation (WHGO) feature [
26]. The gradient is robust for illumination transformation, and reflects the local region information contained in the image; thus, by calculating the gradient edge response, relative gradients, and the occurrence frequency of those gradients in different directions, these two features efficiently express the human face. The proposed multimodal fusion method reduces complexity and improves recognition speed and efficiency.
The contributions of this paper:
Describe a method which can automatically recognize human faces by using depth and intensity maps converted from 3D point cloud data, which are used to provide structural and texture information.
Extract features from multiscale sub-blocks’ bimodal maps for mining essential facial features.
Propose the feature of the local gradient pattern (LGP), and combine LGP with the weighted histogram of gradient orientation (WHGO) to constitute the LGP-WHGO descriptor for extracting the texture and structural features.
The remainder of the paper is organized as follows. In
Section 2, the whole theoretical method of 3D face recognition is given in detail, and the pre-process of 3D facial data is introduced.
Section 3 introduces the specific process of weighted multiscale sub-blocks. In
Section 3, the experiments and analysis are presented. Conclusions and future developments end the paper.
3. Experiments and Results
The experimental environment was a PC, with Inter(R) Core(TM) i5-3210M CPU 2.50 GHz, 4GB RAM, and a Microsoft Windows 7 operating system; the programming platform was MATLAB R2014a. To verify the proposed method, experiments were carried on three public 3D datasets: CASIA, FRGC v2.0, and Bosphorus.
The CASIA database contains 123 subjects, each subject having 37 or 38 images with individual variations of poses, expression, illumination, combined changes in expression under illumination, and poses as expressions. The FRGC v2.0 dataset consists of 4950 3D scans (557 subjects) along with their texture images (2D), in the presence of significant variations in facial expressions, illumination conditions, age, hairstyle, and limited pose variations. The Bosphorus database consists of 4666 3D scans (105 subjects), and each face scan has four files (coordinate file, color image file, 2D landmark file, and 3D landmark file) with neutral poses and expressions, lower face action units, upper face action units, action unit combinations, emotional expressions, yaw rotations, pitch rotations, cross rotations, and occlusions. These three databases are the most widely used in the field of facial recognition.
This paper uses the k-fold cross-validation. The selected dataset is equally divided into nine sub-datasets. The data of each sub-dataset is randomly but uniformly selected. One sub-dataset is used as the testing set, and the remaining are used as training sets, and each experiment will obtain the corresponding recognition rate, which is the average recognition rate of k experiments as a k-fold cross-validation rate of recognition. According to the number of images involved in the training sets and the testing set, the experiments on the CASIA and FRGC v2.0 databases used a nine-fold cross-validation, and the experiments on Bosphorus database used a 10-fold cross-validation.
Each database has been experimenting with two groups of images. For the CASIA database, the first group includes 40 people selected, with 36 pictures randomly selected for each person. An example is shown in
Figure 10. In
Figure 10a,b, there are 18 samples of the depth and intensity maps, respectively, and these samples involve illumination, expressions, and pose variations. The second group is based on the previous increase of 40 people’s data. For the FRGC v2.0 database, the first group selected 80 people (18 pictures per person) in the database randomly, and an example is shown in
Figure 11. In
Figure 11a,b there are nine samples of the depth and intensity maps, respectively, and these samples involve illumination, expressions, and age variations. The second group is based on the previous increase of 80 people’s data. For the Bosphorus database, the first group includes 40 people selected, with 80 pictures per person, and an example is shown in
Figure 12. In
Figure 12a,b, there are 40 samples of the depth and intensity maps, and these samples involve expressions, occlusion (eye occlusion, mouth occlusion, eyeglasses occlusion, and hair occlusion), and pose variations (yaw 10, 20, 30, 45 degrees). The second group is based on the previous increase of 40 people’s data.