A Comparison Study of Kernel Functions in the Support Vector Machine and Its Application for Termite Detection
Abstract
:1. Introduction
2. Materials and Methods
2.1. Selection of Boards
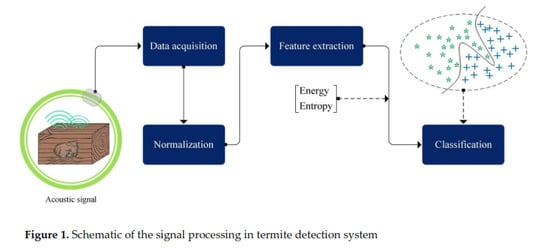
2.2. Acoustic Signal Monitoring
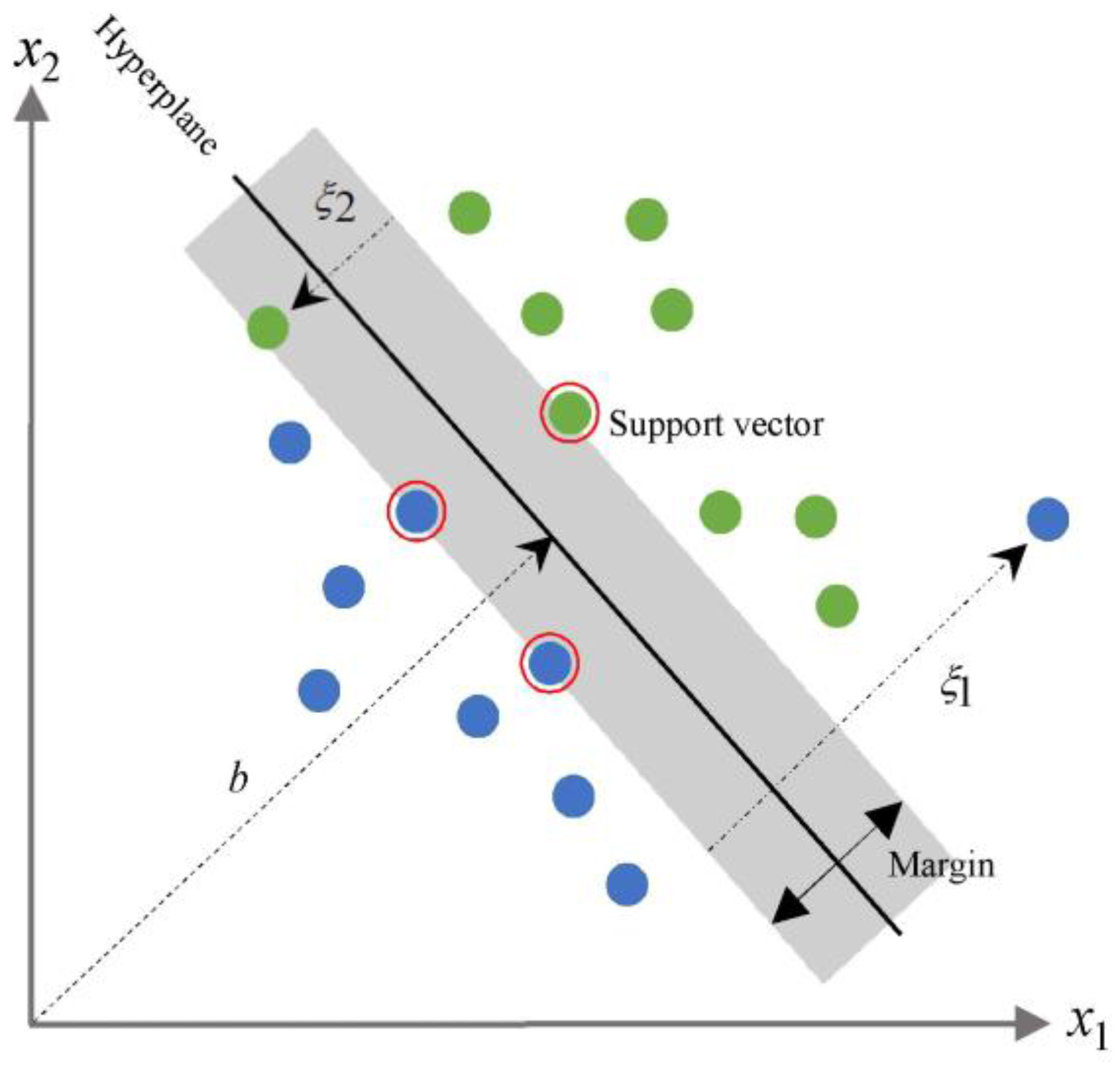
2.3. Support Vector Machine Classifier
2.4. Kernel Function
2.5. Classifier Evaluation
3. Results
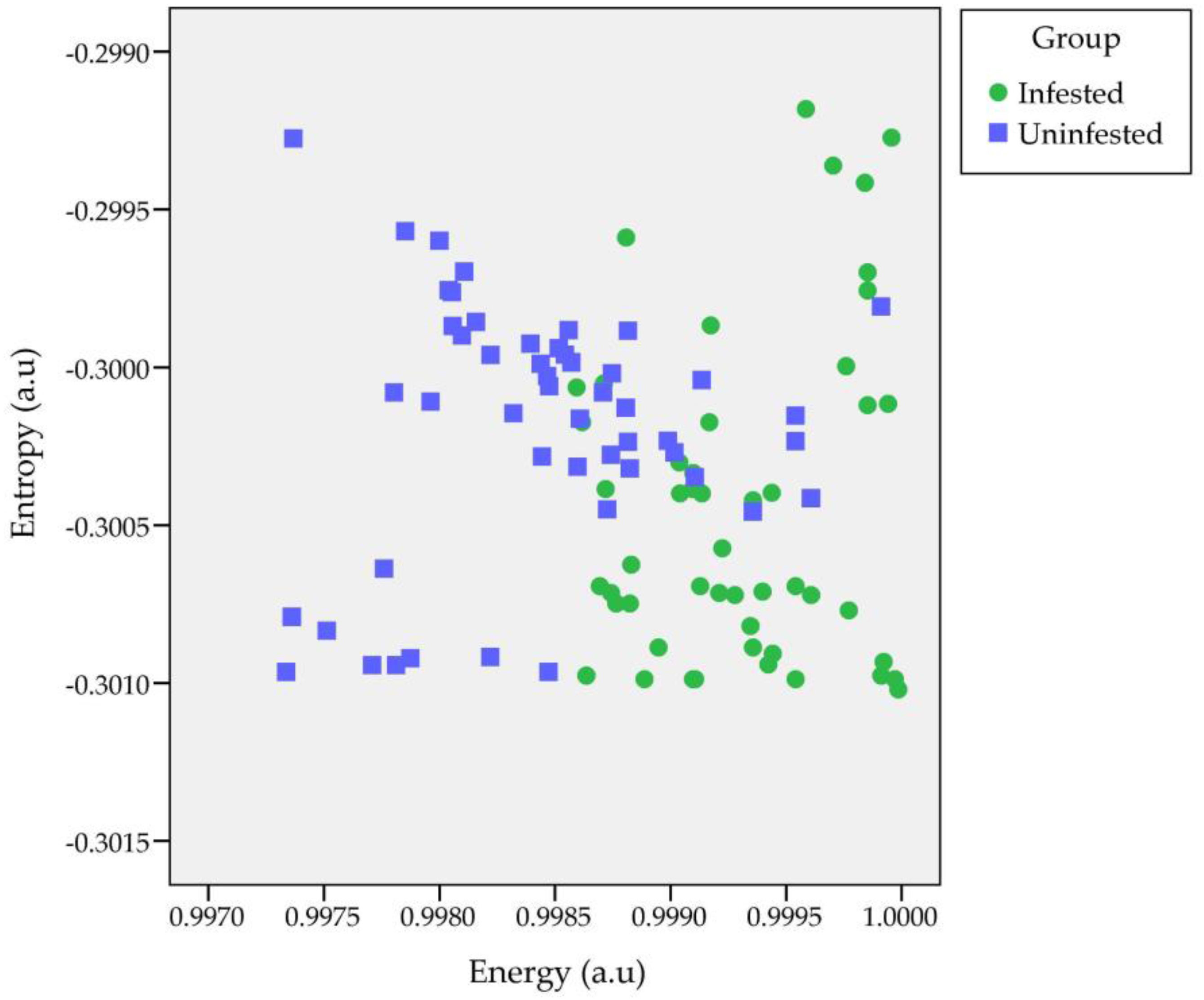
3.1. Acoustic Signal Dispersion
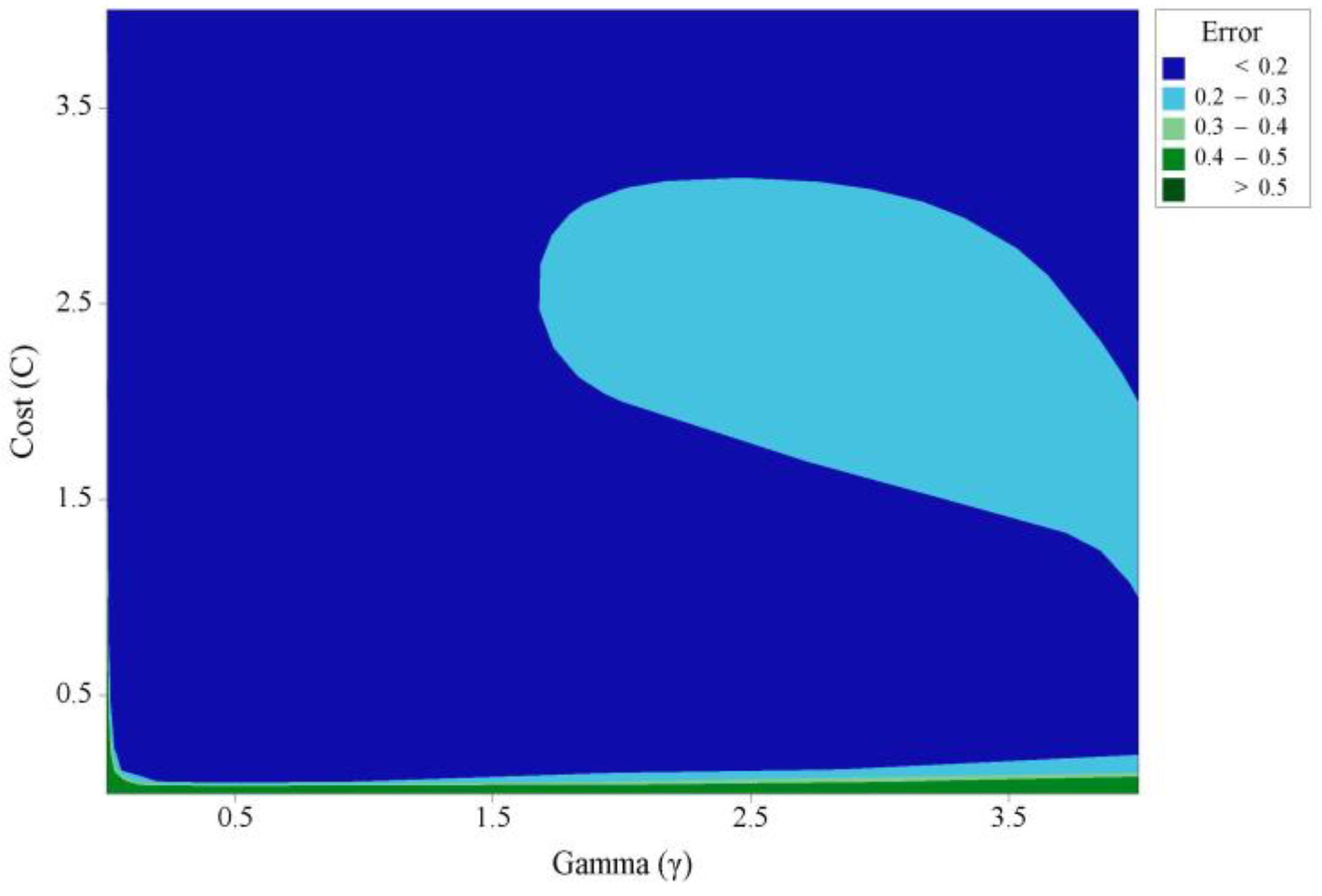
3.2. Grid-Search Optimization
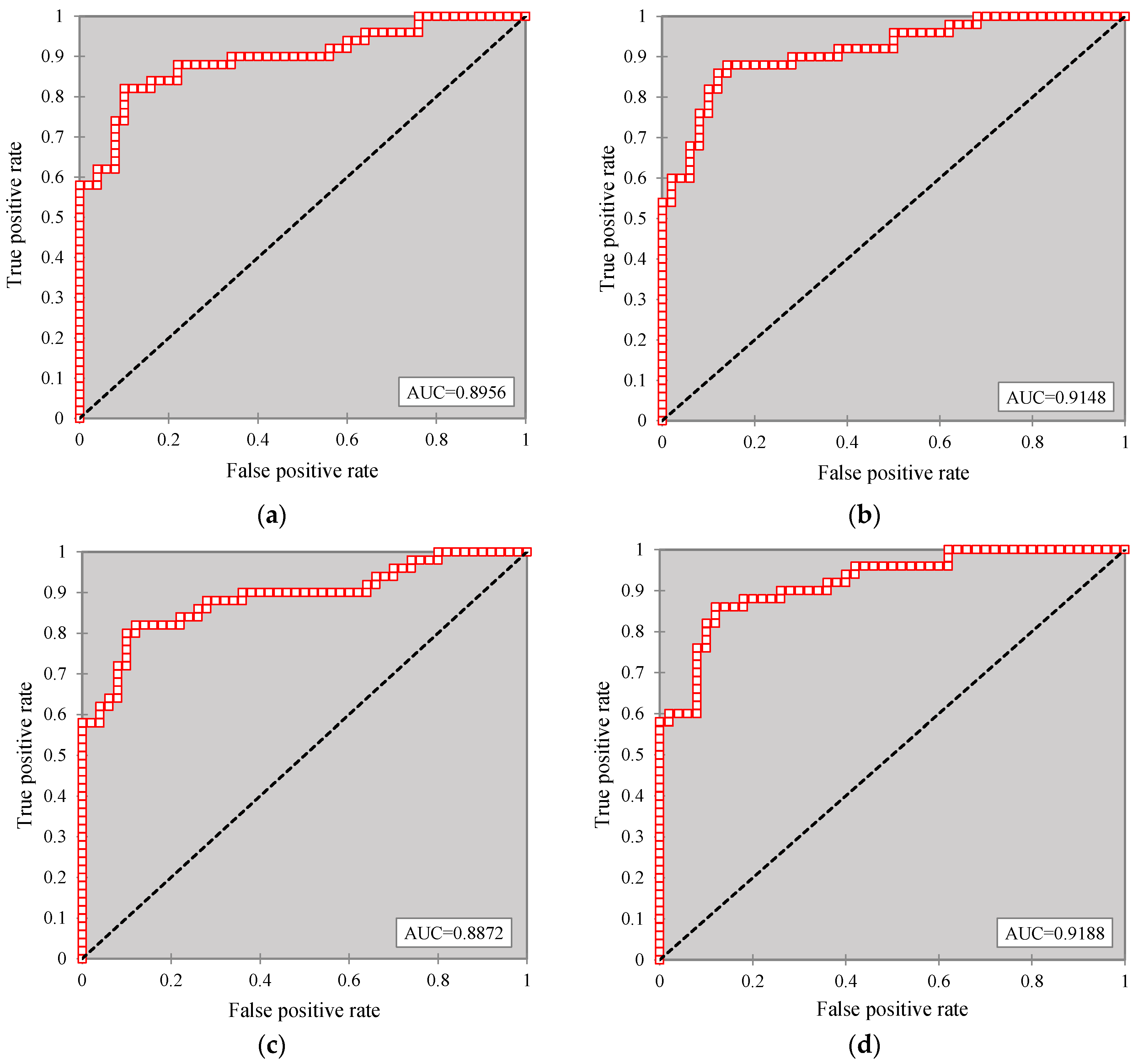
3.3. Performance Evaluation
3.4. Selected Kernel Function
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sukartana, P.; Sumarni, G.; Broadbent, S. Evaluation of chlorfluazuron in controlling the subterranean termite coptotermes curvignathus (isoptera: Rhinotermitidae) in Indonesia. J. Trop. For. Sci. 2009, 21, 13–18. [Google Scholar]
- Nandika, D.; Rismayadi, Y.; Diba, F. Rayap: Biologi dan Pengendaliannya, Edisi ke-2 (Termite: Biology and Its Control), 2nd ed.; Universitas Muhammadiyah Surakarta: Surakarta, Indonesia, 2015; pp. 125–139. [Google Scholar]
- Nandika, D.; Tjahjono, B. Initial Attack of Subterranean Termites on Acacia Crassicarpa Plantation. Available online: http://spma.org.sg/wp-content/uploads/2016/09/Day-2-1430-Dodi-Nandika.pdf (accessed on 25 December 2017).
- Lewis, V.R. Alternative control strategies for termites. J. Agric. Entomol. 1997, 14, 291–307. [Google Scholar]
- Manzoor, F. Biosensors for Termite Control. In Proceedings of the IOP: Materials Science and Engineering, Indus University, Karachi, Pakistan, 24–26 June 2013; IOP Publishing: Bristol, UK, 2013; pp. 1–3. [Google Scholar]
- Indrayani, Y.; Yoshimura, T.; Yanase, Y.; Fujii, Y.; Imamura, Y. Evaluation of the temperature and relative humidity preferences of the western dry-wood termite incisitermes minor (Hagen) using acoustic emission (AE) monitoring. J. Wood Sci. 2007, 53, 76–79. [Google Scholar] [CrossRef]
- Lewis, V.; Leighton, S.; Tabuchi, R.; Haverty, M. Seasonal and daily patterns in activity of the western drywood termite, incisitermes minor (Hagen). Insects 2011, 2, 555–563. [Google Scholar] [CrossRef] [PubMed]
- Lewis, V.R.; Power, A.B.; Haverty, M.I. Surface and subsurface sensor performance in acoustically detecting western drywood termites in naturally infested boards. Forest Prod. J. 2004, 54, 57–62. [Google Scholar]
- Mankin, R.; Osbrink, W.; Oi, F.; Anderson, J. Acoustic detection of termite infestations in urban trees. J. Econ. Entomol. 2002, 95, 981–988. [Google Scholar] [CrossRef] [PubMed]
- Chapman, R.F. The Insects: Structure and Function; Cambridge University Press: Cambridge, UK, 1998; p. 831. [Google Scholar]
- Evans, T.; Inta, R.; Lai, J.C.; Lenz, M. Foraging vibration signals attract foragers and identify food size in the drywood termite, cryptotermes secundus. Insectes Sociaux 2007, 54, 374–382. [Google Scholar] [CrossRef]
- Hussein, W.B.; Hussein, M.A.; Becker, T. Detection of the red palm weevil rhynchophorus ferrugineus using its bioacoustics features. Bioacoustics 2010, 19, 177–194. [Google Scholar] [CrossRef]
- Rach, M.M.; Gomis, H.M.; Granado, O.L.; Malumbres, M.P.; Campoy, A.M.; Martín, J.J.S. On the design of a bioacoustic sensor for the early detection of the red palm weevil. Sensors 2013, 13, 1706–1729. [Google Scholar] [CrossRef] [PubMed]
- Srinivas, S.; Harsha, K.S.; Sujatha, A.; Narendra, K.G. Effcient protection of palms from rpw larvae using wireless sensor networks. Int. J. Comput. Sci. 2013, 10, 192–200. [Google Scholar]
- Glowacz, A. Fault diagnostics of acoustic signals of loaded synchronous motor using smofs-25-expanded and selected classifiers. Teh. Vjesn. 2016, 23, 1365–1372. [Google Scholar] [CrossRef]
- Józwik, J. Identification and monitoring of noise sources of cnc machine tools by acoustic holography methods. Adv. Sci. Technol. Res. J. 2016, 10. [Google Scholar] [CrossRef]
- Glowacz, A.; Glowacz, W.; Glowacz, Z.; Kozik, J. Early fault diagnosis of bearing and stator faults of the single-phase induction motor using acoustic signals. Measurement 2018, 113, 1–9. [Google Scholar] [CrossRef]
- Glowacz, A.; Glowacz, Z. Diagnosis of stator faults of the single-phase induction motor using acoustic signals. Appl. Acoust. 2017, 117, 20–27. [Google Scholar] [CrossRef]
- Glowacz, A. Diagnostics of rotor damages of three-phase induction motors using acoustic signals and smofs-20-expanded. Arch. Acoust. 2016, 41, 507–515. [Google Scholar] [CrossRef]
- Green, F., III; Arango, R.A.; Boardman, C.R.; Bourne, K.J.; Hermanson, J.C.; Munson, R.A. Remote Sensing for Detection of Termite Infestations—Proof of Concept. In Proceedings of the the International Research Group on Wood Protection, Viña del Mar, Chile, 10–14 May 2015; pp. 1–10. [Google Scholar]
- Zhang, Y.; Wu, L. Classification of fruits using computer vision and a multiclass support vector machine. Sensors 2012, 12, 12489–12505. [Google Scholar] [CrossRef] [PubMed]
- SNI (Standar Nasional Indonesia). Wood and Wood Products Resistance Test to Wood Destroying Organism (SNI 01.7207-2006); Indonesian National Standard Bureau: Jakarta, Indonesia, 2006. [Google Scholar]
- Ciptohadijoyo, S.; Litananda, W.; Rivai, M.; Purnomo, M. Electronic nose based on partition column integrated with gas sensor for fruit identification and classification. Comput. Electron. Agric. 2016, 121, 429–435. [Google Scholar] [CrossRef]
- Giannakopoulos, T.; Pikrakis, A. Introduction to Audio Analysis: A Matlab® Approach; Academic Press: Cambridge, MA, USA, 2014; pp. 70–75. [Google Scholar]
- Hemmati, F.; Orfali, W.; Gadala, M.S. Roller bearing acoustic signature extraction by wavelet packet transform, applications in fault detection and size estimation. Appl. Acoust. 2016, 104, 101–118. [Google Scholar] [CrossRef]
- Jain, A.K.; Duin, R.P.W.; Mao, J. Statistical pattern recognition: A review. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 4–37. [Google Scholar] [CrossRef]
- Bakheet, S. An svm framework for malignant melanoma detection based on optimized hog features. Computation 2017, 5, 4. [Google Scholar] [CrossRef]
- Wang, S.; Li, Y.; Shao, Y.; Cattani, C.; Zhang, Y.; Du, S. Detection of dendritic spines using wavelet packet entropy and fuzzy support vector machine. CNS Neurol. Disord. Drug Targets (Former. Curr. Drug Targets-CNS Neurol. Disord.) 2017, 16, 116–121. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.-X.; Zhong, J.-H. A hybrid EEMD-based sampEn and SVD for acoustic signal processing and fault diagnosis. Entropy 2016, 18, 112. [Google Scholar] [CrossRef]
- Glowacz, A. Recognition of acoustic signals of induction motor using fft, smofs-10 and isvm. Eksploat. Niezawodn. 2015, 17. [Google Scholar] [CrossRef]
- Men, S.; Yan, L.; Liu, J.; Qian, H.; Luo, Q. A classification method for seed viability assessment with infrared thermography. Sensors 2017, 17, 845. [Google Scholar] [CrossRef] [PubMed]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin, Germany, 2006; pp. 331–333. [Google Scholar]
- Wang, S.; Phillips, P.; Liu, A.; Du, S. Tea category identification using computer vision and generalized eigenvalue proximal svm. Fundam. Inform. 2017, 151, 325–339. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, Z.; Wang, S.; Ji, G.; Yang, J. Preclinical diagnosis of magnetic resonance (MR) brain images via discrete wavelet packet transform with tsallis entropy and generalized eigenvalue proximal support vector machine (GEPSVM). Entropy 2015, 17, 1795–1813. [Google Scholar] [CrossRef]
- Wilk-Kolodziejczyk, D.; Regulski, K.; Gumienny, G. Comparative analysis of the properties of the nodular cast iron with carbides and the austempered ductile iron with use of the machine learning and the support vector machine. Int. J. Adv. Manuf. Technol. 2016, 87, 1077–1093. [Google Scholar] [CrossRef]
- Karatzoglou, A.; Meyer, D.; Hornik, K. Support vector machines in R. J. Stat. Softw. 2005, 15, 1–28. [Google Scholar]
- Hsu, C.-W.; Chang, C.-C.; Lin, C.-J. A Practical Guide to Support Vector Classification; National Taiwan University: Taipei, Taiwan, 2003. [Google Scholar]
- Min, J.H.; Lee, Y.-C. Bankruptcy prediction using support vector machine with optimal choice of kernel function parameters. Expert Syst. Appl. 2005, 28, 603–614. [Google Scholar] [CrossRef]
- Park, S.H.; Goo, J.M.; Jo, C.-H. Receiver operating characteristic (ROC) curve: Practical review for radiologists. Korean J. Radiol. 2004, 5, 11–18. [Google Scholar] [CrossRef] [PubMed]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Zhu, W.; Zeng, N.; Wang, N. Sensitivity, specificity, accuracy, associated confidence interval and roc analysis with practical sas implementations. In Proceedings of the NESUG: Health Care and Life Sciences, Baltimore, MD, USA, 14–17 November 2010; Volume 19. [Google Scholar]
- Bradley, A.P. The use of the area under the roc curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]
- Lin, S.-W.; Ying, K.-C.; Chen, S.-C.; Lee, Z.-J. Particle swarm optimization for parameter determination and feature selection of support vector machines. Expert Syst. Appl. 2008, 35, 1817–1824. [Google Scholar] [CrossRef]
- Pardo, M.; Sberveglieri, G. Classification of electronic nose data with support vector machines. Sens. Actuators B Chem. 2005, 107, 730–737. [Google Scholar] [CrossRef]
- Zhang, M. Artificial Higher Order Neural Networks for Economics and Business; IGI Global: Derry Township, PA, USA, 2008. [Google Scholar]
- Ben-Hur, A.; Ong, C.S.; Sonnenburg, S.; Schölkopf, B.; Rätsch, G. Support vector machines and kernels for computational biology. PLoS Comput. Biol. 2008, 4, e1000173. [Google Scholar] [CrossRef] [PubMed]
- Hua, S.; Sun, Z. Support vector machine approach for protein subcellular localization prediction. Bioinformatics 2001, 17, 721–728. [Google Scholar] [CrossRef] [PubMed]
- Hager, F.A.; Kirchner, W.H. Vibrational long-distance communication in the termites Macrotermes natalensis and Odontotermes sp. J. Exp. Biol. 2013, 216, 3249–3256. [Google Scholar] [CrossRef] [PubMed]
- Nanda, M.A.; Seminar, K.B.; Nandika, D. Characteristics of acoustic emission for subterranean termite detection in wood. J. Keteknikan Pertan. 2017, 5. in press. [Google Scholar]
- Patel, K. A review on feature extraction methods. Int. J. Adv. Res. Electr. Electron. Instrum. Eng. 2016, 5, 823–827. [Google Scholar] [CrossRef]
- Daud, W.M.B.W.; Yahya, A.B.; Horng, C.S.; Sulaima, M.F.; Sudirman, R. Features extraction of electromyography signals in time domain on biceps brachii muscle. Int. J. Model. Optim. 2013, 3, 515. [Google Scholar] [CrossRef]



| No. | Kernel Function | Formula | Optimization Parameter |
|---|---|---|---|
| 1 | Linear | C and γ | |
| 2 | RBF | C and γ | |
| 3 | Sigmoid | C, γ, and r | |
| 4 | Polynomial | C, γ, r, and d |
| AUC Range | Description |
|---|---|
| 0.9 < AUC < 1.0 | Excellent |
| 0.8 < AUC < 0.9 | Good |
| 0.7 < AUC < 0.8 | Worthless |
| 0.6 < AUC < 0.7 | Not good |
| Kernel Function | Optimal Pair Value | Classification Error | |||
|---|---|---|---|---|---|
| Linear | 2−5 | 2−10 | n/a | n/a | 0.17 |
| RBF | 2−1 | 2−3 | n/a | n/a | 0.15 |
| Sigmoid | 2−3 | 2−2 | 2−6 | n/a | 0.16 |
| Polynomial | 2−8 | 2−1 | 22 | 3 | 0.12 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Achirul Nanda, M.; Boro Seminar, K.; Nandika, D.; Maddu, A. A Comparison Study of Kernel Functions in the Support Vector Machine and Its Application for Termite Detection. Information 2018, 9, 5. https://doi.org/10.3390/info9010005
Achirul Nanda M, Boro Seminar K, Nandika D, Maddu A. A Comparison Study of Kernel Functions in the Support Vector Machine and Its Application for Termite Detection. Information. 2018; 9(1):5. https://doi.org/10.3390/info9010005
Chicago/Turabian StyleAchirul Nanda, Muhammad, Kudang Boro Seminar, Dodi Nandika, and Akhiruddin Maddu. 2018. "A Comparison Study of Kernel Functions in the Support Vector Machine and Its Application for Termite Detection" Information 9, no. 1: 5. https://doi.org/10.3390/info9010005
APA StyleAchirul Nanda, M., Boro Seminar, K., Nandika, D., & Maddu, A. (2018). A Comparison Study of Kernel Functions in the Support Vector Machine and Its Application for Termite Detection. Information, 9(1), 5. https://doi.org/10.3390/info9010005