Image Super-Resolution Algorithm Based on an Improved Sparse Autoencoder
Abstract
:1. Introduction
- A novel training set preprocessing method is proposed. By regarding the high-frequency information of the image as the characterization, we construct the HR and LR image training sets with different methods, and then apply the zero-phase component analysis (ZCA) whitening method to reduce the redundancy of the joint training set to improve the learning efficiency of the SAE.
- An improved SAE (ISAE) is proposed to boost the accuracy and stability of the dictionary. A new sparse regularization term related to the hidden layer is introduced into the cost function of the traditional SAE to further strengthen the sparseness constraint on the hidden layer, so that the number of hidden units whose average activation is close to zero is as many as possible.
- The SR algorithm based on the SAE (SRSAE) and the SR algorithm based on the ISAE (SRISAE) are proposed. The SAE is employed to achieve unsupervised dictionary learning, and then by applying this unsupervised dictionary learning method to the SR algorithm based on sparse representation, the SRSAE can be constructed. By replacing the SAE with the ISAE, the SRISAE can be obtained using the same procedure described above.
2. Related Works
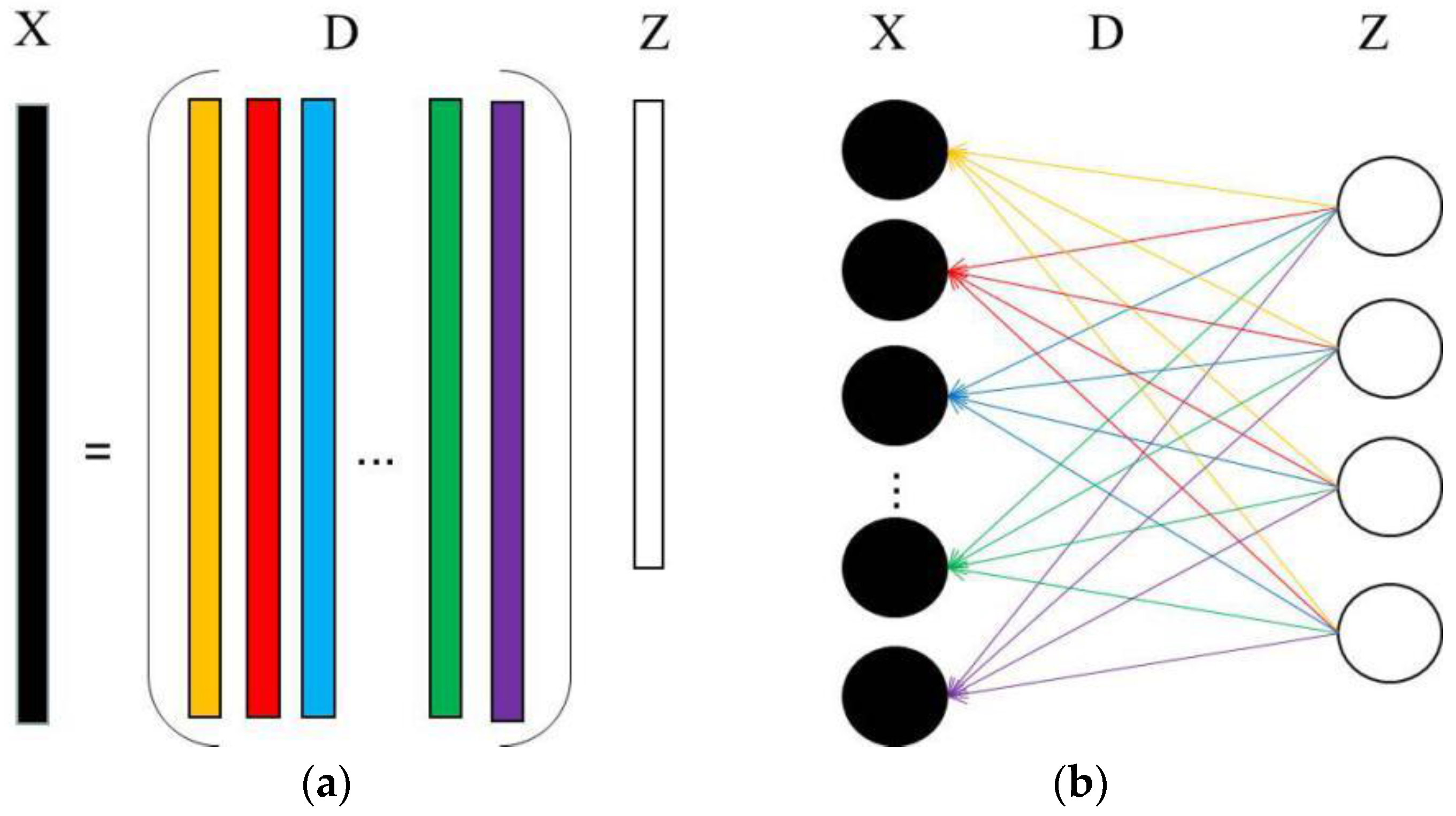
3. Image SR Algorithm Based on Dictionary Learning
4. Proposed Algorithm
4.1. Training Set Preprocessing Method
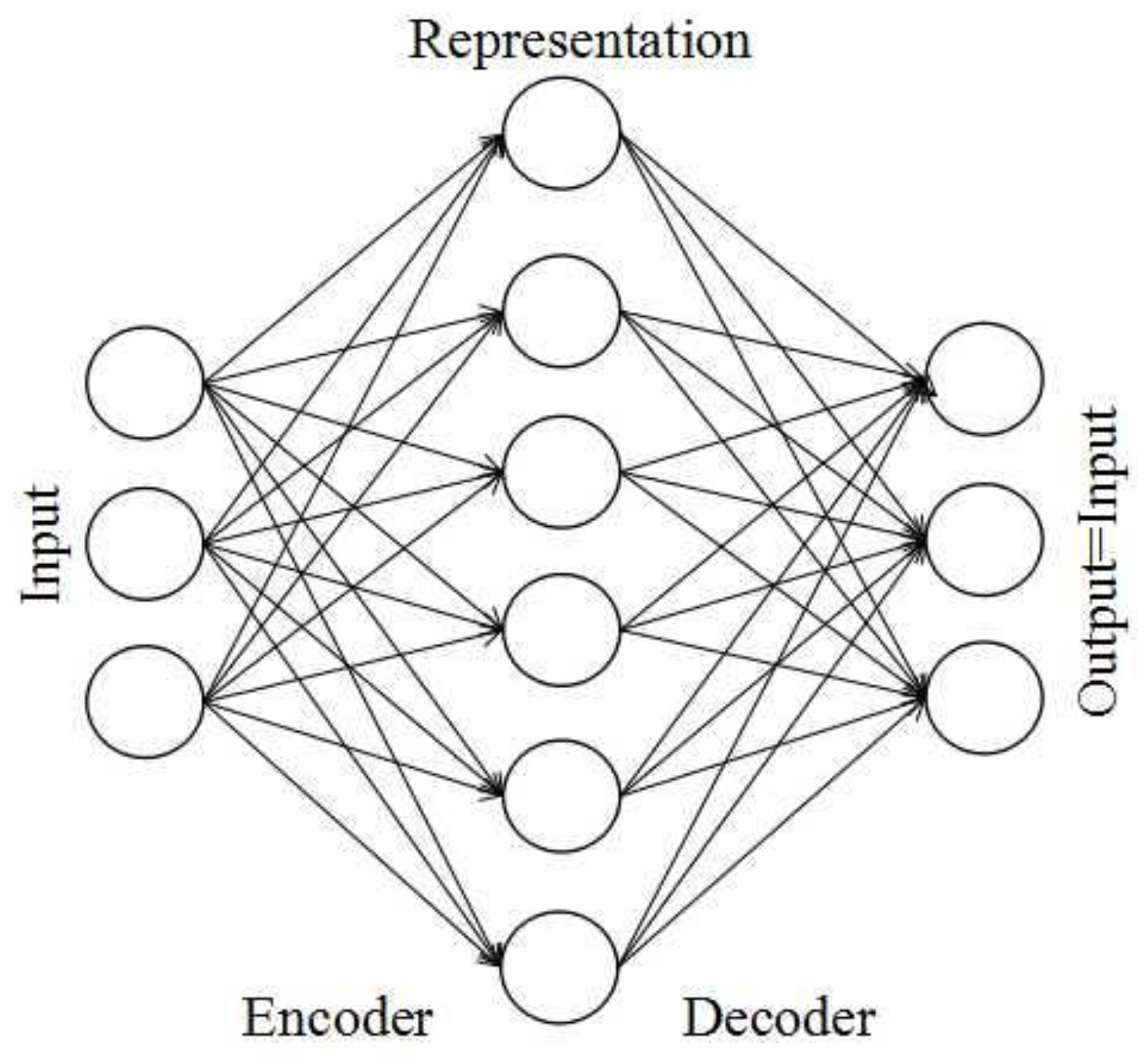
4.2. Unsupervised Dictionary Learning Model Based on ISAE
4.3. The Overall Flow of the Proposed Algorithm
| Algorithm 1: Proposed SR algorithm. |
| Input: an LR image to be reconstructed, the HR sample images for dictionary learning. Step 1: obtain the LR images by down-sampling the HR images , and then obtain the middle images of the same size as the HR images by up-sampling the LR images with Bicubic interpolation. Step 2: obtain the HR and LR joint training set through preprocessing the HR images , the LR images , and the middle images by applying the proposed training set preprocessing method. Step 3: generate the HR dictionary and LR dictionary by utilizing the ISAE to learn the joint training set . Step 4: calculate the sparse representation coefficients of the LR image to be reconstructed under the learned LR dictionary by using the feature-sign search (FSS) algorithm [28]. Step 5: reconstruct the HR image via . Step 6: obtain the final reconstructed HR image by compensating for with the global error compensation model based on the weighted guided filter [29]. Output: HR image . |
5. Experiments
5.1. Samples and Settings
5.2. Experimental Results
5.2.1. Analyze the Influence of Different Number of Hidden Units on the Reconstructed Images
5.2.2. Analyze the Effectiveness of Dictionary Learning Based on SAE or ISAE
5.2.3. Analyze the Performance of Different SR Algorithms on Images Sets
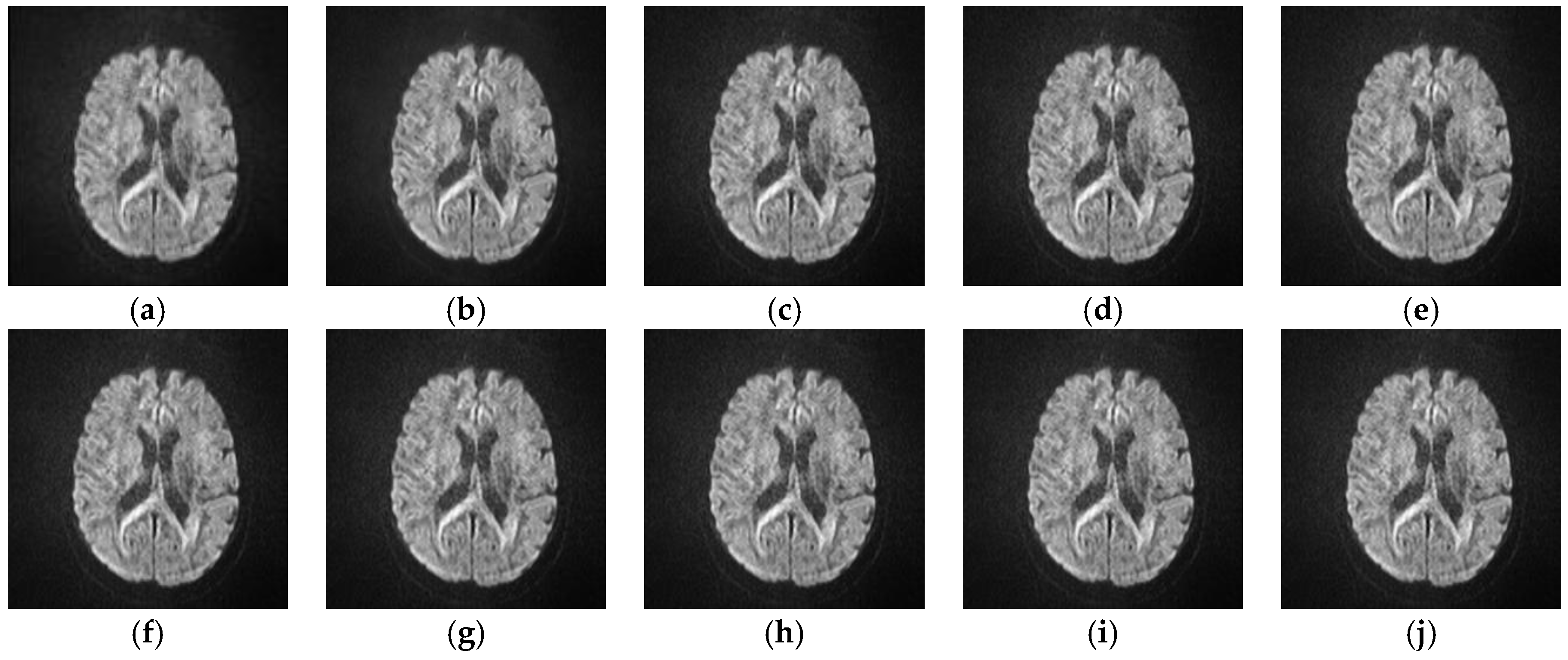
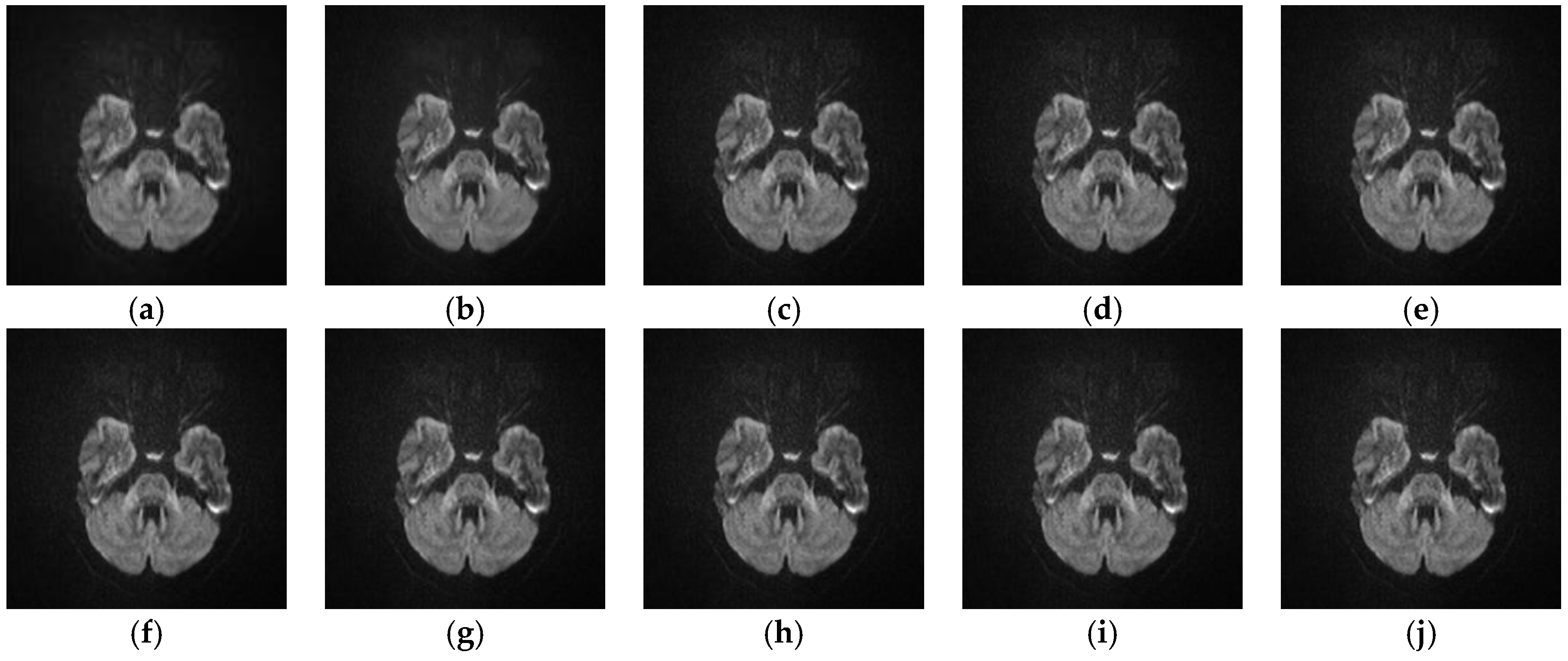
5.2.4. Analyze the Performance of Different SR Algorithms on Real Medical Images
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pan, Z.X.; Yu, J.U.; Xiao, C.B.; Sun, W.D. Single image super resolution based on adaptive multi-dictionary learning. Acta Electron. Sin. 2015, 43, 209–216. [Google Scholar]
- Huang, D.T.; Huang, W.Q.; Huang, H.; Zheng, L.X. Application of regularization technique in image super-resolution algorithm via sparse representation. Optoelectron. Lett. 2017, 13, 439–443. [Google Scholar] [CrossRef]
- Olshausen, B.A.; Field, D.J. Sparse coding with an overcomplete basis set: A strategy employed by V1? Vis. Res. 1997, 37, 3311–3325. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [PubMed]
- Elad, M.; Aharon, M. Image denoisingvia sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar] [CrossRef] [PubMed]
- Koh, M.S.; Rodriguez-Marek, E. Turbo inpainting: Iterative K-SVD with a new dictionary. In Proceedings of the IEEE International Workshop on Multimedia Signal Processing, Rio De Janeiro, Brazil, 5–7 October 2009; pp. 1–6. [Google Scholar]
- Mairal, J.; Elad, M.; Sapiro, G. Sparse representation for color image restoration. IEEE Trans. Image Process. 2008, 17, 53–69. [Google Scholar] [CrossRef] [PubMed]
- Son, C.H.; Choo, H. Local learned dictionaries optimized to edge orientation for inverse halftoning. IEEE Trans. Image Process. 2014, 23, 2542–2556. [Google Scholar] [PubMed]
- Caballero, J.; Price, A.N.; Rueckert, D.; Hajnal, J.V. Dictionary learning and time sparsity for dynamic MR data reconstruction. IEEE Trans. Med. Imaging 2014, 33, 979–994. [Google Scholar] [CrossRef] [PubMed]
- Majumdar, A.; Ward, R. Learning space-time dictionaries for blind compressed sensing dynamic MRI reconstruction. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; pp. 4550–4554. [Google Scholar]
- Jadhav, D.V.; Holambe, R.S. Feature extraction using Radon and wavelet transforms with application to face recognition. Neurocomputing 2009, 72, 1951–1959. [Google Scholar] [CrossRef]
- Dabbaghchian, S.; Ghaemmaghami, M.P.; Aghagolzadeh, A. Feature extraction using discrete cosine transform and discrimination power analysis with a face recognition technology. Pattern Recognit. 2010, 43, 1431–1440. [Google Scholar] [CrossRef]
- Engan, K.; Aase, S.O.; Husoy, J.H. Frame based signal compression using method of optimal directions (MOD). In Proceedings of the IEEE International Symposium on Circuits and Systems, Orlando, FL, USA, 30 May–2 June 1999; Volume 4, pp. 1–4. [Google Scholar]
- Aharon, M.; Elad, M.; Bruckstein, A. rm K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Mairal, J.; Bach, F.; Ponce, J.; Sapiro, G. Online learning for matrix factorization and sparse coding. J. Mach. Learn. Res. 2010, 11, 19–60. [Google Scholar]
- Singhal, V.; Gogna, A.; Majumdar, A. Deep dictionary learning vs deep belief network vs stacked autoencoder: An empirical analysis. In Proceedings of the International Conference on Neural Information Processing, Kyoto, Japan, 16–21 October 2016; Springer: Cham, Switzerland, 2016; pp. 337–344. [Google Scholar]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image super-resolution via sparse representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef] [PubMed]
- Zeyde, R.; Elad, M.; Protter, M. On single image scale-up using sparse-representations. In Proceedings of the International Conference on Curves and Surfaces, Avignon, France, 24–30 June 2010; Volume 6920, pp. 711–730. [Google Scholar]
- Jing, X.Y.; Zhu, X.; Wu, F.; Hu, R.; You, X.; Wang, Y.; Feng, H.; Yang, J.Y. Super-resolution person re-identification with semi-coupled low-rank discriminant dictionary learning. IEEE Trans. Image Process. 2015, 26, 1363–1378. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhou, W.; Duan, Z. Image super-resolution reconstruction based on fusion of K-SVD and semi-coupled dictionary learning. In Proceedings of the Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA), Jeju, Korea, 13–16 December 2016; pp. 1–5. [Google Scholar]
- Zhang, Y.; Liu, Y. Single image super-resolution reconstruction method based on LC-KSVD algorithm. AIP Conf. Proc. 2017, 1521–1527. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, X.; Yang, S.; Yu, L.I. Retrieval of remote sensing images based on semisupervised deep learning. J. Remote Sens. 2017, 21, 406–414. [Google Scholar]
- Donoho, D.L. For most large underdetermined systems of equations, the minimal ℓ1-norm near-solution approximates the sparsest near-solution. Commun. Pure Appl. Math. 2010, 59, 797–829. [Google Scholar] [CrossRef]
- Merola, G.M. SPCA: Sparse principal component analysis. Pattern Recognit. Lett. 2014, 34, 1037–1045. [Google Scholar]
- Krizhevsky, A. Learning Multiple Layers of Features from Tiny Images; Technical Report; University of Toronto: Toronto, ON, Canada, 2009. [Google Scholar]
- Ng, A. Sparse Autoencoder; CS294A Lecture Notes; Stanford University: Stanford, CA, USA, 2011; Volume 72, pp. 1–19. [Google Scholar]
- Miller, F.P.; Vandome, A.F.; Mcbrewster, J. Gradient Descent; Alphascript Publishing: Saarbrücken, Germany, 2010; Volume 20, pp. 235–242. [Google Scholar]
- Li, X.F.; Zeng, L.; Xu, J.; Ma, S.Q. Single image super-resolution based on the feature sign method. J. Univ. Electron. Sci. Technol. China 2015, 44, 22–27. [Google Scholar]
- Huang, D.T.; Huang, W.Q.; Gu, P.T.; Liu, P.Z.; Luo, Y.M. Image super-resolution reconstruction based on regularization technique and guided filter. Infrared Phys. Technol. 2017, 83, 103–113. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Lu, Y.; Fu, Y. Image quality evaluation based on image weighted separating block peak signal to noise ratio. In Proceedings of the IEEE International Conference on Neural Networks and Signal Processing, Nanjing, China, 14–17 December 2003; Volume 2, pp. 994–997. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Bevilacqua, M.; Roumy, A.; Guillemot, C.; Morel, A. Low-complexity single-image super-resolution based on nonnegative neighbor embedding. In Proceedings of the British Machine Vision Conference, Guildford, UK, 3–7 September 2012; pp. 1–10. [Google Scholar]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In Proceedings of the IEEE International Conference on Computer Vision, Vancouver, BC, Canada, 7–14 July 2001; pp. 416–423. [Google Scholar]
- Timofte, R.; De, V.; Gool, L.V. Anchored neighborhood regression for fast example-based super-resolution. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Sydney, Australia, 1–8 December 2013; pp. 1920–1927. [Google Scholar]
- Timofte, R.; Smet, V.D.; Gool, L.V. A+: Adjusted Anchored Neighborhood Regression for Fast Super-Resolution. Asian Conference on Computer Vision; Springer: Cham, Switzerland, 2014; Volume 9006, pp. 111–126. [Google Scholar]
- Clark, K.; Vendt, B.; Smith, K.; Freymann, J.; Koppel, P.; Moore, S.; Phillips, S.; Maffitt, D.; Pringle, M.; Tarbox, L.; et al. The Cancer Imaging Archive (TCIA): Maintaining and operating a public information repository. J. Digit. Imaging 2013, 26, 1045–1057. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.N.; Zhong, W.; Wang, J.; Xia, D.S. Research of measurement for Digital Image Definition. J. Image Graph. 2004, 9, 828–831. [Google Scholar]
- Li, Z.L.; Li, X.H.; Ma, L.L.; Hu, Y.; Tang, L.L. Research of Definition Assessment based on No-reference Digital Image Quality. Remote Sens. Technol. Appl. 2011, 26, 239–246. [Google Scholar]





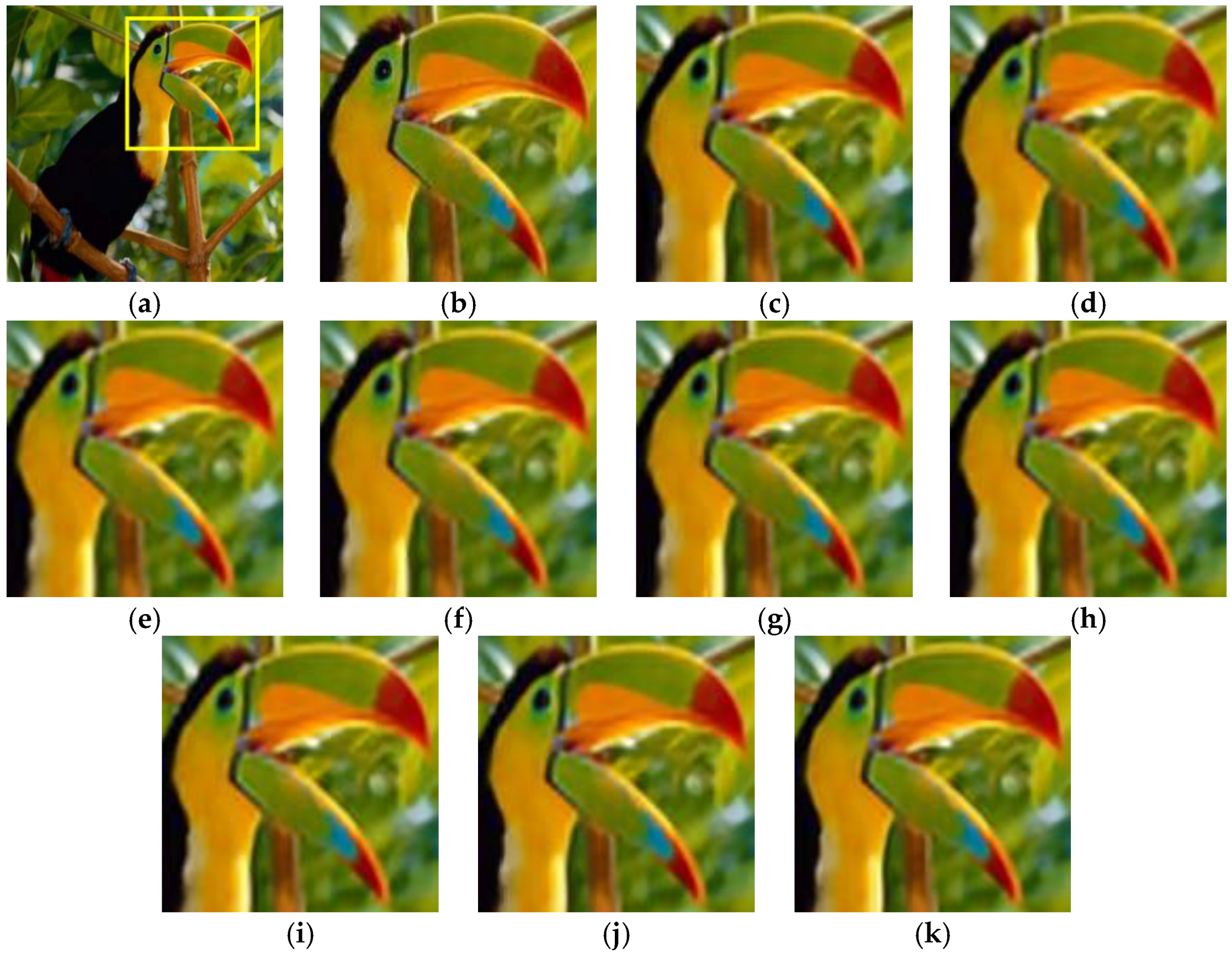
| Images | 256 | 512 | 1024 | 2048 |
|---|---|---|---|---|
| Baby | 35.20/0.9425 | 35.06/0.9411 | 35.23/0.9426 | 35.26/0.9428 |
| Bird | 34.52/0.9616 | 34.68/0.9618 | 35.36/0.9666 | 35.14/0.9658 |
| Butterfly | 25.71/0.8947 | 26.39/0.9077 | 26.63/0.9179 | 26.48/0.9174 |
| Head | 33.61/0.8604 | 33.62/0.8606 | 33.82/0.8624 | 33.71/0.8621 |
| Woman | 30.15/0.9344 | 30.49/0.9370 | 30.81/0.9421 | 30.73/0.9417 |
| Average | 31.84/0.9187 | 32.05/0.9216 | 32.37/0.9263 | 32.26/0.9260 |
| Images | Bicubic | SRSAE | SRISAE |
|---|---|---|---|
| Set5 | 30.40/0.8953 | 32.16/0.9234 | 32.37/0.9263 |
| Set4 | 27.54/0.8107 | 28.90/0.8487 | 28.99/0.8503 |
| BSD100 | 27.15/0.7775 | 28.03/0.8169 | 28.19/0.8180 |
| Images | PSNR/SSIM | L1SR | SISR | ANR | NE + LS | NE + NNLS | NE + LLE | A + (16 Atoms) | ISPSR | SRISAE |
|---|---|---|---|---|---|---|---|---|---|---|
| baby | PSNR | 34.29 | 35.08 | 35.13 | 34.96 | 34.77 | 35.06 | 35.13 | 35.23 | 35.23 |
| SSIM | 0.9226 | 0.9402 | 0.9415 | 0.9390 | 0.9370 | 0.9401 | 0.9409 | 0.9426 | 0.9426 | |
| bird | PSNR | 34.11 | 34.57 | 34.60 | 34.36 | 34.26 | 34.56 | 34.83 | 35.25 | 35.36 |
| SSIM | 0.9530 | 0.9615 | 0.9623 | 0.9602 | 0.9581 | 0.9615 | 0.9629 | 0.9663 | 0.9666 | |
| Head | PSNR | 33.17 | 33.56 | 33.63 | 33.53 | 33.45 | 33.60 | 33.65 | 33.74 | 33.82 |
| SSIM | 0.8382 | 0.8572 | 0.8600 | 0.8569 | 0.8554 | 0.8590 | 0.8606 | 0.8616 | 0.8624 | |
| flowers | PSNR | 28.25 | 28.43 | 28.49 | 28.35 | 28.21 | 28.38 | 28.52 | 28.74 | 28.85 |
| SSIM | 0.8636 | 0.8713 | 0.8739 | 0.8697 | 0.8673 | 0.8718 | 0.8745 | 0.8801 | 0.8818 | |
| Lena | PSNR | 32.64 | 33.00 | 33.08 | 32.98 | 32.82 | 33.01 | 33.17 | 33.37 | 33.53 |
| SSIM | 0.8852 | 0.9002 | 0.9022 | 0.9000 | 0.8981 | 0.9010 | 0.9027 | 0.9050 | 0.9055 | |
| monarch | PSNR | 30.71 | 31.10 | 31.09 | 30.94 | 30.76 | 30.95 | 31.31 | 31.74 | 31.95 |
| SSIM | 0.9422 | 0.9510 | 0.9508 | 0.9499 | 0.9478 | 0.9495 | 0.9518 | 0.9558 | 0.9559 | |
| pepper | PSNR | 33.33 | 34.07 | 33.82 | 33.91 | 33.56 | 33.80 | 34.01 | 34.28 | 34.55 |
| SSIM | 0.8851 | 0.9060 | 0.9045 | 0.9046 | 0.9017 | 0.9041 | 0.9052 | 0.9080 | 0.9098 | |
| ppt3 | PSNR | 24.98 | 25.23 | 25.03 | 25.15 | 24.81 | 24.94 | 25.22 | 25.62 | 25.89 |
| SSIM | 0.9025 | 0.9204 | 0.9123 | 0.9193 | 0.9077 | 0.9111 | 0.9147 | 0.9298 | 0.9291 | |
| Average | PSNR | 31.44 | 31.88 | 31.86 | 31.77 | 31.58 | 31.79 | 31.98 | 32.25 | 32.40 |
| SSIM | 0.8991 | 0.9299 | 0.9098 | 0.9297 | 0.9011 | 0.9054 | 0.9116 | 0.9187 | 0.9195 |
| Image | L1SR | SISR | ANR | NE + LS | NE + NNLS | NE + LLE | A + (16 Atoms) | ISPSR | SRISAE |
|---|---|---|---|---|---|---|---|---|---|
| baby | 194.41 | 1.92 | 0.52 | 1.72 | 9.83 | 2.26 | 0.43 | 1309.44 | 3.28 |
| bird | 63.15 | 0.60 | 0.18 | 0.54 | 3.04 | 0.72 | 0.14 | 408.16 | 1.05 |
| Head | 55.42 | 0.55 | 0.16 | 0.50 | 2.87 | 0.64 | 0.13 | 378.57 | 1.02 |
| flowers | 141.14 | 1.40 | 0.37 | 1.19 | 6.78 | 1.60 | 0.30 | 899.02 | 2.24 |
| Lena | 187.96 | 1.91 | 0.51 | 1.72 | 9.70 | 2.27 | 0.43 | 1296.17 | 3.29 |
| monarch | 81.33 | 2.91 | 0.78 | 2.608 | 15.05 | 3.43 | 0.65 | 1974.27 | 5.06 |
| pepper | 186.37 | 1.92 | 0.53 | 1.73 | 9.87 | 2.25 | 0.44 | 1294.75 | 3.26 |
| ppt3 | 222.23 | 2.30 | 0.68 | 2.17 | 11.91 | 2.94 | 0.57 | 1727.80 | 4.08 |
| Average | 141.50 | 1.69 | 0.47 | 1.52 | 8.63 | 2.01 | 0.39 | 1161.02 | 2.91 |
| B100 | PSNR/SSIM | L1SR | SISR | ANR | NE + LS | NE + NNLS | NE + LLE | A + (16 Atoms) | ISPSR | SRISAE |
|---|---|---|---|---|---|---|---|---|---|---|
| Average | PSNR | 27.72 | 27.87 | 27.89 | 27.83 | 27.73 | 27.85 | 27.94 | 28.07 | 28.19 |
| SSIM | 0.800 | 0.809 | 0.812 | 0.809 | 0.806 | 0.811 | 0.814 | 0.8176 | 0.8180 |
| Indices | L1SR | SISR | ANR | NE + LS | NE + NNLS | NE + LLE | A + (16 Atoms) | ISPSR | SRISAE |
|---|---|---|---|---|---|---|---|---|---|
| Variance | 2446.8651 | 2479.3577 | 2483.4034 | 2480.6194 | 2478.4239 | 2481.2642 | 2483.7900 | 2483.0294 | 2486.2215 |
| Meangradient | 2.8012 | 3.2414 | 3.4120 | 3.2862 | 3.2877 | 3.4117 | 3.4927 | 3.4435 | 3.5033 |
| Entropy | 6.4871 | 6.5141 | 6.5256 | 6.5180 | 6.5170 | 6.5268 | 6.5275 | 6.5231 | 6.5383 |
| Brenner | 4,596,865 | 5,243,693 | 5,568,487 | 5,273,747 | 5,292,623 | 5,457,148 | 5,776,475 | 5,863,142 | 5,914,784 |
| Energy | 4,167,251 | 4,369,326 | 4,644,846 | 4,526,663 | 4,532,565 | 4,544,087 | 4,981,985 | 4,986,970 | 5,098,674 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, D.; Huang, W.; Yuan, Z.; Lin, Y.; Zhang, J.; Zheng, L. Image Super-Resolution Algorithm Based on an Improved Sparse Autoencoder. Information 2018, 9, 11. https://doi.org/10.3390/info9010011
Huang D, Huang W, Yuan Z, Lin Y, Zhang J, Zheng L. Image Super-Resolution Algorithm Based on an Improved Sparse Autoencoder. Information. 2018; 9(1):11. https://doi.org/10.3390/info9010011
Chicago/Turabian StyleHuang, Detian, Weiqin Huang, Zhenguo Yuan, Yanming Lin, Jian Zhang, and Lixin Zheng. 2018. "Image Super-Resolution Algorithm Based on an Improved Sparse Autoencoder" Information 9, no. 1: 11. https://doi.org/10.3390/info9010011
APA StyleHuang, D., Huang, W., Yuan, Z., Lin, Y., Zhang, J., & Zheng, L. (2018). Image Super-Resolution Algorithm Based on an Improved Sparse Autoencoder. Information, 9(1), 11. https://doi.org/10.3390/info9010011





