Predicting DNA Motifs by Using Multi-Objective Hybrid Adaptive Biogeography-Based Optimization
Abstract
:1. Introduction
2. Motif Discovery Problem
- (1)
- Support: Support indicates the level of the support of the candidate motifs to the consensus motif. The consensus motif is built by using the candidate motifs. The level of the support is measured by similarity rate of the candidate motif to the consensus motif. The similarity rate means the same number of the nucleosides between the candidate motif and the consensus motif. When the similarity rate is larger than 50%, the subsequent corresponding to candidate motif can be considered as a Support. For example, the consensus motif is assumed to be GACCTTTTGCAATCCTGG, the candidate motif of the sequence 1, i.e., GACCACTTGCAGTCTTAG, has 13 nucleotides identical to the consensus motif, and the consensus motif has 18 nucleotides, so its similarity rate is 13/18 = 72%.
- (2)
- Motif Length: The motif length points to the number of the nucleotides of the consensus motif. In the example, the motif length is 18. According to real datasets used in this paper, the value of the motif length is limited to between 5 and 60.
- (3)
- Similarity: the similarity objective function of motif is defined as the average of the dominance values of all position weight matrix columns. The similarity is calculated based on Equation (1). In which the in each column (dominant nucleotide) is the dominance value of the dominant nucleotide, it is calculated by Equation (2):where is the score of nucleotide b in column i in the position weight matrix, and l is the motif length.
3. MHABBO Algorithm
3.1. Migration Operator for the MDP
| Algorithm 1: Migration for the MDP (MigrationDo(H, )) Input: Initial population H and migration probability Output: The population H that have been optimized by migration |
| For i = 1 to NP // NP is the size of population If rand < Use to probabilistically decide whether to immigrate to If then For Select the emigrating island with probability If then For j = 1 to Nd // Nd is the dimension size End for End if End for End if End if End for |
3.2. Mutation Operator for the MDP
| Algorithm 2: Mutation for the MDP (Mutation Do(H, )) Input: The population H optimized by migration, mutation probability Output: The population H that have been optimized by mutation |
| For i = 1 to NP // NP is the size of population Select mutating habitat with probability If is selected, then For j = 1 to Nd // Nd is the dimension size End for End if End for |
3.3. Adaptive BBO for MDP
3.4. The Redefinition of the Fitness Function
3.5. Main Procedure of MHABBO for Multi-Objective Motif Discovery Problem
| Algorithm 3: The main pseudo-code of MHABBO algorithm for multi-objective MDP |
| Input: The Sequences S Output: support, motif length, similarity and the non-dominated consensus motif instance and corresponding PWM. 1. Init(number of iterations, elitism parameter keep, migration probability , mutation probability etc.) 2. GenerateInitialRandomPopulation() 3. EvaluateFitness() for each habitat in according to Equation (9). 4. While the halting criterion is not satisfied do 5. Elite(1:keep) 6. Compute for each habitat according to Equations (3) and (4) 7. MigrationDo(, ) Algorithm 1 8. MutationDo(, ) Algorithm 2 9. EvaluateFitness() 10. SortPopulation() 11. ReplaceWorstbyElites (, Elite) 12. ClearDuplicates() 13. [maximum cost, minimum cost, average cost]EvaluateCostItems() 14. [,]updateProbability() Equations (7) and (8) 15. End while |
| GenerateInitialRandomPopulation() |
|
| EvaluateFitness() |
|
4. Simulation and Analysis
4.1. Simulation, Comparison and Discussion
4.1.1. Results Comparisons with Other Methods
4.1.2. The Consensus Motifs Obtained by MHABBO Algorithm
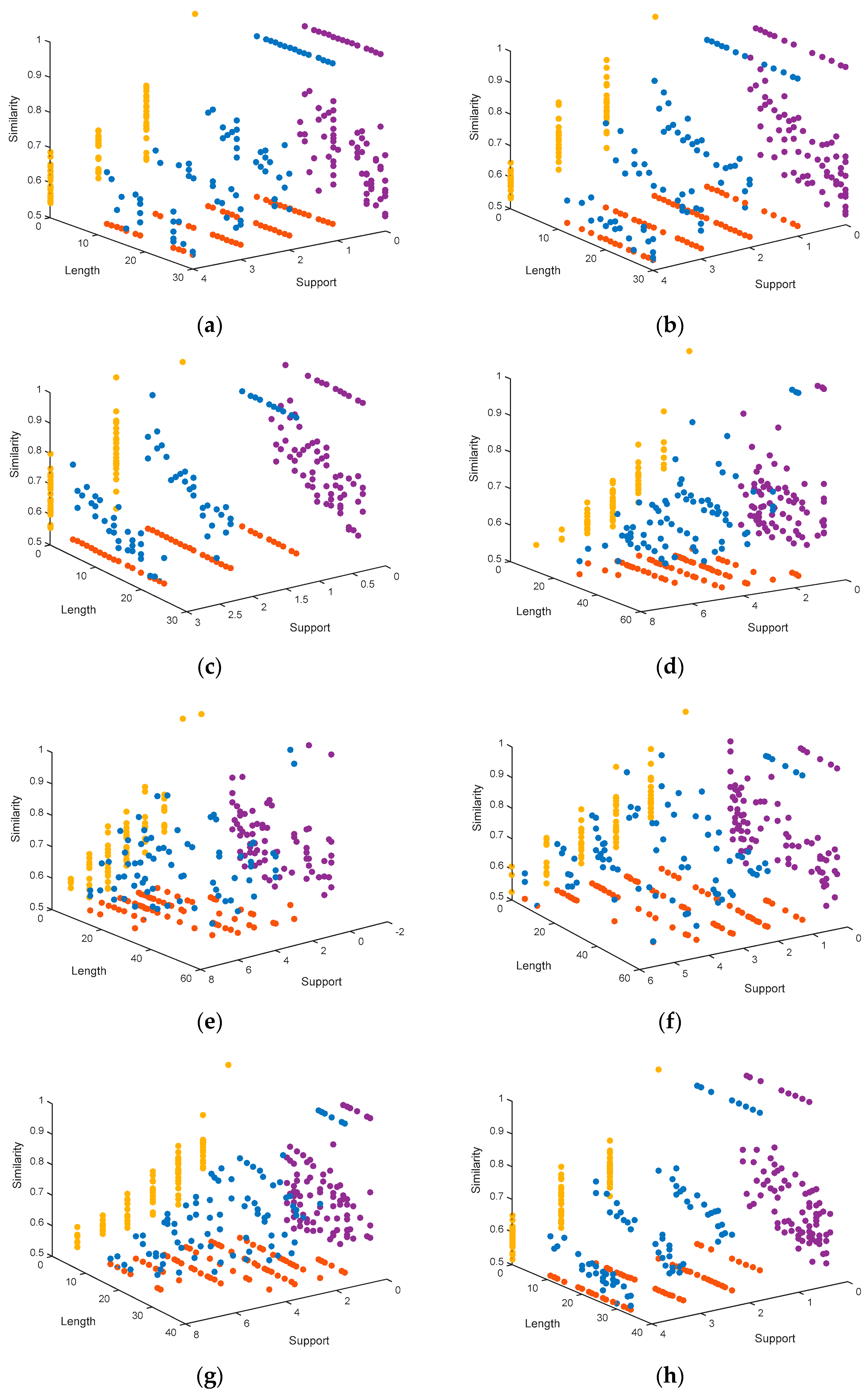
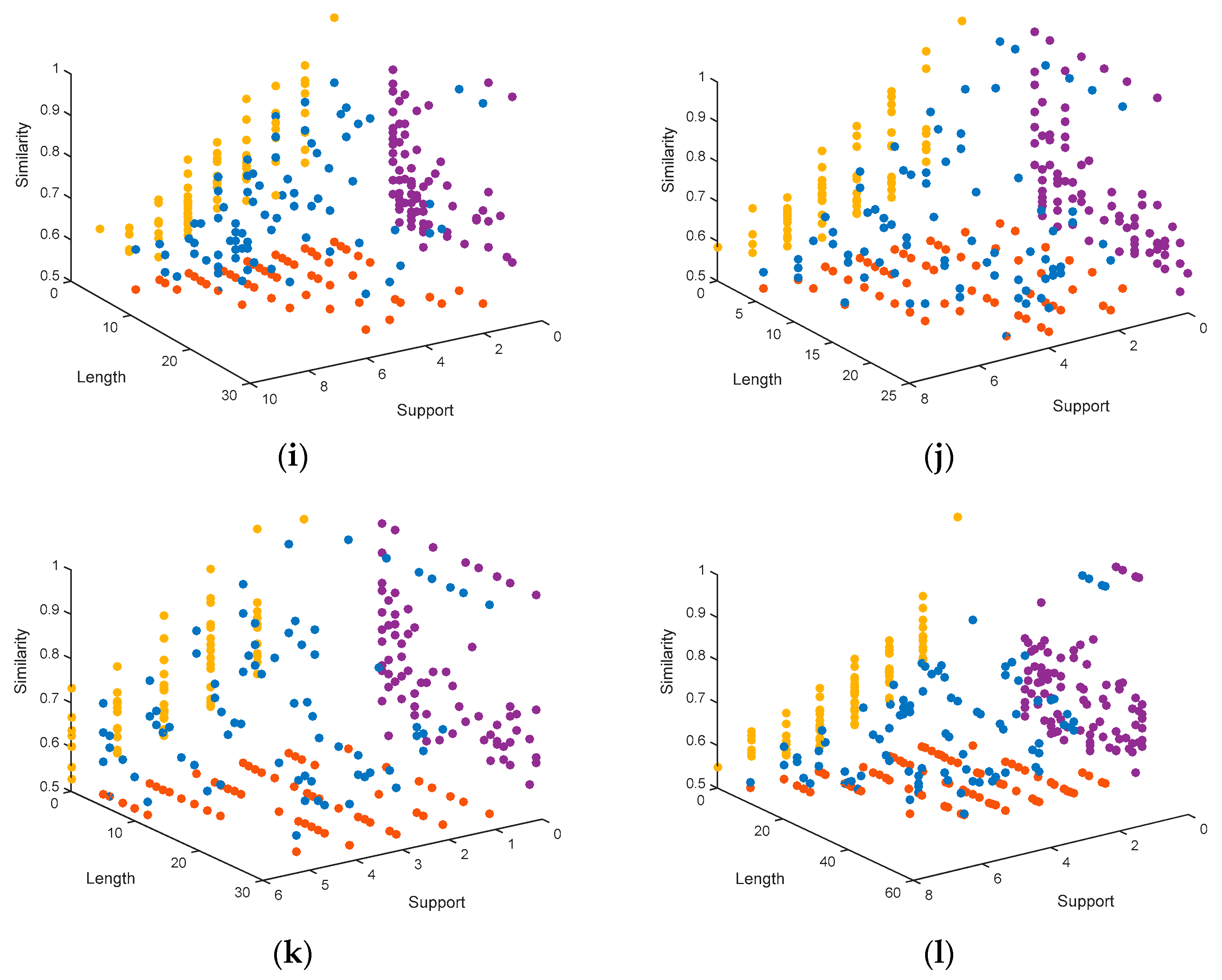
4.1.3. Representation of the Pareto Fronts Obtained by MHABBO Algorithm
4.2. Metrics to Assess Performance
4.2.1. The Nucleotide-Level Performance Coefficient (nPC)
4.2.2. F-Score
5. Conclusions and Future Research
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Patrik, D. What are DNA sequence motifs. Nat. Biotechnol. 2006, 24, 423–425. [Google Scholar]
- Lones, M.A.; Yo, Y.; Tyrrell, A.M. The Evolutionary Computation Approach to Motif Discovery in Biological Sequences. In Proceedings of the 7th Annual Workshop on Genetic and Evolutionary Computation (GECCO’052005), Washington, DC, USA, 25–29 June 2005. [Google Scholar]
- Lou, Y.; Li, J.; Jin, L.; Li, G. A CoEvolutionary Algorithm Based on Elitism and Gravitational Evolution Strategies. J. Comput. Inf. Syst. 2012, 7, 2741–2750. [Google Scholar]
- Che, D.; Song, Y.; Rashedd, K. MDGA: Motif discovery using a genetic algorithm. In Proceedings of the 2005 Conference on Genetic and Evolutionary Computation (GECCO 2005), Washington, DC, USA, 25–29 June 2005; pp. 447–452. [Google Scholar]
- Shao, L.; Chen, Y. Bacterial Foraging Optimization Algorithm Integrating Tabu Search for Motif Discovery. In Proceedings of the IEEE International Conference on Bioinformatics and Biomedicine (BIBM 2009), Washington, DC, USA, 1–4 November 2009; pp. 415–418. [Google Scholar]
- Shao, L.; Chen, Y.; Abraham, A. Motif Discovery using Evolutionary Algorithms. In Proceedings of the International Conference of Soft Computing and Pattern Recognition (SOCPAR 2009), Malacca, Malaysia, 4–7 December 2009; pp. 420–425. [Google Scholar]
- Gonzalez-Álvarez, D.L.; Vega-Rodriguez, M.A.; Gomez-Pulido, J.A.; Sanchez-Pérez, J.M. Predicting DNA Motifs by Using Evolutionary Multiobjective Optimization. IEEE Trans. Syst. Man Cybern. 2012, 42, 913–925. [Google Scholar] [CrossRef]
- González-Álvarez, D.L.; Vega-Rodríguez, M.A.; Pulido, J.A.G.; Sánchez-Pérez, J.M. Finding Motifs in DNA Sequences Applying a Multiobjective Artificial Bee Colony (MOABC) Algorithm. In Proceedings of the 9th European Conference on Evolutionary Computation, Machine Learning and Data Mining in Bioinformatics (EvoBIO), Torino, Italy, 27–29 April 2011; pp. 89–100. [Google Scholar]
- Kaya, M. MOGAMOD: Multi-objective genetic algorithm for motif discovery. Int. J. Expert Syst. Appl. 2009, 36, 1039–1047. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based non-dominated sorting approach. Part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2014, 11, 712–731. [Google Scholar] [CrossRef]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–771. [Google Scholar] [CrossRef]
- Feng, S.L.; Zhu, Q.X.; Gong, X.J.; Zhong, S. Biogeography-Based Optimization for Motif Discovery Problem. J. Comput. Inf. Syst. 2013, 9, 6999–7010. [Google Scholar]
- Feng, S.L.; Zhu, Q.X.; Gong, X.J.; Zhong, S. Hybridizing Biogeography-Based Optimization with Differential Evolution for Motif Discovery Problem. ICIC Express Lett. 2013, 7, 3343–3348. [Google Scholar]
- Feng, S.L.; Zhu, Q.X.; Zhong, S.; Gong, X.J. Hybridizing Adaptive Biogeography-Based Optimization with Differential Evolution for Motif Discovery Problem. Sens. Transducers 2014, 162, 233–237. [Google Scholar]
- Chutima, P.; Wong, N. A Pareto biogeography-based optimisation for multi objective two-sided assembly line sequencing problems with a learning effect. Comput. Ind. Eng. 2014, 69, 89–104. [Google Scholar] [CrossRef]
- E Silva, M.D.A.C.; Coelho, L.D.S.; Lebensztajn, L. Multi objective biogeography-based optimization based on predator-prey approach. IEEE Trans. Magn. 2012, 48, 951–954. [Google Scholar] [CrossRef]
- Ma, H.; Su, S.; Simon, D.; Fei, M. Ensemble multi-objective biogeography-based optimization with application to automated warehouse scheduling. Eng. Appl. Artif. Intell. 2015, 44, 79–90. [Google Scholar] [CrossRef]
- Goudos, S.K.; Plets, D.; Liu, N.; Martens, L.; Joseph, W. A multi-objective approach to indoor wireless heterogeneous networks planning based on biogeography-based optimization. Comput. Netw. 2015, 91, 564–576. [Google Scholar] [CrossRef]
- Feng, S.; Yang, Z.; Huang, M. Hybridizing Adaptive Biogeography-Based Optimization with Differential Evolution for Multi-Objective Optimization Problems. Information 2017, 8, 83. [Google Scholar] [CrossRef]
- Jadon, S.S.; Tiwari, R.; Sharma, H.; Bansal, J.C. Hybrid Artificial Bee Colony algorithm with Differential Evolution. Appl. Soft Comput. 2017, 58, 11–24. [Google Scholar] [CrossRef]
- Loris, V.; Marco, S. Coupling response surface and differential evolution for parameter identification problems. Comput.-Aided Civil Infrastruct. Eng. 2015, 30, 376–393. [Google Scholar] [CrossRef]
- Trivedi, A.; Srinivasan, D.; Biswas, S.; Reindl, T. Hybridizing genetic algorithm with differential evolution for solving the unit commitment scheduling problem. Swarm Evol. Comput. 2015, 23, 50–64. [Google Scholar] [CrossRef]
- Wang, X.; Xu, Z. Multi-objective optimization algorithm based on biogeography with chaos. Int. J. Hybrid Inf. Technol. 2014, 7, 225–234. [Google Scholar] [CrossRef]
- Ma, H.; Simon, D. Analysis of migration models of biogeography-based optimization using Markov theory. Eng. Appl. Artif. Intell. 2011, 24, 1052–1060. [Google Scholar] [CrossRef]
- Ma, H.; Simon, D. Blended biogeography-based optimization for constrained optimization. Eng. Appl. Artif. Intell. 2011, 24, 517–525. [Google Scholar] [CrossRef]
- Boussaïd, I.; Chatterjee, A.; Siarry, P.; Ahmed-Nacer, M. Two-stage update biogeography-based optimization using differential evolution algorithm (DBBO). Comput. Oper. Res. 2011, 38, 1188–1198. [Google Scholar] [CrossRef]
- Cai, Z. A Novel Hybrid Biogeography-based with Differential Mutation. In Proceedings of the International Conference on Electronic & Mechanical Engineering and Information Technology, Harbin, China, 12–14 August 2011; pp. 2710–2714. [Google Scholar]
- Gong, W.; Cai, Z.; Ling, C.X. DE/BBO: A hybrid differential evolution with biogeography-based optimization for global numerical optimization. Soft Comput. 2010, 15, 645–665. [Google Scholar] [CrossRef]
- Bi, X.; Wang, J.; Li, B. Multi-objective optimization based on hybrid biogeography-based optimization. Syst. Eng. Electron. 2014, 36, 179–186. [Google Scholar]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the strength Pareto evolutionary algorithm for multiobjective optimization. In Proceedings of the Evolutionary Methods for Design, Optimization and Control with Applications to Industrial Problems, Athens, Greece, 19–21 September 2001; pp. 95–100. [Google Scholar]
- Wingender, E.; Dietze, P.; Karas, H.; Knüppel, R. TRANSFAC: A database on transcription factors and their DNA binding sites. Nucleic Acids Res. 1996, 24, 238–241. [Google Scholar] [CrossRef] [PubMed]
- Tompa, M.; Li, N.; Bailey, T.L.; Church, G.M.; De Moor, B.; Eskin, E.; Favorov, A.V.; Frith, M.C.; Fu, Y.; Kent, W.J.; et al. Assessing computational tools for the discovery of transcription factor binding sites. Nat. Biotechnol. 2005, 23, 137–144. [Google Scholar] [CrossRef] [PubMed]
- Hughes, J.D.; Estep, P.W.; Tavazoie, S.; Church, G.M. Computational identification of cis-regulatory elements associated with functionally coherent groups of genes in Saccharomyces cerevisiae. J. Mol. Biol. 2000, 296, 1205–1214. [Google Scholar] [CrossRef] [PubMed]
- Bailey, T.L.; Elkan, C. The value of prior knowledge in discovering motifs with MEME. In Proceedings of the Third International Conference on Intelligent Systems for Molecular Biology, Cambridge, UK, 16–19 July 1995; AAAI Press: Menlo Park, CA, USA, 1995; pp. 21–29. [Google Scholar]
- Pavesi, G.; Mereghetti, P.; Mauri, G.; Pesole, G. Weeder Web: Discovery of transcription factor binding sites in a set of sequences from co-regulated genes. Nucleic Acids Res. 2004, 32, W199–W203. [Google Scholar] [CrossRef] [PubMed]
- WebLogo 3. Available online: http://weblogo.threeplusone.com/create.cgi (accessed on 19 September 2017).
- Li, G.; Chan, T.M.; Leung, K.S.; Lee, K.H. A Cluster Refinement Algorithm for Motif Discovery. IEEE Trans. Comput. Biol. Bioinform. 2010, 7, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Sinha, S.; Tompa, M. YMF: A program for discovery of novel transcription factor binding sites by statistical overrepresentation. Nucleic Acids Res. 2003, 31, 3586–3588. [Google Scholar] [CrossRef] [PubMed]
- Favorov, A.V.; Gelfand, M.S.; Gerasimova, A.V.; Mironov, A.A.; Makeev, V.J. Gibbs sampler for identification of symmetrically structured, spaced DNA motifs with improved estimation of the signal length and its validation on the ArcA binding sites. In Proceedings of the Fourth International Conference on Bioinformatics of Genome Regulation and Structure (BGRS 2004), Novosibirsk, Russia, 25–30 July 2004. [Google Scholar]
- Régnier, M.; Denise, A. Rare events and conditional events on random strings. Discrete Math. Theor. Comput. Sci. 2004, 6, 191–214. [Google Scholar]
- Thijs, G.; Lescot, M.; Marchal, K.; Rombauts, S.; De Moor, B.; Rouze, P.; Moreau, Y. A higher-order background model improves the detection of promoter regulatory elements by Gibbs sampling. Bioinformatics 2001, 17, 1113–1122. [Google Scholar] [CrossRef] [PubMed]
- Eskin, E.; Pevzner, P. Finding composite regulatory patterns in DNA sequences. Bioinformatics 2002, 18 (Suppl. 1), S354–S363. [Google Scholar] [CrossRef] [PubMed]
- Workman, C.T.; Stormo, G.D. ANN-Spec: A method for discovering transcription factor binding sites with improved specificity. In Pacific Symposium on Biocomputing; Altman, R., Dunker, A.K., Hunter, L., Klein, T.E., Eds.; Stanford University: Stanford, CA, USA, 2000; pp. 467–478. [Google Scholar]
- Ao, W.; Gaudet, J.; Kent, W.J.; Muttumu, S.; Mango, S.E. Environmentally induced foregut remodeling by PHA-4/FoxA and DAF-12/NHR. Science 2004, 305, 1743–1746. [Google Scholar] [CrossRef] [PubMed]
- Ye, T.; Yang, Z.; Feng, S. Biogeography-Based Optimization of the Portfolio Optimization Problem with Second Order Stochastic Dominance Constraints. Algorithms 2017, 10, 100. [Google Scholar] [CrossRef]
- Sawik, B. Survey of multi-objective portfolio optimization by linear and mixed integer programming. In Applications of Management Science; Lawrence, K.D., Kleinman, G., Eds.; Emerald Group Publishing Limited: Bingley, UK, 2013; Volume 16, pp. 55–79. [Google Scholar]
- Sawik, B. A Review of Multi-Criteria Portfolio Optimization by Mathematical Programming. In Recent Advances in Computational Finance; Dash, G.H., Thomaidis, N., Eds.; Nova Science Publishers: New York, NY, USA, 2013; pp. 149–172. [Google Scholar]

| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 0 | 1 | 0.25 | 0.25 | 0 | 0 | 0 | 0.25 | 0 | 0.25 | 0.75 | 1 | 0 | 0 | 0.25 | 0 | 0.25 | 0 |
| C | 0 | 0 | 0.5 | 0.75 | 0 | 0 | 0 | 0.25 | 0 | 0.5 | 0 | 0 | 0.25 | 1 | 0.5 | 0 | 0.25 | 0 |
| T | 0 | 0 | 0.25 | 0 | 1 | 1 | 0.75 | 0.5 | 0 | 0.25 | 0.25 | 0 | 0.75 | 0 | 0.25 | 1 | 0 | 0 |
| G | 1 | 0 | 0 | 0 | 0 | 0 | 0.25 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 | 1 |
| Motif Length | Seq. 0 | Seq. 1 | Seq. 2 | … | Seq. n |
|---|---|---|---|---|---|
| length | S0 | S1 | S2 | ... | Sn |
| Dataset | #Sequence | Length | #Instance | #Width of Motifs | Time (s) |
|---|---|---|---|---|---|
| Dm01g | 4 | 1500 | 7 | 13–28 | 50 |
| Dm04g | 4 | 2000 | 9 | 10–26 | 51 |
| Dm05g | 5 | 2500 | 14 | 6–21 | 58 |
| Hm03r | 10 | 1500 | 15 | 14–46 | 42 |
| Hm04m | 13 | 2000 | 11 | 7–44 | 37 |
| Hm16g | 7 | 3000 | 7 | 9–54 | 38 |
| Mus02r | 9 | 1000 | 12 | 10–33 | 38 |
| Mus07g | 4 | 1500 | 4 | 15–33 | 53 |
| Mus11m | 12 | 500 | 15 | 6–27 | 42 |
| Yst03m | 8 | 500 | 18 | 6–24 | 44 |
| Yst04r | 7 | 1000 | 7 | 5–25 | 39 |
| Yst08r | 11 | 1000 | 14 | 12–49 | 39 |
| MHABBO | DEPT | MOGAMOD |
|---|---|---|
| Population Size: 100 | Population Size: 200 | Population Size: 200 |
| Migration Probability: 0.75 | Crossover Probability: 0.25 | Crossover: SPX with probability 0.6 |
| Mutation Probability: 0.05 | Mutation Factor: 0.03 | Mutation Factor: 0.5 |
| Maxgen: 100 Elitism parameter: 10 | Selection Scheme: Rand/1/Binomial | Parents choose: Binary Tournament New Generation Selection: Elitist |
| Scaling factor c1: 0.01 | ||
| k1: 0.4, k2: 0.95, k3: 0.05; k4: 0.1 |
| Method | Support | Length | Similarity | Predicted Motif |
|---|---|---|---|---|
| AlignACE [34] | N/A | 10 | N/A | C ATTCCA |
| MEME [35] | N/A | 11 | N/A | C ATTCCCC |
| Weeder [36] | N/A | 10 | N/A | TTTTCT CA |
| MOGAMOD [9] | 5 | 14 | 0.84 | C A CTTCCACTAA |
| 6 | 14 | 0.77 | C ATTCCTCTAT | |
| DEPT | 5 | 22 | 0.854 | TAAATCTTTTACTTTTTTTTCT |
| 6 | 19 | 0.842 | CTAATTCATTCTTTTTCAA | |
| 7 | 15 | 0.847 | TTTCT CAAACACA | |
| MHABBO | 6 | 5 | 0.85 | AAATC* |
| 2 | 19 | 0.82 | GAGCAAGAAGCCAATGAAA | |
| 2 | 10 | 0.8 | TAACCAAGAA* | |
| 3 | 5 | 0.93 | TTTCT |
| Method | Support | Length | Similarity | Predicted Motif |
|---|---|---|---|---|
| AlignACE | N/A | 11 | N/A | CACCCA ACAC |
| N/A | 12 | N/A | T ATT CACT A | |
| MEME | N/A | 11 | N/A | CACCCA ACAC |
| Weeder | N/A | 10 | N/A | ACACCCA AC |
| MOGAMOD | 7 | 15 | 0.84 | C ACT T CCT |
| 8 | 14 | 0.83 | CCA AAAAA C | |
| 8 | 13 | 0.85 | ACACCCA ACATC | |
| DEPT | 7 | 20 | 0.84 | TCAATTTTTTTTTTCTATTC |
| 8 | 19 | 0.83 | TTATTTTTTTCTCTTTC | |
| 8 | 15 | 0.85 | CCATATTTCTTCTA | |
| MHABBO | 2 | 40 | 0.74 | CACTACAATTGCTTTGAGTGGTGTATTCTCAGTCGCCAAG |
| 3 | 16 | 0.75 | GGTGTATGTCCTAATA* | |
| 3 | 34 | 0.68 | AACCAGACAAAC*AAAAGAAAAAAAAAATTAAAAG | |
| 2 | 31 | 0.81 | AGAACAAAAAAAAAAAAAAAAAAAAAAAAAA |
| Method | Support | Length | Similarity | Predicted Motif |
|---|---|---|---|---|
| AlignACE | N/A | 13 | N/A | T T ATAAAAAA |
| MEME | N/A | 20 | N/A | A T TA ATAAAA AAAAAC |
| Weeder | N/A | 10 | N/A | T ATCACT |
| MOGAMOD | 7 | 22 | 0.74 | TATCATCCCT CCTA ACACAA |
| 7 | 18 | 0.82 | T ACTCT TCCCTA TCT | |
| 10 | 11 | 0.74 | TTTTTTCACCA | |
| 10 | 10 | 0.79 | CCCA CTTA | |
| 10 | 9 | 0.81 | A T TCC | |
| DEPT | 7 | 22 | 0.78 | A CTTA T CCT ACACA A A |
| 9 | 12 | 0.83 | A TCTCA T CC | |
| 10 | 9 | 0.85 | T A ACTCA | |
| MHABBO | 2 | 29 | 0.85 | ATCATAGGACCTCCCTTGCTTCCCAATGG |
| 2 | 25 | 0.76 | CCTTTTATTGTTCTATT* | |
| 2 | 13 | 0.85 | AATTAGGAGACAA* | |
| 3 | 36 | 0.68 | AACAACAAAAGATAAAAAGTCAAATGAATGAACTCA |
| Dataset | Predicted Motif |
|---|---|
| Dm01g |  |
| Dm04g | 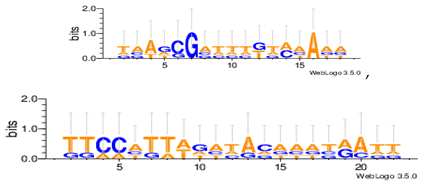 |
| Dm05g | 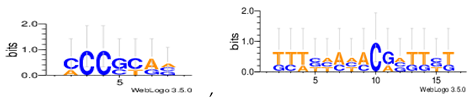 |
| Hm03r | 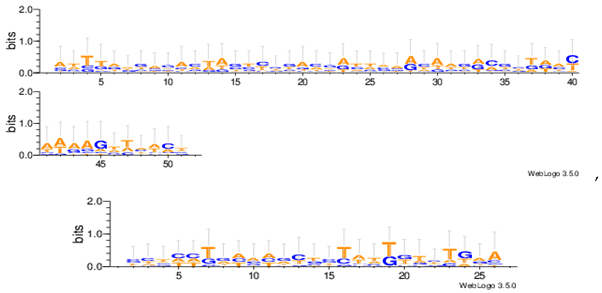 |
| Hm04m | 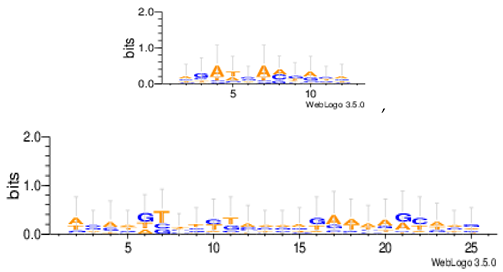 |
| Hm16g | 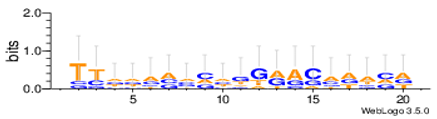 |
| Mus02r | 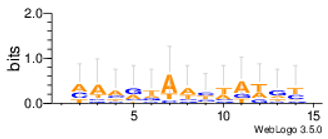 |
| Mus07g |  |
| Mus11m | 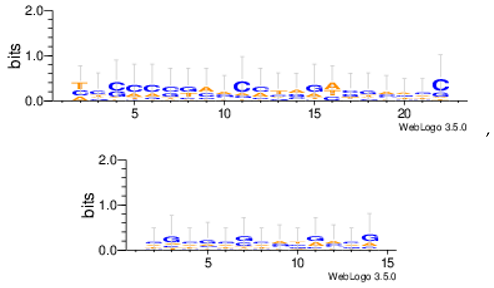 |
| Yst03m | 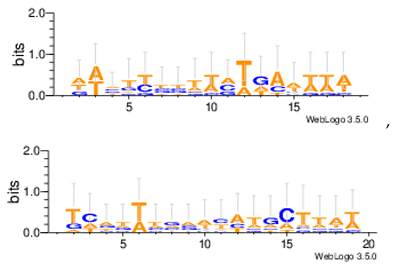 |
| Yst04r |  |
| Yst08r |  |
| Algorithms | Dm 01g | Dm 04g | Dm 05g | Hm 03r | Hm 04m | Hm 16g | Mus 02r | Mus 07g | Mus 11m | Yst 03m | Yst 04r | Yst 08r | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MHABBO | P | 3/100 | 2/20 | 4/20 | 6/20 | 8/20 | 5/10 | 8/20 | 2/10 | 8/20 | 8/20 | 4/10 | 5/20 |
| R | 3/7 | 2/9 | 4/14 | 6/15 | 8/10 | 5/7 | 8/12 | 2/4 | 8/15 | 8/18 | 4/7 | 5/14 | |
| F | 0.06 | 0.14 | 0.24 | 0.34 | 0.53 | 0.59 | 0.5 | 0.29 | 0.46 | 0.42 | 0.47 | 0.29 | |
| Algorithms for MDP | Dataset | Algorithms for MDP | Dataset | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Hm03 | Mu02 | Yst08 | Hm03 | Mu02 | Yst08 | ||||
| YMF [39] | P | 0/25 | 1/12 | 0/11 | AlignACE [34] | P | 0/14 | 0/0 | 9/41 |
| R | 0/15 | 1/12 | 0/14 | R | 0/15 | 0/12 | 9/14 | ||
| F | 0 | 0.08 | 0 | F | 0 | 0 | 0.33 | ||
| SeSiMCMC [40] | P | 1/10 | 0/9 | 0/21 | MEME [35] | P | 1/12 | 2/14 | 6/11 |
| R | 1/15 | 0/12 | 0/14 | R | 1/15 | 2/12 | 6/14 | ||
| F | 0.08 | 0 | 0 | F | 0.074 | 0.154 | 0.48 | ||
| QuickScore [41] | P | 0/22 | 1/22 | 3/56 | MOTIFSAMPLE [42] | P | 0/21 | 1/18 | 7/9 |
| R | 0/15 | 1/12 | 3/14 | R | 0/15 | 1/12 | 7/14 | ||
| F | 0 | 0.06 | 0.08 | F | 0 | 0.07 | 0.61 | ||
| MITRA [43] | P | 0/10 | 0/9 | 1/12 | ANN-SPEC [44] | P | 0/13 | 1/32 | 7/26 |
| R | 0/15 | 0/12 | 1/14 | R | 0/15 | 1/12 | 7/14 | ||
| F | 0 | 0 | 0.08 | F | 0 | 0.05 | 0.35 | ||
| Improbizer [45] | P | 1/20 | 0/18 | 1/22 | MEME3 [35] | P | 0/7 | 0/0 | 9/17 |
| R | 1/15 | 0/12 | 1/14 | R | 0/15 | 0/12 | 9/14 | ||
| F | 0.06 | 0 | 0.06 | F | 0 | 0 | 0.58 | ||
| MHABBO | P | 6/20 | 8/20 | 5/20 | ABBO/DE/GEN [15] | P | 5/30 | 5/30 | 8/30 |
| R | 6/15 | 8/12 | 5/14 | R | 5/15 | 5/12 | 8/14 | ||
| F | 0.34 | 0.5 | 0.29 | F | 0.22 | 0.24 | 0.36 | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, S.; Yang, Z.; Huang, M. Predicting DNA Motifs by Using Multi-Objective Hybrid Adaptive Biogeography-Based Optimization. Information 2017, 8, 115. https://doi.org/10.3390/info8040115
Feng S, Yang Z, Huang M. Predicting DNA Motifs by Using Multi-Objective Hybrid Adaptive Biogeography-Based Optimization. Information. 2017; 8(4):115. https://doi.org/10.3390/info8040115
Chicago/Turabian StyleFeng, Siling, Ziqiang Yang, and Mengxing Huang. 2017. "Predicting DNA Motifs by Using Multi-Objective Hybrid Adaptive Biogeography-Based Optimization" Information 8, no. 4: 115. https://doi.org/10.3390/info8040115
APA StyleFeng, S., Yang, Z., & Huang, M. (2017). Predicting DNA Motifs by Using Multi-Objective Hybrid Adaptive Biogeography-Based Optimization. Information, 8(4), 115. https://doi.org/10.3390/info8040115





