An Extended VIKOR-Based Approach for Pumped Hydro Energy Storage Plant Site Selection with Heterogeneous Information

Abstract

The selection of a desirable site for constructing a pumped hydro energy storage plant (PHESP) plays a vital important role in the whole life cycle. However, little research has been done on the site selection of PHESP, which affects the rapid development of PHESP. Therefore, this paper aims to select the most ideal PHESP site from numerous candidate alternatives using the multi-criteria decision-making (MCDM) technique. Firstly, a comprehensive evaluation criteria system is established for the first time. Then, considering quantitative and qualitative criteria coexist in this system, multiple types of representations, including crisp numerical values (CNVs), triangular intuitionistic fuzzy numbers (TIFNs), and 2-dimension uncertain linguistic variables (2DULVs), are employed to deal with heterogeneous criteria information. To determine the weight of criteria and fully take the preference of the decision makers (DMs) into account, the analytic hierarchy process (AHP) method is applied for criteria weighting. After that, an extended Vlsekriterijumska Optimizacija I Kompromisno Resenje (VIKOR) method is utilized to provide compromise solutions for the PHESP site considering such heterogeneous information. At last, the proposed model is then applied in a case study of Zhejiang province, China to illustrate its practicality and efficiency. The result shows the Changlongshan should be selected as the optimal PHESP.

1. Introduction

In recent years, with the increasingly serious environmental pollution and aggravation of the global energy crisis, developing renewable energy vigorously has become an inevitable choice of mankind. Wind energy and solar energy, as reliable and promising forms of renewable energy, have been developing swiftly worldwide. It is noteworthy that, in 2016, China’s total installed capacity of wind power and solar power both ranked first in the world. However, at the same time, the phenomenon of power curtailment is becoming increasingly prominent since wind and solar energy are characterized by volatility and intermittency [1]. This kind of phenomenon has brought humans huge economic loss and restricted the development of renewable energy. One of the main causes of this phenomenon is that the current peak shaving capacity of the power system is seriously poor. The current power source structure in China is unreasonable, and the thermal power as the main structure of the power source accounts for 71.1%. However, the load response of thermal power is slow, resulting in the shortage of its peak capacity.

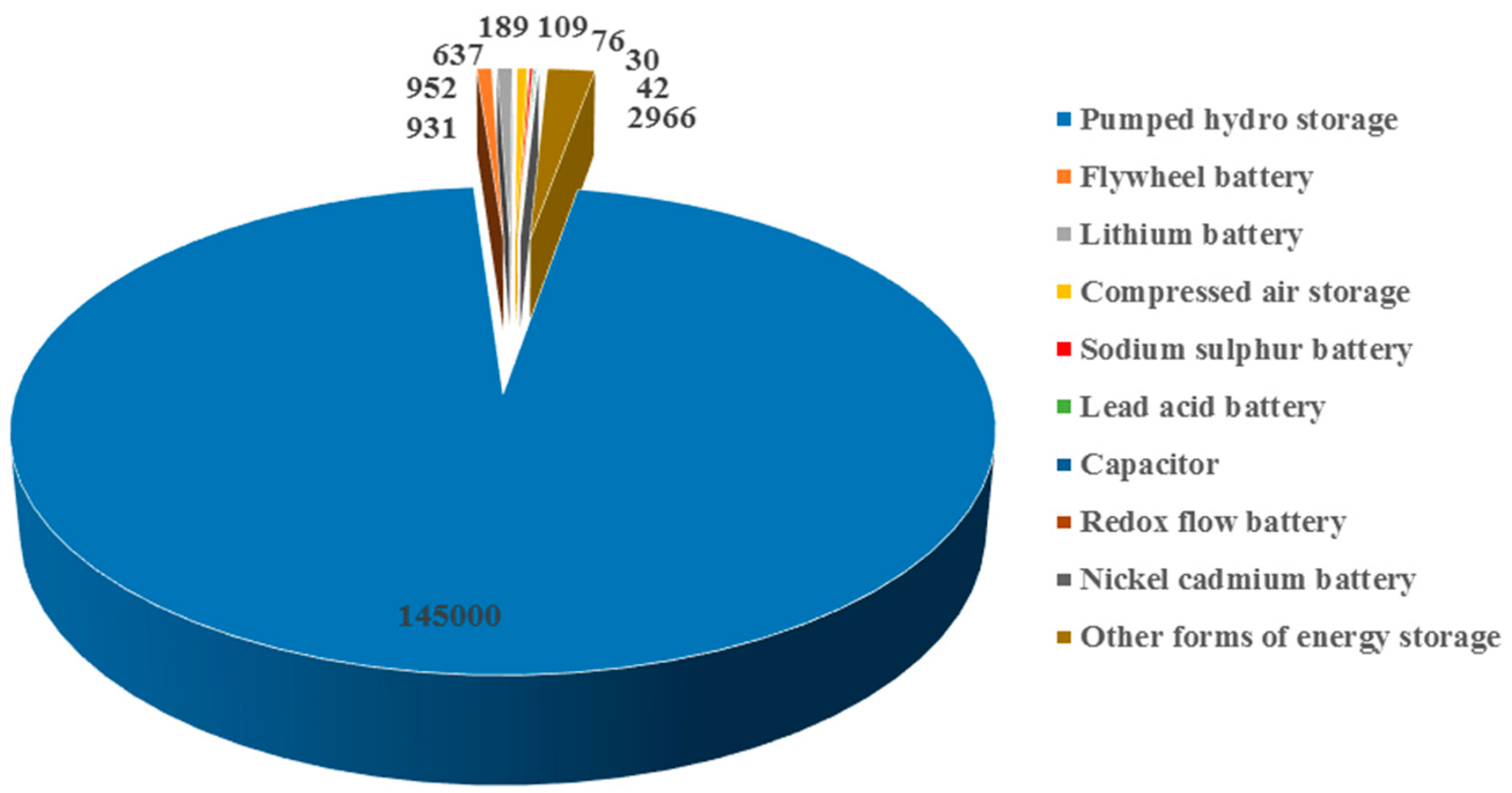
Energy storage systems are one of the possible solutions for mitigating the effects of intermittent renewable resources [2]. Among all energy storage technologies, pumped hydro energy storage (PHES) technology is the most widely used. The share of various storage technologies in the global electricity storage system is shown in Figure 1. Although a lot of forms of energy storage technology have been developed, the PHES technology accounted for the energy storage of absolute dominance. PHES is now one of the most mature and cost-effective technologies since water lifting devices have been invented, used, and improved by humans, for thousands of years [1]. This technique uses electricity produced by other power stations to pump water up to the upper reservoir when the energy demand is low, and release the water back down to the lower reservoir to generate electricity when the energy demand is high [3]. Thanks to the fast response ability of PHESPs, a huge push to build them will ensure that electricity production matches demands at all times.

In June 2017, the installed capacity of PHESPs in China reached 27.73 million kW, surpassed Japan, and became the biggest capacity of PHESP in the world. But despite all that, the proportion of pumped storage in electric power systems in China is less than 2%. Thus, lately, the “13th Five-Year Plan for Electric Power Development” released by the National Energy Administration (NEA) made it clear that the installed capacity of the new pumped hydro energy storage plant must arrive at 60 million kWh by 2020. There is no doubt that the PHES industry is in an important period of strategic opportunities for accelerated development.

In recent years, the existing literature on various aspects of PHESP has become much more enriched. Rogeau et al. [1] proposed a generic method able to evaluate the potential of small-PHESP over a large geographical zone. Gimeno-Gutierrez and Lacal-Arantegui [4] assessed a PHESP potential based on two existing reservoirs in Europe by developing and applying a GIS-based software model. Petrakopoulou et al. [5] conducted a simulation and analysis of a stand-alone solar-wind and PHESP in the Aegean Sea. Pérez-Díaz et al. [6] aimed at assessing the contribution of pumped-hydro energy storage to reduce the scheduling costs of hydrothermal power systems with high wind penetration, which may yield unrealistic results. Pérez-Díaz and Chazarra [7] reviewed the current trends in the PHESP operation, and presented the main challenges faced by PHESP operators. Yang and Jackson [8] analyzed the opportunities and barriers to PHESP in the United States. By contrast, there has been relatively little research on the site selection of PHESP. For example, Lu and Wang [9] provided promising locations of the PHESPs through Geographic Information Science (GIS) analyses. Kucukali [10] found the most suitable existing hydropower reservoirs for the development of PHS by using the multi-criteria scoring technique. Also, Connolly et al. [11] developed a computer program to locate potential sites for pumped hydroelectric energy storage. However, in the entire life cycle of the renewable energy plant, the site selection is important and determines the sustainable development ability and socio-economic values of the power plant [12]. At the meantime, identifying suitable sites for PHESP is a complex task since many potential site alternatives are feasible. Thus, by all appearances, the site selection of PHESP is a valuable research issue.

A number of conflicting criteria need to be taken into account simultaneously in the process of PHESP site selection. So, the site selection of PHESP can be defined as a MCDM problem. MCDM is a well-known branch of decision-making, which aims to find the most suitable solutions from a set of alternatives under multiple criteria conditions [13]. Nevertheless, existing methods for solving MCDM problems that are not applicable for the site selection of PHESP, which are mainly reflected in the loss of information. In detail, the complexity of PHESP site selection is much higher than other MCDM problems since it is very strict with topography and geomorphology. Also, many data are impossible to obtain, and they are also inaccurate. So, in such a complex decision-making environment, the best way to give a reasonable representation of the criteria value and preserve the integrity of the original decision information is very difficult to establish.

Therefore, this paper tries to select the optimal PHESP site and handle the problem of information loss in this process. Firstly, an evaluation criteria system of PHESP site selection is established. Then, according to the properties of the identified criteria, we divide them into three categories: quantitative criteria that can be measured accurately, quantitative criteria that cannot be measured accurately, and qualitative criteria. The values of the three categories are represented by CNVs, TIFNs, and 2DULVs, respectively. In this way, the criteria values with different natures can be better described. Furthermore, based on Hamming distance, the VIKOR method is proposed to rank the PHESP sites. This method is particularly useful for those problems for which the values of the alternatives are not represented by the same units, since there is no need to translate different forms of decision information. The innovations of this paper are as follows: (1) a comprehensive evaluation criteria system is established; (2) an extended VIKOR-based MCDM approach with heterogeneous criteria values comprising CNVs, TIFNs, and 2DULVs is proposed.

2. Literature Review

The values of the criteria involved in site selection not only contain objective quantitative statistical data, but include some subjective judgment data given by DMs with their knowledge and experience. Thus, using a single form of decision information makes it difficult to meet the requirement of site selection decision-making. Most scholars have recognized this problem, and utilized different forms of decision information to represent criteria of different characteristics. Among various information forms, numerical numbers, interval numbers, linguistic variables, and fuzzy numbers are the most commonly used forms. Wu and Chen [14] used CNVs and linguistic variables (LVs) to describe the values of criteria involved in waste-to-energy plant site selection. Wu and Geng [15] applied CNVs and LVs to model the values of criteria involved in solar thermal power plant site selection. Later, both the two studies converted the CNVs into the LVs for convenience of calculation. Sánchez-Lozano et al. [16] utilized CNVs, LVs, and triangular fuzzy numbers (TFNs) to represent the values of criteria involved in onshore wind farm site selection, and then, the CNVs and LVs were both converted into the TIFNs. Wu and Zhang [17] utilized CNVs and LVs to represent the values of criteria involved in offshore wind power station site selection, and transformed both the CNVs and the LVs into intuitionistic fuzzy numbers (IFNs). Also, Wu et al. [18] used CNVs and IFNs in the process of wind farm project plan selection, and then, the CNVs were transformed into the IFNs. In addition, some extended forms of LVs have been also applied, such as 2-tuple linguistic variables. CNVs and 2-tuple linguistic variables are used in the process of low-speed wind farm site selection; after that, both of them are transformed into 2-tuple linguistic variables [19].

The contribution of the above literatures in the field of site selection is understandable. However, there are some problems that have not been well solved. Firstly, for qualitative criteria, their values are generally assessed by DMs with their knowledge and experience. Due to the complexity of PHESP site selection, some DMs may not be very confident about their assessment. In other words, the assessments given by DMs are not very reliable in some cases. However, the current forms of decision information, such as the 2-tuple linguistic variables, have not taken this into account. Secondly, the different forms of decision information in the above studies have been unified into one kind of decision information. Nevertheless, information loss will inevitably occur in such a unification process.

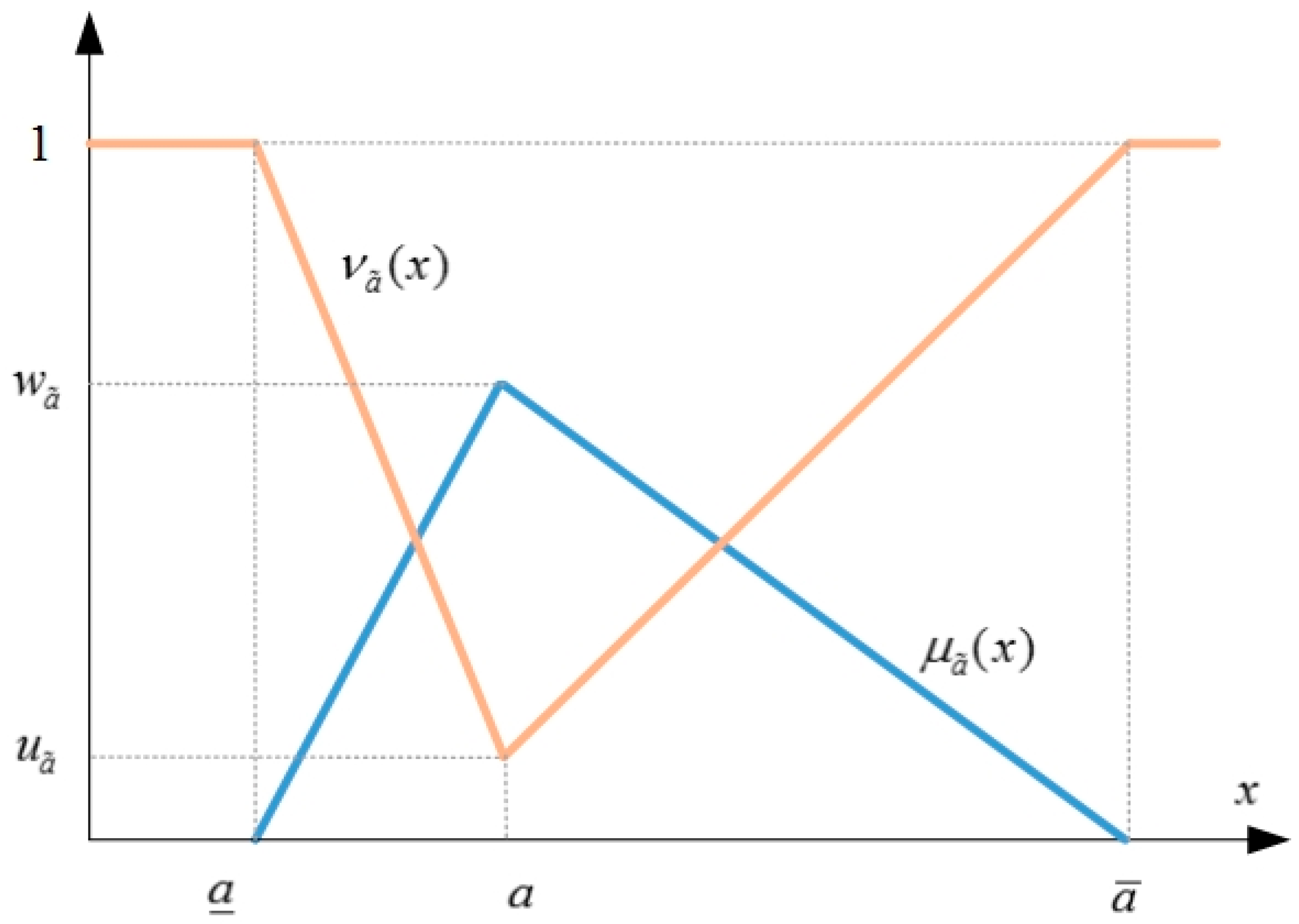
As for the first question, it is necessary to introduce the 2DUIVs. The 2-dimension linguistic variables (2DLVs) were proposed by Zhu et al. [20] in 2009 and include two common linguistic labels to precisely assess alternatives with linguistic information. One dimension is used for describing the evaluation result of alternatives provided by the DM, and the other is used for describing the self-assessment of the DM on the reliability of the given evaluation result. However, due to time pressure, and lack of knowledge and information processing capabilities, the evaluation information provided by DMs may not match any of the original linguistic phrase, and it may be between two linguistic phrases [21]. For this reason, Liu and Zhang [22] extended 2DIVs to 2DULVs, and developed a method to deal with the MCDM problem in which the criteria values take the form of 2-dimension uncertain linguistic information. Naturally, the 2DUIVs spread in the MCDM field [23,24,25]. Thus, introducing the 2DULVs to represent the values of qualitative criteria involved in PHESP site selection is a meaningful work, which reflects more accurately the assessment of DM on alternatives and decreases the information loss.

To solve the second problem, some distance-based techniques play an important role. Among them, the Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) approach and the VIKOR approach are the most commonly used techniques. They are particularly useful for those problems for which the values of the criteria are not represented by the same forms. The core idea of them is to calculate the relative gaps between each alternative and the optimal alternative by means of distance formula associated with hybrid criteria. In view of this, Wu and Xu [26] studied the site selection problem of the tidal power plant with the criteria value as numerical numbers, interval numbers, and random numbers; then, a rank method based on TOPSIS was proposed. Matsui et al. [27] presented a modified VIKOR method based on numerical numbers, fuzzy numbers, interval numbers, and linguistic variables. Sun and Liu [28] handled with numerical numbers, fuzzy numbers, interval numbers, and linguistic variables simultaneously to evaluate the candidate power system restoration alternatives based on an extended VIKOR method. However, it have been proved that the TOPSIS approach cannot reflect the closeness of the alternatives to positive and negative ideal solutions [29]. In contrast, the VIKOR method can overcome the shortcomings of the TOPSIS approach; in addition, it considers a maximum group utility and a minimum of individual regret simultaneously and takes into account the subjective preference of DMs [30,31]. In recent years, the research on the extension and application of VIKOR methods has attracted the attention of some scholars. For example, Mousavi and Jolai [32] used a stochastic VIKOR to evaluate and rank probability distributions for each alternative. Liu and You [33] used a fuzzy VIKOR for failure mode and effects analysis; triangular fuzzy numbers are preferred to express linguistic evaluations. Mokhtarian and Sadi-Nezhad [34] used fuzzy VIKOR on interval-valued fuzzy numbers for facility site selection problems. You and You [35] used the linguistic VIKOR method for supplier selection; the attributes are expressed with 2-tuple linguistic variables. As can be seen from the above, the VIKOR method has been successfully applied in various fields. Therefore, this work tries to adopt the VIKOR method to rank candidate PHESP alternatives.

3. Evaluation Criteria System of PHESP Site Selection

The evaluation criteria are important for the establishment of the criteria system for PHESP site selection. To do this, firstly, a lot of criteria were collected initially in light of the academic literature and feasibility research reports. Then, a total of seven experts whose academic backgrounds are hydrology, geological, engineering, renewable energy, and social, economic, and environmental fields were invited and an expert meeting was organized. In this meeting, the list of initial criteria were distributed to the experts and each expert issued his/her judgement. After several rounds of discussion, experts reached an agreement; the final criteria and sub-criteria of PHESP site selection are established and listed in

Table 1. The criteria and sub-criteria of PHESP site selection.

Criteria	Symbol	Sub-Criteria	Symbol
Terrain and geography	C1	Permeability	C11
		Altitude	C12
		Storage capacity	C13
		Proximity to electricity grid	C14
		Length-height ratio	C15
Social effect	C2	Employment	C21
		Economy improvement	C22
		Disasters withstand	C23
Economic effect	C3	Loan repayment period	C31
		Assets liabilities ratio	C32
		Pay back period	C33
		Financial internal rate of return	C34
Environmental effect	C4	Carbon emission reduction	C41
		Nitrogen oxide emission reduction	C42
		Sulfur dioxide emission reduction	C43

. The first criteria reflect the impacts of various local conditions on the potential PHESP; the last three criteria are the impacts induced by the PHESP after completion. The analysis of these criteria and sub-criteria is given in Appendix A.

PHESP site selection involves selecting the optimal one through comparing the alternatives against a series of qualitative and quantitative criteria. The sub-criteria values can be divided into three types: quantitative criteria can be measured accurately, quantitative criteria cannot be measured accurately, and qualitative criteria. (1) The first type of sub-criteria include C11, C12, C13, C14, and C15. The value of such sub-criteria can be measured definitely and expressed by CNVs; (2) the second type of sub-criteria include C31, C32, C33, C34, C41, C42, and C43. Due to the restriction of measuring and forecasting technology, the sub-values of criteria C11, C13, and C31 is expressed by TIFNs; (3) the last type of sub-criteria include C21, C22, and C23. It’s difficult to quantify their values by measurement methods, so it’s common to invite experts to score those sub-criteria with respect to the alternatives. Because of the inherent vagueness of human thinking, DMs express their preferences or assessments by using 2DUIVs.

4. Preliminaries

4.1. Triangular Intuitionistic Fuzzy Number

In this section, we review the definition and operation rules of TIFNs and give the Hamming distance for TIFNs.

4.1.1. Definition of Triangular Intuitionistic Fuzzy Number

Definition 1 [36]. 

A TIFN $\tilde{a}=((\underset{\_}{a},a,\overline{a});w_{\tilde{a}},u_{\tilde{a}})$ is a special IFS on the real number set $R$, whose membership function and non-membership function are defined as follows:

$${\mu }_{\tilde{a}}\left(x\right)=\{\begin{array}{l}\left(x-\underset{\_}{a}\right)u_{\tilde{a}}/\left(a-\underset{\_}{a}\right)\\ u_{\tilde{a}}\\ \left(\overline{a}-x\right)u_{\tilde{a}}/\left(\overline{a}-a\right)\\ 0\end{array}\begin{array}{ll}\mathrm{if}\hfill & \underset{\_}{a}\le x<a,\hfill \\ \mathrm{if}\hfill & x=a,\hfill \\ \mathrm{if}\hfill & a<x\le \overline{a},\hfill \\ \mathrm{if}\hfill & \begin{array}{ccc}x<\underset{\_}{a}& \mathrm{or}& x>\overline{a},\end{array}\hfill \end{array}and$$

$${\nu }_{\tilde{a}}\left(x\right)=\{\begin{array}{l}\left[a-x+v_{\tilde{a}}\left(x-\underset{\_}{a}\right)\right]/\left(a-\underset{\_}{a}\right)\\ v_{\tilde{a}}\\ \left[x-a+v_{\tilde{a}}\left(\overline{a}-x\right)\right]/\left(\overline{a}-a\right)\\ 0\end{array}\begin{array}{ll}\mathrm{if}\hfill & \underset{\_}{a}\le x<a,\hfill \\ \mathrm{if}\hfill & x=a,\hfill \\ \mathrm{if}\hfill & a<x\le \overline{a},\hfill \\ \mathrm{if}\hfill & \begin{array}{ccc}x<\underset{\_}{a}& \mathrm{or}& x>\overline{a},\end{array}\hfill \end{array}$$

respectively, depicted as in Figure 2; the values $w_{\tilde{a}}$ and $u_{\tilde{a}}$ represent the maximum membership degree and the minimum non-membership degree such that they satisfy the conditions: $0\le w_{\tilde{a}}\le 1,0\le u_{\tilde{a}}\le 1$ and $w_{\tilde{a}}+u_{\tilde{a}}\le 1$. Let ${\pi }_{\tilde{a}}(x)=1-w_{\tilde{a}}(x)-u_{\tilde{a}}(x)$ is called an intuitionistic fuzzy index of the TIFN $\tilde{a}$, which reflects hesitancy degree of the element $x$ to $\tilde{a}$.

4.1.2. Operation Rules of Triangular Intuitionistic Fuzzy Number

Definition 2 [36]. 

Let ${\tilde{a}}_1=(({\underset{\_}{a}}_1,a_1,{\overline{a}}_1);w_{a_1},u_{a_1})$ and ${\tilde{a}}_2=(({\underset{\_}{a}}_2,a_2,{\overline{a}}_2);w_{a_2},u_{a_2})$ be two TIFNs and $\lambda$ be a real number. Then the arithmetical operations for TIFNs are defined as follows:

(1) 

${\tilde{a}}_1+{\tilde{a}}_2=(({\underset{\_}{a}}_1+{\underset{\_}{a}}_2,a_1+a_2,{\overline{a}}_1+{\overline{a}}_2);w_{{\overline{a}}_1}\wedge w_{{\overline{a}}_2},u_{{\overline{a}}_1}\vee u_{{\overline{a}}_2})$

(2) 

$\lambda {\tilde{a}}_1=\{\begin{array}{c}((\lambda {\underset{\_}{a}}_1,\lambda a_1,\lambda {\overline{a}}_1);w_{{\overline{a}}_1},u_{{\overline{a}}_1}),\mathrm{if}\lambda >0\\ ((\lambda {\overline{a}}_1,\lambda a_1,\lambda {\underset{\_}{a}}_1);w_{{\overline{a}}_1},u_{{\overline{a}}_1}),\mathrm{if}\lambda <0\end{array}$

where the symbols “$\wedge$” and “$\vee$” mean min and max operators, respectively.

4.1.3. Distance between Two Triangular Intuitionistic Fuzzy Numbers

Definition 3 [37]. 

Let ${\tilde{a}}_1=(({\underset{\_}{a}}_1,a_1,{\overline{a}}_1);w_{a_1},u_{a_1})$ and ${\tilde{a}}_2=(({\underset{\_}{a}}_2,a_2,{\overline{a}}_2);w_{a_2},u_{a_2})$ be two TIFNs. The Hamming distance between ${\tilde{a}}_1$ and ${\tilde{a}}_2$ is defined as follows:

$$\begin{array}{ll}\hfill d({\tilde{a}}_1,{\tilde{a}}_2)=& \frac{1}{6}(\left|(1+w_{{\tilde{a}}_1}-u_{{\tilde{a}}_1}){\underset{\_}{a}}_1-(1+w_{{\tilde{a}}_2}-u_{{\tilde{a}}_2}){\underset{\_}{a}}_2\right|\hfill \\ & +\left|(1+w_{{\tilde{a}}_1}-u_{{\tilde{a}}_1})a_1-(1+w_{{\tilde{a}}_2}-u_{{\tilde{a}}_2})a_2\right|\hfill \\ & +\left|(1+w_{{\tilde{a}}_1}-u_{{\tilde{a}}_1}){\overline{a}}_1-(1+w_{{\tilde{a}}_2}-u_{{\tilde{a}}_2}){\overline{a}}_2\right|)\hfill \end{array}$$

(1)

4.2. 2-Dimension Uncertain Linguistic Variable

4.2.1. Definition of 2-Dimension Uncertain Linguistic Variable

Definition 4 [38]. 

Let $\widehat{s}=([{\dot{s}}_a,{\dot{s}}_b],[{\ddot{s}}_c,{\ddot{s}}_d])$, where $[{\dot{s}}_a,{\dot{s}}_b]$ is I class uncertain linguistic information, which represents decision maker’s judgment to an evaluated object, and ${\dot{s}}_a,{\dot{s}}_b$ are the elements from the predefined linguistic assessment set $S_I=({\dot{s}}_0,{\dot{s}}_1,\dots ,{\dot{s}}_{l-1})$, while $[{\ddot{s}}_c,{\ddot{s}}_d]$ is II class uncertain linguistic information, which represents the subjective evaluation on the reliability of their given results, and ${\ddot{s}}_c,{\ddot{s}}_d$ are the elements from the predefined linguistic assessment set $S_{II}=({\ddot{s}}_0,{\ddot{s}}_1,\dots ,{\ddot{s}}_{t-1})$, then $\widehat{s}$ is called the 2-dimension uncertain linguistic variable.

4.2.2. Operational Rules of 2-Dimension Uncertain Linguistic Variable

(1)

$\begin{array}{ll}\hfill {\widehat{s}}_1\oplus {\widehat{s}}_2& =([{\dot{s}}_{a_1},{\dot{s}}_{b_1}],[{\ddot{s}}_{c_1},{\ddot{s}}_{d_1}])\oplus ([{\dot{s}}_{a_2},{\dot{s}}_{b_2}],[{\ddot{s}}_{c_2},{\ddot{s}}_{d_2}])\hfill \\ & =([{\dot{s}}_{a_1+a_2},{\dot{s}}_{b_1+b_2}],[{\ddot{s}}_{\min (c_1,c_2)},{\ddot{s}}_{\min (d_1,d_2)}])\hfill \end{array}$

(2)

$\lambda {\widehat{s}}_1=\lambda ([{\dot{s}}_{a_1},{\dot{s}}_{b_1}],[{\ddot{s}}_{c_1},{\ddot{s}}_{d_1}])=([{\dot{s}}_{\lambda \times a_1},{\dot{s}}_{\lambda \times b_1}],[{\ddot{s}}_{c_1},{\ddot{s}}_{d_1}]),\lambda \ge 0$

4.2.3. Distance between Two 2-Dimension Uncertain Linguistic Variables

Definition 6 [38]. 

Let ${\widehat{s}}_1=([{\dot{s}}_{a1},{\dot{s}}_{b1}],[{\ddot{s}}_{c1},{\ddot{s}}_{d1}])$ and ${\widehat{s}}_2=([{\dot{s}}_{a2},{\dot{s}}_{b2}],[{\ddot{s}}_{c2},{\ddot{s}}_{d2}])$ be two 2DULVs, the Hamming distance of ${\widehat{s}}_1$ and ${\widehat{s}}_2$ is defined as follows:

$$\begin{array}{ll}\hfill d({\widehat{s}}_1,{\widehat{s}}_2)=& \frac{1}{4(l-1)}(\left|a_1\times \frac{c_1}{t-1}-a_2\times \frac{c_2}{t-1}\right|+\left|a_1\times \frac{d_1}{t-1}-a_2\times \frac{d_2}{t-1}\right|\hfill \\ & +\left|b_1\times \frac{c_1}{t-1}-b_2\times \frac{c_2}{t-1}\right|+\left|b_1\times \frac{d_1}{t-1}-b_2\times \frac{d_2}{t-1}\right|)\hfill \end{array}$$

(2)

4.3. VIKOR Method

The VIKOR method, proposed by Opricovic [39], would be an effective tool for the MCDM process when the DM is unable to take a decision or doesn’t know to express their preferences at the beginning stage [40]. This method generates a multi-criteria ranking index, which is developed from an aggregating function representing ‘‘closeness” to “ideal” solution. The ranking index is developed from $L_p-$metric, an aggregating function in compromise programming. The VIKOR method uses a linear normalization method to eliminate the units of criteria and determines a compromise solution, which represents maximum “group utility” and a minimum individual regret for the “majority” and “opponent”, respectively [31].

Allow that there are $m$ alternatives $A_1,A_2,\dots ,A_m$ generated for any complex problem of decision making. As an alternative, $A_i$; $f_{ij}$ is the performance value of $j$-th criterion function. The $L_p-$metric, which was used for starting the development of the ranking measure of the VIKOR method, is as follows:

$$L_{pi}={\left\{{\displaystyle \sum _{j=1}^n{\left[(f_j{}^{*}-f_{ij})/(f_j{}^{*}-f_j{}^{-})\right]}^p}\right\}}^{1/p}1\le p\le \infty ;i=1,2,\dots ,m.$$

(3)

$L_{1,i}$ and $L_{\infty ,i}$ are used to formulate the ranking measures $S_i$ and $R_i$ in the VIKOR method, respectively. The maximum group utility (“majority rule”) and minimum individual regret of the “opponent” is calculated by min $S_i$ and min $R_i$, respectively.

5. An Extended, VIKOR-Based MCDM Approach with Heterogeneous Information

Consider a MCDM problem with three types of values: CNVs, TIFNs, and 2DULVs. The alternatives set is $A=\{A_1,A_2,\dots ,A_m\}$, and the criteria set is $C=\{C_1,C_2,\dots ,C_n\}$. Among it, the criteria set with CNVs is $C_I=\{C_1,C_2,\dots ,C_{n_1}\}$, TIFNs is $C_{II}=\{C_{n_1+1},C_{n_1+2},\dots ,C_{n_2}\}$, and 2DULVs is $C_{III}=\{C_{n_2+1},C_{n_2+2},\dots ,C_n\}$. A CNV is expressed as $x$, a TIFN is expressed as $\tilde{a}=((\underset{\_}{a},a,\overline{a});w_{\tilde{a}},u_{\tilde{a}})$, and a 2DULV is expressed as $\widehat{s}=([{\dot{s}}_a,{\dot{s}}_b],[{\ddot{s}}_c,{\ddot{s}}_d])$. The pre-defined linguistic assessment sets are $S_I=({\dot{s}}_0,{\dot{s}}_1,\dots ,{\dot{s}}_{l-1})$ and $S_{II}=({\ddot{s}}_0,{\ddot{s}}_1,\dots ,{\ddot{s}}_{t-1})$.

Step 1: Normalize decision matrix.

This step performs the normalization process of the decision matrix. The data in the decision matrix are normalized to unify different measurement scales. The normalized matrix $\tilde{D}$, composed by a mixture of CNVs, TIFNs, and 2DULVs, can be expressed as follows:

$$\tilde{D}=\left[\underset{\mathrm{CNVs}}{\underbrace{\begin{array}{ccc}{\tilde{x}}_{1,1}& \dots & {\tilde{x}}_{1,n_1}\\ {\tilde{x}}_{2,1}& \dots & {\tilde{x}}_{2,n_1}\\ ⋮& & ⋮\\ {\tilde{x}}_{m,1}& & {\tilde{x}}_{m,n_1}\end{array}}}\underset{\mathrm{TIFNs}}{\underbrace{\begin{array}{ccc}{\tilde{\tilde{a}}}_{1,n_1+1}& \dots & {\tilde{\tilde{a}}}_{1,n_2}\\ {\tilde{\tilde{a}}}_{2,n_1+1}& \dots & {\tilde{\tilde{a}}}_{2,n_2}\\ ⋮& & ⋮\\ {\tilde{\tilde{a}}}_{m,n_1+1}& & {\tilde{\tilde{a}}}_{m,n_2}\end{array}}}\underset{2\mathrm{DULVs}}{\underbrace{\begin{array}{ccc}{\tilde{\widehat{s}}}_{1,n_2+1}& \dots & {\tilde{\widehat{s}}}_{1,n}\\ {\tilde{\widehat{s}}}_{2,n_2+1}& \dots & {\tilde{\widehat{s}}}_{2,n}\\ ⋮& & ⋮\\ {\tilde{\widehat{s}}}_{m,n_2+1}& & {\tilde{\widehat{s}}}_{m,n}\end{array}}}\right]$$

(4)

The normalized values for benefit- and cost-related criteria are calculated using the following equations:

$${\tilde{x}}_{ij}=\{\begin{array}{c}\frac{x_{ij}-\underset{j}{\min }\{x_{ij}\}}{\underset{j}{\max }\{x_{ij}\}-\underset{j}{\min }\{x_{ij}\}},j\in C_b\\ \frac{\underset{j}{\max }\{x_{ij}\}-x_{ij}}{\underset{j}{\max }\{x_{ij}\}-\underset{j}{\min }\{x_{ij}\}},j\in C_c\end{array}$$

(5)

$${\tilde{\tilde{a}}}_{ij}=\{\begin{array}{c}\left(\left(\frac{{\underset{\_}{a}}_{ij}-\underset{j}{\min }{\underset{\_}{a}}_{ij}}{\underset{j}{\min }{\overline{a}}_{ij}-\underset{j}{\min }{\underset{\_}{a}}_{ij}},\frac{a_{ij}-\underset{j}{\min }{\underset{\_}{a}}_{ij}}{\underset{j}{\min }{\overline{a}}_{ij}-\underset{j}{\min }{\underset{\_}{a}}_{ij}},\frac{{\overline{a}}_{ij}-\underset{j}{\min }{\underset{\_}{a}}_{ij}}{\underset{j}{\min }{\overline{a}}_{ij}-\underset{j}{\min }{\underset{\_}{a}}_{ij}}\right);w_{{\tilde{a}}_{ij}},u_{{\tilde{a}}_{ij}}\right),j\in C_b\\ \left(\left(\frac{\underset{j}{\max }{\overline{a}}_{ij}-{\overline{a}}_{ij}}{\underset{j}{\max }{\overline{a}}_{ij}-\underset{j}{\min }{\underset{\_}{a}}_{ij}},\frac{\underset{j}{\max }{\overline{a}}_{ij}-a_{ij}}{\underset{j}{\max }{\overline{a}}_{ij}-\underset{j}{\min }{\underset{\_}{a}}_{ij}},\frac{\underset{j}{\max }{\overline{a}}_{ij}-{\underset{\_}{a}}_{ij}}{\underset{j}{\max }{\overline{a}}_{ij}-\underset{j}{\min }{\underset{\_}{a}}_{ij}}\right);w_{{\tilde{a}}_{ij}},u_{{\tilde{a}}_{ij}}\right),j\in C_c\end{array}$$

(6)

$${\tilde{\widehat{s}}}_{ij}=\{\begin{array}{c}{\widehat{s}}_{ij}=([{\dot{s}}_a,{\dot{s}}_b],[{\ddot{s}}_c,{\ddot{s}}_d]),j\in C_b\\ {\widehat{s}}_{ij}=([{\dot{s}}_{n-b},{\dot{s}}_{n-a}],[{\ddot{s}}_c,{\ddot{s}}_d]),j\in C_c\end{array}$$

(7)

Step 2: Determine PIS and NIS, respectively:

$$F_i{}^{+}=\{\begin{array}{c}\underset{i}{\max }{x}_{ij},j\in N_1\\ ((\underset{i}{\max }{\underset{\_}{a}}_{ij},\underset{i}{\max }{a}_{ij},\underset{i}{\max }{\overline{a}}_{ij}),\underset{i}{\max }{w}_{ij},\underset{i}{\min }{u}_{ij}),j\in N_2\\ ({\dot{s}}_{\max a_{ij}},{\dot{s}}_{\max b_{ij}}),({\ddot{s}}_{\max c_{ij}},{\ddot{s}}_{\max d_{ij}}),j\in N_3\end{array}$$

(8)

$$F_i{}^{-}=\{\begin{array}{c}\underset{i}{\min }{x}_{ij},j\in N_1\\ ((\underset{i}{\min }{\underset{\_}{a}}_{ij},\underset{i}{\min }{a}_{ij},\underset{i}{\min }{\overline{a}}_{ij}),\underset{i}{\min }{w}_{ij},\underset{i}{\max }{u}_{ij}),j\in N_2\\ ({\dot{s}}_{\min a_{ij}},{\dot{s}}_{\min b_{ij}}),({\ddot{s}}_{\min c_{ij}},{\ddot{s}}_{\min d_{ij}}),j\in N_3\end{array}$$

(9)

where $F_i^{+}$ is PIS and $F_i^{-}$ is NIS; $N_1,N_2,N_3$ denote the set of CNVs, TIFNs and 2DULVs, respectively.

Step 3: Calculate the separation measures

The calculation of the separation of each alternative with respect to the PIS and NIS, respectively, based on the Hamming distance. The distance between two CNVs is an absolute value of difference, and the distance between two TIFNs and 2DULVs is calculated according to Formulas (1) and (2).

Step 4: Calculate criteria weight

Reasonable weights for decision criteria may be obtained by many techniques, one of which is the AHP [41]. It utilizes pair-wise comparisons for a set of criteria to judge the relative importance between one attribute and another. In this context, the fundamental “1–9 scale” defined by Saaty is employed for DMs to evaluate the priority score. The judgment matrix is constructed as follows:

$$A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ \cdots & \cdots & \cdots & \cdots \\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right]$$

(10)

where the element $a_{ij}$ indicates representation of relative importance between criteria $i$ and $j$.

Step 5: Calculate the values of $S_i$, $R_i$, and $Q_i$ by the relations:

$$S_i={\displaystyle \sum _{j=1}^n{w}_j}\frac{D(F_i{}^{+},f_{ij})}{D(F_i{}^{+},F_i{}^{-})}, R_i=\max \left(w_j\frac{D(F_i{}^{+},f_{ij})}{D(F_i{}^{+},F_i{}^{-})}\right)R_i$$

(11)

$$Q_i=v\frac{S_i-\min S_i}{\max S_i-\min S_i}+(1-v)\frac{R_i-\min R_i}{\max R_i-\min R_i}{C}_1:Q(A^{(2)})-Q(A^{(1)})\ge 1/(\text{n}-1)$$

(12)

where $S_i$ is the group utility of alternative; $a_i$ is the individual regret of the worst index of $a_i$; $v\in [0,1]$ is the weight of majority criteria; and $(1-v)$ is the weight of individual regret.

Step 6: Rank the alternatives and obtain the evaluation results.

Rank the alternatives by $Q_i$ in an increasing order. The new order is expressed as $A^{(1)},\dots ,A^{(i)},\dots ,A^{(m)}$. If $A^{(1)}$ satisfies the conditions $C_1$ and $C_2$, $A^{(1)}$ is considered as the optimal alternative with the minimum $Q_i$.

• $C_1$: $Q(A^{(2)}-Q{A}^{(1)})\ge 1/(n-1)$
• $C_2$: $A^{(1)}$ is also considered optimal according to the value of $S_i$ or/and $R_i$.

6. A Case Study

6.1. Background

Zhejiang Province is located in the southern wing of the Yangtze River Delta and has experienced rapid economic growth in recent decades. However, with the continuously expanding demand for electricity in Zhejiang province, the contradiction of load capacity is more and more prominent. Fortunately, the amount of potential PHESP sites of Zhejiang province are second to none in China. A total of 47 potential PHESPs, with an installed capacity of more than 30 million kW, have been initially identified by local government. At present, the total installed capacity of PHESPs in Zhejiang province is 458 million kW, including 308 million kW operating capacity and 150 kW under-constricting capacity. According to the “12th five-year Electric Development Planning for Zhejiang Province”, the forecast value of maximum load and Peak-valley in 2020 are 102 million kW and 37 million kW, respectively. It is estimated that about 370–700 kW PHES units are required by 2020. Therefore, it is urgent and necessary to pay close attention to the construction of a new round of PHESPs.

In April 2013, the NEA issued the “Reply on the pumped hydro energy storage plant location planning of Zhejiang province”, in which nine potential PHESP sites have been recommended. On further investigation, four promising PHES sites from these sites are selected using GIS technology. There are Changlongshan PHESP (30°28′21.68″ N, 119°37′28.30″ E), Ninghai PHESP (29°23′20.47″ N, 121°36′1.77″ E), Jinyun PHESP (28°31′32.77″ N, 120°10′31.82″ E), and Tiantai PHESP (29°13′30.17″ N, 121°02′39.18″ E). The distribution and general situation of the four sites are shown in Figure 3 To select the optimal one, the seven experts who were invited to screen criteria were invited again. Also, the second expert meeting was held. The main tasks of this meeting are to determine the weights of criteria and to define the evaluation scale of criteria values. After several rounds of consultation, the experts’ opinions tend to converge. The pair-wise comparison judgment matrices were collected. Also, the scales of the 2DULVs for each criteria were determined as $S_I=({\dot{s}}_0,{\dot{s}}_1,\dots ,{\dot{s}}_4)=\{\mathrm{highly}\mathrm{poor},\mathrm{poor},\mathrm{fair},\mathrm{good},\mathrm{highly}\mathrm{good}\}$ and $S_{II}=({\dot{s}}_0,{\dot{s}}_1,{\dot{s}}_2)=\{\mathrm{partial}\mathrm{familiar},\mathrm{familiar},\mathrm{very}\mathrm{familiar}\}$. As mentioned previously, the decision criteria values of PHESP site selection are heterogeneous. The relative data or information are collected and shown in

Table 2. Performance numerical values of the first type sub-criteria.

Alternative	C11 (m/h)	C12 (m)	C13 (m2)	C14 (m)	C15
A1	339.45	567	99,152	4258	2.49
A2	570.46	485	34,493	3692	5.42
A3	405.94	486	13,457	7307	4.36
A4	542.16	339	7102	4412	7.59

. The performance numerical and triangular intuitionistic fuzzy numbers (TIFNs) values of the second type sub-criteria and the performance 2DUIVs values of the last type sub-criteria are shown in

Table 3. Performance numerical and triangular intuitionistic fuzzy numbers (TIFNs) values of the second type sub-criteria.

Alternative		C31 (a)	C32	C33 (a)	C34	C41 (10 × 4CNY)	C42 (10 × 4CNY)	C43 (10 × 4CNY)
A1	Value	≈8.5	≈75.35	≈13.6	≈17.56	≈2530	≈4208	≈406
	TIFN	((8.3, 8.5, 8.7); 0.7, 0.1)	((75.21, 75.35, 75.46); 0.7, 0.1)	((13.5, 13.6, 13.8); 0.7, 0.2)	((17.4, 17.56, 17.7); 0.6, 0.3)	((2518, 2530, 2543); 0.7, 0.2)	((4187, 4208, 4223); 0.8, 0.1)	((389, 406, 419); 0.8, 0.2)
A2	Value	≈9.8	≈70.35	≈15.7	≈19.62	≈1246	≈2106	≈210
	TIFN	((9.5, 9.8, 9.8); 0.8, 0.1)	((70.12, 70.35, 70.43); 0.8, 0.2)	((15.5, 15.7, 15.8); 0.6, 0.3)	((19.5, 19.62, 19.7); 0.7, 0.2)	((1230, 1246, 1261); 0.8, 0.1)	((2092, 2106, 2122); 0.7, 0.1)	((198, 210, 223); 0.7, 0.2)
A3	Value	≈13.2	≈80	≈18.4	≈15.33	≈623	≈1362	≈108
	TIFN	((12.9, 13.2, 13.4); 0.6, 0.2)	((79.83, 80, 80.15); 0.7, 0.2)	((18.1, 18.4, 18.6); 0.8, 0.1)	((15.1, 15.33, 15.5); 0.9, 0.1)	((609, 623, 642); 0.7, 0.1)	((1254, 1362, 1378); 0.7, 0.2)	((98, 108, 121); 0.8, 0.2)
A4	Value	≈12.8	≈78	≈17.2	≈16.97	≈589	≈1052	≈96
	TIFN	((12.6, 12.8, 13); 0.7, 0.2)	((77.9, 78, 78.17); 0.6, 0.3)	((17.1, 17.2, 17.3); 0.8, 0.2)	((16.9, 16.97, 17.2); 0.8, 0.1)	((573, 589, 603); 0.6, 0.3)	((1013, 1052, 1070); 0.8, 0.1)	((87, 96, 106); 0.8, 0.1)

and

Table 4. Performance 2DUIVs values of the last type sub-criteria.

Alternative	C21	C22	C23
A1	(S2, S3), (S1, S2)	(S2, S3), (S1, S2)	(S1, S3), (S1, S2)
A2	(S1, S2), (S1, S2)	(S1, S2), (S0, S1)	(S2, S3), (S0, S1)
A3	(S3, S4), (S0, S1)	(S1, S2), (S1, S2)	(S0, S1), (S1, S2)
A4	(S1, S2), (S0, S1)	(S3, S4), (S0, S1)	(S3, S4), (S1, S2)

respectively.

6.2. Sitting Decision-Making Process

Firstly, the normalized decision-making matrix composed by a mixture of CNVs, TIFNs, and 2DULVs is calculated and shown in Appendix B.

Secondly, the PIS and NIS are identified, and the separation of each alternative with respect to the PIS and NIS is calculated, which is shown in

Table 5. The separation of each alternative from positive and negative ideal solution.

Criteria	PIS	NIS	A1		A2		A3		A4
			d1j+	d1j−	d1j+	d1j−	d1j+	d1j−	d1j+	d1j−
C11	A1	A2	0	1	1	0	0.289	0.712	0.877	0.123
C12	A1	A4	0	1	0.360	0.640	0.355	0.645	1	0
C13	A1	A2	0	1	0.702	0.298	0.931	0.069	1	0
C14	A2	A3	0.157	0.843	0	1	1	0	0.199	0.801
C15	A1	A4	0.000	1.000	0.576	0.424	0.367	0.633	1	0
C21	A1	A4	0	0.475	0.300	0.175	0.350	0.125	0.475	0
C22	A1	A2	0	0.200	0.200	0	0.050	0.150	0.100	0.100
C23	A4	A3	0.225	0.250	0.400	0.075	0.475	0	0	0.475
C31	A3	A1	0.850	0.000	0.575	0.275	0	0.850	0.010	0.841
C32	A3	A2	0.429	0.535	0.964	0	0	0.964	0.302	0.662
C33	A3	A1	1.059	0.000	0.714	0.345	0	1.059	0.309	0.749
C34	A2	A3	0.518	0.406	0	0.924	0.924	0	0.510	0.414
C41	A1	A4	0	0.987	0.606	0.380	0.966	0.021	0.987	0
C42	A1	A4	0	1.116	0.764	0.351	1.026	0.090	1.116	0
C43	A1	A4	0	0.990	0.650	0.340	0.952	0.038	0.990	0

.

Thirdly, pair-wise comparison judgment matrices are provided by the experts (see Appendix C). Based on these matrices, the weights of criteria are obtained using the method of AHP, shown as follows:

• $w(C1,C2,C3,C4)={(0.531,0.068,0.147,0.254)}^T$;
• $w(C11,C12,C13,C14,C15)={(0.459,0.123,0.118,0.124,0.176)}^T$; $w(C21,C22,C23)={(0.443,0.169,0.387)}^T$;
• $w(C31,C32,C33,C34)={(0.227,0.073,0.473,0.227)}^T$; $w(C41,C42,C43)={(0.443,0.169,0.387)}^T$.

Fourthly, let the value of $v$ be 0.5, then the values $S_i$, $R_i$, and $Q_i$ of each alternative are calculated, which is shown in

Table 6. Values of $S_i$, $R_i$, and $Q_i$ of each alternative.

	Alternative	Value		Alternative	Value		Alternative	Value
$S_i$	A1	0.127	$R_i$	A1	0.059	$Q_i$	A1	0
	A2	0.668		A2	0.207		A2	0.883
	A3	0.629		A3	0.194		A3	0.810
	A4	0.813		A4	0.211		A4	1

.

Fifthly, the raking result can be obtained as $A1\succ A3\succ A2\succ A4$ by comparing $Q_i$ value in an increasing order. Also, $A1$ satisfies the conditions $C_1$ and $C_2$, so it is considered as the optimal alternative.

6.3. Sensitivity Analysis

A sensitivity analysis is performed to test whether the ranking results would qualitatively change if the criteria weights fluctuated. Figure 4 shows those cases where the four criteria have 10%, 20%, and 30% less weight and 10%, 20%, and 30% more weight than the base weight. It can be seen that although the sequencing of alternative A2 and A3 is changeable, A1 is always the best alternative in all 24 tests. So it could be concluded that the method proposed in this study is effective and suitable for the optimal site selection of PHESP. In conclusion, the alternative A1 should be selected as the optimal PHESP site for construction in priority.

7. Conclusions

This paper establishes a VIKOR-based, multi-criteria site selection model for the PHESP site selection. This study has the following advantages compared with existing research: (i) it has constructed a comprehensive evaluation index system, which consists of four criteria and 15 sub-criteria, which reflects the inherent characteristics of PHESP site selection comprehensively; (ii) it can decrease the information distortion and losing that exists in criteria value representation and the information transformation process by considering the different properties of the criteria. When applied to a case from Zhejiang province, China, the decision model shows good suitability. This study provides a clear decision process for DMs to improve management efficiency. Moreover, the decision model could also be applied to solve other comprehensive and multi-criteria optimal location problems, such as tidal power station.

Although the proposed method in this paper helps improve the decision accuracy, there is still some room for improvement. It would be very interesting to extend our study to the case in a more sophisticated situation, such as introducing the behavior theory of DMs. Besides, this paper only considers the case that opinions of all experts arrive at a consensus. But, in some cases, the experts are divided in their opinions since they have different background knowledge. Thus, extending our study to group decision-making is meaningful work.