A Method for Multi-Criteria Group Decision Making with 2-Tuple Linguistic Information Based on Cloud Model

Abstract

This paper presents a new approach to solve the multi-criteria group decision making (MCGDM) problem where criteria values take the form of 2-tuple linguistic information. Firstly, a 2-tuple hybrid ordered weighted geometric (THOWG) operator is proposed, which synthetically considers the importance of both individual and the ordered position so as to overcome the defects of existing operators. Secondly, combining the advantages of the cloud model and 2-tuple linguistic variable, a new generating cloud method is proposed to transform 2-tuple linguistic variables into clouds. Thirdly, we further define some new cloud algorithms, such as cloud possibility degree and cloud support degree which can be respectively used to compare clouds and determine the criteria weights. Furthermore, a new approach for 2-tuple linguistic group decision making is presented on the basis of the THOWG operator, the improved generating cloud method as well as the new cloud algorithms. Finally, an example of assessing the social effects of biomass power plants (BPPS) is illustrated to verify the application and feasible of the developed approach, and a comparative analysis is also conducted to validate the effectiveness of the proposed method.

1. Introduction

Multi-criteria group decision-making (MCGDM) problems are wide-spread in real-life decision-making situations, especially with the increasing complexity of the socio-economic environment [1,2]. In reality, decision-making information is usually uncertain or fuzzy, due to the complexity of things and in recognition of the limitations of decision makers. In order to thoroughly describe fuzzy information, Herrera and Martinez [3] proposed the 2-tuple linguistic model, composed of a linguistic term and a real number, to represent assessment information in a way that can effectively avoid information loss. Consequently, 2-tuple linguistic MCGDM problems have captured the attention of many researchers in recent years [4,5,6]. 2-tuple linguistic information can describe the fuzziness of decision-making information, while it seems imperfect and inaccurate to deal with information in terms of randomness. In fact, randomness and fuzziness are the most important and fundamental of all kinds of uncertainty [7,8]. For instance, for a linguistic decision-making problem, decision maker A may think that 75% fulfillment of a task is “good”, while decision maker B may hold that less than 80% fulfillment of the same task cannot be considered to be “good” with the same linguistic term scale. So in such a way, when considering the degree of certainty of an element belonging to a qualitative concept in a specific universe, it is more feasible to allow a stochastic disturbance of the membership degree encircling a determined central value than to allow a fixed number [9,10]. Fortunately, the cloud model can easily overcome this weakness and make decision-making processes more realistic. The cloud model, which is a quantitative and qualitative uncertainty conversion model proposed by Professor Deyi Li based on traditional fuzzy set theory and probability statistics [11], has distinct advantages in terms of dealing with vague and random decision-making information. It not only easily characterizes the concept of uncertainty in the natural language, but also reflects the intrinsic connection between randomness and fuzziness. Therefore, the cloud model can be used to depict the randomness of 2-tuple linguistic information. To the best of the authors’ knowledge, however, research on converting 2-tuple linguistic variables into clouds has not been reported in the existing literature.

One aim of this paper is to propose a 2-tuple hybrid ordered weighted geometric (THOWG) operator which synthetically considers the importance of both individual and the ordered position to overcome the defect of the existing operators. Another aim of this paper is to develop a new cloud generation method to transform 2-tuple linguistic variables into clouds. The novelty of this paper is as follows:

(i) We develop a new THOWG operator. Traditional 2-tuple linguistic operators either ignore the importance of the individual or neglect the importance of ordered position. To overcome the limitations of existing 2-linguistic power aggregation operators, we develop a new THOWG operator. The THOWG operator combines the advantages of TWG operators and TOWG operators. In this way, it can synthetically consider the importance of both individuals and the ordered position. Moreover, both the TWG operator and the TOWG operator are proved to be special cases of the THOWG operator.

(ii) We present a new cloud generation method to transform 2-tuple linguistic variables into clouds. In real life, fuzziness and randomness are used to describe the uncertainty of natural languages. In addition, randomness and fuzziness are tightly related and inseparable. However, the 2-tuple linguistic variable finds it hard to deal with information in terms of randomness, which will lead to the loss of decision information. To deal with this limitation, we present a new cloud generating method to transform 2-tuple linguistic variables into clouds. This method integrates the significant advantages of the cloud model, so that it can deal with the randomness of natural languages, which will significantly improve the decision quality.

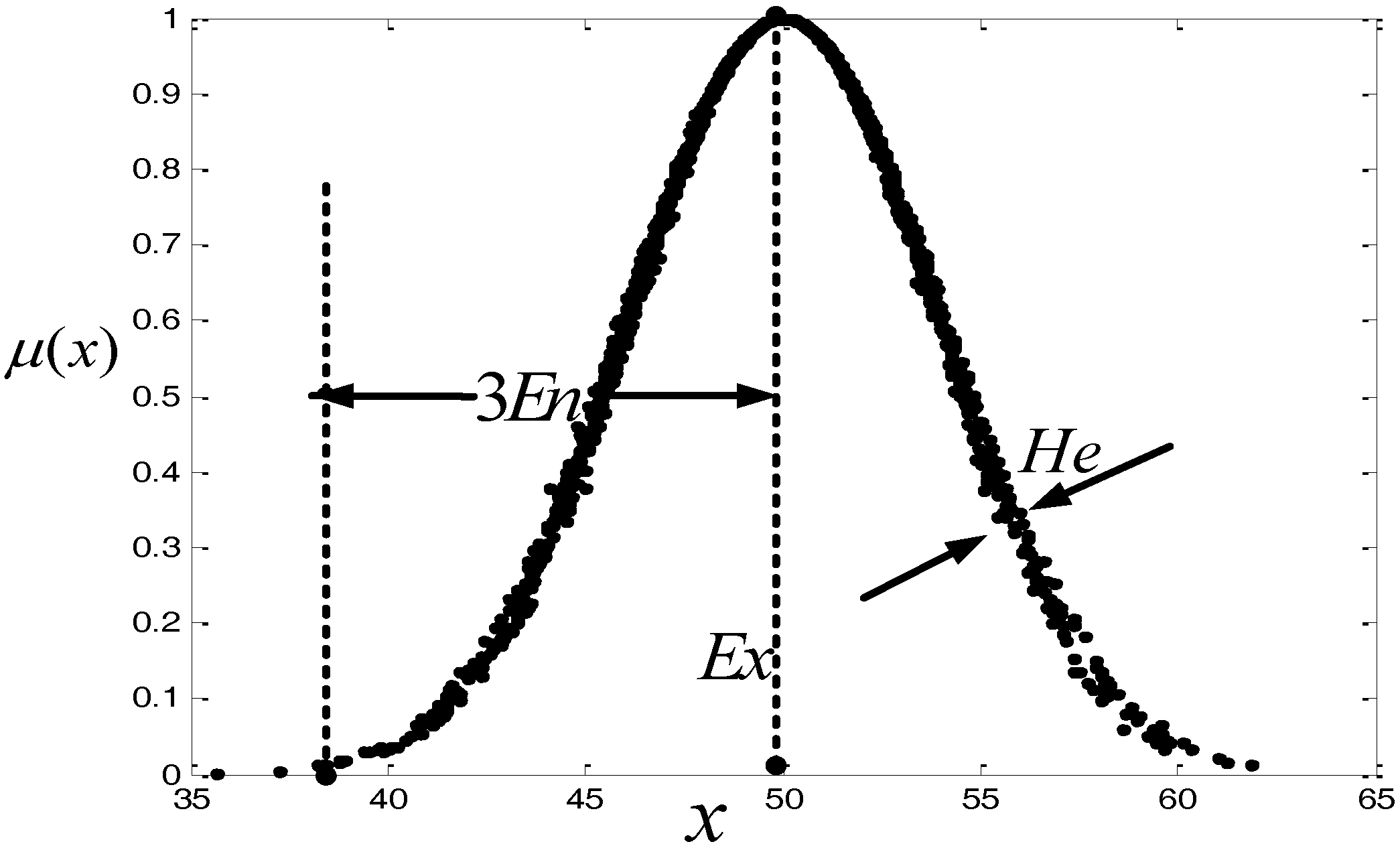
(iii) We address some new cloud algorithms: cloud distance, cloud possibility degree and cloud support degree. Based on the “3En rules” of cloud models, a cloud distance is defined. We further put forward a cloud possibility degree according to this cloud distance, which can be used to compare clouds, and define a cloud support degree which is a similarity index. That is, the greater the similarity is, the closer the two clouds are, and consequently the more they support each other. The support degree can be used to determine the weights of aggregation operators.

To verify the application of the developed approach, a case study of social effect evaluation for BPPs in China is illustrated, and a comparative analysis of the existing approach and the proposed one is carried out to prove the effectiveness of the new developed approach.

The rest of this paper is organized as follows. Section 2 reviews some recent studies regarding 2-tuple linguistic MCGDM problems and aggregating operators, as well as cloud models. Section 3 introduces the fundamental conceptions of 2-tuple linguistic variables and cloud models. Section 4 develops a new averaging operator, and discusses its properties. Section 5 introduces a method for converting a 2-tuple linguistic into a corresponding normal cloud and defines some new algorithms of the cloud model. Section 6 proposes a 2-tuple linguistic MCGDM approach based on the cloud model. Section 7 presents a case study to verify the application of the proposed method and Section 8 draws conclusions.

2. Literature Review

The decision information in some practical MAGDM situations may be unquantifiable due to its nature, or cannot be precisely assessed in a quantitative form, but may be assessed in a qualitative one. Thus, it may take the form of linguistic variables [12], such as “poor”, “fair”, and “very good”. To utilize linguistic variables, a pre-defined linguistic assessment set is needed. Unfortunately, the traditional linguistic assessment set is discrete. So in many cases, the decision information provided by DMs may not match any of the original linguistic phrases in the linguistic assessment sets, resulting in loss of information. To overcome these limitations, Herrera and Martinez [3] introduced the 2-tuple linguistic representation model of which the significant advantage is to be continuous in its domain. Therefore, it can express any counting of information in the universe of the discourse. Recently, the 2-tuple linguistic model has been widely studied. Dong, et al. [13] developed two different models based on linguistic 2-tuples to address term sets that are not uniformly and symmetrically distributed. Truck [14] stressed a comparison between the 2-tuple semantic model and the 2-tuple symbolic model, and then proved that links can be made between them. Zhu et al. [15] utilized two 2-tuples in a 2-dimension linguistic lattice implication algebra to represent a 2-dimension linguistic label for more precise computing and aggregating 2-dimension linguistic information. Xu et al. [16] proposed a four-way procedure to estimate missing preference values when dealing with acceptable incomplete 2-tuple fuzzy linguistic preference relations in group decision-making. Gong et al. [17] established an optimization model of group consensus of 2-tuple linguistic preferential relations. In addition, the 2-tuple linguistic variable has been applied to many practical MCGDM problems such as supplier selection [18,19], material selection [20], site selection [21], emergency response capacity evaluation [22] and in-flight service quality evaluation [23].

In light of the fact that information aggregation always plays an important role in decision-making processes, many 2-tuple aggregation operators have been proposed to aggregate information. The ordered weighted averaging (OWA) operator is one of the most common aggregation methods [24,25,26,27]. It provides a parameterized family of aggregation operators that include as special cases the maximum, the minimum and the average [28]. Motivated by the idea of the OWA operator, Xu and Wang [29] developed the 2-tuple linguistic power ordered weighted averaging (2TLPOWA) operator, which can take all the decision arguments and their relationships into account. Jiang and Fan [30] proposed the 2-tuple ordered weighted geometric (TOWG) operator on the basis of the 2-tuple OWA operator. Li et al. [28] developed the 2-tuple linguistic induced generalized ordered weighted averaging distance (2LIGOWAD) operator. Zeng et al. [31] developed the 2-tuple linguistic generalized ordered weighted averaging distance (2LGOWAD) operator, which is an extension of the OWA operator that utilizes generalized means, distance measures and uncertain information represented as 2-tuple linguistic variables. Wang and Hao [32] introduced the quantifier-guided OWA aggregation operator and anchoring value-based OWA aggregation operator for 2-tuples. However, it needs to point out that these above operators only take into account the importance degrees of relative position and fail to consider the individual importance. On the other hand, some operators just consider individual significance, but neglect the importance of ordered position. For instance, Liu et al. [33] developed a dependent interval 2-tuple weighted averaging (DITWA) operator and a dependent interval 2-tuple weighted geometric (DITWG) operator.

Randomness and fuzziness are the most important and fundamental of all kinds of uncertainties [8]. Here, fuzziness mainly refers to uncertainty regarding the range of extension of concept, and randomness implies that any concept is related to the external world in various ways [10]. However, it is necesssary to point out that the 2-tuple linguistic variable can describe the fuzziness of decision making information, whereas it seems imperfect and inaccurate in dealing with information in terms of randomness. Cloud models, proposed by Professor Deyi Li, has distinct advantages in terms of dealing with vague and random decision-making information. The cloud model depicts the fuzziness and randomness of a qualitative concept with three numerical characteristics perfectly, in such a way that objective and interchangeable transformation between qualitative concepts and quantitative values becomes possible [11]. Therefore, the cloud model makes it possible to improve the accuracy of decisions. With the rapid development of the cloud model theory, successful applications were carried out in various fields, such as intelligent control [34], network security [35], and algorithm improvement [36]. In particular, since Wang and Feng [37] introduced the conversion between linguistic variables and clouds, the cloud model has also been applied to the field of decision-making [9,38,39,40].

From what has been discussed above, it is necessary to develop a new 2-tuple linguistic variable aggregation operator which considers the importance degrees of relative position and individual importance simultaneously. In addition, regarding the significant advantages of 2-tuple linguistic variable and cloud model, it is meaningful to combine them together to deal with MCGDM problems. On the basis of the aforementioned improvements, the decision results will be more reasonable than before.

3. Preliminaries

In this section, we briefly review the fundamental concepts and properties of 2-tuple linguistic and cloud model.

3.1. 2-Tuple Linguistic Variable

Herrera and Martinez [3] developed the 2-tuple fuzzy linguistic representation model based on the concept of symbolic translation. It is used for representing the linguistic assessment information by means of a 2-tuple $(s_i,a_i)$, where $s_i$ is a linguistic label from predefined linguistic term set S and $a_i$ is the value of symbolic translation, and $a_i\in [-0.5,0.5)$.

Definition 1

[3]. Let $S=\left\{s_0,s_1,s_2,\cdots ,s_t\right\}$ be a finite and totally ordered discrete linguistic term set with odd cardinality, where $s_i$ represents a possible value for a linguistic variable. $\beta \in \left[0,t\right]$ is a number value representing the aggregation result of linguistic symbolic. Then the function $\Delta$ used to obtain the 2-tuple linguistic information is defined as:

$$\Delta :[0,Q]\to S\times [-0.5,0.5),\beta \to \Delta \left(\beta \right)=\left(s_i,\alpha \right)$$

(1)

where $i=round\left(\beta \right),\alpha =\beta -i,\alpha \in [-0.5,0.5),round(\cdot )$ is the usual round operation, $s_i$ has the closest index label to $\beta$ and $\alpha$ is the value of the symbolic translation.

Definition 2

[3]. Let $S=\left\{s_0,s_1,s_2,\cdots ,s_t\right\}$ be a linguistic term set and $\left(s_i,\alpha \right)$ a linguistic 2-tuple. There is always a function ${\Delta }^{-1}$, such that, from a 2-tuple it returns its equivalent numerical value, $\beta \in \left[0,t\right]\subset R$, which is

$${\Delta }^{-1}:S\times [-0.5,0.5)\to [0,t],{\Delta }^{-1}\left(s_i,\alpha \right)=i+\alpha =\beta$$

(2)

From Definitions 1 and 2, we can conclude that the conversion of a linguistic term into a linguistic 2-tuple consists of adding a value 0 as symbolic translation:

$$\Delta \left(s_i\right)=\left(s_i,0\right)$$

(3)

Definition 3

[41]. Let $\left(s_k,{\alpha }_k\right)$ and $\left(s_l,{\alpha }_l\right)$ be two 2-tuples, they should have the following properties.

(1) 

If k < l then $\left(s_k,{\alpha }_k\right)$ is smaller than $\left(s_l,{\alpha }_l\right)$, denoted by $\left(s_k,{\alpha }_k\right)<\left(s_l,{\alpha }_l\right)$;

(2) 

If k > l then $\left(s_k,{\alpha }_k\right)$ is bigger than $\left(s_l,{\alpha }_l\right)$, denoted by $\left(s_k,{\alpha }_k\right)>\left(s_l,{\alpha }_l\right)$;

(3) 

If k = l then

(a) 

If ${\alpha }_k={\alpha }_l$, then $\left(s_k,{\alpha }_k\right)=\left(s_l,{\alpha }_l\right)$ representing the same information;

(b) 

If ${\alpha }_k<{\alpha }_l$, then $\left(s_k,{\alpha }_k\right)<\left(s_l,{\alpha }_l\right)$;

(c) 

If ${\alpha }_k>{\alpha }_l$, then $\left(s_k,{\alpha }_k\right)>\left(s_l,{\alpha }_l\right)$.

3.2. Cloud Model

The cloud theory is a model that contains the procedure for transferring uncertainty between quality concepts and quantity data representation by using natural language [7], which was proposed by Professor Deyi Li based on the traditional fuzzy set theory and probability statistics.

Definition 4

[7]. Suppose U is a quantitative domain expressed by precise values, and C is a qualitative concept on the domain. If the quantitative value $x\in U$, and x is a random realization to the qualitative concept C, whose membership $\mu \left(x\right)\in \left[0,1\right]$ for C is a random number with stable tendency:

$$\mu :U\to [0,1],\forall x\in U,x\to \mu \left(x\right)$$

then, the distribution of x on the domain is called as cloud, and each x is called as droplet.

A cloud is made up of many cloud droplets, and a single cloud droplet is a specific realization of the qualitative value in number. Its abscissa value represents the quantitative value corresponding to qualitative concept, and the ordinate value expresses the membership degree of the quantitative value on behalf of the qualitative concepts. The three number features of cloud are expectation Ex, entropy En and hyper entropy He.

• Ex: Expectation best representatives the value of the qualitative concept, and it is usually the x value corresponding to the gravity of the cloud, reflecting the center value of corresponded qualitative concepts.
• En: Entropy represents the measure of the fuzzy degree of the qualitative concept, the size of which directly determines the number of elements that can be accepted by the qualitative concept on the domain, and also reflects the margin of qualitative value based on both this and that.
• He: Hyper entropy expresses the uncertainty measurement of entropy; that is, the entropy of entropy. The size of hyper entropy indirectly reflects the cloud’s thickness.

The 3En rules for clouds refer to the fact that the total contribution of all elements on the domain U to the qualitative concept $C$ is 1. That is, 99.7% of the cloud droplets will fall into the range $(Ex-3En,Ex+3En)$. Thus, cloud droplets falling outside of this scope are small probability events for a qualitative linguistic values concept, and can be ignored. A normal cloud is used most commonly to express the linguistic values. Figure 1 shows the cloud (50, 3.93, 0.01).

4. A New 2-Tuple Aggregation Operator

The use of the fuzzy linguistic approach provides a direct way to manage the uncertainty and model the linguistic assessments by means of linguistic variables. In order to effectively avoid the loss and distortion of information in linguistic information processing processes, Herrera and Martinez [3] proposed a 2-tuple linguistic model, composed of a linguistic term and a real number, to represent the assessment information.

Definition 5

[30]. Let $\left\{\left(s_1,a_1\right),\left(s_2,a_2\right),\cdots ,\left(s_n,a_n\right)\right\}$ be a set of 2-tuple and $\omega ={\left({\omega }_1,{\omega }_2,\cdots ,{\omega }_n\right)}^T$ be the weighting vector of 2-tuple $\left(s_j,a_j\right)\left(j=1,2,\dots ,n\right)$ and ${\omega }_j\in \left[0,1\right],{\displaystyle \sum _{j=1}^n{\omega }_j}=1$, the 2-tuple weighted geometric (TWG) operator $\left(\phi \right)$ is

$$\left(\tilde{s},\tilde{\alpha }\right)=\phi \left(\left(s_1,{\alpha }_1\right),\left(s_2,{\alpha }_2\right),\cdots ,\left(s_n,{\alpha }_n\right)\right)=\Delta \left({\displaystyle \prod _{j=1}^n{\left({\Delta }^{-1}\left(s_j,{\alpha }_j\right)\right)}^{{\omega }_j}}\right),\tilde{s}\in S,\tilde{\alpha }\in [-0.5,0.5).$$

(4)

Definition 6

[30]. Let $\left\{\left(s_1,a_1\right),\left(s_2,a_2\right),\cdots ,\left(s_n,a_n\right)\right\}$ be a set of 2-tuple, a 2-tuple ordered weighted geometric operator $\left(\varphi \right)$ of dimension n is a mapping $TOWG:R^n\to R$ that has an associated vector $\omega ={\left({\omega }_1,{\omega }_2,\cdots ,{\omega }_n\right)}^T$ such that $w_j>0$ and ${\displaystyle \sum _{j=1}^n{\omega }_j}=1$. Furthermore,

$$\left(\overline{s},\overline{\alpha }\right)=\varphi \left(\left(s_1,{\alpha }_1\right),\left(s_2,{\alpha }_2\right),\cdots ,\left(s_n,{\alpha }_n\right)\right)$$

(5)

Where $\left(\pi \left(1\right),\pi \left(2\right),\cdots ,\pi \left(n\right)\right)$ is a permutation of $\left(1,2,\cdots ,n\right)$ such that $\left(s_{\pi \left(j-1\right)},{\alpha }_{\pi \left(j-1\right)}\right)\ge \left(s_{\pi \left(j\right)},{\alpha }_{\pi \left(j\right)}\right)$ for all $j=2,\cdots ,n$.

It is obvious that the two operators have their own defect by Definitions 5 and 6. That is to say, the fundamental aspect of the TWG operator just considers individual significance, but the importance of ordered position is neglected. On the contrary, the TOWG operator only takes the importance degrees of relative position into account and ignores the individual importance.

Therefore, in this section, we propose a new 2-tuple aggregation operator by combining with the advantages of two kinds of operators.

Definition 7.

Let $\left\{\left(s_1,a_1\right),\left(s_2,a_2\right),\cdots ,\left(s_n,a_n\right)\right\}$ be a set of 2-tuple, A 2-tuple hybrid ordered weighted geometric operator $\left(\psi \right)$ of dimension n is a mapping $THOWG:R^n\to R$ that has an associated vector $\omega ={\left({\omega }_1,{\omega }_2,\cdots ,{\omega }_n\right)}^T$ such that ${\omega }_j>0$ an d ${\displaystyle \sum _{j=1}^n{\omega }_j}=1$. Furthermore,

$$\left(\widehat{s},\widehat{\alpha }\right)=\psi \left(\left(s_1,{\alpha }_1\right),\left(s_2,{\alpha }_2\right),\cdots ,\left(s_n,{\alpha }_n\right)\right)=\Delta \left({\displaystyle \prod _{j=1}^n{\left({\Delta }^{-1}\left({\stackrel{⌢}{s}}_{\pi (j)},{\stackrel{⌢}{\alpha }}_{\pi (j)}\right)\right)}^{{\omega }_j}}\right),\widehat{s}\in S,\widehat{\alpha }\in [-\mathrm{0.5.0.5}).$$

(6)

where $\left(\pi \left(1\right),\pi \left(2\right),\cdots ,\pi \left(n\right)\right)$ is a permutation of $\left(1,2,\cdots ,n\right)$, such that $\left({\stackrel{⌢}{s}}_{\pi \left(j-1\right)},{\stackrel{⌢}{\alpha }}_{\pi \left(j-1\right)}\right)\ge \left({\stackrel{⌢}{s}}_{\pi \left(j\right)},{\stackrel{⌢}{\alpha }}_{\pi \left(j\right)}\right)$ $=\Delta \left({\Delta }^{-1}\left(s_j,{\alpha }_j\right)/n{w}_j\right)$ for all $j=2,\cdots ,n$, in which $w={\left(w_1,w_2,\cdots ,w_n\right)}^T$ is the weighting vector of 2-tuple $\left(s_j,a_j\right)$ and $w_j\in \left[0,1\right],{\displaystyle \sum _{j=1}^n{w}_j}=1$. $n$ is the balance factor. The advantage of taking the expression $\Delta \left({\Delta }^{-1}\left(s_j,{\alpha }_j\right)/n{w}_j\right)$ is that it ranks 2-tuple variables by taking the difference and balance into account.

Proposition 1.

If $w={\left(1/n,1/n,\cdots ,1/n\right)}^T$, then THOWG operator can degenerate into TOWG operator.

Proof. 

If $w={\left(1/n,1/n,\cdots ,1/n\right)}^T$, then $\Delta \left({\Delta }^{-1}\left(s_j,{\alpha }_j\right)/n{w}_j\right)=\left(s_j,{\alpha }_j\right)$.

Thus, $\psi \left(\left(s_1,{\alpha }_1\right),\left(s_2,{\alpha }_2\right),\cdots ,\left(s_n,{\alpha }_n\right)\right)=\varphi \left(\left(s_1,{\alpha }_1\right),\left(s_2,{\alpha }_2\right),\cdots ,\left(s_n,{\alpha }_n\right)\right)$. ☐

Proposition 2.

If $w={\left(1/n,1/n,\cdots ,1/n\right)}^T$ and $\left(s_{j-1},{\alpha }_{j-1}\right)\ge \left(s_j,{\alpha }_j\right)$, then THOWG operator can degenerate into TWG operator.

Proof. 

If $w={\left(1/n,1/n,\cdots ,1/n\right)}^T$, then THOWG operator can degenerate into TOWG operator by Proposition 1.

Moreover, $\left(s_{j-1},{\alpha }_{j-1}\right)\ge \left(s_j,{\alpha }_j\right)$. That is to say, the corresponding weight of $\left(s_j,{\alpha }_j\right)$ is ${\omega }_j$.

Thus $\psi \left(\left(s_1,{\alpha }_1\right),\left(s_2,{\alpha }_2\right),\cdots ,\left(s_n,{\alpha }_n\right)\right)=\phi \left(\left(s_1,{\alpha }_1\right),\left(s_2,{\alpha }_2\right),\cdots ,\left(s_n,{\alpha }_n\right)\right)$. ☐

Proposition 3.

If $(s_j,{\alpha }_j)=\left(s,\alpha \right)$ for all $j=1,2,\cdots ,n,$ then $\psi \left(\left(s_1,{\alpha }_1\right),\left(s_2,{\alpha }_2\right),\cdots ,\left(s_n,{\alpha }_n\right)\right)=\left(s,\alpha \right).$

Proposition 4.

Let $\left(s_1,{\alpha }_1\right),\left(s_2,{\alpha }_2\right),\cdots ,\left(s_n,{\alpha }_n\right)$ and $\left(s_1^{\prime },{\alpha }_1^{\prime }\right),\left(s_2^{\prime },{\alpha }_2^{\prime }\right),\cdots ,\left(s_n^{\prime },{\alpha }_n^{\prime }\right)$ be two set of 2-tuple, if $\left(s_j,{\alpha }_j\right)\le \left({s^{\prime }}_j,{{\alpha }^{\prime }}_j\right)$ for all $j=1,2,\cdots ,n$ and the rest of the conditions are not changed, then $\psi \left(\left(s_1,{\alpha }_1\right),\left(s_2,{\alpha }_2\right),\cdots ,\left(s_n,{\alpha }_n\right)\right)\le \psi \left(\left(s_1^{\prime },{\alpha }_1^{\prime }\right),\left(s_2^{\prime },{\alpha }_2^{\prime }\right),\cdots ,\left(s_n^{\prime },{\alpha }_n^{\prime }\right)\right)$.

Proof. 

According to Equation (6), $\psi \left(\left(s_1,{\alpha }_1\right),\left(s_2,{\alpha }_2\right),\cdots ,\left(s_n,{\alpha }_n\right)\right)=\Delta \left({\displaystyle \prod _{j=1}^n{\left({\Delta }^{-1}\left({\stackrel{⌢}{s}}_j,{\stackrel{⌢}{\alpha }}_j\right)\right)}^{{\omega }_j}}\right)$, $\psi \left(\left(s_1^{\prime },{\alpha }_1^{\prime }\right),\left(s_2^{\prime },{\alpha }_2^{\prime }\right),\cdots ,\left(s_n^{\prime },{\alpha }_n^{\prime }\right)\right)=\Delta \left({\displaystyle \prod _{j=1}^n{\left({\Delta }^{-1}\left({{\stackrel{⌢}{s}}_j}^{\prime },{{\stackrel{⌢}{\alpha }}_j}^{\prime }\right)\right)}^{{\omega }_j}}\right).$

If $\left(s_j,{\alpha }_j\right)\le \left({s^{\prime }}_j,{{\alpha }^{\prime }}_j\right)$, then ${\Delta }^{-1}\left(s_j,{\alpha }_j\right)/n{w}_j\le {\Delta }^{-1}\left({s_j}^{\prime },{{\alpha }_j}^{\prime }\right)/n{w}_j.$ so $\left({\stackrel{⌢}{s}}_j,{\stackrel{⌢}{\alpha }}_j\right)=\Delta \left({\Delta }^{-1}\left(s_j,{\alpha }_j\right)/n{w}_j\right)\le \Delta \left({\Delta }^{-1}\left({s_j}^{\prime },{{\alpha }_j}^{\prime }\right)/n{w}_j\right)=\left({{\stackrel{⌢}{s}}_j}^{\prime },{{\stackrel{⌢}{\alpha }}_j}^{\prime }\right)$, ${\Delta }^{-1}\left({\stackrel{⌢}{s}}_j,{\stackrel{⌢}{\alpha }}_j\right)\le {\Delta }^{-1}\left({{\stackrel{⌢}{s}}_j}^{\prime },{{\stackrel{⌢}{\alpha }}_j}^{\prime }\right)$.

Therefore, $\Delta \left({\displaystyle \prod _{j=1}^n{\left({\Delta }^{-1}\left({\stackrel{⌢}{s}}_j,{\stackrel{⌢}{\alpha }}_j\right)\right)}^{{\omega }_j}}\right)\le \Delta \left({\displaystyle \prod _{j=1}^n{\left({\Delta }^{-1}\left({{\stackrel{⌢}{s}}_j}^{\prime },{{\stackrel{⌢}{\alpha }}_j}^{\prime }\right)\right)}^{{\omega }_j}}\right)$.

Thus, $\psi \left(\left(s_1,{\alpha }_1\right),\left(s_2,{\alpha }_2\right),\cdots ,\left(s_n,{\alpha }_n\right)\right)\le \psi \left(\left(s_1^{\prime },{\alpha }_1^{\prime }\right),\left(s_2^{\prime },{\alpha }_2^{\prime }\right),\cdots ,\left(s_n^{\prime },{\alpha }_n^{\prime }\right)\right)$. ☐

Remark 1.

Definition 7 shows that the new 2-tuple aggregation operator not only considers individual significance, but also considers the importance of ordered position.

5. An Improved Cloud Generating Method and Cloud Algorithms

5.1. An Improved Cloud Generating Method

This section introduces a cloud generating method in which a 2-tuple linguistic variable is converted into a corresponding normal cloud.

Let decision-makers’ linguistic evaluation scale be $n$. If $U=[X_{\min },X_{\max }]$ is the effective universe given by experts, then a normal cloud is generated by the given 2-tuple linguistic variable $(s_j,{\alpha }_j)$. The intermediate normal cloud is expressed as $C_0(E{x}_0,E{n}_0,H{e}_0)$, so the respective representations of the adjacent normal cloud are:

$$C_{-1}(E{x}_{-1},E{n}_{-1},H{e}_{-1}),C_{+1}(E{x}_{+1},E{n}_{+1},H{e}_{+1}),\cdots ,C_{-\frac{n-1}{2}}(E{x}_{-\frac{n-1}{2}},E{n}_{-\frac{n-1}{2}},H{e}_{-\frac{n-1}{2}}),C_{+\frac{n-1}{2}}(E{x}_{+\frac{n-1}{2}},E{n}_{+\frac{n-1}{2}},H{e}_{+\frac{n-1}{2}})$$

Based on golden section method, we present a model that the 2-tuple linguistic variable can be converted into the corresponding normal cloud. In order to be convenient, let $\xi ={\Delta }^{-1}\left(s_j,{\alpha }_j\right)/j,\eta =\frac{1-\xi }{1+\xi }$. To generate the five normal cloud, for example, the transformation process of three numerical characters of normal cloud is as follows:

Step 1. Compute $Ex$

$$E{x}_0=\frac{X_{\min }+X_{\max }}{2}\cdot \xi ,E{x}_{(n-1)/2}=X_{\max }\cdot \xi ,E{x}_{-(n-1)/2}=X_{\min }\cdot \xi ;$$

$$E{x}_i=E{x}_0+0.382\cdot i\cdot (\frac{X_{\max }-X_{\min }}{2})/\frac{(n-3)}{2}\cdot \xi ,$$

$$E{x}_{-i}=E{x}_0-0.382\cdot i\cdot (\frac{X_{\max }-X_{\min }}{2})/\frac{(n-3)}{2}\cdot \xi ,(1\le i\le \frac{n-3}{2})$$

Step 2. Compute $En$

$$E{n}_{-1}=E{n}_{+1}=\left(1+\eta \right)\cdot 0.382\cdot (X\max -X\min )/6,E{n}_0=0.618\left(1+\eta \right)\cdot E{n}_{+1};$$

$$E{n}_{-i}=E{n}_{+i}=\left(1+\eta \right)\cdot E{n}_{i-1}/0.618;(2\le i\le \frac{n-1}{2}).$$

Step 3. Calculate $He$

$H{e}_{-i}=H{e}_{+i}=H{e}_{i-1}/0.618,1\le i\le \left(n-1\right)/2$, here $H{e}_0$ is given beforehand.

If ${\alpha }_j=0$, that is to say, the 2-tuple linguistic variable can degenerate into natural language. In this case, the cloud generating model, in which the 2-tuple linguistic variable is converted into the corresponding normal cloud, can degenerate into the corresponding model.

The following Theorem proves that our method can overcome the weaknesses of method given by [37].

Theorem 1.

The expectations of clouds are different from each other and all fall into the range of the universe.

Proof. 

(1) First, we prove that the expectations of clouds are different from each other.

Without loss of generality, we assume $i>j$, then

$$\begin{gathered} E{x}_i-E{x}_j=E{x}_0+0.382\cdot i\cdot (\frac{X_{\max }-X_{\min }}{2})/\frac{(n-3)}{2}\cdot {\xi }_i-E{x}_0-0.382\cdot j\cdot (\frac{X_{\max }-X_{\min }}{2})/\frac{(n-3)}{2}\cdot {\xi }_j \\ =0.382\cdot (\frac{X_{\max }-X_{\min }}{2})/\frac{(n-3)}{2}\cdot \left[(1-\frac{m}{k})\cdot (k+{\alpha }_k)-(1-\frac{m}{l})\cdot (l+{\alpha }_l)\right] \\ =0.382\cdot (\frac{X_{\max }-X_{\min }}{2})/\frac{(n-3)}{2}\cdot \left[\frac{(kl-ml)\cdot (k+{\alpha }_k)-(kl-mk)\cdot (l+{\alpha }_l)}{kl}\right] \\ >0.382\cdot (\frac{X_{\max }-X_{\min }}{2})/\frac{(n-3)}{2}\cdot \left[\frac{(kl-ml)\cdot (l+{\alpha }_l)-(kl-mk)\cdot (l+{\alpha }_l)}{kl}\right] \\ =0.382\cdot (\frac{X_{\max }-X_{\min }}{2})/\frac{(n-3)}{2}\cdot \left[\frac{mk-ml}{kl}\right]>0 \end{gathered}$$

$m,k,l$ are constant, and $i=k-m,j=l-m$.

Therefore, $E{x}_i>E{x}_j$, this is to say,$E{x}_i\ne E{x}_j$.

(2) Second, we prove that all the expectations of clouds fall into the range of the universe.

From Step 1 of the procedure for transforming linguistic variables into clouds, we see that

$$E{x}_1=\min \left\{E{x}_i\right\},E{x}_{(n-1)/2}=\max \left\{E{x}_i\right\},\left(1\le i\le (n-1)/2\right).$$

Since $E{x}_1=X_{\max }-(0.5-\frac{0.382}{n-3})\times l_U$, it can be concluded that

$$X_{\min }<E{x}_1<X_{\max }.$$

(7)

Similarly, note that $E{x}_{\left(n-1\right)/2}=X_{\max }-0.309\times l_U$, we then have

$$X_{\min }<E{x}_{\frac{(n-1)}{2}}<X_{\max }.$$

(8)

Therefore, the expectations of clouds $Y_i\left(1\le i\le \frac{n-1}{2}\right)$ fall into the range of the universe. ☐

By the same token, it is easy to verify that the expectations of clouds $Y_{-i}\left(1\le i\le \frac{n-1}{2}\right)$ fall into the range of the universe. Based on the above analysis, we can conclude that all the expectations of clouds fall into the range of the universe.

Remark 2.

Theorem 1 shows that the improved cloud generating method can guarantee that all the expectations fall into the range of the universe, and meanwhile this method can effectively distinguish the linguistic evaluation scale over the symmetrical interval and transform linguistic term sets of any odd labels into a cloud rather than only five labels.

5.2. New Algorithms of the Cloud Model

This subsection firstly defines the cloud distance, based on it, cloud possibility degree and cloud support degree are also defined, which will be used for cloud comparison and weight determination, respectively.

Based on the “3En rules” of normal cloud models, the distance of clouds is defined as follows.

Definition 8.

Let $Y_1=Y_1(E{x}_1,E{n}_1,H{e}_1)$ and $Y_2=Y_2(E{x}_2,E{n}_2,H{e}_2)$ be two normal clouds in universe U. Then, the distance $d(Y_1,Y_2)$ of two normal clouds $Y_1$ and $Y_2$ is given by:

$$d(Y_1,Y_2)=\frac{1}{2}\left(\underset{\_}{d}(Y_1,Y_2)+\overline{d}(Y_1,Y_2)\right),$$

(9)

where $\underset{\_}{d}(Y_1,Y_2)=\left|(1-3\sqrt{E{n}_1^2+H{e}_1^2}/E{x}_1)E{x}_1-(1-3\sqrt{E{n}_2^2+H{e}_2^2}/E{x}_2)E{x}_2\right|,$ and $\overline{d}(Y_1,Y_2)=|(1+3\sqrt{E{n}_1^2+H{e}_1^2}/E{x}_1)E{x}_1-(1+3\sqrt{E{n}_2^2+H{e}_2^2}/E{x}_2)E{x}_2|.$

Proposition 5.

The cloud distance satisfies the following properties:

(i) 

$d(Y_1,Y_2)\ge 0$;

(ii) 

$d(Y_1,Y_2)=d(Y_2,Y_1)$;

(iii) 

For $\forall Y_3\in F,d(Y_1,Y_3)\le d(Y_1,Y_2)+d(Y_2,Y_3)$.

Proof. 

See Appendix. ☐

Remark 3.

If $E{n}_1=H{e}_1=E{n}_2=H{e}_2=0$, then the normal cloud will degenerate into a real number, in this case, $d(Y_1,Y_2)=\left|E{x}_1-E{x}_2\right|.$

Based on the cloud distance, a cloud possibility degree can be defined as follows.

Definition 9.

Let $Y_1=Y_1(E{x}_1,E{n}_1,H{e}_1)$ and $Y_2=Y_2(E{x}_2,E{n}_2,H{e}_2)$ be two normal clouds in universe U, and $Y^{*}=Y(max E{x}_i,\min E{n}_i,\min H{e}_i)(i=1,2)$ be the positive ideal cloud, then the cloud possibility degree is defined as

$$p(Y_1\ge Y_2)=\frac{d(Y^{*},Y_2)}{d(Y^{*},Y_1)+d(Y^{*},Y_2)}$$

(10)

where $d(Y^{*},Y_1)$ and $d(Y^{*},Y_2)$ are the distances between $Y^{*}$ and $Y_1,Y_2$, respectively.

Definition 9 shows that the cloud possibility degree $p(Y_1\ge Y_2)$ is described by the distance $d(Y^{*},Y_1)$ and $d(Y^{*},Y_2)$. The larger the distance between $Y_2$ and $Y^{*}$ is, the larger the cloud possibility degree $p(Y_1\ge Y_2)$ is. The cloud possibility degree can be used for cloud comparison.

From Definition 9, we can easily obtain the following properties of cloud possibility degree.

Proposition 6.

Let $Y_1=Y_1(E{x}_1,E{n}_1,H{e}_1)$, $Y_2=Y_2(E{x}_2,E{n}_2,H{e}_2)$ and $Y_3=Y_3(E{x}_3,E{n}_3,H{e}_3)$ be three cloud variables. Then, the cloud possibility degree satisfies the following properties:

(i) 

$0\le p(Y_1\ge Y_2)\le 1$;

(ii) 

$p\left(Y_1\ge Y_2\right)=1\iff Y^{*}=Y_1$;

(iii) 

$p\left(Y_1\ge Y_2\right)=0\iff Y^{*}=Y_2$;

(iv) 

$p(Y_1\ge Y_2)+p(Y_1<Y_2)=1,$ particularly, $p\left(Y_1\ge Y_1\right)=0.5$;

(v) 

if $p(Y_1\ge Y_2)\ge 1$ and $p(Y_2\ge Y_3)\ge 1$, then $p(Y_1\ge Y_3)\ge 1$;

(vi) 

if $p(Y_1\ge Y_2)=1$, then $p(Y_1\ge Y_3)\ge p(Y_2\ge Y_3)$.

To rank clouds $Y_i(i=1,2,\cdots ,m),$ following Wan and Dong [42] who ranked interval-valued intuitionistic fuzzy numbers via possibility degree, we can construct a fuzzy complementary matrix of cloud possibility degree as follows:

$$P=\left[\begin{array}{cccc}{p}_{11}& p_{12}& \cdots & p_{1m}\\ p_{21}& p_{22}& \cdots & p_{2m}\\ ⋮\\ p_{m1}& p_{m2}& \cdots & p_{mm}\end{array}\right]$$

(11)

where $Y^{*}=Y(\max E{x}_i,\min E{n}_i,\min H{e}_i),$ $p_{ij}\ge 0,$ $p_{ij}+p_{ji}=1$ and $p_{ii}=0.5$. It is noteworthy that it is possible for there to be different sets of $Y_1$ and $Y_2$ results in the same value $p_{12}$. In other words, if ${Y_1}^{\prime }\ne {Y_1}^{\prime }$, ${Y_2}^{\prime }\ne {Y_2}^{\prime }$, ${Y_3}^{\prime }\ne {Y_3}^{\prime }$, then it could be ${p_{12}}^{\prime }=p_{12}$. However, these cases have no effect on the final ranking. The aim of the introduction of possibility degree is to make a rank.

Then, the ranking vector $V={(v_1,v_2,\cdots ,v_m)}^T$ is determined by

$$v_i=\frac{1}{m\left(m-1\right)}\left({\displaystyle \sum _{j=1}^m{p}_{ij}}+\frac{m}{2}-1\right)\left(i=1,2,\cdots ,m\right),$$

(12)

and consequently, the clouds $Y_i(i=1,2,\cdots ,m)$ can be ranked in descending order via values of $v_i$ $(i=1,2,\cdots ,m)$. That is, the smaller the value of $v_i$ is, the larger the corresponding order of $Y_i$ $(i=1,2,\cdots ,m)$ is.

The advantage of utilizing the vector $V={(v_1,v_2,\cdots ,v_m)}^T$ for ranking clouds lies in the fact that it fully uses the decision making information and makes the calculation simple.

Proposition 7.

Suppose that $Y_1(E{x}_1,E{n}_1,H{e}_1)$ and $Y_2(E{x}_2,E{n}_2,H{e}_2)$ are two normal clouds in universe, if $E{x}_1\ge E{x}_2$, $E{n}_1\le E{n}_2$, $H{e}_1\le H{e}_2$, then $Y_1\ge Y_2$.

Proof. 

See Appendix. ☐

Note that the positive ideal cloud $Y^{*}=Y(7.58,0.663,0.09)$ and according to Equation (9), we have that $d(Y^{*},Y_1)=3.78$, $d(Y^{*},Y_2)=3.28$, $d(Y^{*},Y_3)=1.96$ and $d(Y^{*},Y_4)=2.82$.

Consequently, based on Equation (10), the possibility degree matrix can be derived as follows:

$$P=\left[\begin{array}{cccc}0.500& 0.465& 0.344& 0.427\\ 0.535& 0.500& 0.377& 0.462\\ 0.656& 0.623& 0.500& 0.587\\ 0.573& 0.538& 0.413& 0.500\end{array}\right].$$

According to Equation (12), we further derive the ranking vector $V={(0.228,0.240,0.280,0.252)}^T$. So the ranking of the normal clouds is: $Y_3>Y_4>Y_2>Y_1.$

Following [43] we can define the cloud support degree.

Definition 10.

Let F be the set of all normal clouds and support (hereafter, Sup) a mapping from $F\times F$ to R. For any $Y_{\alpha }$ and $Y_{\beta }$, if the term Sup satisfies:

(i) 

$Sup(Y_a,Y_{\beta })\in \left[0,1\right]$;

(ii) 

$Sup(Y_a,Y_{\beta })=Sup(Y_{\beta },Y_a)$;

(iii) 

$Sup(Y_a,Y_{\beta })\ge Sup(Y_i,Y_j)$ if $d(Y_{\alpha },Y_{\beta })<d(Y_i,Y_j),$ where $d$ is a distance measure for clouds.

Then, $Sup(Y_a,Y_{\beta })$ is called the support degree for $Y_{\alpha }$ from $Y_{\beta }$.

Note that Sup measure is essentially a similarity index, meaning that the greater the similarity is, the closer the two clouds are, and consequently the more they support each other. The support degree will be used to determine the weights of aggregation operator.

6. 2-Tuple Linguistic Multi-Criteria Group Decision Making Approach

This section presents an approach to dealing with the 2-tuple linguistic MCGDM problems.

6.1. Solution Procedure

For a 2-tuple linguistic MCGDM problem, Let $A=\left\{A_1,\cdots ,A_i,\cdots ,A_m\right\}$ be a discrete set of alternatives, $C=\left\{C_1,\cdots ,C_j,\cdots ,C_n\right\}$ a finite set of criteria, and $w={(w_1,\cdots ,w_j,\cdots w_n)}^T$ be the weight vector of criteria, where ${\displaystyle \sum _{j=1}^n{w}_j=1,w_j\ge 0,j=1,2,\cdots ,n}.$ Let $D=\left\{D_1,\cdots ,D_l,\cdots D_t\right\}$ be a finite set of decision-makers, whose weight vector is $\lambda ={({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_t)}^T$, with ${\displaystyle \sum _{l=1}^t{\lambda }_l=1,{\lambda }_l\ge 0,l=1,2,\cdots ,t}$.

Figure 2 illustrates the solution procedure about solving the above 2-tuple linguistic MCDM problem.

From Figure 2, we notice that the solution procedure can be decomposed into six sub-procedures. First, a 2-tuple linguistic decision matrix is constructed according to decision-makers’ preferences. Second, the 2-tuple linguistic decision matrices are aggregated into a collective decision matrix by the THOWG operator. Third, based on generating cloud method, the collective decision matrix is converted into the corresponding cloud decision matrix. Fourth, a cloud support degree is defined to determine the criteria weights. Fifth, the integrated value of each alternative is calculated by aggregating the cloud prospect values. Last, the ranking of alternatives is determined by comparing the integrated cloud values based on the cloud possible degree.

6.2. Decision Making Approach

Based on the THOWG operator, we propose the decision-making approach which is shown as follows.

Step 1. Construct the 2-tuple linguistic decision matrix ${\tilde{R}}_l={\left({r_{ijk}}^{\left(l\right)},0\right)}_{m\times n}$.

Step 2. Utilize the decision information given in matrix ${\tilde{R}}_l$, and the THOWG operator which has the associated weighting vector $\omega ={({\omega }_1,\cdots ,{\omega }_l,\cdots {\omega }_t)}^T$

$$x_{ijk}=\left(r_{ijk},{\alpha }_{ijk}\right)=\psi \left(\left(r_{ijk}^{\left(1\right)},0\right),\cdots \left(r_{ijk}^{\left(l\right)},0\right),\cdots ,\left(r_{ijk}^{\left(t\right)},0\right)\right)=\Delta \left({\displaystyle \prod _{l=1}^t{\left({\Delta }^{-1}\left({\widehat{r}}_{ijk}^{\left(l\right)},{\widehat{\alpha }}_{ijk}^{\left(l\right)}\right)\right)}^{{\omega }_l}}\right),r_{ijk}^{\left(l\right)}\in S,{\alpha }_{ijk}^{\left(l\right)}\in [-\mathrm{0.5.0.5}),k=1,2,\cdots s.$$

(13)

to aggregate all the decision matrices ${\tilde{R}}_l\left(l=1,2,\cdots ,t\right)$ into a collective decision matrix $\tilde{R}={\left(r_{ijk},{\alpha }_{ijk}\right)}_{m\times n}$, where $\left({\widehat{r}}_{ijk}^{\left(l\right)},{\widehat{\alpha }}_{ijk}^{\left(l\right)}\right)$ is jth element of $\{\Delta \left({\Delta }^{-1}\left(r_{ijk}^{\left(1\right)},0\right)/t{\lambda }_1\right),\Delta \left({\Delta }^{-1}\left(r_{ijk}^{\left(2\right)},0\right)/t{\lambda }_2\right),\cdots ,$ $\Delta \left({\Delta }^{-1}\left(r_{ijk}^{\left(t\right)},0\right)/t{\lambda }_t\right)\}$ based on descending order, and $\lambda ={\left({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_t\right)}^T$ the weighting vector of decision makers.

Step 3. Based on the generating cloud method, the collective decision matrix $\tilde{R}$ is converted into the corresponding normal cloud decision matrix $R$.

Step 4. Determine the criteria weights.

Calculate the cloud support degrees:

$$Sup\left({\widehat{r}}_{sj}^k,{\widehat{r}}_{qj}^k\right)=1-\frac{2d\left({\widehat{r}}_{sj}^k,{\widehat{r}}_{qj}^k\right)}{{\displaystyle \sum _{\begin{array}{l}q=1\\ q\ne s\end{array}}^{n}d\left({\widehat{r}}_{sj}^k,{\widehat{r}}_{qj}^k\right)+{\displaystyle \sum _{\begin{array}{l}s=1\\ s\ne q\end{array}}^{n}d\left({\widehat{r}}_{qj}^k,{\widehat{r}}_{sj}^k\right)}}},\begin{array}{c}q=1,2,\cdots ,n\end{array},$$

(14)

which satisfy the support conditions (i)–(iii) in Definition 10. Here, the cloud distance measure is expressed by Equation (9), and $Sup\left({\widehat{r}}_{sj}^k,{\widehat{r}}_{qj}^k\right)$ denotes the similarity between the sth largest cloud preference value ${\widehat{r}}_{sj}^k$ and the qth largest cloud preference value ${\widehat{r}}_{qj}^k$. We further calculate the weights of criteria by means of Equation (14).

Step 5. Aggregate the criteria values of each alternative into a collective value.

Utilize Equation (14) to aggregate all cloud decision matrices ${\widehat{R}}^k={\left({\widehat{r}}_{ij}^{(k)}\right)}_{m\times n}\left(k=1,2,\cdots ,t\right)$ into a collective cloud decision matrix $R={\left(r_{ij}\right)}_{m\times t}$.

Step 6. Rank the alternatives and choose the best one(s).

According to the cloud possibility degree and the ranking vector, we can rank the collective overall preference values $r_i(i=1,2,\cdots ,m)$ in descending order and consequently select the best one in the light of the collective overall preference values $r_i(i=1,2,\cdots ,m)$.

7. A Case Study

7.1. Social Effect Evaluation of BPPs in China

Fossil fuels are the main cause of many of the environmental impacts that limit human beings [44]. Biomass, as an important kind of renewable energy, is a promising energy source alternative to traditional fossil fuel [45]. In China, a lot of BBPs are beginning to emerge with the support of national policies. According to this country’s “The 12th Five Year Plan for Renewable Energy Development”, electricity generated by biomass will have reached a total installed capacity of 13 GW by 2015. This value will have been doubled by 2020, and is supposed to account for 4% of the total energy consumption [46,47].

Recently, a thermal power corporation in Beijing, China, intends to enter into the field of biomass energy. Given the advantages of electricity market share in South China and energy information, the decision-makers consider southern Fujian and Guangdong are suitable for establishing a BPP. Many proposals have been put forward for this project. The local government and people share the concern of social problems for establishing a BPP. Thus, it is strongly recommended that the social effects of the BPP proposals must be assessed before any BPP proposal is chosen for development. An expert committee, which consists of three expert groups whose academic backgrounds are in the energy, social, and mathematical fields, is organized temporarily for the social effects assessment of BPP proposals. The major tasks of the three expert groups are as follows: (1) expert group I is responsible for the selection of prospective BPP proposals and the identification of the most significant criteria involved in assessing social effects of BPPs; (2) expert group II is responsible for expressing their preference on the prospective BPP proposals with respect to every criterion; (3) the task of expert group III is to calculate the ranking results by the proposed method.

Firstly, by using GIS and satellite images, expert group I preliminarily screens out four prospective proposals, which are denoted A_1, A₂, A₃ and A₄. In fact, A₁ and A₂ lie in Fujian province, A₃ and A₄ in Guangdong province. Then, the most significant criteria for the assessment of social effects of BPPs are also identified: effect on local economic development (C₁), effect on local employment boost (C₂), and effect on local cultural development (C₃). Secondly, three experts in expert group II express their preference on the four BPP proposals with respect to the three criteria by using 2-tuple linguistic information. The information is collected and shown in

Table 1. 2-Tuple linguistic decision matrix ${\tilde{R}}_l$.

		A1	A2	A3	A4
$D_1$	$C_1$	$\left(EG,0\right)$	$\left(M,0\right)$	$\left(M,0\right)$	$\left(G,0\right)$
	$C_2$	$\left(G,0\right)$	$\left(EG,0\right)$	$\left(G,0\right)$	$\left(EG,0\right)$
	$C_3$	$\left(EG,0\right)$	$\left(G,0\right)$	$\left(EG,0\right)$	$\left(EG,0\right)$
$D_3$	$C_1$	$\left(G,0\right)$	$\left(S,0\right)$	$\left(G,0\right)$	$\left(G,0\right)$
	$C_2$	$\left(G,0\right)$	$\left(G,0\right)$	$\left(M,0\right)$	$\left(G,0\right)$
	$C_3$	$\left(EG,0\right)$	$\left(EG,0\right)$	$\left(G,0\right)$	$\left(EG,0\right)$
$D_3$	$C_1$	$\left(S,0\right)$	$\left(M,0\right)$	$\left(M,0\right)$	$\left(G,0\right)$
	$C_2$	$\left(G,0\right)$	$\left(EG,0\right)$	$\left(G,0\right)$	$\left(EG,0\right)$
	$C_3$	$\left(EG,0\right)$	$\left(G,0\right)$	$\left(EG,0\right)$	$\left(EG,0\right)$

. In addition, the weight vector of the three experts is $\lambda ={\left(0.3,0.4,0.3\right)}^T$ and the used linguistic term set is $S=\{ES=\mathrm{extremely}\mathrm{small},S=\mathrm{small},M=\mathrm{medium},G=\mathrm{great},EG=\mathrm{extremely}\mathrm{great}\}$. Thirdly, expert group III calculates the ranking results. The process is as follows: (i) Based on the THOWG operator, expert group III calculates the collective overall 2-tuple linguistic decision matrix $\tilde{R}={\left(r_{ijk},{\alpha }_{ijk}\right)}_{4\times 3},k=1,2,3$ given in

Table 2. Collective decision matrix $R$.

	Y1	Y2	Y3	Y4
$C_1$	$\left(G,-0.17\right)$	$\left(M,-0.5\right)$	$\left(M,0.3\right)$	$\left(G,-0.03\right)$
$C_2$	$\left(G,-0.03\right)$	$\left(EG,-0.47\right)$	$\left(G,-0.47\right)$	$\left(EG,-0.47\right)$
$C_3$	$\left(EG,-0.04\right)$	$\left(G,0.33\right)$	$\left(EG,-0.47\right)$	$\left(EG,-0.04\right)$

, where $\omega ={(0.3,0.3,0.4)}^T$ is the associated weight vector with THOWG operator; (ii) According to the cloud generating method, the collective overall 2-tuple linguistic decision matrix is converted into the corresponding normal cloud decision matrix, as shown in

Table 3. Cloud decision matrix $Y$.

	A1	A2	A3	A4
$C_1$	$Y_{+1}(65.18,6.56,0.16)$	$Y_0(37.50,4.50,0.10)$	$Y_0(57.50,3.66,0.10)$	$Y_{+1}(68.41,6.40,0.16)$
$C_2$	$Y_{+1}(68.41,6.40,0.16)$	$Y_{+2}(77.84,10.95,0.26)$	$Y_{+1}(58.27,6.91,0.16)$	$Y_{+2}(77.84,10.95,0.26)$
$C_3$	$Y_{+2}(87.32,10.35,0.26)$	$Y_{+1}(76.70,6.03,0.16)$	$Y_{+1}(77.84,10.95,0.26)$	$Y_{+2}(87.32,10.35,0.26)$

; (iii) Based on the cloud support degree, the criteria weights are derived. Then, the criteria values of each alternative are aggregated into a collective value, as shown in

Table 4. Weights of criteria.

	A1	A2	A3	A4
$C_1$	0.355	0.298	0.344	0.313
$C_2$	0.366	0.350	0.351	0.354
$C_3$	0.280	0.352	0.305	0.333

; (iv) Equation (14) is utilized to compute the collective overall preference value of the alternatives:$A_1:Y(72.56,7.760,0.19)$, $A_2:Y(65.42,7.797,0.19)$, $A_3:Y(63.98,7.613,0.18)$ and $A_4:Y(78.05,9.538,0.23)$; (v) The positive ideal cloud is $Y^{*}=Y(78.05,7.613,0.18)$. The ranking vector, then, is derived by Equations (11) and (12): $V={(0.1965,0.1572,0.1522,0.1941)}^T$; (vi) The ranking order in light of the overall collective preference values $r_i(i=1,2,3,4)$ is $A_1>A_4>A_2>A_3.$

The ranking results show that the social effects of BPP proposal $A_1$ is the greatest. It implies that the local government and people highly encourage the corporation to establish a BPP. So, the proposal $A_1$ should be the primary choice for establishing a BPP.

7.2. Comparative Analysis

To validate the effectiveness of the proposed method, a comparative study is conducted by applying the 2-tuple weighted averaging (2TWA) operator. And the dependent 2-tuple ordered weighted averaging (D2TOWA) operator of Wei [48]. This comparative analysis is based on the same illustrative example given in Section 7.1. The weights of criteria are taken from Table 4 to make it easy to compare these results with our method.

Table 5. Individual overall preference value by utilizing 2TWA operator.

	E1	E2	E3
$Z_1$	$(EG,-0.36)$	$(G,0.28)$	$(G,-0.43)$
$Z_2$	$(G,0.05)$	$(G,-0.22)$	$(G,0.05)$
$Z_3$	$(G,-0.04)$	$(G,-0.35)$	$(G,-0.05)$
$Z_4$	$(EG,-0.31)$	$(G,0.33)$	$(EG,-0.31)$

shows the individual overall preference value by utilizing 2TWA operator and

Table 6. Overall preference values of the alternatives.

	Z1	Z2	Z3	Z4
2TWA and D2TOWA	$(G,0.21)$	$(G,-0.02)$	$(G,-0.12)$	$(EG,-0.4)$

presents the overall preference values of the alternatives. It is easily seen from

Table 7. Ordering of the alternative.

Sources	Operators	Ordering
This paper	THOWG	$A_1>A_4>A_2>A_3.$
Wei’s paper	2TWA and D2TOWA	$A_4>A_1>A_2>A_3.$

that the ranking results obtained by the 2TWA and D2TOWA operator of Wei and the method of this paper are slightly different. Disparities are manifested in the ranking order of $A_1$ and $A_4$. The best alternative by the former is $A_4$, while the best alternative by the latter is $A_1$. However, it is difficult to judge which one is close to the original expert judgments since multiple experts are involved. So we judge it indirectly from the comparison of two methods. Compared with the two operators of Wei, the main advantages of our method mainly lie in the following:

(i) Our method sufficiently takes the importance degrees of different experts into consideration. The 2TWA and D2TOWA operators are based on the ET-WG and ETOWG operators, which don’t consider the importance degrees of different experts at all. In fact, different experts act in different roles in the decision process. Some experts may assign unduly high or unduly low uncertain preference values to their preferred or non-preferred objects. To reduce the influence of these unfair arguments on the decision results and reflect the importance degrees of all the experts, the proposed method calculates the collective overall 2-tuple linguistic decision matrix by using the weighting vector of decision makers and the weighting vector of ordered position based on the THOWG operator. Therefore, the THOWG operator can make the decision results more reasonable through assigning low weights to those “false” or “biased” arguments. These advantages cannot be reflected in the former.

(ii) Our method utilizes the cloud model which can easily overcome this weakness and make decision processes more realistic. The 2TWA and D2TOWA operators cannot deal with information in terms of fuzziness and randomness. However, randomness and fuzziness are the most important and fundamental in all kinds of uncertainty. It will produce a consequent loss of information and then result in a lack of precision if randomness or fuzziness are ignored. Our method transforms the collective 2-tuple linguistic decision matrix into the corresponding normal cloud decision matrix by applying generating cloud method. Thus, our method could better depict the fuzziness and randomness of the 2-tuple linguistic variables. It demonstrates that our method is of flexibility and accuracy.

In conclusion, we hold that the ordering result from the proposed methodology is superior to the Wei’s methodology.

8. Conclusions

This paper has investigated MCGDM problems where the criteria values of the alternatives are 2-tuple linguistic information and the information of criteria weights is partially known. A new 2-tuple aggregation operator is developed so as to aggregate the evaluation value into the group’s comprehensive evaluation information. In addition, taking the fuzziness and randomness of linguistic information into account, a cloud generating method is proposed in which a 2-tuple linguistic is converted into a corresponding normal cloud. Based on this method, we developed some new cloud algorithms such as the cloud possibility degree and cloud support degree, which can be used for cloud comparison and the weight determination, respectively. In particular, based on the new cloud generating method and THOWG operator, an approach for the 2-tuple linguistic MCGDM problems is developed. Finally, to show the effectiveness and the good performance of our approach in practice, we provide an example and make a comparative analysis.

In further research about the 2-tuple linguistic MCGDM problems, it would be very interesting to extend our analysis to the case of more sophisticated situations, such as dynamic group decisions, etc. Nevertheless, we leave that point to future research, since our methodology cannot be applied to that extended framework, which will result in more sophisticated calculations and which we cannot tackle here.