A Quick Artificial Bee Colony Algorithm for Image Thresholding
Abstract
:1. Introduction
2. Related Works
3. Formulation of the Multilevel Thresholding
3.1. Pixel Grouping Based on Thresholding
3.2. Concept of Kapur’s Entropy for Image Thresholding
4. Brief Introduction of the Quick Qrtificial Bee Colony Algorithm
4.1. Standard Artificial Bee Colony Algorithm
| Algorithm 1 (Main steps of the ABC algorithm) |
| Step 1: Initialization Phase Step 2: Repeat Step 3: Employed Bee Phase Step 4: Onlooker Bee Phase Step 5: Scout Bee Phase Step 6: Memorize the best solution achieved so far Step 7: Continue until the termination criteria is satisfied or Maximum Cycle Number has been achieved. |
4.2. Modified Quick Artificial Bee Colony Algorithm for Image Thresholding
| Algorithm 2 (Main steps of the MQABC algorithm for image thresholding): |
| Step 1: Initialization of the population size SN, setting the number of thresholds M and maximum cycle number CN, and initialization the population of source foods by Equation (5). Step 2: Evaluate the population via the specified optimization function, while a termination criterion is not satisfied or Cycle Number < CN. Step 3: (for j = 1 to SN) Produce new solutions (food source positions) vj in the neighborhood of tj for the employed bees using Equation (6). Step 4: Apply the greedy selection process between the corresponding and vj. Step 5: Calculate the probability values for the solutions by means of their fitness values using Equation (8). Step 6: Calculate the Euclidean distance by Equation (10), search for the neighborhood food sources with distance less than in the existing population, amd then choose the best food source by Equation (11) in . Step 7: Produce the new solutions (new positions) for the onlookers from the solutions using Equation (9). Then select them depending on and evaluate them. Step 8: Apply the greedy selection process for the onlookers between and . Step 9: Determine the abandoned solution (source food), if it exists, and replace it with a new randomly produced solution tj for the scout. Step 10: Memorize the best food source position (solution) achieved so far. Step 11: end for Step 12: end while |
5. Experiments and Result Discussions
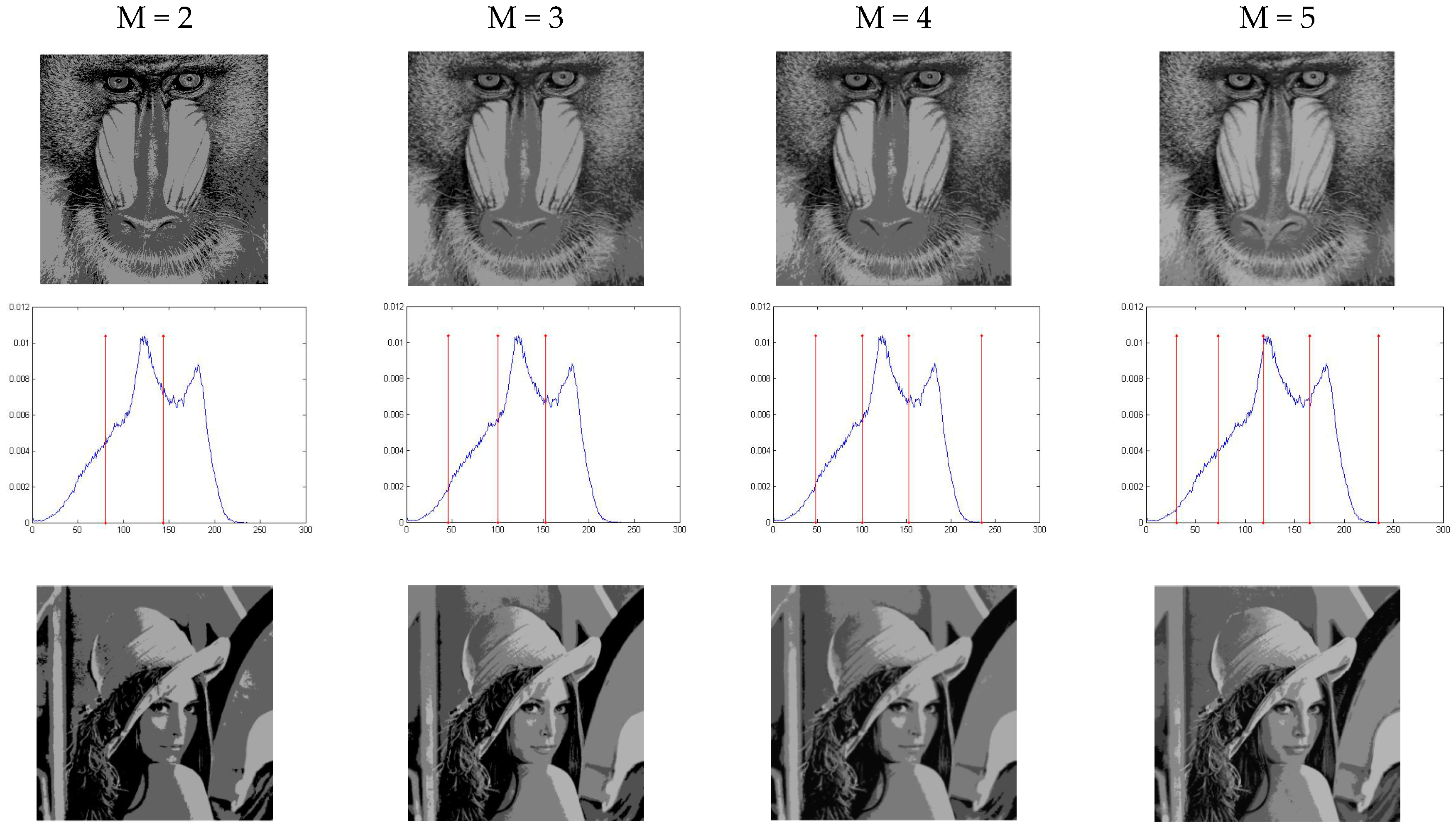
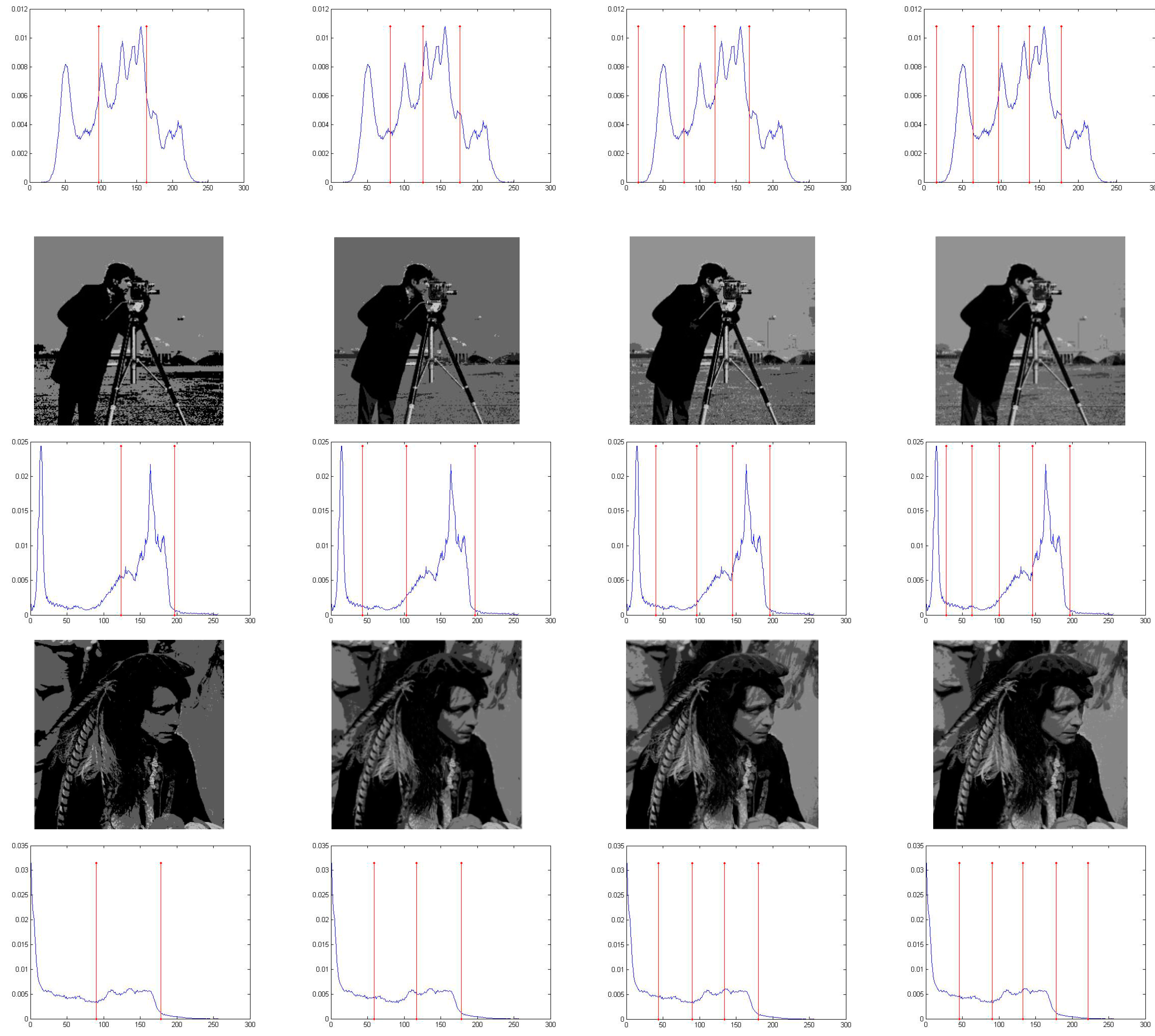
5.1. The Modified Quick Artificial Bee Colony Image Segmentation Results with Different Thresholds
5.2. Comparison of Best Objective Function Values and Their Corresponding Thresholds between EMO, ABC, MDFWO and MQABC
5.3. The Multilevel Image Segmentation Quality Assessment by PSNR and FSIM
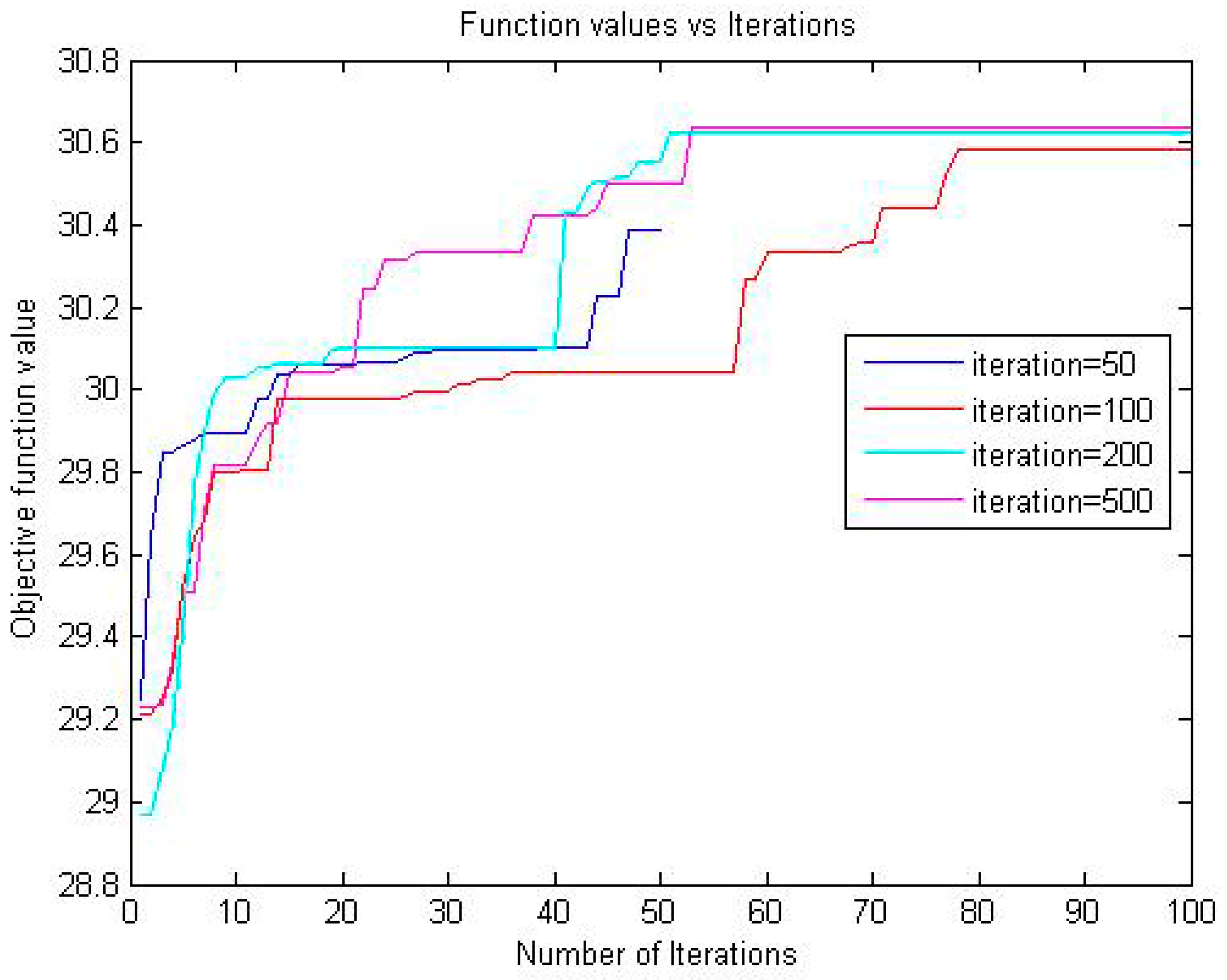
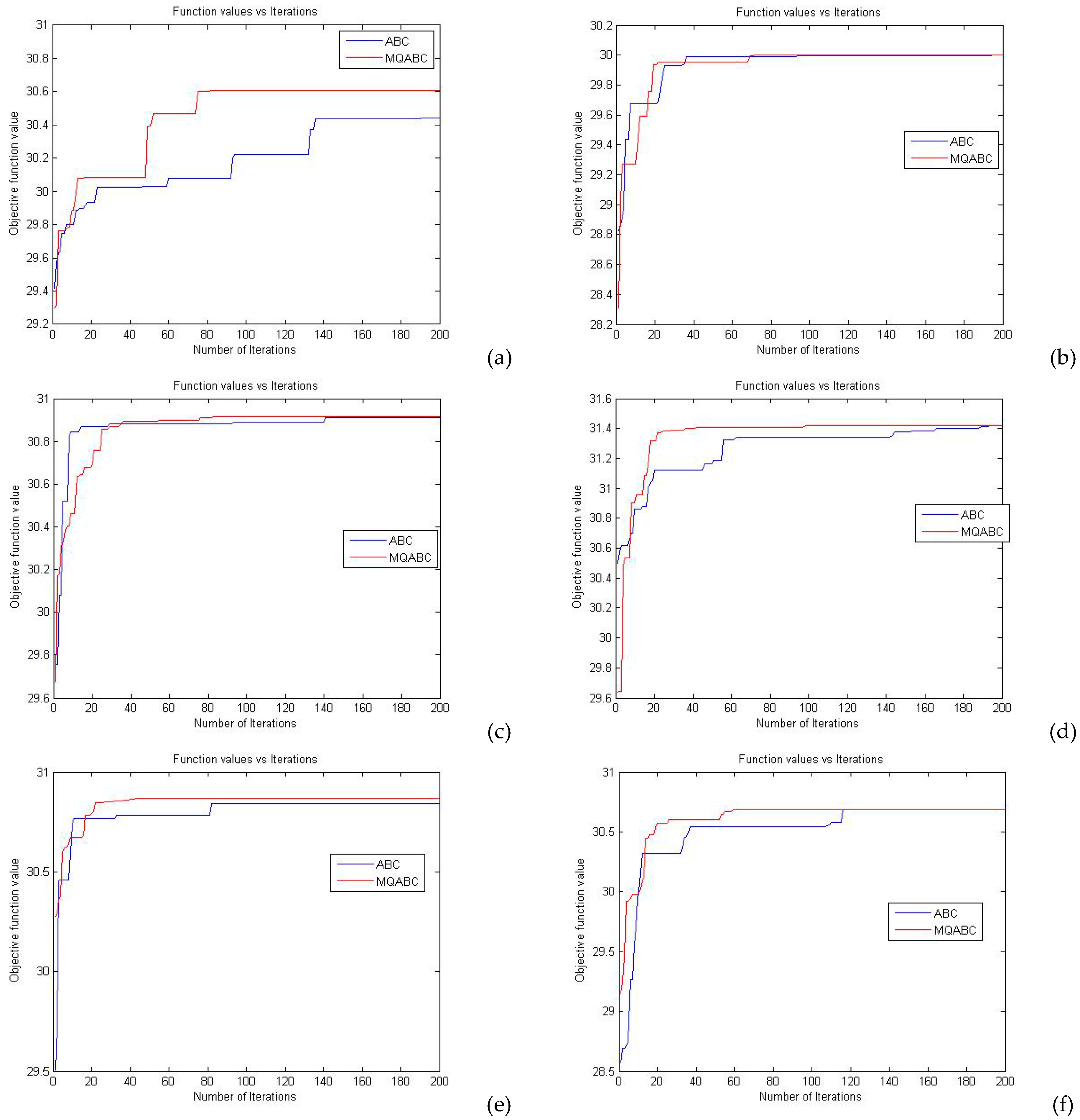
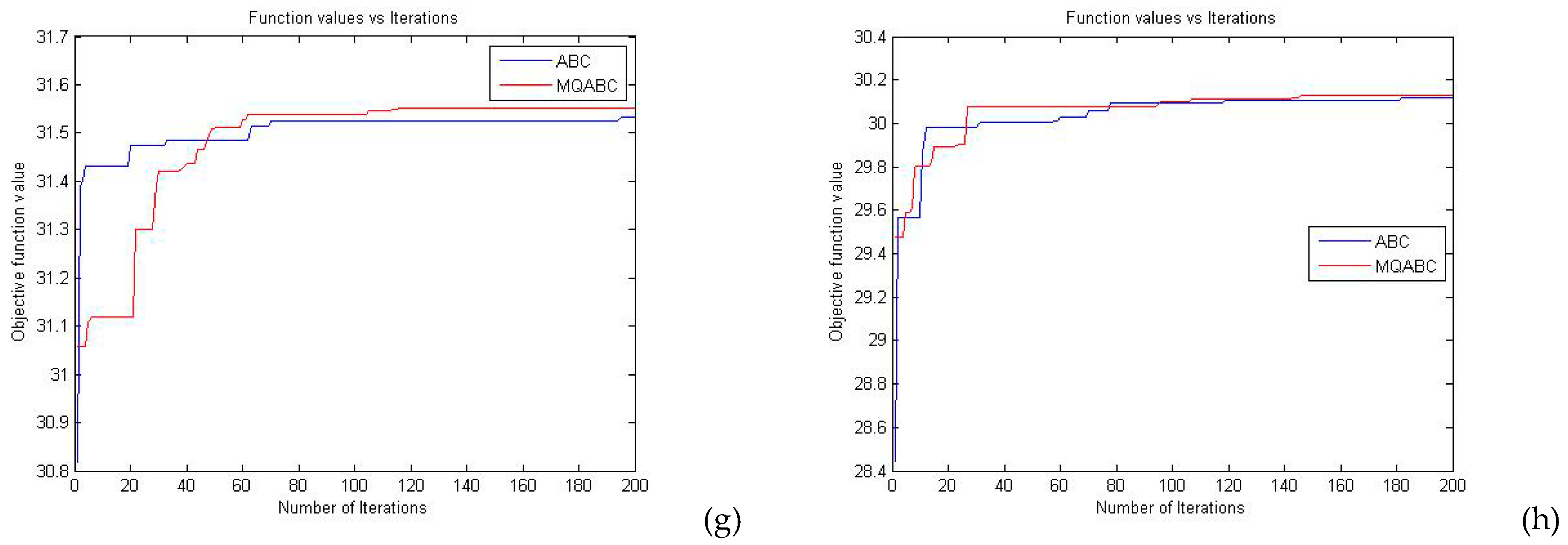
5.4. Comparison of the Characteristics of Running Time and Convergence
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Khan, M.W. A Survey: Image segmentation techniques. Int. J. Future Comput. Commun. 2014, 3, 89–93. [Google Scholar] [CrossRef]
- Masood, S.; Sharif, M.; Masood, A. A Survey on medical image segmentation. Curr. Med. Imaging Rev. 2015, 11, 3–14. [Google Scholar] [CrossRef]
- Ghamisi, P.; Couceiro, M.S.; Martins, F.M.L. Multilevel image segmentation based on fractional-order Darwinian particle swarm optimization. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2382–2394. [Google Scholar] [CrossRef]
- Sonka, M.; Hlavac, V.; Boyle, R. Image Processing, Analysis, and Machine Vision; Cengage Learning: Boston, MA, USA, 2014; pp. 179–321. [Google Scholar]
- Oliva, D.; Cuevas, E.; Pajares, G.; Zaldivar, D.; Osuna, V. A Multilevel Thresholding algorithm using electromagnetism optimization. Neurocomputing 2014, 139, 357–381. [Google Scholar] [CrossRef]
- Nakib, A.; Oulhadj, H.; Siarry, P. Non-supervised image segmentation based on multiobjective optimization. Pattern Recognit. Lett. 2008, 29, 161–172. [Google Scholar] [CrossRef]
- Hammouche, K.; Diaf, M.; Siarry, P. A comparative study of various meta-heuristic techniques applied to the multilevel thresholding problem. Eng. Appl. Artif. Intell. 2010, 23, 676–688. [Google Scholar] [CrossRef]
- Akay, B. A study on particle swarm optimization and artificial bee colony algorithms for multilevel thresholding. Appl. Soft Comput. 2013, 13, 3066–3091. [Google Scholar] [CrossRef]
- Cuevas, E.; Sossa, H. A comparison of nature inspired algorithms for multi-threshold image segmentation. Expert Syst. Appl. 2013, 40, 1213–1219. [Google Scholar]
- Kurban, T.; Civicioglu, P.; Kurban, R. Comparison of evolutionary and swarm based computational techniques for multilevel color image thresholding. Appl. Soft Comput. 2014, 23, 128–143. [Google Scholar] [CrossRef]
- Sarkar, S.; Das, S.; Chaudhuri, S.S. A multilevel color image thresholding scheme based on minimum cross entropy and differential evolution. Pattern Recognit. Lett. 2015, 54, 27–35. [Google Scholar] [CrossRef]
- Kapur, J.N.; Sahoo, P.K.; Wong, A.K.C. A new method for gray-level picture thresholding using the entropy of the histogram. Comput. Vis. Gr. Imag. Process. 1985, 29, 273–285. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. Automatica 1975, 11, 23–27. [Google Scholar] [CrossRef]
- Li, X.; Zhao, Z.; Cheng, H.D. Fuzzy entropy threshold approach to breast cancer detection. Inf. Sci. Appl. 1995, 4, 49–56. [Google Scholar] [CrossRef]
- Kittler, J.; Illingworth, J. Minimum error thresholding. Pattern Recognit. 1986, 19, 41–47. [Google Scholar] [CrossRef]
- Sathya, P.D.; Kayalvizhi, R. Optimal multilevel thresholding using bacterial foraging algorithm. Expert Syst. Appl. 2011, 38, 15549–15564. [Google Scholar] [CrossRef]
- Oliva, D.; Cuevas, E.; Pajares, G. Multilevel thresholding segmentation based on harmony search optimization. J. Appl. Math. 2013, 2013. [Google Scholar] [CrossRef]
- Ghamisi, P.; Couceiro, M.S.; Enediktsson, J.A. An efficient method for segmentation of images based on fractional calculus and natural selection. Expert Syst. Appl. 2012, 39, 12407–12417. [Google Scholar] [CrossRef]
- Hussein, W.A.; Sahran, S.; Abdullah, S.N.H.S. A fast scheme for multilevel thresholding based on a modified bees algorithm. Knowl.-Based Syst. 2016, 101, 114–134. [Google Scholar] [CrossRef]
- Li, L.; Sun, L.; Kang, W.; Jian, G.; Han, C.; Li, S. Fuzzy Multilevel Image Thresholding Based on Modified Discrete Grey Wolf Optimizer and Local Information Aggregation. IEEE Access 2016, 4, 6438–6450. [Google Scholar] [CrossRef]
- Horng, M.H. Multilevel thresholding selection based on the artificial bee colony algorithm for image segmentation. Expert Syst. Appl. 2011, 38, 13785–13791. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, L. Optimal multi-level thresholding based on maximum Tsallis entropy via an artificial bee colony approach. Entropy 2011, 13, 841–859. [Google Scholar] [CrossRef]
- Cuevas, E.; Sención, F.; Zaldivar, D. A multi-threshold segmentation approach based on Artificial Bee Colony optimization. Appl. Intell. 2012, 37, 321–336. [Google Scholar] [CrossRef]
- Ye, Z.W.; Wang, M.W.; Liu, W. Fuzzy entropy based optimal thresholding using bat algorithm. Appl. Soft Comput. 2015, 31, 381–395. [Google Scholar] [CrossRef]
- Bhandari, A.K.; Kumar, A.; Singh, G.K. Modified artificial bee colony based computationally efficient multilevel thresholding for satellite image segmentation using Kapur’s, Otsu and Tsallis functions. Expert Syst. Appl. 2015, 42, 1573–1601. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization. Available online: https://pdfs.semanticscholar.org/cf20/e34a1402a115523910d2a4243929f6704db1.pdf (accessed on 24 January 2016).
- Karaboga, D.; Bahriye, B. On the performance of artificial bee colony (ABC) algorithm. Appl. soft Comput. 2008, 8, 687–697. [Google Scholar] [CrossRef]
- Akay, B.; Dervis, K. A modified artificial bee colony algorithm for real-parameter optimization. Inf. Sci. 2012, 192, 120–142. [Google Scholar] [CrossRef]
- Karaboga, D.; Bahriye, A. A survey: Algorithms simulating bee swarm intelligence. Artif. Intell. Rev. 2009, 31, 61–85. [Google Scholar] [CrossRef]
- Singh, A. An artificial bee colony algorithm for the leaf-constrained minimum spanning tree problem. Appl. Soft Comput. 2009, 9, 625–631. [Google Scholar] [CrossRef]
- Sonmez, M. Artificial bee colony algorithm for optimization of truss structures. Appl. Soft Comput. 2011, 11, 2406–2418. [Google Scholar] [CrossRef]
- Hsieh, T.J.; Hsiao, H.F.; Yeh, W.C. Forecasting stock markets using wavelet transforms and recurrent neural networks: An integrated system based on artificial bee colony algorithm. Appl. Soft Comput. 2011, 11, 2510–2525. [Google Scholar] [CrossRef]
- Dervis, K.; Akay, B. A modified artificial bee colony (ABC) algorithm for constrained optimization problems. Appl. Soft Comput. 2011, 11, 3021–3031. [Google Scholar]
- Karaboga, D.; Beyza, G. A quick artificial bee colony-qABC-algorithm for optimization problems. In Proceedings of the 2012 International Symposium on Innovations in Intelligent Systems and Applications (INISTA), Trabzon, Turkey, 2–4 July 2012; IEEE: Trabzon, Turkey, 2012; pp. 1–5. [Google Scholar]
- Arbelaez, P.; Maire, M.; Fowlkes, C. Contour detection and hierarchical image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 898–916. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhang, L.; Mou, X. FSIM: A feature similarity index for image quality assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef] [PubMed]
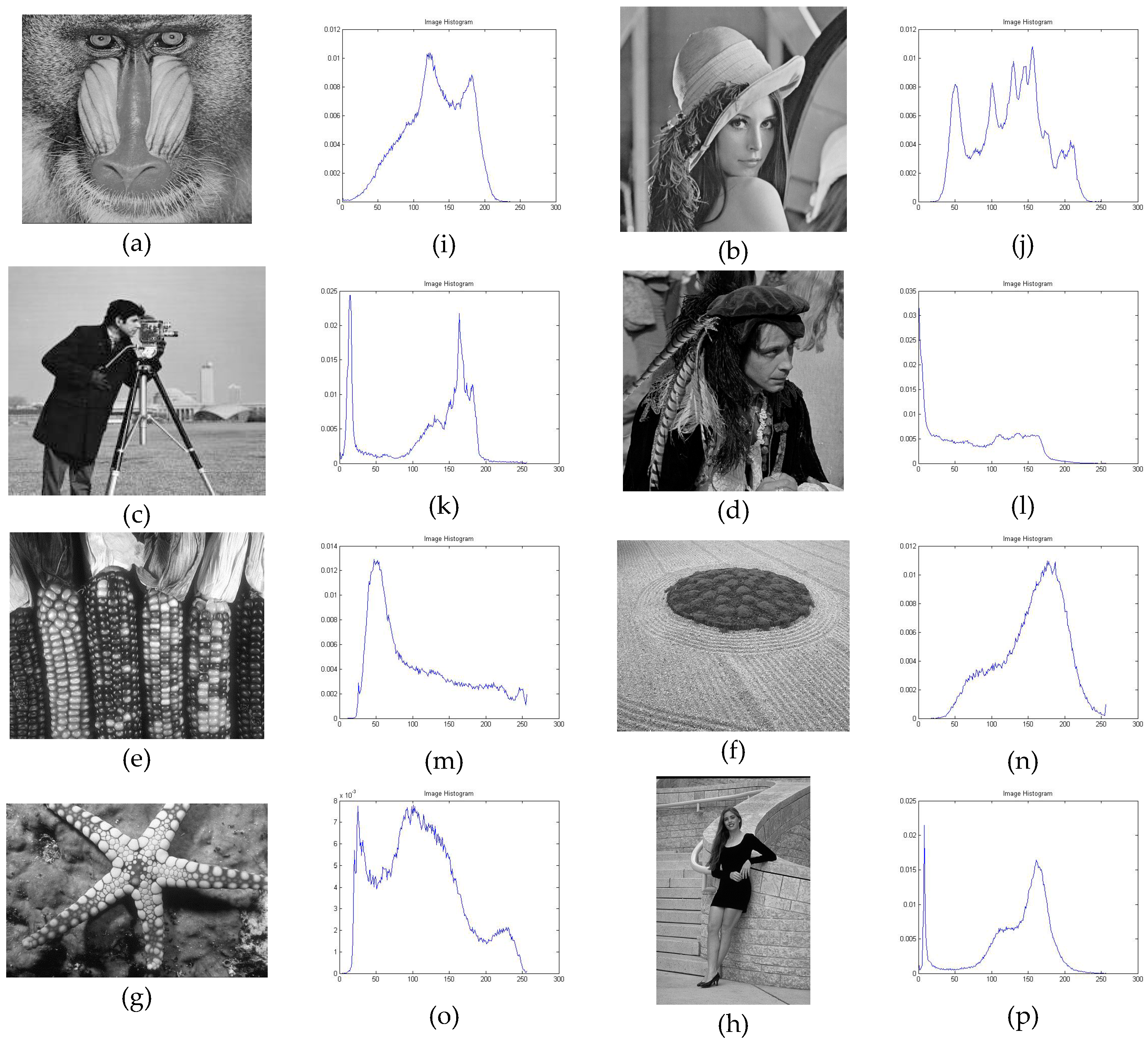
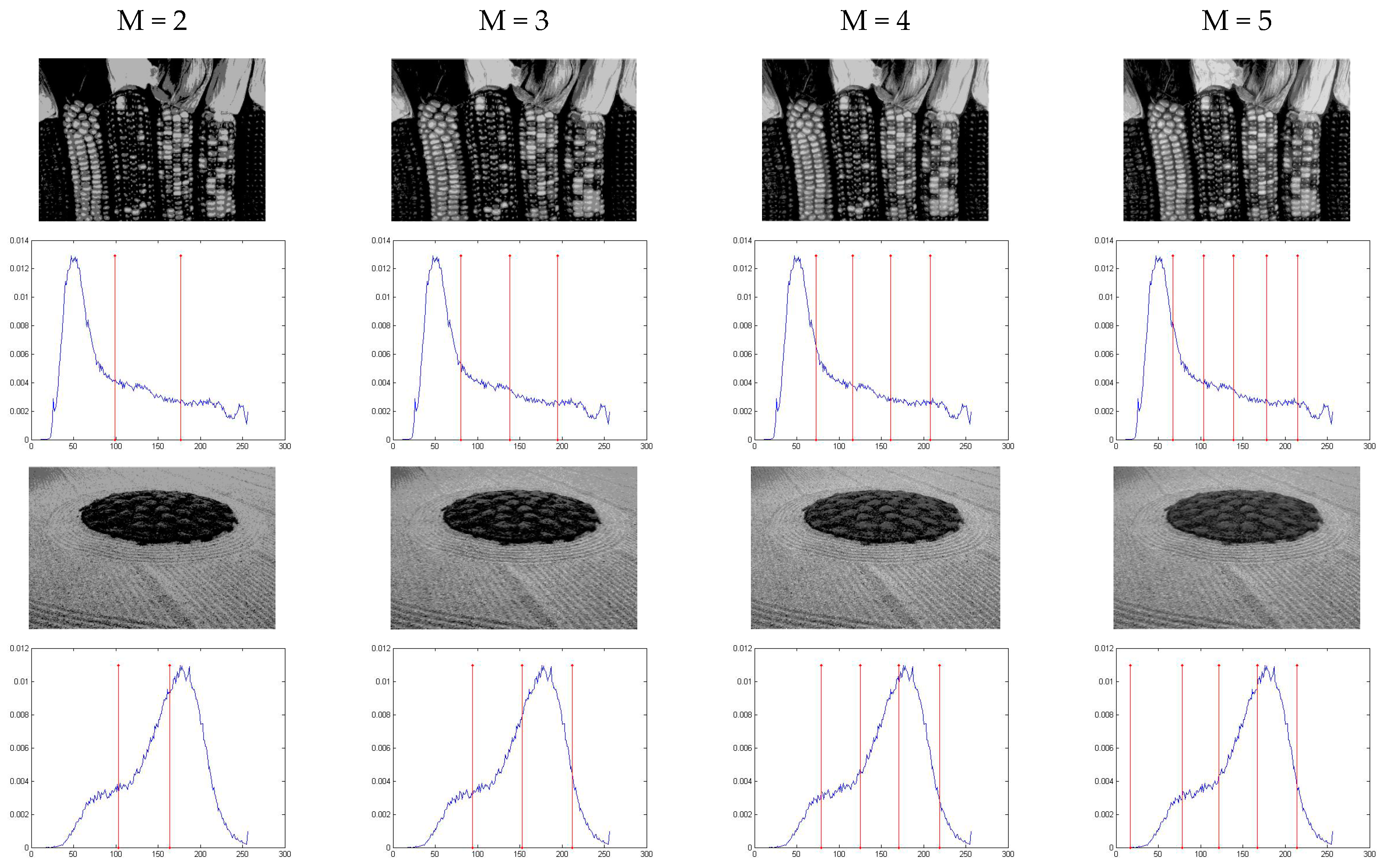

| Parameters | Population Size | No. of Iterations | Lower Bound | Upper Bound | Trial Limit |
|---|---|---|---|---|---|
| Value | 30 | 200 | 1 | 256 | 10 |
| Population Size | 10 | 20 | 30 | 40 | 50 |
|---|---|---|---|---|---|
| PSNR | 20.3650 | 20.4675 | 20.7193 | 20.4243 | 20.4071 |
| FSIM | 0.9259 | 0.9192 | 0.9318 | 0.9206 | 0.9207 |
| Image | M | Optimum Threshold Values | |||
|---|---|---|---|---|---|
| EMO | ABC | MDGWO | MQABC | ||
| Baboon | 2 3 4 5 | 78 143 46 100 153 46 100 153 235 34 75 115 160 235 | 80 144 46 101 153 45 100 153 236 34 75 116 161 236 | 80 144 46 100 153 34 89 147 235 27 65 107 154 235 | 80 144 46 100 153 48 100 153 235 31 73 118 165 235 |
| Lena | 2 3 4 5 | 97 164 81 126 177 16 82 127 177 16 64 97 137 179 | 97 164 83 127 178 16 87 123 174 16 65 96 133 178 | 97 164 81 126 177 16 82 127 177 16 64 97 138 179 | 97 164 81 126 176 16 83 126 174 16 64 97 137 178 |
| Camera man | 2 3 4 5 | 124 197 43 103 197 40 96 145 197 40 96 145 191 221 | 124 197 43 103 197 41 96 1 45 197 28 63 98 145 197 | 124 197 43 103 197 36 95 145 197 25 61 100 145 197 | 124 197 43 103 197 40 95 144 197 28 65 102 147 197 |
| Corn | 2 3 4 5 | 99 177 82 140 198 73 118 164 211 69 107 144 181 219 | 99 177 82 140 199 73 115 158 207 68 106 145 179 216 | 99 177 82 140 198 73 118 164 211 67 105 142 180 218 | 99 177 80 138 195 73 116 161 208 67 104 139 178 215 |
| Hunter | 2 3 4 5 | 90 178 58 117 178 44 89 133 180 44 89 132 176 213 | 90 178 60 118 178 43 87 132 180 51 95 135 179 220 | 90 178 60 118 178 45 90 133 180 41 86 131 178 222 | 90 178 59 117 178 44 90 134 180 46 91 133 178 222 |
| Soil | 2 3 4 5 | 104 166 95 151 213 78 124 169 218 17 82 128 172 218 | 104 166 94 152 212 84 129 172 218 17 64 113 159 216 | 104 166 95 151 213 82 128 171 218 64 103 141 180 220 | 103 164 94 153 212 79 125 171 219 17 78 122 167 214 |
| Starfish | 2 3 4 5 | 90 170 74 131 185 68 117 166 208 57 96 135 173 211 | 90 170 73 127 182 63 111 161 207 55 94 132 170 210 | 90 170 74 131 185 67 114 161 205 54 92 131 170 209 | 90 170 72 127 182 69 119 167 206 53 90 130 170 210 |
| Lady | 2 3 4 5 | 108 197 95 144 207 36 84 140 203 36 84 134 179 211 | 109 197 94 143 207 35 84 140 203 35 85 136 181 211 | 108 197 95 144 206 34 84 140 203 32 82 132 179 211 | 108 197 94 145 206 36 84 139 203 34 83 136 180 211 |
| Image | M | Best Objective Function Values | |||
|---|---|---|---|---|---|
| EMO | ABC | MDGWO | MQABC | ||
| Baboon | 2 3 4 5 | 17.6799 22.1331 26.5254 30.6432 | 17.6802 22.1331 26.5249 30.4394 | 17.6802 22.1331 26.4671 30.5622 | 17.6802 22.1331 26.5248 30.6111 |
| Lena | 2 3 4 5 | 17.8234 22.1102 26.1107 30.0052 | 17.8234 22.1091 26.1064 29.9870 | 17.8234 22.1102 26.1107 30.0045 | 17.8234 22.1101 26.1062 30.0029 |
| Cameraman | 2 3 4 5 | 17.7870 22.3541 26.9258 30.8656 | 17.7870 22.3541 26.9231 30.9041 | 17.7870 22.3541 26.9150 30.9071 | 17.7870 22.3541 26.9232 30.9098 |
| Corn | 2 3 4 5 | 18.6341 23.2676 27.5028 31.4310 | 18.6341 23.2668 27.4910 31.4183 | 18.6341 23.2676 27.5028 31.4305 | 18.6341 23.2661 27.4976 31.4205 |
| Hunter | 2 3 4 5 | 17.9294 22.6077 26.8221 30.8369 | 17.9294 22.6076 26.8094 30.8709 | 17.9294 22.6076 26.8216 30.8744 | 17.9294 22.6076 26.8213 30.8784 |
| Soil | 2 3 4 5 | 17.7911 22.4002 26.6100 30.7030 | 17.7911 22.3949 26.6079 30.6860 | 17.7911 22.4002 26.6152 30.5266 | 17.7902 22.3922 26.6067 30.6872 |
| Starfish | 2 3 4 5 | 18.7518 23.3205 27.5691 31.5536 | 18.7518 23.3192 27.5609 31.5338 | 18.7518 23.3205 27.5696 31.5537 | 18.7518 23.3192 27.5675 31.5519 |
| Lady | 2 3 4 5 | 17.3196 21.8911 26.0155 30.1406 | 17.3195 21.8901 26.0140 30.1187 | 17.3196 21.8908 26.0137 30.1276 | 17.3196 21.8882 26.0147 30.1282 |
| Image | M | PSNR | |||
|---|---|---|---|---|---|
| EMO | ABC | MDGWO | MQABC | ||
| Baboon | 2 3 4 5 | 15.9947 18.5921 18.5921 20.5234 | 16.0070 18.5921 18.5435 20.5058 | 16.0070 18.5921 17.7340 19.9261 | 16.0070 18.5921 18.6718 20.7193 |
| Lena | 2 3 4 5 | 14.5901 17.2122 18.5488 20.3250 | 14.5901 17.1178 18.3798 20.2440 | 14.5901 17.2122 18.5488 20.3152 | 14.5901 17.2328 18.6011 20.3360 |
| Cameraman | 2 3 4 5 | 13.9202 14.4620 20.1078 20.2439 | 13.9202 14.4620 20.1172 20.6463 | 13.9202 14.4620 20.0183 20.7726 | 13.9202 14.4620 20.1187 21.0713 |
| Corn | 2 3 4 5 | 13.5901 15.1819 16.3460 17.1081 | 13.5901 15.1772 16.3688 17.2131 | 13.5901 15.1819 16.3460 17.3272 | 13.5901 15.2913 16.7947 17.3402 |
| Hunter | 2 3 4 5 | 15.1897 18.5073 21.0490 21.1563 | 15.1897 18.5091 21.0204 21.0040 | 15.1897 18.5091 21.0584 21.0582 | 15.1897 18.5116 21.0668 21.1618 |
| Soil | 2 3 4 5 | 15.0106 15.9665 18.5457 19.2186 | 15.0106 16.0513 18.2730 18.9467 | 15.0106 15.9665 18.3966 18.6843 | 15.0813 16.0565 18.6280 19.3609 |
| Starfish | 2 3 4 5 | 14.3952 16.9727 18.1811 20.0649 | 14.3952 17.1199 18.4836 20.2304 | 14.3952 16.9727 18.3818 20.2925 | 14.3952 17.1430 18.5054 20.3400 |
| Lady | 2 3 4 5 | 13.5137 18.0864 18.8255 19.7622 | 13.5108 18.1279 18.8180 19.7680 | 13.5137 18.1007 18.8099 19.4766 | 13.5137 18.1559 18.9093 19.8081 |
| Image | M | FSIM | |||
|---|---|---|---|---|---|
| EMO | ABC | MDGWO | MQABC | ||
| Baboon | 2
3 4 5 | 0.8586
0.9004 0.9004 0.9218 | 0.8601
0.9004 0.8997 0.9218 | 0.8601
0.9004 0.8863 0.9131 | 0.8601
0.9004 0.9012 0.9318 |
| Lena | 2
3 4 5 | 0.7262
0.7911 0.8018 0.8457 | 0.7262
0.7886 0.7952 0.8415 | 0.7262
0.7911 0.8018 0.8455 | 0.7262
0.7919 0.8036 0.8455 |
| Cameraman | 2
3 4 5 | 0.6776
0.7893 0.8433 0.8470 | 0.6776
0.7893 0.8431 0.8636 | 0.6776
0.7893 0.8426 0.8689 | 0.6776
0.7893 0.8439 0.8743 |
| Corn | 2
3 4 5 | 0.6902
0.7661 0.8092 0.8364 | 0.6902
0.7653 0.8096 0.8363 | 0.6902
0.7661 0.8092 0.8370 | 0.6902
0.7676 0.8107 0.8373 |
| Hunter | 2
3 4 5 | 0.7117
0.8175 0.8815 0.8851 | 0.7117
0.8156 0.8828 0.8741 | 0.7117
0.8156 0.8801 0.8871 | 0.7117
0.8168 0.8804 0.8880 |
| Soil | 2
3 4 5 | 0.7805
0.8182 0.8761 0.8977 | 0.7805
0.8216 0.8649 0.9074 | 0.7805
0.8182 0.8694 0.9014 | 0.7779
0.8229 0.8789 0.9100 |
| Starfish | 2
3 4 5 | 0.6058
0.6870 0.7336 0.7913 | 0.6058
0.6924 0.7417 0.7956 | 0.6058
0.6870 0.7417 0.7951 | 0.6058
0.6922 0.7450 0.7957 |
| Lady | 2
3 4 5 | 0.5895
0.7205 0.7645 0.8261 | 0.5900
0.7222 0.7646 0.8230 | 0.5895
0.7223 0.7645 0.8220 | 0.5895
0.7254 0.7667 0.8277 |
| Image | M | Running Time (S) | |||
|---|---|---|---|---|---|
| EMO | ABC | MDGWO | MQABC | ||
| Baboon | 4 5 | 2.887928 8.747538 | 1.369329 1.870215 | 1.616275 1.676552 | 1.269490 1.559394 |
| Lena | 4 5 | 3.923755 5.297557 | 1.537726 1.997193 | 1.571869 1.703536 | 1.180458 1.471279 |
| Cameraman | 4 5 | 4.171417 6.263097 | 1.375140 1.699723 | 1.637016 1.751039 | 1.246388 1.494485 |
| Corn | 4 5 | 4.221177 9.523326 | 2.481717 2.989686 | 2.707189 2.958905 | 2.402332 2.702894 |
| Hunter | 4 5 | 3.187744 6.207372 | 1.572262 2.044084 | 1.600798 1.654322 | 1.479363 1.596739 |
| Soil | 4 5 | 4.546173 8.693048 | 2.359536 2.822248 | 2.748231 2.853070 | 2.122324 2.481809 |
| Starfish | 4 5 | 4.651453 5.812047 | 2.537318 2.972738 | 2.790188 2.954895 | 2.308098 2.647345 |
| Lady | 4 5 | 4.621457 9.362831 | 2.524725 3.055700 | 2.736448 2.947035 | 2.437168 2.837646 |
| Image | M | Iterations to Convergence | |||
|---|---|---|---|---|---|
| EMO | ABC | MDGWO | MQABC | ||
| Baboon | 4 5 | 15 53 | 55 140 | 145 141 | 46 81 |
| Lena | 4 5 | 29 42 | 127 194 | 149 148 | 20 78 |
| Cameraman | 4 5 | 19 49 | 82 140 | 149 149 | 49 82 |
| Corn | 4 5 | 33 60 | 80 193 | 148 150 | 54 100 |
| Hunter | 4 5 | 17 26 | 97 183 | 145 147 | 64 89 |
| Soil | 4 5 | 23 50 | 113 115 | 58 147 | 17 61 |
| Starfish | 4 5 | 30 35 | 131 194 | 149 150 | 59 117 |
| Lady | 4 5 | 29 61 | 100 188 | 147 150 | 33 145 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Sun, L.; Guo, J.; Han, C.; Zhou, J.; Li, S. A Quick Artificial Bee Colony Algorithm for Image Thresholding. Information 2017, 8, 16. https://doi.org/10.3390/info8010016
Li L, Sun L, Guo J, Han C, Zhou J, Li S. A Quick Artificial Bee Colony Algorithm for Image Thresholding. Information. 2017; 8(1):16. https://doi.org/10.3390/info8010016
Chicago/Turabian StyleLi, Linguo, Lijuan Sun, Jian Guo, Chong Han, Jian Zhou, and Shujing Li. 2017. "A Quick Artificial Bee Colony Algorithm for Image Thresholding" Information 8, no. 1: 16. https://doi.org/10.3390/info8010016
APA StyleLi, L., Sun, L., Guo, J., Han, C., Zhou, J., & Li, S. (2017). A Quick Artificial Bee Colony Algorithm for Image Thresholding. Information, 8(1), 16. https://doi.org/10.3390/info8010016





