1. Introduction
Speech coding is a critical technology for digital cellular communications, voice over Internet protocol (VoIP), voice response applications, and videoconferencing systems. In this paper, we present an abridged history of speech compression, a development of the dominant speech compression techniques, and a discussion of selected speech coding standards and their performance. We also discuss the future evolution of speech compression and speech compression research. We specifically develop the connection between rate distortion theory and speech compression, including rate distortion bounds for speech codecs. We use the terms speech compression, speech coding, and voice coding interchangeably in this paper. The voice signal contains not only what is said but also the vocal and aural characteristics of the speaker. As a consequence, it is usually desired to reproduce the voice signal, since we are interested in not only knowing what was said, but also in being able to identify the speaker. All of today’s speech coders have this as a goal [
1,
2,
3].
Compression methods can be classified as either lossless or lossy. Lossless compression methods start with a digital representation of the source and use encoding techniques that allow the source to be represented with fewer bits while allowing the original source digital representation to be reconstructed exactly by the decoder. Lossy compression methods relax the constraint of an exact reproduction and allow some distortion in the reconstructed source [
4,
5].
Thus, given a particular source such as voice, audio, or video, the classic tradeoff in lossy source compression is rate versus distortion—the higher the rate, the smaller the average distortion in the reproduced signal. Of course, since a higher bit rate implies a greater channel or network bandwidth or a larger storage requirement, the goal is always to minimize the rate required to satisfy the distortion constraint or to minimize the distortion for a given rate constraint. For speech coding, we are interested in achieving a quality as close to the original speech as possible within the rate, complexity, latency, and any other constraints that might be imposed by the application of interest. Encompassed in the term quality are intelligibility, speaker identification, and naturalness. Note that the basic speech coding problem follows the distortion rate paradigm; that is, given a rate constraint set by the application, the codec is designed to minimize distortion. The resulting distortion is not necessarily small or inaudible, just acceptable for the given application.
The distortion rate structure is contrasted with the rate distortion formulation wherein the constraint is on allowable distortion and the rate required to achieve that distortion is minimized. Notice that for the rate distortion approach, a specified distortion is the goal and the rate is adjusted to obtain this level of distortion. Voice coding for digital cellular communications is an example of the distortion rate approach, since it has a rate constraint, while coding of high quality audio typically has the goal of transparent quality, and hence is an example of the rate distortion paradigm.
The number of bits/s required to represent a source is equal to the number of bits/sample multiplied by the number of samples/s. The first component, bits/sample, is a function of the coding method, while the second component, samples/s, is related to the source bandwidth. Therefore, it is common to distinguish between speech and audio coding according to the bandwidth occupied by the input source.
Narrowband or telephone bandwidth speech occupies the band from 200 to 3400 Hz, and is the band classically associated with telephone quality speech. The category of
wideband speech covers the band 50 Hz to 7 kHz, which is a bandwidth that originally appeared in applications in 1988 but has come into prominence in the last decade. Audio is generally taken to cover the range of 20 Hz to 20 kHz, and this bandwidth is sometimes referred to today as
fullband audio. More recently, a few other bandwidths have attracted attention, primarily for audio over the Internet applications, and the bandwidth of 50 Hz to 14 kHz, designated as
superwideband, has gotten considerable recent attention [
6]. The interest in wider bandwidths comes from the facts that wider bandwidths improve intelligibility, naturalness, and speaker identifiability. Furthermore, the extension of the bandwidth below 200 Hz adds to listener comfort, warmth, and naturalness. The focus in this paper is on narrowband and wideband speech coding; however, codecs for these bands often serve as building blocks for wider bandwidth speech and audio codecs. Audio coding is only discussed here as it relates to the most prevalent approaches to narrowband and wideband speech coding.
As the frequency bands being considered move upward from narrowband speech through wideband speech and superwideband speech/audio, on up to fullband audio, the basic structures for digital signal processing and the desired reproduced quality change substantially. Interestingly, all of these bands are incorporated in the latest speech coders, and the newest speech coding standard, EVS, discussed later, utilizes a full complement of signal processing techniques to produce a relatively seamless design.
The goal of speech coding is to represent speech in digital form with as few bits as possible while maintaining the intelligibility and quality required for the particular application [
1,
4,
5]. This one sentence captures the fundamental idea that rate and distortion (reconstructed speech quality) are inextricably intertwined. The rate can always be lowered if quality is ignored, and quality can always be improved if rate is not an issue. Therefore, when we mention the several bit rates of various speech codecs, the reader should remember that as the rate is adjusted, the reconstructed quality changes as well, and that a lower rate implies poorer speech quality.
The basic approaches for coding narrowband speech evolved over the years from waveform following codecs to the code excited linear prediction (CELP) based codecs that are dominant today [
1,
5]. This evolution was driven by applications that required lower bandwidth utilization and by advances in digital signal processing, which became implementable due to improvements in processor speeds that allowed more sophisticated processing to be incorporated. Notably, the reduction in bit rates was obtained by relaxing prior constraints on encoding delay and on complexity. This later relaxation of constraints, particularly on complexity, should be a lesson learned for future speech compression research; namely, the complexity constraints of today will almost certainly be changed in the future.
With regard to complexity, it is interesting to note that most of the complexity in speech encoding and decoding resides at the encoder for most voice codecs; that is, speech encoding is more complex, often dramatically so, than decoding. This fact can have implications when designing products. For example, voice response applications, wherein a set of coded responses are stored and addressed by many users, require only a single encoding of each stored response (the complex step) but those responses may be accessed and decoded many times. For real time voice communications between two users, however, each user must have both an encoder and a decoder, and both the encoder and the decoder must operate without noticeable delay.
As we trade off rate and distortion, the determination of the rate of a speech codec is straightforward, however, the measurement of the distortion is more subtle. There are a variety of approaches to evaluating voice intelligibility and quality. Absolute category rating (ACR) tests are subjective tests of speech quality and involve listeners assigning a category and rating for each speech utterance according to the classifications, such as, Excellent (5), Good (4), Fair (3), Poor (2), and Bad (1). The average for each utterance over all listeners is the Mean Opinion Score (MOS) [
1].
Of course, listening tests involving human subjects are difficult to organize and perform, so the development of objective measures of speech quality is highly desirable. The perceptual evaluation of speech quality (PESQ) method, standardized by the ITU-T as P.862, was developed to provide an assessment of speech codec performance in conversational voice communications. The PESQ has been and can be used to generate MOS values for both narrowband and wideband speech [
5,
7]. While no substitute for actual listening tests, the PESQ and its wideband version have been widely used for initial codec evaluations. A newer objective measure, designated as P.863 POLQA (Perceptual Objective Listening Quality Assessment) has been developed but it has yet to receive widespread acceptance [
8]. For a tutorial development of perceptual evaluation of speech quality, see [
9]. More details on MOS and perceptual performance evaluation for voice codecs are provided in the references [
1,
7,
8,
9,
10].
The emphasis in this paper is on linear prediction based speech coding. The reason for this emphasis is that linear prediction has been the dominant structure for narrowband and wideband speech coding since the mid-1990’s [
11] and essentially all important speech coding standards since that time are based on the linear prediction paradigm [
3,
11]. We do not discuss codec modifications to account for channel or network effects, such as bit errors, lost packets, or delayed packets. While these issues are important for overall codec designs, the emphasis here is on compression, and the required modifications are primarily add-ons to compensate for such non-compression issues. Further, these modifications must be matched to the specific compression method being used, so understanding the speech compression techniques is an important first step for their design and implementation.
We begin with the fundamentals of linear prediction.
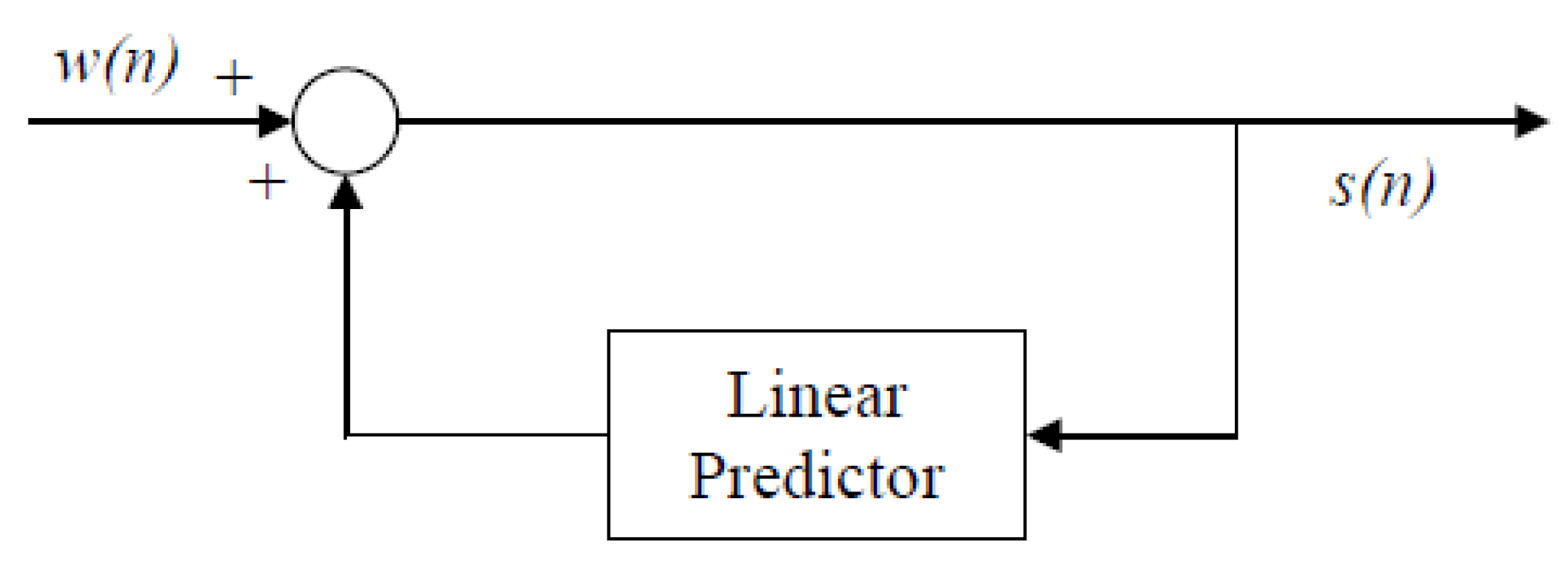
2. The Basic Model: Linear Prediction
The linear prediction model has served as the basis for the leading speech compression methods over the last 45 years. The linear prediction model has the form
where we see that the current speech sample at time instant
n can be represented as a weighted linear combination of
N prior speech samples plus a driving term or excitation at the current time instant. The weights,
, are called the linear prediction coefficients. A block diagram of this model is depicted in
Figure 1.
We can write the z-domain transfer function of the block diagram in
Figure 1 by assuming zero initial conditions to obtain
where
represents the weighted linear combination of past samples as indicated [
4,
5]. This model is also known as an autoregressive (AR) process or AR model in the time series analysis literature. It is helpful to envision the linear prediction model as a speech synthesizer, wherein speech is reconstructed by inserting the linear prediction coefficients and applying the appropriate excitation in order to generate the set of speech samples. This is the basic structure of the decoders in all linear prediction based speech codecs [
12]. However, the encoders carry the burden of calculating the linear prediction coefficients and choosing the excitation to allow the decoder to synthesize acceptable quality speech [
4,
5].
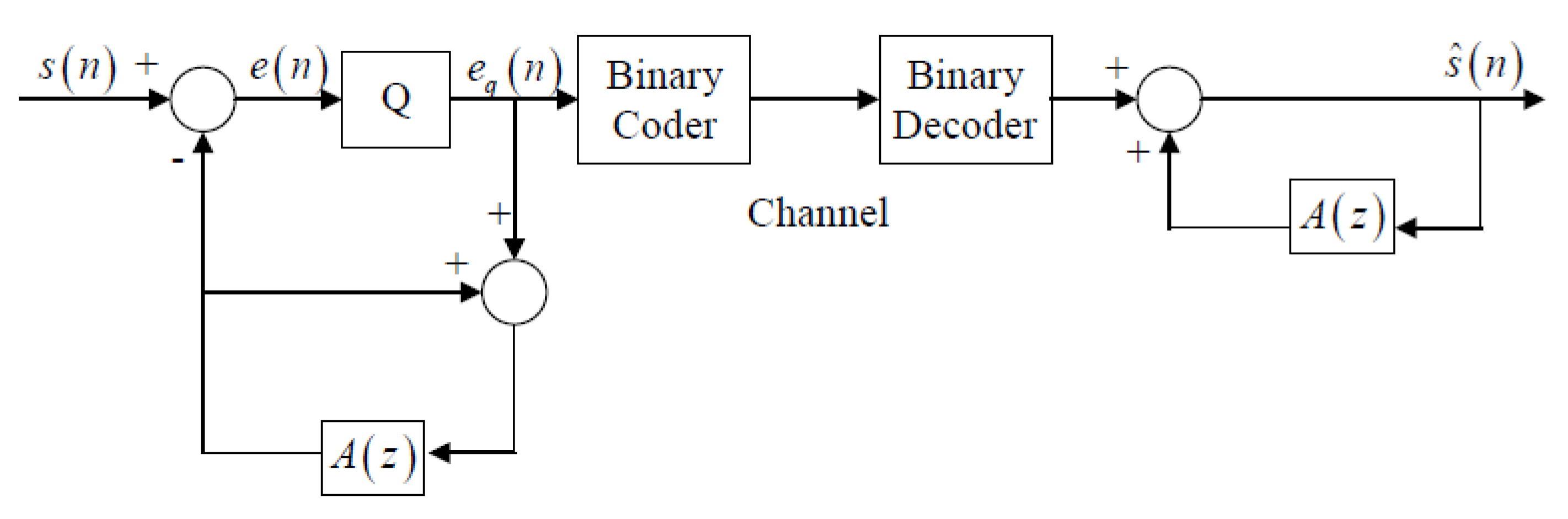
The earliest speech coder to use the linear prediction formulation was differential pulse code modulation (DPCM) shown in
Figure 2. Here we see that the decoder has the form of the linear prediction model and the excitation consists of the quantized and coded prediction error at each sampling instant. This prediction error is decoded and used as the excitation and the linear prediction coefficients are either computed at the encoder and transmitted or calculated at both the encoder and decoder on a sample-by-sample basis using least mean squared (LMS) or recursive least squares (RLS) algorithms that are adapted based on the reconstructed speech samples. The LMS approach served as the basis for the ITU-T international standards G.721, G.726, and G.727, which have transmitted bit rates from 16 kilobits/s up to 40 kilobits/s, with what is called “toll quality” produced at 32 kbits/s. See the references for a further development of DPCM and other time domain waveform following variants as well as the related ITU-T standards [
1,
4,
5].
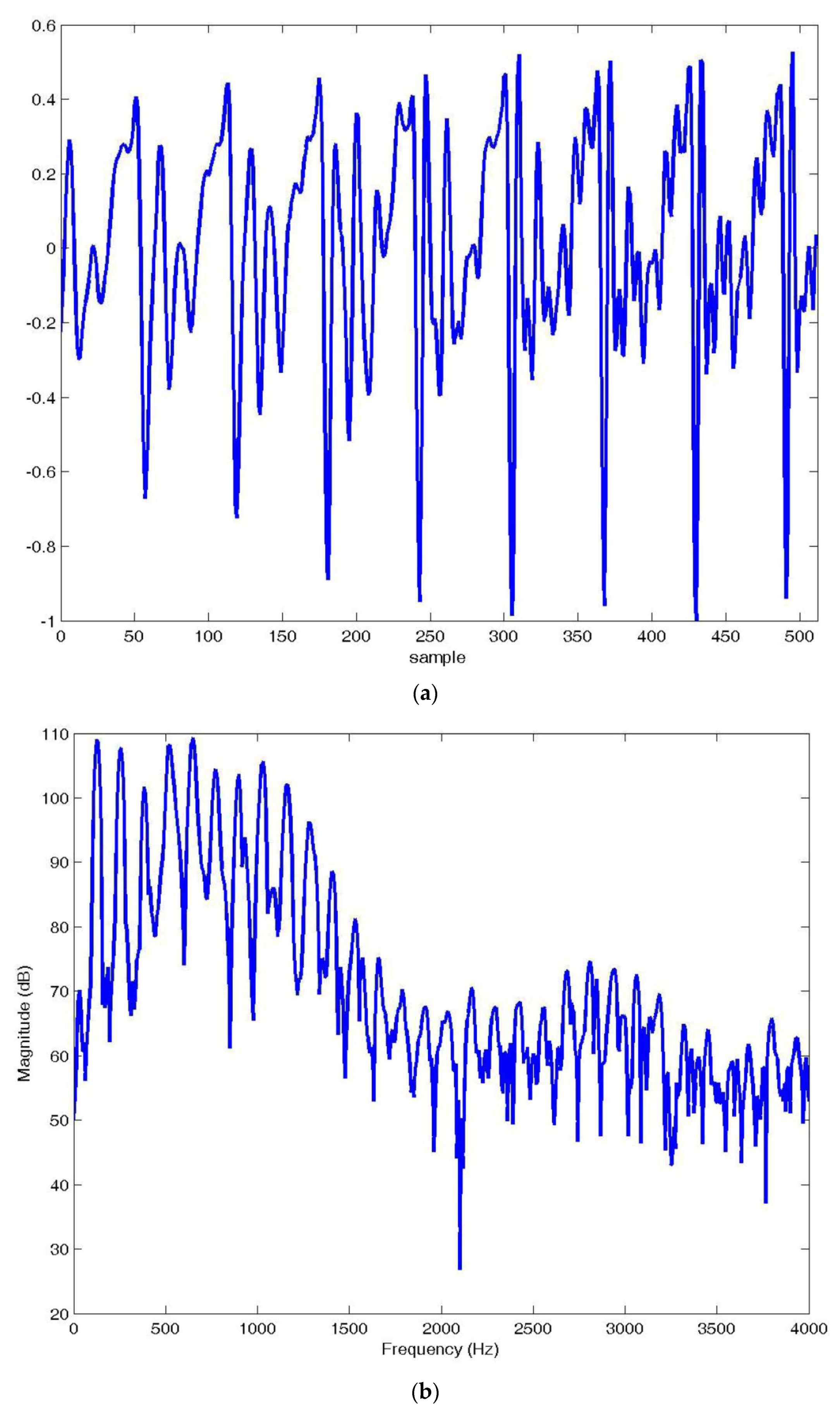
Of course, for many applications these rates were too high, and to lower these rates, while maintaining reconstructed speech quality, required a more explicit use of the linear prediction model. It is instructive to investigate the usefulness of the linear prediction model for speech spectrum approximation. To do this, consider the voiced speech segment shown in
Figure 3a. If we take the Fast Fourier Transform (FFT) of this segment, we obtain the spectrum shown in
Figure 3b.
The very pronounced ripples in the spectrum in
Figure 3b are the harmonics of the pitch period visible in
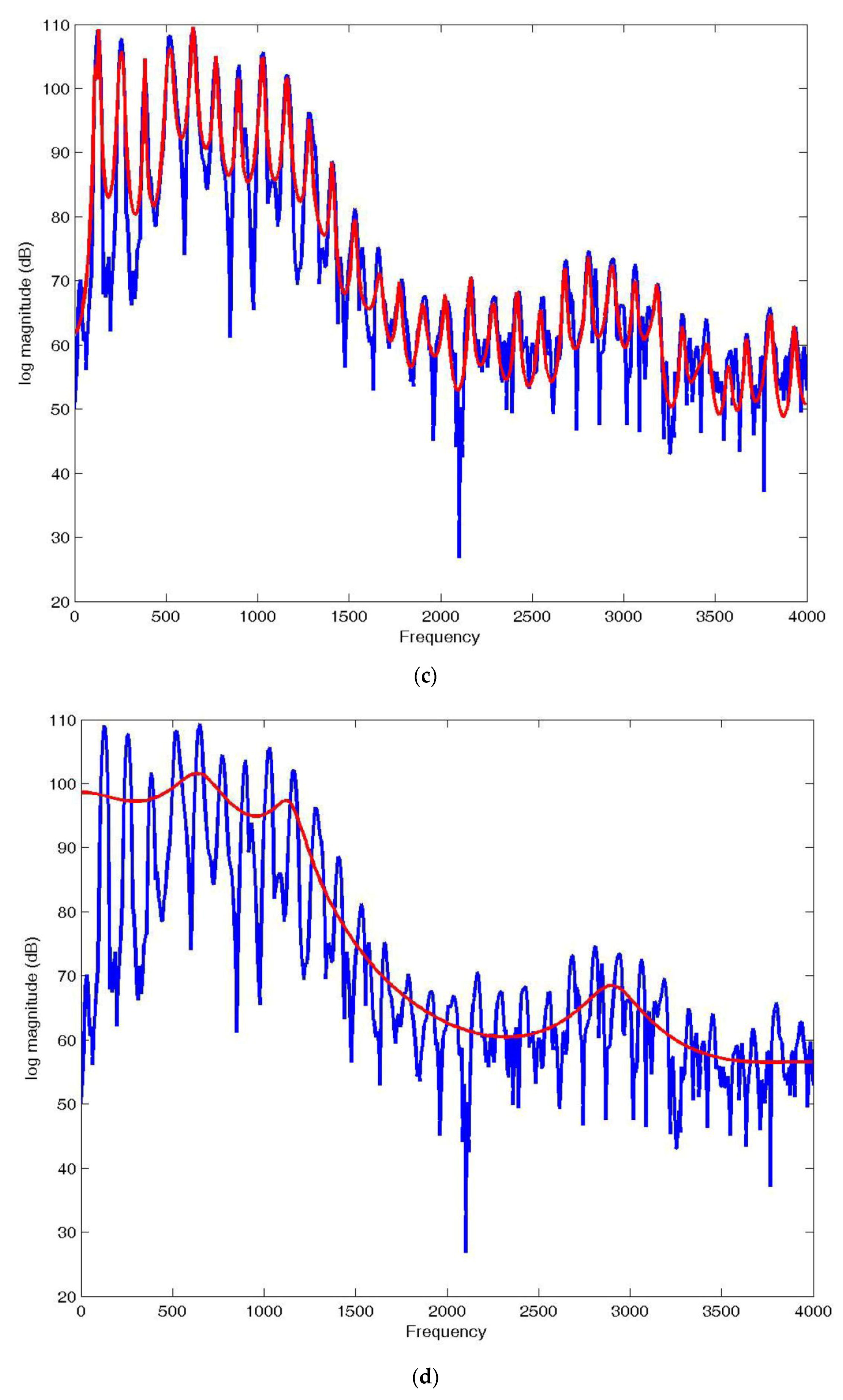
Figure 3a as the periodic spikes in the time domain waveform. As one might guess, these periodicities are due to the periodic excitation of the vocal tract by puffs of air being released by the vocal cords. Can the linear prediction model provide a close approximation of this spectrum? Letting the predictor order
N = 100, the magnitude spectrum can be obtained from the linear prediction model in
Figure 1, and this is shown in red in
Figure 3c. We see that the model is able to provide an excellent approximation to the magnitude spectrum, reproducing all of the pitch harmonics very well. However, for speech coding, this is not a very efficient solution since we would have to quantize and code 100 frequency locations plus their amplitudes to be transmitted to reproduce this spectrum. This is a relatively long speech segment, about 64 ms, so if we needed (say) 8 bits/frequency location plus 8 bits for amplitude for accurate reconstruction, the transmitted bit rate would be about 25,000 bits/s. This rate is about the same or slightly lower than DPCM for approximately the same quality but still more than the 8 kbits/s or 4 kbits/s that is much more desirable in wireline and cellular applications. Further, speech sounds can be expected to change every 10 ms or 20 ms so the transmitted bit rate would be 3 to 6 times 25 kbits/s, which is clearly not competitive.
So, what can be done? The solution that motivated the lower rate linear predictive coding methods was to use a lower order predictor, say
N = 10, to approximate the envelope of the spectrum as shown in red in
Figure 3d, and then provide the harmonic structure using the excitation.
Thus, we only need to quantize and code 10 coefficients and so if the rate required for the excitation is relatively low, the bit rate should be much lower, even with 10 ms frame sizes for the linear prediction analysis.
The linear predictive coder (LPC) was pioneered by Atal and Hanauer [
13], Makhoul [
14], Markel and Gray [
15], and others and took the form shown in
Figure 4, where with
N = 10 uses the explicit split between the linear prediction fit of the speech envelope and the excitation to provide the spectral fine structure. In
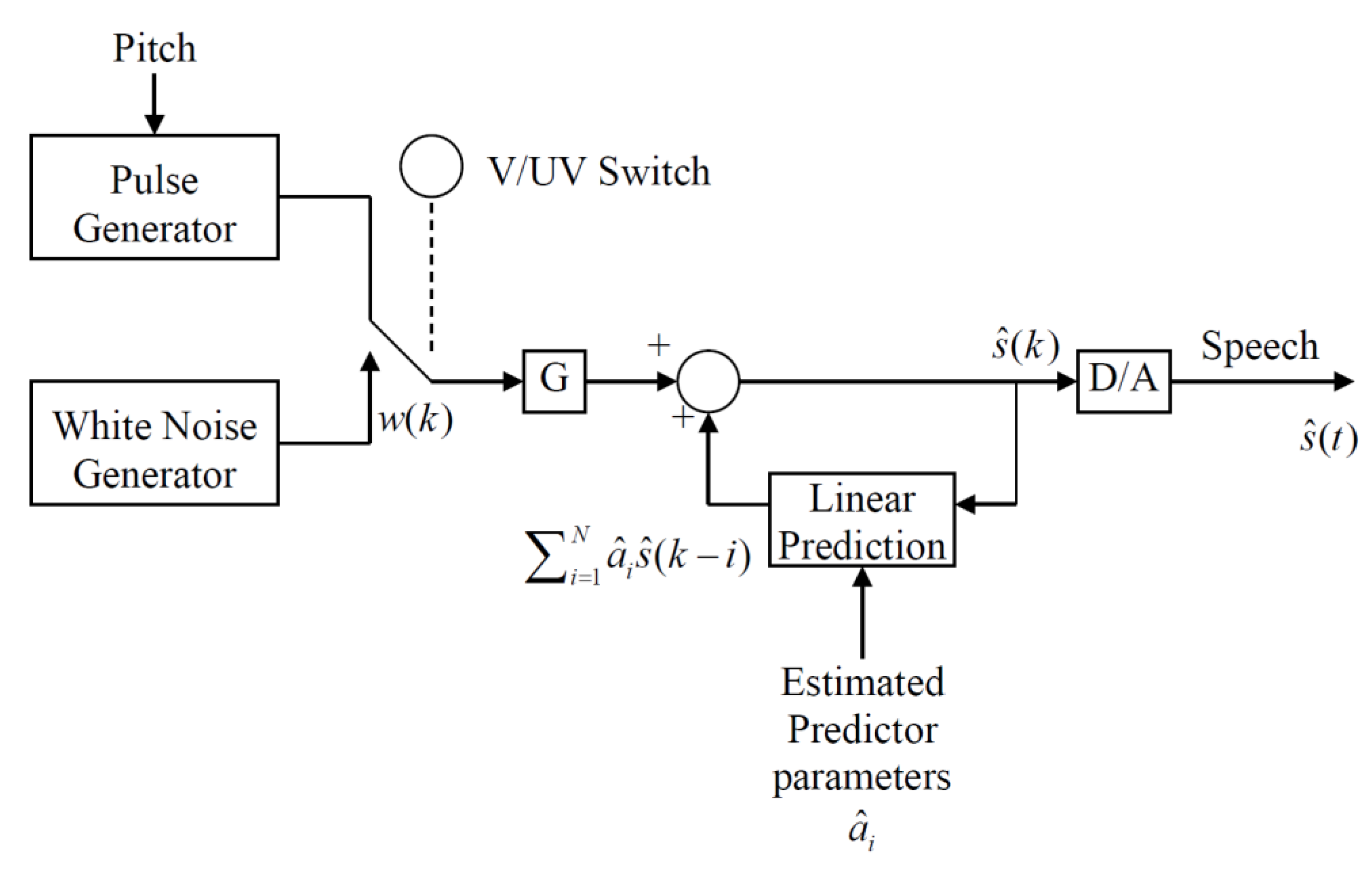
Figure 4, the excitation consists of either a periodic impulse sequence if the speech is determined to be Voiced (V) or white noise if the speech is determined to be Unvoiced (UV) and G is the gain of the excitation used to match the reconstructed speech energy to that of the input. A depiction of the two components, namely the speech envelope and the spectral fine structure, for a particular speech spectrum is shown in
Figure 5 [
16].
The linear prediction coefficients and the excitation (V/UV decision, gain, and pitch) are calculated based on a block or frame of input speech using, which are since the 1970’s, well known methods [
4,
5,
14,
15]. These parameters are quantized and coded for transmission to the receiver/decoder and they must be updated regularly in order to track the time varying nature of a speech signal [
3,
4,
5,
11,
17,
18]. The resulting bit rate was usually 2.4 kbits/s, 4 kbits/s, or 4.8 kbits/s depending on the application and the quality needed. For LPC-10 at a rate of 2.4 kbits/s, the coding of the linear prediction coefficients was allocated more than 1.8 kbits/s and the gain, voicing, and pitch (if needed) received the remaining 600 bits/s [
5]. This structure in
Figure 4 served as the decoder for the LPC-10 (for a 10th order predictor) Federal Standard 1015 [
19], as well as the synthesizer in the Speak ‘N Spell toy [
20]. The speech quality produced by the LPC codecs was intelligible and retained many individual speaker characteristics, but the reconstructed speech can be “buzzy” and synthetic-sounding for some utterances.
Thus, the power of the linear prediction model is in its ability to provide different resolutions of the signal frequency domain representation and the ability to separate the calculation of the speech spectral envelope from the model excitation, which fills in the harmonic fine structure. Today’s speech coders are a refinement of this approach.
7. The Relationship between Speech and Audio Coding
The process of breaking the input speech into subbands via bandpass filters and coding each band separately is called subband coding [
4,
5,
28,
29]. To keep the number of samples to be coded at a minimum, the sampling rate for the signals in each band is reduced by decimation. Of course, since the bandpass filters are not ideal, there is some overlap between adjacent bands and aliasing occurs during decimation. Ignoring the distortion or noise due to compression, quadrature mirror filter (QMF) banks allow the aliasing that occurs during filtering and subsampling at the encoder to be cancelled at the decoder [
28,
29]. The codecs used in each band can be PCM, ADPCM, or even an analysis-by-synthesis method, however, the poorer the coding of each band, the more likely aliasing will no longer be cancelled by the choice of synthesizer filters. The advantage of subband coding is that each band can be coded to a different accuracy and that the coding error in each band can be controlled in relation to human perceptual characteristics [
4,
5].
Transform coding methods were first applied to still images but later investigated for speech. The basic principle is that a block of speech samples is operated on by a discrete unitary transform and the resulting transform coefficients are quantized and coded for transmission to the receiver. Low bit rates and good performance can be obtained because more bits can be allocated to the perceptually important coefficients, and for well-designed transforms, many coefficients need not be coded at all, but are simply discarded, and acceptable performance is still achieved [
30].
Although classical transform coding has not had a major impact on narrowband speech coding and subband coding has fallen out of favor in recent years (with a slight recent resurgence for Bluetooth audio [
31]), filter bank and transform methods play a critical role in high quality audio coding, and several important standards for wideband, superwideband, and fullband speech/audio coding are based upon filter bank and transform methods [
32,
33,
34,
35]. Although it is intuitive that subband filtering and discrete transforms are closely related, by the early 1990’s, the relationships between filter bank methods and transforms were well-understood [
28,
29]. Today, the distinction between transforms and filter bank methods is somewhat blurred, and the choice between a filter bank implementation and a transform method may simply be a design choice. Often a combination of the two is the most efficient [
32].
The basic very successful paradigm for coding full band audio in the past two decades has been the filter bank/transform based approach with perceptual noise masking using an iterative bit allocation [
32,
35]. This technique does not lend itself to real time communications directly because of the iterative bit allocation method and because of complexity, and to a lesser degree, delay in the filter bank/transform/noise masking computations. As a result, the primary impact of high quality audio coding has been to audio players (decoders) such as MP3 and audio streaming applications, although the basic structure for high quality audio coding has been expanded in recent years to conversational applications with lower delay [
34].
A high level block diagram of an audio codec is shown in
Figure 9. In this diagram, two paths are shown for the sampled input audio signal, one path is through the filter bank/transform that performs the analysis/decomposition into spectral components to be coded, and the other path into the psychoacoustic analysis that computes the noise masking thresholds. The noise masking thresholds are then used in the bit allocation that forms the basis for the quantization and coding in the analysis/decomposition path. All side information and parameters required for decoding are then losslessly coded for storage or transmission.
The primary differences among the different coding schemes that have been standardized and/or found wide application are in the implementations of the time/frequency analysis/decomposition in terms of the types of filter banks/transforms used and their resolution in the frequency domain. Note that the frequency resolution of the psychoacoustic analysis is typically finer than the analysis/decomposition path since the perceptual noise masking is so critical for good quality. There are substantive differences in the other blocks as well, with many refinements over the years.
The strengths of the basic audio coding approach are that it is not model based, as in speech coding using linear prediction, and that the perceptual weighting is applied on a per-component basis, whereas in speech coding, the perceptual weighting relies on a spectral envelope shaping. A weakness in the current approaches to audio coding is that the noise masking theory that is the foundation of the many techniques is three decades old; further, the masking threshold for the entire frame is computed by adding the masking thresholds for each component. The psychoacoustic/audio theory behind this technique of adding masking thresholds has not been firmly established.
Other key ideas in the evolution of the full band audio coding methods have been pre- and post-masking and window switching to capture transients and steady state sounds. Details of the audio coding methods are left to the very comprehensive references cited [
4,
5,
32,
33,
34].
8. Speech Coding Standards
Although the ITU-T had set standards for wireline speech coding since the 1970’s, it was only with the worldwide digital cellular industry that standards activities began to gain momentum, and by the 1990’s, speech coding standardization activities were expanding seemingly exponentially. We leave the historical development of speech coding standards and the details of many of the standards to the references [
1,
2,
3,
5,
11]. Here, however, we present some key technical developments of standards that have greatly influenced the dominant designs of today’s leading speech coding standards.
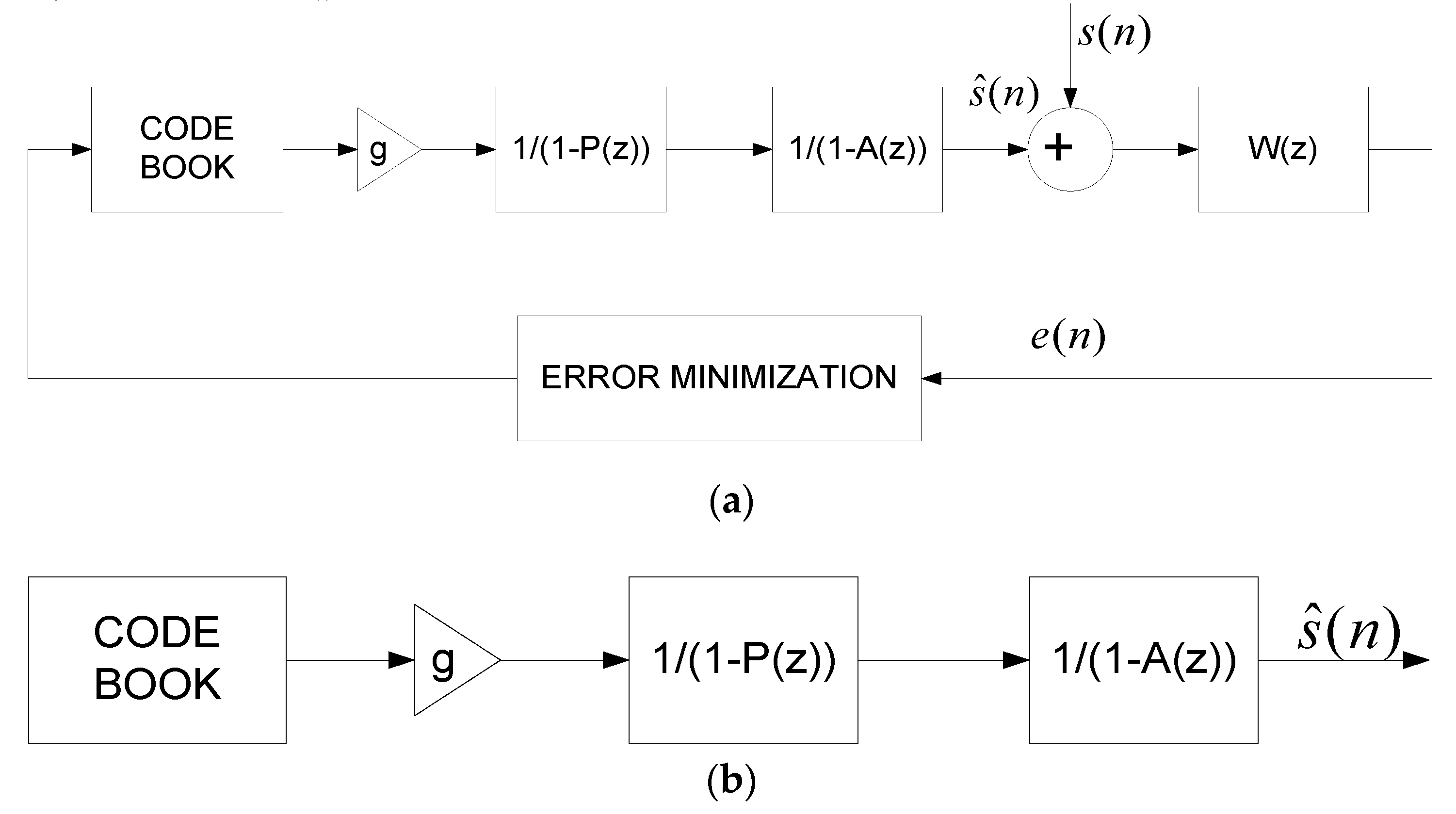
By the early 1990’s, the analysis-by-synthesis approach to speech coding was firmly established as the foundation of the most promising speech codecs for narrowband speech. The research and development efforts focused on designing good excitation codebooks while maintaining manageable search complexity and simultaneously improving reconstructed speech quality and intelligibility.
What might be considered two extremes of codebook design were the Gaussian random codebooks, made up of Gaussian random sequences, and the multipulse excitation type of codebook, which consisted of a limited number of impulses (say 8) placed throughout a speech frame, each with possibly different polarity and amplitude [
36]. In the former case, encoding complexity was high since there needed to be a sufficient number of sequences to obtain a suitably rich excitation set, while in the latter, encoding was complex due to the need to optimally place the impulses and determine their appropriate amplitude. The breakthrough idea came through the work of Adoul and his colleagues who showed that a relatively sparse set of positive and negative impulses, all of the same amplitude (!), would suffice as a codebook to produce good quality speech, while at the same time, managing complexity due to the sparseness of the impulses and the need to determine only one amplitude [
22,
23]. These ideas were motivated by codes from channel coding, and while it should be noted that others had proposed and investigated using excitations motivated by channel coding structures [
37,
38], Adoul and his colleagues provided the demonstration that the needed performance could be achieved.
This sparse excitation codebook, called an algebraic codebook, served as the basis for the G.729 analysis-by-synthesis speech coding standard set by the ITU-T for speech coding at 8 kbits/s. The speech coding method in G.729 was designated as Algebraic Code Excited Linear Prediction (ACELP) and served to define a new class of speech codecs. We leave further development of the G.729 standard to the references [
3,
23], but we turn our attention now to ACELP codecs in general and the most influential and widely deployed speech codec in the 2000’s to date.
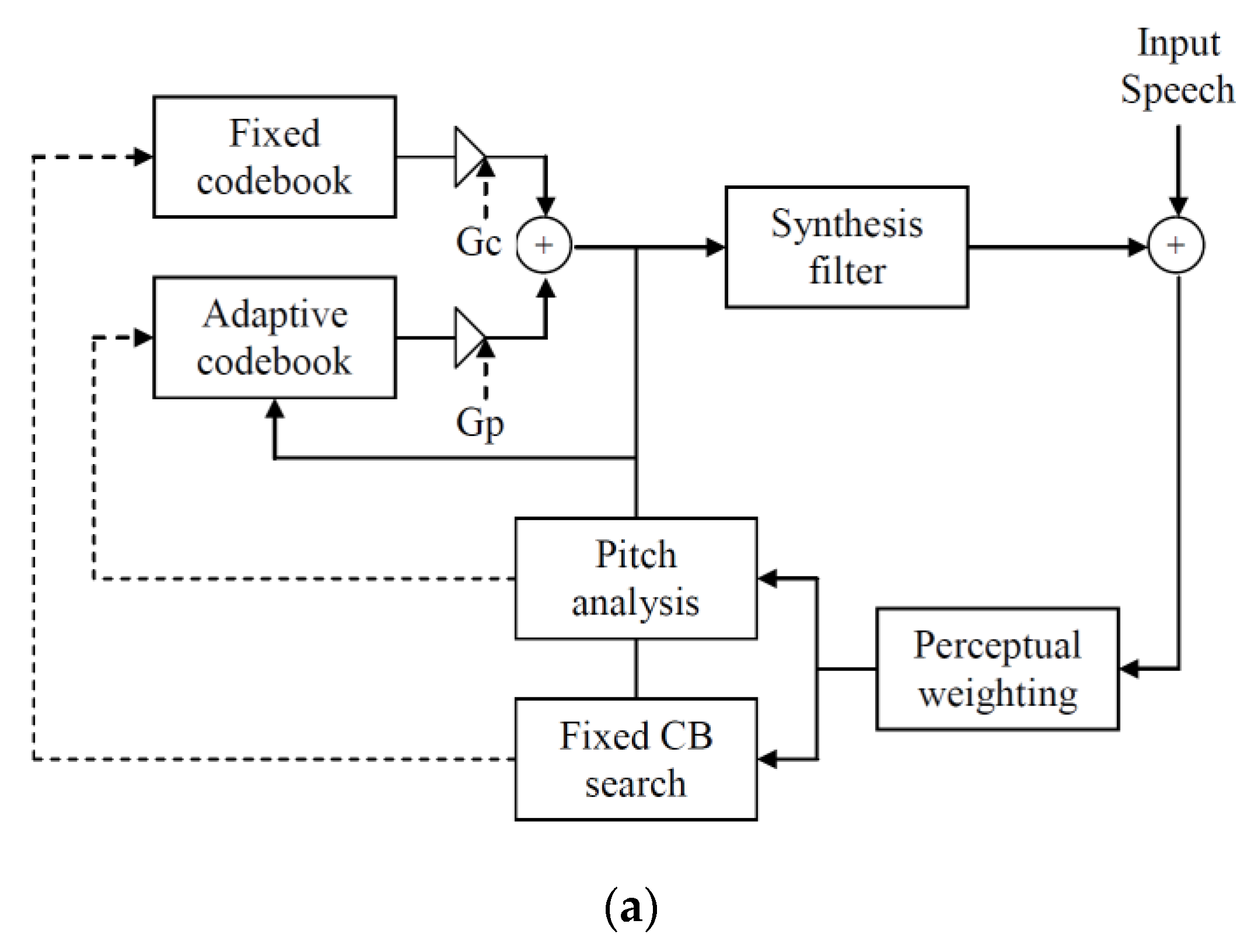
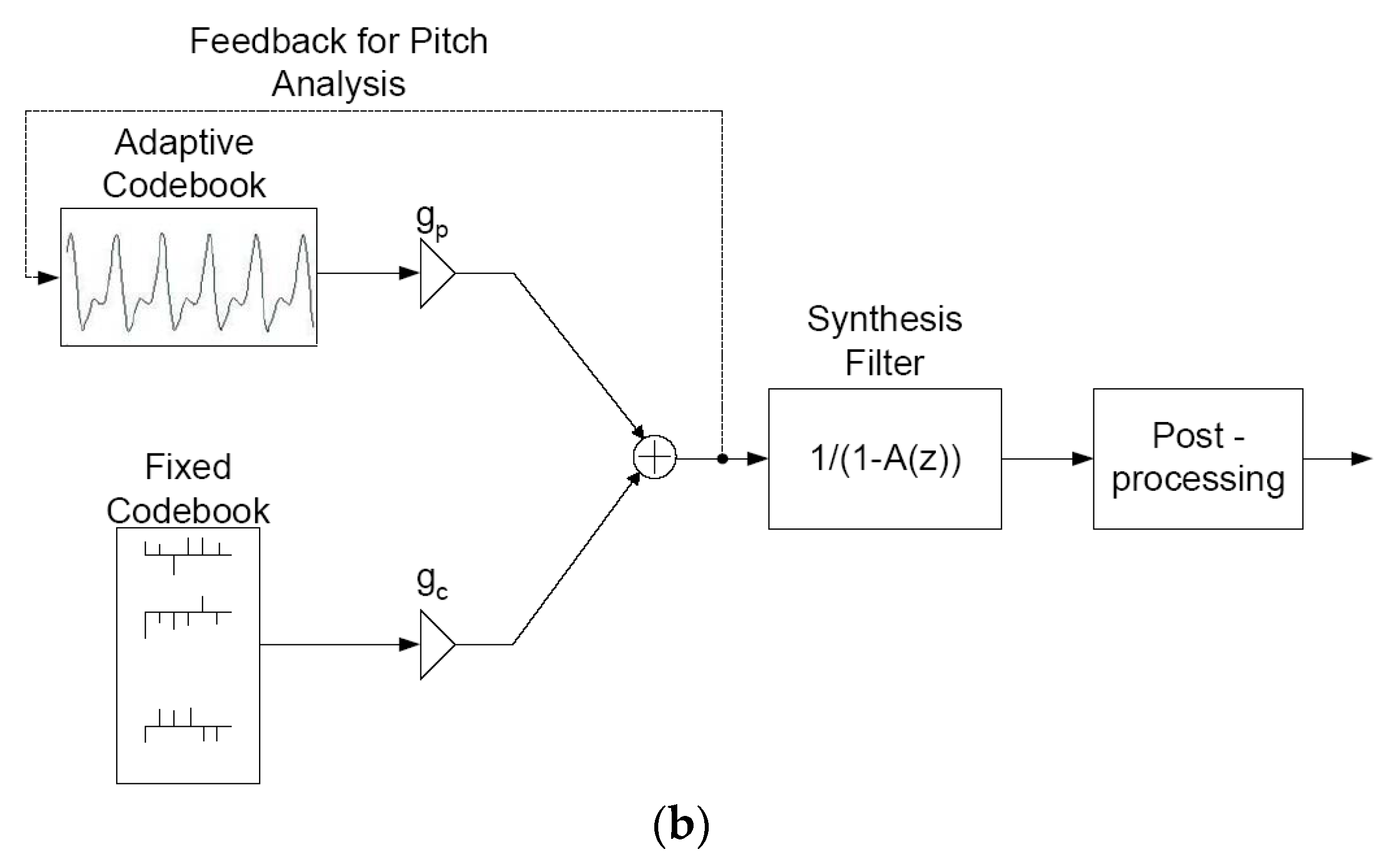
The Adaptive Multirate (AMR) codec uses the ACELP method but improves on the G.729 standard in several ways, including using a split vector quantization approach to quantize and code the linear prediction parameters on a frame/subframe basis. The AMR narrowband (AMR-NB) codec was standardized and widely deployed and operated at the bit rates of 4.75, 5.15, 5.9, 6.7, 7.4, 7.95, 10.2, and 12.2 kbits/s [
3]. The bit rate can be changed at any frame boundary and the “adaptive” in AMR refers to the possible switching between rates at frame boundaries in response to instructions from the base station/mobile switching center (MSC) or eNodeB in LTE (long term evolution), which is referred to as “network controlled” switching. The AMR-NB codec standardization was then followed by the AMR-WB (wideband) speech codec, which operates at bit rates of 6.6, 8.85, 12.65, 14.25, 15.85, 18.25, 19.85, 23.05, and 23.85 kbits/s [
27]. These codecs have been implemented in 3rd generation digital cellular systems throughout the world and have served as the default codecs for VoLTE (voice over long term evolution) in 4th generation digital cellular, designated as LTE, while a new codec standard was developed. The AMR-WB codec is the basis for claims of HD (High Definition) Voice for digital cellular in industry press releases and the popular press, where HD simply refers to wideband speech occupying the band from 50 Hz to 7 kHz.
After the development of the AMR codecs, another speech codec, called the Variable Multirate (VMR) codec, was standardized [
39]. This codec allowed rate switching at the frame boundaries not only as a result of network control but also due to the analysis of the input speech source. This type of rate switching is called “source controlled” switching. Although the VMR codec was standardized, it was not widely deployed, if at all.
The newest speech codec to be standardized is the Enhanced Voice Services (EVS) codec designed specifically for 4th generation VoLTE but is expected to be deployed in many applications because of its performance and its wide-ranging set of operable modes [
40]. The new EVS codec uses the ACELP codec structure and builds on components of the AMR-WB codec. The EVS codec achieves enhanced voice quality and coding efficiency for narrowband and wideband speech, provides new coding modes for superwideband speech, improves quality for speech, music, and mixed content, has a backward compatible mode with AMR-WB with additional post-processing, and allows fullband coding at a bit rate as low as 16.4 kbit/s. The EVS codec has extensive new pre-processing and post-processing capabilities. It builds on the VMR-WB codec and the ITU-T G.718 codec by using technologies from those codecs for classification of speech signals. Further, the EVS codec has source controlled variable bit rate options based on the standardized ERVC-NW (enhanced variable rate narrowband-wideband) codec. There are also improvements in coding of mixed content, voice activity detection, comfort noise generation, low delay coding, and switching between linear prediction and MDCT (modulated discrete cosine transform) coding modes. Further details on the EVS codec can be found in the extensive set of papers cited in [
40].
The impact of rate distortion theory and information theory in general can be seen in the designs of the excitation codebooks over the years, starting with the tree/trellis coding work of Anderson [
24], Becker and Viterbi [
37], and Stewart, Gray, and Linde [
38], among others, through the random Gaussian sequences employed by Atal and Schroeder [
21] and then continuing with the algebraic codes pioneered by Adoul,
et al. Additionally, this influence appears in the use of vector quantization for some codebook designs over the years and also for quantization of other parameters, such as the linear prediction coefficients in AMR codecs [
27]. More recently, rate distortion theoretic bounds on speech codec performance have been developed as described in the following section.
9. Fundamental Limits on Performance
Given the impressive performance of the EVS codec and the observably steady increase in speech codec performance over the last 3 decades, as evidenced by the standardized speech codec performance improvements since the mid-1980’s, it would be natural to ask, “what is the best performance theoretically attainable by any current or future speech codec design?” Apparently, this question is not asked very often. Flanagan [
41] used Shannon’s expression for channel capacity to estimate the bit rate for narrowband speech to be about 30,000 bit/s, and further, based on experiments, concluded that the rate at which a human can process information is about 50 bits/s. Later, in his 2010 paper [
42], Flanagan reported experiments that estimated a rate of 1000 to 2000 bits/s preserved “quality and personal characteristics”. Johnston [
43] performed experiments that estimated the perceptual entropy required for transparent coding of narrowband speech to be about 10 kbit/s on the average up to a maximum of about 16 kbits/s. See also [
44]. Given the wide range of these bit rates and since these are all estimates of the bit rate needed for a representative bandwidth or averaged over a collection of speech utterances, they do not provide an indication of the minimum bit rate needed to code a specific given utterance subject to a perceptually meaningful distortion measure.
In standardization processes, the impetus for starting a new work item for a new speech codec design comes not only from a known, needed application, but also from experimental results that indicate improvement in operational rate distortion performance across the range of desirable rates and acceptable distortion is possible. However, the question always remains as to what is the lowest bit rate achievable while maintaining the desired quality and intelligibility with any, perhaps yet unexplored, speech coding structure.
Other than the broad range of estimated rates cited earlier, there have been only a few attempts to determine such performance limits in the past [
45]. There are two challenges in determining any rate distortion bound: specifying the source model and defining an analytically tractable, yet meaningful, distortion measure. For real sources and human listeners, both of these components are extraordinarily difficult, a fact that has been recognized since the 1960’s. Recently however, the author and his students have produced some seemingly practical rate distortion performance bounds as developed in some detail in a research monograph [
45].
In order to develop such bounds, it is necessary to identify a good source model and to utilize a distortion measure that is relevant to the perceptual performance of real speech coders. The approach used in [
45] is to devise speech models based on composite sources, that is, source models that switch between different modes or subsources, such as voiced, unvoiced, onset, hangover, and silence speech modes. Then, conditional rate distortion theory for the mean squared error (MSE) distortion measure is used to obtain rate distortion curves subject to this error criterion. Finally, a mapping function is obtained that allows the rate
versus MSE curves to be mapped into rate
versus PESQ-MOS bounds. Since the PESQ-MOS performance of real speech codecs can be determined from [
7], direct comparisons are possible. These steps are performed for each speech utterance consisting of one or two short sentences of total length of a few seconds, such as those that are used in evaluating voice codec performance using [
7]. A complete list of references and details of the approach are left to [
45].
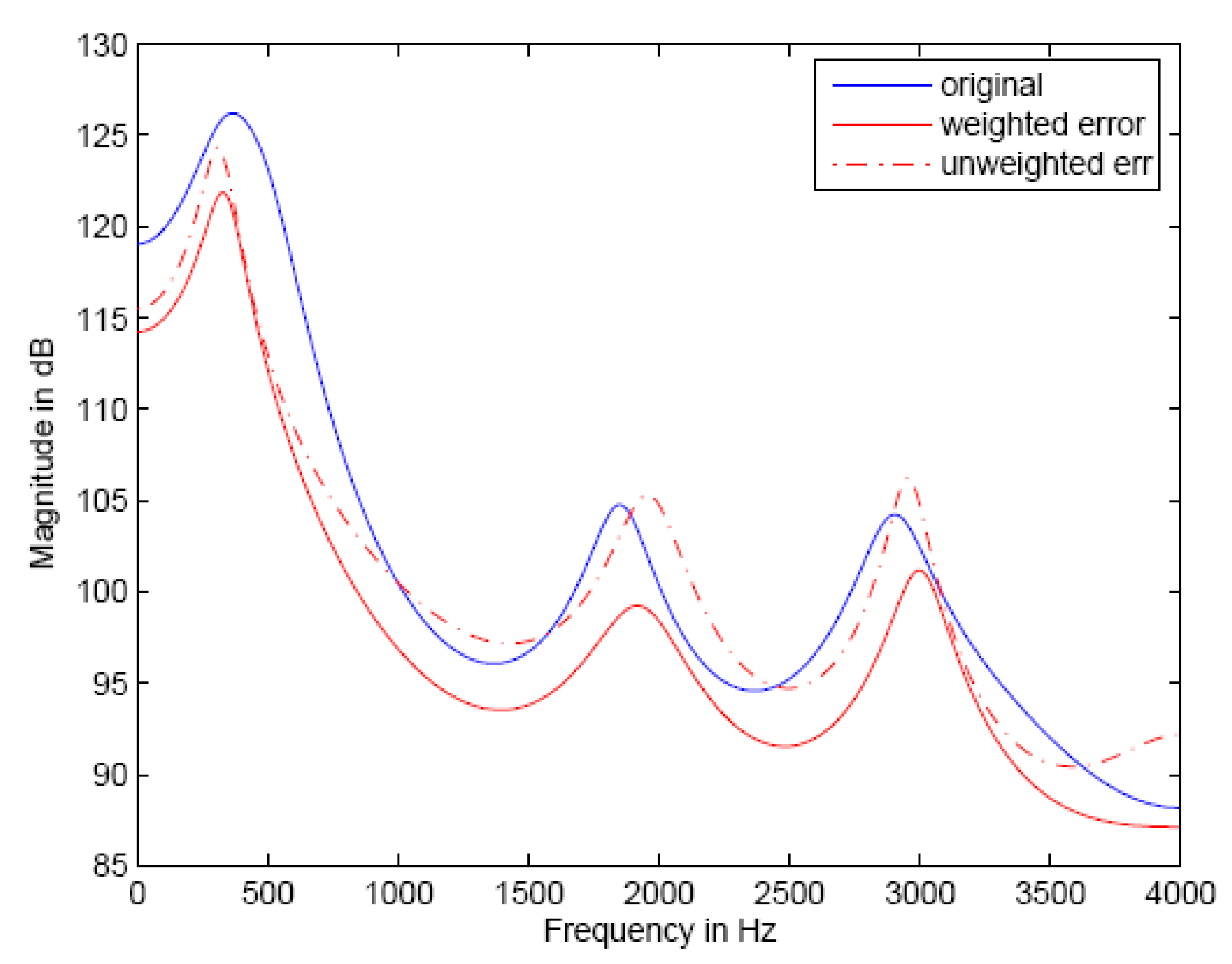
While these bounds have not been compared to all standardized codecs, the bounds are shown to lower bound the performance of many existing speech codecs, including the AMR-NB and AMR-WB codecs, and additionally, these bounds indicate that speech codec performance can be improved by as much as 0.5 bit/sample or 50%! Further, by examining how the different codecs perform for the different source sequences, it is possible to draw conclusions at to what types of speech sources are the most difficult for current codec designs to code [
45], thus pointing toward new research directions to improve current codecs.
Therefore, practically significant rate distortion bounds that express the best performance theoretically attainable for the given source model and distortion measure address at least these two questions: (1) Is there performance yet to be achieved over that of existing codecs; and (2) what types of speech codecs might be worthy of further research? Furthermore, answers to these questions can be provided without implementing new speech codecs; seemingly a very significant savings in research and development effort.
It is critical to emphasize what has already been said: The rate distortion bounds obtained thus far are based on certain specified source models, composite source models in this case, and on using a particular method to create a distortion measure expressible in terms of MOS, mean opinion score, which can be interpreted in terms of subjective listening tests. Therefore, it is clear that the current bounds can be refined further by developing better source (speech) models and by identifying a more precise, perceptually relevant distortion measure. As a result, it would appear that future research to extend rate distortion performance bounds for speech is highly desirable.
11. First Responder Voice Communications
Emergency first responder voice communications in the U.S. and Europe rely on entirely different communications systems than the telephone network or digital cellular systems used by the public. These emergency first responder systems have much lower transmitted data rates and as a result, the voice codecs must operate at much lower bit rates. Additionally, the voice codecs must operate in much more hostile environments, such as those experienced by firefighters for example, wherein the background noise consists of chain saws, sirens, and alarms, among other noise types. Furthermore, first responders depend critically on voice communications in these dynamic, unpredictable environments.
In the U.S., the Emergency First Responder Systems are called Land Mobile Radio (LMR), which started out as a purely analog system but in recent years has evolved toward digital transmission via the designation Project 25 (P25) Radio Systems [
49]. The standard used for first responder communications in Europe and the United Kingdom is TETRA, originally Trans European Trunked Radio but now Terrestrial Trunked Radio, and TETRA includes a comprehensive set of standards for the network and the air interface. TETRA was created as a standard for a range of applications in addition to public safety [
49].
For P25 in the U.S., the speech codecs used are the IMBE, AMBE, and AMBE +2 codecs, all of which are based upon the Multiband Excitation (MBE) coding method [
49,
50]. In P25 Phase I, the Improved MBE, or IMBE, codec at 4.4 kbits/s is used for speech coding and then an additional 2.8 kbits/s is added for error control (channel) coding. This 7.2 kbits/s total then has other synchronization and low-speed data bits incorporated to obtain the final 9.6 kbits/s presented to the modulator. For P25 Phase II, the total rate available for speech and channel coding is half of 7.2 kbits/s or 3.6 kbits/s, which is split as 2.45 kbits/s for voice and 1.15 kbits/s for channel coding [
49,
50].
These bit rates, namely, 4 kbits/s and below, are in the range of what is called low bit rate speech coding [
51]. Speech coding at these rates has not been able to achieve quality and intelligibility sufficient for widespread adoption. In fact, there have been standards activities directed toward establishing an ITU-T standard at 4 kbits/s for over a decade, and while some very innovative codecs have been developed, none have yet achieved toll quality across the desired range of conditions. The public safety first responder requirements include a much harsher operational environment in terms of background noises as well as a desire for quality equivalent to analog narrowband speech communications, which is similar to toll quality.
We do not provide block diagrams of the IMBE based codecs here but we describe the basic IMBE codec in the following. The IMBE vocoder models each segment of speech as a frequency-dependent combination of voiced (more periodic) and unvoiced (more noise-like) speech. The encoder computes a discrete Fourier transform (DFT) for each segment of speech and then analyzes the frequency content to extract the model parameters for that segment, which consists of the speaker pitch or fundamental frequency, a set of Voiced/Unvoiced (V/UV) decisions, which are used to generate the mixture of voiced and unvoiced excitation energy, and a set of spectral magnitudes, to represent the frequency response of the vocal tract. These model parameters are then quantized into 88 bits, and the resulting voice bits are then output as part of the 4.4 kbits/s of voice information produced by the IMBE encoder [
5,
49,
50].
At the IMBE decoder the model parameters for each segment are decoded and these parameters are used to synthesize both a voiced signal and an unvoiced signal. The voiced signal represents the periodic portions of the speech and is synthesized using a bank of harmonic oscillators. The unvoiced signal represents the noise-like portions of the speech and is produced by filtering white noise. The decoder then combines these two signals and passes the result through a digital-to-analog converter to produce the analog speech output.
For TETRA, the voice codec is based on code excited linear prediction (CELP) and the speech is coded at 4.567 kbits/s, or alternatively, if the speech is coded in the network or in a mobile handset, the AMR codec at 4.75 kbits/s is used [
3,
49]. Block diagrams of the TETRA encoder and decoder are essentially the same as the CELP codecs already discussed. The TETRA codecs based on the CELP structure are clearly a very different coding method than IMBE.
The algorithmic delay of the TETRA voice codec is 30 ms plus an additional 5 ms look ahead. Such a delay is not prohibitive, but a more thorough calculation in the standard estimates an end-to-end delay of 207.2 ms, which is at the edge of what may be acceptable for high quality voice communications. A round trip delay near 500 ms is known to cause talkers to talk over the user at the other end, thus causing difficulty in communications, especially in emergency environments [
49].
Codec performance in a noisy environment is much more of a challenge than for clean speech, wherein for these hostile environments, the speech codecs must pass noisy (PASS (Personal Alert Safety System) alarms, chainsaws,
etc.) input speech and speech from inside a mask (Self-Contained Breathing Apparatus (SCBA) that is essential in firefighting) [
49,
52]. Recent extensive test results by the Public Safety Research Program in the U. S. has shown that the IMBE codecs at these low rates perform poorly compared to the original analog FM voice systems and that the AMR codecs at a rate of 5.9 kbit/s, which is higher than the 4.75 kbits/s used in TETRA, perform poorly as well [
52]. Emergency first responder voice communications is clearly an area in need of intensive future research.