An Approach to the Match between Experts and Users in a Fuzzy Linguistic Environment

Abstract

Knowledge management systems are widely used to manage the knowledge in organizations. Consulting experts is an effective way to utilize tacit knowledge. The paper aims to optimize the match between users and experts to improve the efficiency of tacit knowledge-sharing. Firstly, expertise, trust and feedback are defined to characterize the preference of users for experts. Meanwhile, factors including trust, relationship and knowledge distance are defined to characterize the preference of experts for users. Then, a new method for the measurement of satisfaction based on the principle of axiomatic design is proposed. Afterwards, in order to maximize the satisfaction of both experts and users, the optimization model is constructed and the optimal solution is shown in the matching results. The evaluation results show the approach is feasible and performs well. The approach provides new insights for research on tacit knowledge-sharing. It can be applied as a tool to match experts with users in the development of knowledge management systems. The fuzzy linguistic method facilitates the expression of opinions, and as a result, the users-system interaction is improved.

1. Introduction

In today’s highly competitive environment, knowledge is a kind of strategic resource for organizations [1,2]. It can enhance an organization’s advantage in responding to new and unusual situations. The knowledge management system (KMS) has been widely implemented to serve the needs of managing the valuable knowledge in organizations [2,3].

Tacit knowledge such as know-how and experience exists in experts’ minds. It is subjective and difficult to formalize. Tacit knowledge is more important to a produce competitive advantage since it is harder to imitate than explicit knowledge [4,5,6]. Consulting experts is an efficient way to share tacit knowledge [7,8,9,10].

Many approaches have been proposed to help consult experts. For example, expert profiles are constructed manually or automatically, and are stored in the knowledge repository by systems administrators or system users [11,12,13]. Users search for a suitable expert for help by categories, passively. For a specific category, the list of information about experts is provided to users. In order to ease the burden of browsing categories one by one, the list is provided to users actively based on their needs [14,15,16,17]. Then they can choose the expert from the list for help manually.

These approaches are based on the assumption that experts are willing to help any person without discrimination. Experts’ preferences are ignored. Moreover, these approaches only focus on knowledge needs and other preferences of users are neglected. In fact, consulting experts is a communication process between experts and users. Tacit knowledge is transferred by face-to-face interactions. Many factors affect knowledge-sharing in the communication. Besides expertise, users care about trust [18,19,20] and feedback [18]. Factors including trust [18,19,20], relationship [21] and knowledge distance [18] influence the willingness of experts to share their knowledge [18,21].

Satisfying both experts and users from types of preferences facilitates the communication and promotes knowledge-sharing [18]. Being instructed by favorable experts can result in a higher satisfaction of users. Meanwhile, experts are glad to help preferred users. Therefore, the first problem arises as how to characterize preferences of both experts and users comprehensively. Meanwhile, a method is required for making the global optimum match between experts and users. Intuitively, choosing done by users and experts themselves directly may derive the match. However, the user who is satisfied with the expert may not be preferred by the chosen expert, and vice versa. Moreover, the number of users that one expert can help is restricted because of limited time and spirit. In the condition, only a few matches can be made. Other experts and users are excluded from the match. Therefore, there needs to be a matching method for satisfying both users and experts as much as possible to derive the maximum satisfaction globally.

In order to resolve the above problems, in this paper, an approach to the match between experts and users in a fuzzy linguistic environment is proposed. Factors including expertise, trust, relationship, knowledge distance and feedback are defined in the fuzzy linguistic environment. Then methods for the measurement of satisfaction and for the match between experts and users are constructed. The remainder of this paper is organized as follows. In the next section, related works are reviewed. In Section 3, we present the approach to matching between experts and users. Then, in Section 4, the evaluation of the proposed approach is given. Finally, conclusions are presented.

2. Related Works

2.1. Tacit Knowledge-Sharing

Knowledge is divided into tacit knowledge and explicit knowledge [1]. Explicit knowledge refers to knowledge that can be codified. On the contrary, knowledge which is difficult to codify is called tacit knowledge. Since tacit knowledge resides in owners’ brains, it is often shared and transferred via instruction or face-to-face interactions [2]. Information technologies for supporting tacit knowledge-sharing focus on assisting users in finding appropriate experts and facilitating communications between them.

In the initial stage, the expert database is built, in which the expert profile is constructed and stored. Each expert belongs to a category. Users who are in need of help search related categories for appropriate experts. The focus of research in the field is on profiling experts. In most previous research [11,12], experts have been profiled manually by system administrators or system users. Afterwards, the automatic expert profiling method based on registered documents is proposed [13]. However, it will fail when there are no or few documents, especially in the early stage of the implementation of knowledge management systems.

With the increasing complexity of tasks, categories develop rapidly. At the same time, more and more tasks are involved in multiple categories. It consumes more time to find the appropriate experts by searching categories. In order to ease the burden of finding experts passively, researchers propose methods for providing a list of experts to users actively according to the needs of users [14,15,16,17]. Then users can choose the expert from the list for help manually. In most studies, the needs of users only refer to knowledge needs. In fact, besides knowledge needs, users care about many other factors. Moreover, these studies are based on the assumption that experts are willing to help users without discrimination. However, tacit knowledge is transferred through a mutual communication process and it resides in experts’ brains [18,20]. Experts’ satisfaction is more important in tacit knowledge-sharing. However, in the previous research, experts’ preferences have been ignored. Considering these limitations, it is ideal to match users with experts by integrating both experts’ and users’ preferences.

2.2. Fuzzy Linguistic Method

The fuzzy linguistic method is used to handle linguistic information [22]. Linguistic terms are often represented by fuzzy numbers such as triangular and trapezoidal fuzzy numbers [23,24]. A triangular fuzzy number is a special case of a trapezoidal fuzzy number. When the two vertexes of the trapezoidal fuzzy number have the same value, the trapezoidal fuzzy number becomes a triangular fuzzy number [24]. It can be used to cope with more general situations. In the following, the trapezoidal fuzzy number and corresponding operators are reviewed [25].

A trapezoidal fuzzy number can be defined as $\tilde{A}=\left(a,b,c,d\right)$, where $a\le b\le c\le d$. The corresponding membership function ${\mathsf{\mu }}_{\tilde{A}}$ of $\tilde{A}$ is shown in Figure 1,

$${\mathsf{\mu }}_{\tilde{A}}=\{\begin{array}{c}\frac{x-a}{b-a} \left(a\le x\le b\right)\\ 1 \left(b\le x\le c\right)\\ \frac{d-x}{d-c} \left(c\le x\le d\right)\end{array}$$

(1)

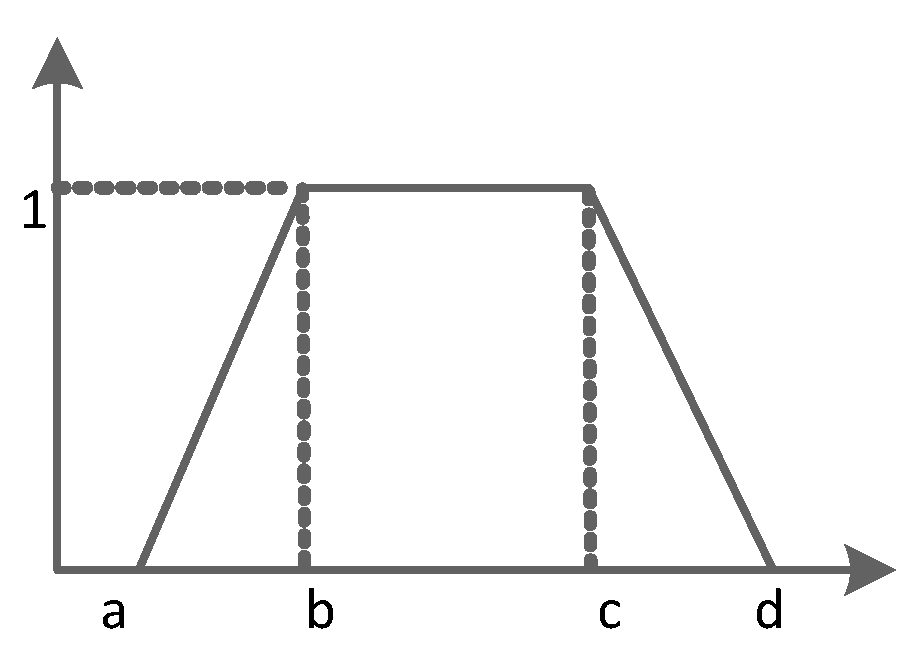
Figure 1. A trapezoidal fuzzy number.

Let $\tilde{A}$ and $\tilde{B}$ be two positive trapezoidal fuzzy numbers parameterized by $\left(a_1,b_1,c_1,d_1\right)$ and $\left(a_2,b_2,c_2,d_2\right)$. Some algebraic operations of trapezoidal fuzzy numbers $\tilde{A}$ and $\tilde{B}$ can be expressed as follows [26,27].

Definition 1. 

Addition operator

$$\tilde{A}\oplus \tilde{B}=\left(a_1,b_1,c_1,d_1\right)+\left(a_2,b_2,c_2,d_2\right)=\left(a_1+a_2,b_1+b_2,c_1+c_2,d_1+d_2\right)$$

(2)

Definition 2. 

Subtraction operator

$$\tilde{A}\ominus \tilde{B}=\left(a_1,b_1,c_1,d_1\right)-\left(a_2,b_2,c_2,d_2\right)=\left(a_1-a_2,b_1-b_2,c_1-c_2,d_1-d_2\right)$$

(3)

Definition 3. 

Multiplication operator

$$\tilde{A}\otimes \tilde{B}=\left(a_1,b_1,c_1,d_1\right)\otimes \left(a_2,b_2,c_2,d_2\right)=\left(a_1{a}_2,b_1{b}_2,c_1{c}_2,d_1{d}_2\right)$$

(4)

Definition 4. 

Division operator

$$\tilde{A}∕\tilde{B}=\left(a_1,b_1,c_1,d_1\right)∕\left(a_2,b_2,c_2,d_2\right)=\left(a_1∕a_2,b_1∕b_2,c_1∕c_2,d_1∕d_2\right)$$

(5)

Definition 5. 

Multiplication operator of real number $k$ and a trapezoidal fuzzy number

$$k\tilde{A}=\left(k{a}_1,k{b}_1,k{c}_1,k{d}_1\right)$$

(6)

Definition 6. 

Reciprocal operator

$${(\tilde{A})}^{-1}=\left(1/d_1,1/c_1,1/b_1,1/a_1\right)$$

(7)

Definition 7. 

Defuzzification operator

$$N=D(\tilde{A})=\frac{\left(a_1+2b_1+2c_1+d_1\right)}{6}$$

(8)

where $N$ is the defuzzified crisp value.

2.3. Axiomatic Design

Axiomatic design (AD) principles are proposed to provide the systematic scientific basis for designers in the area of product design and software design [28,29]. The advantage of AD principles is that not only the best alternative but also the most appropriate alternative can be selected.

Information axiom is one of concepts in AD principles. The principle states that the alternative that has the smallest information content is deemed the best design. The information axiom provides a way to select appropriate alternatives. It is symbolized by the information content which refers to the probability of reaching design goals. Information content ($I$) is defined as [28,29,30,31]

$$I={\log }_2\frac{1}{p}$$

(9)

where $p$ is the probability of meeting a specific function requirement.

When there is more than one function requirement, the information content can be derived by summing all probabilities,

$$I={\displaystyle \sum }_{i=1}^t{I}_i=-{\log }_2\left({\displaystyle \prod }_{i=1}^t{p}_i\right)$$

(10)

The probability of meeting the function requirement is given by the design range, the system range and the common area. Design range refers to the object of the design and the system range is the capacity that the system achieves. The common area is the intersection area of the design range and the system range, which is just the acceptable solution, as is shown in Figure 2 [28].

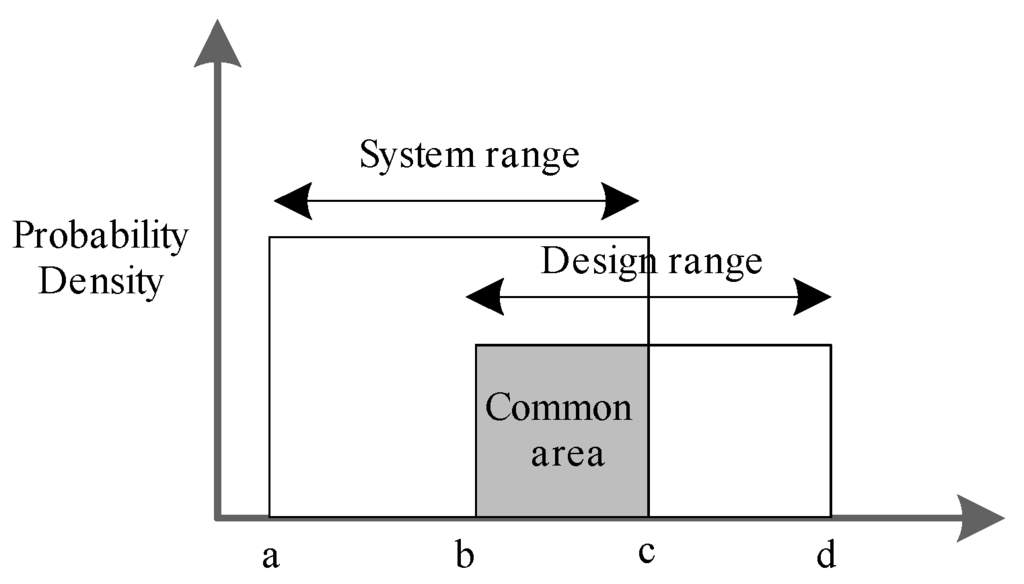
Figure 2. Design range, system range and common area of the function requirement.

Therefore, the information content $I$ can be defined as [28]

$$I={\log }_2\frac{1}{p}={\log }_2\frac{1}{\frac{\text{Common range}}{\text{System range}}}={\log }_2\frac{\text{System range}}{\text{Common range}}$$

(11)

3. Approach to the Match between Experts and Users

3.1. Establishing Criteria for the Match

The establishment of the proper criteria is the basis of the match between users and experts. For evaluating users, trust, relationship and knowledge distance are considered. Meanwhile, expertise, trust and feedback are used to evaluate experts. In the following, the detailed definitions of the criteria are given.

3.1.1. Expertise

As a consulting expert is there to learn from, his expertise with regard to knowledge needs of users is the first criterion for users to evaluate experts.

The expert is always involved in multiple knowledge areas with different expertise levels. The predefined expertise level of expert $E_j$ in knowledge area $K_j$ is denoted as ${\widetilde{VE}}_{ji}$.

In order to identify knowledge needs, user $U_i$ is required to rate the relevance of completed tasks to knowledge needs. Based on linguistic evaluations, the relevant degree ${\widetilde{VN}}_{ik}$ of user $U_i$’s knowledge needs to the knowledge area $K_k$ can be obtained by

$${\widetilde{VN}}_{ik}=\frac{{{\displaystyle \sum }}_{T_t\in ST{S}_i}{\widetilde{ϵ}}_{ti}\times {\widetilde{\mathit{VT}}}_{tk}}{{{\displaystyle \sum }}_{T_t\in ST{S}_i}{\widetilde{ϵ}}_{ti}}$$

(12)

where $ST{S}_i$ is the set of retrieved similar completed tasks, ${\widetilde{ϵ}}_{ti}$ is the rating of completed task $T_t$ to the knowledge needs of user $U_i$ on relevance, and ${\widetilde{VT}}_{tk}$ is the belonging degree of task $T_t$ to the knowledge area $K_k$.

The degree ${\widetilde{VM}}_{ij}$ of the match of the expertise between expert $E_j$ and the knowledge needs of user $U_i$ is determined by

$${\widetilde{VM}}_{ij}=\frac{{{\displaystyle \sum }}_{k=1}^n\left({\widetilde{VP}}_{\mathit{ik}}\times {\widetilde{VN}}_{\mathit{jk}}\right)}{{{\displaystyle \sum }}_{k=1}^n\left({\widetilde{VN}}_{\mathit{jk}}\right)}$$

(13)

where $n$ is the number of knowledge areas, and ${\widetilde{VP}}_{jk}$ is the expertise level of expert $E_j$ in knowledge area $K_k$.

3.1.2. Trust

Trust is people’s subject belief in the other people, which includes ambiguity and subjectivity [18]. In the evaluation of experts, trust represents the subject belief in the expert which is generated from authority and reputation. When evaluating users, trust means the expert has confidence in the user that the user will not misuse knowledge and take unjust credit for it.

Users and experts are allowed to rate trust in each other with linguistic terms directly. When there are unrated experts and users, for the unrated trust people, the max-min aggregation method [32] among shorted paths is extended to propagate indirect trust in others.

Firstly, the strength of the trust path from expert $E_j$ to user $U_i$ is obtained through

$${\widetilde{ST}}_{j,t}=\underset{u_k\in OTS\left(e_j\right)}{\mathit{max}}[min\{{\tilde{\rho }}_{j,k},{\widetilde{ST}}_{k,t}\}]$$

(14)

where $OTS\left(u_i\right)$ is the set of users whom user $U_i$ directly trusts, and${\tilde{\rho }}_{i,k}$ is the direct linguistic rating of user $U_k$ given by expert $E_j$ on trust.

Then, among the inlink-neighbor of $U_i$, the user who is trusted most by $U_i$ can be derived by

$$U_{t^{*}}=\mathit{arg}\underset{u_t\in ITS\left(u_i\right)}{\mathit{max}}{\widetilde{ST}}_{j,t}$$

(15)

where $ITS\left(u_i\right)$ is the set of users who trust user $U_i$.

Afterwards, expert $E_j$’s indirect trust ${\tilde{T}}_{j,i}$ in user $U_i$ is estimated by

$${\tilde{T}}_{j,i}=\min \left\{{\widetilde{\mathit{ST}}}_{j,t^{*}}^{*},{\tilde{\varpi }}_{t^{*},i}\right\}$$

(16)

where ${\tilde{\varpi }}_{t^{*},i}$ is the direct linguistic rating of user $U_i$ given by user $U_{t^{*}}$.

In the same way, user $U_i$’s indirect trust ${\tilde{T}}_{i,j}$ in expert $E_j$ can be estimated by

$${\tilde{T}}_{i,j}=\min \left\{{\widetilde{\mathit{ST}}}_{i,t^{*}}^{*},{\tilde{\varpi }}_{t^{*},j}\right\}$$

(17)

$$E_{t^{*}}=\mathit{arg}\underset{e_t\in ITS\left(e_j\right)}{\mathit{max}}{\widetilde{ST}}_{i,t}$$

(18)

$${\widetilde{ST}}_{i,t}=\underset{e_k\in OTS\left(u_i\right)}{\mathit{max}}[min\{{\tilde{\rho }}_{i,k},{\widetilde{ST}}_{k,t}\}]$$

(19)

where ${\tilde{\varpi }}_{t^{*},j}$ is the direct linguistic rating of expert $E_j$ given by expert $E_{t^{*}}$,$ITS\left(e_j\right)$ is the set of experts who trust expert $e_j$, $OTS\left(u_i\right)$ is the set of experts whom user $U_i$ directly trusts, ${\tilde{\rho }}_{i,k}$ is the direct linguistic rating of expert $E_k$ given by user $U_i$ on trust.

3.1.3. Relationship

In organizations, especially in inter-organizations, there often exist relationships such as cooperative relationships and competitive relationships between experts and users. These relationships determine by expected benefits of knowledge-sharing and influence experts’ willingness to share the knowledge [21]. Thus, relationship is selected as the criterion for experts to evaluate users.

Experts are allowed to use linguistic terms to declare the relationship with users or groups. A user may join in more than one group and there probably exist conflicts in relationships of groups that the user belongs to. The relationship ${\tilde{R}}_{ij}$ of expert $E_i$ with user $U_j$ is aggregated by

$${\tilde{R}}_{ij}=\{\begin{array}{c}\underset{O_h\in O{C}_j}{\max }{\tilde{c}}_{ih}^{\text{'}}, \mathrm{if} \mathrm{the} \mathrm{expert} \mathrm{has} \mathrm{the} \mathrm{generous} \mathrm{preference}. \\ \underset{O_h\in O{C}_j}{\min }{\tilde{c}}_{ih}^{\text{'}},\mathrm{if} \mathrm{the} \mathrm{expert} \mathrm{has} \mathrm{the} \mathrm{cautious} \mathrm{preference}.\end{array}$$

(20)

where $O{C}_j$ is the collection of groups that user $U_j$ belongs to, and ${\tilde{c}}_{ih}^{\text{'}}$ is the linguistic declaration of the relationship given by expert $E_i$ to group $O_h$.

3.1.4. Feedback

Consulting the same expert who was used to ask for help can ease the burden of introducing background information repeatedly, and more personalized help can be given. The feedback of the user denotes whether he is willing to get help from the expert next time. Experts with a higher degree of feedback will be matched with the user in a higher priority.

As an expert may be consulted and rated more than once and the effect decreases as time goes on, by integrating the time factor [33], the aggregated rating ${\tilde{F}}_{ij}$ of expert $E_j$ on feedback given by user $U_i$ can be derived by

$${\tilde{F}}_{ij}=\frac{{{\displaystyle \sum }}_{k=1}^m{\tilde{f}}_{ijk}^{\text{'}}\times \frac{1}{e^{\tau \left(t_{now}-t_k\right)}}}{{{\displaystyle \sum }}_{k=1}^m\frac{1}{e^{\tau \left(t_{now}-t_k\right)}}},$$

(21)

where ${\tilde{f}}_{ijk}^{\text{'}}$ is the linguistic rating given by user $U_i$ to expert $E_j$ at the $k$th time, $t_{now}$ is the present date, $t_k$ is the date of the rating at the $k$th time, and τ is a tunable parameter.

3.1.5. Knowledge Distance

The efficiency of consultation will decrease because of the lower knowledge level of recipients. The expert has his own preference for a user with a certain level of knowledge. Thus, knowledge distance is used as the criterion for the expert to evaluate users. It can be derived by calculating the gap between experts’ expected knowledge level of users and the real knowledge level of users.

In the aggregation of knowledge distances, the knowledge needs are used as weights. The distance ${\tilde{D}}_{ij}$ between expert $E_i$ and user $U_j$ is defined by

$${\tilde{D}}_{ij}={\displaystyle \sum }_{k=1}^{n}distance\left({\widetilde{\mathit{VE}}}_{ik},{\widetilde{\mathit{VU}}}_{jk}\right){\tilde{w}}_{jk}$$

(22)

where ${\tilde{w}}_{jk}$ denotes the weight of the knowledge needs of user $U_j$ in knowledge area $K_k$, and ${\widetilde{VE}}_{ik}$ and ${\widetilde{VU}}_{jk}$ represent expert $E_i$’s expected knowledge level for users and the actual knowledge level of user $U_j$ in knowledge area $K_k$, respectively.

3.2. Constructing the Matching Approach

The architecture of the proposed matching approach is shown in Figure 3. Among the five criteria, only the criterion of trust can be used directly. For the criteria feedback, the direct ratings need to be aggregated along with the rating time. For the criteria expertise, knowledge distance and relationship, values need to be derived from the linguistic ratings with respect to the indirect criteria. These indirect criteria include the relevance of completed tasks to knowledge needs (task relevance), the relationship with users or groups (direct relationship) and the expected expertise level of users (expected level of expertise). In the proposed approach, firstly, besides trust and feedback, users and experts are required to rate each other with respect to the indirect criteria. Then the rating values are processed. Afterwards, based on the processed values, the satisfactions are measured. Finally, the optimization model is constructed to derive the optimal match.

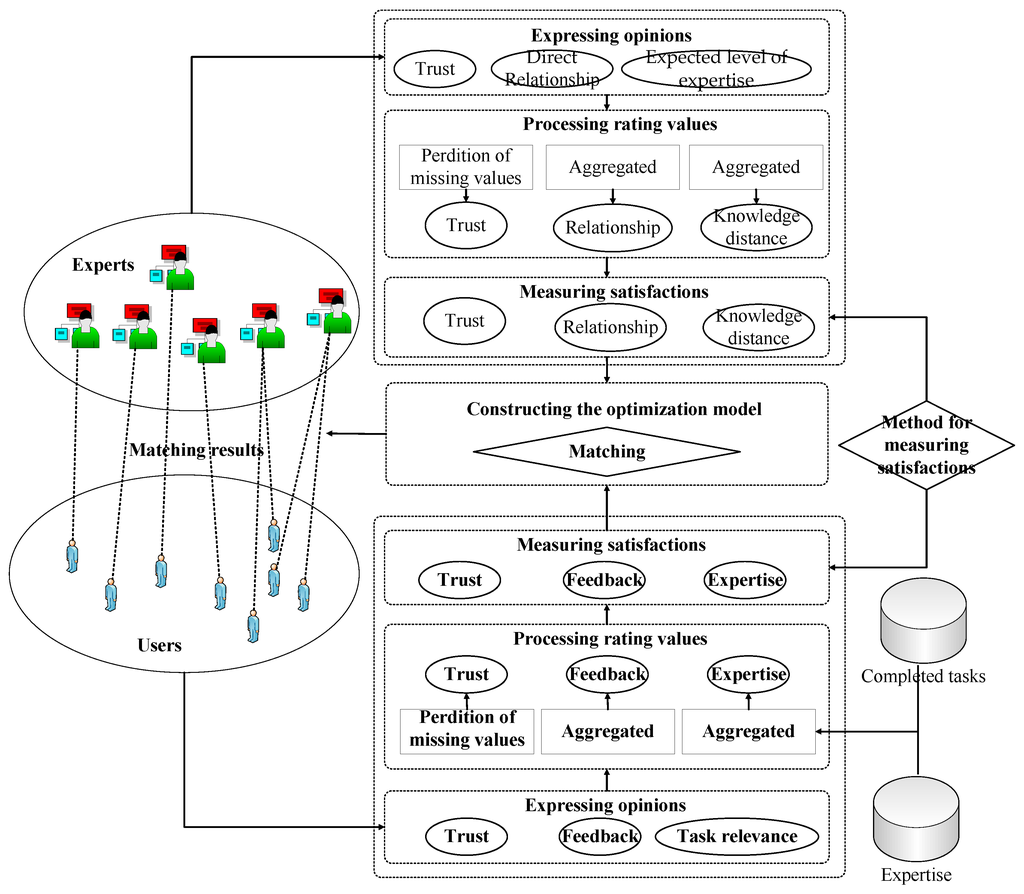
Figure 3. Structure of the matching approach.

The detail of these modules is presented in the following sections.

Let $E=\left\{E_1,E_2,\cdots ,E_p\right\}$ and $U=\left\{U_1,U_2,\cdots ,U_q\right\}$ be collections of experts and users, and $\tilde{W}=\left\{{\tilde{w}}_1,{\tilde{w}}_2,\cdots ,{\tilde{w}}_p\right\}$ and $\tilde{V}=\left\{{\tilde{v}}_1,{\tilde{v}}_2,\cdots ,{\tilde{v}}_q\right\}$ be corresponding weights. The criteria $C^e=\left\{C_1^e=\text{expertise},C_2^e=\text{trust},C_3^e=\text{feedback}\right\}$ are used to evaluate experts. In order to evaluate users, the criteria $C^u=\left\{C_1^u=\text{trust},C_2^u=\text{relationship},C_3^u=\text{knowledge distance}\right\}$ are taken into account. The predefined profile of expert $E_j$ is $V{P}_j=\left({\widetilde{vp}}_{j1},{\widetilde{vp}}_{j2},\cdots ,{\widetilde{vp}}_{jn}\right)$ and the predefined profile of user $U_i$ is $V{U}_i=\left({\widetilde{vu}}_{i1},{\widetilde{vu}}_{i2},\cdots ,{\widetilde{vu}}_{in}\right)$. The predefined relevance of completed task $T_t$ to knowledge areas is $V{T}_t=\left({\widetilde{vt}}_{i\mathrm{t}},{\widetilde{vt}}_{i\mathrm{t}},\cdots ,{\widetilde{vt}}_{tn}\right)$. The collection of groups that user $U_i$ belongs to is denoted by $O{C}_i$. The set of user $U_i$’s retrieved completed tasks is denoted by $ST{S}_i$.

3.2.1. Expressing Opinions and Processing Rating Values

The weight vector of criteria $C^u$ given by expert $E_j$ is denoted by ${\tilde{\zeta }}_j=\{{\tilde{\zeta }}_{j1},{\tilde{\zeta }}_{j2},{\tilde{\zeta }}_{j3}\}$. The weight vector of criteria $C^e$ given by user $U_i$ is denoted by ${\tilde{\eta }}_i=\left\{{\tilde{\eta }}_{i1},{\tilde{\eta }}_{i2},{\tilde{\eta }}_{i3}\right\}$.

Besides the criteria of trust and feedback, experts and users rate each other using linguistic terms with respect to the corresponding indirect criteria. Meanwhile, they are also required to give their opinions on the value of goals.

As for the criterion of expertise, the linguistic rating of completed task $T_t$ to the knowledge needs on relevance given by user $U_i$ is denoted by ${\widetilde{ϵ}}_{ti}$. With Equations (12) and (13), the evaluation value of expert $E_j$ on expertise given by user $U_i$. can be derived by

$${\widetilde{VE}}_{ij}=\frac{{{\displaystyle \sum }}_{k=1}^n\left({\widetilde{VE}}_{\mathrm{ik}}\times \frac{{{\displaystyle \sum }}_{T_t\in ST{S}_i}{\widetilde{ϵ}}_{ti}\times {\widetilde{VT}}_{tk}}{{{\displaystyle \sum }}_{T_t\in ST{S}_i}{\widetilde{ϵ}}_{ti}}\right)}{\frac{{{\displaystyle \sum }}_{T_t\in {\mathit{STS}}_i}{\widetilde{ϵ}}_{\mathit{ti}}\times {\widetilde{VT}}_{\mathit{tk}}}{{{\displaystyle \sum }}_{T_t\in {\mathit{STS}}_i}{\widetilde{ϵ}}_{\mathit{ti}}}}$$

(23)

With respect to the criterion of knowledge distance, expert $E_j$’s expected knowledge level of users is denoted by ${\widetilde{VE}}_{jk}$. With Equation (22), the distance ${\tilde{D}}_{ji}$ between the expert $E_j$ and the user $U_i$ is derived by

$${\tilde{D}}_{ji}={\displaystyle \sum }_{k=1}^{n}distance\left({\widetilde{\mathit{VE}}}_{jk},{\widetilde{\mathit{VU}}}_{ik}\right){\tilde{w}}_{ik}$$

(24)

Concerning the criterion relationship, the linguistic declaration of the relationship given by expert $E_j$ with group $O_h$ is denoted by ${\tilde{c}}_{jh}^{\text{'}}$, and$O{C}_i$ is the collection of groups that user $U_i$ belongs to. According to Equation (20), the relationship ${\tilde{R}}_{ji}$ of expert $E_j$ with user $U_i$ is aggregated by

$${\tilde{R}}_{ji}=\{\begin{array}{c}\underset{O_h\in O{C}_i}{\max }{\tilde{c}}_{jh}^{\text{'}}, \mathrm{if} \mathrm{the} \mathrm{expert} \mathrm{has} \mathrm{the} \mathrm{generous} \mathrm{preference}. \\ \underset{O_h\in O{C}_i}{\min }{\tilde{c}}_{jh}^{\text{'}},\mathrm{if} \mathrm{the} \mathrm{expert} \mathrm{has} \mathrm{the} \mathrm{cautious} \mathrm{preference}.\end{array}$$

(25)

With regard to the criterion of feedback, the linguistic rating given by user $U_i$ to expert $E_j$ at the $k$th time is denoted by ${\tilde{f}}_{ijk}^{\text{'}}$. With Equation (21), the evaluation value of expert $E_j$ on feedback can be aggregated by

$${\tilde{F}}_{ij}=\frac{{{\displaystyle \sum }}_{k=1}^m{\tilde{f}}_{ijk}^{\text{'}}\times \frac{1}{e^{\tau \left(t_{now}-t_k\right)}}}{{{\displaystyle \sum }}_{k=1}^m\frac{1}{e^{\tau \left(t_{now}-t_k\right)}}}$$

(26)

For the criterion of trust, it can be rated directly. If expert $E_j$ does not rate user $U_i$ on trust, then the missing value needs to be propagated with Equations (14)–(16).$ITS\left(u_i\right)$ is the set of users who trust user $U_i$, $OTS\left(u_i\right)$ is the set of users whom user $U_i$ directly trusts. The direct linguistic rating of user $U_i$ given by user $U_{t^{*}}$ is represented by ${\tilde{\varpi }}_{t^{*},i}$, and the direct linguistic rating of user $U_k$ given by expert $E_j$ on trust is denoted by ${\tilde{\rho }}_{i,k}$. Firstly, with Equation (14), the strength ${\widetilde{ST}}_{j,t}$ of the trust path from expert $E_j$ to user $U_i$ is obtained. Then the reliable inlink-neighbor of $U_i$ is derived by $U_{t^{*}}=\mathit{arg}\underset{u_t\in ITS\left(u_i\right)}{\mathit{max}}{\widetilde{ST}}_{j,t}$. Finally, with Equation (16), expert $e_j$’s indirect trust ${\tilde{T}}_{j,i}$ in user $u_i$ is estimated by ${\tilde{T}}_{j,i}=\min \left\{{\widetilde{\mathit{ST}}}_{j,t^{*}}^{*},{\tilde{\varpi }}_{t^{*},i}\right\}$.

3.2.2. Measuring the Satisfaction

Let the value derived from the ratings of user $U_i$ given expert $E_j$ on the criterion $C_y^u$ be represented ${\tilde{u}}_{jyi}=\left(a_1,a_2,a_3,a_4\right)$ and the corresponding value of the goal provided by expert $E_j$ be ${\tilde{G}}_{jy}^{u*}=\left(A_1,A_2,A_3,A_4\right)$. If the value of goals is not provided, the default value is set by

$${\tilde{G}}_{jy}^{u*}=\underset{i}{\max }\left\{{\tilde{u}}_{jyi}\right\}$$

(27)

As the value of a goal and the rating value are both represented by trapezoidal fuzzy numbers, the common area [24] can be used as the satisfaction area to measure the satisfaction, as is shown in Figure 4.

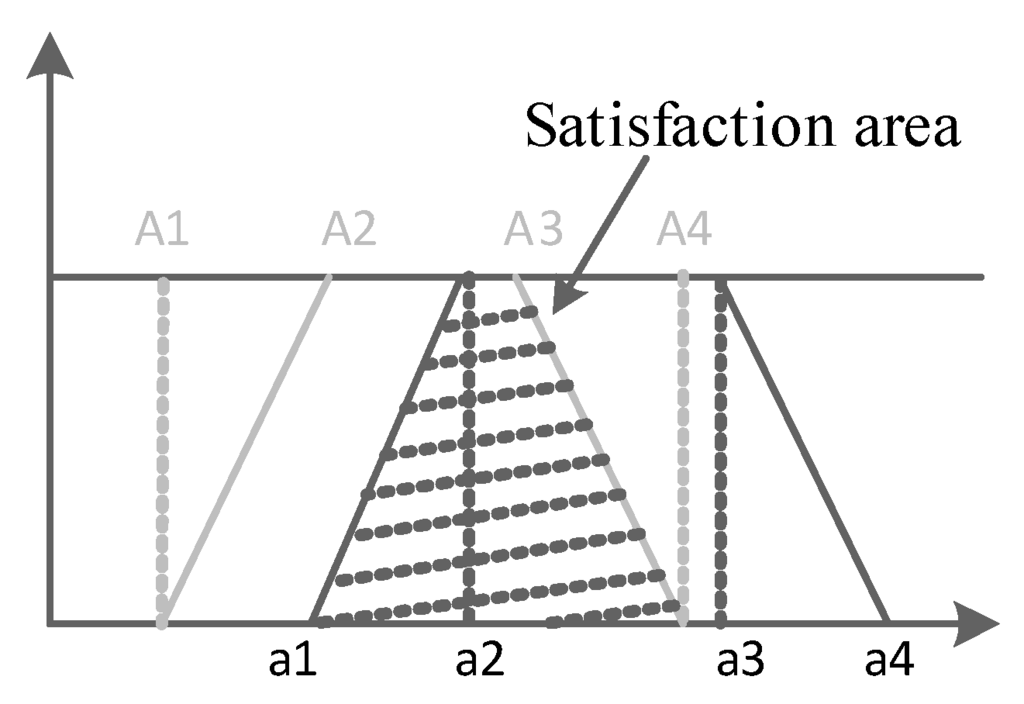
Figure 4. Satisfaction area.

The smaller the gap area is, the less the dissatisfaction is.

The information content of expert $E_j$’s satisfaction with the user $U_i$ with respect to the criterion $C_y^u$ can be defined as

$$\begin{array}{l}{S}_{jyi}={\log }_2\frac{\text{System Area}}{\text{Satisfaction Area}}\\ =\{\begin{array}{c}{\log }_2\frac{\left(a_4-a_1+a_3-a_2\right)\times \left(A_2-A_1-a_3+a_4\right)}{{\left(a_4-A_1\right)}^2} if\left(A_2\ge a_3\right)\wedge \left(A_1<a_4\right)\\ {\log }_2\frac{\left(a_4-a_1\right)+\left(a_3-a_2\right)}{\left(a_3-A_2\right)+\left(a_4-A_1\right)} if\left(A_3\ge a_3\ge A_2\right)\\ {\log }_2\frac{\left(a_4-a_1\right)+\left(a_3-a_2\right)}{\left(A_3-a_2\right)+\left(A_4-a_1\right)} if\left(A_3\ge a_2\ge A_2\right)\\ {\log }_2\frac{\left(a_4-a_1+a_3-a_2\right)\left(a_2-a_1-A_3+A_4\right)}{{\left(A_4-a_1\right)}^2} if\left(A_3\le a_2\right)\wedge \left(A_4>a_1\right)\end{array}\end{array}$$

(28)

When there are no common areas, the gap area [31] between the system area and design area represents dissatisfactions, and the gap area can be used as a dissatisfaction area, as is shown in Figure 5. The smaller the dissatisfaction area is, the less the dissatisfaction is.

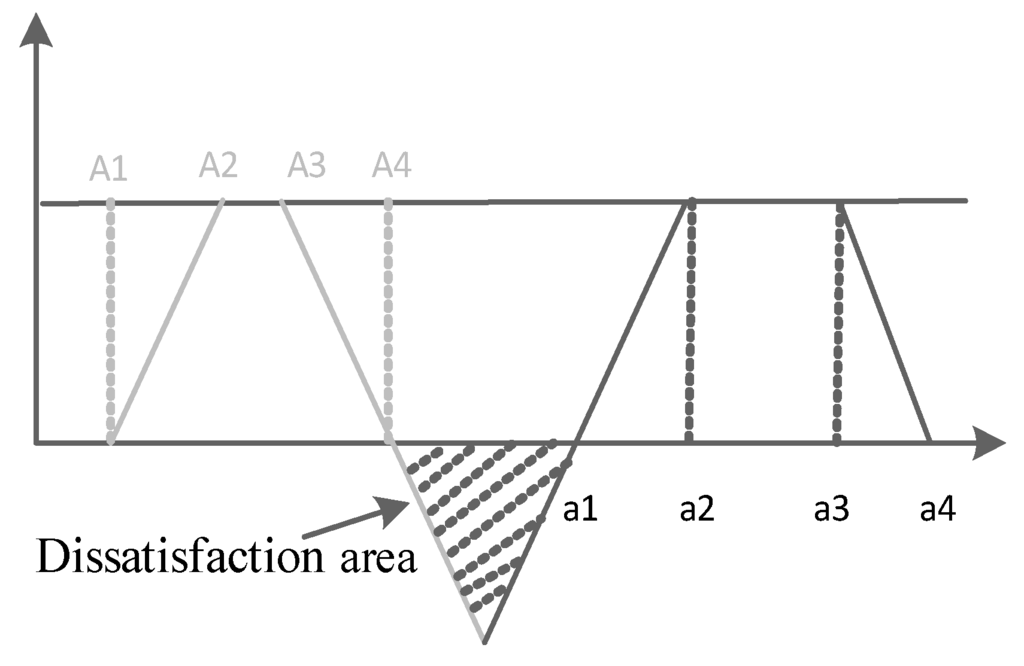
Figure 5. Dissatisfaction area.

Thus, the information content of expert $E_j$’s dissatisfaction with user $U_i$ with respect to criterion $C_y^u$ is defined as

$${\widetilde{DF}}_{jyi}=\{\begin{array}{c}{\log }_2\frac{\left(a_4-a_1+a_3-a_2\right)\left(A_3-A_4-a_2+a_1\right)}{{\left(a_1-A_4\right)}^2} if \left(a_1>A_4\right)\\ {\log }_2\frac{\left(a_4-a_1+a_3-a_2\right)\left(a_3-a_4-A_2+A_1\right)}{{\left(A_1-a_4\right)}^2} if \left(a_4<A_1\right)\end{array}$$

(29)

In fact, the opposite number of the information content of dissatisfaction indicates the information content of satisfaction. Thus, the information content of expert $E_j$’s satisfaction with user $U_i$ can be defined as

$$S_{jyi}=\{\begin{array}{c}{\log }_2\frac{\left(a_4-a_1+a_3-a_2\right)\times \left(A_2-A_1-a_3+a_4\right)}{{\left(a_4-A_1\right)}^2} if\left(A_2\ge a_3\right)\wedge \left(A_1<a_4\right)\\ {\log }_2\frac{\left(a_4-a_1\right)+\left(a_3-a_2\right)}{\left(a_3-A_2\right)+\left(a_4-A_1\right)} if\left(A_3\ge a_3\ge A_2\right)\\ {\log }_2\frac{\left(a_4-a_1\right)+\left(a_3-a_2\right)}{\left(A_3-a_2\right)+\left(A_4-a_1\right)} if\left(A_3\ge a_2\ge A_2\right)\\ \begin{array}{c}{\log }_2\frac{\left(a_4-a_1+a_3-a_2\right)\left(a_2-a_1-A_3+A_4\right)}{{\left(A_4-a_1\right)}^2} if\left(A_3\le a_2\right)\wedge \left(A_4>a_1\right)\\ -{\log }_2\frac{\left(a_4-a_1+a_3-a_2\right)\left(A_3-A_4-a_2+a_1\right)}{{\left(a_1-A_4\right)}^2} if\left(a_1>A_4\right)\\ \begin{array}{c}-{\log }_2\frac{\left(a_4-a_1+a_3-a_2\right)\left(a_3-a_4-A_2+A_1\right)}{{\left(A_1-a_4\right)}^2} if\left(a_4<A_1\right)\\ \begin{array}{c}{\log }_2\frac{\left(a_4-a_1\right)+\left(a_3-a_2\right)}{2\epsilon } if a_1=A_4 or a_4=A_1\end{array}\end{array}\end{array}\end{array}$$

(30)

where $\epsilon$ is the positive value that is far smaller than the minimal common area.

Accordingly, user $U_i$’s satisfaction with expert $E_j$ with respect to each criterion can be measured in the same way.

The overall satisfaction can be measured by summing the information content with regard to each criterion along with the corresponding weights. The overall information content of expert $E_j$’s satisfaction with user $U_i$ can be derived by

$${\alpha }_{ji}=D\left({\displaystyle \sum }_{y=1}^m{\tilde{\zeta }}_{jy}\times S_{jyi}\right)$$

(31)

Correspondingly, the overall information content of user $U_j$’s satisfaction with expert $E_i$ can be derived by

$${\beta }_{ij}=D\left({\displaystyle \sum }_{z=1}^n{\tilde{\eta }}_{iz}\times S_{izj}\right)$$

(32)

3.2.3. Constructing the Optimization Model

The match is optimal when the sum of the information content of the satisfaction is at its minimum [30]. Let $x_{ij}$ $\left(i=1,2,\cdots ,p,j=1,2,\cdots ,q\right)$ be a binary variable that denotes whether expert $E_j$ $\left(j=1,2,\cdots ,p\right)$ is matched with user $U_i$ $\left(i=1,2,\cdots ,q\right)$ or not, i.e., if expert $E_j$ $\left(j=1,2,\cdots ,p\right)$ is matched with user $U_i$ $\left(i=1,2,\cdots ,q\right)$, then $x_{ji}$ = 1; otherwise, $x_{ji}$ = 0. The optimization model is established as

$$\begin{gathered} \min Z={\displaystyle \sum }_{i=1}^q{\displaystyle \sum }_{j=1}^{p}D\left({\alpha }_{ji}\times {\tilde{w}}_j\right)\times x_{ji}+{\displaystyle \sum }_{i=1}^q{\displaystyle \sum }_{j=1}^{p}D\left({\beta }_{ij}\times {\tilde{v}}_i\right)\times x_{ji} \\ \text{s.t.\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}} \\ {\displaystyle \sum }_{i=1}^q{x}_{ji}\le {\eta }_j^{max} \\ {\eta }_j^{min}\le {\displaystyle \sum }_{i=1}^q{x}_{ji} \\ {\displaystyle \sum }_{j=1}^p{x}_{ji}\le {\lambda }_i^{max} \\ {\lambda }_i^{min}\le {\displaystyle \sum }_{j=1}^p{x}_{ji} \\ x_{ji}\in \left\{0,1\right\},j=1,2,\cdots ,p, i=1,2,\cdots ,q \end{gathered}$$

(33)

where ${\eta }_j^{max}$ and ${\eta }_j^{min}$ are the maximum and minimum numbers of users that can be accepted by expert $E_j$, ${\lambda }_i^{max}$ and ${\lambda }_i^{min}$ are the maximum and minimum numbers of experts that user $U_i$ can consult. By resolving the model, according to the value of variable $x_{ji}$, the optimal match with the global highest level of satisfaction can be obtained.

4. Evaluations

In this section, the feasibility and effectiveness of the proposed approach are evaluated. The experiment is carried out with the match between users and experts in a scene of information system design and development. Novices are users and the people that have rich experience in system design and development are experts. Each user and each expert is required to use linguistic terms in Table 1 to express their opinions.

Table 1. Linguistic terms.

Linguistic Variables	Fuzzy Numbers
Very low (VL)	(0,1,2,3)
Low (L)	(1,2,3,4)
Medium (M)	(3,4,5,6)
High (H)	(4,5,6,7)
Very low (VH)	(5,6,7,8)

The criteria of expertise ($C_1^e$), trust ($C_2^e$) and feedback ($C_3^e$) are used to evaluate experts and trust ($C_1^u$), relationship ($C_2^u$) and knowledge distance ($C_3^u$) are used to evaluate users. Since the expertise, knowledge distance and relationship cannot be rated directly, the corresponding indirect criteria, which include task relevance $\left(C_1^{\prime e}\right)$, direct relationship ($C_2^{\prime u}$) and expected expertise ($C_3^{\prime u}$), are used. The criteria of trust and feedback are rated directly. Besides the criteria of trust and feedback, users and experts give ratings with respect to the indirect criteria. The rating values are processed to drive the value of ratings with respect to the criteria.

In the following, the definition and measurement of criteria in a fuzzy linguistic setting along with the calculation of satisfaction degrees are explained.

The derived information content of users’ satisfaction with experts is shown in Table 2. In the table, we can see the level of satisfaction with respect to each criterion. The smaller the value is, the higher the level of satisfaction is. For example, considering criterion $C_1^e$, user $U_6$ is more satisfied with expert $E_1$ than expert $E_2$.

Table 2. Information content of users’ satisfaction with experts.

User	${\mathit{E}}_{\mathbf{1}}$			${\mathit{E}}_{\mathbf{2}}$			${\mathit{E}}_{\mathbf{3}}$			${\mathit{E}}_{\mathbf{4}}$
	${\mathit{C}}_{\mathbf{1}}^{\mathit{e}}$	${\mathit{C}}_{\mathbf{2}}^{\mathit{e}}$	${\mathit{C}}_{\mathbf{3}}^{\mathit{e}}$	${\mathit{C}}_{\mathbf{1}}^{\mathit{e}}$	${\mathit{C}}_{\mathbf{2}}^{\mathit{e}}$	${\mathit{C}}_{\mathbf{3}}^{\mathit{e}}$	${\mathit{C}}_{\mathbf{1}}^{\mathit{e}}$	${\mathit{C}}_{\mathbf{2}}^{\mathit{e}}$	${\mathit{C}}_{\mathbf{3}}^{\mathit{e}}$	${\mathit{C}}_{\mathbf{1}}^{\mathit{e}}$	${\mathit{C}}_{\mathbf{2}}^{\mathit{e}}$	${\mathit{C}}_{\mathbf{3}}^{\mathit{e}}$
${\mathit{U}}_{\mathbf{1}}$	0.14	1.00	1.00	0.41	3.00	1.00	0.37	0.00	1.00	−6.65	3.00	3.00
${\mathit{U}}_{\mathbf{2}}$	0.14	1.00	0.00	0.36	1.00	0.00	0.22	0.00	0.00	−5.06	1.00	0.00
${\mathit{U}}_{\mathbf{3}}$	0.15	1.00	1.00	0.37	4.99	3.00	0.28	0.00	0.00	−4.96	1.00	3.00
${\mathit{U}}_{\mathbf{4}}$	0.11	0.00	0.00	0.39	1.00	3.00	0.31	0.00	0.00	−6.04	1.00	3.00
${\mathit{U}}_{\mathbf{5}}$	0.18	1.00	1.00	0.38	0.00	1.00	0.28	0.00	0.00	−5.35	3.00	3.00
${\mathit{U}}_{\mathbf{6}}$	0.22	1.00	3.00	0.33	3.00	3.00	0.20	0.00	3.00	−3.94	0.00	0.00
${\mathit{U}}_{\mathbf{7}}$	0.21	0.00	3.00	0.38	0.00	0.00	0.23	0.00	1.00	−5.03	3.00	3.00
${\mathit{U}}_{\mathbf{8}}$	0.05	3.00	1.00	0.43	3.00	1.00	0.50	0.00	1.00	−14.09	3.00	1.00
${\mathit{U}}_{\mathbf{9}}$	0.19	1.00	0.00	0.39	3.00	3.00	0.30	1.00	0.00	−5.44	1.00	3.00
${\mathit{U}}_{\mathbf{10}}$	0.19	3.00	1.00	0.38	3.00	0.00	0.21	0.00	0.00	−4.99	1.00	3.00
${\mathit{U}}_{\mathbf{11}}$	0.21	0.00	1.00	0.40	1.00	3.00	0.24	0.00	1.00	−5.23	1.00	1.00
${\mathit{U}}_{\mathbf{12}}$	0.14	0.00	0.00	0.40	0.00	1.00	0.36	0.00	0.00	−6.39	3.00	1.00
User	${\mathit{E}}_{\mathbf{5}}$			${\mathit{E}}_{\mathbf{6}}$			${\mathit{E}}_{\mathbf{7}}$			${\mathit{E}}_{\mathbf{8}}$
	${\mathit{C}}_{\mathbf{1}}^{\mathit{e}}$	${\mathit{C}}_{\mathbf{2}}^{\mathit{e}}$	${\mathit{C}}_{\mathbf{3}}^{\mathit{e}}$	${\mathit{C}}_{\mathbf{1}}^{\mathit{e}}$	${\mathit{C}}_{\mathbf{2}}^{\mathit{e}}$	${\mathit{C}}_{\mathbf{3}}^{\mathit{e}}$	${\mathit{C}}_{\mathbf{1}}^{\mathit{e}}$	${\mathit{C}}_{\mathbf{2}}^{\mathit{e}}$	${\mathit{C}}_{\mathbf{3}}^{\mathit{e}}$	${\mathit{C}}_{\mathbf{1}}^{\mathit{e}}$	${\mathit{C}}_{\mathbf{2}}^{\mathit{e}}$	${\mathit{C}}_{\mathbf{3}}^{\mathit{e}}$
${\mathit{U}}_{\mathbf{1}}$	0.88	3.00	3.00	0.30	1.00	3.00	0.00	0.00	3.00	1.95	3.00	3.00
${\mathit{U}}_{\mathbf{2}}$	0.68	1.00	0.00	0.28	1.00	3.00	0.00	1.00	3.00	1.64	1.00	0.00
${\mathit{U}}_{\mathbf{3}}$	0.58	1.00	3.00	0.25	0.00	3.00	0.00	0.00	1.00	1.56	4.99	−3.00
${\mathit{U}}_{\mathbf{4}}$	0.83	1.00	3.00	0.26	0.00	3.00	0.00	0.00	1.00	1.80	1.00	−3.00
${\mathit{U}}_{\mathbf{5}}$	0.69	1.00	3.00	0.29	−3.00	3.00	0.00	0.00	3.00	1.81	−3.00	3.00
${\mathit{U}}_{\mathbf{6}}$	0.38	3.00	3.00	0.12	3.00	3.00	0.00	1.00	3.00	1.50	1.00	3.00
${\mathit{U}}_{\mathbf{7}}$	0.56	−3.00	3.00	0.24	−3.00	3.00	0.00	1.00	3.00	1.74	1.00	3.00
${\mathit{U}}_{\mathbf{8}}$	1.16	1.00	1.00	0.51	0.00	3.00	0.05	0.00	3.00	2.10	−3.00	1.00
${\mathit{U}}_{\mathbf{9}}$	0.69	3.00	3.00	0.29	1.00	1.00	0.00	0.00	1.00	1.85	0.00	3.00
${\mathit{U}}_{\mathbf{10}}$	0.54	3.00	−3.00	0.23	1.00	3.00	0.00	1.00	1.00	1.64	3.00	−3.00
${\mathit{U}}_{\mathbf{11}}$	0.53	0.00	3.00	0.24	4.99	1.00	0.00	0.00	1.00	1.73	4.99	0.00
${\mathit{U}}_{\mathbf{12}}$	0.88	1.00	3.00	0.29	0.00	1.00	0.00	0.00	1.00	1.94	−3.00	3.00

In order to measure the satisfaction of users on expertise ($C_1^e$), users are required to evaluate the relevance of completed tasks to knowledge needs. For example, $U_6$’s ratings of the four completed tasks are L, L, VH and VH. The predefined belonging degrees of the four completed tasks to each knowledge area are (L, L, VL, VH, L), (VL, VH, VH, M, M), (VH, L, H, M, M) and (VL, VL, VL, L, VH), respectively. Then, with Equation (12), the knowledge needs of user $U_6$ can be derived as

$$\begin{array}{l}{\widetilde{VN}}_6\hfill \\ =\left(\begin{array}{c}\frac{L\otimes L\oplus L\otimes VL\oplus VH\otimes VH\oplus VH\otimes VL}{L\oplus L\oplus VH\oplus VH},\frac{L\otimes L\oplus L\otimes VL\oplus VH\otimes VH\oplus VH\otimes VL}{L\oplus L\oplus VH\oplus VH},\\ \frac{L\otimes L\oplus L\otimes VL\oplus VH\otimes VH\oplus VH\otimes VL}{L\oplus L\oplus VH\oplus VH},\frac{L\otimes L\oplus L\otimes VL\oplus VH\otimes VH\oplus VH\otimes VL}{L\oplus L\oplus VH\oplus VH},\frac{L\otimes L\oplus L\otimes VL\oplus VH\otimes VH\oplus VH\otimes VL}{L\oplus L\oplus VH\oplus VH}\end{array}\right)\hfill \\ =\left(\left(2.10,2.93,3.83,4.77\right),\left(1.00,2.21,3.33,4.41\right),\left(2.10,3.14,4.17,5.18\right),\left(2.40,3.57,4.67,5.73\right),\left(3.60,4.43,5.33,6.27\right)\right)\hfill \end{array}$$

The predefined profile of expert $E_1$ is (VL, VH, VH, H, H). With Equation (13), the value of expertise ($C_1^e$) of expert $E_1$ for user $U_6$ can be obtained by

$$\begin{array}{l}{\widetilde{VM}}_{6,1}\hfill \\ =\frac{\begin{array}{c}\hfill \left(2.10,2.93,3.83,4.77\right)\otimes VL\oplus \left(1.00,2.21,3.33,4.41\right)\otimes VH\oplus \left(2.10,3.14,4.17,5.18\right)\otimes VH\oplus \left(2.40,3.57,4.67,5.73\right)\otimes H\hfill \\ \oplus \left(3.60,4.43,5.33,6.27\right)\otimes H\end{array}}{\left(2.10,2.93,3.83,4.77\right)\oplus \left(1.00,2.21,3.33,4.41\right)\oplus \left(2.10,3.14,4.17,5.18\right)\oplus \left(2.40,3.57,4.67,5.73\right)\oplus \left(3.60,4.43,5.33,6.27\right)}\hfill \\ =\left(3.53,4.61,5.63,6.64 \right)\hfill \end{array}$$

In the same way, the values of expertise ($C_1^e$) of other experts for user $U_6$ are derived. The derived maximum value is (3.84, 4.87, 5.88, 6.87). Based on Equation (30), the information content of user $U_6$’s satisfaction with expert $E_1$ on expertise ($C_1^e$) is obtained by

$$\begin{array}{cc}{S}_{6,1,1}\hfill & ={\log }_2\frac{\text{System Area}}{\text{Satisfaction Area}}\hfill \\ & ={\log }_2\frac{\left(6.64-3.53+5.63-4.61\right)\times \left(4.87-3.84-5.63+6.64\right)}{{\left(6.64-3.53\right)}^2}\\ & =0.22\end{array}$$

User $U_6$ consulted with expert $E_4$ once and the rating value is VH. With Equation (21), the aggregated rating of expert $E_4$ for user $U_6$ on feedback ($C_3^e$) can be derived by

$${\tilde{F}}_{6,4}^u=\frac{VH\left(\frac{1}{e^{\tau \left(12-10\right)}}\right)}{\left(\frac{1}{e^{\tau \left(12-10\right)}}\right)}=VH=\left(5,6,7,8\right)$$

Likewise, the derived maximum value of feedback for user $U_6$ is $VH$. According to Equation (29), the information content of user $U_6$’s satisfaction with expert $E_4$ on feedback ($C_3^e$) is obtained by

$$S_{6,2,4}={\log }_2\frac{\left(8-5\right)+\left(7-6\right)}{\left(7-6\right)+\left(8-5\right)}=0$$

For trust ($C_2^e$), the rating value of expert $E_1$ given by user $U_6$ is missing. The direct rating of expert $E_2$ and expert $E_4$ on trust given by user $U_6$ are M and VH, respectively. Meanwhile, the direct trust rating of $E_1$ given by experts $E_2$ and $E_4$ are M and H. Therefore, Equations (14)–(16) are used to predict trust rating values as follows:

$$E_{*}=\arg \text{max}\left\{{\widetilde{ST}}_{6,2},{\widetilde{ST}}_{6,4}\right\}=\arg \text{max}\left\{M,VH\right\}=E_4$$

$${\tilde{T}}_{6,1}=\min \left\{\text{max}\left\{{\widetilde{\mathit{ST}}}_{6,2},{\widetilde{\mathit{ST}}}_{6,4}\right\},{\varpi }_{*,1}\right\}=\min \left\{VH,H\right\}=H$$

As the derived maximum value of $U_6$’s trust on experts is VH, according to Equation (21), the information content of user $U_6$’s satisfaction with expert $E_1$ on trust ($C_2^e$) is 1.

The derived information content of experts’ satisfaction with users is shown in Table 3.

Table 3. Information content of experts’ satisfaction with users.

Expert	${\mathit{U}}_{\mathbf{1}}$			${\mathit{U}}_{\mathbf{2}}$			${\mathit{U}}_{\mathbf{3}}$			${\mathit{U}}_{\mathbf{4}}$
	${\mathit{C}}_{\mathbf{1}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{2}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{3}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{1}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{2}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{3}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{1}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{2}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{3}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{1}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{2}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{3}}^{\mathit{u}}$
${\mathit{E}}_{\mathbf{1}}$	0.00	2.00	2.23	1.00	2.00	0.64	1.00	2.00	1.74	1.00	2.00	2.37
${\mathit{E}}_{\mathbf{2}}$	4.99	−0.25	0.59	1.00	−0.25	2.29	1.00	−0.25	0.93	1.00	−0.25	0.67
${\mathit{E}}_{\mathbf{3}}$	0.00	1.00	1.80	0.00	1.00	1.86	0.00	1.00	1.98	0.00	1.00	0.22
${\mathit{E}}_{\mathbf{4}}$	0.00	−0.25	2.87	1.00	−0.25	0.59	1.00	−0.25	1.51	1.00	−0.25	3.00
${\mathit{E}}_{\mathbf{5}}$	0.00	2.00	2.43	1.00	2.00	0.17	0.00	2.00	2.52	0.00	2.00	1.17
${\mathit{E}}_{\mathbf{6}}$	0.00	1.00	0.44	3.00	1.00	3.54	1.00	1.00	0.71	3.00	1.00	2.13
${\mathit{E}}_{\mathbf{7}}$	0.00	−0.25	2.31	1.00	−0.25	0.18	1.00	−0.25	1.74	1.00	−0.25	1.81
${\mathit{E}}_{\mathbf{8}}$	0.00	2.00	3.00	1.00	2.00	0.26	0.00	2.00	2.00	0.00	2.00	1.11
Expert	${\mathit{U}}_{\mathbf{5}}$			${\mathit{U}}_{\mathbf{6}}$			${\mathit{U}}_{\mathbf{7}}$			${\mathit{U}}_{\mathbf{8}}$
	${\mathit{C}}_{\mathbf{1}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{2}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{3}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{1}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{2}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{3}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{1}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{2}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{3}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{1}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{2}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{3}}^{\mathit{u}}$
${\mathit{E}}_{\mathbf{1}}$	1.00	2.00	1.65	1.00	1.00	1.84	4.99	1.00	0.68	0.00	1.00	0.50
${\mathit{E}}_{\mathbf{2}}$	0.00	−0.25	1.95	1.00	2.00	1.37	4.99	2.00	1.71	0.00	2.00	0.23
${\mathit{E}}_{\mathbf{3}}$	3.00	1.00	0.76	3.00	2.00	2.46	3.00	2.00	0.50	0.00	2.00	−0.69
${\mathit{E}}_{\mathbf{4}}$	1.00	−0.25	0.12	0.00	2.00	−0.59	1.00	2.00	1.63	1.00	2.00	0.50
${\mathit{E}}_{\mathbf{5}}$	1.00	2.00	2.59	1.00	1.00	3.79	1.00	1.00	2.79	0.00	1.00	−0.19
${\mathit{E}}_{\mathbf{6}}$	1.00	1.00	−0.72	−3.00	2.00	0.81	0.00	2.00	−1.01	1.00	2.00	0.68
${\mathit{E}}_{\mathbf{7}}$	1.00	−0.25	−1.41	1.00	2.00	−0.97	1.00	2.00	−0.93	0.00	2.00	1.27
${\mathit{E}}_{\mathbf{8}}$	1.00	2.00	2.20	1.00	1.00	2.52	1.00	1.00	1.40	0.00	1.00	0.50
Expert	${\mathit{U}}_{\mathbf{9}}$			${\mathit{U}}_{\mathbf{10}}$			${\mathit{U}}_{\mathbf{11}}$			${\mathit{U}}_{\mathbf{12}}$
	${\mathit{C}}_{\mathbf{1}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{2}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{3}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{1}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{2}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{3}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{1}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{2}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{3}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{1}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{2}}^{\mathit{u}}$	${\mathit{C}}_{\mathbf{3}}^{\mathit{u}}$
${\mathit{E}}_{\mathbf{1}}$	1.00	1.00	2.03	0.00	1.00	2.71	1.00	1.00	2.03	0.00	2.00	2.52
${\mathit{E}}_{\mathbf{2}}$	1.00	2.00	0.93	0.00	2.00	−1.07	0.00	2.00	1.77	0.00	−0.25	1.21
${\mathit{E}}_{\mathbf{3}}$	0.00	2.00	−0.05	0.00	2.00	−1.98	3.00	2.00	0.78	3.00	1.00	0.26
${\mathit{E}}_{\mathbf{4}}$	1.00	2.00	−0.10	1.00	2.00	−0.50	1.00	2.00	4.02	1.00	−0.25	3.52
${\mathit{E}}_{\mathbf{5}}$	1.00	1.00	1.62	1.00	1.00	2.22	1.00	1.00	2.87	0.00	2.00	3.31
${\mathit{E}}_{\mathbf{6}}$	0.00	2.00	1.44	0.00	2.00	−0.47	3.00	2.00	0.51	−3.00	1.00	0.00
${\mathit{E}}_{\mathbf{7}}$	0.00	2.00	0.85	0.00	2.00	0.33	1.00	2.00	1.98	0.00	−0.25	1.68
${\mathit{E}}_{\mathbf{8}}$	0.00	1.00	1.67	1.00	1.00	2.33	1.00	1.00	2.58	0.00	2.00	3.09

The rating of user $U_6$ given by expert $E_4$ with respect to relationship ($C_2^u$) is VH. The expert chooses the caution preference. According to Equation (20), the corresponding value is obtained by

$${\tilde{R}}_{4,6}=\max \left(VH\right)=VH$$

The derived maximum value of expert $E_4$’s relationship with users is VH. With Equation (30), the obtained information content of the corresponding satisfaction is 0.

The rating of the expected knowledge level of users given by expert $E_4$ in the five knowledge areas is (VL, VL, L, M, VH) and the predefined profile of user $U_6$ is (VL, VL, VL, M, VL). The information content of user $E_4$’s satisfaction with expert $U_6$ on knowledge distance ($C_3^u$) in each knowledge area can be calculated directly with Equation (30). The calculation results are 0, 0, 1, 0 and 4. The knowledge needs of user $U_6$ in each knowledge area are used as weights. With Equation (22), the weighted overall information content can be derived by

$$S_{4,3,6}^{\text{'}}=\frac{\left(0\times 3.40+0\times 2.75+ 1\times 3.65+0\times 4.10-4 \times 4.90\right)}{3.40+2.75+3.65+4.10+4.90}=-0.59$$

The weights of criteria are given directly by experts and users. The weight of the criteria for evaluating experts and the weight of the criteria for evaluating users are shown in Table 4 and Table 5, respectively. Each person has his or her own preference about the importance. The two tables show the importance of the criteria for each person. In Table 4, we see that user $U_1$. thinks the first two criteria are more important for him. In the calculation of his satisfaction degrees, the two criteria play more important roles.

Table 4. Weight of the criteria for evaluating experts given by users.

	${\mathit{U}}_{\mathbf{1}}$	${\mathit{U}}_{\mathbf{2}}$	${\mathit{U}}_{\mathbf{3}}$	${\mathit{U}}_{\mathbf{4}}$	${\mathit{U}}_{\mathbf{5}}$	${\mathit{U}}_{\mathbf{6}}$	${\mathit{U}}_{\mathbf{7}}$	${\mathit{U}}_{\mathbf{8}}$	${\mathit{U}}_{\mathbf{9}}$	${\mathit{U}}_{\mathbf{10}}$	${\mathit{U}}_{\mathbf{11}}$	${\mathit{U}}_{\mathbf{12}}$
${\mathit{C}}_{\mathbf{1}}^{\mathit{e}}$	VH	H	VH	H	VH	VH	H	VH	H	VH	M	VH
${\mathit{C}}_{\mathbf{2}}^{\mathit{e}}$	VH	VH	VH	H	H	VH	M	M	VH	M	M	H
${\mathit{C}}_{\mathbf{3}}^{\mathit{e}}$	H	VH	H	H	VH	H	L	M	VH	VH	M	VH

Table 5. Weight of the criteria for evaluating users given by experts.

	${\mathit{E}}_{\mathbf{1}}$	${\mathit{E}}_{\mathbf{2}}$	${\mathit{E}}_{\mathbf{3}}$	${\mathit{E}}_{\mathbf{4}}$	${\mathit{E}}_{\mathbf{5}}$	${\mathit{E}}_{\mathbf{6}}$	${\mathit{E}}_{\mathbf{7}}$	${\mathit{E}}_{\mathbf{8}}$
${\mathit{C}}_{\mathbf{1}}^{\mathit{u}}$	VH	H	H	H	H	M	L	M
${\mathit{C}}_{\mathbf{2}}^{\mathit{u}}$	M	H	VL	M	M	VL	VH	M
${\mathit{C}}_{\mathbf{3}}^{\mathit{u}}$	M	M	M	H	M	VH	H	H

In the evaluation, weights of experts and users are equal. In order to guarantee each user can get help and avoid the selection of experts from the matching results again, the values of ${\mathsf{\lambda }}_i^{min}$ and ${\mathsf{\lambda }}_i^{max}$ $\left(j=1,2,\cdots ,12\right)$ are set to 1, which means one user can only accept one expert. In order to avoid concentrating on the small number of experts, the value of ${\mathsf{\eta }}_j^{max}\left(j=1,2,\cdots ,8\right)$ is set to 2 and the value of ${\mathsf{\eta }}_j^{min}\left(j=1,2,\cdots ,8\right)$ is set to 1. Each expert can accept two users at most.

According to Equation (33), the objective function is defined as

$$\min Z^{\prime }={\displaystyle \sum }_{j=1}^8{\displaystyle \sum }_{i=1}^{12}{\displaystyle \sum }_{y=1}^{3}D\left({\tilde{\zeta }}_{jy}\times S_{jyi}\right)\times x_{ji}+{\displaystyle \sum }_{j=1}^8{\displaystyle \sum }_{i=1}^{12}{\displaystyle \sum }_{z=1}^{3}D\left({\tilde{\eta }}_{iz}\times S_{izj}\right)\times x_{ji}$$

Thus, the optimal model is constructed as

$$\begin{array}{c}\min Z^{\prime }={\displaystyle {\displaystyle \sum }_{j=1}^8{\displaystyle \sum }_{i=1}^{12}}\left({\displaystyle {\displaystyle \sum }_{y=1}^3}D\left({\tilde{\zeta }}_{iy}\times S_{jyi}\right)+{\displaystyle {\displaystyle \sum }_{z=1}^3}D\left({\tilde{\eta }}_{jz}\times S_{izj}\right)\right)\times x_{ji}\\ \begin{array}{cc}=31.90x_{11}& +25.62x_{12}+36.30x_{13}+26.78x_{14}+36.06x_{15}+43.69x_{16}+48.69x_{17}+25.09x_{18}\\ & +27.69x_{19}+37.88x_{110}+25.61x_{111}+21.23x_{112}+56.49x_{21}+22.92x_{22}\hfill \\ & +59.68x_{23}+31.26x_{24}+16.39x_{25}+60.77x_{26}+48.29x_{27}+33.27x_{28}\hfill \\ & +61.82x_{29}+22.15x_{210}+38.73x_{211}+13.19x_{212}+18.02x_{31}+11.61x_{32}\hfill \\ & +12.25x_{33}+4.67x_{34}+34.81x_{35}+48.35x_{36}+26.03x_{37}+8.14x_{38}+11.37x_{39}\hfill \\ & -3.98x_{310}+29.00x_{311}+22.03x_{312}+93.92x_{41}+41.94x_{42}+67.88x_{43}\hfill \\ & +76.11x_{44}+75.83x_{45}+31.36x_{46}+72.16x_{47}-56.37x_{48}+69.88x_{49}\hfill \\ & +68.17x_{410}+69.14x_{411}+88.29x_{412}+61.71x_{51}+25.59x_{52}+47.33x_{53}\hfill \\ & +40.91x_{54}+55.77x_{55}+65.78x_{56}+19.78x_{57}+20.20x_{58}+60.24x_{59}\hfill \\ & +17.72x_{510}+38.98x_{511}+54.64x_{512}+13.40x_{61}+46.00x_{62}+28.71x_{63}\hfill \\ & +47.30x_{64}+6.20x_{65}+31.523x_{66}-8.24x_{67}+15.72x_{68}+26.97x_{69}\hfill \\ & +25.46x_{610}+47.91x_{611}-3.02x_{612}+11.08x_{71}+8.38x_{72}+15.94x_{73}\hfill \\ & +16.33x_{74}+12.63x_{75}+33.18x_{76}+22.38x_{77}+20.11x_{78}+24.18x_{79}\hfill \\ & +25.84x_{710}+30.89x_{711}+14.10x_{712}+74.15x_{81}+30.46x_{82}+46.12x_{83}\hfill \\ & +14.05x_{84}+40.37x_{85}+55.59x_{86}+38.24x_{87}+11.89x_{88}+43.39x_{89}\hfill \\ & +26.49x_{810}+53.47x_{811}+41.58x_{812}\hfill \\ & \mathrm{s}.\mathrm{t}.\hfill \end{array}\end{array}$$

$$1\le {\displaystyle \sum }_{i=1}^{12}{x}_{ji}\le 2,j=1,2,\cdots ,8$$

$${\displaystyle \sum }_{j=1}^8{x}_{ji}=1,i=1,2,\cdots ,12$$

$$x_{ji}\in \left\{0,1\right\},j=1,2,\cdots 8;i=1,2,\cdots ,12.$$

By resolving the model, the derived optimal match is $\{\left(U_1,E_7\right), \left(U_2,E_5\right), \left(U_3,E_7\right),\left(U_4,E_8\right),$ $\left(U_5,E_2\right),\left(U_6,E_4\right),\left(U_7,E_6\right),\left(U_8,E_4\right),\left(U_9,E_3\right),\left(U_{10},E_3\right),\left(U_{11},E_1\right),\left(U_{12},E_6\right)\}$.

The matching results are based on ratings given by experts and users. With the optimized matching results, the maximum satisfaction degree can be obtained. It is the only optimum solution. Therefore, this match is better than any other one.

Compared with the manual selection of experts, both experts and users are more satisfied with the proposed approach.

(1)

With the proposed approach, the needs of both users and experts are identified more comprehensively because of the expression of preferences from multiple aspects. The burden of finding experts is reduced. The only requirements of users are to express their preferences instead of strenuously searching each category and browsing the descriptions of experts. Since the match is made based not only on users’ preferences but also on experts’ preferences, the experts’ satisfaction with users is improved. As a result, experts are more willing to help the users and users can get more fitting help with higher quality. Moreover, searching and contacting experts repeatedly when the one-sided chosen expert is reluctant to help the user due to disagreement with their preferences or limited interest is avoided.

(2)

For experts, especially those whose expertise level is higher, the amount of users that ask them for help is reduced and the matched users are better fits for the experts’ preferences. It eases the burden of experts and makes the matched users more acceptable. As the match is based on the rating with respect to the criteria but not rating the people directly, users can be matched with suitable but unfamiliar experts. These unfamiliar experts will be consulted and will not be excluded from the tacit knowledge-sharing. The valuable tacit knowledge resources are utilized fully and efficiently.

It can be deduced that deriving the optimized match with the integration of preferences of both users and experts leads to a higher level of satisfaction and superior performance.

5. Conclusions

In this paper, we propose an approach to matching experts and users in a fuzzy linguistic environment. The criteria for the matching are constructed and defined in the fuzzy linguistic environment. Satisfaction of both experts and users is measured based on the AD. The optimal match is made by maximizing the overall satisfaction of both experts and users. The evaluation results show that the proposed approach performs well and reveals a better satisfaction of users and experts. This study has important implications both for the development of the knowledge management system and the research of tacit knowledge-sharing. Consulting the appropriate expert is the key for tacit knowledge-sharing. With the proposed approach, the satisfaction of both users and experts is improved and the sharing of tacit knowledge is promoted.