A Minimum-Entropy Based Residual Range Cell Migration Correction for Bistatic Forward-Looking SAR

Abstract

For bistatic forward-looking synthetic aperture radar (BFSAR), motion errors induce two adverse effects on the echo, namely, azimuth phase error and residual range cell migration (RCM). Under the presumption that residual RCM is within a range resolution cell, residual RCM can be neglected, and azimuth phase error can be compensated utilizing autofocus methods. However, in the case that residual RCM exceeds the range resolution, two-dimensional defocus would emerge in the final image. Generally speaking, residual RCM is relatively small and can be neglected in monostatic SAR, while the unique characteristics of BFSAR makes the residual RCM exceeding range resolution cell inevitable. Furthermore, the excessive residual migration is increasingly encountered as resolutions become finer. To cope with such a problem, minimum-entropy based residual RCM correction method is developed in this paper. The proposed method eliminates the necessity of the parametric model when estimating the residual RCM. Moreover, it meets the practical needs of BFSAR owing to no requirement of exhaustive computation. Simulations validate the effectiveness of the proposed method.

1. Introduction

Synthetic aperture radar (SAR) has been used in many civilian and military fields with its all-weather and day/night ability [1]. However, the azimuth resolution is greatly limited in the forward-looking terrain for monostatic SAR, which restricts the application in airplane navigation, landing, etc. Then, bistatic forward-looking SAR (BFSAR) arouses researchers’ concern, and the radar platform configuration mode, resolution theory, field test, and imaging algorithms are studied [2,3,4,5,6].

In order to obtain the desired azimuth resolution, relative motion between platforms and the desired scene is the key point. Nevertheless, it introduces range cell migration (RCM), which induces a strong azimuth-range coupling [7] in BFSAR, at the same time. RCM correction is essential to compensate the RCM and eliminate the azimuth-range coupling in frequency domain imaging algorithms. However, due to the motion errors and approximations in imaging algorithms, RCM cannot be compensated completely. When the residual RCM is within a range resolution cell, residual RCM can be neglected. This is the general presumption for almost all the existing autofocus algorithms, such as phase gradient autofocus (PGA) [8], Mapdrift (MD) [9], phase difference (PD) [10] and metric-based autofocus [11,12,13,14].

Generally speaking, residual RCM is relatively small and can be neglected in monostatic SAR, while the unique characteristics of BFSAR makes the residual RCM exceeding range resolution cell inevitable. On one hand, the separated platforms of BFSAR induce motion errors much larger than the errors in monostatic SAR raw data. On the other hand, range walk, the linear component of RCM, is only taken into consideration in the imaging algorithms of BFSAR, while the range curvature and the higher order terms are neglected. However, the impacts of these higher order terms become serious when the squint angle gets larger [15,16] and the resolution gets higher. In this situation, residual RCM correction becomes a necessary procedure for BFSAR imaging.

In principle, it is possible to compute the excessive residual RCM from orbit and altitude data provided by an ancillary instrument such as inertial measurement units (IMU) and global positioning system (GPS). Nevertheless, measurement uncertainties on the data would limit the accuracy, and the data remain unknown for some unmanned aerial vehicles without ancillary instruments. Thus, signal-based residual RCM correction is indispensable.

To correct residual RCM, two alternative strategies are available. One is to estimate the azimuth phase errors firstly, and then calculate the residual RCM from the estimated azimuth phase errors by exploiting their analytical relationship. In [17], the range compressed data is processed to a new coarser range resolution so that the presumption for autofocus is met. Therefore, the azimuth phase errors can be obtained using autofocus from the new range compressed data and then the residual RCM can be calculated and compensated. However, as the azimuth phase errors are estimated in coarse resolution, the estimation precision of azimuth phase errors and residual RCM can not satisfy the demands of high resolution BFSAR. Furthermore, range curvature and the higher order terms, which are neglected in the imaging algorithms, cannot be compensated.

The other one is to estimate the residual RCM independently. The residual RCM correction method proposed in [18] is based on the image quality metrics in [19]. The residual RCM of the echoes is modeled as a polynomial, and the coefficients of this polynomial are chosen to optimize a global quantity by minimizing the image entropy or maximizing the image contrast. However, the parametric model of the residual RCM restricts the estimation accuracy.

In this paper, based on the entropy metric, we present a relatively simple non-parametric correction algorithm for BFSAR to estimate the residual RCM. In this algorithm, a coordinate descent scheme is employed, where we minimize the entropy by sequentially updating the residual RCM parameters one at a time. From the derivation, the optimal single entropy-minimizing residual RCM parameter can be obtained in analytical form as the solution of a polynomial equation, thus enabling a fast focusing of the range focusing procedure with no computation exhaustive steps such as line-search.

The remainder of this paper is organized as follows: Section 2 establishes the signal model of BFSAR in the presence of motion errors. Based on the signal model, the migration property of BFSAR is analyzed and a range focusing procedure is conducted in order to obtain the coarse range focusing echo. Section 3 analyzes the influence of residual RCM, verifies the necessity of residual RCM correction, and proposes a residual RCM estimation method based on minimal entropy. Numerical simulations are given in Section 4. Section 5 concludes this paper.

2. Problem Formulation

Signal Model of BFSAR

The emphasis of this section lies in eliminating the range migration and realizing coarse range focusing in the presence of motion errors.

The geometric model in Figure 1 provides the basis for BFSAR imaging. In an ideal condition, the transmitter and receiver are moving along parallel tracks with equal velocity. The squint angles ${\varphi }_T$, ${\varphi }_R$ and initial ranges $R_{Tcen}$, $R_{Rcen}$ shown in Figure 1 are measured at the composite beam center crossing time of target P.

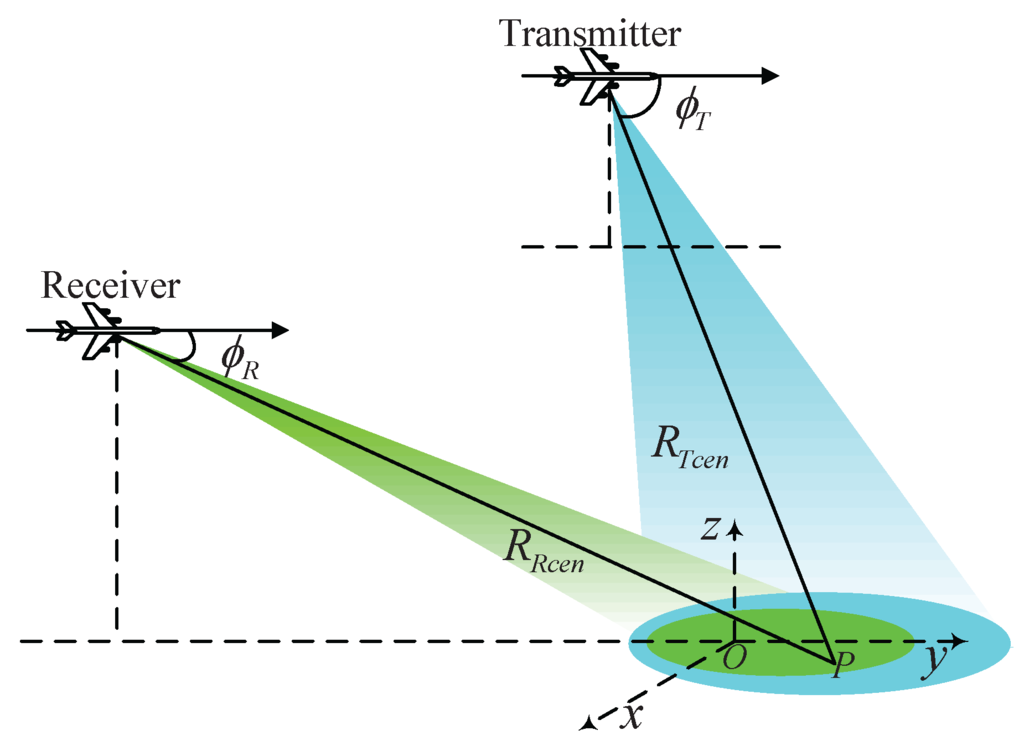
Figure 1. Geometric model of BFSAR.

Figure 1. Geometric model of BFSAR.

Assume that Linear Frequency Modulated (LFM) pulses are transmitted by the radar. The demodulated signal from the reference target in the presence of motion errors can be adequately described by

$$\begin{array}{c}\hfill s(\tau ,t)=rect\left[\frac{\tau -\overline{R}\left(t\right)/c}{T_r}\right]rect\left(\frac{t}{T_a}\right)\text{exp}\left\{-j\pi K_r{[\tau -\frac{\overline{R}\left(t\right)}{c}]}^2\right\}\text{exp}\left\{-j2\pi \frac{\overline{R}\left(t\right)}{\lambda }\right\}\end{array}$$

(1)

where $K_r$ is the transmitted chirp rate, $T_r$ is the timewidth of the LFM pulse, and $T_a$ is the synthetic aperture time. The range time is given by τ, and t denotes the cross-range time, λ is the wave-length, c is the speed of propagation.

In Equation (1), $\overline{R}\left(t\right)$ is the instantaneous two-way range of reference target P in the presence of motion errors. $\overline{R}\left(t\right)$ can be formulated as

$$\begin{array}{c}\hfill \overline{R}\left(t\right)=R\left(t\right)+\delta R\left(t\right),\end{array}$$

(2)

where $\delta R\left(t\right)$ denotes the instantaneous range displacement induced by motion errors, and $R\left(t\right)$ represents the nominal instantaneous two-way range,

$$\begin{array}{cc}\hfill R\left(t\right)& =\sqrt{R_{Tcen}^2+{\left(Vt\right)}^2-2R_{Tcen}Vt \text{cos} {\varphi }_T}+\sqrt{R_{Rcen}^2+{\left(Vt\right)}^2-2R_{Rcen}Vt \text{cos} {\varphi }_R}.\hfill \end{array}$$

(3)

Expand (3) at $t=0$ to its Taylor series and $R\left(t\right)$ can be rewritten as

$$\begin{array}{c}\hfill R\left(t\right)=R_{Tcen}+R_{Rcen}-(V \text{cos} {\varphi }_R+V \text{cos} {\varphi }_R)t+(\frac{V^2{\text{sin}}^2{\varphi }_R}{2R_{Rcen}}+\frac{V^2{\text{sin}}^2{\varphi }_T}{2R_{Tcen}})t^2+o\left(t\right).\end{array}$$

(4)

The linear and quadratic terms in Equation (4) are called the range walk and range curvature, respectively. Using the Doppler centroid estimation method in [20], range walk migration can be estimated. After range compression and range walk compensation, a coarse range focusing signal $s^{\prime }(\tau ,t)$ is obtained.

$$\begin{array}{c}\hfill s^{\prime }(\tau ,t)=\text{sin} c[\tau -\frac{R_{Tcen}+R_{Rcen}+\Delta R\left(t\right)}{c}]rect\left(\frac{t}{T_a}\right)\text{exp}[-j\frac{2\pi }{\lambda }\overline{R}\left(t\right)]\end{array}$$

(5)

where $\Delta R\left(t\right)$ in the range profile is residual range cell migration (RCM)

$$\begin{array}{c}\hfill \Delta R\left(t\right)=\delta R\left(t\right)+(\frac{V^2{\text{sin}}^2{\varphi }_R}{2R_{Rcen}}+\frac{V^2{\text{sin}}^2{\varphi }_T}{2R_{Tcen}})t^2+o\left(t\right).\end{array}$$

(6)

Residual RCM introduces a 2D defocus in the final image. In order to obtain high resolution BFSAR image, residual RCM correction is essential before the azimuth procedures such as autofocus, nonlinear chirp scaling (NLCS) [21] and azimuth compression. In the following section, a residual RCM correction method based on minimum entropy is proposed.

3. Residual RCM Correction

In this section, dominant scatterers are selected from the BFSAR image as the input of the proposed residual RCM correction method. The reason for the adoption of dominant scatterers is that the signal-noise ratio (SNR) in the area of dominant scatters is high, which can directly cause high residual RCM estimation accuracy. At first, quality range cells are picked out based on the contrast measurement because high contrast indicates a range cell containing more prominent scatterers than a cell with low contrast. M means the number of range cells picked out based on the based on the contrast measurement. Then, the brightest scatterers of the M range cells are selected. In order to consider the computation burden and the generalizability, M is always set to be quarter of the range cell numbers. For the sake of convenience in subsequent processing, these scatterers are shifted to the image center. The next important step is windowing these shifted scatterers in order to preserve the width of the dominant blur and meanwhile suppress the noise and interference from the neighboring clutter. The size of the window can be determined by the average response of these shifted scatterers. The Gaussian window is adopted in the whole processing. Finally, quality scatterers are chosen from these windowed scatterers based on the criteria that the main lobe energy is much higher than the background noise and the interference is negligible for both the main lobe and sidelobes [1].

The specific implement steps are performed as follows. (1) Estimate the main lobe width utilizing the average response of selected scatterers. (2) Calculate the proportion of the main lobe energy to the total signal energy for each selected scatterer. (3) Set a threshold, and select dominant scatterers. The threshold should ensure that selected scatterers are prominent and not influenced by neighboring clutter interference. In the actual situation, the threshold is set to be half of the amplitude of the brightest scatterers. Then, these selected dominant scatterers will be utilized to estimate phase errors.

In addition, the residual RCM is assumed to be identical for all the selected dominant scatterers in the BFSAR data. Strictly, residual RCMs of scatterers located at different ranges are not the same. However, this space variance can be solved by dividing the BFSAR data into several blocks along the range, whereby residual RCMs in each block are similar. After the segmenting operation, the problem of residual RCM correction can be formulated as [19]

$$\begin{array}{c}\hfill z(m,n)={\displaystyle \sum _{k=0}^{M-1}}{s}^{\prime }(k,n)\text{exp}\left(j\frac{2\pi }{M}mk\right)\text{exp}(j2\pi k\Delta R_n)\end{array}$$

(7)

where m, n and k are the indices of range, azimuth bins, and range frequency, respectively, and M, N are the numbers of range and azimuth samples, respectively. $s^{\prime }(k,n)$ denotes the fast Fourier transformation (FFT) results of $s^{\prime }(\tau ,t)$ with respect to range yields, and $\Delta R_n$ is the residual RCM in the nth azimuth bin. An entropy-based residual RCM estimation method is proposed to estimate the $\Delta R_n(n=1,2,\cdots ,N)$ in Equation (7).

3.1. Minimum-Entropy Estimation

In the minimum-entropy residual RCM correction algorithm, $\Delta R_n$ is designed to minimize the entropy of $z(m,n)$.

$$\begin{array}{c}\hfill E=\text{ln}S-\frac{1}{S}{\displaystyle \sum _{m=0}^{M-1}\sum _{n=0}^{N-1}}{\left|z(m,n)\right|}^2\text{ln}{\left|z(m,n)\right|}^2\end{array}$$

(8)

where

$$\begin{array}{c}\hfill S={\displaystyle \sum _{m=0}^{M-1}\sum _{n=0}^{N-1}}{\left|z(m,n)\right|}^2.\end{array}$$

(9)

Entropy can be used to measure the smoothness of a distribution function. It is generally acknowledged that the BFSAR images with better range focusing quality have smaller entropy. Owing to this property, BFSAR residual RCM correction is performed by satisfying the global minimum-entropy criterion to find $\Delta R_n(n=1,2,\cdots ,N)$. The minimum-entropy residual RCM estimate can be obtained by

$$\begin{array}{c}\hfill \Delta R={\displaystyle \underset{\Delta R}{\text{arg min}}} E(\Delta R)\end{array}$$

(10)

where $\Delta R=[\Delta R_1,\Delta R_2,\cdots ,\Delta R_N]$ is a vector of residual RCM correction parameter. Since there is no closed-form solution for Equation (10), an iterative numerical minimization procedure is needed to solve the optimal range displacement parameters.

3.2. Coordinate Descent

In this subsection, an iterative method based on coordinate descent to solve for the optimal residual RCM parameters in Equation (10) is discussed. In the coordinate descent optimization, each parameter is optimized in turn, while holding the remaining parameters constant. For our application, coordinate descent is applied to maximize the objective function in Equation (10).

Suppose that the residual RCM at the qth iteration for the nth parameter is estimated. In coordinate descent scheme, an iteration is defined as a complete cycle through all N range displacement parameters. All the other residual RCM variables are fixed at constants, where the first $(n-1)$ parameters have already been updated in the qth iteration. Now, the objective function reduces to a function of a single variable $\Delta R_n$,

$$\begin{array}{c}\hfill \Delta R_n^q={\displaystyle \underset{\Delta R_n}{\text{arg min}}}\left[E(\Delta R_1^q,\cdots ,\Delta R_{n-1}^q,\Delta R_n,\Delta R_{n+1}^{q-1},\cdots ,\Delta R_N^{q-1})\right].\end{array}$$

(11)

3.3. Analytical Solution

Function (11) is a typical scalar minimization problem, and a computationally expensive numerical line-search can be utilized. Here, the optimal single minimum-entropy parameter can be obtained in analytical form, thus enabling a fast procedure with no line-search steps.

Expand $E(\Delta R_n)$ in (11) at $\Delta R_n^q$ to its Taylor series as follows and the cubic and higher order items are ignored:

$$\begin{array}{c}\hfill E(\Delta R_n)=E{|}_{\Delta R_n=\Delta R_n^q}+E^{\prime }{|}_{\Delta R_n=\Delta R_n^q}(\Delta R_n-\Delta R_n^q)+E^{″}{|}_{\Delta R_n=\Delta R_n^q}{(\Delta R_n-\Delta R_n^q)}^2\end{array}$$

(12)

The first and second order derivatives of entropy with respect to $\Delta R_n$ are obtained in the following:

$$\begin{array}{c}\hfill E^{\prime }=-{\displaystyle \sum _{m=0}^{M-1}\sum _{n=0}^{N-1}}[1+\text{ln}{\left|z(m,n)\right|}^2]\frac{d{\left|z(m,n)\right|}^2}{d\Delta R_n}\end{array}$$

(13)

$$\begin{array}{c}\hfill E^{″}=-{\displaystyle \sum _{m=0}^{M-1}\sum _{n=0}^{N-1}}\frac{1}{{\left|z(m,n)\right|}^2}\frac{d^2{\left|z(m,n)\right|}^2}{d\Delta R_n^2}.\end{array}$$

(14)

Since ${\left|z(m,n)\right|}^2=z(m,n)z^{*}(m,n)$,

$$\begin{array}{cc}\hfill \frac{d{\left|z(m,n)\right|}^2}{d\Delta R_n}=2Re& [z^{*}(m,n)\frac{dz(m,n)}{d\Delta R_n}]\hfill \\ \hfill =-\frac{4\pi }{Mc}Im& \left\{\left[{\displaystyle \sum _{k=0}^{M-1}}k{s}^{\prime }(k,n)\text{exp}\left(j\frac{2\pi }{M}km\right)\text{exp}(j2\pi k\Delta R_n)\right]z^{*}(m,n)\right\}\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill \frac{d^2{\left|z(m,n)\right|}^2}{d\Delta R_n^2}=& -\frac{8{\pi }^2}{M^2{c}^2}Re\left\{\left[{\displaystyle \sum _{k=0}^{M-1}}{k}^2{s}^{\prime }(k,n)\text{exp}\left(j\frac{2\pi }{M}km\right)\text{exp}(j2\pi k\Delta R_n)\right]z^{*}(m,n)\right\}\hfill \\ & +\frac{8{\pi }^2}{M^2{c}^2}{\left|{\displaystyle \sum _{k=0}^{M-1}}{k}^2{s}^{\prime }(k,n)\text{exp}\left(j\frac{2\pi }{M}km\right)\text{exp}(j2\pi k\Delta R_n)\right|}^2.\hfill \end{array}$$

(16)

By solving for $E^{\prime }(\Delta R_n)=0$, a closed-form solution for (11) is obtained, which results in the following update equation.

$$\begin{array}{c}\hfill \Delta R_n^{q+1}=\Delta R_n^q-\frac{E^{\prime }{|}_{\Delta R_n=\Delta R_n^q}}{E^{″}{|}_{\Delta R_n=\Delta R_n^q}}.\end{array}$$

(17)

The proposed iterative method constructs a local quadratic curve to gradually approach the extremum of the objective function (11). Moreover, in order to make the iteration converge towards a minimum point, these quadratic curves should be convex and namely satisfy (18)

$$\begin{array}{c}\hfill E^{″}{|}_{\Delta R_n=\Delta R_n^q}>0.\end{array}$$

(18)

At this stage, residual RCM can be estimated and corrected precisely. Then, azimuth procedures, such as autofocus, NLCS, and azimuth compression, should be performed to get the well-focused BFSAR images.

4. Numerical Results

Simulation experiment is performed to verify the theoretical analysis and proposed residual RCM correction method. Table 1 lists the main parameters used in the simulation.

Table 1. Simulation parameters.

Parameter	Value
Carrier frequency	10 GHz
Band width	40 MHz
Synthetic aperture time	0.75 s
Nominal Radar platform velocity	120 m/s
Pulse repetition frequency	600 Hz
Coordinates of transmitter	(-6000,0,8000) m
Coordinates of receiver	(0,-6000,8000) m
Coordinates of scene center	(0,0,0) m

Table 1. Simulation parameters.

Parameter	Value
Carrier frequency	10 GHz
Band width	40 MHz
Synthetic aperture time	0.75 s
Nominal Radar platform velocity	120 m/s
Pulse repetition frequency	600 Hz
Coordinates of transmitter	(-6000,0,8000) m
Coordinates of receiver	(0,-6000,8000) m
Coordinates of scene center	(0,0,0) m

Two nominal parallel linear flight paths are assumed for BFSAR imaging. However, in reality, deviations from these nominal linear trajectories of transmitter and receiver are introduced in X, Y and Z direction. The deviation in the X-direction accounts for along-track nominal velocity changes that are generally compensated via an on-board adjustment of the pulse repetition frequency or, via azimuth re-sampling of SAR raw data. Therefore the forward velocity errors are assumed to be negligible, and we focus on how the deviations of the other two directions affect the residual RCM. The motion errors in Y and Z direction are shown in Figure 2. A ground point target is assumed to be located in the scene center and the coordinates of the other two target are (100,0,0) m and (–100,0,0) m, respectively. Therefore, all the targets in the echo signal are related to range displacements induced by the radars’ maneuver.

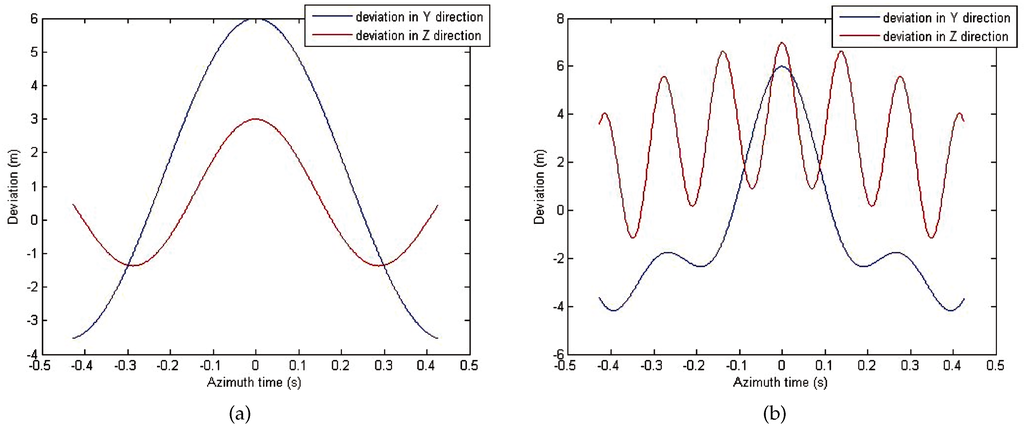
Figure 2. (a) Deviations of transmitter from the nominal flight path. (b) Deviations of receiver from the nominal flight path.

Figure 2. (a) Deviations of transmitter from the nominal flight path. (b) Deviations of receiver from the nominal flight path.

The simulation results are shown in Figure 3a,b. Figure 3a is the data after range compression and RCM correction while Figure 3b denotes the residual RCM corrected data. The figures suggest that the residual RCM is corrected well for the case of multiple point targets.

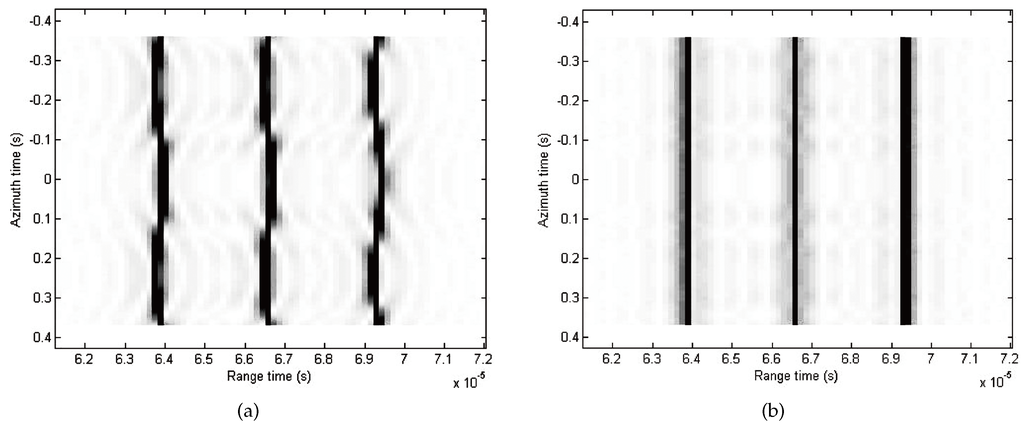
Figure 3. (a) Data after range compression and RCM correction. (b) Data after residual RCM correction.

Figure 3. (a) Data after range compression and RCM correction. (b) Data after residual RCM correction.

The true range displacement and the estimated range displacement are shown in Figure 4a. It can be clearly seen that the estimated range displacement matches quite well with the true range displacement. In terms of estimation performance, the estimation error is shown in Figure 4b, and the variation of the root mean square (RMS) of an overall estimation error is smaller than 0.04 m with the default estimation accuracy Δr = 0.004 m. The nondefocus validity constraint of the estimation error is λ/16 = 0.01875 m, and the maximum estimation error is 0.004 m. Hence, the nondefocus validity constraint is satisfied, and, therefore, the range displacement estimated can be utilized to compensate for the azimuth phase errors (APE).

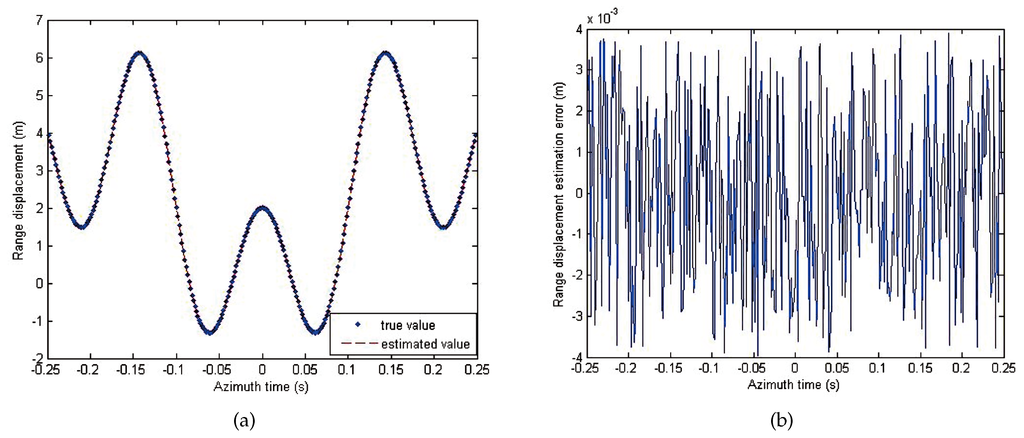
Figure 4. (a) Range displacement. (b) Range displacement estimation errors.

Figure 4. (a) Range displacement. (b) Range displacement estimation errors.

Then, the effect of noise on estimation accuracy is evaluated. White Gaussian noise with different signal-to-noise ratios (SNR) is added to the range-compressed data. A Monte Carlo simulation is conducted and the RMS of estimation error is shown in Figure 5 with SNR ranging from 10 to 30 dB. It is obvious that the proposed algorithm is insensitive to noise and can provide reliable estimation even for the data with low SNR.

Figure 5. RMS of estimated range displacement error versus SNR.

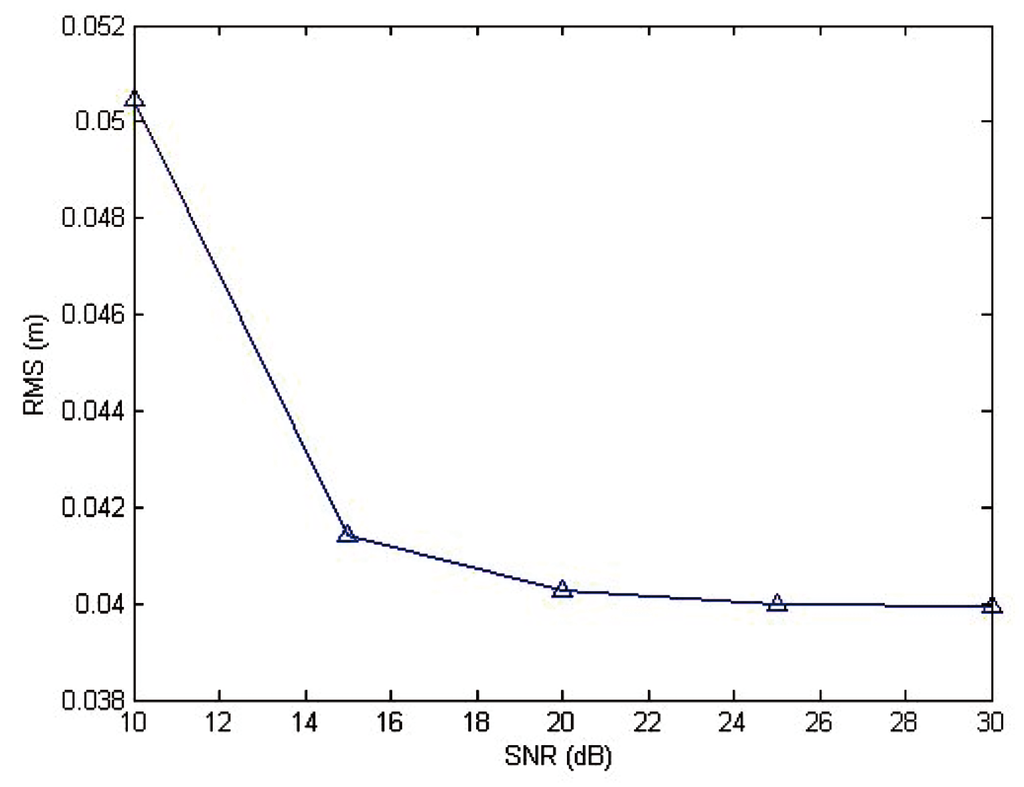
Figure 5. RMS of estimated range displacement error versus SNR.

5. Conclusions

This paper proposes the signal model of BFSAR in the presence of motion errors and analyzes in detail the influence of excessive residual RCM on the full compressed image. A minimal-entropy based residual RCM correction method is presented in this paper. By utilizing the coordinate decent scheme, we minimize the entropy by sequentially updating the residual RCM parameters one at a time. In the coordinate decent scheme, the optimal single entropy-minimizing residual RCM parameter can be obtained in analytical form. The proposed method eliminates the necessity of the parametric model and improves the estimation accuracy. Moreover, it meets the practical needs of BFSAR owing to no requirement of exhaustive computation. This method can be used in other SAR configuration modes with excessive residual RCM. Simulations and experiments using real BFSAR data are carried out to confirm the effectiveness of the algorithm.