Throughput Capacity of Selfish Wireless Ad Hoc Networks with General Node Density
Abstract
:1. Introduction
- (1)
- Comparing to previous research, we firstly consider the model of selfish wireless ad hoc network, which is more realistic.
- (2)
- We derive the asymptotic throughput capacity of the network combining selfish feature and general node density, which is different from the previous works of dense or extended networks.
- (3)
- We observe that the selfishness degrades the achievable throughput with a factor , where is the probability of forwarding transmission. In addition, the node density impacts the throughput trivially.
2. System Assumption
- (1)
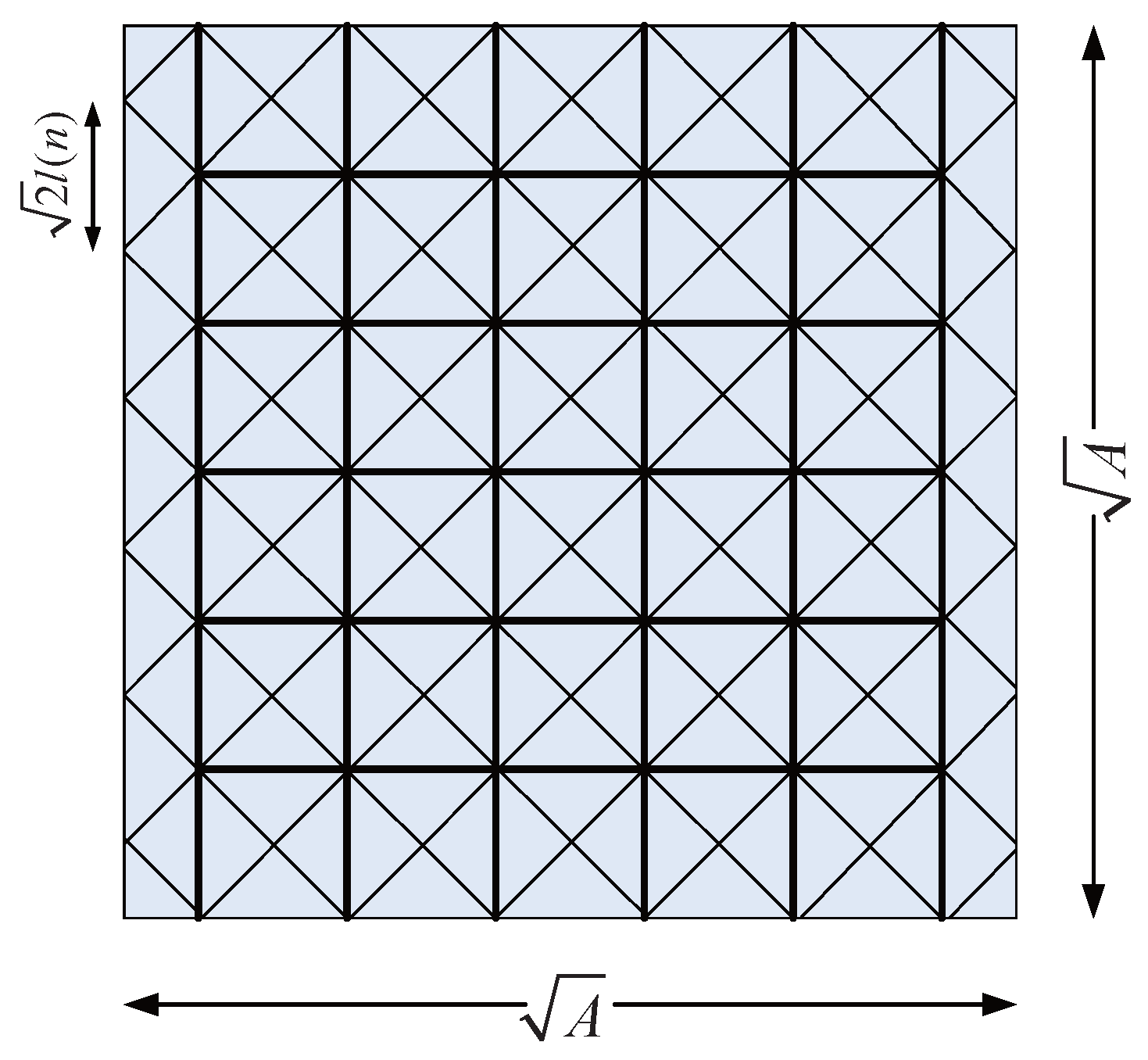
- We assume n static nodes uniformly and independently placed over an area , where .
- (2)
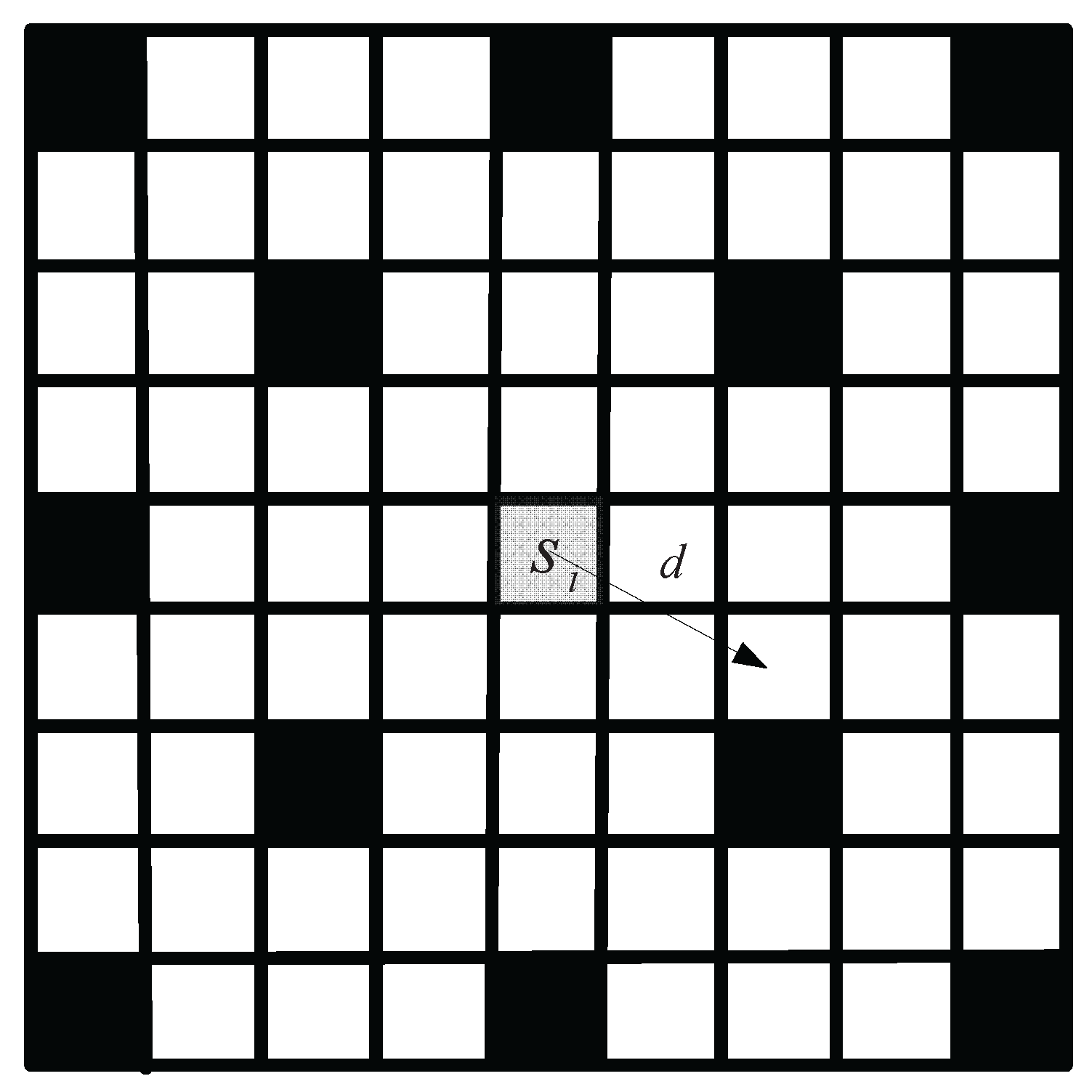
- The node is classified by whether it will forward other transmission. As shown in Figure 1, if a node will forward other transmission, we define the node as an altruistic node (AN, empty points in Figure 1). Otherwise the node is a Selfish Node (SN, solid points in Figure 1). In this work, we assume each node may be selfish, and define the probability that a node i will forward other transmission as . For simplicity, we assume the probability that each node forwards other transmission is .
- (3)
- Each node randomly chooses a destination node and each node is the destination of exactly one node.
- (4)
- The transmission model we adopted is General Physical Model [4], where the channel gain ignores shadowing and fading, and only depends on the distance between the transmitter and receiver. Let S denote the subset of nodes transmitting simultaneously. Based on the point-to-point coding and decoding [4], the transmission rate between node i to node j is:where is the transmission power of node i. We assume each employs identical power P to transmit. denotes the distance between an arbitrary pair of nodes i and j. is the ambient noise power at the receiver. α is the path loss exponent, and . The notations of this paper are summarized in Table 1.
- (5)
- We say that the throughput capacity of a network [4] is of the order bits per second if there is a deterministic constant such thatand is of order bits per second if there are deterministic constants such that
3. Achievable Rate
3.1. Construction of the Backbone Network
3.2. Routing Protocol
- (1)
- Draining phase: In the draining phase, source node s drops packets to an entry point on the nearest horizontal crossing highway.
- (2)
- Highway phase: In the highway phase, packets are first moved along horizontal highway, and then along the vertical highway until they arrive at an exit point that is close to the destination node D.
- (3)
- Delivery phase: In this phase, packets are delivered to the destination node D from the exit point located on the highway.
3.3. The Rate for Transporting a Packet
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zuhairi, M.; Zafar, H.; Harle, D. Wireless Machine-to-Machine Routing Protocol with Unidirectional Links. Smart Comput. Rev. 2011, 1, 58–68. [Google Scholar] [CrossRef]
- Cho, K.H.; Ryu, M.W. A survey of greedy routing protocols for vehicular ad hoc networks. Smart Comput. Rev. 2012, 2, 125–137. [Google Scholar] [CrossRef]
- Zaman, K.; Shafiq, M.; Choi, J.G.; Iqbal, M. The Life Cycle of Routing in Mobile Ad Hoc Networks. Smart Comput. Rev. 2015, 5, 135–150. [Google Scholar]
- Gupta, P.; Kumar, P.R. The capacity of wireless networks. IEEE Trans. Inf. Theory 2000, 46, 388–404. [Google Scholar] [CrossRef]
- Franceschetti, M.; Dousse, O.; David, N.C. Closing the gap in the capacity of wireless networks via percolation theory. IEEE Trans. Inf. Theory 2007, 53, 1009–1018. [Google Scholar] [CrossRef]
- Grossglauser, M.; Tse, D. Mobility increases the capacity of ad-hoc wireless networks. In Proceedings of the Twentieth Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM), Anchorage, AK, USA, 22–26 April 2001; volume 3, pp. 1360–1369.
- Li, P.; Zhang, C.; Fang, Y. The capacity of wireless ad hoc networks using directional antennas. IEEE Trans. Mob. Comput. 2011, 10, 1374–1387. [Google Scholar] [CrossRef]
- Zhang, G.; Xu, Y.; Wang, X. Capacity of hybrid wireless networks with directional antenna and delay constraint. IEEE Trans. Commun. 2010, 58, 2097–2106. [Google Scholar] [CrossRef]
- Sadjadpour, H.R.; Wang, Z.; Garcia-Luna-Aceves, J.J. The capacity of wireless ad hoc networks with multi-packet reception. IEEE Trans. Commun. 2010, 58, 600–610. [Google Scholar] [CrossRef]
- Ozgur, A.; Leveque, O.; Tse, D.N.C. Hierarchical cooperation achieves optimal capacity scaling in ad hoc networks. IEEE Trans. Inf. Theory 2007, 53, 3549–3572. [Google Scholar] [CrossRef]
- Shin, W.Y.; Jeon, S.W.; Devroye, N. Improved capacity scaling in wireless networks with infrastructure. IEEE Trans. Inf. Theory 2011, 57, 5088–5102. [Google Scholar] [CrossRef]
- Shila, D.M.; Cheng, Y. Ad hoc wireless networks meet the infrastructure: Mobility, capacity and delay. In Proceedings of the 2012 Proceedings IEEE INFOCOM, Orlando, FL, USA, 25–30 March 2012; pp. 3031–3035.
- Gamal, A.E.; Mammen, J.; Prabhakar, B. Throughput-delay trade-off in wireless networks. In Progress of the Twenty-Third AnnualJoint Conference of the IEEE Computer and Communications Societies, Hong Kong, China, 7–11 March 2004.
- Lin, X.; Shroff, N.B. The fundamental capacity-delay tradeoff in large mobile ad hoc networks. In Proceedings of the Third Annual Mediterranean Ad Hoc Networking Workshop, Bodrum, Turkey, 27–30 June 2004.
- Yao, S.; Wang, X.; Tian, X.; Zhang, Q. Delay-Throughput Tradeoff with Correlated Mobility of Ad-Hoc Networks. In Proceedings of the 2014 Proceedings IEEE INFOCOM, Toronto, ON, Canada, 27 April–2 May 2014.
- Neely, M.J.; Modiano, E. Capacity and delay tradeoffs for ad hoc mobile networks. IEEE Trans. Inf. Theory 2005, 51, 1917–1937. [Google Scholar] [CrossRef]
- Lu, N.; Shen, X. Scaling Laws for Throughput Capacity and Delay in Wireless Networks—A Survey. IEEE Commun. Surveys Tutor. 2014, 16, 642–657. [Google Scholar] [CrossRef]
- Jiang, C.; Shi, Y.; Hou, Y.; Lou, W.; Kompella, S.; Midkiff, S.F. Toward Simple Criteria to Establish Capacity Scaling Laws for Wireless Networks. In Proceedings of the IEEE INFOCOM, Orlando, FL, USA, 25–30 March 2012.
- Mao, G.; Lin, Z.; Ge, X.; Yang, Y. Towards a Simple Relationship to Estimate the Capacity of Static and Mobile Wireless Networks. IEEE Trans. Wirel. Commun. 2013, 12, 3883–3895. [Google Scholar] [CrossRef]
- Liu, E.; Zhang, Q.; Leung, K.K. Connectivity in selfish, cooperative networks. IEEE Commun. Lett. 2010, 14, 936–938. [Google Scholar] [CrossRef]
- Lee, S.; Levin, D.; Gopalakrishnan, V. Backbone construction in selfish wireless networks. ACM SIGMETRICS Perform. Eval. Rev. 2007, 35, 121–132. [Google Scholar] [CrossRef]
- Jo, M.; Han, L.; Kim, D.; In, H.P. Selfish attacks and detection in cognitive radio ad-hoc networks. IEEE Netw. 2013, 27, 46–50. [Google Scholar]
- Kesten, H. The critical probability of bond percolation on the square lattice equals 1/2. Commun. Math. Phys. 1980, 74, 41–59. [Google Scholar] [CrossRef]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Keshavarz-Haddad, A.; Ribeiro, V.; Riedi, R. Broadcast capacity in multihop wireless networks. In Proceedings of the 12th Annual International Conference on Mobile Computing and Networking, Los Angeles, CA, USA, 24–29 September 2006; pp. 239–250.



| Notation | Definition |
|---|---|
| n | Total number of nodes in the network. |
| ζ | Node density. |
| A | Network area; . |
| Probability that a node will forward other transmission. | |
| S | Set of simultaneous nodes. |
| Point to point rate. | |
| P | Power of transmission. |
| The distance between node i and j. | |
| Power of noise. | |
| α | Path loss exponent. |
| The achievable throughput. |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Luo, Y.; Ling, Y.; Zheng, J. Throughput Capacity of Selfish Wireless Ad Hoc Networks with General Node Density. Information 2016, 7, 16. https://doi.org/10.3390/info7010016
Liu Q, Luo Y, Ling Y, Zheng J. Throughput Capacity of Selfish Wireless Ad Hoc Networks with General Node Density. Information. 2016; 7(1):16. https://doi.org/10.3390/info7010016
Chicago/Turabian StyleLiu, Qiuming, Yong Luo, Yun Ling, and Jun Zheng. 2016. "Throughput Capacity of Selfish Wireless Ad Hoc Networks with General Node Density" Information 7, no. 1: 16. https://doi.org/10.3390/info7010016
APA StyleLiu, Q., Luo, Y., Ling, Y., & Zheng, J. (2016). Throughput Capacity of Selfish Wireless Ad Hoc Networks with General Node Density. Information, 7(1), 16. https://doi.org/10.3390/info7010016






