Modeling of Experimental Adsorption Isotherm Data
Abstract
:1. Introduction
2. Experiments
2.1. The Experimental Isotherm Data
| C0\Samples | M1 | M2 | M3 | M4 | ||||
|---|---|---|---|---|---|---|---|---|
| Ce | qe | Ce | qe | Ce | qe | Ce | qe | |
| 0.5 | 0.49 | 0.021 | 0.061 | 0.93 | 0.037 | 0.98 | 0.052 | 0.95 |
| 1.0 | 0.78 | 0.39 | 0.023 | 1.91 | 0.013 | 1.92 | 0.017 | 1.94 |
| 5.0 | 3.67 | 1.91 | 0.35 | 8.56 | 0.036 | 9.26 | 0.034 | 9.26 |
| 10.0 | 9.03 | 3.88 | 2.45 | 17.18 | 0.15 | 19.49 | 0.33 | 18.97 |
| 25.0 | 23.98 | 4.82 | 16.43 | 19.74 | 5.74 | 42.22 | 4.12 | 44.95 |
| 55.0 | 53.25 | 5.01 | 44.40 | 20.91 | 29.54 | 44.30 | 26.09 | 52.14 |
2.2. Non-linear Forms of the Isotherm Models
2.3. Linear Forms of the Isotherm Models
| Isotherm models | Linear form | |
|---|---|---|
| Langmuir | I | |
| II | ||
| III | ||
| IV | ||
| Freundlich | ||
| Dubinin-Radushkevich |
3. Results and Discussion
3.1. Non-linear Fitting of the Isotherm Models
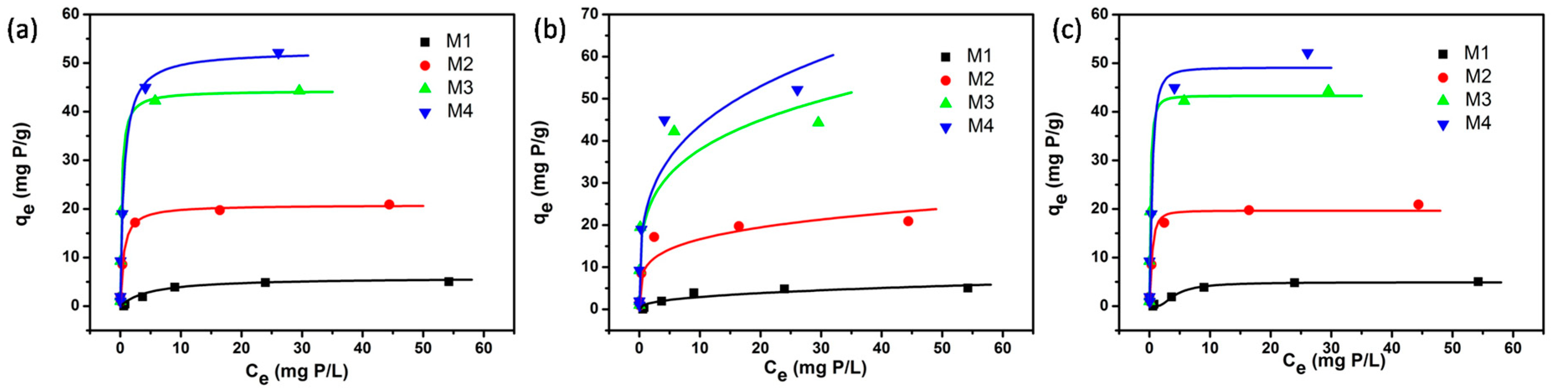
| Model/parameters | M1 | M2 | M3 | M4 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Value | S.E. | Value | S.E. | Value | S.E. | Value | S.E. | ||
| Langmuir | qm (mg P/g) | 5.92 | 0.51 | 20.82 | 0.62 | 44.36 | 2.38 | 52.53 | 3.24 |
| b (L/mg P) | 0.152 | 0.045 | 1.890 | 0.310 | 4.470 | 1.154 | 1.682 | 0.518 | |
| r2 | 0.973 | - | 0.993 | - | 0.979 | - | 0.978 | - | |
| Freundlich | KF | 1.18 | 0.45 | 9.91 | 1.96 | 21.61 | 4.17 | 22.88 | 4.32 |
| n | 2.541 | 0.729 | 4.440 | 1.259 | 4.103 | 1.096 | 3.572 | 0.853 | |
| r2 | 0.858 | - | 0.857 | - | 0.868 | - | 0.894 | - | |
| Dubinin-Radushkevich | qs (mg P/g) | 4.93 | 0.16 | 19.67 | 0.82 | 43.32 | 2.17 | 49.10 | 3.72 |
| KD (mol2/kJ2) | 2.79 | 0.37 | 0.074 | 0.014 | 0.032 | 0.005 | 0.080 | 0.024 | |
| r2 | 0.989 | - | 0.977 | - | 0.975 | - | 0.946 | - | |
3.2. Linear Fitting of the Isotherm Models
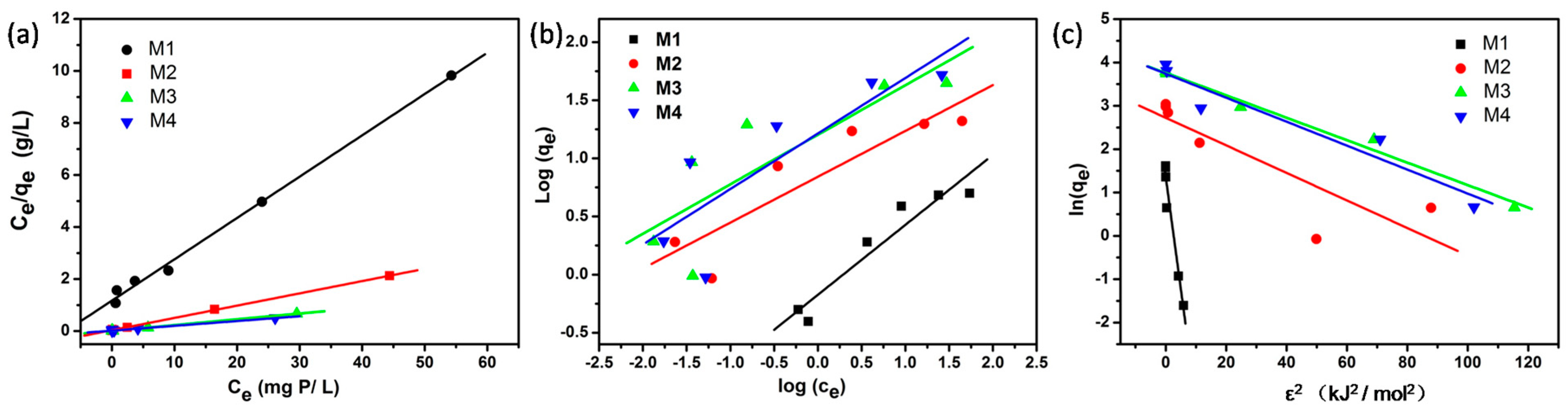
| Model | M1 | M2 | M3 | M4 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Value | S.E. | Value | S.E. | Value | S.E. | Value | S.E. | ||
| Langmuir | qm (mg P/g) | 6.29 | 0.19 | 21.18 | 0.26 | 45.17 | 1.11 | 54.23 | 2.59 |
| b (L/mg P) | 0.135 | 0.018 | 1.352 | 0.442 | 1.815 | 1.01 | 0.985 | 0.524 | |
| r2 | 0.995 | - | 0.999 | - | 0.997 | - | 0.990 | - | |
| Freundlich | KF | 0.67 | 0.14 | 6.95 | 1.87 | 15.97 | 7.15 | 16.38 | 7.19 |
| n | 1.661 | 0.254 | 2.535 | 0.625 | 2.346 | 0.791 | 2.094 | 0.666 | |
| r2 | 0.916 | - | 0.806 | - | 0.701 | - | 0.714 | - | |
| Dubinin-Radushkevich | qs (mg P/g) | 3.87 | 0.63 | 15.25 | 5.82 | 42.99 | 4.83 | 42.14 | 10.74 |
| KD (mol2/kJ2) | 0.52 | 0.06 | 0.032 | 0.009 | 0.026 | 0.002 | 0.028 | 0.005 | |
| r2 | 0.946 | - | 0.688 | - | 0.980 | - | 0.900 | - | |
3.3. Comparison of Maximum Adsorption Capacities (qm)
| Adsorbents | Isotherm models | qm (mg P/g) | Da (mg P/g) | References |
|---|---|---|---|---|
| M1 | Nonlinear Langmuir | 5.92 | 0.91 | Present work |
| Linear Langmuir | 6.29 | 1.28 | ||
| M2 | Nonlinear Langmuir | 20.82 | 0.09 | Present work |
| Linear Langmuir | 21.18 | 0.27 | ||
| M3 | Nonlinear Langmuir | 44.36 | 0.06 | Present work |
| Linear Langmuir | 45.17 | 0.87 | ||
| M4 | Nonlinear Langmuir | 52.53 | 0.39 | Present work |
| Linear Langmuir | 54.23 | 2.09 | ||
| activated carbon fiber (ACF-NanoHFO) | Linear Langmuir | 12.86 | - | [3] |
| Fe-Zr binary oxide | Nonlinear Langmuir | 13.65 | - | [4] |
| aluminum pillared bentonites | Nonlinear Langmuir | 12.70 | - | [5] |
| Fe(III)-coordinated amino-functionalized SBA-15 | Linear Langmuir | 20.70 | - | [9] |
4. Conclusions
Acknowledgements
Conflicts of Interest
References
- Yuan, X.; Pan, G.; Chen, H.; Tian, B. Phosphorus fixation in lake sediments using LaCl3-modified clays. Ecol. Eng. 2009, 35, 1599–1602. [Google Scholar] [CrossRef]
- Eilbeck, W.J.; Mattock, G. Chemical Processes in Wastewater Treatment; Wiley: New York, NY, USA, 1987; pp. 12–96. [Google Scholar]
- Zhou, Q.; Wang, X.; Liu, J.; Zhang, L. Phosphorus removal from wastewater using nano-particulates of hydrated ferric oxide doped activated carbon fiber prepared by Sol-Gel method. Chem. Eng. J. 2012, 200, 619–626. [Google Scholar] [CrossRef]
- Long, F.; Gong, J.; Zeng, G.; Chen, L.; Wang, X.; Deng, J.; Niu, Q.; Zhang, H.; Zhang, X. Removal of phosphate from aqueous solution by magnetic Fe-Zr binary oxide. Chem. Eng. J. 2011, 171, 448–455. [Google Scholar] [CrossRef]
- Yan, L.; Xu, Y.; Yu, H.; Xin, X.; Wei, Q.; Du, B. Adsorption of phosphate from aqueous solution by hydroxy-aluminum, hydroxy-iron and hydroxy-iron-aluminum pillared bentonites. J. Hazard. Mater. 2010, 79, 244–250. [Google Scholar] [CrossRef]
- Rodrigues, L.; Maschio, L.; Coppio, L.; Thim, G.; da Silva, M. Adsorption of phosphate from aqueous solution by hydrous zirconium oxide. Environ. Technol. 2012, 33, 1345–1351. [Google Scholar] [CrossRef] [PubMed]
- Mao, Y.; Pham, A.N.; Xin, Y.; Waite, T.D. Effects of pH, floc age and organic compounds on the removal of phosphate by pre-polymerized hydrous ferric oxides. Sep. Purif. Technol. 2012, 91, 38–45. [Google Scholar] [CrossRef]
- Huang, W.; Li, D.; Zhu, Y.; Xu, K.; Li, J.; Han, B.; Zhang, Y. Fabrication of Fe-coordinated diamino-functionalized SBA-15 with hierarchical porosity for phosphate removal. Mater. Lett. 2013, 99, 154–157. [Google Scholar] [CrossRef]
- Huang, W.; Li, D.; Yang, J.; Liu, Z.; Zhu, Y.; Tao, Q.; Xu, K.; Li, J.; Zhang, Y. One-pot synthesis of Fe(III)-coordinated diamino-functionalized mesoporous silica: Effect of functionalization degrees on structures and phosphate adsorption. Microporous Mesoporous Mater. 2013, 170, 200–210. [Google Scholar] [CrossRef]
- Thompson, G.; Swain, J.; Kay, M.; Forster, C.F. The treatment of pulp and paper mill effluent: A review. Bioresour. Technol. 2001, 77, 275–286. [Google Scholar] [CrossRef] [PubMed]
- Langmuir, I. The constitution and fundamental properties of solids and liquids. J. Am. Chem. Soc. 1916, 38, 2221–2295. [Google Scholar] [CrossRef]
- Freundlich, H.M.F. Over the adsorption in solution. J. Phys. Chem. 1906, 57, 385–471. [Google Scholar]
- Temkin, M.I.; Pyzhev, V. Kinetics of Ammonia Synthesis on Promoted Iron Catalyst. Acta Physiochim. URSS 1940, 12, 217–222. [Google Scholar]
- Dubinin, M.M.; Radushkevich, L.V. The equation of the characteristic curve of the activated charcoal. Proc. Acad. Sci. USSR Phys. Chem. Sect. 1947, 55, 331–337. [Google Scholar]
- Foo, K.Y.; Hameed, B.H. Insights into the modeling of adsorption isotherm systems. Chem. Eng. J. 2010, 156, 2–10. [Google Scholar] [CrossRef]
- Huang, W.; Yang, J.; Zhang, Y. One-pot synthesis of mesoporous MCM-41 with different functionalization levels and their adsorption abilities to phosphate. Adv. Mater. Res. 2012, 476, 1969–1973. [Google Scholar] [CrossRef]
- Kinniburgh, D.G. General purpose adsorption isotherms. Environ. Sci. Technol. 1986, 20, 895–904. [Google Scholar] [CrossRef] [PubMed]
- Ho, Y.S. Isotherms for the sorption of lead onto peat: Comparison of linear and non-linear methods. Pol. J. Environ. Stud. 2005, 15, 81–86. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X. Modeling of Experimental Adsorption Isotherm Data. Information 2015, 6, 14-22. https://doi.org/10.3390/info6010014
Chen X. Modeling of Experimental Adsorption Isotherm Data. Information. 2015; 6(1):14-22. https://doi.org/10.3390/info6010014
Chicago/Turabian StyleChen, Xunjun. 2015. "Modeling of Experimental Adsorption Isotherm Data" Information 6, no. 1: 14-22. https://doi.org/10.3390/info6010014
APA StyleChen, X. (2015). Modeling of Experimental Adsorption Isotherm Data. Information, 6(1), 14-22. https://doi.org/10.3390/info6010014





