A Model for Information
Abstract
:1. Introduction
2. Information and Selection
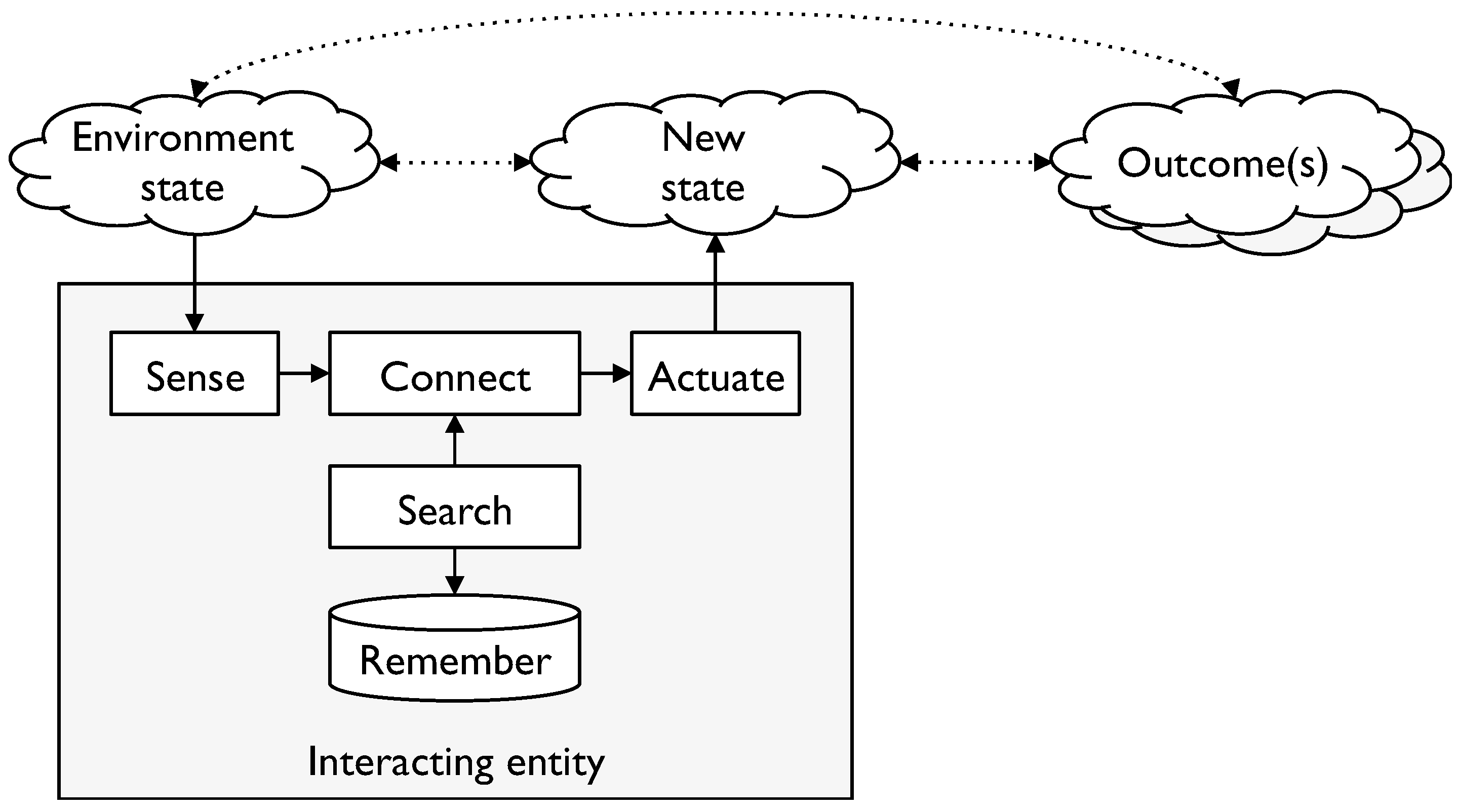
- to sense what is taking place in the environment
- to actuate—to cause an impact on the environment
- to remember, search and retrieve what has been remembered
- to connect the various elements together to enable the IE to link environment states to actions and potential outcomes and choose more favourable alternatives from the options.
“System 1 operates automatically and quickly, with little or no effort and no sense of voluntary control. System 2 allocates attention to the effortful mental activities that demand it, including complex computations. The operations of System 2 are often associated with the subjective experience of agency, choice and concentration.”“…most of what you (your System 2) think and do originates in your System 1, but System 2 takes over when things get difficult, and it normally has the last word. The division of labour between System 1 and System 2 is highly efficient: it minimizes effort and optimizes performance. ... System 1 has biases, however, systematic errors that it is prone to make in specified circumstances.”
The distinction between Systems 1 and 2 highlights one of the impacts of selection pressures. Changes may improve efficiency or quality or both, but their reconciliation is not always elegant.“When information is scarce, which is a common occurrence, System 1 acts as a machine for jumping to conclusions.”“System 1 is radically insensitive to both the quality and quantity of information that gives rise to impressions and intuitions.”
3. The Model for Information (MfI)
- Physical Connection Models (PCM) which model physical entities and their interactions;
- Extended Connection Models (ECM) which model aggregations of entities and interactions;
- Virtual Connection Models (VCM) which model more abstract connections;
- Information Artefact Models (IAM) which model Information Artefacts (IAs).
3.1. Definitions
- properties: each slice has a set of properties and for each property there is one or more physical processes (which we call measurement) that takes the slice as input and generates the value of the property for the slice;
- entity: a type of slice corresponding to a substance;
- interaction: a physical process that relates the properties of two entities.
- l is a label: lab (c);
- S is a set which is the set of all possible values of the pointer: cont (c);
- v is the value (a member of S or ∅): val (c).
- the set of properties of x, Px = {pi: pi is a pointer representing the i-th property of x};
- the number of properties of x, |x| = |Px|;
- a disposition δ is an |x|-tuple (val (p1),..., val (p|x|)), pi∈ Px ;
- the set of all dispositions of x, or disposition space of x, Δx.
- Pxoα the set of properties which can trigger α (“o” stands for output);
- Δxoα the corresponding disposition space (the projection of Δx onto Pxoα);
- Pyiα the set of properties altered by α (“i” stands for input);
- Δyiα the corresponding disposition space (the projection of Δy onto Pyiα).
- the output function, oα: Δxoα x T → Δxoα which maps any disposition of x before α is output to the disposition afterwards;
- the input function, iα: Δyiα x T → Δyiα which maps any disposition of y before α is input to the disposition afterwards.
- oα: (δx, t)→ δxoα for δx in the domain of oα;
- iα: (δy, t) → δyiα for δy in the domain of iα.
- tα: Δxoα x Δyiα x T → Δyiα and tα(δx, δy, t) = δyiα.
- tα(δx, δy, t) = tα(δx, δ’y, t) for all δy, δ’y∈ Δy and for all t ∈ T.
- tα: Δxoα → Δyiα and tα(δx) = δyiα.
- tβ: Δx1oα x…x Δxioα x…x Δxniαm → Δxniαm and tβ(δ1, …,δi, …,δn) = δniαm.
- V is a finite set of vertices;
- E is a finite set of connectors;
- V and E are disjoint;
- N is the set of connections of D where N ⊆ {(a, e, b): a, b ∈ V ∪ E, e ∈ E};
- if e ∈ E and (a, e, b), (a’, e, b’) ∈ N, then a = a’ and b = b’.
- V(C) ⊆ V(D);
- E(C) ⊆ E(D);
- N(C) ⊆ N(D).
- V(DC) = ∪ V(Ci) and E(DC) = ∪ E(Ci)
- instantiated if all the pointers in V(C) and E(C) are instantiated;
- uninstantiated if all the pointers in V(C) and E(C) are uninstantiated;
- partially instantiated if it is not instantiated.
3.2. Physical Connection Models
- let v(xik) be the pointer with label xi and value δxik, where δxik is the disposition of xi at time tk;
- let e(ejk) be the pointer with label ej and value δejk, where δejk is the disposition of ej at time tk;
- let V(Ck) = ∪i {v(xik)} and E(Ck) = ∪j {e(ejk)};
- N(Ck) = {(v, e, w}: v, w ∈ V(Ck), e ∈ E(Ck), the d-interaction represented by e connects the entities represented by v and w};
- Ck = (V(Ck), E(Ck), N(Ck)).
3.3. Extended Connection Models
- X = {xj: 1 ≤ j ≤ n} is a set of entities;
- Y = {xj: 1 ≤ j ≤ m} for some m < n;
- Α is a set of interactions between elements of X;
- A|Y = {α ∈ Α: α is an interaction between elements of Y}.
- C is a linnet;
- e is an edge of C corresponding to the connection (v1, e, v2);
- v ∉ V(C) ∪ E(C)
- V(C\e) = (V(C) ∪ {v})\{v1, v2};
- E(C\e) = E(C)\{e};
- N(C\e) = N(C)\{n: n ∈ N(C), e ∈ n};
- any occurrence of v1 or v2 in C is replaced with v in C\e;
- any occurrence of e in C is replaced with v in C\e.
- ΔY = Δx1 x ... x Δxm.
3.4. Connections and Relations
- the symbols which are used;
- the structure of IAs and the rules that apply to them;
- the ways in which concepts are connected;
- the syntax of IAs and how they are created;
- the channels which are used to interact (and the associated sensor and actuator patterns).
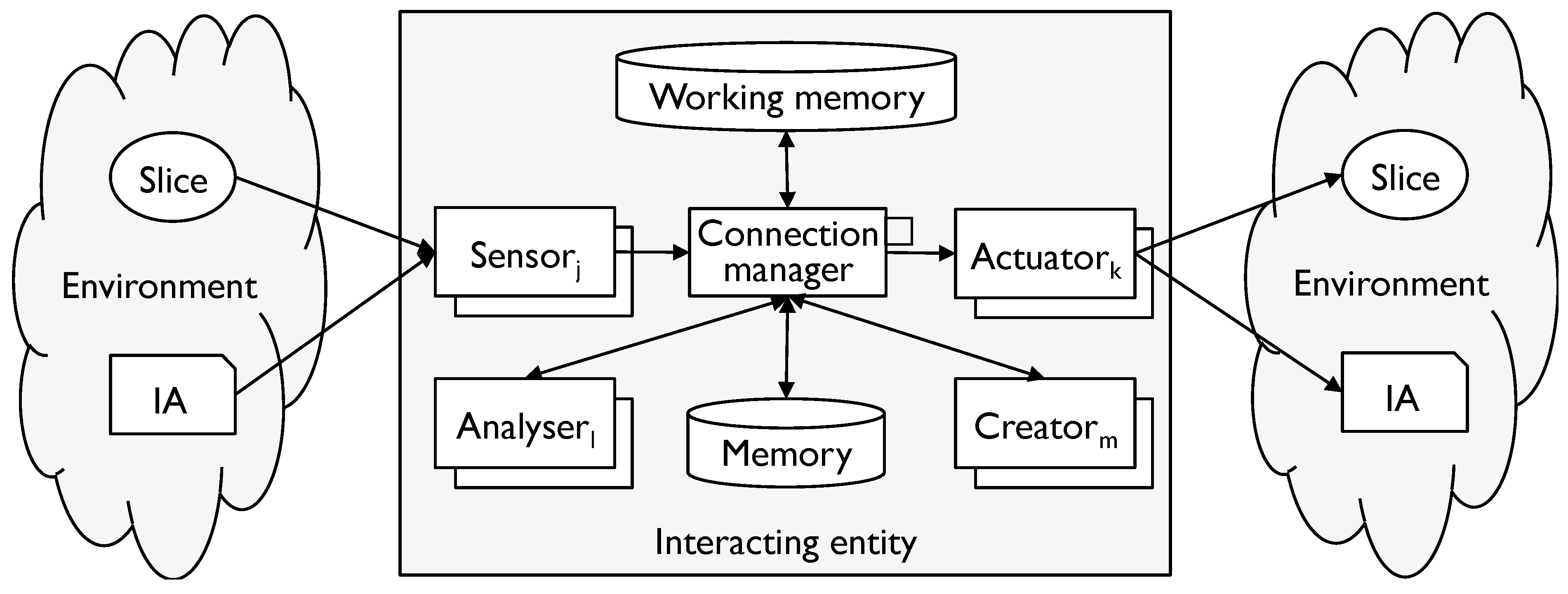
- E is a set of IEs in an ecosystem corresponding to a modelling tool M;
- A is a set of IAs in the ecosystem;
- AP is a pattern for each instance of the M analysers for all e ∈ E (the existence of a modelling tool and ecosystem guarantees the existence of such a pattern).
- ∀ e ∈ E, a ∈ A, ∃ δa∈ Δa such that Pe maps each δa to the same disposition δe and each δe represents each other δe with respect to all M interactions.
- a set of IE patterns, I = IE(M) (each including patterns for sensing, actuation, analysing, creating and connecting);
- a set of symbol types, S = ST(M);
- a set of content patterns, based on ST(M), Cp = CT(M);
- a set of IA patterns, based on ST(M), A = IA(M);
- a set of channel patterns, Ch = CH(M);
- each sensor instance consistent with a pattern in IE(M) consumes IAs which are consistent with a pattern in IA(M) over a channel consistent with a pattern in CH(M);
- each actuator instance consistent with a pattern in IE(M) produces IAs which are consistent with a pattern in IA(M) over a channel consistent with a pattern in CH(M);
- each IA consistent with a pattern in IA(M) is consumed or produced by all IEs consistent with at least one pattern in IE(M);
- each IA consistent with a pattern in IA(M) contains content consistent with at least one pattern in CT(M);
- each channel consistent with a pattern in CH(M) is used by at least one IE consistent with a pattern in IE(M).
- E = {e: e is an instance of some pattern in IE(M)};
- A = {a: a is an instance of some pattern in IA(M)};
- C = {c: c is an instance of some pattern in Chan(M)}.
| # | Type of connection | Equivalent as physical process |
|---|---|---|
| 1 | Physical process instance | Physical process instance (as in PCMs or ECMs) |
| 2 | m slices satisfy relation | There is an ecosystem process, which is an instance of a modelling tool pattern, which takes m slices as input and generates a content instance which is part of the content type “true” as output when the relation is satisfied |
| 3 | m slices have a property | There is an ecosystem process, which is an instance of a modelling tool pattern, which takes m slices as input and generates a content instance which is part of the ecosystem content type as output representing the value of the property |
3.5. Virtual Connection Models
- let v(xik) be the pointer with label xi and value δxik, where δxik is the disposition of xi at time tk;
- let e(ejk) be the pointer with label ej and value δejk, where δejk is the disposition of ej at time tk;
- let c(clk) be a pointer with label lab(c(clk)) ∈ C and value representing the relevant ecosystem process;
- let V(Ck) = ∪i {v(xi)}, E1(Ck) = ∪j {e(ejk)}, E2(Ck) = ∪l {c(clk)} and E(Ck) = E1(Ck) ∪ E2(Ck);
- N1(Ck) = {(v, e, w}: v, w ∈ V(Ck), e ∈ E1(Ck), the d-interaction represented by e connects the entities represented by v and w};
- N2(Ck) = {(x, e, y}: x, y ∈ V(Ck) ∪ E(Ck), e ∈ E2(Ck), the process represented by e supports x and y};
- N(Ck) = N1(Ck) ∪ N2(Ck);
- Ck = (V(Ck), E(Ck), N(Ck)).
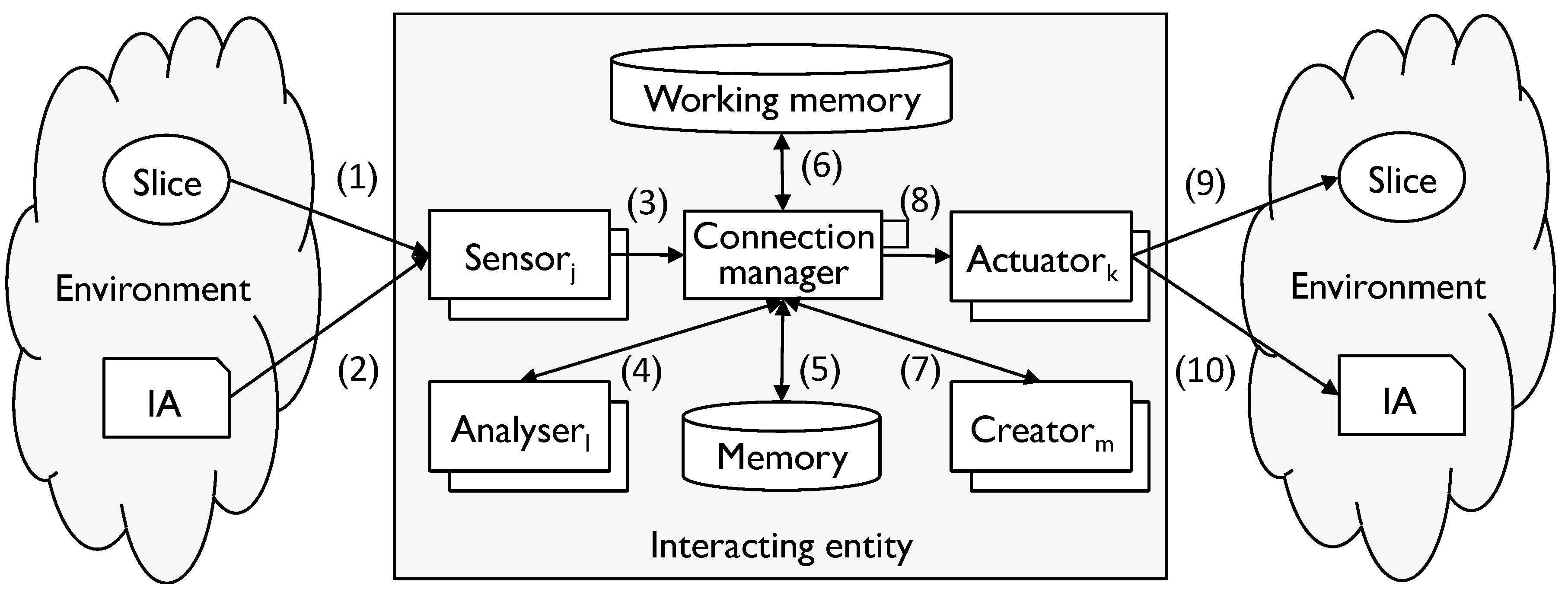
- (1)
- Environment input: an input interaction with the environment;
- (2)
- IA input: an input interaction with the environment in which the source of the input is an IA;
- (3)
- Converted input: the input converted into a form which can be manipulated by the IE;
- (4)
- MT-converted input: the input converted into a form consistent with the relevant modelling tool (if any);
- (5)
- Memories: material collected from memory;
- (6)
- Attention: the short-term picture created by the IE in working memory;
- (7)
- MT-converted output: output converted into a form consistent with the rules of a modelling tool;
- (8)
- Converted output, environment output, IA output: the reverse of the corresponding input.
3.6. Information Artefact Models
- SS(M) to be the set of ordered sequences of elements of ST(M);
- CS(M) to be the subset of SS(M) containing permissible modelling tool content.
- lab(c) ∈ CS(N) (where N is the modelling tool for consumers of the model);
- val(c) ∈ CS(M).
- ap ∈ IA(M) for a modelling tool M;
- UV(ap) is the set of uninstantiated pointers in ap.
- instantiating c ∈ UV(ap) means that val(c) is given the value vc for some vc ∈ CS(M);
- an Information Artefact Linnet (IAL) conforming to ap is obtained by instantiating all elements of UV(ap).
4. Information Quality (IQ)
- the human memory is fallible;
- digital media wear out and fail (as anyone who has suffered a computer disc head crash can attest);
- transmission over a network can be unreliable.
- how well does x represent what it is intended to represent?
- how useful is x in what an IE needs to achieve?
4.1. Interpretation
- the whodunit question: what is the “something” (the subject) that some information describes?
- the completeness question: what other information is there about the subject?
- Sc = slices corresponding to people wearing coats;
- Sj = slices corresponding to people called John;
- Sr = slices corresponding to people from Rome.
- atom: the fundamental indivisible level of content in the modelling tool (note that this definition is different from the definition of “atom” in [17]) ;
- chunk: groups of atoms;
- assertion: the smallest piece of content that is a piece of information—again composed of two chunks in a manner that conforms to an assertion pattern;
- passage: a related sequence of assertions.
| Component | Examples | Interpretation |
|---|---|---|
| Atom | Language: a word Mathematics: a variable Programming: a variable | A set of slices |
| Chunk | Language: a phrase Mathematics: a function with variables Programming: an expression | A set of slices that further constrains the slices corresponding to individual atoms |
| Assertion | Language: a sentence Mathematics: an equation Programming: an assignment statement | A set theoretic relationship between two sets of differently defined slices |
| Passage | Language: a paragraph (of assertions about the same things) Mathematics: simultaneous equations Programming: a function or subroutine | Multiple set theoretic relationships between sets of differently defined slices |
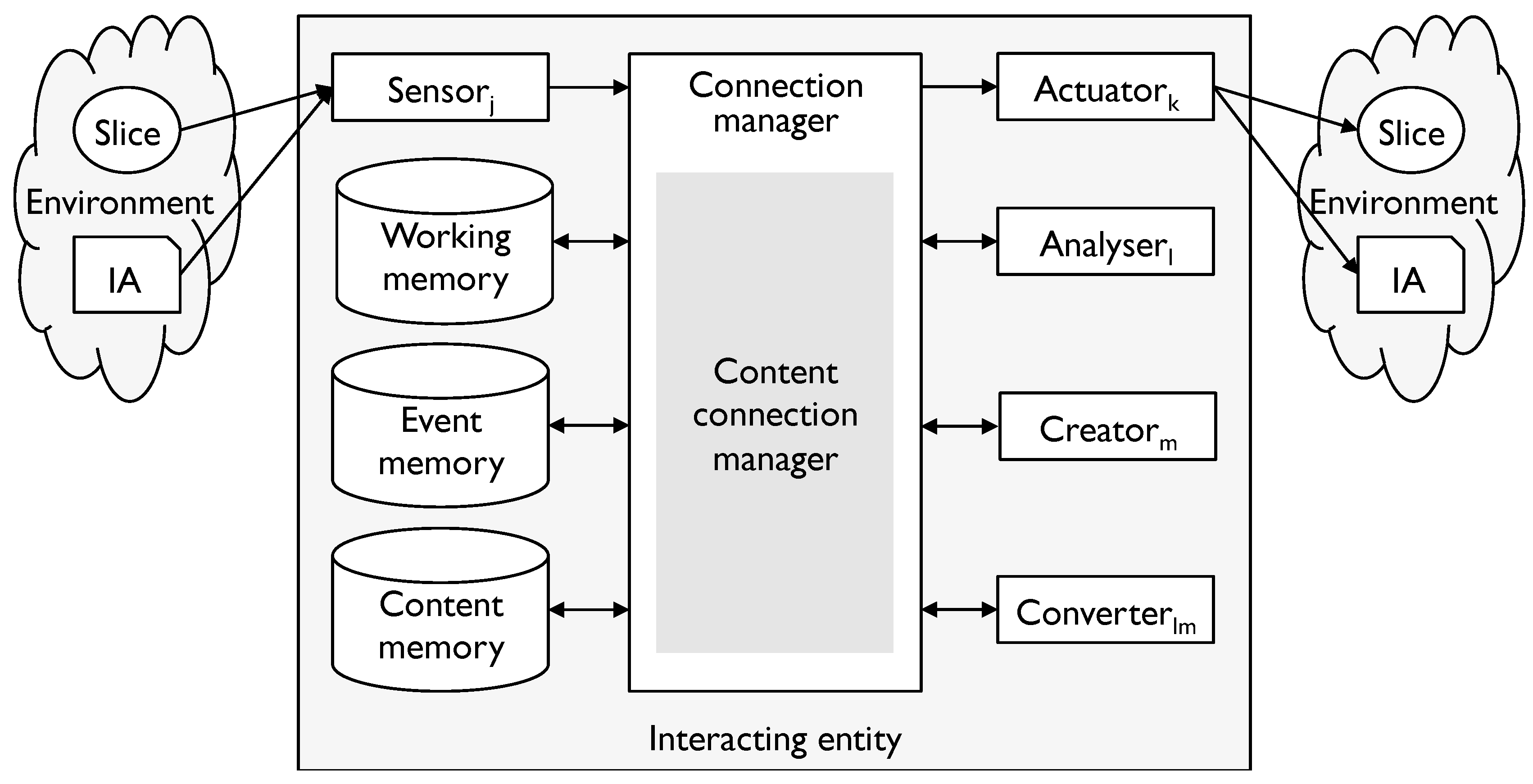
- humans converting between French and English;
- computer programs converting between messages using a banking protocol and their database structure.
- ΓΜ is the set of content in M;
- ΓcΜ is the set of chunk content in M;
- ΓaΜ is the set of assertion content in M;
- ΓpΜ is the set of passage content in M;
- Ξ is the set of set theoretic relationships (including ⊆, ⊇, ⊂, ⊃, ∩ = ∅, ∩ ≠ ∅);
- Σ is the set of all slices and Σ’ ∈ Σ;
- T is a set of discrete times.
- analysis (M) dcMα: Δxoα x T → ΓΜ (from disposition to content with modelling tool M);
- creation (M) cdMα: ΓΜ x T→ Δyiα (from content to disposition with modelling tool M);
- conversion (M,M) ccMα: ΓΜ x T→ ΓΜ (from content to content within modelling tool M);
- conversion (M, M’) ccMM’α: ΓΜ x T→ ΓΜ’ (from content to content, converting from M to M’).
- chunk interpretation (M) ciM: ΓcΜ x T → 2Σ’ (the set of slices which is the interpretation of a chunk with modelling tool M at a specific time);
- assertion interpretation (M) aiM: ΓaΜ x T → 2Σ’ x Ξ x 2Σ’ (the sets of slices and relation which is the interpretation of an assertion with modelling tool M at a specific time).
- passage interpretation (M) piM: ΓpΜ x T → 2Σ’ x Ξ x 2Σ’ (the sets of slices and relation which is the interpretation of a passage with modelling tool M at a specific time).
- S iλt = {s ∈ Σ’: i(λ, t) = (s, r, u), for some u ∈ Σ};
- U iλt = {u ∈ Σ’: i(λ, t) = (s, r, u) for some s ∈ Σ}.
4.2. Geometry and Information
- When are two pieces of information the same with respect to the quantity?
- When does one piece of information have more of the quantity than another?
| # | Example | Disposition pointer(s) | Content pointer(s) | Order |
|---|---|---|---|---|
| 1 | Temperature | Continuous, single dimensional | Discrete, single dimensional | Total |
| 2 | Length of the mercury in a tube | Continuous, single dimensional | Discrete, single dimensional | Total |
| 3 | A number as a finite string of digits | Discrete, single dimensional | Discrete, single dimensional | Total |
| 4 | Personal assessment of temperature into one of {cool, cold, warm, hot} | Discrete, single dimensional | Discrete, single dimensional | Partial (there may be an overlap between “cool” and “cold” for example) |
| 5 | Shape | Continuous, multi-dimensional | Discrete, multi-dimensional | Partial (induced by the total order for each dimension) |
| 6 | Species (e.g., lion, cheetah, leopard) | Discrete, single dimensional | Discrete, single dimensional | No order |
- The range is discrete;
- The range is continuous and contains two or more disjoint subsets.
| Example | Domain | Range | Transmission function | Metric |
|---|---|---|---|---|
| Reading a mercury thermometer | Continuous, total order | Continuous, total order | Tonic | Yes |
| Reading a digital thermometer | Continuous, total order | Discrete, total order | Tonic | Yes |
| Personal assessment of temperature into one of {cold, cool, warm, hot} | Continuous, total order | Discrete, partial order | P-tonic, discriminating | No |
| Recognition of cat species into {lion, leopard, cheetah} | Continuous, multi-dimensional, no order | Discrete | Discriminating | No |
4.3. Measurement
- Accuracy is the degree to which a measurement is close to the true value;
- Precision defines the extent to which repeated measurements give the same result;
- Resolution defines the size of change in a property which produces a change in the measurement.
- c < λt c’ if c (λ, t) ⊂ c’ (λ, t);
- c ≤ λt c’ if c (λ, t) ⊆ c’ (λ, t);
- c = λt c’ if c (λ, t) = c’ (λ, t).
- c is accurate (with respect to t and λ) if c =λt cE;
- c is inaccurate (with respect to t and λ) if c (λ, t) ∩ cE (λ, t) = ∅;
- c is more accurate than c’ (with respect to t and λ) if cE ≤λt c <λt c’ or cE ≥λt c >λt c’; (and similarly less accurate);
- c is as accurate as c’ (with respect to t and λ) if cE ≤λt c ≤λt c’ or cE ≥λt c ≥λt c’;
- c is partially accurate if it is not accurate, inaccurate, or more or less accurate than cE.
- res (c, Σ’, t) = |{λ ∈ ΓcΜ: σ ∈ c(λ, t), for some σ ∈ Σ’}|;
- c has greater resolution than c’ (with respect to t and Σ’) if res (c, Σ’, t) > res (c’, Σ’, t);
- c has lower resolution than c’ (with respect to t and Σ’) if res (c, Σ’, t) < res (c’, Σ’, t);
- c has resolution as good as c’ (with respect to t and Σ’) if res (c, Σ’, t) ≥ res (c’, Σ’, t);
- c has the same resolution as c’ (with respect to t and Σ’) if res (c, Σ’, t) = res (c’, Σ’, t).
- the ∩-range of c with respect to λ, ∩-ran (c, λ) = {σ: σ ∈ c (λ, t) ∀ t ∈ T};
- the ∪-range of c with respect to λ, ∪-ran (c, λ) = {σ: ∃ t ∈ T such that σ ∈ c (λ, t)};
- c is precise (with respect to λ) if ∩-ran (c, λ) = ∪-ran (c, λ);
- c is imprecise (with respect to λ) if ∩-ran (c, λ) = ∅;
- c is more precise than c’ (with respect to λ) if
- ∩-ran (c, λ) ⊃ ∩-ran (c’, λ) and ∪-ran (c, λ) ⊆ ∪-ran (c’, λ), or
- ∩-ran (c, λ) ⊇ ∩-ran (c’, λ) and ∪-ran (c, λ) ⊂ ∪-ran (c’, λ);
- c is as precise as c’ (with respect to λ) if
- ∩-ran (c, λ) ⊇ ∩-ran (c’, λ) and ∪-ran (c, λ) ⊆ ∪-ran (c’, λ).
- a1 is an assertion interpretation with induced chunk interpretations c1 and c1’ and relationship r1;
- a2 is an assertion interpretation with induced chunk interpretations c2 and c2’ and relationship r2;
- t ∈ T, Σ’ ∈ Σ, λ ∈ ΓcΜ.
- a1 is accurate (with respect to t and λ) if c1 is accurate and c1’ is accurate and r1 = rE (where rE has the obvious definition);
- a1 is more accurate than a2 (with respect to t and λ) if
- r1 = r2 and
- c1 is more accurate than c2 and c1’ is as accurate as c2’, or
- c1 is as accurate as c2 and c1’ is more accurate than c2’;
- a1 has greater resolution than a2 (with respect to t and Σ’)
- r1 = r2 and
- c1 has greater resolution than c2 and c1’ has resolution as good as c2’, or
- c1 has resolution as good as c2 and c1’ has greater resolution than c2’;
- a1 is more precise than a2 (with respect to λ) if
- r1 = r2 and
- c1 is more precise than c2 and c1’ is as precise as c2’, or
- c1 is as precise as c2 and c1’ is more precise than c2’.
- coverage: does the IA contain content which is derived from enough properties?
- resolution: does the interpretation provide sufficient resolution to discriminate between the options available?
- a chunk c is the subject of assertions a1, …, an;
- λn is the passage which contains a1 to an in sequence.
4.4. Assessing IQ
| Ecosystem | MT | Assessment of IQ | Characteristics |
|---|---|---|---|
| Science | Mathematics (often) | Careful design of experiments Peer review Transparency | High IQ Resource intensive |
| English Law | Legal English | Rigorous evidence gathering Trials and cross-examination | Relatively high IQ Resource intensive |
| Computer protocols | Tools like XML | Careful specification Careful implementation and testing Message validation | IQ linked to quality of definition Relatively resource intensive definition and implementation but efficient use (generally) |
| English speakers | Spoken English | Questions and answers | Variable IQ Relatively efficient |
- people trust brands for information just as they trust brands for other products (think of news organisations, for example);
- when users use a computer system they rely on the testing that has been carried out.
In these cases, the IE trusts that the IE providing the IA is reliable and that the reliability will transfer to the IA. This trust is not universal—it is an attribute of information ecosystems. The topic of trust in relation to IT is analysed in [23].“For information has trouble, as we all do, testifying on its own behalf. Its only recourse in the face of doubt is to add more information. ... Piling up information from the same source doesn’t increase reliability. In general, people look beyond information to triangulate reliability.”
5. Information Friction (IF)
- Φ is the set of all d-interaction function types;
- Ψ is the set of all space-time locations;
- N is the set of natural numbers;
- translation from one (human) language to another
- translation from one computer data structure to another (perhaps storing an incoming message in a database).
- interacting with a computer (in which both parties are trying to interpret the other!)
- deciphering an ancient document
- reading a news story.
6. Floridi’s Questions
- (P1) “what is information?”;
- (P12) “the informational circle: how can information be assessed? If information cannot be transcended but can only be checked against further information—if it is information all the way up and all the way down—what does this tell us about our knowledge of the world?”.
6.1. What is Information?
MfI provides a response to this statement and shows how these different elements combine. Consider each element in turn.“Information can be understood as range of possibilities (the opposite of uncertainty); as correlation (and thus structure), and information can be viewed as code, as in DNA .... Furthermore, information can be seen as dynamic rather than static; it can be considered as something that is transmitted and received, it can be looked upon as something that is processed, or it can be conceived as something that is produced, created, constructed .... It can be seen as objective or as subjective. It can be seen as thing, as property or as relation. It can be seen from the perspective of formal theories or from the perspective of informal theories .... It can be seen as syntactic, as semantic or as pragmatic phenomenon, and it can be seen as manifesting itself throughout every realm of our natural and social world.”
- the information ecosystem(s) under consideration;
- information quality;
- the degree of connection implied in an IA or created in an IE.
6.2. How can Information be Assessed?
The different MfI models show how information is linked directly to the properties of physical entities. Consider, in turn, the different elements of this question.“The informational circle: how can information be assessed? If information cannot be transcended but can only be checked against further information—if it is information all the way up and all the way down—what does this tell us about our knowledge of the world?”
In MfI, the relationship between physical properties and content is the distinction between PCMs and IAMs (discussed in Section 3), and the development of these elements of MfI shows the relationship. As an example, consider sunlight shining on a rock to which a thermometer is attached, which person A reads and tells person B, as in the following diagram (Figure 5).“If information cannot be transcended but can only be checked against further information— if it is information all the way up and all the way down…”
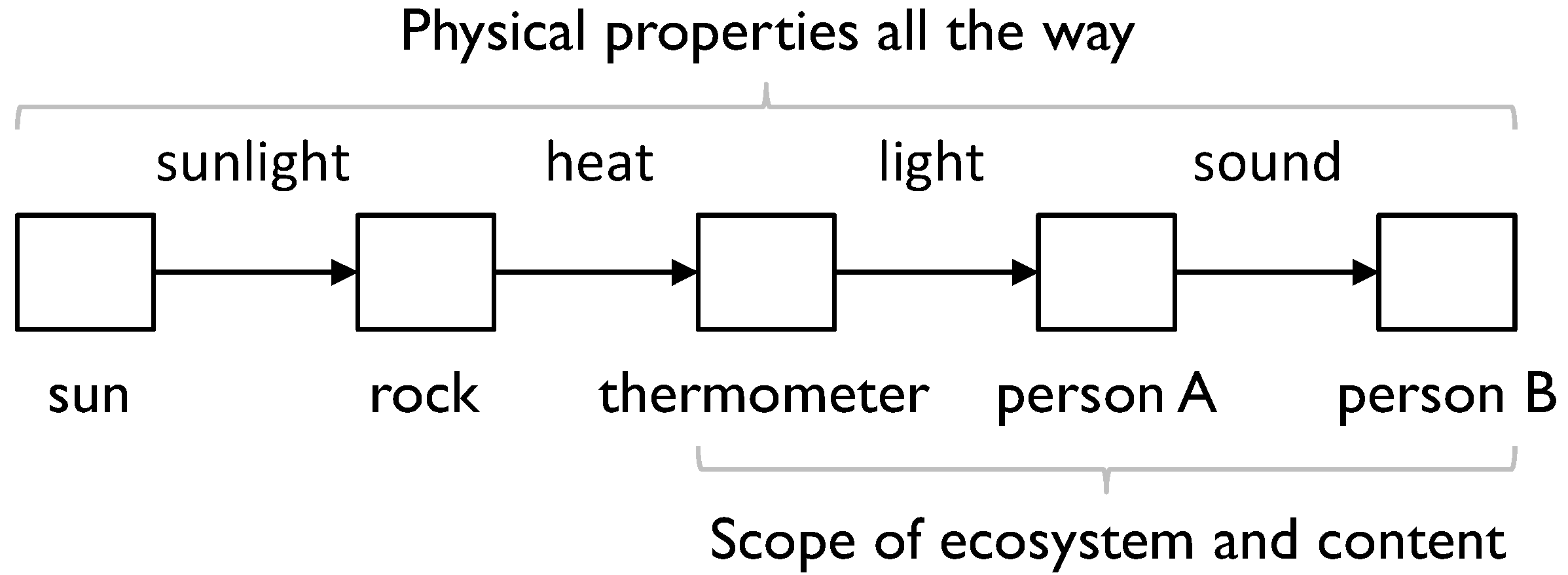
- through interaction (as in the example above);
- through processing existing content within an IE, in which case the new content is derived from the properties of the physical entities which represent the existing content within the IE by some physical processes;
- through the creation of the IE, in which case it is based on a set of physical processes acting on a pattern (which again comprises some properties of physical entities—see Section 2).
“It is properties of physical entities all the way up and all the way down and, according to ecosystem conventions, some are treated as content.”
According to MfI the premise for this is incorrect, so the question as posed becomes immaterial. However, MfI shines some light on this question when separated from the premise. As described in Section 4, information purports to describe set theoretic relationships between slices characterised using different combinations of properties. This purpose is subject to the vagaries of IQ and, as a result, is delivered with varying degrees of success. This purpose enables IEs to link environment states with potential outcomes in order to help the IE navigate towards a relatively favourable outcome.“What does this tell us about our knowledge of the world?”
7. Conclusions
Acknowledgments
Conflicts of Interest
References
- Silver, G.; Silver, M. Systems Analysis and Design; Addison Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Floridi, L. The Philosophy of Information; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Del Moral, R.; Navarro, J.; Marijuán, P. New Times and New Challenges for Information Science: From Cellular Systems to Human Societies. Information 2014, 5, 101–119. [Google Scholar]
- Hofkirchner, W. Emergent Information: A Unified Theory of Information Framework; World Scientific Publishing: Singapore, Singapore, 2013. [Google Scholar]
- Burgin, M. Evolutionary Information Theory. Information 2013, 4, 124–168. [Google Scholar]
- Darwin, C. On the Origin of Species by Means of Natural Selection, or the Preservation of Favoured Races in the Struggle for Life; John Murray: London, UK, 1859. [Google Scholar]
- Smith, A. An Inquiry into the Nature and Causes of the Wealth of Nations; Strahan and Cadell: London, UK, 1776. [Google Scholar]
- Avgeriou, P.; Uwe, Z. Architectural patterns revisited: A pattern language. In Proceedings of 10th European Conference on Pattern Languages of Programs (EuroPlop 2005), Bavaria, Germany, July 2005.
- Wolff, J. The SP Theory of Intelligence: Benefits and Applications. Information 2014, 5, 1–27. [Google Scholar]
- Kahneman, D. Thinking, Fast and Slow; Macmillan: London, UK, 2011. [Google Scholar]
- Burgin, M. Theory of Information: Fundamentality, Diversity and Unification; World Scientific Publishing: Singapore, Singapore, 2010. [Google Scholar]
- Harary, F. Graph Theory; Addison-Wesley: Reading, MA, USA, 1969. [Google Scholar]
- Harary, F.; Gupta, G. Dynamic Graph Models. Math. Comput. Model. 1997, 25, 79–87. [Google Scholar]
- ISO/IEC 9075-11: Information technology—Database languages—SQL—Part 11: Information and Definition Schemas (SQL/Schemata). Available online: http://www.iso.org/iso/catalogue_detail.htm?csnumber=38645 (accessed on 15 September 2014).
- Tulving, E. Episodic and semantic memory. In Organization of Memory; Tulving, E., Donaldson, W., Eds.; Academic Press: New York, NY, USA, 1972; pp. 381–403. [Google Scholar]
- Macknik, S.L.; Martinez-Conde, S. Sleights of Mind; Picador: Surrey, UK, 2011. [Google Scholar]
- Kohlas, J.; Schmid, J. An Algebraic Theory of Information: An Introduction and Survey. Information 2014, 5, 219–254. [Google Scholar]
- Popper, K.R. The Logic of Scientific Discovery; Hutchinson: London, UK, 1959. [Google Scholar]
- Huang, K.-T.; Lee, Y.W.; Wang, R.Y. Quality Information and Knowledge; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Fields, C. Equivalence of the Symbol Grounding and Quantum System Identification Problems. Information 2014, 5, 172–189. [Google Scholar] [CrossRef]
- Brenner, J. Information: A Personal Synthesis. Information 2014, 5, 134–170. [Google Scholar]
- Brown, J.S.; Duguid, P. The Social Life of Information; Harvard Business Press: Boston, MA, USA, 2000. [Google Scholar]
- DeVries, W. Some Forms of Trust. Information 2011, 2, 1–16. [Google Scholar]
- Gates, B.; Myhrvold, N.; Rinearson, P. The Road Ahead; Viking Penguin: New York, NY, USA, 1995. [Google Scholar]
- Dodig Crnkovic, G.; Hofkirchner, W. Floridi’s “Open Problems in Philosophy of Information”, Ten Years Later. Information 2011, 2, 327–359. [Google Scholar]
- Mackay, D.M. Information, Mechanism and Meaning; MIT Press: Cambridge, MA, USA, 1969. [Google Scholar]
- Bateson, G. Steps to an Ecology of Mind; Ballantine Books: New York, NY, USA, 1972. [Google Scholar]
- Lenski, W. Information: A Conceptual Investigation. Information 2010, 1, 74–118. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Walton, P. A Model for Information. Information 2014, 5, 479-507. https://doi.org/10.3390/info5030479
Walton P. A Model for Information. Information. 2014; 5(3):479-507. https://doi.org/10.3390/info5030479
Chicago/Turabian StyleWalton, Paul. 2014. "A Model for Information" Information 5, no. 3: 479-507. https://doi.org/10.3390/info5030479
APA StyleWalton, P. (2014). A Model for Information. Information, 5(3), 479-507. https://doi.org/10.3390/info5030479




