Abstract
Simulating organizational processes characterized by interacting human activities, resources, business rules and constraints, is a challenging task, because of the inherent uncertainty, inaccuracy, variability and dynamicity. With regard to this problem, currently available business process simulation (BPS) methods and tools are unable to efficiently capture the process behavior along its lifecycle. In this paper, a novel approach of BPS is presented. To build and manage simulation models according to the proposed approach, a simulation system is designed, developed and tested on pilot scenarios, as well as on real-world processes. The proposed approach exploits interval-valued data to represent model parameters, in place of conventional single-valued or probability-valued parameters. Indeed, an interval-valued parameter is comprehensive; it is the easiest to understand and express and the simplest to process, among multi-valued representations. In order to compute the interval-valued output of the system, a genetic algorithm is used. The resulting process model allows forming mappings at different levels of detail and, therefore, at different model resolutions. The system has been developed as an extension of a publicly available simulation engine, based on the Business Process Model and Notation (BPMN) standard.
1. Introduction and Motivation
Inadequate process design increases inefficiency and yields ineffectiveness. As a consequence, internally observable circumstances, such as backlog, long response times, poorly performing activities, unbalanced utilization of resources and low service levels, may produce external events of interest for the end user, such as increasing damage claims, angry customers and loss of goodwill. Hence, it is important to analyze business processes (BPs) before starting production and also while producing, for finding design flaws and for diagnosis/decision support.
BPs can be seen as a set of partially ordered activities intended to reach a goal. An interesting point from a scientific perspective is to separate the management of the BPs from the technological applications and methods developed for specific domains. Since the 1980s, researchers have been pursuing standard and unified ways of representing and measuring processes [1].
This section is structured into three subsections: modeling, parameterization and simulation of BPs.
1.1. Business Process Modeling
BP modeling is an established way of documenting BPs. A BP model is a generic description of a class of BPs. BP models describe how BP instances have to be carried out. They highlight certain aspects and omit others. A conceptual BP model is independent of a particular technology or organizational environment, whereas an executable BP model is specialized to a particular environment. The development of business process models is very labor-intensive [2]. There is a multitude of languages to support BP modeling, such as textual language (e.g., formal or natural language) and visual language (e.g., flow chart), and there are several representation standards. The interested reader is referred to [3] for a comparative analysis of such languages. Business Process Model and Notation (BPMN) [4] has been an Object Management Group (OMG) standard since 2005, aimed at providing a notation readily understandable by all business stakeholders. The BPMN structure is similar to well-known flow charts and activity diagrams. However, BPMN provides support to represent the most common control-flow patterns occurring when defining process models [5]. In this paper, BPMN is considered a reference standard in BP modeling.
In the process-based approach, quantifiable measurements must be defined, so-called key performance indicators (KPIs). KPIs can be related to a marketing-based perspective (e.g., customer satisfaction), to internal quality (non-compliance) and efficiency (cost, duration). KPIs are created on the basis of business objectives and are the detailed specifications used to track business objectives. A KPI is then associated with a specific process and is generally represented by a numeric value. A KPI may have a target and allowable margins, or lower and upper limits, forming a range of performances that the process should achieve. KPIs can be made up of one or more metrics. The calculated results of the metrics during process monitoring are used to determine whether the target of the KPI has been met. For example, waiting time, processing time, cycle time, process cost and resource utilization are commonly used KPIs [6,7]. To choose the right KPIs of a process requires a good understanding of what is important to the organization [8].
1.2. Business Process Parameterization
Business process simulation (BPS) [9] can be of great help in the quantitative measurement of KPIs. To simulate a process, it must first be defined as a workflow, showing the flow of work from trigger to result, with its main paths (scenarios) [2]. To simulate scenarios of a defined workflow, the availability of data input and parameters is critical. For instance, each case to be simulated must contain a number of process instances and their arrival rate. Moreover, the number of available resources must be declared for the process instances defined in the model. Furthermore, execution data has to be defined. For instance: the duration of each task, the branching proportion of each alternative flow, the number of resources needed by each task execution, and so on. Cost and other quality parameters can also be defined.
There are several possible outcomes of a BPS tool. The output can be a detailed process log that can be analyzed with a process mining framework [10], a set of benchmarks with related diagrams, a set of KPIs values, etc. Some simulation tools provide also support for animation (see [11]) and other criteria. The interested reader is referred to [12] for an analysis of such criteria at the application level.
This paper is focused on an important aspect of a BPS tool, i.e., the ability to capture the inherent uncertainty, inaccuracy, variability and dynamicity of a process [13,14]. Most business systems contain variability in the demand of the system (e.g., customer arrivals), as well as in the duration of processes (e.g., customer service times) within the system. In such cases, the use of average values does not provide reliable performance information. To model such variability is crucial when comparing as-is and to-be models, or in customer-based systems, where performance should not drop below a certain level. A great source of uncertainty is also related to the modeling of human resources [15].
A response to the above limits is to make more detailed models. However, a simulation model should have the right level of detail, and adding further detail does not always solve the problem [9]. Hence, it is very difficult to calibrate BPS models. For this reason, BPS tools permit the incorporation of statistical distributions, to provide an indication of both the range and variability of the performance of the process. Hence, task execution times and process arrival rates can be defined by an average value plus some distribution information, commonly standard, uniform or exponential distribution. In addition, BPS tools can incorporate statistical distributions to model non-deterministic decision flows.
A different representation dealing with uncertainty is the fuzzy-valued variable. In contrast with probability, which is an indicator of the frequency or likelihood that an element is in a class, fuzzy set theory quantifies the similarity of an element to a class by means of a membership function valued in the real unit interval [0,1]. While single-valued and probability-valued variables take numerical values, in fuzzy-valued variables, non-numeric values are often used to facilitate the expression of facts. For instance, variable, such as temperature, may have a value, such as cold, warm and hot, represented by three related functions mapping a temperature scale onto similarity values. Thus, a temperature value, such as 25 °C, can belong to both cold and warm with degree 0.2 and 0.8, respectively. In practice, fuzzy sets generalize classical sets whose membership degrees only take values of zero or one.
A special case of a classical bivalent set is the interval, i.e., a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. An interval-valued parameteris [x, x] is the simplest representation of uncertainty, asserting that measured values in a set of process instances range from x to x. As an example, consider the temperature of a chemical process, which may have values ranging in [19,27]°C. With an interval, no information about the distribution of the measured values is provided, which means that the shape of the probability density function is unknown. In contrast, a uniform probability distribution, U[x, x], asserts that the probability density function is known to be 1 / (x − x) for x ≤ x ≤ x and zero for x < x or x > x, which is much more detailed information on the outcomes of a process.
Depending on the scale of modeling, a certain amount of important data about the processes needs to be collected and analyzed in order to be incorporated in a model. Data is usually collected through discussions with experts and particularly with people involved in the processes to be modeled, through observation of the existing processes and studying the documentation about processes. Unfortunately, process traceability is, in general, a very difficult task [16]. In practice, in many cases, the available data is inaccurate and not sufficiently precise to parameterize the model, and there are no sufficient sample values to calculate a probability distribution. Indeed, data gathering is one of the major barriers to BPS methods. In the field of data-based fuzzy modeling, the construction of fuzzy sets is often difficult, even for process experts, and practicable for applications with a small number of variables. In the literature for the design of fuzzy sets, different approaches can be found, as the interpolation between pairs of observation values and given membership values or the data-based extraction via a clustering algorithm [17,18]. Similarly, to determine the most fitting probability distribution with an estimation of the parameters on the basis of observed data is an expensive task. Indeed, even to select the simplest model (e.g., the uniform probability distribution) in a group of candidate models needs statistical methods based on a number of sample data.
In contrast, interval-valued data refer to the data observed as a range instead of as a distribution of values. Interval data require simply the determination of the lower and upper bounds, which often can be easily asked from people who are involved in the activity. Thus, with respect to probability- and fuzziness-valued data, the modeling of interval-valued data requires less data collecting and processing.
1.3. Business Process Simulation
Statistical and interval-based simulation engines are very different in design. A statistical simulation engine evaluates the model on some stochastically extracted input data. This method does not produce an exact, reliable and deterministic output, as multiple executions of the method would produce different results. Moreover, a statistical engine is not scalable, because it requires an exploding number of evaluation points for increasing parameters of the model. In contrast, in a business model with interval-valued parameters, the output interval is determined by the highest and lowest KPI values that can be provided by giving to parameters all possible values within the related intervals. As an example, consider the temperature and the relative humidity of a chemical process, which may have values ranging in [19,27] °C and [74,81] %, respectively, producing a solidification time ranging in [187,231] min.
The problem of processing an output interval can actually be split into two sub-problems; for a given prefixed input: (i) to find the highest KPI value in the output; and (ii) to find the lowest KPI value in the output, under the constraints established by the intervals-valued parameters. As a matter of fact, each of these sub-problems is based on an optimization problem: (i) a maximization problem; and (ii) a minimization problem; respectively.
In the literature, different solution methods have been applied for the optimization of business processes [19]. Basically, search is the solving method for such problems whose solution cannot be determined a priori via a sequence of steps. Search can be performed with either heuristic or blind strategies, depending on the use or not of domain knowledge to guide the search, respectively. Further, a search strategy can be more or less based on exploitation and exploration, i.e., using the best available solution for possible improvement and exploring the search space with new solutions, respectively. For instance, Hill-climbing and random search are two examples of strategies based on exploitation and exploration, respectively [20]. A genetic algorithm (GA) is a general-purpose search method, based on principles of natural biological evolution, which combines directed and stochastic strategy to make a balance between exploration and exploitation. GAs have been successfully applied to many industrial engineering problems that are impracticable for conventional optimization methods [21,22]. In a conventional optimization method, a single solution is increasingly improved through iterations, via problem-dependent progress strategies.
In this paper, we propose a novel approach of BPS consisting of the use of interval-valued parameters as an alternative to conventional single-valued or probability-valued parameters. With regard to this problem, we designed and developed a simulation system, called Interval Bimp (IBimp), whose optimization module is based on a GA. The IBimp system has been tested on pilot scenarios, as well as on real-world scenarios. The proposed simulator has been publicly released as an extension of Bimp, see [23], a publicly available simulation engine based on the BPMN standard. Unlike the approaches proposed in the literature, our interval-based simulator can be used in two ways: (i) as a generator of characteristic curves of models subject to uncertainty associated with their input parameters; (i) as a tool to evaluate the worst/best cases within a constrained operating area.
The paper is structured as follows. Section 2 introduces the background notions required to understand the proposed approach. Section 3 discusses existing work in BPS, with attention to parameterization approaches. Section 4 provides specification and design details on our interval-valued BPS approach. Architectural implementation details are provided in Section 5. In Section 6, five scenarios are introduced to illustrate the basic concepts of our approach. Section 7 covers conclusion and future works.
2. Background
The importance of conceptual modeling is largely recognized in the literature [24]. Modeling is a learning process allowing business analysts to make clear requirements, express domain knowledge and provide rough solutions. BP models should have a formal foundation. Indeed, formal models do not allow ambiguity and increase the potential for analysis [25]. In addition, a BP model should be easily understood by all the involved stakeholders. This important requirement can be achieved through the use of visual notations. Once consensus among stakeholders has been reached, the BP model can be deployed on BP management platforms and, if a formal language was used, its behavior can be unambiguously implemented by vendors. BP models may involve core business or complex business transactions. Hence, the analysis of BP models is important to reduce the risk of costly corrections at a later stage, as well as to investigate ways of improving processes. Visual models act as communication channels between business managers and technicians and provide documentation to manage post-project activities.
The strength of BPMN resides in two important aspects: (i) simplicity, which is due to the abstraction level provided by the standard; and (ii) the possibility of being automatically translated into a business execution language and, then, to generate a machine-readable prototype of business processes. BPMN was developed with a solid mathematical foundation provided by exploiting process calculus theory [26]. This theory is an essential requirement for a good business process modeling language, in order to automate execution and to easily provide proofs of general consistency properties, as is widely recognized in the literature [10,27]. Hence, BPMN was conceived of with the specific intention of creating a bridge from the business perspective to the technical perspective about processes [26].
To describe BPs, BPMN offers the BP diagram. Figure 1 shows the basic elements of a BP diagram that are supported by the Bimp simulator: event, gateway (split node) and merge node, task and activity [4]. Key concepts are briefly defined in the following. Events are representations of something that can happen during the BP; a business flow is activated by a start event and terminated by an end event, while intermediate events can occur anywhere within the flow. Business activities can be atomic (tasks) or compound (processes and sub-processes, as a connection of tasks); gateways represent decision points to control the business flow. The sequence flow is represented by solid arrows and shows the order of execution of activities in the BP.
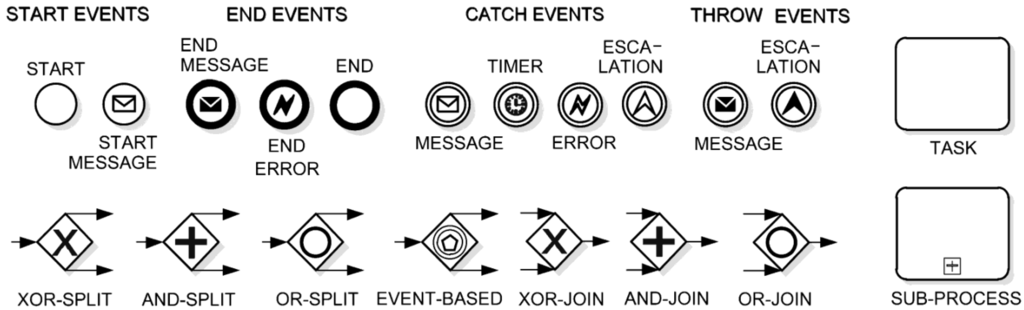
Figure 1.
Business Process Model and Notation (BPMN) elements supported by the Bimp simulator.
To define the BPMN process model, we employ the concept of a token traversing the sequence flow and passing through the elements in the process. A token is a theoretical concept that is used to define the behavior of a process that is being performed. During the simulation, any BPMN element in the process model has its own state per process instance. In Figure 2, a UML (Unified Modeling Language) state diagram shows the lifecycle of a BPMN element supported by the Bimp simulator. More specifically, an element becomes enabled when it has been selected by the simulation engine as an element to be handled. When a resource is assigned to a task, it is said that the task has been started. Elements other than tasks do not have the state, started, because resources can be assigned only to tasks. If the element gets completed without interruptions, the element is said to be completed. Otherwise, it changes to withdrawn.
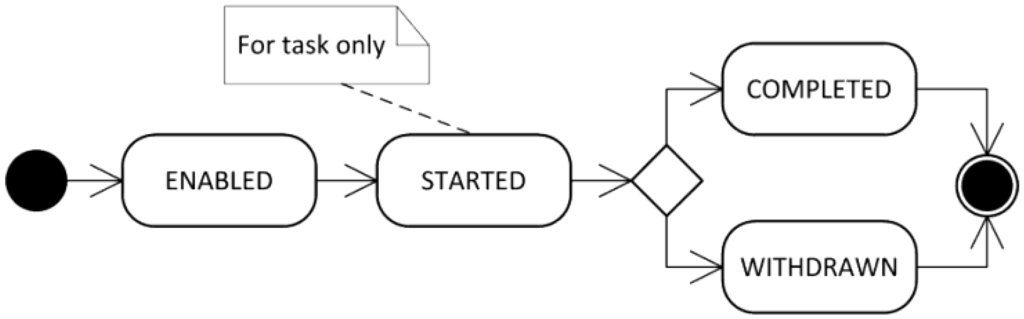
Figure 2.
A UML (Unified Modeling Language) state diagram representing the lifecycle of a BPMN element supported by the Bimp simulator.
In general, a BP diagram is organized in terms of interacting pools (partners), represented as labeled rectangular containers. A pool can be divided into lanes, represented as internal labeled rectangular containers, to express a detailed categorization of activities. Finally, message flows, represented as dashed white arrow, express messages exchanged between business entities. An example of a BP diagram is shown in Figure 3. It represents the macro processes of bag manufacturing in a leather workshop. More specifically, the start event in the leather workshop pool indicates where the process starts. Then, a cutting activity is performed on a leather sheet. At this point, there are two possibilities: either the bag components are prepared internally, via a preparing components activity, or externally, by means of outsourcing. In the latter case, an outsourcing management activity is in charge of appointing a third party to the task, which will be carried out by a craftsman. Subsequently, an assembling activity can be either performed internally or externally, as done with the previous activity. Finally, the quality check and packing activity is carried out, and final products are made. The end event indicates where the process ends.
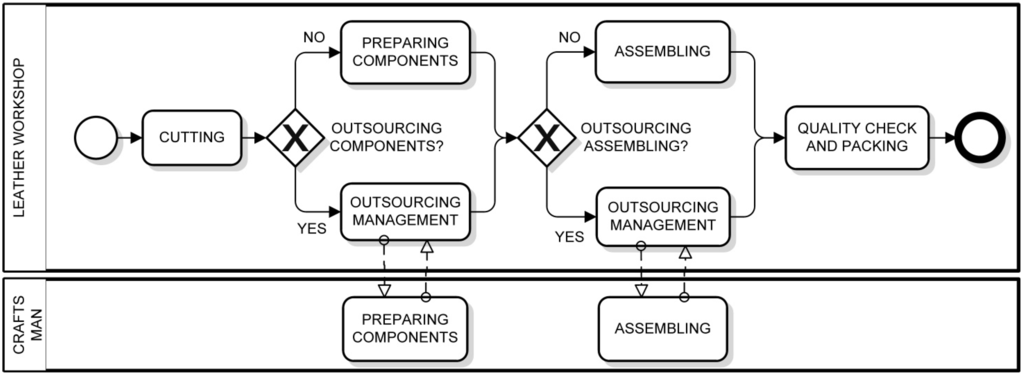
Figure 3.
A BPMN process diagram representing the macro processes of bag manufacturing in a leather workshop.
3. Related Work
3.1. Business Process Management Lifecycle
The BP management initiative aims at making processes visible and measurable, to continuously improve them. The BP management lifecycle is made of iterative improvements via identification, discovery, analysis, improvement, implementation and monitoring-and-controlling phases [4,8,28,29]. The identification phase determines an overall view of the process, whereas the discovery and analysis phases take an as-is view of the process and determine the issues of the process to be improved, respectively. The improvement and the implementation phases identify changes to address the above issues and make the to-be model effective. Finally, in the monitoring and control phase, process instances are inspected for the next iteration of the BP management lifecycle. Thus, managing a process requires a continuous effort, avoiding degradation. This is why the phases in the BP management lifecycle should be circular, i.e., the output of the monitoring-and-control phase feeds back into the discovery, analysis and improvement phases.
BP analysis, which is the focus of this paper, includes a rather broad meaning encompassing simulation, diagnosis, verification and performance analysis of BPs [1,28]. BP analysis should offer both supply-chain-level and company-level views of the processes, paying attention to roles and responsibilities. BP analysis tools should be usable by organizational managers rather than by specialists. Three types of analysis can be considered in the field [30]: (i) diagrammatic analysis, related to visual workflow-based models, which enable high-level specification of system interactions, improve system integration and support performance analysis [31]; (ii) formal/mathematical analysis, which is aimed at setting performance indicators related to the attainment of strategic goals [9]; and (iii) language-based analysis, which enables algorithmic analysis for validation, verification and performance evaluation [32]. In particular, performance evaluation aims at describing, analyzing and optimizing the dynamic, time-dependent behavior of systems [30]. The performance level focuses on evaluating the ability of the workflow to meet requirements with respect to some KPIs target values.
A performance measure or KPI is a quantity that can be unambiguously determined for a given BP; for example, several costs, such as the cost of production, the cost of delivery and the cost of human resources. Further refinement can be made via an aggregation function, such as count, average, variance, percentile, minimum, maximum or ratios; for instance, the average delivery cost per item. In general, time, cost and quality are basic dimensions for developing KPIs. The definition of performance measures is tightly connected to the definition of performance objectives. An example of a performance objective is “customers should be served in less than 30 min”. A related example of a performance measure with an aggregation function is “the percentage of customers served in less than 30 min”. A more refined objective based on this performance measure is “the percentage of customer served in less than 30 min should be higher than 99%”.
BPS facilitates process diagnosis (i.e., analysis) in the sense that by simulating real-world cases, what-if analyses can be carried out. Simulation is a very flexible technique to obtain an assessment of the current process performance and/or to formulate hypotheses about possible process redesign. BPS assists decision-making via tools allowing the current behavior of a system to be analyzed and understood. BPS also helps predict the performance of the system under a number of scenarios determined by the decision-maker.
3.2. Business Process Simulation
Modern simulation packages allow for both the visualization and performance analysis of a given process and are frequently used to evaluate the dynamic behavior of alternative designs. Visualization and a graphical user interface are important in making the simulation process more user-friendly. The main advantage of simulation-based analysis is that it can predict process performance using a number of quantitative measures [13]. As such, it provides a means of evaluating the execution of the business process to determine inefficient behavior. Thus, business execution data can feed simulation tools that exploit mathematical models for the purpose of business process optimization and redesign. Dynamic process models can enable the analysis of alternative process scenarios through simulation by providing quantitative process metrics, such as cost, cycle, time, service-ability and resource utilization [30]. These metrics form the basis for evaluating alternatives and for selecting the most promising scenario for implementation.
However, BPS has some disadvantages. Some authors report the large costs involved and the large amount of time to build a simulation model, due to the complexity and knowledge required. The main reason is that business processes involves human-based activities, which are characterized by uncertainty, inaccuracy, variability and dynamicity. Even though simulation is well-known for its ability to assist in long-term planning and strategic decision-making, it has not been considered a main stream technique for operational decision-making, due to the difficulty of obtaining real-time data in a timely manner to set up the simulation experiments [33]. Reijers et al. [22] introduced the concept of “short-term simulation”. They went on to experiment with short-term simulations from a “current” system state to analyze the transient behavior of the system, rather than its steady-state behavior [34]. In [35], a short-term analysis architecture was designed, in the context of widely-used, off-the-shelf workflow tools and without a specific focus on resourcing. An example of a typical question for a simulation scenario might be “How long will it take to process?” Using conventional tools for BPS, it is possible to answer this question with an average duration, assuming some “typical” knowledge regarding the available resources. Another question might be “What are the consequences of adding some additional resources of a given type to assist in processing?” Again, the question cannot be answered with precision using the “average” results produced by a conventional simulation.
Basic performance measures in BPS are cycle time, process instances count, resource utilization, and activity cost [33]. Cycle time represents the total time a running process instance spends traversing a process, including value-added process time, waiting time, movement time, etc. The calculation of minimum, average and maximum cycle time based on all running process instances is a fundamental output of a BPS. The process instance count includes the total number of completed or running process instances. During a simulation, resources change their states from busy to idle, from unavailable to reserved. Current resource utilization, for a given type or resource, defines the percentage of a resource type that has been spent in each state. The availability and assignment of resources dictate the allocation of resources to activities. Hence, resource utilization provides useful indexes to measure and analyze under-utilization or over-utilization of resources. A resource can be defined by the number of available units, usage costs (i.e., a monetary value), setup costs and fixed costs. Cost can include the variable cost related to the duration (e.g., hourly wages of the involved human resources), as well as a fixed additional cost (e.g., shipping cost). When an activity is defined, it is also defined by the resources required to perform it, the duration for the activity and the process instances that it processes. During simulation, the BPS tool keeps track of the time each process instance spends in an activity and the time each resource is assigned to that activity. Hence, activity cost calculations provide a realistic way for measuring and analyzing the costs of activities. BPS tools allow a detailed breakdown of activity costs by resource or process instance type, as well as aggregated process costs.
Table 1 summarizes some important simulation parameters. A simulation is divided into scenarios, and each scenario must contain a well-defined path (from a start event to an end event), with a number of process instances and their arrival rate. Moreover, the available resources must be declared for the process instances defined in the model. Furthermore, element execution data has to be defined; for instance, the duration of each task, the branching proportion of each outgoing flow of a XOR and OR gateway, the resources needed by each task. Cost and other quality parameters can also be defined.
There are several possible outputs of a BPS tool, as represented in Figure 4:
- (i)
- A detailed process log of each process instance, which can be analyzed with a process mining framework [10]. Logs are finite sets of transactions involving some process items, such as customers and products. For example: (1) Jane Doe buys pdt1 and pdt2; (2) John Doe buys pdt1; (3) Foo buys pdt2, pdt3 and pdt4. Logs are usually represented in a format used by the majority of process-mining tools, known as MXML (Mining XML) [36].
- (ii)
- A set of benchmarks with some diagrams. Benchmarking is a popular technique that a company can use to compare its performance with other best-in-class performing companies in similar industries [37,38]. For example, a comparative plot of the compliance to international warranty requirements in a specific industrial sector.
- (iii)
- A set of KPIs values, as exemplified in Table 2.
Unfortunately, for a large number of practical problems, to gather knowledge, modeling is a difficult, time-consuming, expensive or impossible task. For example, let us consider chemical or food industries, biotechnology, ecology, finance, sociology systems, and so on. The stochastic approach is a traditional way of dealing with uncertainty. However, it has been recognized that not all types of uncertainty can be dealt with within the stochastic framework. Various alternative approaches have been proposed [39], such as fuzzy logic and set theory. Figure 5 shows some different representations of a simulation parameter. Here, in Figure 5a, the single-valued representation is shown. The possible (true) value is a unique value, and all other values are false (Boolean membership). With this kind of parameter, any process instance performs the same way (determinism). Figure 5b shows the interval-valued representation. The true values are fully established, and all other values are false (Boolean membership). Again, with this kind of parameter, any process instance performs the same way (determinism).
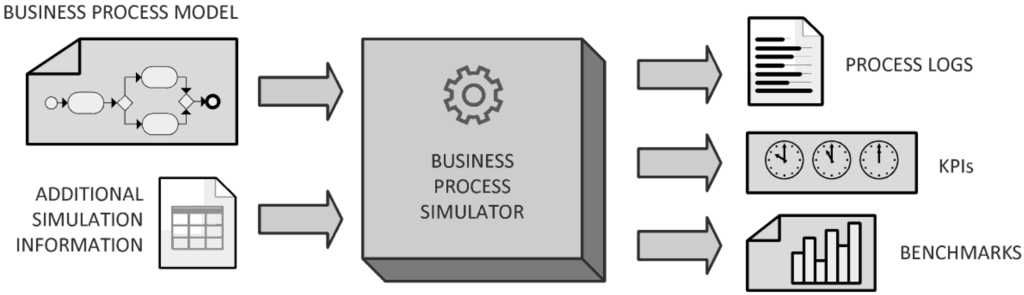
Figure 4.
Representation of the input and output data of a business process simulator.

Table 1.
Basic simulation parameters.
| Parameter | Description |
|---|---|
| task duration | the time taken by the task to complete |
| branching proportion | the percentage of process instances for each outgoing flow of an XOR/OR gateway |
| resource allocation | the resources needed by each task |
| task cost | a monetary value of the task execution instance |
| available resources | the number of pools, lanes, actors or role available for tasks |
| number of instances | the number of running process instances for the scenario |
| arrival rate | the time interval between the arrivals of two process instances |

Table 2.
Some general purpose key performance indicators. KPI, key performance indicator.
| KPI | Description |
|---|---|
| waiting time | time measured from enabling a task to the time when task was actually started |
| processing time | time measured from the beginning to the end of a single process path |
| cycle time | sum of time spent on all possible process paths considering the frequencies of the path to be taken in a scenario; cycle time corresponds to the sum of processing and waiting times |
| process cost | sum of all costs in a process instance |
| resource utilization | rate of allocated resources during the period that was inspected |
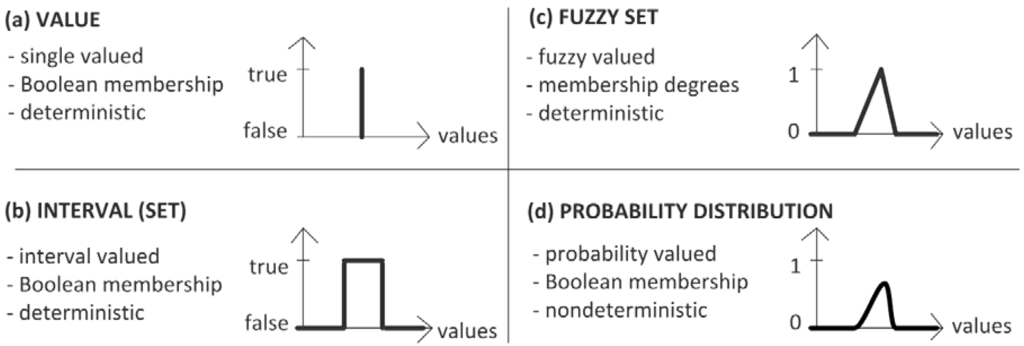
Figure 5.
Some different representations of a simulation parameter.
Figure 5c,d represents fuzzy and probabilistic values, respectively. Fuzziness is a type of deterministic uncertainty, which measures the similarity degree of a value to a set. In contrast, probability arises from the question of whether or not a value occurs as a Boolean event. An interval can be considered as a special fuzzy set whose elements have the same similarity to the set. The example of Figure 5c represents a triangular membership function, where there is a unique value that is fully a member of the set (i.e., the abscissa of the triangle vertex). Fuzziness and probability are orthogonal concepts that characterize different aspects of human experience. A detailed theoretical discussion of the relationships between the fuzziness and probability can be found in [40].
An example to show the conceptual difference between probability and fuzzy modeling is described as follows. An insolvent investor is given two stocks. One stock’s label says that it has a 0.9 membership in the class of stocks known as non-illegal business. The other stock’s label states that it has a 90% probability of being a legal business and a 10% probability of being an illegal business. Which stock would you choose? In the example, the probability-assessed stock is illegal, and the investor is imprisoned. This is quite plausible, since there was a one in 10 chance of it being illegal. In contrast, the fuzzy-assessed stock is an unfair business, which, however, does not cause imprisonment. This also makes sense, since an unfair business would have a 0.9 membership in the class of non-illegal business. The point here is that probability involves conventional set theory and does not allow for an element to be a partial member in a class. Probability is an indicator of the frequency or likelihood that an element is in a class. Fuzzy set theory deals with the similarity of an element to a class. Another distinction is in the idea of observation. Suppose that we examine the contents of the stocks. Note that, after observation, the membership value for the fuzzy-based stock is unchanged while the probability value for the probability-based stock changes from 0.9 to 1 or 0. In conclusion, fuzzy memberships quantify similarities of objects to defined properties, whereas probabilities provide information on expectations over a large number of experiments.
Simulation functionality is provided by many business process modeling tools based on notations, such as EPC (Event-driven Process Chain) or BPMN. These tools offer user interfaces to specify basic simulation parameters, such as arrival rate, task execution time, cost and resource availability. They allow users to run simulation experiments and to extract statistical results, such as average cycle time and total cost. Table 3 provides a summary of the main features of some commercial BPS tools [41].

Table 3.
A summary of commercial business process simulation (BPS) tools supporting BPMN.
| BPS Tool Engine | Short Functional Description |
|---|---|
| ARIS (Architecture of Integrated Information Systems) Business Simulator | Locate process weaknesses and bottlenecks; identify best practices in your processes; optimize throughput times and resource utilization; determine resource requirements, utilization levels and costs relating to workflows; analyze potential process risks; establish enterprise-wide benchmarks |
| Bizagi BPM (Business Process Management) Suite | Identify bottlenecks, over-utilized resources, under-resourced elements in the process and opportunities for improvement. Create multiple what-if scenarios |
| Bonita Open Solution | Generate business process simulation reports that detail per iteration and cumulative process duration, resource consumption, costs and more |
| Sparx Systems Enterprise Architect | Identify potential bottlenecks, inefficiencies and other problems in a business process |
| IBM Business Process Manager | Simulate process performance; identify bottlenecks and other issues; compare actual process performance to simulations; compare simulations to historical performance data; simultaneously analyze multiple processes from a single or multiple process applications |
| iGrafx Process | Mapping real time simulation to show how transactions progress through the process highlighting bottlenecks, batching and wasted resources. Process improvement and what-if analysis, resource utilization, cycle time, capacity and other pre-defined and customizable statistics |
| Visual Paradigm Logizian | Simulate the execution of business process for studying the resource consumption (e.g., human resources, devices, etc.) throughout a process, identifying bottlenecks, quantifying the differences between improvement options which help study and execute process improvements |
| MEGA Simulation | Customizable dynamic simulation dashboards; build multiple simulation scenarios for isolated business processes or for covering entire value chains of coordinated business processes; indicators and associated customizable metrics link simulation results with the objectives of the optimization project; indicators can be defined by simple mathematical formulations, such as an MS-Excel formula, or by complex Visual Basic algorithms. Comparisons between indicators and simulation objectives assess the relevance of proposed scenarios |
| Signavio Process Editor | Visualize process runs and run analysis based on configurable one-case and multiple-case scenarios in order to gain information about cost, cycle times, resources and bottlenecks |
| TIBCO Business Studio | Perform cost and time analysis and examine workload requirements for the system |
4. Interval-Valued Business Process Simulation: Specification and Design
4.1. The Output of the Interval-Valued BPS As an Optimization Problem
In this subsection, the basic requirements of our interval-valued BPS model are formally introduced. We employ an implementation of the parameter in terms of interval-valued variable, which is defined as:
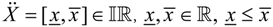 where
where  is the set of all closed and bounded intervals in the real line and x and x are the boundaries of the intervals. An F-dimensional array of parameters is then represented by a vector of interval-valued variables as follows:
is the set of all closed and bounded intervals in the real line and x and x are the boundaries of the intervals. An F-dimensional array of parameters is then represented by a vector of interval-valued variables as follows:
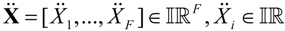
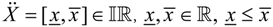
 is the set of all closed and bounded intervals in the real line and x and x are the boundaries of the intervals. An F-dimensional array of parameters is then represented by a vector of interval-valued variables as follows:
is the set of all closed and bounded intervals in the real line and x and x are the boundaries of the intervals. An F-dimensional array of parameters is then represented by a vector of interval-valued variables as follows:
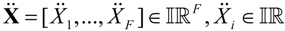
It is worth noting that real numbers can be considered as special intervals, called degenerated intervals, with x = x [42].
Let 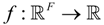 be an F-dimensional single-valued business process model. The corresponding interval-valued model
be an F-dimensional single-valued business process model. The corresponding interval-valued model 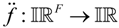 is defined as follows:
is defined as follows:
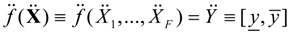 where:
where:
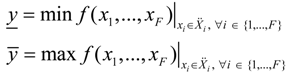
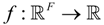 be an F-dimensional single-valued business process model. The corresponding interval-valued model
be an F-dimensional single-valued business process model. The corresponding interval-valued model 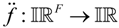 is defined as follows:
is defined as follows:
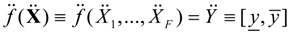
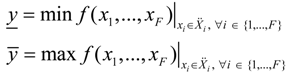
Formulas (3) and (4) represent the interval-valued BPS as an optimization problem. Figure 6 shows a simple case of interval-valued BPMN model, made of three tasks and two exclusive gateways. Here, each task is measured by an interval-valued parameter [xi, xi] (e.g., duration [12,15] min.), as well as the branching proportion of the upper flow of the XOR splitting gateway (e.g., [70,75] %). It is worth noting that the lower flow is constrained by the upper flow, because the total flow must be 100%. For this reason, there is a unique independent interval parameter associated with the gateway, i.e., 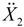 .
.
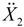 .
. For a given set of input interval parameters and a given output KPI (y), the interval-valued output of the process model [y, y] (e.g., total cycle time) can be theoretically determined by simulating the execution of the model for all possible single-valued parameter values x1,…,x4.
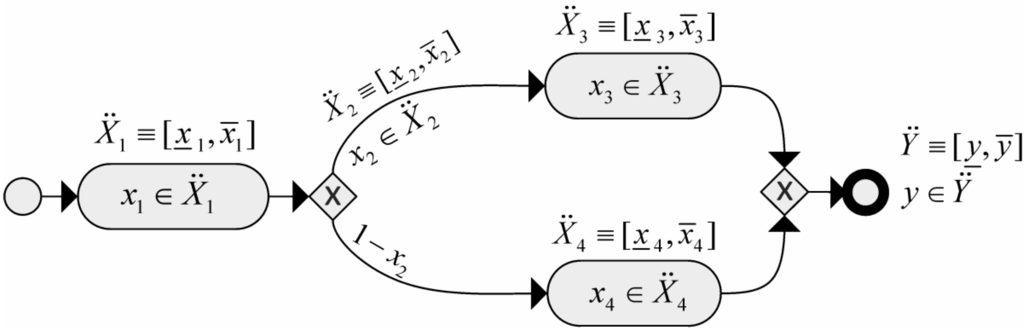
Figure 6.
A simple case of interval-valued BPMN model.
Figure 7 gives an exemplification of a mono-dimensional single-valued system function with its interval-valued form, by means of a black solid line and a grey stripe, respectively. Three evaluations of input-output are also included, as single points and rectangles, respectively.
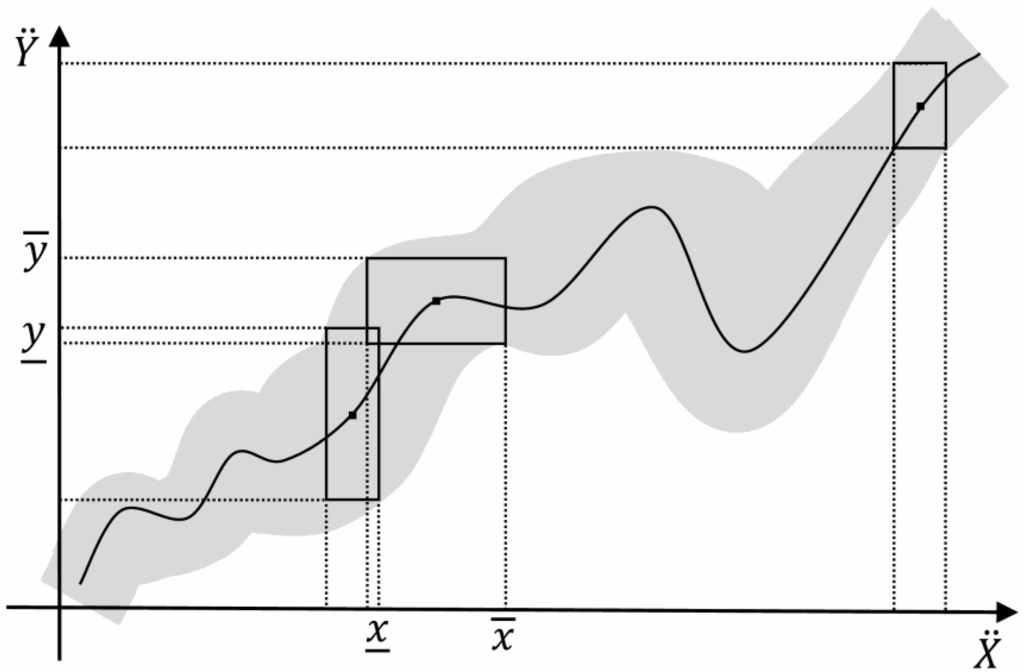
Figure 7.
An exemplification of a system with single-valued and interval-valued inputs-outputs.
4.2. The Genetic-Based Optimization
As expressed by Formulas (3) and (4), the problem of evaluating an interval-valued model can be designed as an optimization problem, where the boundaries of the output interval are determined as a minimization and a maximization problem. In our approach, to efficiently compute the interval-valued output of the system, a GA is used. A GA is a search method based on the analogy with the mechanisms of biological evolution [21,43]. A GA is typically made of the following main steps. For a given optimization problem, an initialization process provides a set of randomly generated approximated solutions. Each solution is then evaluated, using a problem-specific measure of fitness. If the termination criteria are satisfied, a solution is then elected as (sub-)optimal for the problem. If not, each solution is encoded as a chromosome (a serialized form). The chromosomes evolve through successive generations (iterations) of the GA. During each generation, a set of new chromosomes, called an offspring, is formed by: (i) the selection of a mating pool, i.e., a quota of parent chromosomes from the current population, according to the fitness values; (ii) a combination of pairs of parents via the crossover genetic operator; and (iii) modification of offspring chromosomes via the mutation genetic operator. The new chromosomes are then decoded in terms of domain solutions. Finally, a new generation is formed by reinserting, according to their fitness, some of the parents and offspring and rejecting the remaining individuals, so as to keep the population size constant [43]. Figure 8 shows the general structure of the GA.
The design of a GA for a given domain problem requires the specification of the following major elements: the chromosome coding of a solution, a fitness function to evaluate a solution and a choice of genetic operators and genetic parameters. The fitness function is represented by the output KPI, the interval-valued output of the process model. The next subsections are devoted to the specification of the other major elements.
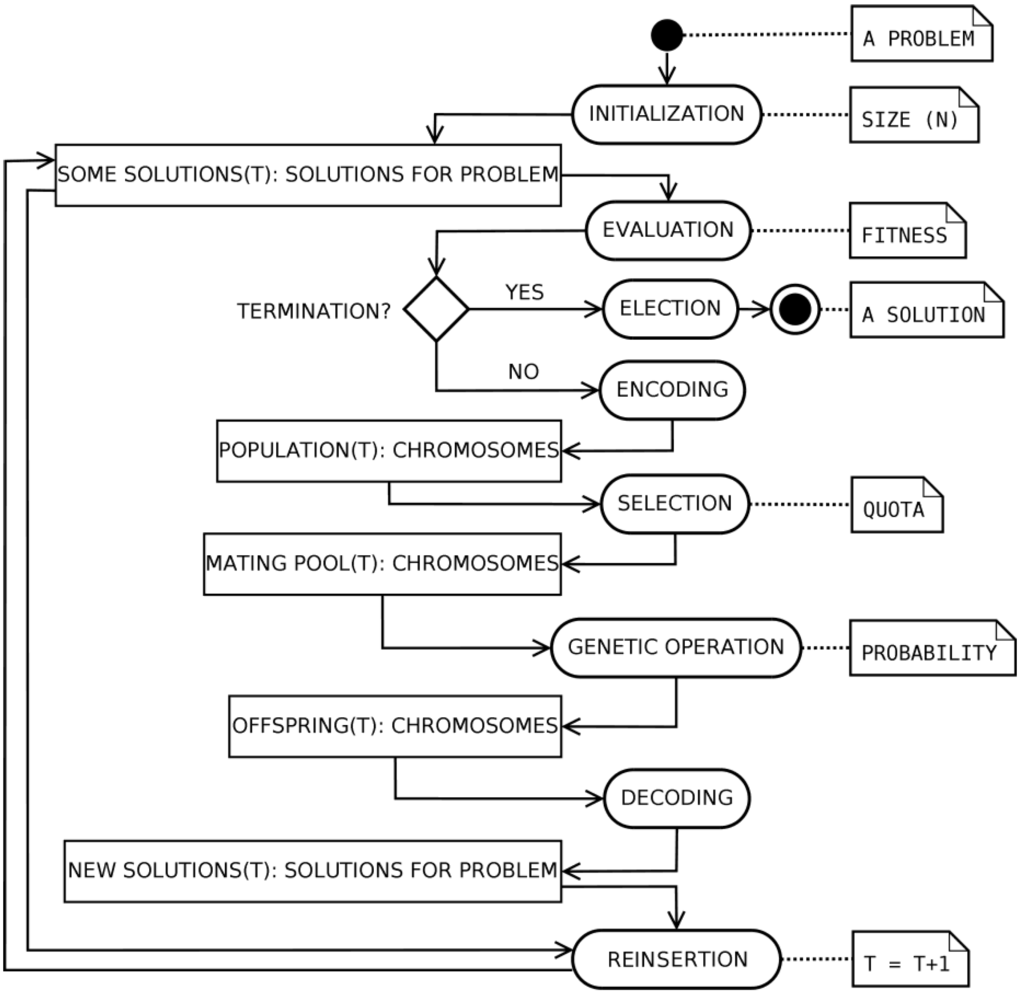
Figure 8.
The general structure of the GA.
4.3. The Genetic Coding
In a GA, a chromosome (or genome) is made of the set of parameters that define a proposed solution to the problem to solve. The chromosome is often represented as a string. Representation is a key issue, because a GA directly manipulates the coded representation of the problem and because the representation schema can severely limit the window by which it observes the search space [44]. Fixed-length and binary coded strings dominate GA research, since there are theoretical results showing their effectiveness and the availability of simple implementations. However, the GA’s good properties do not stem from the use of bit strings. One of the most important representations is the real number representation, which is particularly natural to tackle optimization problems with variables in continuous search spaces. More specifically, a chromosome is a vector of floating point numbers whose size is kept the same as the length of the vector, which is the solution to the problem. A GA based on a real number representation is called real-coded GA [44]. A real-coded GA offers a number of advantages in numerical function optimization over binary encodings. The efficiency of the GA is increased, as there is no need to convert chromosomes to phenotypes before each function evaluation; less memory is required as efficient floating-point internal computer representations can be used directly; there is no loss in precision by discretization to binary or other values; and there is greater freedom to use different genetic operators. Figure 9a,b shows the chromosome coding used in the GA. Here, each gene (box) encodes a single-valued parameter of the model. The chromosome contains the minimum number of variables. For instance, a decision point with N outgoing flows is represented via N-1 variables, because a variable can be calculated from the other ones, supposing that their summation must be equal to one.
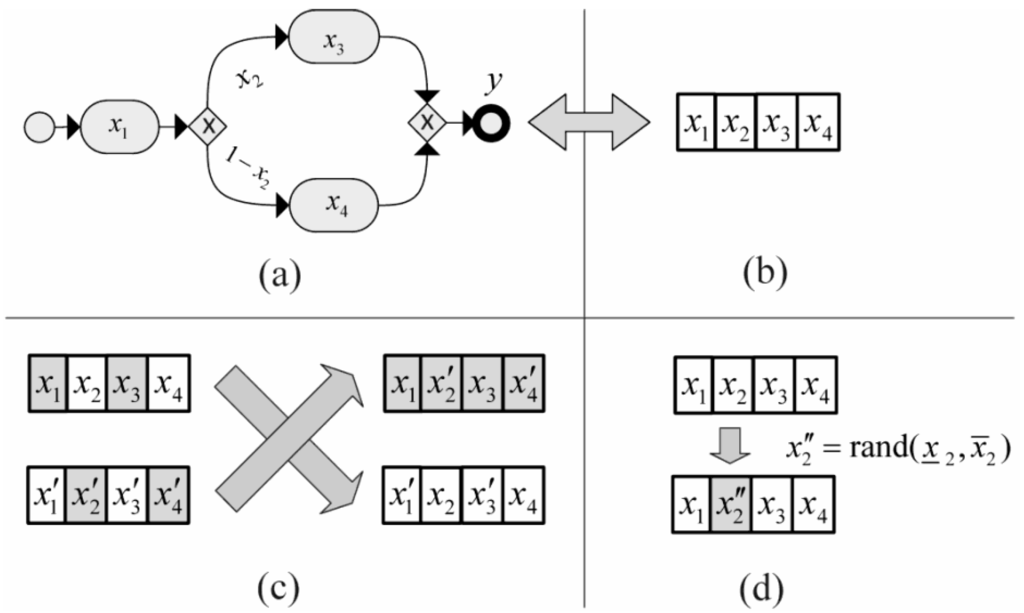
Figure 9.
The chromosome coding (a,b), the crossover (c) and the mutation (d) operators.
4.4. The Crossover and Mutation Genetic Operators
Crossover is the main genetic operator. It consists of splitting two chromosomes into two or more sub-sequences and obtaining two new chromosomes by exchanging gene sub-sequences between the two original chromosomes. More specifically, we adopted a scattered crossover, in which a binary mask is randomly created of the same length as parents chromosomes. The child is produced by combining parts of chromosomes that lie on the place of Number 1 in the mask from one parent and the rest from the other parent and vice versa. Figure 9c shows an example of such a crossover, where zero and one are represented by white and gray colors, respectively. The rationale for this choice is summarized in the following considerations. The idea behind the scattered crossover operator is that the segments contributing to most of the performance of a particular individual may not necessarily be contained in adjacent substrings. Further, the disruptive nature of such a crossover encourages the exploration of the search space, rather than favoring the convergence to highly fit individuals early in the search, thus making the search more robust [21].
The crossover operator is applied with a probability, pc (crossover rate), on the selected pair of individuals. When the operator is not applied, the offspring is a pair of identical copies, or clones, of the parents. A higher crossover rate allows a better exploration of the space of solutions. However, too high a crossover rate causes unpromising regions of the search space to be explored. Typical values are in the order of 10−1 [44].
Mutation is an operator that produces random alteration of the value of a gene, under the constraints enforced by the interval-valued parameter. Figure 9d shows a mutation operator applied on a gene. Mutation is used to maintain genetic diversity. Mutation is randomly applied. The mutation rate, pm, is defined as the probability that an arbitrary gene is complemented. If it is too low, many genes that would have been useful are never discovered, but if it is too high, there will be much random perturbation, the offspring lose their resemblance to the parents and the GA loses the efficiency in learning from the search history. Typical values of pm are in the order of 10−2 [44]. In our system, we used the adaptive feasible mutation, in which the default mutation function, when there are constraints, randomly generates directions that are adaptive with respect to the last successful or unsuccessful generation. The mutation chooses a direction and step length that satisfies bounds and linear constraints.
4.5. Selection, Reinsertion and Termination Methods
A selection operator chooses a subset of chromosomes from the current population. Various stochastic selection techniques are available. In this work, the roulette wheel method [43] is used. With this method, an individual is selected with a probability that is directly proportional to its fitness. Each individual is mapped to an arc of a circle, whose length equals the individual’s fitness. The circumference is then equal to the sum of the fitness. The selection is made by choosing a random number with a uniform distribution between zero and the circumference. The selected individual is the one mapped to the arc containing the chosen point. This ensures that better-fit individuals have a greater probability of being selected; however, all individuals have a chance.
Once a new population has been produced by selection, the crossover and mutation of individuals from the old population, the fitness of the individuals in the new population may be determined. To maintain the size of the original population, the new individuals have to be reinserted into the old population. Similarly, if not all the new individuals are to be used at each generation or if more offspring are generated than the size of the old population, then a reinsertion scheme must be used to determine which individuals are to exist in the new population. If one or more of the best individuals is deterministically reinserted in the next generation, the GA is said to use an elitist strategy. A mutation rate that is too high may lead to the loss of good solutions, unless there is elitist reinsertion. For this reason, we adopted this kind of feature.
As the GA is a stochastic search method, it may be difficult to formally specify convergence criteria. A common practice is to terminate the GA after a prefixed number of generations and then test the quality of the best individual of the population against the problem definition. As the fitness of a population may remain static for a number of generations before a superior individual is found, the application of conventional termination criteria may become problematic. For this reason, we used a more adaptive criterion: the GA terminates if there is no improvement in the best fitness of the population over a predetermined number of generations (called stall generations) or when the preset maximum number of generations is reached.
4.6. Overall Genetic-Based Optimization Algorithm
Let P be the current population, PM the mating pool (Section 4.2), PO the offspring (Section 4.2, the set of individuals resulting from crossover and mutation), PU the set of individuals passed unchanged to the next generation and q and s the cardinality of the mating pool and the cardinality of the current population, respectively. Function select(P) returns an individual from P, selected with the roulette wheel method, and function getPair(PM) returns a pair of parents from PM, selected with the roulette wheel method. Function crossover(x, y, pc) returns the offspring of a pair of parents (Section 4.4). Function mutate(x, PM) is applied to the selected parent with probability PM., whereas function reinsert(P, e) returns the first e best individuals from P. Note that the cardinality of the set, PU, is s − q, with individuals drawn from the population, P, passed to the algorithm. It may be observed that all sets used in the algorithm may contain pairs of identical individuals, due to the random character of the various operators. However, each individual is identifiable, even when it is structurally identical to another one. Therefore, all sets are proper sets (not multi-sets). As a consequence, the cardinality of P is a constant.
The optimization algorithm can be formally defined as follows.
| Algorithm 1: the genetic-based optimization algorithm. | |
| 01: | t ← 0; |
| 02: | initialize(P(t)); |
| 03: | evaluate(P(t)); |
| 04: | while not termination(P(t)) do |
| 05: | t ← t + 1; |
| 06: | P(t) = Generation (P(t – 1)); |
| 07: | evaluate(P(t)); |
| 08: | end while |
| 09: | return best(P(t)); |
| Algorithm 2: a generation of the genetic-based optimization algorithm. | |
| 01: | Procedure Generation(P) |
| 02: | begin |
| 03: | PM ← Ø; PO ← Ø; PU ← Ø; |
| 04: | for i = 1 to q do |
| 05: | x ← select(P); |
| 06: | PM ← PM ⋃ x; |
| 07: | end for |
| 08: | for i = 1 to q/2 do |
| 09: | (x, y) ← getPair(PM); |
| 10: | (x', y') ← crossover(x, y, pc); |
| 11: | x'' ← mutate(x', pm); |
| 12: | y'' ← mutate(y', pm); |
| 13: | PO ← PO ⋃ {x'', y''}; |
| 14: | end for |
| 15: | for i = 1 to s − q do |
| 16: | if i ≤ e |
| 17: | x ← reinsert(P, e); |
| 18: | else |
| 19: | x ← select(P, pc); |
| 20: | end if |
| 21: | PU ← PU ⋃ x; |
| 22: | end for |
| 23: | P ← PO ⋃ PU; |
| 24: | return P; |
| 25: | end |
4.7. The Parameter Tuning Process
Some sensitive user parameters for controlling GAs are the following [21,43]: (i) the maximum number of generations allowed; (ii) the population size, which is the number of individuals managed within a generation; (iii) the crossover fraction, i.e., the percentage of chromosomes (from a single generation) that get effectively involved in the crossover operation; and (iv) the elite count, which is the number of individuals with the best fitness values in the current generation that are guaranteed to survive to the next generation. Table 4 summarizes the parameters of the algorithm, together with their typical values. Such parameter values shown have been set according to a generic optimization strategy. In practice, when using evolutionary techniques on a specific case, a number of application constraints narrow down the choice of parameter values. In addition, parameters that cannot be chosen from application constraints can be tuned by using sensitivity analysis. Sensitivity is informally defined as the effect of uncertainty in the parameter on the final results [45].
For the purposes of this paper, application-dependent parameters have been set to the prototypical value of Table 4. With regard to genetic operators, many alternatives are available in the literature. Most of them are used for very specific purposes, unrelated to the aims of this paper.
5. Architectural Implementation
Many GA implementations can be employed in our system. Over the last few decades, considerable research has focused on improving GAs, by producing many types of genetic operators and algorithmic strategies. The interested reader is referred to [21,44] for a comparison of GA methods. It is worth noting that the optimization performed by the IBimp system usually lasts just a few generations. The coexistence of multiple GA implementations is an important requirement in order to allow inspecting the way in which the optimization is carried out, rather than its performance. Indeed, the analyst could be interested in accessing the steps performed by a GA, to better understand the criticalities of some parameters. The management of multiple GAs is, however, intended for advanced users and for experimental purposes, rather than for business users.

Table 4.
Parameters of the algorithm and their typical values.
| Parameter | Description | Value | Reference |
|---|---|---|---|
| s | population size | 50 | Section 4.6 |
| pc | crossover rate | 0.7 | Section 4.4 |
| pm | mutation rate | 0.1 | Section 4.4 |
| e | elite count | 2 | Section 4.5 |
| q | mating pool size | 25 | Section 4.6 |
| gmax | maximum number of generations allowed | 50 | Section 4.5 |
| gstall | number of generations considered for stall | 20 | Section 4.5 |
| εfit | fitness tolerance to detect an improvement | 10−6 | Section 4.5 |
Figure 10 shows how the overall modules of the system are wired together, via a UML component diagram. All the components are executed on the Java Runtime environment. The architecture has been developed and integrated with the MATLAB framework. The source code of our IBimp simulator has been publicly released on the MATLAB Central File Exchange [46] as an extension of Bimp [23] a publicly available java-based business process simulator.
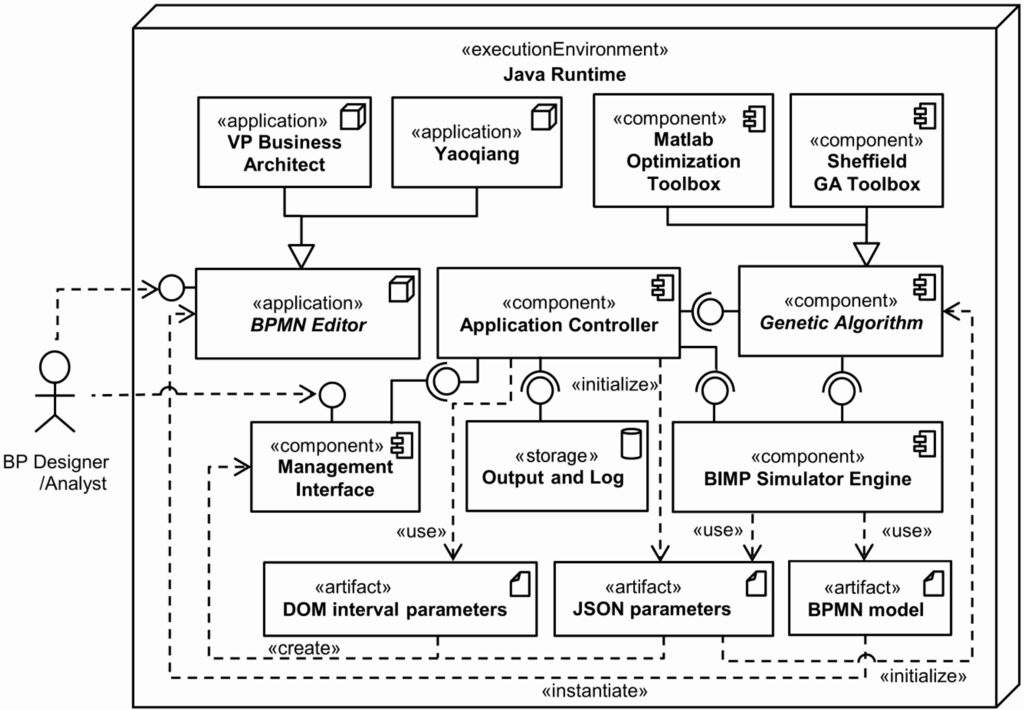
Figure 10.
IBimp, overall system architecture.
More specifically, the BP Designer/Analyst (the stick man on the left) first uses a BPMN editor to create a BPMN model (the artifact on the bottom right). For this purpose, any editor can be used, provided that a BPMN interchange format XML file can be exported. We mainly used the Visual Paradigm Business Architect [11] and the Yaoqiang [47] BPMN editors. Once created, the BPMN model artifact can be imported in another software product that supports BPMN interchange XML format. The BPMN model is then enriched by the BP Designer/Analyst with two types of parameters, namely JSON parameters and DOM (Document Object Model) interval parameters, via a management interface. The former represents the additional simulation information of Table 1 and Figure 4, whereas the latter represents the intervals related to some JSON parameters. DOM and JSON are the formats in which such parameters are generated and transferred to other components. More specifically, DOM stands for Document Object Model [48], a cross-platform and language-independent convention for representing and interacting with objects, whereas JSON stands for JavaScript Object Notation, a lightweight data-interchange format [49] that is used to send such parameters to the Bimp Simulator Engine, a core component of the architecture [50]. Bimp is the java-based business process simulator. It takes a file written in BPMN and allows you to add simulation information in JSON format, then outputs process logs and KPIs values. It can be used as a numerical (single-valued) or statistical simulator. We exploited the numerical features only, because the statistical ones are not adequate for our (deterministic) interval-valued approach.
Figure 11 shows the implementation of the management interface. More specifically, Figure 11a shows the main interface for setting both single-valued and interval-valued parameters. Once the XML/BPMN file has been loaded, the main interface shows a number of panes with the input data related to that specific process: general-purpose parameters, resources, tasks, intermediate events and gateways. Further simulation parameters can be set by an advanced user via a plain text configuration file.
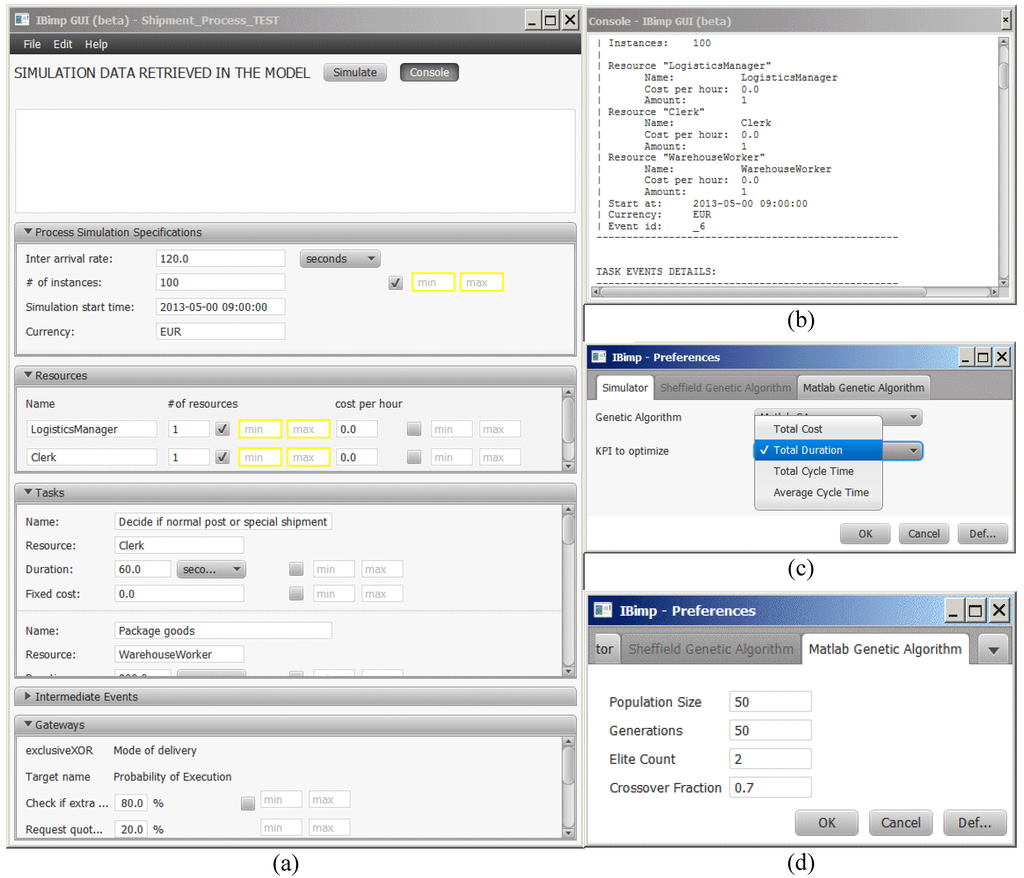
Figure 11.
IBimp management interface.
Once all parameters have been set, the management interface triggers the Application Controller, a component that acts as an orchestrator, by managing the interconnections and the interactions between the main system components. More specifically, the Application Controller is in charge of: (i) taking the parameters; (ii) executing the core simulation components; and (iii) taking the output and log data. Figure 11b shows the simulation console, with detailed information about the status of the simulation. Figure 11c shows the preferences pane, with the focus on the KPI choice (The Bimp engine currently supports four KPIs: total cost, total duration, total cycle time and average cycle time. In the Java source code of the engine, the class, KpiCalculator, can be extended to implement other KPIs). The other output and log data can be derived via log files in comma-separated values (csv) format. Moreover, the system is able to produce some plot of the optimization process, as shown in the experimental section.
The optimization is carried out by the genetic algorithm, a core component that is triggered by the Application Controller. The genetic algorithm is able to control the Bimp Simulator Engine and to instantiate the JSON parameters artifact, so as to carry out a high number of single-valued output evaluations, each with different JSON parameters. When the parameters are all single-valued, the Application Controller does not take into account the genetic algorithm, and the simulation output is computed via the Bimp Simulator Engine only.
The system can be used with different GA implementations. In our implementation, we included the MATLAB Optimization Toolbox [51] and the Sheffield GA Toolbox [52]. Figure 11d shows the common parameters for the MATLAB GA. Further genetic parameters can be set by an advanced user via plain text configuration files. The interested reader is referred to [21,44] for a detailed discussion of the genetic parameters.
6. Experimental Studies
Although several works have been published in the field of BPS, unfortunately, there is still a lack of benchmark scenarios in the literature. In this section, we discuss the application of our system to three pilot scenarios and to two real-world scenarios. The aim of this section is to briefly illustrate the possibilities offered by the IBimp simulator rather than to focus on completely solving the scenarios.
In all cases, the simulation is aimed at capturing the process efficiency under a certain variability expressed by some interval-valued parameters. Moreover, each scenario allows exploiting different features of the simulation tool. Depending on the scenario, the total duration and the average cycle time have been used as the main KPIs.
We adopted the MATLAB GA version in the optimization process, by setting the values of population size, elite count and crossover fraction to 50, 2 and 0.7, respectively. We also tested the Sheffield GA version, just to verify that the general properties of the optimization process are kept valid.
6.1. Pilot Scenario: Shipment of a Hardware Retailer
As a first scenario, consider a hardware retailer preparing some steps to fulfill before the ordered goods can actually be shipped to the customer. The scenario comes from [53] and allows testing queuing phenomena in synchronized flows. Figure 12 shows the related BPMN business process diagram. Here, the plain start event “goods to ship” indicates that the preparation is going to be done. After the instantiation of the process, two flows are carried out in parallel: while the clerk has to decide whether this is a normal postal or a special shipment, the warehouse worker can already start packaging the goods. This clerk’s task is followed by the exclusive gateway “mode of delivery”: only one of the following two branches can be traversed. If a special shipment is needed, the clerk requests quotes from different carriers, then assigns a carrier and prepares the paperwork. If a normal post shipment is fine, the clerk needs to check if an extra insurance is necessary. If that extra insurance is required, the logistics manager has to take out that insurance. In any case, the clerk has to fill in a postal label for the shipment. By means of the inclusive gateway, it can be shown that one branch is always taken, while the other one only if the extra insurance is required. If this is the case, this can happen in parallel to the first branch. Because of this parallelism, we need the synchronizing inclusive gateway right behind “fill in a post label” and “take out extra insurance”. Furthermore, we also need the synchronizing parallel gateway before the last task “add paperwork and move package to pick area”, to be sure that everything has been fulfilled before the last task is executed.
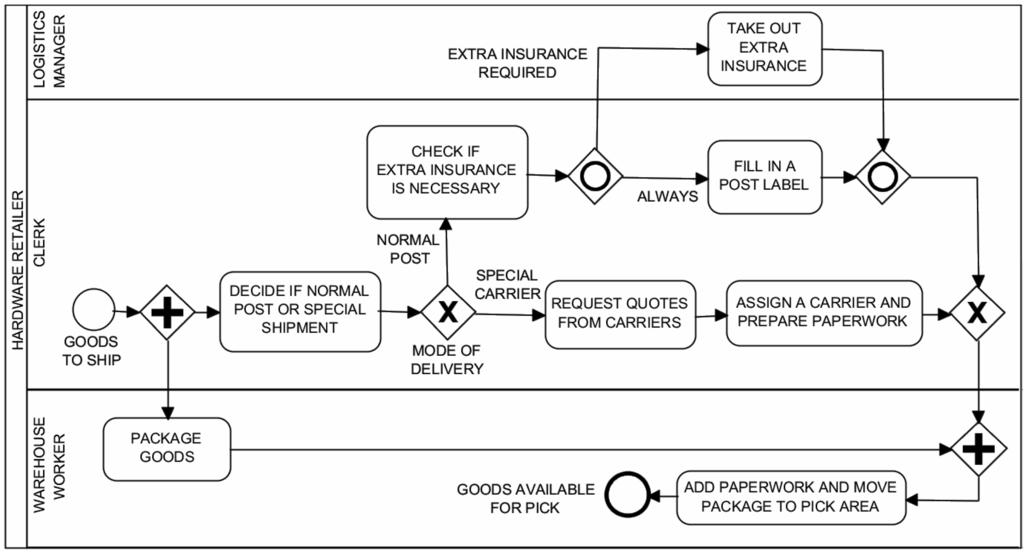
Figure 12.
Shipment process of a hardware retailer: BPMN process diagram.
Table 5 shows the model parameters, some of which are interval-valued. First, a single-valued simulation of 100 instances has been carried out, by using single-valued parameters only.
Table 6 and Table 7 show the result. It can be noted that there are very long queues, especially on the last activities, which wait for the management of the extra insurance. Subsequently, an interval-valued simulation has been carried out, by using intervals on some tasks and resources as expressed in the right column of Table 5.
Figure 13a,b shows the optimization processes performed by the GA, which are characterized by a very fast convergence: 15 generations only, carried out in 4 min (results were obtained on a computer with an Intel Dual Core i3-3220, 3.30 GHz, 8GB RAM).
As a result, the total duration interval provided by the system is [577, 4363] h. This outcome is the interval-valued total duration, due to the variability of some parameters in Table 5. Considering the abstraction of Figure 7, the result represent a single evaluation of a specific interval-valued function with 6 input parameters 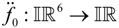 . By varying the interval-valued parameters on a region of interest, an interval-valued curve similar to Figure 7 can be generated.
. By varying the interval-valued parameters on a region of interest, an interval-valued curve similar to Figure 7 can be generated.
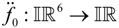 . By varying the interval-valued parameters on a region of interest, an interval-valued curve similar to Figure 7 can be generated.
. By varying the interval-valued parameters on a region of interest, an interval-valued curve similar to Figure 7 can be generated. Thus, the tool can be used in two ways: (i) as a generator of characteristic curve of models subject to uncertainty associated with some input parameters; and (ii) as a tool to evaluate the worst/best cases within a constrained area.
To illustrate the second way of using the system, Table 8 shows the values of the parameters that were used by the GA to have the minimum and maximum KPI, i.e., the best individual of both optimization processes. Here, it can be noted that the KPI minimization occurs by using a high number of resources and a low duration of tasks. Moreover, the KPI maximization occurs by using a low number of resources. This seems logical, since new resources speed up the entire process, whereas tasks duration needs to be adapted to the duration of other synchronized tasks, so as to reduce the queuing phenomena.
Different genetic operators and strategies may find different solutions to the problem. A comparative study can be proficiently handled as future work.

Table 5.
Parameters and their values for the shipment scenario.
| Parameter Name | Parameter Type | Parameter Value | Parameter Interval |
|---|---|---|---|
| Inter-arrival rate | time rate | 120 s | |
| Decide if normal post | duration | 60 s | |
| Check if extra | duration | 60 s | |
| Request quotes | duration | 1300 s | [1200, 2400] s |
| Assign a carrier & | duration | 500 s | [300, 600] s |
| Take out extra | duration | 900 s | [600, 1200] s |
| Fill in a post label | duration | 500 s | |
| Add paperwork | duration | 900 s | |
| Package goods | duration | 900 s | |
| Normal post | percentage | 80% | |
| Special carrier | percentage | 20% | |
| Extra insurance required | percentage | 20% | |
| Logistics manager | units | 1 | [1, 5] |
| Clerk | units | 1 | [1, 5] |
| Warehouse worker | units | 1 | [1, 5] |

Table 6.
KPIs, by using single-valued parameters, for 100 instances.
| KPI | Duration (h) |
|---|---|
| Shortest execution | 7.5 |
| Longest execution | 68.7 |
| Total duration | 4289.6 |
| Average duration | 46.9 |

Table 7.
Average waiting time, on 100 instances.
| Task | Average Waiting Time (s) |
|---|---|
| Add paperwork | 60,498 |
| Assign a carrier | 30,724 |
| Check if extra insurance | 28,017 |
| Decide if normal post | 9,272 |
| Fill in a post label | 31,607 |
| Package goods | 39,258 |
| Request quotes | 23,799 |
| Take out extra insurance | 432 |

Table 8.
Interval-valued results.
| Parameter/KPI | Optimization: Final Parameters | |
|---|---|---|
| Minimization | Maximization | |
| Logistics managers | 5 | 5 |
| Clerks | 5 | 1 |
| Warehouse workers | 5 | 1 |
| Request quotes | 1605 s | 1449 s |
| Assign a carrier | 301 s | 557 s |
| Take out extra | 667 s | 601 s |
| Total duration | 577 h | 4363 h |
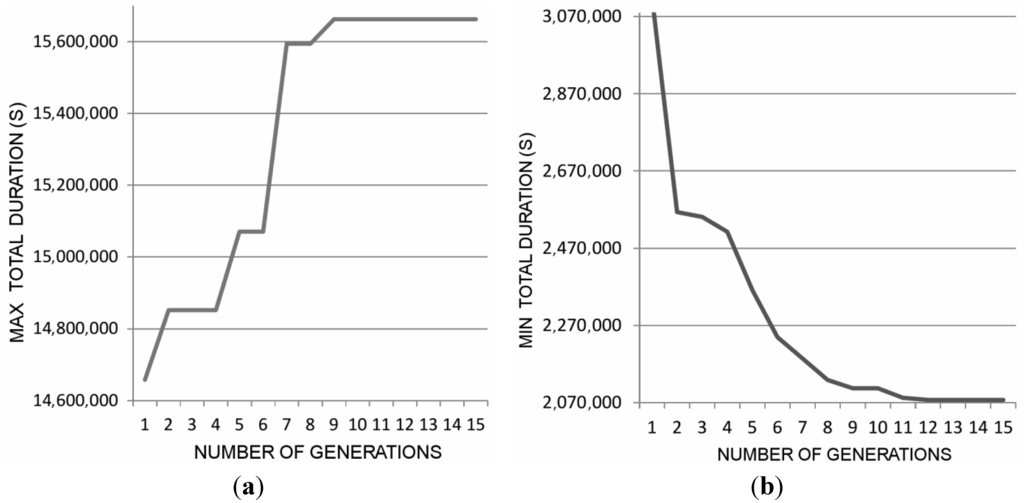
Figure 13.
Total duration vs. number of generations for the Shipment process.
6.2. Pilot Scenario: Hospital Emergency Center
The second pilot scenario comes from [54] and allows testing models with multiple exclusive flows. Figure 14 shows the BPMN process diagram. Consider the operations of a hospital emergency center (HEC). The process begins when a patient arrives through the admission process in the entrance room of the HEC and ends when a patient is either released from the HEC or admitted into the hospital for further treatment. Patients arriving on their own, after admission, sign in and then are assessed in terms of their condition (Triage). Depending on their condition, patients must then go through the registration process and through the treatment process. Arriving patients are classified into different codes (levels), according to their condition. With the red code, patients are more critical. Patients coming by ambulance are first assigned to the red code and taken to an emergency room (ER) immediately after admission. Once in the room, they undergo their treatment. Finally, they complete the registration process before being either released or admitted into the hospital for further treatment. In contrast, the yellow and green code patients must first sign in with an administrative clerk. After signing in, their condition is assessed by a triage nurse. Such patients must first complete their registration and then go on to receive their treatment. Finally, they are either released or admitted into the hospital for further treatment. The HEC has the following resources: nurses, physicians, technicians, administrative clerks, medical and administrative rooms.
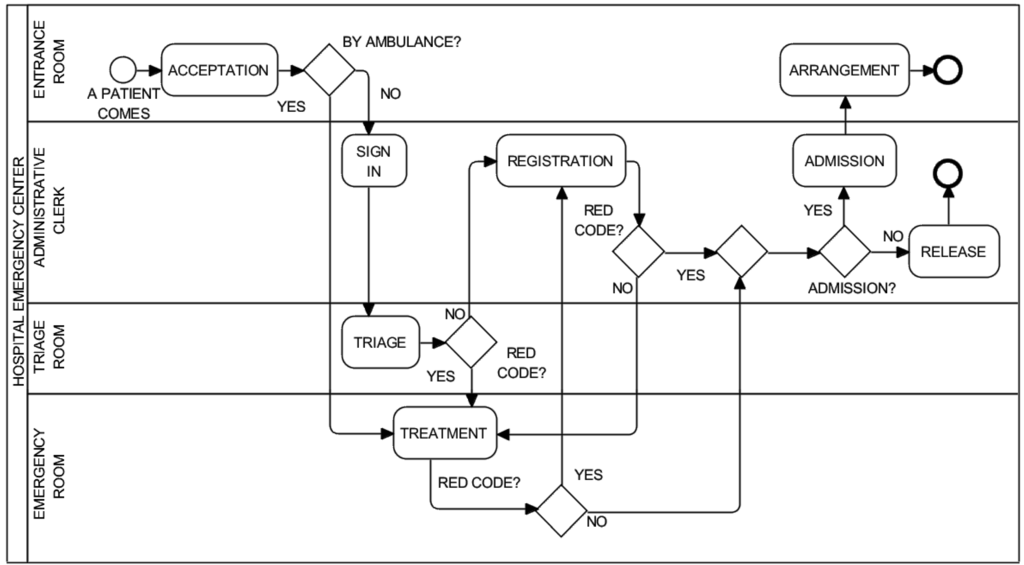
Figure 14.
Hospital emergency center: BPMN process diagram.
Table 9 shows the model parameters, five of which are interval-valued. First, a single-valued simulation of 100 instances has been carried out, by using single-valued parameters only. Table 10 shows the result. Subsequently, an interval-valued simulation has been carried out, by using intervals on some tasks and resources, as expressed in the last column of Table 9. Figure 15a,b shows the optimization processes performed by the GA. In terms of convergence, 50 generations were carried out. The total simulation lasted 12 min (results were obtained on a computer with an Intel Dual Core i3-3220, 3.30 GHz, 8GB RAM).

Table 9.
Parameters and their values for the hospital scenario.
| Parameter Name | Parameter Type | Parameter Value | Parameter Interval |
|---|---|---|---|
| Inter-arrival rate | time rate | 900 s | |
| Acceptation | duration | 30 s | |
| Acceptation | cost | 0.24 € | |
| Sign in | duration | 192 s | [100, 200] s |
| Sign in | cost | 1.55 € | |
| Triage | duration | 324 s | [150, 400] s |
| Triage | cost | 11.95 € | |
| Registration | duration | 570 s | [300, 700] s |
| Registration | cost | 4.59 € | |
| Admission | duration | 223 s | |
| Admission | cost | 1.79 € | |
| Release | duration | 132 s | |
| Release | cost | 1.06 € | |
| Treatment | duration | 1554 s | |
| Treatment | cost | 80.69 € | |
| Arrangement | duration | 1275 s | |
| Arrangement | cost | 10.28 € | |
| By ambulance? | percentage | 6% (yes) | |
| Red code (after triage)? | percentage | 10% (yes) | |
| Red code (after registration)? | percentage | 18% (yes) | |
| Red code (after treatment)? | percentage | 14.5% (yes) | |
| Admission? | percentage | 10% (yes) | |
| Emergency Room | units | 3 | [2, 5] |
| Triage Room | units | 2 | [1, 3] |

Table 10.
KPIs, by using single-valued parameters, for 100 instances.
| KPI | Duration |
|---|---|
| Shortest execution | 20.8 m |
| Longest execution | 256.3 m |
| Total duration | 116.3 h |
| Average duration | 69.8 m |
As a result, the total duration interval provided by the system is [62.25, 124.26] h. Table 11 shows the values of the parameters, which were used by the GA to have the minimum and maximum KPI, i.e., the best individual of both optimization processes. It can be noted that the KPI minimization occurs by using a high number of emergency rooms and a low number of triage rooms.

Table 11.
Interval-valued results.
| Resource/KPI | Optimization: Final Parameters | |
|---|---|---|
| Minimization | Maximization | |
| Emergency room | 4 | 2 |
| Triage room | 1 | 1 |
| Registration | 300 s | 696 s |
| Triage | 165 s | 360 s |
| Sign in | 132 s | 165 s |
| Total duration | 62.25 h | 124.26 h |
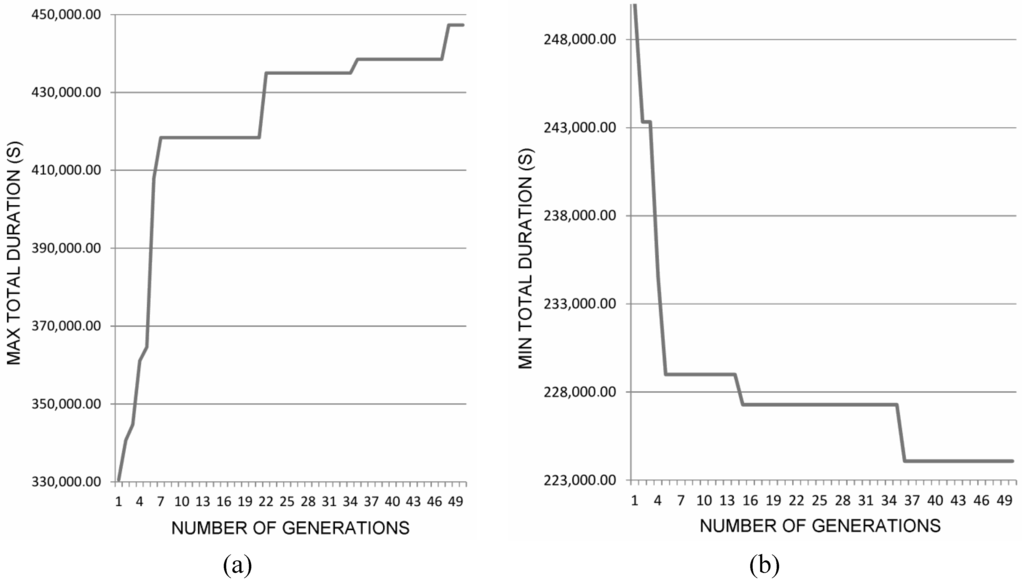
Figure 15.
Total duration vs. number of generations for the hospital process.
To better investigate the sensitivity of the number of emergency rooms, we can inspect the detailed progress of the KPI during the minimization and maximization steps, shown in Table 12 and Table 13, respectively. More specifically, it is worth noting in Table 12 that a reduction of about 6 h in the total duration is due to a reduction of a handful of seconds of the triage and registration durations, in spite of the fact that the number of triage rooms has also been reduced. It is worth noting in Table 13 that an increase of about 20 h in the total duration can be ascribed to less triage rooms and a small increase of the registration and sign-in durations.

Table 12.
KPI along generations during the minimization phase.
| Total Duration (h) | Emergency Room | Triage Room | Registration (m) | Triage (m) | Sign in (m) |
|---|---|---|---|---|---|
| 69.45 | 4 | 2 | 5.51 | 4.36 | 1.72 |
| 67.59 | 3 | 3 | 5.71 | 2.75 | 2.05 |
| 67.59 | 3 | 3 | 5.71 | 2.75 | 2.05 |
| 65.16 | 3 | 1 | 5.71 | 2.75 | 2.05 |
| 63.61 | 4 | 1 | 5.03 | 2.75 | 2.20 |

Table 13.
KPI along generations during the maximization phase.
| Total Duration (h) | Emergency Room | Triage Room | Registration (m) | Triage (m) | Sign in (m) |
|---|---|---|---|---|---|
| 95.76 | 2 | 2 | 11.20 | 5.98 | 2.35 |
| 100.30 | 2 | 2 | 11.60 | 5.48 | 2.74 |
| 101.29 | 2 | 2 | 11.60 | 5.79 | 2.75 |
| 113.32 | 2 | 2 | 11.20 | 5.98 | 2.78 |
| 116.23 | 2 | 1 | 11.60 | 5.98 | 2.75 |
6.3. Pilot Scenario: Insurance Company
The third pilot scenario comes from [54] and allows testing optimization in the use of resources. A personal claims department in an insurance company handles claims made by their clients. Figure 16 shows the BPMN process diagram. The first lane corresponds to work done by a claims handler located at the client’s local service center. Upon the arrival of a claim, the assessor determines if the client has a valid policy. If not, then the case is terminated; otherwise, the assessor enters the appropriate information in the system. In the second lane, an assessor located at the service center receives data from the claims handler. The assessor first determines if the claim is covered by the client’s policy. If not, the case is terminated; otherwise, the assessor approves the preliminary estimate of the damage. If the damage exceeds $2000, the claim is sent to an assessor at headquarters for approval; otherwise, it is sent directly to a senior assessor. Lane 3 corresponds to the assessor at headquarters. The assessor first authorizes the on-site investigation of the accident. If the investigation determines that the incident is not covered by the client’s policy, then the case is terminated; otherwise, a final price is determined, and the case is approved. In Lane 4, the senior assessor receives the claim, checks it, completes it and provides the final approval. Once the claim is approved, it is sent to documentation control. Documentation control, in Lane 5, is in charge of processing the payment to the client, closing the case and, finally, filing the claim. The problem in this example is to find the most efficient staffing levels for each of the five resource types.
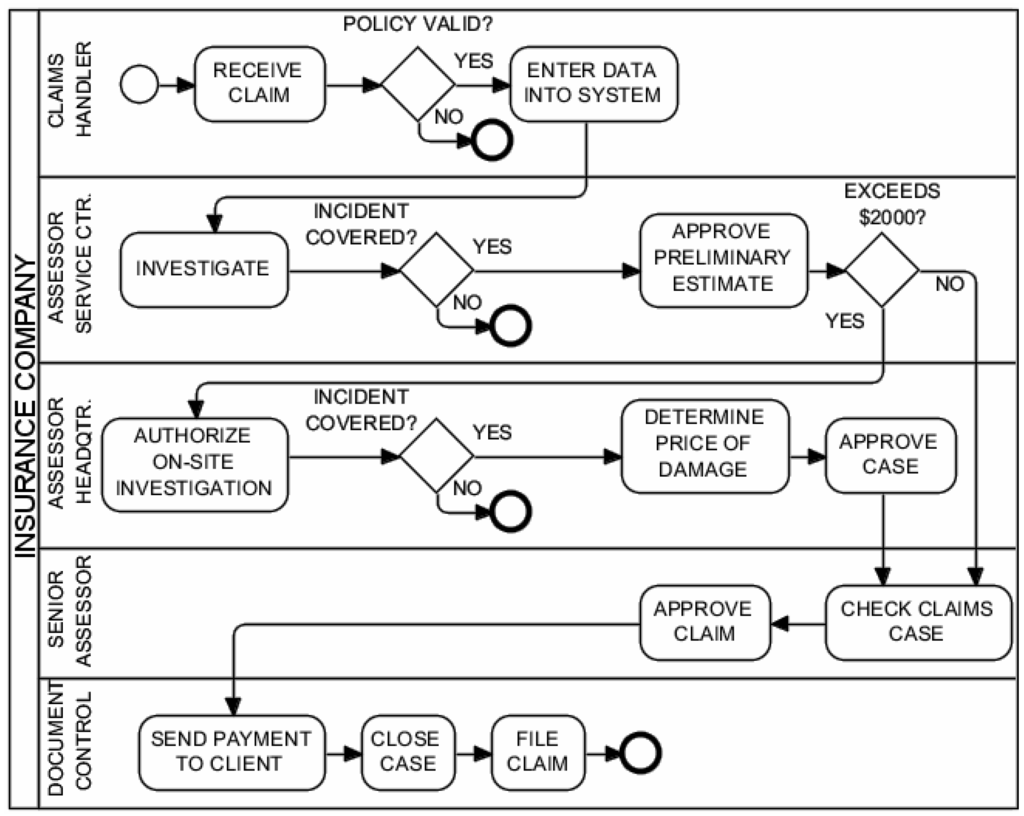
Figure 16.
Personal claims process at an insurance company: BPMN process diagram.
Table 14 shows the model parameters. First, a single-valued simulation of 100 instances has been carried out. Table 15 shows the resulting KPIs.

Table 14.
Parameter and their values for the insurance scenario.
| Parameter Name | Parameter Type | Parameter Value |
|---|---|---|
| Inter-arrival rate | time rate | 5 min |
| Receive claim | duration | 2 min 12 s |
| Enter data into system | duration | 10 min 32 s |
| Investigate | duration | 19 min 28 s |
| Approve preliminary… | duration | 3 min 54 s |
| Authorize on-site… | duration | 2 min 46 s |
| Determine price of… | duration | 37 min 16 s |
| Approve case | duration | 2 min 10 s |
| Check claims case | duration | 3 min 38 s |
| Approve claim case | duration | 1 min 18 s |
| Send payment to client | duration | 7 min 11 s |
| Close case | duration | 1 min 46 s |
| File claim | duration | 3 min 22 s |
| Policy valid? | percentage | 95% (yes) |
| Incident covered (Assessor Service Center)? | percentage | 95% (yes) |
| Incident covered (Assessor Headquarter)? | percentage | 98% (yes) |
| Exceeds $2000? | percentage | 35% (yes) |
| Claims handler | units | 10 |
| Assessor service center | units | 10 |
| Assessor HQ | units | 10 |
| Senior assessor | units | 10 |
| Document control | units | 10 |

Table 15.
KPIs, by using single-valued parameters, for 100 instances.
| KPI | Duration |
|---|---|
| Shortest execution | 132 s |
| Longest execution | 95.6 m |
| Total duration | 107 h |
| Average duration | 64.3 m |
Subsequently, an interval-valued simulation has been carried out, by using intervals [5,20] on resources. The GA converged in 40 generations, carried out in 11 min (results were obtained on a computer with an Intel Dual Core i3-3220, 3.30 GHz, 8GB RAM). As a result, the total duration interval provided by the system is [96.5, 109.7] h. Surprisingly, using fewer resources produces a shorter total duration. Table 16 shows the values of the parameters, which were used by the GA to have the minimum and maximum KPI, i.e., the best individual of both optimization processes. Here, it can be noted that the best is to use a very low number of assessor service centers. Moreover, the main difference between minimization and maximization could be ascribed to the number of assessor HQ resources. This can be easily verified by reducing the intervals and restarting the simulator. Thus, our interval-valued simulator allows forming mappings at different levels of detail and, therefore, at different model resolutions.

Table 16.
Interval-valued results.
| Resource/KPI | Optimization: Final Parameters | |
|---|---|---|
| Minimization | Maximization | |
| Claims handler | 14 | 16 |
| Assessor Service Center | 5 | 8 |
| Assessor HQ | 13 | 6 |
| Senior assessor | 10 | 11 |
| Document control | 19 | 19 |
| Total duration | 96.5 h | 109.7 h |
6.4. Real-World Scenario: Marine Container Terminal
This scenario presents a real-world experience of the application of our interval-valued simulation in the context of a marine container terminal located in the Port of Leghorn (Italy). A marine container terminal is the place where containers arriving by sea vessels are transferred to inland carriers, such as trucks, trains and vice versa. Every marine container terminal performs four basic functions: receiving, storage, staging and loading for both import and export. Receiving involves container arrival at the terminal, either as an import or export, recording its arrival, retrieving relevant logistics data and adding it to the current inventory. Storage is the function of placing the container in a known and recorded location in order to retrieve it when it is needed. Staging is the function of preparing a container to leave the terminal. The containers that are to be exported are identified and organized so as to optimize the loading process. Import containers follow similar processes, although staging is not always performed. An exception is a group of containers leaving the terminal via rail. Finally, the loading function involves placing the correct container on the ship, truck or other mode of transportation.
In this work, the emphasis has been put on internal logistics. More specifically, the aim of the study was to assess the extent to which information technology solutions can improve the overall efficiency of the process. The as-is model is made of 5 lanes, 22 tasks, 9 gateways and 7 types of resources (different types of machinery). Interval parameters were derived by a number of interviews and measurements. A simulation was carried out by considering 20 individuals in the population, 2000 containers and converged in 6 generations, which lasted 16 min (results were obtained on a computer with an Intel Dual Core i3-3220, 3.30 GHz, 8GB RAM). It is worth noting that this simulation time strongly depends on the relatively high number of containers used in a single Bimp simulation, rather than on the number of Bimp simulations requested by the GA. As a result, a minimum total duration of 86.63 h was evaluated. Moreover, a large waiting time was estimated, mostly due to lack of synchronization between resources.
To improve the process, wireless tracking technologies, such as RFID and GPS, were adopted. The to-be model is made of a number of settings able to improve synchronization between machineries. A new simulation was made considering again 20 individuals in the population, 2000 containers and converged in 17 generations, which lasted 38 min (results were obtained on a computer with an Intel Dual Core i3-3220, 3.30 GHz, 8GB RAM). As a result, a minimum total duration of 18.19 h was evaluated, with a better resource utilization, as shown in Figure 17.
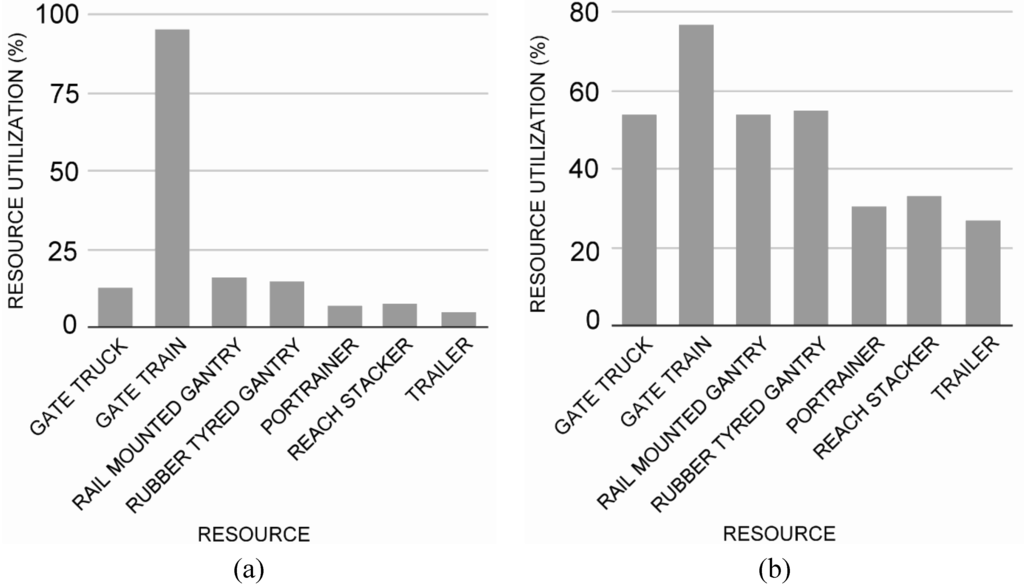
Figure 17.
Resource utilization in the as-is (a) and to-be (b) model.
6.5. Real-World Scenario: Manufacturing Company
This scenario presents a real-world experience of application of our interval-valued simulation tool in the context of the buying process of a leading auto and truck parts manufacturing company.
More specifically, the aim of the study was to improve the overall efficiency of the purchase order process. The as-is model is made of 2 pools, 7 lanes, 24 tasks and 7 gateways. Interval parameters were derived by a number of interviews and measurements. The KPI is the average cycle time (ACT). A single-valued simulation was first performed, considering 25 purchase orders. The resulting ACT was about 42 days. In order to assess this result, an interval simulation was performed, which converged in 15 generations and employed 20 individuals in the population. The simulation lasted 6 min (results were obtained on a computer with an Intel Dual Core i3-3220, 3.30 GHz, 8GB RAM). As a result, the measured ACT was about [28,54] days. Hence, the ACT can be sensibly reduced. Figure 18 shows the parameter values for the as-is, the minimum and maximum KPI.
It can be noted that the maximum KPI may be mainly ascribed to a large duration of the “chief financial officer approval” and “materials and delivery note approval” tasks. This may be easily verified by reducing the intervals and restarting the simulator. Indeed, the interval-valued parameterization allows sensibly reducing the number of trials in incremental investigations.
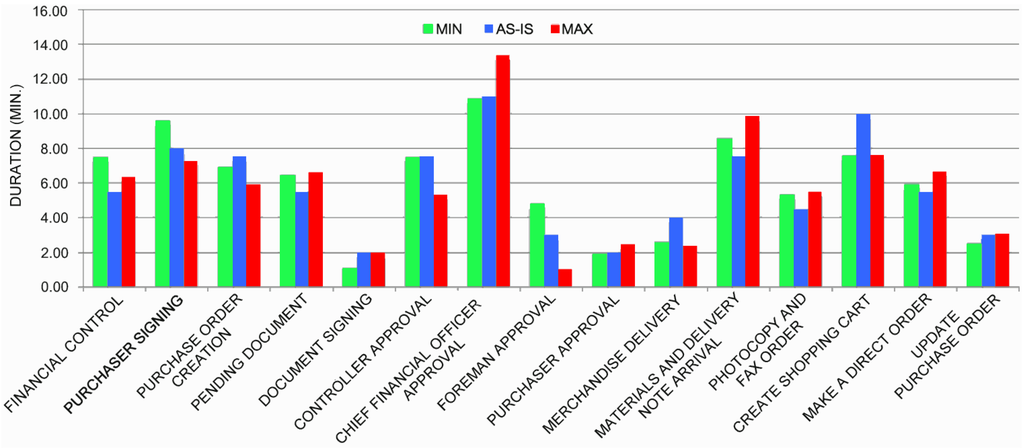
Figure 18.
Duration of the relevant tasks, in the minimum KPI, as-is and maximum KPI models.
7. Conclusions and Future Works
In this paper, a novel approach of business process simulation is presented. The approach is based on the representation of business process parameters in terms of intervals, to efficiently characterize human-driven processes. An interval-valued simulation tool is designed, developed and tested on five scenarios. Given input intervals, the system employs a numerical simulation engine, based on the BPMN standard, and a genetic algorithm to compute the output interval (KPI). The use of BPMN allows the tool to be used by process owners, which is an important condition in BP simulation studies. However, the most important strength point is the possibility of dealing with interval-valued parameters offered by our extension. Indeed, the proposed approach solves a fundamental weakness of existing tools dealing with multi-valued representations, which require an expensive data collection. Moreover, interval-valued data are deterministic and then more suitable for decision-making.
Experimental results have shown that the adopted GA has been an adequate choice, since our approach allowed an efficient analysis of interesting the properties of the observed processes: (i) the worst/best cases within a constrained area; (ii) the parameter values corresponding to the cases of interest; (iii) the importance of some parameter values with respect to the cases of interest; and (iv) the analysis at different levels of detail. Other genetic-based strategies may be effective in solving the type of optimization problem tackled in this work, providing different kinds of solutions. Thus, as future research, we plan to investigate the use of different genetic-based optimization methods, so as to make a comparative analysis. The simulation time performance of the IBimp simulator can be a limitation with respect to the simulation time performance of the lightning fast Bimp simulator, because GAs do not scale well with complexity. In future work, this limitation could be lifted by exploring meta-heuristics, such as simulated annealing, which strike a good trade-off between accuracy and performance. Finally, to conduct performance evaluations of our simulation tool on other KPIs (such as the total cost), as well as on multiple KPIs (i.e., multi-objective optimization) is considered a key investigation activity for future work.
Author Contributions
Mario G. C. A. Cimino and Gigliola Vaglini are both responsible for the concept of the paper, the results presented and the writing. Both authors have read and approved the final published manuscript.
Conflict of Interest
The authors declare no conflict of interest.
References
- Van der Aalst, W.M.P. Challenges in business process management: Verification of business processes using petri nets. Bull. Eur. Assoc. Theor. Comput. Sci. 2003, 80, 174–199. [Google Scholar]
- Sharp, A.; McDermott, P. Workflow Modeling, 2nd ed.; Artech House: Boston, MA, USA, 2009. [Google Scholar]
- Barros, A.P.; Gal, A.; Kindler, E. (Eds.) Business Process Management: 10th International Conference, BPM 2012, Tallinn, Estonia, September 3–6, 2012; Proceedings; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2012; Volume 7481.
- Object Management Group. Business Process Model and Notation (BPMN), Version 2.0. Official specification. Available online: http://www.omg.org/spec/BPMN/2.0 (accessed on 20 November 2013).
- Wohed, P.; van der Aalst, W.M.P.; Dumas, M.; ter Hofstede, A.H.M.; Russell, N. On the suitability of BPMN for business process modelling. In Business Process Management; Lecture Notes in Computer Sciences; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4102, pp. 161–176. [Google Scholar]
- Bozarth, C.C.; Handfield, R.B. Introduction to Operations and Supply Chain Management, 3rd ed.; Pearson: Upper Saddle River, NJ, USA, 2013. [Google Scholar]
- Anupindi, R.; Chopra, S.; Deshmukh, S.D.; van Mieghem, J.A.; Zemel, E. Managing Business Process Flows: Principles of Operations Management, 3rd ed.; Pearson: Upper Saddle River, NJ, USA, 2012. [Google Scholar]
- Van der Aalst, W.M.P. A decade of business process management conferences: Personal reflections on a developing discipline. In Business Process Management; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7481, pp. 1–16. [Google Scholar]
- Van der Aalst, W.M.P. Business process simulation revisited. In Enterprise and Organizational Modeling and Simulation; Lecture Notes in Business Information Processing; Springer: Berlin/Heidelberg, Germany, 2010; Volume 63, pp. 1–14. [Google Scholar]
- Rozinat, A. Process mining. In Process-oriented Information Systems; Report on the Seminar; Hasso Plattner Institute for Software Systems Engineering, University of Potsdam: Potsdam, Germany, 2003; pp. 156–171. [Google Scholar]
- VP Business Architect. Available online: http://www.visual-paradigm.com/product/lz/ (accessed on 20 November 2013).
- Bosilj-Vuksic, V.; Hlupic, V. Criteria for the evaluation of business process simulation tools. Interdiscip. J. Inf. Knowl. Manag. 2007, 2, 73–88. [Google Scholar]
- Greasley, A. Using business process simulation within a business process reengineering approach. Bus. Process Manag. J. 2003, 9, 408–420. [Google Scholar] [CrossRef]
- Völkner, P.; Werners, B. A simulation-based decision support system for business process planning. Fuzzy Set. Syst. 2002, 125, 275–287. [Google Scholar] [CrossRef]
- Van der Aalst, W.M.P.; Nakatumba, J.; Rozinat, A.; Russell, N. Business process simulation: How to get it right? In Handbook on Business Process Management; International Handbooks on Information Systems; Springer: Berlin/Heidelberg, Germany, 2010; pp. 317–342. [Google Scholar]
- Cimino, M.G.C.A.; Marcelloni, F. Autonomic tracing of production processes with mobile and agent-based computing. Inf. Sci. 2011, 181, 935–953. [Google Scholar] [CrossRef]
- Pedrycz, W. Knowledge-based Clustering: From Data to Information Granules; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Babuška, R. Fuzzy Systems, Modeling and Identification; Technical Report; Delft University of Technology, Department of Electrical Engineering: Delft, The Netherlands, 1999. [Google Scholar]
- Hofacker, I.; Vetschera, R. Algorithmical approaches to business process design. Comput. Oper. Res. 2001, 28, 1253–1275. [Google Scholar] [CrossRef]
- Russell, S.J.; Norvig, P. Artificial Intelligence: A Modern Approach, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2003; pp. 111–114. [Google Scholar]
- Gen, M.; Cheng, R. Genetic Algorithms and Engineering Design; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Reijers, H.A.; van der Aalst, W.M.P. Short-term simulation: Bridging the gap between operational control and strategic decision making. In Proceedings of the IASTED Conference on Modeling and Simulation, Philadelphia, PA, USA, 5–8 May 1999; pp. 417–421.
- Bimp-simulator. Available online: http://code.google.com/p/bimp-simulator/ (accessed on 15 May 2014).
- Wand, Y.; Weber, R. Research commentary: Information systems and conceptual modeling—a research agenda. Inf. Syst. Res. 2002, 13, 363–376. [Google Scholar] [CrossRef]
- Van Der Aalst, W.M.P.; ter Hofstede, A.H.M.; Weske, M. Business process management: A survey. In Business Process Management; Lecture Notes in Computer Sciences; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2678, pp. 1–12. [Google Scholar]
- White, S.A. Introduction to BPMN. Available online: http://www.bptrends.com/bpt/wp-content/publicationfiles/07-04 WP Intro to BPMN - White.pdf (accessed on 20 November 2013).
- Puhlmann, F. On the suitability of the Pi-Calculus for business process management. In Technologies for Business Information Systems; Springer: Berlin/Heidelberg, Germany, 2007; pp. 51–62. [Google Scholar]
- Ciaramella, A.; Cimino, M.G.C.A.; Lazzerini, B.; Marcelloni, F. Using BPMN and tracing for rapid business process prototyping environments. In Proceedings of the 11th International Conference on Enterprise Information Systems (ICEIS’09), Milan, Italy, 6–10 May 2009; pp. 206–212.
- Dumas, M.; La Rosa, M.; Mendling, J.; Reijers, H.A. Fundamentals of Business Process Management; Springer: Berlin/Heidelberg, Germany, 2013; pp. 21–23. [Google Scholar]
- Vergidis, K.; Tiwari, A.; Majeed, B. Business process analysis and optimization: Beyond reengineering. IEEE Trans. Syst. Man C. Appl. Rev. 2008, 38, 69–82. [Google Scholar] [CrossRef]
- Li, L.; Hosking, J.G.; Grundy, J.C. EML: A tree overlay-based visual language for business process modeling. In Proceeding of 9th International Conference on Enterprise Information Systems (ICEIS’07), Funchal, Madeira, Portugal, 12–16 June 2007; pp. 13–19.
- Van Breugel, F.; Koshkina, M. Models and Verification of BPEL; Technical Report. York University: Toronto, ON, Canada, 2006; pp. 1–19. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.85.882.
- Tumay, K. Business process simulation. In Proceedings of the 1996 Winter Simulation Conference (WSC), Coronado, CA, USA, 8–11 December 1996; pp. 93–98.
- Reijers, H.A. Design and Control of Workflow Processes; Springer: Secaucus, NJ, USA, 2003. [Google Scholar]
- Wynn, M.T.; Dumas, M.; Fidge, C.J.; ter Hofstede, A.H.M.; van der Aalst, W.M.P. Business process simulation for operational decision support. In Proceedings of the International Workshop on Business Process Intelligence (BPI), Brisbane, Australia, 24 September 2007; pp. 55–66.
- Pérez-Castillo, R.; Weber, B.; Pinggera, J.; Zugal, S.; García-Rodríguez de Guzmán, I.; Piattini, M. Generating event logs from non-process-aware systems enabling business process mining. Enterp. Inf. Syst. 2011, 5, 301–335. [Google Scholar]
- Van der Aalst, W.; Desel, J.; Oberewis, A. (Eds.) Business Process Management: Models, Techniques, and Empirical Studies; Springer: Berlin/Heidelberg, Germany, 2000.
- Laguna, M.; Marklund, J. Business Process Modeling, Simulation, and Design; Pearson Education Dorling Kindersley: New Delhi, India, 2011. [Google Scholar]
- Smets, P.; Mamdani, E.H.; Dubois, D.; Prade, H. (Eds.) Non-Standard Logics for Automated Reasoning; Academic Press: London, UK, 1988.
- Dubois, D.; Prade, H. Fuzzy sets and probability: Misunderstandings, bridges and gaps. In Proceedings of the 2nd IEEE International Conference on Fuzzy Systems (FUZZ-IEEE’93), San Francisco, CA, USA, 28 March–1st April 1993; Volume 2, pp. 1059–1068.
- Jansen-vullers, M.H.; Netjes, M. Business process simulation—a tool survey. In Presented at Workshop and Tutorial on Practical Use of Colored Petri Nets and the CPN Tools, Aarhus, Denmark, 24–26 October 2005.
- Alefeld, G.; Claudio, D. The basic properties of interval arithmetic, its software realizations and some applications. Comput. Struct. 1998, 67, 3–8. [Google Scholar] [CrossRef]
- Bernardeschi, C.; Cassano, L.; Cimino, M.G.C.A.; Domenici, A. GABES: A Genetic Algorithm Based Environment for SEU Testing in SRAM-FPGAs. J. Syst. Architect. 2013, 59, 1243–1254. [Google Scholar] [CrossRef]
- Herrera, F.; Lozano, M.; Verdegay, J.L. Tackling Real-Coded Genetic Algorithms: Operators and Tools for Behavioural Analysis. Artif. Intell. Rev. 1998, 12, 265–319. [Google Scholar] [CrossRef]
- Pinel, F.; Danoy, G.; Bouvry, P. Evolutionary algorithm parameter tuning with sensitivity analysis. In Proceedings of the 2011 International Conference on Security and Intelligent Information Systems (SIIS’11), Warsaw, Poland, 13–14 June 2011; Springer: Berlin/Heidelberg, Germany, 2012; pp. 204–216. [Google Scholar]
- Ibimp. Available online: http://www.mathworks.com/matlabcentral/fileexchange/46211-ibimp (accessed on 16 May 2014).
- Yaoqiang BPMN Editor. Available online: http://bpmn.sourceforge.net (accessed on 20 May 2014).
- Document Object Model (DOM). Available online: http://www.w3.org/DOM/ (accessed on 20 May 2014).
- JavaScript Object Notation (JSON). Available online: http://www.json.org (accessed on 20 May 2014).
- Abel, M. Lightning Fast Business Process Simulator. Master’s Thesis, Institute of Computer Science, Faculty of Mathematics and Computer Science, University of Tartu, Tartu, Estonia, 2011. [Google Scholar]
- MatLab Optimization Toolbox. Available online: http://www.mathworks.it/it/help/optim/ (accessed on 20 May 2014).
- Genetic Algorithms Toolbox. Available online: http://codem.group.shef.ac.uk/index.php/ga-toolbox (accessed on 20 May 2014).
- OMG, Object Management Group. BPMN 2.0 by Example, version 1.0. OMG Document Number dtc/2010–06–02. Available online: http://www.omg.org/spec/BPMN/2.0/examples/PDF (accessed on 20 November 2013).
- April, J.; Better, M.; Glover, F.; Kelly, J.P.; Laguna, M. Enhancing Business Process Management with simulation optimization. 2005. Available online: http://www.bptrends.com/enhancing-bpm-with-simulation-optimization/ (accessed on 20 November 2013).
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).