1. Introduction
As Floridi states in his General Definition of Information (GDI), meaning is an essential element of information [
1,
2]. This essentiality has often been considered since the beginning of the scientific understanding of information. Right after Shannon’s oblivion of meaning, the development of a proper account of the relation between meaning and information has comprised a continuous effort in the integral understanding of information. It was, for instance, the endeavor of Bar-Hillel & Carnap in the 1950s; the algorithmic approaches of Solomonov, Kolmogov, and Chaitin offered new insights in the 1960s; the study of self-organized systems suggested different perspectives, arisen from a broad spectrum of sciences, in the 1970s; Dretske, as well as Barwise and Perry advanced new analytic approaches in the 1980s; and many other semiotic frameworks have considered the centrality of the relation between meaning and information in the last decades [
3,
4,
5]. Furthermore, this is something to which even Shannon agreed, though he decided to focus on the syntactical aspects aiming at solving the technical problems he was interested in [
6,
7].
However, as Floridi lucidly points out, the clue for a consistent understanding of information concerns the very grounding of such meaning (which he addresses in terms of the Symbol Grounding Problem—[
1], Chapter 5). Certainly, if—according to the sciences—our world is significantly populated by information well beyond human contexts, and if information comprises meaning, we cannot ignore the question of how information acquires meaning in the first place and for the different contexts. In other words, how does meaning come into existence within the world? This is the quest for the emergence of meaning.
We agree with Floridi in the importance of action for the emerging of meaning, though beyond the epistemic constraint of Floridi, we adopt a more existential stance close to the aforementioned Spinozist reflection, in which effectiveness of action, meaning and being are tightly linked. Floridi’s solution to the grounding of meaning—through his “action based semantics” (Ibid. Chapter 7)—is attached to a given minimal set of levels of abstraction (LoA, namely a set of observables, understood as interpreted typed variables), implemented in the systems within which Floridi searches for the grounding of meaning relations. But pitifully this given LoA provides—as we argue below—an implicit semantics whose origin should also be sought. Thus the question is merely displaced to the origin of the LoA, breaching the purpose of finding a real ground without semantic commitment. Hence the question remains opens and we shall pursue a more fundamental anchoring for the grounding of meaning and therefore information.
Finding a more robust ground for the concept of information might solve indeed the lack of common understanding of information throughout the sciences as we have discussed elsewhere [
3,
4,
5]. If such a ground is found, the road for the developing of a
Unified Theory of Information (UTI) as proposed by Hofkirchner and others would be clear [
8]. To this respect, it is worth recalling that the arousing of the scientific concept of information since the 1920s was rooted in a new insight of nature within statistical physics as started by Boltzmann, Gibbs and Maxwell in the nineteenth century. As J. Segal [
9] clearly showed in his thorough study of the scientific development of the information concept, relevant contributions—from the 1920s onwards—by Marjan von Smoluchowsky, Leo Szilard, Gilbert N. Lewis, John von Neuman and Ronald A. Fisher constitutes the emerging of a new understanding of information from such a matrix. Moreover, the development within telecommunications as promoted at the North American research milieu in those decades was heavily influenced by the new insights in physics—e.g., the works of Ralph Hartley and Harry Nyquist ([
9], Chapter 1). Thus it was the framework very much constituted by the conceptualization within physics—together with the target of some technical achievements—the actual matrix for the development of the scientific concept of information in the 1940s. Therefore Shannon should not be surprised to find the Boltzmannian formulation in his own quantitative definition of information, because this was implicitly there since the beginning.
It should neither be surprising that—as we show in
Section 2—some remarkable conceptualizations within fundamental physics since the 1960s foster new insights into the information understanding; particularly in the solution of one of the most challenging problems for the unification of the sciences, namely the junction of the theories of relativity and quanta—as it is pursued in the field of
quantum gravity. Upon these new insights in physics,
energy and
information might be regarded as two aspects of a same underlying primordial structure of the world, which does not imply a reduction of beings to its physicals constituents, but an attempt to give an account of the emergence of irreducible beings throughout the ladder of complexity in a progressive perspective—in chemical structures, in organisms, in cognition, in consciousness, in societies.
To this purpose, we adopt a viewpoint which can be understood from Spinoza’s proposition, recalled at the beginning: an effective and contingent interaction constitutes an agency, a new being with respect to its underlying components, whose course(s) of action conforms its own
meaning(s). The space of action defines its level of complexity. As explained in
Section 3, this vision extends Kauffman’s conception of autonomous agency, which requires an important review of Floridi’s GDI with respect to the related neutrality principles and the truthfulness commitment.
Reviewing the aspects of truthfulness drives to the need of overcoming some limitations of the standard approach to information, as articulated commonly into the syntactic, semantic and pragmatic dimensions. This endeavor is embraced in
Section 4, where the pragmatic sense of meaning is stressed (as it is also to some extent in Floridi’s action-based semantics, mentioned above) though in our case, we aim at covering the different levels of complexity from pre-geometry to consciousness. In a sense that is deepened in the last section, we supersede the former trinity into the one constituted by syntax, lexicology, and semantics. But before reaching up to the higher level of consciousness, an interim step in biology has to be given. This is done in
Section 4.2 by embracing Barbieri’s epigenetic approach, which offers a non-stagnant code-making as it is in fact the case of cooperation—following Floridi’s model—between interacting parts possessing a given set of LoA. By reaching the level of reflexive being, the originally rejected truthfulness aspects of the GDI can be transformed into the proper utilization of the meaning implicit in any type of information throughout the different kinds of beings. The possibility of attaining such proper use of meaning is considered in
Section 4.3 recalling Manfred Frank’s hermeneutics which provides a stage for the study of interpretation in the sciences altogether.
Upon these roots in
Section 5, both pre-reflexive and reflexive types of meaning are appropriately handled. Here,
emergence is put forward in both ontological and epistemological terms, referred to microscopic and macroscopic levels, by means of a consistent evolutionary approach. This offers, on the one hand, a ground for a sound regressive perspective; on the other hand, a way for overcoming
Capurro’s trilema [
10], which states the necessity of choosing among univocity, analogy or equivocy when speaking of information throughout different contexts; something that was indeed overcome in the nineteenth century with respect to energy. Relying on a similar abstraction,
information can be understood alongside
energy—distinguished from each other—no matter the context, and referred to the potentiality of selecting or producing changes respectively. Correspondingly,
structure and
matter can be visualized as the actualization of the related changes. Furthermore, the semiological realm, rephrased in
Section 4, is further developed by means of Thom’s semiological approach which offers a sound approach for the emergence of reflexive meanings in both societal and cognitive senses. This framework enables us to go beyond the mentioned limits of Floridi’s approach concerning both the action semantics and the Correctness Theory of Truth ([
1], Chapters 5 and 6).
In the Appendix, a more elaborated view of the agent-based approach is provided, which embraces: Kauffman’s insight (Section 1), its adaptation to spin networks for an adequate starting at the pre-geometrical level (Section 2, Section 3, Section 4 and Section 5), its extension to the skeleton-of-the-universe-view for moving through the hierarchy of complexity up to social games (Section 6); unveiling at the end the whole proposal in its epistemological flesh; thus pointing to a cognitive meta-theory (Section 7).
2. Fundamental Physics as an Anchor for a General Understanding of Information
After roughly 35 years of development in the theories of self-organization and related variants (chaos, self-organized criticality and so forth), it is somewhat of a surprise that physics proper has not yet sufficiently found its entry into the ongoing quest for a precise concept of information. Hence, even the most optimistic volume of collected essays on what has often been called Unified Theory of Information, or UTI in short (edited by Hofkirchner in 1999 [
11]), is introduced by Haefner with the remark that “… at the physical level, we encounter a set of physical theories that have never considered information as an appropriate term to understand physical phenomena …. Quantum theories are not using the term information at all; instead, they are fixed to formulations of field theory” ([
12], p. xv).
In fact, although the Vienna conference meeting took place in 1996 rather than 1999, this remark (and similar remarks as to that) do(es) not actually refer to the reality of ongoing research: As Seth Lloyd points out in his book from 2006 ([
13], p. 52), already as early as in the sixties of the last century Fredkin and Zuse visualized the universe as a digital computer, a line of argument that Wolfram has followed more recently in his work on cellular automata published in 2002. Not to speak of the more recent theories on quantum information [
14,
15,
16] which generically couple to theories of quantum gravity: One of the leading protagonists is David Deutsch here for whom “… [b]its, Boolean variables, and classical computation are all emergent or approximate properties of qubits, manifested mainly when they undergo decoherence” ([
17], p. 93). In other words: “The world is made of qubits …. What we perceive to some degree of approximation as a world of single-valued variables is actually part of a larger reality in which the full answer to a yes-no question is not just yes or no, nor even both yes and no in parallel, but a quantum-observable—something that can be represented as a large Hermitian matrix” (
Ibid., p. 100).
This line of argument goes actually back as far as to John Wheeler in 1977 for whom “… [a] true observation of the physical world … must not only produce an indelible record, [but] somehow in part
meaningful information.” ([
18], p. 8—my emphasis) For him, “… [m]easurement implies a transition from the realm of mindless material stuff to the realm of knowledge. So it [is] not enough … that a measurement should record a bit of information, that lowly bit had
to mean something.” (
Ibid.—my emphasis) This perspective led at the time to the famous “it-from-bit” thesis proposing that “the universe be fundamentally an information processing system from which the appearance of matter emerges at a higher level of reality.” (
Ibid., p. 10) In fact, it is Seth Lloyd himself who after all has developed the cosmological implications in most detail when presenting his work on the computational universe [
13,
19,
20]. For him,
the big bang was also a bit bang ([
20], p. 96).
Within the theories of quantum gravity, these aspects have gained even more pertinence. This is because the quantum viewpoint itself typically tends to conceptualize information (contrary to Haefner’s assertion, mentioned above). As Carlo Rovelli has concluded: “… what precisely quantum mechanics is about is the information that physical systems have about one another” ([
21], p. 219). The quantum aspect itself however, turns out to be somewhat more involved than expected, as Roger Penrose has pointed out in his more recent works when he talks, e.g., of what he calls
quanglement in demonstrating his reluctance to utilize the concept of quantum information. As he says: “Quantum is not information, but [it] can be used in conjunction with ordinary information channels, to enable these to achieve things that ordinary signaling alone cannot achieve” ([
22], p. 603, p. 607).
It is especially in
loop quantum gravity that these features are most prominent: The idea is that “[j]ust as a polymer … the fundamental 1-dimensional excitation of geometry can be packed appropriately to provide a geometry which, when coarse-grained on scales much larger than the Planck length, resembles continuous geometries” ([
23], p. 181). The theory is named after the Wilson-type loops which are essentially closed curves carrying quantized electric flux and being organized into hexagonal networks called
spin networks ([
24], p. 135; [
25], p. 504). To be more precise, the significant objects are not just the loops, but their holonomies: They represent a generalized kind of parallel transport that can be described in terms of a Lie group element in the fiber bundle attached to the chosen base manifold. Hence, holonomies can be visualized as homomorphisms from some group structure defined in terms of equivalence classes of closed curves onto a Lie group. We can see then that essentially, “the result of evaluating a Wilson loop about a very small planar circle around a point X is proportional to the area enclosed by this circle times the corresponding value of the curvature tensor of the gauge field evaluated at X” ([
26], p. 79,
cf. [
27]). Hence, the holonomy has the same information as the curvature at this point (
cf. [
28], p. 1f). A spin network then, is a linear combination of products of holonomies of closed curves that wrap along the graph ([
29], p. 237). Louis Kauffman who dealt with a representation of loops and knots in terms of (mathematical) category theory, has shown that in principle, the binor identity characterizing spin networks, the skein identity of the bracket polynomial in knot theory, and the trace identity are really all the same. Hence, space altogether shows up then as one of the possible targets of the many functors that extract information from the network ([
30], p. 277f) (For general networks see [
31], for categories see in particular [
32], for an alternative approach in terms of strings see [
33]. As to the relationship between functors and knots see also [
34,
35,
36]
As preliminary conclusions of all of this we can note the following:
(1) The physicist’s quest for a unified theory from the outset (an enterprise in fact that already starts at the end of the 19th century) is the reason for the fact that the concept of information is always present in the sense that comparatively early it became necessary to map the physical processes involved by means of thermodynamical (and statistical) techniques. From the beginning on therefore, for Penrose, the entropy of a state is described as a measure of the volume of that compartment which contains the phase-space point which actually represents this very state ([
37], p. 313).
Hence, if a theory of cosmology must, as Smolin puts forward ([
38], p. 291, [
39]), in order to be self-consistent, be a theory of the self-organization of the universe, the very aspect of organization entails a concept of information on an equal footing with the concept of energy. (A point, in fact, also Floridi would agree to [
1], p. 135. See also Jantsch [
40]). This idea has become popular back in the late seventies of the last century following the international reception of the theories of René Thom and Ilya Prigogine (Thom [
41,
42,
43]; Prigogine [
44,
45,
46];
cf. Zimmermann [
47,
48,
49,
50,
51,
52,
53]). As one can clearly recognize from this development, the problem of organization is closely related to the problem of a unified theory of physical interactions. Although significant progress has been achieved here, starting with Maxwell’s theory of electromagnetism and with Einstein’s theories of relativity, leading forward to a further unification including weak interactions (Salam-Weinberg-Glashow) and even to a GUT, gravitation (completing a true TOE) has not yet been successfully integrated into this enterprise. And the reason for this may be a deficiency in the proper co-ordination of energy and information within the theories of the cosmological beginnings. Looking particularly for characteristic differences in the entropy of the universe, in 1979, Roger Penrose [
54] has claimed a principle of time-asymmetry which shows up as a direct consequence of this evolution of entropy and can be formulated as an explicit energy condition (called the Weyl curvature hypothesis) (
cf. [
55,
56]). In fact, this is why recent approaches to quantum gravity try to explicitly reconcile energy and information. This is particularly apparent when dealing with black holes. But there is still another point to this.
(2) As it is obvious from the underlying intention of unified theories, they also refer to a kind of secularized grounding problem which in metaphysical philosophy is traditionally dealt with when talking about the concept of substance and its attributes [
57,
58,
59,
60,
61,
62]. From time to time this perspective is mentioned more or less at random, but altogether, the philosophical perspectives taken by physicists are very often far from being relevant and precise. This is mainly due to the terminology utilized according to somewhat arbitrary criteria and to the mixing up of ontological and epistemological problems: First of all, there are serious attempts to conceptualize the underlying physics with a view to basic principles which give a kind of philosophical grounding to physics normally absent when discussing physical details. Roger Penrose, e.g., in his 1995 Tanner Lectures, is comparatively prudent in his formulations when stating that “[w]hat we need is a criterion to enable us to estimate when two space-times differ significantly and this will lead to a
time-scale for Nature’s choice between them. Thus, the viewpoint is that Nature chooses one or the other according to some rule we do not understand yet” ([
63], p. 86). In that case he points to the theory of consciousness which he has developed himself together with Stuart Hameroff. Therefore, for him the solution must be somewhere in the quantum domain: “It seems to me that consciousness is something global. Therefore, any physical process responsible for consciousness would have to be something with an essentially global character. Quantum coherence certainly fits the bill in this respect.” (
Ibid., p. 133) He thus concludes that “[m]entality … be ontologically fundamental in the Universe” and mentions some kind of “proto-mentality”. (
Ibid., p. 176) This is something we can subscribe to: If there is a choice for Nature, then Nature is acting in a sense, it is subjective rather than objective. This is indeed an idea that is present in philosophical theories from Schelling to Bloch. And in particular it is the idea of characteristic time-scales that fits nicely to Schelling’s worldly epochs [
58,
59,
60,
61,
62].
But unfortunately, aside from the fact that Penrose is known officially as a serious Platonist (which is somewhat out of date to say the least), Hameroff does not share his modesty and claims that their results would point towards a philosophy of some “… funda-mental panexperiential view in which primitive experience exists at the Planck scale of spacetime geometry” ([
64], p. 154). And Lee Smolin adds that “[p]hysics should be more than a set of formulae that predict what we will observe in an experiment; it should give a picture of what reality
is …. It cannot be that reality depends on our experience” ([
65], p. 7). As to the first statement we notice that the vagueness in formulation actually destroys the strong argument provided by Penrose, because automatically, we envision a world which is some sort of living creature and loose the aspect of “proto-entities” (we will briefly come back to this).
On the other hand, the same vagueness in Smolin’s statement renders the whole approach to end up with a false idea: This is mainly so because it is not quite the task of physics to say what there actually is. And it is a mere claim that reality cannot depend on our existence (Because it is this very reality that produced us in the first place). But the main point is here that the concept of reality is far from clear: Because traditionally, reality refers to what the world is like in absolute truth but to what we cannot actually perceive at all, because the cognitive capacity of human beings is limited. Hence, the world as we see it is its modality, the world as it really is we call reality. Obviously, the former can only be an approximation to the latter. And this is what in the physics of quantum gravity we would also like to call approximation or emergence ([
23], p. 181, [
66], [
18], p. 10, [
67], pp. 93, 100, see also: [
17], [
68], p. 603). Hence, in the strict sense of the concept, Smolin would be right (but then, physics could not help). Or, if he has mistaken the concept and refers to modality instead, he is simply wrong, because the latter is indeed depending on our existence. A similar critique is adequate when referring to the recent book of Vedral’s [
69] when the author struggles (unsuccessfully) with the concepts of nothingness and
creatio ex nihilo (
Ibid., p. 2, p. 5). In fact, he does not actually answer the questions he is presenting in the beginning (“… why is there a reality at all and where does it come from?”), because on the one hand, he shares with Smolin the same difficulty referring to the correct meaning of “reality”, and because on the other hand, he forgets that information (as well as energy) is a worldly concept which is utilized for human modeling, but not part of reality proper (we leave aside here the astonishing point that the author is, as far as we can see, not referring to the works of Seth Lloyd at all).
Now, in order to summarize this rash view on the contributions made within fundamental physics during the last decades with respect to the conceptualization of information (which turns out to be a kind of “discourse on the method”), we can say the following: Similar to the concept of energy, information is already always present in fundamental physics. Both energy (and the matter which it is manifesting) and information are two different aspects of the same underlying primordial structure of the world we will know not before there is a consistent TOE. Within this theory, both concepts have to be unified, and by doing so, there will also enter the aspect of some cognitive meta-theory which tells us how human modeling is coming about as part of a process actually performed by nature. Such an approach will also establish an innovative relationship between philosophy and the sciences, because epistemologically, all of them have to rely on each other. Hence, the appropriate TOE cannot be found, if not a philosophical framework for the grounding of the world is also developed which in turn is only possible, if philosophical research gets interdisciplinarily entangled with the other fields of the sciences. What this attitude is actually up to shall be discussed in this present paper.
3. Starting from Floridi’s Viewpoint
Much of what we have said in the introduction is the foundation for the results announced here earlier. The generic tendency of these results is already entailed in the role which is attributed to the concept of information when applied within the framework of fundamental physics. So, Floridi is certainly right when mentioning that “information can be said in many ways just as being can” and that “th[is] correlation is probably not accidental” ([
2], p. 40). But it is not clear why a UTI project should be necessarily reductionistic, because—different from the unified projects in physics—it deals with a conceptual rather than physical unification, because primarily it aims at a conceptualization which is for information what it was before for energy and mass. In other words: Unification means here
unifying energy and information rather than unifying different types of information. Hence, it is also a project of unifying a catalogue of terminologies, but at the same time one of unifying two irreducible phenomena. Similar to quantum physics where the difficulty is to differ between what is axiomatic and what is empirical, modern information theories have to differ between what is substantial and what is accidental. (This is summarized somewhat in Capurro’s Trilemma mentioned in the introduction [
18]). In the first case, the result is a bundle of interpretations of quantum physics altogether, and it is hoped that eventually it will be possible to decide which one is the master interpretation. In the second case, the task is practically the same. The crucial difference may be the fact that certainly, an adequate UTI will not be grounded on the mathematical theory of communication in the sense of Shannon, but will instead turn out to be part of a physical TOE, which does not imply a reductionist stance—as argued in the introduction. But the more is it necessary to actually determine what
meaning is all about, a notion which according to common terminology obviously surpasses the concept of mere information. In so far, it is quite to the point that Floridi stresses the advent of hermeneutic theories (
Ibid., p. 41), but it is possibly insufficient to let things be as they are without going into further detail as to a possible definition of the underlying basis of meaning (See also [
70,
71,
72,
1]).
This is mainly so because the concept of meaning enters the discussion very early: For starting with a proper definition in the first place, it is immediately part of what Floridi calls the
General Definition of Information (GDI). This definition states that an instance of information visualized as objective semantic content is given, if and only if (iff) it consists of n data (n ³ 1) which are well-formed and
meaningful ([
2], p. 42, [
1], p. 84—our emphasis). There we are: From the beginning on we have to deal with meaning. And if having a look on Floridi’s list of possible data within definition’s range (
Ibid., p. 85f) we notice that primary and secondary data, metadata, as well as operational data can be found throughout nature. They are not restricted to social systems proper. Only derivative data extracted from the first three types are possibly reserved for the latter. The question is whether this is also true for meaning,
i.e., whether meaning can be generally found. If there is no information without data, and if “a datum is a relational entity” (
Ibid., p. 87), then obviously, throughout nature, there is information which by its very relational quality always entails meaning in the first place. This requires reviewing what Floridi means by meaningful data and what we mean by stating the intrinsic meaningful value of data itself. But before coming into such examination of Floridi’s account, it is worth pointing out that according to other approaches, information cannot properly be conceived as meaningful data. For instance in Luhman’s theory of social systems, information concerns the selection of meaning, though it is not constituted by the meaning itself [
4]. Similarly, Brier conceives his semiotic approach—and particularly meaning—as necessarily transcending information ([
73]; a comparative appraisal of Brier’s account with respect to our approach is done in the second part [
74]). From our viewpoint there is some kind of redundancy when speaking of “meaningful data”, since we conceive data as intrinsically meaningful. Nevertheless, there is some kind of immeasurability among the different approaches concerning the relation between information and meaning due to an often radically different understanding of meaning, as we argue in the following paragraphs.
3.1. Reviewing Floridi’s Account of Meaning, Data and Information
Taking into account Floridi’s Method of the
Levels of Abstraction (LoA), his solution to the
Symbol Grounding Problem (SGP) as well as his
Correctness Theory of Truth (CTT)—the three conforming a self-consistent approach to semantics [
1], it can be straightforward observed that his understanding of meaning is clearly attached to a particular vision of
meaning as reference, which follows the line represented by Frege, Russell, Tarsky and Davidson; adopting—instead of Russell or Tarsky’s ontological commitment—an
ontological neutrality similar to Davidson’s. Such referential (or extensional, though ontologically neutral) value of meaning is particularly explicit in his definition of
observable and
system behavior, which constitute the basic elements of his LoA and the modeling of observed systems respectively.
Observables—which are conceptual entities according to Floridi—determine the scrutable and interpreted “features of the system under consideration”, whereas system behavior refers to the “values for such observables that make the predicate true” (Ibid., p. 49). Through this referential approach to information semantics, in which behaviors correspond to the expectancies of the informee with respect to observable features of the system (pragmatically achieved by the agent’s interaction with its environment, as modeled in Floridi’s Action Semantics as solution to the SGP), Floridi’s approach resembles Shannon’s syntactical model in terms of semantic uncertainty. Indeed, emergence is a change in the reference, related to a Gradient of Abstraction (GoA, which in turn implies the existence of at least two interrelated levels of abstraction), namely a failure in the correspondence of the behaviors between observables as represented by its relations (Ibid., p. 64); not the relations themselves; not the observables themselves (in the limiting case of empty behaviors, meaning would also be empty; in the other extreme, saturated behaviors, i.e., applicable to all possible values of the referred observables, they would be a kind of tautology, thus detached from information according to Floridi). Hence, it is the degree of uncertainty (as in Shannon), determined by the extension of the reference (similar to code frequencies), what enables an informational (i.e., meaningful) exchange. As discussed in his CTT, the semantic agreement is feasible upon a harmony in the LoA, Context and Purpose (which is similar to the implicit agreement on code in Shannon’s approach). Therefore information is conceived within a predetermined frame of interpretation, which is environmentally and pragmatically situated.
Data—for Floridi—consist of not-yet-interpreted differences (
Ibid., p. 85); by filtering them through the network of observables (namely, the LoA) they gain meaning in terms of the corresponding behaviors. In other terms, as long as they actualize the reference by reducing the uncertainty, they convey information. Data are “constraining affordances—answers waiting for the relevant questions” (p. 77), which are transformed into “
factual information” by being processed at a given LoA. Therefore, information can be optimized struggling for a better tuning “to the constraining affordances available”,
i.e., data (
ibid.). But as we see, there is an insurmountable boundary between the “systems under consideration” and informational agents, established by observables, which has a clear Kantian resemblance. Although we may agree with Floridi concerning the fundamentally bounded access to reality by a subject in terms of a constructive modeling of his experience—as we mentioned above, in
Section 2, referring to modality of the world, we cannot support the limits that he assume concerning the given interpretation frame. On the one hand, we consider this leaves the question of the emergence of meaning actually unanswered, or displaced: If meaning consists of references for an already given conceptual frame, then we are forced to further ask: “How does this conceptual frame come into existence?” On the other hand, if speaking of information requires such conceptual framework, we could hardly state that Floridi’s GDI is actually so general and consistent with Wheeler or Wiener’s accounts of information, which can be predicated for more simple agents, detached from conceptualization. (It is also worth noticing that Floridi typifies Wheeler’s and Wiener’s accounts as consistent with his
Ontological Neutrality (ON), named in [
2] as ON. 2 and ON. 3 respectively).
In sum, Floridi’s approach may be appropriate if restricted to the case of
factual information in which symbolic agents experiment a very limited change in the modeling of reality, just referred to the change in the expectancy of observables and relations (which Floridi names “informational spaces”). Nevertheless in order to refer properly to information in physical or biological contexts, on one side, or information that may cause a radical change in perception or scientific discovery, on the other, GDI—together with meaning and data—has to be significantly reviewed. For instance, the exclusion of contradictions ([
1], p. 101f) prevents from taking into account revolutionary changes in science, or generally the emergence of more significant epistemic emergencies.
All this drives us to reject two fundamental aspects of Floridi’s account in order to properly generalize the understanding of information—as the GDI seems to intend:
(1) The intrinsic conceptual value of information and meaning, as derived from the nature of observable as long as it is a typed variable. Though this is, for instance, consistent with his formulation of ON “No Information without data representation” (representation implicitly points at conceptualization), it contradicts his Genetic Neutrality (GeN), but what is more important, it clearly excludes a significant amount of cases in which we would also like to speak properly of information.
(2) The exclusively extensional sense of meaning. On the one hand because it veils its actual conceptual grounds, intrinsically referred to intension; on the other hand, because it leaves the question of meaning with respect to its intension unanswered.
Hence by unveiling the implicit intension of meaning, we observe that Floridi’s action semantics is actually breaching the objective of finding a proper foundation of meaning without semantic commitment in the outset. Nevertheless, we completely agree with Floridi in the importance of action for the emergence of meaning, but we must move beyond the epistemic terrain to which Floridi confines himself. In his action semantics, Floridi tries to ground the meaning (as reference), preserving the ontological neutrality, by stressing the relational character of the meaning achieved, but detached from involving, for instance, a change of the wiring of the artificial agent. However, it is the wiring of the LoA that provides an implicit semantics (in terms of intension, even if not self-reflected); and it is such wiring that implies an obvious ontological commitment even if its concrete implementation is contingent. Furthermore, also the physical realization of the reflected reference (Floridi’s meaning) in terms of states of registers is nothing but a more flexible implementation than a wired structure directly reflecting the Gradient of Abstractions. Indeed, contingency is not a ground for arguing ontological neutrality, rather a motivation for speaking of ontological contingency, which in turn is important for the understanding of ontological emergence.
3.2. Broadening the Frame of Meaning and Information
Coming back to the relation between
data,
information and
meaning: If Bateson is right, and “information is the difference which makes a difference” (referred to by Floridi as type 4 of Ontological Neutrality, ON. 4, [
2], p. 44), then it is quite straightforward to notice that the existence of a difference (mere data according to Floridi) immediately implies the means of recognizing a difference as difference, in other words of interpreting differences (
i.e., information;
cf. [
75,
76]). This is so because the mere existence of such relational difference in reality implies that the informee—as a part of reality too—can likewise reflect a similar or corresponding relational difference as to detect it whenever it gets in touch with the former difference. We can also say, there is a minimal nucleus of proto-type forms of cognition and communication essentially comprised of a
detection device which is able to differ between what a signal actually shows and what this actually means for the informee [
77,
78,
79]—independent of whether this informee (be it a living structure or not) is able to also reflect about the fact that presently, it
possesses knowledge of this process.
Concerning the extension vs. intension of meaning, if we move beyond an extensional account, it is clear that acknowledging a value of the observable (extension) requires in the informee an heterogeneous structure which is somehow homomorphic with respect to the inhomogeneity, feature or relation to which the observable points (constituting the intension; for instance, an asymmetric molecule located at the cell membrane which is able to react whenever a gradient relevant for the survival of the cell appears across the membrane, and thereafter causing a beneficial effect for its survival). This is linked to the aforementioned detection device through which an intensional account of meaning can be blended with an extensional one by means of a functional agency. These three elements intension, extension and functional effectiveness are very dependent from each other, and stand upon the common ground of the possibility of existence of particular relations throughout nature, whose specific realizations are contingent with respect to the interacting parts constituting such relation. This is what is behind our statement of “the intrinsic meaningful value of data”.
As to the concept of meaning we find this line of argument confirmed from time to time, if often only as a side-remark. Seth Lloyd, e.g., is quite clear with respect to meaning: “If you adopt Wittgenstein’s perspective that the meaning of a piece of information is to be found in the action this information provokes, the meaning of a computer program written in a particular computer language is to be found in the actions the computer performs as it interprets that program” ([
13], p. 26). And we remember that action is already there from the beginning on, namely speaking of spin networks as the fundamental fabric of space which actually processes the information which is produced by means of the organizing action of the loops co-operating in order to constitute the network in the first place.
This has an interesting consequence: A loop in the above sense fulfills what Stuart Kauffman calls the criteria for
autonomous agents, namely, the ability of performing full thermodynamic work cycles for the provision of its own needs and the participation in natural games according to the constraints of its environment [
80,
81,
82]. This aspect has already been mentioned in the recently emerged field of biosemiotics ([
83,
75], [
84], p. 192). Some more details are given here in the appendix.
Hence, we can live with Floridi’s formulations of
Ontological Neutrality, ON. 1 through 4 with respect to adequate data realizations (as referred to in [
2]), though following our previous arguing, we prefer not speaking of representations, on one side, and rephrasing the principles in terms of
ontological contingency, on the other. Beyond appearances, this actually represents a significant distance with respect to Floridi’s stance: First, because in [
1], Floridi clearly rejects ON. 1, namely “no information without physical implementation”; second because, as argued above, ON. 2 and ON. 3 (
i.e., Wheeler’s and Wiener’s positions) are actually not really consistent with Floridi’s account of information; finally ON. 4 is not even mentioned in [
44]. Furthermore, we dispute formulation GeN (
Genetic Neutrality,
i.e., “data can have a semantics independently of any informee”, p. 91) and also the viewpoint that false information is no information, therefore restoring what he names
Alethic Neutrality ([
2], pp. 44f, [
1], p. 93). We argue against GeN because it is the emergence of a difference in nature at a given level of complexity that entails at the same time an effective autonomous agency (constituted at the lower levels), a kind of regularity in which the difference have sense, and the possibility to be reproduced (therefore detected) somewhere else in nature. Then it is the actual and potential agency in the first place that provides both semantics and informee.
Concerning Floridi’s rejection of
falsehood, we can support it only if we confine ourselves within the abovementioned limits of factual information in which no change in LoA is experienced. Herein, Floridi´s CTT (explicitly referred to a distal access to an observed and pragmatically situated reality) is consistent with respect to the fact that falsehood represents a kind of failure in such distal access, thus falling out of the model. However, we consider the necessity of restoring
Alethic Neutrality in order to properly generalize GDI. Indeed, the fact of not having an actual extension—given a set of intentional meanings—is no reason to reject something as informative. On the contrary, it may cause a new emergence in both epistemological and ontological senses, therefore informative in a deeper sense. We referred to epistemic emergencies above (
Section 3.1), but there are a number of well-known examples that can be understood as ontological emergencies under an information-theoretical perspective. For instance, in genetics, a copy error of the DNA can be clearly seen as false information, whereas it produces a mutation which may be able to survive and even grow, bringing about a new population with new functionalities and regularities, that is, meanings. This very well-known productive effect of false information is however not restricted to biological systems, it can indeed be applied to fundamental physical systems (the difference being that copy errors in spin foams have not yet been studied sufficiently so as to determine what a surviving mutation would be in practice).
But alethic neutrality refers also to information processes not only linked to false information, but to extensional emptiness. This is for instance the case of biological preadaptations in which (as described by S. Kauffman [
82], p. 514): “Before [a] particular causal feature began to confer selective advantage the world was such that the particular causal feature was not yet distinguished from among all the other causal properties of the organism and its parts”; thus, being non-informative until it actually becomes an advantageous feature, that is, becoming actually meaningful.
Summing up, though we would like to stay with the GDI, another interpretation has to be chosen in order to embrace the real diversity of information adequately. In fact, what we would aim at can be illustrated in more detail when looking at the catalogue of main concepts assembled in the handbook edited by Floridi on philosophy of computing and information [
85]: Beside information, there is computation, complexity, and system. From elaborating on the first [
86], we obtain the importance of Goedel’s theorem which restricts the power of computability from the beginning on. Complexity however, is visualized exclusively as
computational complexity which is probably a little too narrow after all [
87]. Finally, Mainzer [
88] is quite correct in stressing the origin of systems which is in
dynamical systems (in the mathematical sense). The importance of this insight lies in the idea that one cannot describe any dynamical system without describing its state space at the same time. And as we know from more recent developments, the KAM (Kolmogorov-Arnold-Moser) theorem points to the ubiquity of mixed systems such that dynamical forms of deterministic chaos dominate the processes throughout nature (
cf.
ibid., p. 31). Now, if structures in nature and society can be explained by the dynamics of complex systems and their attractors (
Ibid., p. 33), then indeed, the existence of observable structures is essentially grounded in their underlying information and its inherent meaning: Hence, “[a] dynamical system can be considered as an
information processing machine, computing a present state as output from an initial state of input. Thus, the
computational efforts to determine the states of a system characterize the
complexity of a dynamical system.” (
Ibid., p. 36) The point is here that as far as computation goes, this formulation is certainly correct. But in view of the Goedel theorem, computational complexity is not quite satisfactory after all. The solution may be found in what Mainzer calls “computational ecologies”: Possibly, it is self-organizing agents as they are already available in computer networks which open a new perspective here (see also what we said above on S. Kauffman’s autonomous agents, as well as what is clarified below in the appendix). But then, game theory becomes relevant again [
40,
89,
90,
91,
92].
Hence, in order to summarize, we can state that the GDI is confirmed as to the emergence of meaning which is visualized as a concept to be handled parallel when dealing with information: Information is always meaningful indeed, and it is the emergence of an
autonomous agency within a particular context that comprises at the same time:
Meanings (as the courses of efficient and functional actions with respect to eventual interactions within its context, embodied in constraints that enable the driving of work;
cf. [
93]) and
information (as what enables the selection of courses of action for both the fulfillment of agent’s needs and the participation in natural games within its context; see note [
94]). Therefore to this respect, we adhere to Burgin’s general understanding of information as the capability to generate changes in the system (agent), no matter at what level of organization or abstraction (in case of cognitive agents), even if they entail the emergence of a new agency [
95]. However, as we stress below (
Section 5), we prefer to make a clearer difference between information and energy. First we need to delve into the relationship between information and meaning throughout nature, from fundamental agents to reflexive ones.
Appendix—Agent-Based Meaningful Games as the Foundation of Systems, Spaces and Networks
1. Following an idea of Stuart Kauffman’s, we think of
agents in the generalized sense as systems which achieve a new kind of closure in a given space of catalytic and work tasks propagating work out of non-equilibrium states and playing natural games according to the constraints of their environment (see note [
133]). In particular, (physical) space is visualized then, as being comprised of autocatalytic autonomous Planck scale agents coevolving with each other serving at the same time as some sort of crystallization of seeds of classicity (in the physical sense). This co-evolution is taking place according to what Kauffman calls
4th Law of Thermodynamics: The maximum growth of the adjacent possible in the flow of a non-ergodic Universe maximizes the rate of decoherence and thus the emergence of classicity. There is also a hierarchy of such agents depending on the explicit complexity of those in question (“higher-order agents”) such that
human agents in particular (as constituents of social systems) represent a stage of higher complexity as compared to physical, chemical, or biological systems, respectively (games of various types of agents are nicely illustrated by Szabó and Fáth [
134]). But on the fundamental level of physics, Kauffman mentions the possibility to visualize
spin networks as knots acting on knots to create knots in rich coupled cycles not unlike a metabolism. Hence, they (or their constituents) show up as a sort of “fundamental agents” (see note [
135]).
2. If we take up the viewpoint of Kauffman’s, then it appears to be straightforward to find the fundamental agents in the loops of loop quantum gravity (and the associated quantum information theory) in the first place: This is so because it is the loops which combine in order to form spin networks. In fact, six of them co-operate in order to produce one hexagon of the network.
With a
loop (
cf. e.g., [
21,
136]) we mean here a closed curve
α such that
T[
α] =
Tr [
Uα], where
is the parallel propagator of the vector field Aα along α defined by (the si being points of α)
The SO(3)-field A is here essentially the difference of the SU(2)-spin connection and the extrinsic 3-curvature called real Ashtekar connection:
The important result (
cf. [
21]) is that each spin network state can be decomposed into a finite linear combination of products of loop states.
3. Obviously, this bears a strong resemblance to the Wilson loop representation (hence, we think here of a kind of loop transport according to Stuart Kauffman’s idea of agents), and is also essentially a Feynman-type integral which gives the probability for a (physical) system to go from one state to another:
where S is the action of the form
(The probability is the above expression squared. This is equivalent to the Schroedinger picture of quantum physics on the one hand and a model for quantum computation on the other). As Freidel and Krasnov [
28,
137,
138] as well as Reisenberger and Rovelli [
139] have shown, spin networks and spin foams, respectively, can be visualized as Feynman integrals of that sort such that the formal Feynman perturbation series of the partition function
is given by
where J is a 2-complex, and the vertices, edges, and faces are labelled accordingly. It is N(J) the number of vertices of J divided by the number of symmetries of J.
4. There is a number of important cross-relationships which connect the notion of loops with the notion of knots: Louis Kauffman’s bracket algebra (the boundary algebra of containers and extainers) turns out to be the precursor of the Temperley-Lieb algebra important in order to construct representations of the Artin braid group related to the Jones polynomial in the theory of knot invariants (Kauffman [
113,
140], Grand [
129], Neuman [
141], p. 11, p. 48, pp. 91ff). As the elementary bracket algebra is to
biologic what Boolean logic is to classical logic, this has important epistemological consequences [
75]. On the other hand, the Jones polynomial can itself be visualized in terms of quantum computers, because a similar partition function of the form
ZK = < cup □
M □ cap > with creation and annihilation operations, respectively,
M being the braiding, and <
K>:=∑
σ<
K□
σ>
d║σ║ can be related to the process of quantum computation (as can, by the way, the spin network formalism itself). As spin networks are nothing but graphs, the
agency in question here is motion on graphs or
percolation in networks such that phase transitions can be represented in terms of an appropriate cluster formation of connected components. This is what points to a close relationship to cellular automata utilized for the simulation of evolutionary processes (
cf. Conway’s game of life or Wolfram’s approach [
142]). Stuart Kauffman has associated this with the emergence of collectively autocatalytic sets of polymers, and in fact with the onset of forming classicity with regards to physics. It is straightforward (in epistemic terms) to generalize this (with a view to higher-order agents) to chemical, biological, and other systems.
5. But there is still another point to that: In the approach of Barrett and Crane [
143,
144], the idea is to generalize topological state sum models in passing from three to four dimensions by replacing the characteristic SO(3) group with SO(4), or its appropriate spin covering, SU(2) × SU(2), respectively. The concept of spin networks is also generalized then, by introducing graphs with edges labeled by non-negative real numbers (called “relativistic spin networks”). Applying this kind of “spin foam” model to Lorentzian state sums demonstrates their finiteness in turn implying a number of choices made from physical and/or geometrical arguments [
145]. The really interesting aspect of this is its relation to the group SL(2,C): because this is the double cover of SO(3,1) and the complexification of SU(2) which in turn is the double cover of SO(3). On the other hand, SL(2,C) is the group of linear transformations of C
2 that preserve the volume form. Thanks to an e-mail crash course on these matters referring to the Barrett-Crane model and made available online by John Baez and Dan Christensen [
146], where they use the terminology of the former’s quantum gravity seminar [
147], it is easy to understand that constructions in the sense of Barrett-Crane turn out to be invariant under SL(2,C). In other words, we essentially deal with states in C
2 which are spinors. And it is from quantum theory and special relativity that we know about their relevance. On the other hand, as Baez notes [
146], and as we will see shortly, a state in C
2 can also be called a
qubit. So “[w]hat we [a]re really doing, from the latter viewpoint, is writing down‚ quantum logic gates’ which manipulate
qubits in an SU(2)-invariant [in fact, SL(2,C)-invariant] way. We [a]re seeing how to build little Lorentz-invariant quantum computers. From this viewpoint, what the Barrett-Crane model does is to build a theory of quantum gravity out of these little Planck-scale quantum computers”. This is obviously very much on line with the arguments of Zizzi, Lloyd and others. Moreover, it is referring to the explicit level of spin networks: That is, the aforementioned “boundary layer” between the physical world and its foundation shows up as a “shift of quantum computing” processing the fundamental information necessary for performing the transition from foundation to world (or in other words: For actually
producing a world out of its foundation).
6. Utilizing the “skeleton-of-the-universe view” [
59,
148], the idea would be to insert various steps of a hierarchy of complexity in the overall functor diagram from topological quantum field theory (
cf. [
149]):
This diagram is commutative, if an adequate emergence (em) mapping is being defined. Here, SpinF is the category of spin foams, and nCob is the category of n-dimensional cobordisms (for the time being, we can safely set n = 4). Hence, there remain three things to do:
If we accept this viewpoint for a moment, then all of this is compatible with the idea of humans being complex agents organized in complex communities of agents playing natural games which in their case specialize to
social games and are called meaningful. The cognitive activity of humans then, thinking, and modeling the world, is a complex activity defined according to their complexity as agents [
153]. Hence, humans show up as collectives of fundamental agents which co-evolve in an organized community. A social system is a community of communities then (in fact, this viewpoint is also compatible with the theory of systems according to Edgar Morin).
7. However, while talking about all of that, we notice that this is the outcome of the modeling procedure. In other words, the systematic approach outlined above is itself a model,
i.e., a mapping of the world, not the world itself. We utilize the concepts of
space,
network, and
system according to our epistemological principles: As such networks serve as a formal skeleton for a space and for a system, respectively, while they are graphical representations of both of them. The concept of space serves also the graphical representation of what we call a system. The system is the concept we have of what we are able to observe in concrete terms. But what we observe is only part of the world (our ontological directive is: The world is not as we observe it). But we are products of that world ourselves. Hence, there is the necessity of a
cognitive metatheory for our other theories which tells us something about the basic limitations of our possible knowledge. This entails the necessity of a self-loop: Humans model the world by inventing theories according to the cognitive constraints this same world is imposing upon humans. Theories constitute categories of meaning. If humans show up then as communities of communities of fundamental (natural) agents, they are, with respect to the latter,
emergent structures in nature. And so are all of their reflexive concepts. Hence, the concept of (human) meaning itself is emergent with respect to fundamental
proto-meaning defined in terms of the directed behaviour of fundamental agents. This may be utilized as a grounding of the concepts of
pre-reflexive and
reflexive meaning, respectively. (For „reflexive mentation“ see also Jantsch [
40], p. 237, and as early as 1748 La Mettrie [
154];
cf. Grand [
129], p. 6) Hence, the Universe is meaningful from the outset, but it is only humans who develop reflexive meaning such that they actually know that there
is meaning.
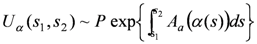
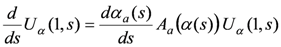
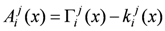

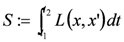
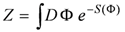
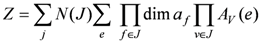
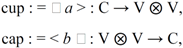
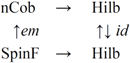
∑ =
Ω
ΩC as adequate tensor product of the associated Hilbert spaces such that
. In particular, for the loops of this theory, the appropriate Hilbert spaces are defined by the cyclic functions of an SU(2) connection A. Hence: {ψ; ψ(A) = f(U(A, γ1)…U(A, γL))}, where
is a spin network state. The density matrix of the underlying graph Γ turns out as the Laplacian matrix L(Γ) (essentially the difference between degree matrix and adjacency matrix) divided by the degree-sum of such graph. Then, ∮γdSE(Ω) ≥ 0 fulfills Stuart Kauffman’s condition for an autonomous agent.