Empirical Information Metrics for Prediction Power and Experiment Planning
Abstract
: In principle, information theory could provide useful metrics for statistical inference. In practice this is impeded by divergent assumptions: Information theory assumes the joint distribution of variables of interest is known, whereas in statistical inference it is hidden and is the goal of inference. To integrate these approaches we note a common theme they share, namely the measurement of prediction power. We generalize this concept as an information metric, subject to several requirements: Calculation of the metric must be objective or model-free; unbiased; convergent; probabilistically bounded; and low in computational complexity. Unfortunately, widely used model selection metrics such as Maximum Likelihood, the Akaike Information Criterion and Bayesian Information Criterion do not necessarily meet all these requirements. We define four distinct empirical information metrics measured via sampling, with explicit Law of Large Numbers convergence guarantees, which meet these requirements: Ie, the empirical information, a measure of average prediction power; Ib, the overfitting bias information, which measures selection bias in the modeling procedure; Ip, the potential information, which measures the total remaining information in the observations not yet discovered by the model; and Im, the model information, which measures the model's extrapolation prediction power. Finally, we show that Ip + Ie, Ip + Im, and Ie − Im are fixed constants for a given observed dataset (i.e. prediction target), independent of the model, and thus represent a fundamental subdivision of the total information contained in the observations. We discuss the application of these metrics to modeling and experiment planning.1. Introduction
1.1. The Need for Information Metrics for Statistical and Scientific Inference
Information theory as formulated by Shannon [1], Kolmogorov and others provides an elegant and general measure of information (or coupling) that connects variables. As such, it might be expected to be universally applied in the “Information Age” (see, for example, the many fields to which it is relevant, described in [2]). Identifying and measuring such information connections between variables lies at the heart of statistical inference (infering accurate models from observed data) and more generally of scientific inference (performing experimental observations to infer increasingly accurate models of the universe).
However, information theory and statistical inference are founded on rather different assumptions, which greatly complicate their union. Statistical inference draws a fundamental distinction between observable variables (operationally defined measurements with no uncertainty) and hidden variables (everything else). It seeks to estimate the likely probability distribution of a hidden variable(s), given a sample of relevant observed variables. Note that from this point of view, probability distributions are themselves hidden, in the sense that they can only be estimated (with some uncertainty) via inference. For example, individual values of an observable are directly observed, but their true distribution can only be inferred from a sample of many such observations.
Traditional information theory, by contrast, assumes as a starting point that the joint probability distribution p(X, Y, Z…) of all variables of interest is completely known, as a prerequisite for beginning any calculations. The basic tools of information theory – entropy, relative entropy, and mutual information – are undefined unless one has the complete joint probability distribution p(X, Y, Z…) in hand. Unfortunately, in statistical inference problems this joint distribution is unknown, and precisely what we are trying to infer.
Thus, while “marrying” information theory and statistical inference is by no means impossible, it requires clear definitions that resolve these basic mismatches in assumptions. In this paper we begin from a common theme that is important to both areas, namely the concept of prediction power, i.e., a model's ability to accurately predict values of the observable variable(s) that it seeks to model. Prediction power metrics have long played a central role in statistical inference. Fisher formulated prediction power as simply the total likelihood of the observations given the model, and developed Maximum Likelihood estimators, based on seeking the specific model that maximizes this quantity. This concept remains central to more recent metrics such as the Akaike Information Criterion (AIC) [3], and Bayesian Information Criterion (BIC) [4], which add “corrections” based on the number of model parameters being fitted.
In this paper we define a set of statistical inference metrics that constitute statistical inference proxies for the fundamental metrics of information theory (such as mutual information, entropy and relative entropy). We show that they are vitally useful for statistical inference (for precisely the same properties that make them useful in information theory), and highlight how they differ from standard statistical inference metrics such as Maximum Likelihood, AIC and BIC. We present a series of metrics that address distinct aspects of statistical inference:
prediction power, as it is ordinarily defined, as the likelihood of future observations (e.g., “test data”) under a given set of conditions that we have already observed (“training data”).
bias: A measure of any systematic difference in the model's prediction power on future observations vs. on its original training data.
completeness: We define a modeling process as “complete” when no further improvements in prediction power are possible (by further varying the model). Thus a completeness metric measures how far we are from obtaining the best possible model.
extrapolation prediction power:We will introduce a measure of how much the model's prediction power exceeds the prediction power of our existing observation density, when tested on future observations. If this value is zero (or negative) one might reasonably ask to what extent its results can truly be called a “prediction”, but instead are only a summary (or “interpolation”) of our existing observation data.
To clarify the challenges that such metrics must solve, we wish to highlight several characteristics they must possess:
objective or model-free: One important criterion for such a metric is whether it is model-free; that is, whether or not the calculation of the metric itself involves a process that is equivalent to modeling. If it does, the metric can only be considered to yield a “subjective” evaluation – how well one model fits to the expectations of another model. By contrast, a model-free metric aims to provide an objective measure of how well a model fits the empirical observations. While this criterion may seem very simple to achieve, it poses several challenges, which this paper will seek to clarify.
unbiased: Like any estimator calculated from a finite sample, these metrics are expected to suffer from sampling errors, but they must be mathematically proven to be free from systematic errors. Such errors are an important source of overfitting problems, and it is important to understand how to exclude them by design.
convergent: These metrics must provide explicit Law of Large Numbers proofs that they converge to the “true value” in the limit of large sample size. The assumption of convergence is implicit in the use of many methods (such as Maximum Likelihood), but unfortunately the strict requirements of the Law of Large Numbers are sometimes violated, breaking the convergence guarantee and resulting in serious errors. To prevent this, a metric must explicitly show that it meets the requirements of the Law of Large Numbers.
bounded: These metrics must provide probabilistic bounds that measure the level of uncertainty about their true value, based on the limitations of the available evidence.
low computational complexity: Ideally, the computational complexity for computing a metric should be O(N log N) or better, where N is the number of sample observations.
In this paper we define a set of metrics obeying these requirements, which we shall refer to as empirical information metrics. As a Supplement, we also provide a tutorial that shows how to calculate these metrics using darwin, an easy-to-use open source software package in Python, available at https://github.com/cjlee112/darwin.
2. Empirical Information
2.1. Standard Prediction Power Metrics
Fisher defined the prediction power of a model Ψ for an observable variable X in terms of the total likelihood of a sample of independent and identically distributed (I.I.D.) draws X1,X2, …Xn
Fisher's Maximum Likelihood method seeks the model that maximizes the total likelihood or, equivalently, the sample average log-likelihood L̅. Similarly, minimizing the Akaike Information Criterion (AIC) [3]
Vapnik-Chervonenkis theory also supplies a correction factor that penalizes model complexity for classifier problems [6]. For example, consider the simplest case of a binary classifier that predicts the class of each data point with a confidence factor C (by assigning that class a likelihood of , and the other class a likelihood of ). In this case the classification error probability on the training data, Rtrain, converges for large C to , and structural risk minimization indicates choosing the model that minimizes the upper bound of the classification error probability:
2.2. Prediction Power and the Law of Large Numbers
These metrics are best understood by highlighting the critical role that the Law of Large Numbers plays in inference metrics. Say we want to find a model Ψ that maximizes the total likelihood of many draws of X, or equivalently the expectation value of the log-likelihood, which depends on the true distribution Ω(X):
Since we do not know the true distribution Ω(X) we cannot use this definition directly. However, we can apply the Law of Large Numbers (LLN) to the log-likelihood of a sample of observations, whose sample average must converge
Since the Xi are indeed conditionally independent given Ω and identically distributed as X, we expect for large sample size n to be able to use L̅ as a proxy for E(L). In that case maximizing L̅ also maximizes E(L), which it is convenient to separate into one term dependent only on Ω and another term dependent on Ψ:
2.3. The Problem of Selection Bias
Unfortunately, there is a catch. This guarantee can only be extended to maximization of the sample log-likelihood L̅, if the Li are identically distributed as L. All of these metrics (L̅, AIC, BIC) were designed for use with model selection; that is, we compute the metric for each of a large set of models, then select the model that maximizes the likelihood (or minimizes the AIC or BIC). And the very nature of model selection introduces bias into the sample likelihoods [8]. Briefly, if the model Ψ was chosen specifically to maximize the values Li, we cannot assume that the Li are identically distributed as L. Indeed, we expect that the Li will be biased to higher values than L in general. Therefore the Law of Large Numbers convergence guarantee collapses, and we cannot prove that model selection using L̅ will yield the true distribution Ω. Vapnik-Chervonenkis theory seeks to protect against this bias by deriving an upper bound on the possible error due to selection bias [6], based on the model's VC dimension.
First, let's examine this problem from an empirical point of view, by simply defining a metric for measuring the bias. We define a test data criterion:
a set of sample values are valid test data for a model Φ predicting an observable X if the are exchangeable, identically distributed as X, and conditionally independent of Φ given the true distribution Ω, i.e., . Equivalently, Φ contains no information about the except via their shared dependence on the hidden distribution Ω. Note that for any model Φ generated by model selection, its training data do not meet this requirement, since Φ is not conditionally independent of the training data given Ω.
We desire an estimator for L̅ − E(L). Since the are identically distribured as X and conditionally independent of Φ given Ω, the are identically distributed as log Φ(X) i.e., L. So by the Law of Large Numbers we can define an overfitting bias information metric
Ib has the corresponding lower bound estimator (under the simplifying assumption that the sample sizes for L and Le are the same (m = n)):
2.4. Example: The BIC Optimal Model for a Small Sample from a Normal Distribution
The BIC adds a correction term k log n to the total log-likelihood, which penalizes against models with larger numbers of parameters. Note that this correction is designed specifically to protect against overfitting. This correction is referred to as the Bayesian Information Criterion because it is based on choosing the model with maximum Bayesian posterior probability, and by this criterion is provably optimal for the exponential family of models [4].
However, several caveats about such corrections should be understood:
a given correction addresses a particular kind of overfitting, for example, for the AIC and BIC, excessive number of model parameters k.
a given correction is based on specific assumptions about the model, and may not behave as expected under other conditions;
Such corrections do not guarantee that the model they select will be optimal, or even unbiased.
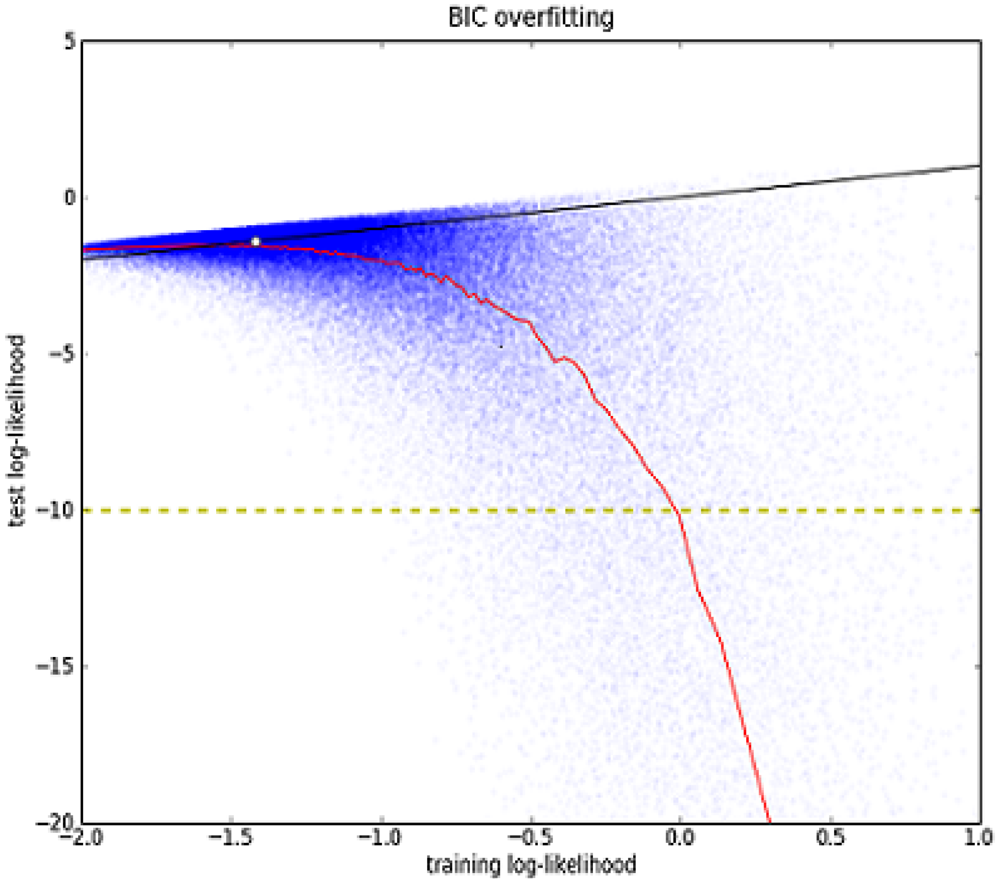
As an example, Figure 1: Overfitting analysis of BIC models on a small sample from a normal distribution shows the distribution of L̅ vs. for BIC-optimal models generated using a sample of three observations drawn from a unit normal distribution. (Note that in this case BIC-optimality is just equivalent to AIC-optimality and Maximum Likelihood, since the set of all possible normal models share the same value of k = 2). This simple example illustrates several points:
A large fraction of the models strongly overfit the observations as indicated by a large deviation from the L̅ = diagonal.
L̅ and are strongly and non-linearly anti-correlated. That is, the better the apparent fit to the training data, the worse the actual fit to the test data.
2.5. The Empirical Information Metric
Based on these considerations, we use the unbiased estimator Le to define the empirical information, a signed measure of prediction power relative to the uninformative distribution p(X):
Note that Ie can be negative, if the model's prediction power is even worse than that of theuninformative distribution.
Whereas most metrics for model selection such as the AIC and BIC contain correction terms dependent on the model complexity k (or VC dimension h), Ie needs no such corrections because it is unbiased by definition. Excessive model complexity will not increase Ie but instead will reduce it. Ie contains no bias and therefore needs no correction. In this sense, it follows a similar approach as cross-validation [9].
Note that we do not need to incorporate the sample size directly into the metric definition (as in the case of the BIC [4], Vapnik-Chervonenkis upper-bound error Rvc [6], and “small-sample corrected” versions of the AIC such as the AICc [10]). Instead, the effect of sample size emerges naturally from the Law of Large Numbers lower bound estimator for our empirical information metrics (e.g., Le,ε, Ib,ε, Ie,ε). Fundamentally, the importance of sample size is simply the uncertainty due to sampling error, and the Law of Large Numbers probabilistic bound captures this in a general way.
2.6. Empirical Information as A Sampleable Form of Mutual Information
Consider the following “mutual information sampling problem”:
draw a specific inference problem (hidden distribution Ω(X)) from some class of real-world problems (e.g., for weight distributions of different animal species, this step would mean randomly choosing one particular animal species);
draw training data and test data X from Ω(X);
find a way to estimate the mutual information I( ; X) on the basis of this single case (single instance of Ω).
The standard definition of mutual information does not enable such a calculation. Even if we draw many pairs , X to estimate this value, we will just get a value of zero, because , X are conditionally independent given Ω. The mutual information I( ; X) is defined only over the complete joint distribution p(Ω, , X); it does not appear meaningful to talk about calculating it from a single instance of Ω.
By contrast with mutual information, we do calculate empirical information for a specific value of Ω, i.e., we use it to measure the prediction power of our model Ψ on observations emitted by that specific value of Ω. It is therefore interesting to investigate the relationship of the empirical information vs. the mutual information. We follow the usual information theory approach of taking its expectation value over the complete joint distribution:
for one specific inference problem (hidden value of Ω), we draw a training dataset , use it to train a model Ψ(X|), and measure the empirical information on a set of test data drawn from the same distribution.
We repeat this procedure for multiple inference problems Ω(1), Ω(2), …, Ω(m), and take the average of their empirical information values .
If the model Ψ(X| ) approximates the true conditional distribution p(X| ) more and more closely, the relative entropy term D(p(X|)‖Ψ(X|)) will vanish, and we expect the average of the empirical information values to converge simply to I(X; ). Under these conditions, the empirical information becomes a “sampleable form” of the mutual information. Note that the mutual information itself does not have this property; as shown above, the mutual information cannot be computed “piecewise” for individual instances of Ω and then averaged. By contrast, if we compute the empirical information for each inference problem, and then take the average, it will converge to the mutual information.
3. The Problem of Convergence
If we wish to maximize prediction power, our ultimate goal must be convergence, namely that our model will converge to the true, hidden distribution Ω. So we must ask the obvious question, how do we know when we're done? Two basic strategies present themselves:
self-consistency tests: We can use our model as a reference to test whether the observations exactlymatch its expectations, as must be true if Ψ → Ω.
convergence distance metric: If we knew the value of the absolute maximum prediction power L(Ω) possible for our target observable X, we could define a distance metric δ = L(Ω) − L(Ψ), which measures how “far” our current model is from convergence, in terms of its relative prediction power.
We will define empirical information metrics for both these approaches.
3.1. The Inference “Halting Problem”
As an example of the need for a convergence metric, we consider the process of Bayesian inference in modeling scientific data. In scientific research, we cannot easily restrict the set of possible models a priori either to closed-form analytic solutions or to finite sets of models that we can fully compute in practical amounts of CPU time. That is, the set of all possible models of the universe is not strictly bounded, and generally can be reduced only by calculating likelihoods for different terms of this set vs. experimental observations.
What is the computational complexity for Bayesian inference to find the correct term Ω or any term within some distance δ of it? We can view this as a form of the Halting Problem, in the sense that it requires a metric that indicates when it has found a term that is less than δ distance from Ω, at which point the algorithm halts. Unfortunately, the standard form of Bayes' Law
In real-world practice this “halting problem” often grows into an even worse problem of “model misspecification” [11]. That is, Bayesian computational methods typically lack a mechanism for generating all possible models even in theory. Instead they are limited to assuming a specific mathematical form for the model. Unless by good fortune the true distribution exactly fits this mathematical form, the computation will simply exclude it. Therefore, a reliable convergence metric becomes essential as an external indicator for whether the computational model is “misspecified” in this way. It should be noted that this is not addressed by asking whether a given Bayesian modeling process has “converged” in the sense of a Markov Chain Monte Carlo sampling process converging to its stationary distribution [12]. Any such process is still restricted by its assumptions of a specific mathematical form for the model; there is no guarantee that this will contain the correct answer.
3.2. Potential Information
We define I∞ as the total information content obtainable from a set of observations by considering the infinite set of all possible models. By analogy to the classical physics division of kinetic vs. potential energy components, we divide this into one part representing the model terms we've actually calculated (Ie, the empirical information), and a second part for the remaining uncomputed terms, which we define as Ip, the potential information:
This density estimation problem poses one conceptual problem that requires clarification. Since the ultimate purpose of the potential information calculation is to catch possible errors in modeling, no part of its calculation (such as the empirical entropy calculation) should itself be equivalent to a form of modeling. If we used such a form of modeling to compute the empirical entropy, that would introduce a strongly subjective element, i.e., simply comparing one model (Ψ) versus another (the model used for estimating He). To obtain an objective Ip metric, the empirical entropy calculation should be model-free. It should be a purely empirical procedure with a Law of Large Numbers convergence guarantee for large sample size n → ∞.
3.3. The Empirical Entropy
For the case where the observable X is restricted to a set of discrete values, we define an indicator label κx(X) which equals 1 if X equals a desired value x, otherwise zero. Then by the Law of Large Numbers
Of course, the empirical entropy has the usual lower bound estimator from the Law of Large Numbers
3.4. Potential Information Estimators
This gives us mean and lower bounds estimators for the potential information
Note that since the potential information is computed in “observation space” instead of “model space”, the computational complexity of its calculation depends primarily on the observation sample size. This can be very efficient. First of all, the calculation divides into two parts that can be done separately; since the empirical entropy has no dependence on the model Ψ, it need only be calculated once and can then used for computing Ip for many different models. Second, the empirical entropy calculation can have low computational complexity. For the simple implementation outlined above, it is simply O(mn) (where m is a small constant for the nearest-neighbor density calculation; this assumes the observations are already sorted in order. If not, an additional O(n log n) step is required to sort them). For high dimensional data, the computational complexity scales as O(n2), due to the need to calculate pairwise distances. Of course, the details of the computational complexity will vary depending on what empirical entropy implementation is used.
3.5. Convergence to the Kullback-Leibler Distance
In the limit of large sample size, the potential information converges to
We may thus consider the potential information to represent a distance estimator from the true distribution Ω. Specifically, it estimates the difference in prediction power of our current model vs. that of the true distribution. Thus it solves the Inference Halting metric problem; if we are searching for a model with prediction power within distance δ of the maximum, we simply halt when
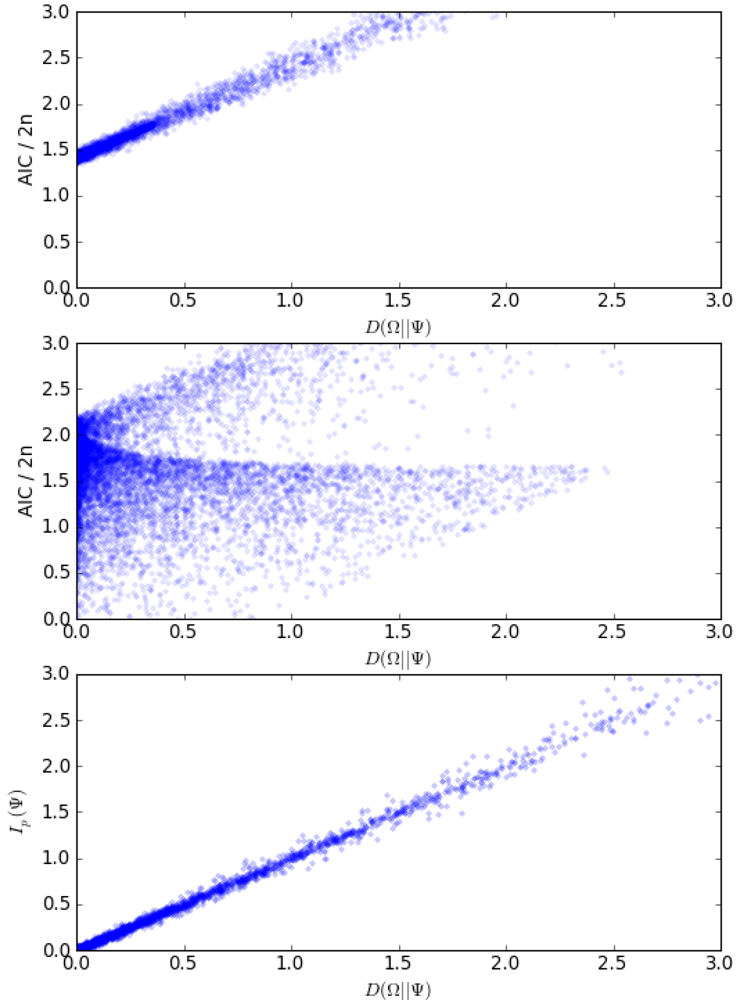
The Akaike Information Criterion (AIC) [3] and related information metrics [16] are often referred to as representing the Kullback-Leibler (KL) divergence of the true distribution vs. the model [17]. So it is logical to ask how the potential information differs from these well-known metrics. The AIC and related metrics were designed for model selection problems, in which the observable (characterized by the true distribution Ω) is treated as a fixed constant, and the model is varied in search of the best fit. As shown in part A of Figure 2: Comparing AIC and Potential Information to the Theoretical Kullback-Leibler Divergence, the AIC does indeed correlate directly with the KL divergence D(Ω‖Ψ) under this assumption (holding the true distribution fixed as a constant). Specifically, for a sample of exchangeable observations ,
However, if the true distribution Ω is not treated as a fixed constant, and instead is allowed to vary, this simple relationship breaks. In that case, the AIC no longer correlates with the KL divergence (Figure 2B). By contrast, the potential information metric Ip̅ correlates with the KL divergence under all conditions (Figure 2C). The main difference between the potential information and the AIC is simply the empirical entropy term, which is included in the potential information metric but missing from the AIC:
we need an estimate of the absolute value of the Kullback-Leibler divergence, rather than simply comparing its relative value for two models;
or we need to consider possible variation between different true distributions Ω (or equivalently, different observable variables X). For example, in experiment planning problems, we consider different possible experiments (different observable variables) in order to estimate how much information they are likely to yield [18].
3.6. Unbiased Empirical Posteriors
Standard Bayesian inference can grossly overestimate the posterior probability of a model term, because the sum of calculated terms is biased to underestimate the total p(X) summed over the complete infinite series. The empirical entropy provides a resolution to this problem. By the Asymptotic Equipartition theorem [1], for a sample = {X1, X2, …XN} of exchangeable observations of size N
3.7. The Model Self-Consistency Test
We note that a more limited convergence test is possible, by reversing the procedure, and calculating the entropy of the model (which can be done directly, either analytically or by simulation). We define a self-consistency measure
For Ψ → Ω, δSC → 0. We use this fact to construct a test
4. Model Information
4.1. What is “Prediction”?
We defined our empirical information metric as a measure of prediction power. However, it seems worthwhile to ask again what exactly we mean by “prediction”. The empirical density estimation procedure outlined above suggests that in the limit of large sample size there is always a trivial way of obtaining perfect prediction power: Copy the empirical density for X as our “likelihood model” for X, and show that it accurately predicts new observations of X. Such a procedure does not seem to qualify as “prediction”; we simply copied the observed density. In this case all the information for the “prediction” came from the observed data, and none at all from the modeling procedure itself. This suggest several conclusions:
We desire a metric for the intrinsic prediction power of a model, above and beyond just copying the existing observation density. We will refer to this as Im, the model information.
Generalizing our original definition of “prediction power”, we wish to maximize our prediction accuracy not only for situations that we have already observed, but also for novel situations that we have never encountered before. In other words, we adopt the conservative position that our data may be incomplete, so we cannot assume that future experience will simply mirror past experience. To maximize future prediction power, we must seek models that predict future observations more accurately than simply interpolating from past observations.
Of course, we do not know a priori that such models even exist; that is a strictly empirical question. We simply generate models and measure whether they have such intrinsic prediction power, i.e., Im > 0.
By definition, such a measurement can only be performed via new observations, e.g., a regionof observation space that we have not observed before. As we will show in a moment, a regionthat has already been observed (thoroughly) cannot yield significant model information, becausethe past observations already provide a good density image for predicting future observations inthis region.
Thus, we can consider the adoption of a new model to be a cut on the temporal sequence ofobservations, partitioning them into two sets: The “old” observations (those taken before theadoption of the model), and the “new” observations (those taken after the adoption of the model).
4.2. Defining Model Information
The key question of model information is whether the model yields better prediction power than simple interpolation from past observations. As the interpolation reference, we simply use the empirical density calculation defined previously. Specifically, for a model Ψ we define its model information as
Thus, measures whether the model's empirical log-likelihood on the new observations exceeds the average log-likelihood of the new observations computed from the old observation density, i.e., . As for the potential information, we define a lower bound estimator for Im with confidence level 1 − ∈ based on the Law of Large Numbers:
In the case nold → 0 we make the density function converge to the uninformative prior based on the detector range for the observable X. That is, if the range of detectable values for X is [0,10] then Pe,old(X) → 1/10.
Note that the model information can be negative, indicating that the model has worse prediction power than the old empirical density estimator.
4.3. Example: The Normal Distribution
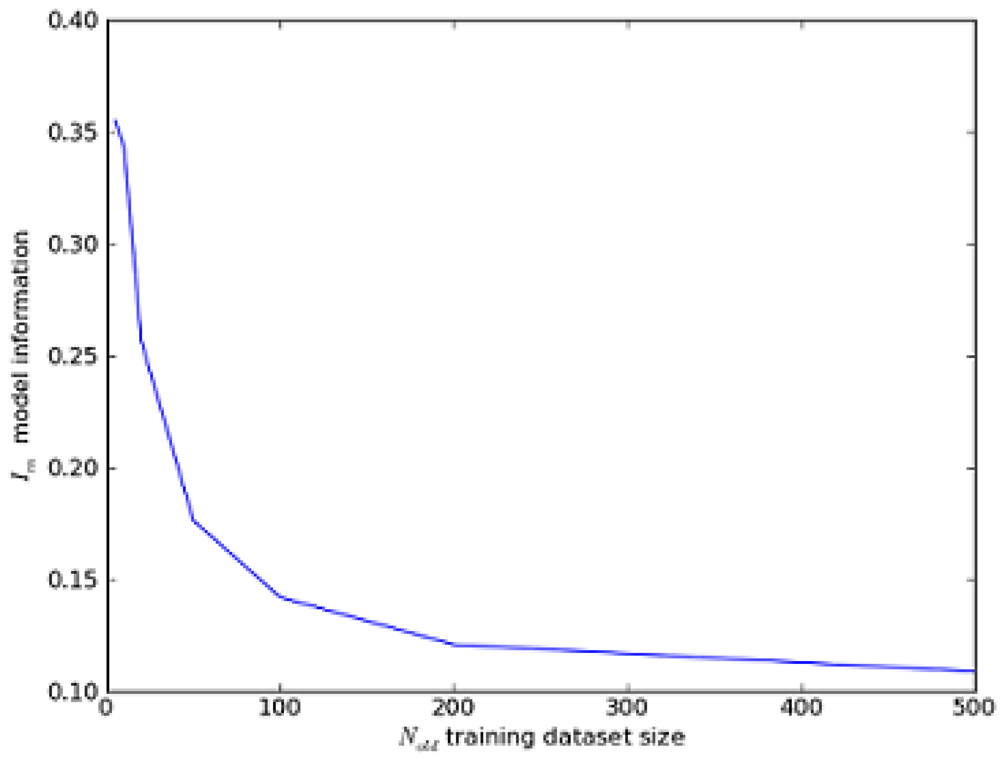
Figure 3: Model Information of the Normal Distribution. We draw nold observations from the unit normal distribution N(0,1) and compute the posterior likelihood distribution for this sample. We then draw a new sample of 100 observations from the same distribution and use it to measure Im for our model. The model information is initially high because the normal model predicts the shape of the distribution much more accurately than simple interpolation from the old observation sample.
4.4. Example: The Binomial Distribution
By contrast, the binomial distribution doesn't yield significant model information, because the observable has only two possible states (success or failure) for the model to predict, and the binomial model's prediction of its probability is just equivalent to the empirical probability in the training data:
5. Empirical Information Partition Rules
5.1. The Ip + Ie, Ie − Im, Ip + Im Partitions
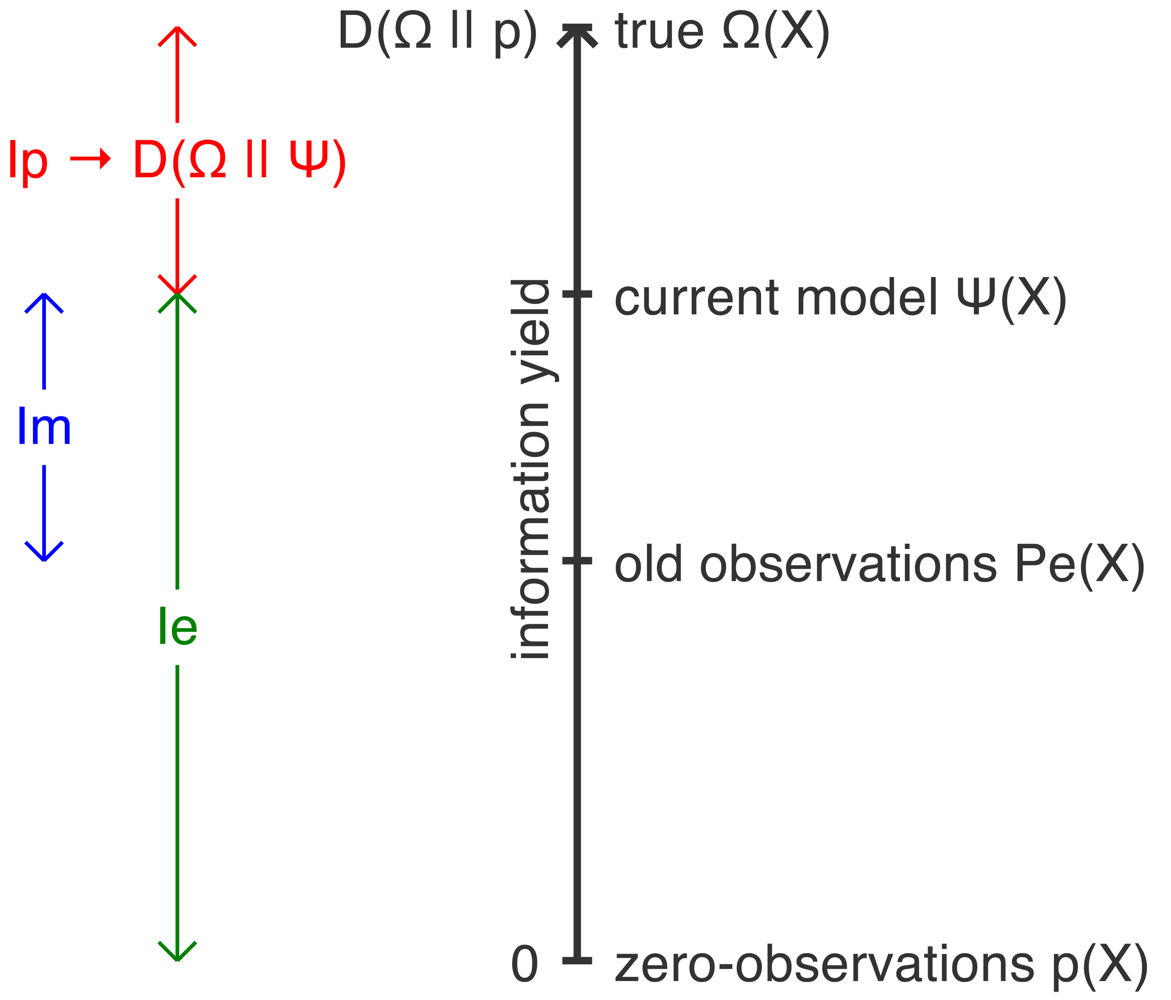
We now briefly consider the relationships between potential information, empirical information and model information, illustrated in Figure 4: Empirical Information Partition Rules.
All information originates as potential information. That is, before we have a successful model for a set of observations, our prediction power is no better than random, and this manifests as positive Ip and zero Ie.
For a given observable X, the sum of Ip + Ie is a constant (i.e., independent of the model Ψ(X)). That is, for any observation sample ,
where p(X) is the uninformative distribution for X. For large sample size nwhich is simply the relative entropy of the true distribution relative to the uninformative distribution p(X).Thus potential information is converted to empirical information by modeling. As the model Ψ becomes a more accurate image of the observation density, Ip decreases and Ie increases by the same amount.
relation to mutual information: It must be emphasized that the mutual information I(X; Ω) is defined only if we know the complete joint distribution p(X, Ω). Since we do not know this joint distribution, we would like a sampling-based estimator for I(X; Ω). We can do this by simply sampling different inference cases Ω(1), Ω(2), … Ω(m) (represented by different observation samples Taking the average of + over a large number m of inference cases converges:
If we explicitly assume that the uninformative distribution used for computing the empirical information matches the true marginal distribution of X, thenThus, Ip + Ie may be considered to be a “sampleable version of the mutual information”; that is, it can be measured for any individual inference case, and its average over multiple inference problems will converge to the mutual information of the observable vs. hidden variables.For a given observable X, the sum of Ie − Im is a constant. (i.e., independent of the model Ψ(X)).Assuming both Ie, Im are calculated on the same test data,
where Pe,old(X) is the distribution of X computed from past observations (as described above). So for n → ∞Thus Ie − Im measures the amount of information supplied by the past observations (in the form of Pe,old(X)).Moreover, in the asymptotic limit, − ≥ 0 since for nold → 0 we guarantee that Pe,old(X) → p(X) and for nold → ∞ we have .
Thus, Im partitions Ie into the part that is simply provided by the training observations themselves, versus the part that actually constitutes “value added” predictive power of the model itself.
For a given observable X, the sum of Ip + Im is a constant (i.e., independent of the model Ψ(X)). Specifically, assuming both Ip, Im are calculated on the same test data,
which simply measures the amount of information available to be learned about the true distribution of X above and beyond that already provided by past observations (in the form of Pe,old(X)).Relation of Im to relative entropy: Note that since , this also implies that . This simply restates the principle that the model information representsthe increase in model prediction power relative to the empirical density of the past observations.
5.2. Asymptotic Conversion of Potential and Model Information to Empirical Information
Consider the following asymptotic modeling protocol: For a large sample size nold → ∞ we simply adopt the empirical density Pe,old as our model Ψ. We then measure Ie,Ip,Im on a set of new observations.
As nold → ∞, Pe,old (X) converges to the true density Ω (X), so and
This scenario illustrates a simple point about the distinct meanings of empirical information vs. model information. The overriding goal of model selection is maximizing empirical information (likelihood). However, this scenario shows that maximizing the empirical information is in a sense trivial if one can collect a large enough observation sample. By contrast, there is no trivial way to produce positive model information; note that the very procedure that automatically maximizes Ie also ensures that Im ≤ 0.
This suggests several changes in how we think about the value of modeling. In model selection, the value of a model is often thought of in terms of data compression; that is, that the best model encodes the underlying pattern of the data in the most efficient manner possible. Metrics such as the AIC and BIC seek to enforce this principle by adding “correction terms” that penalize the number of model parameters. However, to be truly valuable for prediction, a model should meet this data compression criterion not only retrospectively (i.e., it can yield a more efficient encoding of the past observations) but also prospectively (i.e., it can predict future observations more accurately than simply interpolating from the past observations). Whereas the total empirical information metric fails to draw this distinction, the model information explicitly measures it. That is, it partitions the total Ie into a “trivial” part that represents the prediction power implicit in the observation dataset itself, and a non-trivial part that represents true “predictions” coming from the model.
6. Conclusion
We wish to suggest that these empirical information metrics represent a useful extension of existing statistical inference metrics, because they provide “sampleable” measures of key information theory metrics (such as mutual information and relative entropy), with explicit Law of Large Numbers convergence guarantees. That is, each empirical information metric can be measured via sampling on an individual inference problem (unlike the conventional definition of mutual information); Yet its average value over multiple inference problems will converge to the true, hidden value of its associated metric from information theory (such as the mutual information). On such a foundation, one can begin to recast statistical and scientific inference problems in terms of the very useful and general tools of information theory. For example, the “inference halting problem”, which imposes a variety of problems and limitations in Bayesian inference, can be easily resolved by the potential information metric, which directly measures the distance of the current model from the true distribution in standard information theoretic terms. Similarly, the model information metric measures the “value-added” prediction power of a model relative to its training data.
Acknowledgments
The author wishes to thank Marc Harper, Esfan Haghverdi, John Baez, Qing Zhou, Alex Alekseyenko, and Cosma Shalizi for helpful discussions on this work. This research was supported by the Office of Science (BER), U. S. Department of Energy, Cooperative Agreement No. DE-FC02-02ER63421.
References
- Shannon, C. A Mathematical Theory of Communication. Bell System Tech. J. 1948, 27, 379–423. [Google Scholar]
- Cover, T.; Thomas, J. Elements of Information Theory; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Automat. Contr. 1974, AC-19, 716–23. [Google Scholar]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar]
- de Finetti, B. La pre′vision: ses lois logiques, ses sources subjectives. Ann. Inst. Henri Poincare′ 1937, 7, 168. [Google Scholar]
- Vapnik, V.N. Statistical Learning Theory; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Efron, B. Nonparametric estimates of standard error: The jackknife, the bootstrap and other methods. Biometrika 1981, 68, 589–599. [Google Scholar]
- Breiman, L. The little bootstrap and other methods for dimensionality selection in regression: X-fixed prediction error. J. Am. Stats. Assoc. 1992, 87, 738–754. [Google Scholar]
- Geisser, S. Predictive Inference; Chapman and Hall: New York, NY, USA, 1993. [Google Scholar]
- McQuarrie, A.; Tsai, C.L. Regression and Time Series Model Selection; World Scientific: Singapore, 1998. [Google Scholar]
- Shalizi, C.R. Dynamics of Bayesian Updating with Dependent Data and Misspecified Models. Electron. J. Statist. 2009, 3, 1039–1074. [Google Scholar]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Rubin, D.B. Bayesian Data Analysis, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Bonnlander, B.; Weigend, A. Selecting input variables using mutual information and nonparametric density estimation. Proceedings of the 1994 International Symposium on Artificial Neural Networks (ISANN 94), Taiwan; 1994; pp. 42–50. [Google Scholar]
- Kraskov, A.; Stogbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar]
- Kullback, S.; Leibler, R. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar]
- Sawa, T. Information Criteria for Discriminating among Alternative Regression Models. Econometrica 1978, 46, 1273–1291. [Google Scholar]
- Vuong, Q. Likelihood ratio tests for model selection and non-nested hypotheses. Econometrica 1989, 57, 307–333. [Google Scholar]
- Paninski, L. Asymptotic theory of information-theoretic experimental design. Neural Computat. 2005, 17, 1480–1507. [Google Scholar]
- Laplace, P.S. Essaiphilosophique sur lesprobabilités; Courcier: Paris, France, 1814. [Google Scholar]
© 2011 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)
Share and Cite
Lee, C. Empirical Information Metrics for Prediction Power and Experiment Planning. Information 2011, 2, 17-40. https://doi.org/10.3390/info2010017
Lee C. Empirical Information Metrics for Prediction Power and Experiment Planning. Information. 2011; 2(1):17-40. https://doi.org/10.3390/info2010017
Chicago/Turabian StyleLee, Christopher. 2011. "Empirical Information Metrics for Prediction Power and Experiment Planning" Information 2, no. 1: 17-40. https://doi.org/10.3390/info2010017
APA StyleLee, C. (2011). Empirical Information Metrics for Prediction Power and Experiment Planning. Information, 2(1), 17-40. https://doi.org/10.3390/info2010017



