Accuracy in Biological Information Technology Involves Enzymatic Quantum Processing and Entanglement of Decohered Isomers
Abstract
: Genetic specificity information “seen by” the transcriptase is in terms of hydrogen bonded proton states, which initially are metastable amino (−NH2) and, consequently, are subjected to quantum uncertainty limits. This introduces a probability of arrangement, keto-amino → enol-imine, where product protons participate in coupled quantum oscillations at frequencies of ∼ 1013 s−1 and are entangled. The enzymatic ket for the four G′-C′ coherent protons is | ψ > = α| + − + − > + β| + − − + > + γ| − + + − > + δ| − + − + >. Genetic specificities of superposition states are processed quantum mechanically, in an interval Δt ≪ 10−13 s, causing an additional entanglement between coherent protons and transcriptase units. The input qubit at G-C sites causes base substitution, whereas coherent states within A-T sites cause deletion. Initially decohered enol and imine G′ and *C isomers are “entanglement-protected” and participate in Topal-Fresco substitution-replication which, in the 2nd round of growth, reintroduces the metastable keto-amino state. Since experimental lifetimes of metastable keto-amino states at 37 °C are ≥ ∼3000 y, approximate quantum methods for small times, t < ∼100 y, yield the probability, P(t), of keto-amino → enol-imine as Pρ(t) = ½ (γρ/ħ)2 t2. This approximation introduces a quantum Darwinian evolution model which (a) simulates incidence of cancer data and (b) implies insight into quantum information origins for evolutionary extinction.1. Introduction
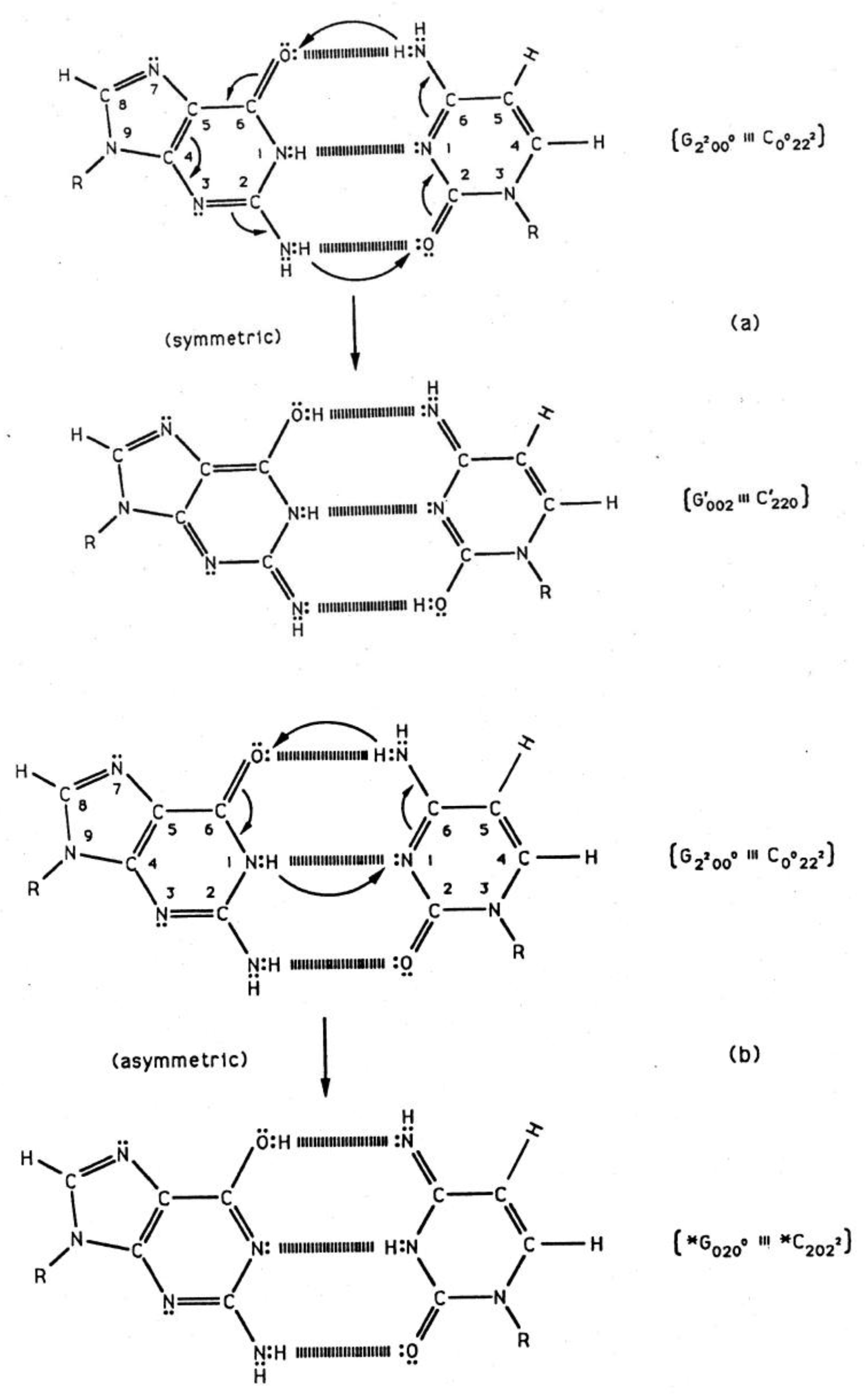
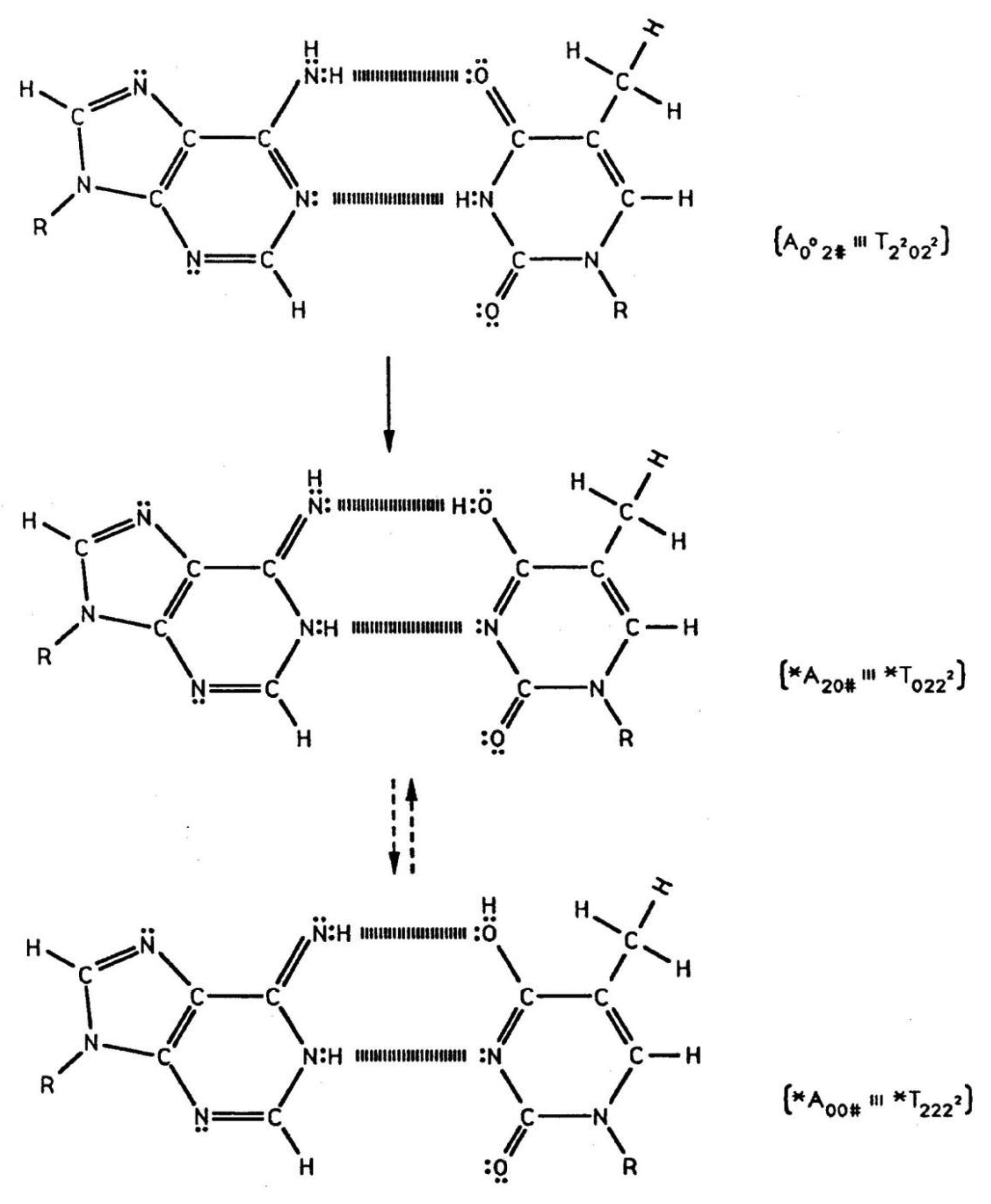
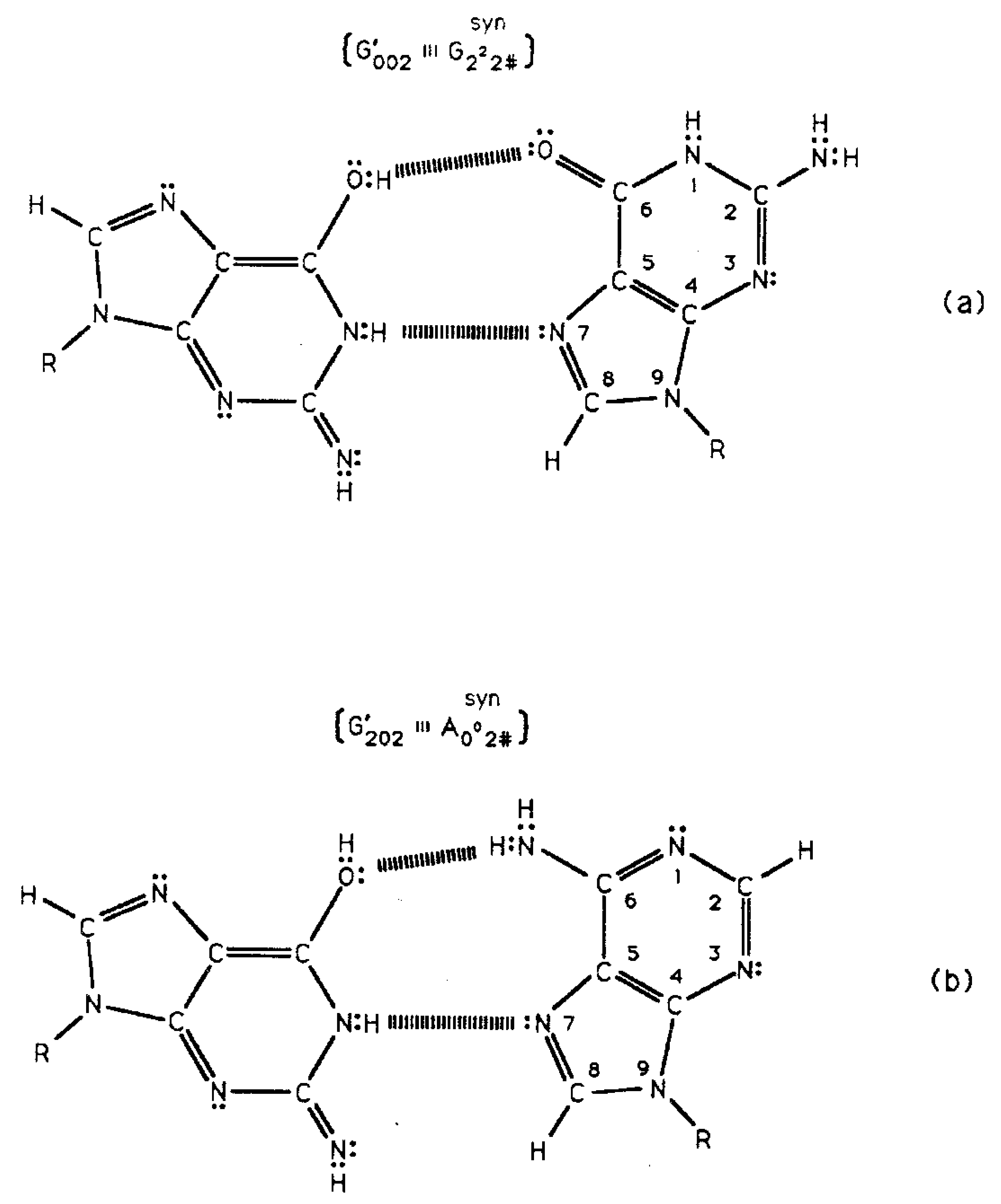
Quantum information science seeks to exploit applications of quantum theory to enhance the versatility of acquiring, storing, transmitting and processing information, using encoded information systems that exhibit unique quantum properties [1-3]. If successful, quantum information processing by a quantum computer would significantly enhance computational power and thus expand the range of computational applications [4,5]. In the context of discussing an example quantum information system [6,7], this report presents a review of evolutionarily designed quantum information processing routinely implemented by enzyme systems of bacteriophage T4 [8,9] and human DNA systems [10-13]. This model of genetic specificity implies a quantum Darwinian evolution treatment for intrinsic time-dependent DNA instabilities. Although most molecular genetic experiments did not attempt to measure consequences of quantum effects, time-dependent point mutations exhibited by T4 phage require quantum coherence for explanation. In this case, molecular genetic observations [8] and quantum chemical calculations [9-13] demonstrate that the replicase introduces metastable keto-amino complementary DNA pairs. As a consequence, quantum uncertainty limits—Δx Δpx ≥ ½ ħ—operate on amino DNA protons which drive arrangements, keto-amino → enol-imine (Figures 1 to 3). This populates accessible reduced energy enol-imine duplex states at rates consistent with time-dependent DNA evolution [14-18], exhibited as stochastic mutations. Evolution data exhibited by T4 phage DNA [8,17,18] demonstrate that the two classes of time-dependent point lesion, G-C → G′-C′ & G-C → *G-*C, are consequences of hydrogen bond arrangements, keto-amino → enol-imine, by symmetric and asymmetric channels [18-20]. Product enol-imine protons are shared between two indistinguishable sets of electron lone-pairs and, thus, participate in coupled quantum oscillations (Figure 2) at frequencies of ∼1013 s−1. Observable long-term stability of coherent state G′-C′ and *G-*C sites [8,9,17,18] implies existence of decoherence-free subspaces [10,21-24] where coupled enol-imine protons are entangled and H2O is excluded [8,12]. Genetic specificity at a coherent superposition site—G′-C′, *G-*C (Figure 2) or *A-*T (Figure 3)—is stored as an input qubit, the quantum counterpart to the classical information bit [4]. Before decoherence [25], genetic specificities of coherent states are measured and processed by the transcriptase as an output qubit in an interval Δt ≪ 10−13 s, causing an additional entanglement between coherent protons and transcriptase components [9,26-28]. This entanglement ultimately yields an ensemble of decohered enol and imine isomers [8]—G′, C′, *G, *C (Table 1)—that participate in Topal-Fresco [29] substitution replication, i.e., G′2 0 2 → T, G′0 0 2 → C, *G0 2 00 → A & *C2 0 22 → T (see Figure 2 for notation).
However, coherent states within *A-*T sites are deleted. These time-dependent substitutions, ts, and deletions, td, contribute to the spectrum of stochastic mutations [14-18] and imply a modest evolutionary shift favoring A-T richness, consistent with observation [30]. Since T4 phage DNA systems are susceptible to (i) fine scale genetic mapping [31], (ii) reversion analysis [32,33] and (iii) strand analysis [8,18], an individual G′-C′ or *G-*C genetic site can be assayed at the resolution of the particular G′ or *C coherent state at the time of transcriptase measurement. Consistent with data [8,18], Figure 4 illustrates a “snap shot” of quantum information “seen by” the transcriptase viewing coherent states G′2 0 2, G′0 0 2 & *C2 0 22 and the keto-amino state, T22 0 22. In the case of *C on the template strand, the transcriptase deciphers genetic specificities of quantum states, *C2 0 22-*G0 2 00 ⇄ *C0 0 22-*G2 2 00, on the basis of measurements on the cytosine carbon-6 imine proton, which participates in coupled quantum oscillation (Figure 2f to g). Similarly in the G′ case, genetic specificities residing within quantum states, G′2 0 2-C′0 2 0 (Figure 2c) ⇄ G′0 0 2-C′2 2 0 (Figure 2b), are deciphered by coherent state measurements on the guanine carbon-6 enol proton. These quantum measurements of coherent states, *C2 0 22 and G′2 0 2, yield information corresponding to normal thymine, T22 0 22 (Figure 4), and consequently, phenotypically express substitutions, *C2 0 22 → T and G′2 0 2 → T, by transcription before replication [8,18]. Specificity determination by the transcriptase is independent of the proton or electron lone-pair at the “outside” position (in the major and minor groves) on keto, enol and imine groups (Figure 2). Otherwise, enol and imine groups on quantum states *C2 0 22 and G′2 0 2 could not simulate keto groups on T22 0 22 at transcription as observed. Also, this mode of determining genetic specificity is tolerant of gross structural dissimilarities between the dual ring purine, G′2 0 2, and single ring pyrimidines, *C2 0 22 & T22 0 22, as observed.
Transcriptase quantum processing [8-13] of coherent enol-imine states includes selecting particular decohered enol and imine isomers to participate in time-dependent substitutions, ts, or time-dependent deletions, td. The fact that mutation frequencies, G′2 0 2 → T & *C2 0 22 → T, phenotypically expressed via quantum transcription are identical to subsequent substitution frequencies, G′2 0 2 → T & *C2 0 22 → T, expressed as a consequence of Topal-Fresco replication of decohered isomers indicates that consequences of keto-amino → enol-imine arrangements are “hard wired” into the DNA code [8,9]. In these cases of G′2 0 2 → T and *C2 0 22 → T, transcriptase quantum processing specifies subsequent DNA replication substitution at G′ and *C sites. Otherwise one cannot explain how ∼100% of the expressed coherent state population, e.g., G′2 0 2, exhibited by transcription is subsequently decohered to form the complementary mispair, G′2 0 2–syn-A00 2 # (Table 1; Figure 5), all of which successfully participate in the G′2 0 2 → T substitution at replication [8,18]. The observed absence of reequilibration implies quantum entanglement participation [8,9]. In the next round of replication, coherent states and entanglement are absent, so ∼20% of imine *C2 0 22 exhibits reequilibration, *C2 0 22 → C00 2 22. Data [8,17,18] and the model [9-13] provide evidence that evolutionary pressures have selected quantum probability laws over laws of classical kinetics for (i) introducing time-dependent “point” genetic alterations, (ii) transcription of coherent states occupying decoherence-free subspaces and (iii) subsequent replication-substitution or deletion of selected decohered isomers. The present and previous reports [8-13] imply that the classical double helix of duplex DNA contains an embedded microphysical subset of hydrogen bonded protons and electron lone-pairs that (a) obey quantum probability laws and (b) govern time-dependent specificity of DNA information. These evolutionarily acquired quantum mechanisms for operating microphysical genetic systems imply gains in evolutionary advantages. Enhanced advantages include (A) possibilities of favorable population responses to changing environmental conditions and, concomitantly, (B) mechanisms of protecting the gene pool against acquiring unsafe levels of mutation [8,13,34]. As a consequence of identifying quantum origins of stochastic mutations, ts + td, a quantum Darwinian evolution model is developed that simulates manifestation of cancer as a function of intrinsic DNA instability [35], and further, implies a quantum mechanism for evolutionary extinction.
Based on molecular genetic data [8,14-18] and the attendant model [9-13], genetic specificity within a DNA base pair is dependent on states of hydrogen-bonded DNA protons, which are allowed the possibility of transitioning through a cycle of physical states. This sequence of proton states can be visualized in terms of qualitative terminology: classical amino → unperturbed coherent quantum entangled (enol-imine) → transcriptase quantum entanglement → entanglement-decoherence → decohered isomer → classical amino. This model is a combination of the Löwdin [19] and Topal-Fresco [29] models, referred to as the LTF model, where consequences of entanglement are included. The next section identifies available genetic information as a function of hydrogen bonded proton states. Section 3 discusses molecular genetic observations requiring quantum theory for explanations. This is followed by introducing a two qubit model for coupled enol-imine proton oscillations created by quantum uncertainty limits on metastable amino protons. Section 5 develops a quantum Darwinian evolution model for time-dependent DNA instabilities. The model simulates incidence of cancer data and implies insight into evolutionary extinction. The final section contains the discussion. The Appendix develops an approximate quantum model for keto-amino → enol-imine arrangement.
2. Biological Information as a Function of Proton States: Classical Amino → Coherent Entangled Enol-imine → Transcriptase Entanglement → Decoherence-Entanglement → Decohered → Classical Amino
Consistent with evolutionary design, standard replication creates metastable, complementary keto-amino DNA base pairs where quantum uncertainty limits operate on amino DNA protons. The physical state of hydrogen bonded DNA protons plays a significant role in determining the nature of genetic information available to the biological system. The different hydrogen bond DNA proton environments at G-C sites are first (i), after replication, keto-amino protons are subjected to quantum uncertainty limits which introduces a probability of keto-amino → enol-imine arrangement via symmetric or asymmetric channels (Figures 1 to 2). Second (ii), unperturbed and entangled enol-imine hydrogen bonded protons participate in coupled quantum oscillations between near symmetric double minima at frequencies of ∼1013 s−1 (Figure 2). Third (iii), the transcriptase implements its measurement on coherent protons, generating an output qubit of genetic specificity. Forth (iv), an entanglement state is created between coherent protons and transcriptase components. Fifth (v), an enzyme-entanglement participates in creating complementary Topal-Fresco mispairs (Table 1; Figure 5) consisting of non-reequilibrated enol and imine isomers, G′, C′, *G, & *C. Sixth (vi), entanglement ultimately generates a decoherent transition from quantum to classical, which allows non-reequilibrated enol and imine isomers to form complementary mispairs that are incorporated as ts. Seventh (vii), in the next round of replication, quantum coherence and entanglement are absent; so, reequilibration is allowed and keto-amino states are replicated into DNA.
As a consequence of transcriptase quantum processing of coherent states at G′-C′ and *G-*C sites, an entanglement is created between coherent protons and transcriptase components. This entanglement state is evidently responsible for recognizing an initially “measured” quantum state (e.g., G′2 0 2) and preserving this particular state and information through its decoherent transition, i.e., G′2 0 2 (coherent) → G′2 0 2 (decohered isomer). After transcriptase quantum processing within an interval Δt ≪ 10−13 s [8,9], the initial round of replication involves the formation of complementary mispairs [8,18,29], e.g., G′2 0 2-syn-A00 2 # (Table 1; Figure 5b), between an entanglement preserved decohered enol-imine isomer (e.g., G′2 0 2) and, in this case, syn-A00 2 #. In the absence of entanglement between coherent G′2 0 2 protons and transcriptase components, the originally transcribed G′2 0 2 state would be exposed to H2O. This would cause decoherence and introduce reequilibration, i.e., G′2 0 2 (enol-imine) → G22 0 00 (keto-amino). In fact, observation [8] shows that ∼100% of quantum processed coherent G′2 0 2 and *C2 0 22 states subsequently contribute—in their decohered isomer form—to the replication-substitution step required for finalizing molecular clock substitutions, ts. In the absence of entanglement protection of enol and imine states, the observed ts—G′2 0 2 → T, *C2 0 22 → T, G′0 0 2 → C, *G0 2 00 → A—would be at classical background levels governed by reequilibration, thereby eliminating detection of a time-dependent molecular clock [8,13,14,18]. These data further imply that enzymes responsible for quantum information processing of coherent states also participate in replicating particular ts. As noted, in the second round of replication after transcriptase quantum processing, coherent states and entanglement are absent. This allows ∼20% of imine *C2 0 22 to exhibit reequilibration [8].
Metastable keto-amino duplex DNA implies the arrangement, keto-amino → enol-imine, and subsequent ts + td (stochastic mutations) should be observable in human DNA systems. Hwang and Green [13] have clearly shown that mammalian DNA exhibits time-dependent, replication independent molecular clock events, CpG → TpG substitutions, at the DNA level. The terminology, “CpG substitutions”, indicates C → T and/or G → A substitutions at a CpG site. Time-dependent CpG substitutions are the most frequent point mutation observed in the human genome and the rate is ∼15-fold greater when cytosine is methylated [16]. Since replicated keto-amino DNA duplex is metastable [8-13] and the observed CpG substitutions, C → T and G → A [14,16], are two of the four time-dependent substitutions exhibited by the high resolution T4 phage DNA system (i.e., also, G2 0 2 → T and G′0 0 2 → C), the argument is made that a significant component of CpG substitution is a consequence of keto-amino → enol-imine arrangements, which are ultimately replicated as ts + td stochastic mutations [15]. A consequence of methylated cytosine (at carbon-5) is an enhancement of quantum uncertainty limits on cytosine −NH2 protons, i.e., −NH2 - - H3C−From the uncertainty relation, Δx Δpx ≥ ½ ħ, amino proton momentum can be expressed, approximately, as p ≈ ħ/Δx; so, proton kinetic energy can be approximated by mv2/2 = p2/2m = ħ2/[2m(Δx)2]. However additional proton-proton interactions, −NH2 - - H3C−, would increase the probability of confining cytosine amino protons to too small of space, Δx. This would create more energetic cytosine amino (−NH2) protons which would enhance the rates of keto-amino → enol-imine via the asymmetric channel, introducing C → *C → T and G→ *G → A as observed [8,16-18]. Thus the ∼15-fold increase in CpG → TpG when cytosine is methylated is consistent with the quantum origin of ts. Also Elango et al. [16] note that vague mechanisms responsible for inserting H2O between DNA strands are invoked if time-dependent CpG → TpG [14] events are explained in terms of hydrolytic deamination of cytosine.
Observations consistent with quantum origins of stochastic mutations, ts and td, include (i) the prediction of a modest evolutionary shift favoring A-T richness [14]. Second (ii), when G′ or *C is on the template strand, mutation frequencies, G′ 2 0 2 → T & *C2 0 22 → T, phenotypically expressed by quantum transcription—before replication—are identical to subsequent frequencies, G′2 0 2 → T & *C2 0 22 → T, exhibited as consequences of genotypic incorporation by replication from decohered isomers. This implies participation of quantum entanglement [10,26-28]. In the next round of replication, quantum coherence and entanglement are absent; so, ∼20% of imine cytosine (5HMC), *C2 0 22, exhibits reequilibration, *C2 0 22 → C00 0 22. This eliminates deamination of cytosine as the mechanism responsible for these time-dependent C00 2 22→ *C2 0 22 → T events [8,17]. Third (iii), quantum processing by the transcriptase explains how enol and imine groups on quantum states G′2 0 2 and *C 2 0 22 can simulate keto groups on normal T22 0 22 at transcription, as observed [8,9]. This mode of determining specificity distinguishes the quantum state G′2 0 2 (G′2 0 2 → T) from quantum state G′0 0 2 (G′0 0 2 → C) and is tolerant of gross structural dissimilarities between the dual ring purine, G′2 0 2, and the single ring pyrimidines, *C2 0 22 and T22 0 22, as observed [8,9]. Forth (iv), the fact that the yield of G′2 0 2 → T is ∼3-fold (rather than 2-fold) greater than G′0 0 2 → C is explained by arguments that the duplex quantum state, G′2 0 2-C′0 2 0 (Figure 2c), is “preferred” compared to the duplex quantum state, G′0 0 2-C′2 2 0 (Figure 6). Fifth (v), the ∼15-fold increase in CpG → TpG rates when cytosine is methylated is consistent with quantum expectations for increased proton-proton interactions, −NH2 - - H3C−, causing enhanced reaction rates, C00 2 22 → *C2 0 22 → T, via the asymmetric channel. Since time-dependent CpG substitutions are the most frequent point mutation observed in the human genome [16], these CpG → TpG events should contribute to the stochastic mutation spectrum in Equation (18). However, deamination of cytosine disallows the quantum mechanical term, βt, in Equation (13). Thus, deamination of cytosine is not in agreement with a model, Equation (18), which satisfies data, Figure 7 [35]. Also the facts that (a) after *C2 0 22 → T, imine *C2 0 22 exhibits reequilibration, *C2 0 22 → C00 2 22, in the second round of growth [8] and (b) mechanism for inserting H2O between DNA strands exhibit difficulties [16] argue against deamination of cytosine as the mechanism responsible for time-dependent CpG → TpG [13]. Additionally, the extensive investigation by Ripley [17] could not identify evidence supporting deamination of cytosine (5HMC) as the mechanism responsible for the time-dependent substitution, C → *C → T. Sixth (vi), the time-dependent substitutions observed at a mammalian CpG site, C → T and/or G → A, represent 50% of coherent state ts exhibited by the higher resolution T4 phage DNA system, i.e., also G′2 0 2 → T, G′0 0 2 → C and *A-*T → deletion [8,9]. These six observations are consistent with quantum uncertainty limits operating on metastable amino DNA protons, which drive the arrangements, keto-amino → enol-imine, thereby populating accessible lower energy enol- imine coherent states, G′-C′, *G-*C and *A-*T (Figures 1 to 3). Since the wave function for coherent enol-imine protons cannot be expressed as a tensor product, these protons are entangled [27,28]. Subsequent transcriptase quantum processing introduces a new entanglement between coherent protons and transcriptase components. Ultimately this entanglement yields decohered enol and imine isomers that are replicated as ts and td, which contribute to the spectrum of stochastic mutations [8-18].
3. Explicit Evidence Exhibiting Quantum Information Technology by a Biological System
3.1. Multiple Genetic Specificities Exhibited by a ‘Point’ Mutation G′ Site
Time-dependent transversions originate at G′-C′ sites [8,17,18] where a complementary duplex contains a superposition of four quantum states illustrated in Figure 2b-e. In the case of rUV74 rII → r+ transversion revertants, G′ is on the T-strand. Data demonstrate that 350 of the 460 (76%) revertants detected express G′2 0 2 →T as a consequence of transcription before replication was initiated, but 110 of the 460 (24%) revertants required replication (passage) to express G′0 0 2 → C. In this case, genetic specificities originating within quantum states, G′2 0 2-C′0 2 0 (Figure 4b) ⇄ G′0 0 2-C′2 2 0 (Figure 4d), are deciphered by the transcriptase on the basis of different coherent states for the guanine carbon-6 enol proton, which participates in coupled quantum oscillation. State G′0 0 2 communicates that it is not a transcription analog of C00 2 22 or T22 0 22; so, passage (replication) is required for expression of the G′0 0 2 → C substitution, which involves Topal-Fresco replication of the complementary mispair, G′0 0 2-syn-G22 2 # (Figure 5), to insert normal C00 2 22. Compared to state G′0 0 2, expression of state G′2 0 2 was enhanced by a single round of transcription before replication was initiated. After transcription and before replication, the template quantum state, G′2 0 2, was not subjected to H20 and reequilibration, but was preserved by entanglement between coherent protons and transcriptase components. Additionally, all decohered G′2 0 2 isomers formed complementary mispairs, G′2 0 2-syn-A00 2 # (Table 1; Figure 5), required for the G′2 0 2 → T substitution resulting from Topal-Fresco replication. Given these two conditions, straightforward analysis predicts the number of G′2 0 2 → T events should be ∼2-fold greater (after passage) than the number of G′0 0 2 → C events. However observation shows G′2 0 2 → T (76%) is ∼3-fold more numerous than G′0 0 2 → C (24%). Since the quantum state G′2 0 2 is “preferred” compared to state G′0 0 2 (Figure 6; Section 3.2), this would cause an enhanced availability of quantum G′2 0 2 at transcription and a corresponding increased yield of the decohered G′2 0 2 isomer at replication, which would explain the greater than expected yield, i.e., 3-fold rather than 2-fold, of G′2 0 2 → T compared to G′0 0 2 → C.
3.2. Consequences of the “Favored Status” for the Quantum State, G′2 0 2
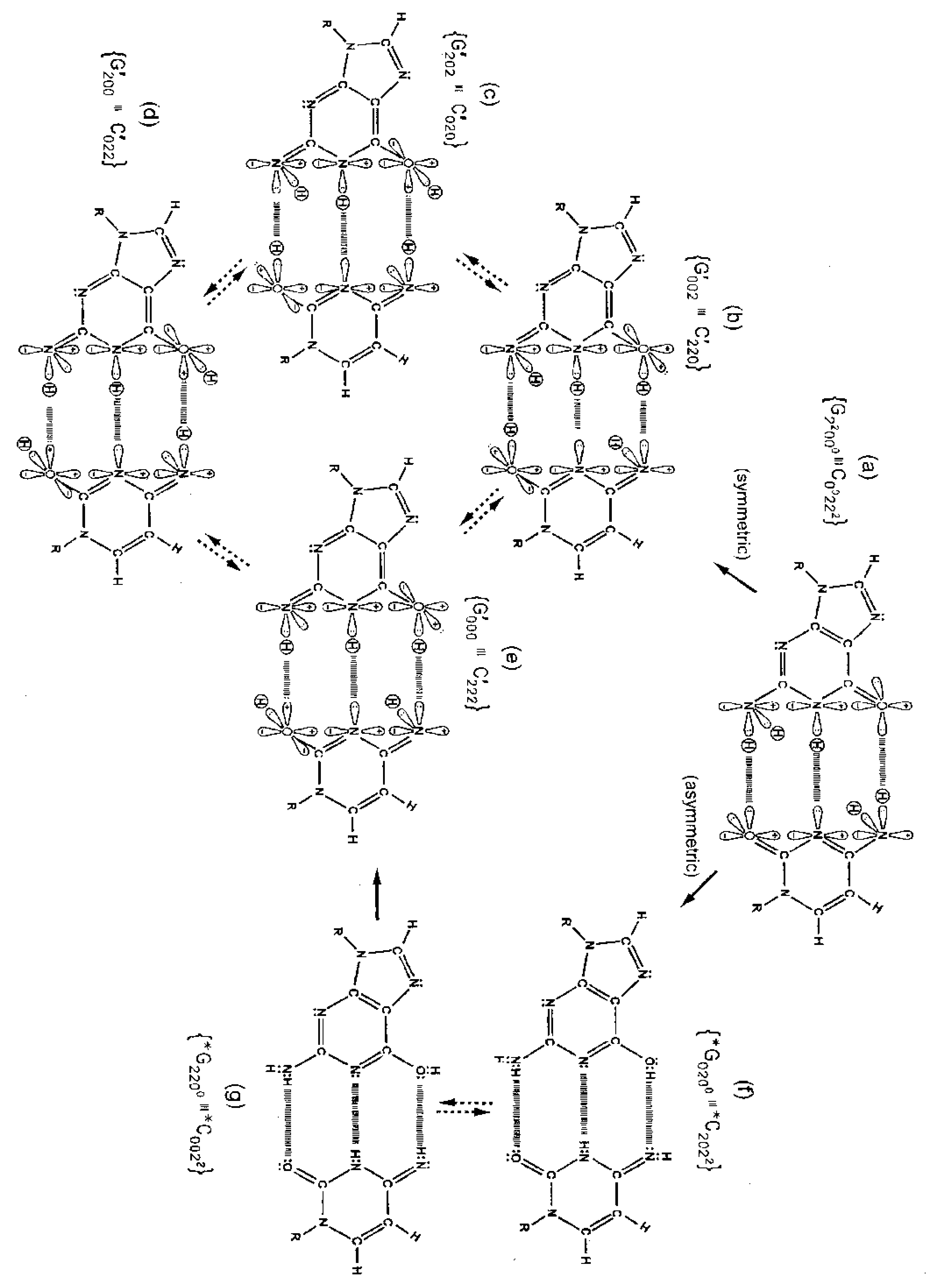
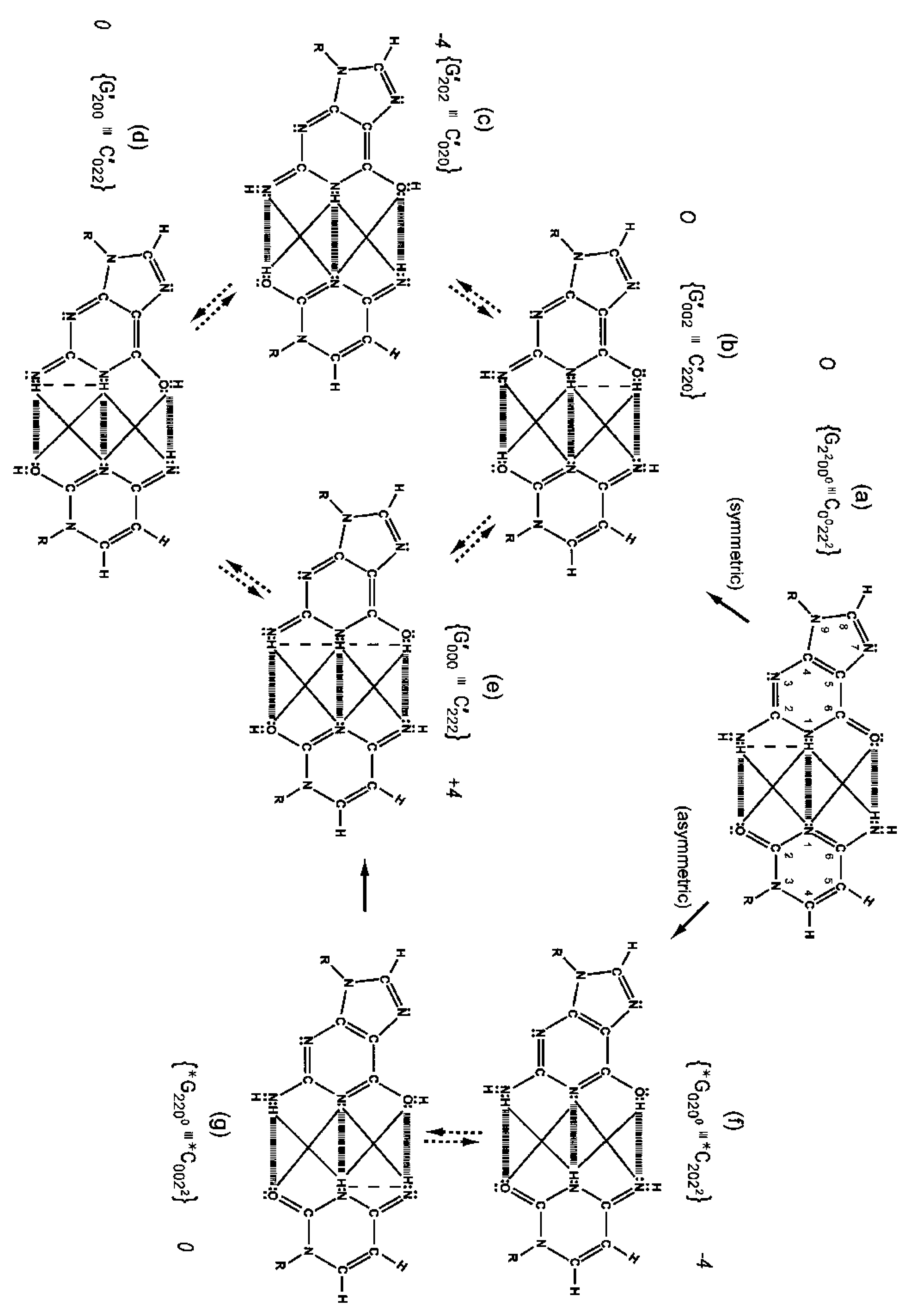
Although quantum proton oscillations are the order of ∼ 1013 s−1 [9,10], the relative distribution of quantum duplex G′-C′ states can be qualitatively estimated, using Jorgensen's model [36,37] for secondary electrostatic interactions within a superposition of complementary duplex states. This is illustrated in Figure 6 where the duplex state G′000–C′222 (Figure 6e) exhibits the maximum intramolecular proton-proton repulsion and thus is the least preferred configuration. This state is identified by an energy pairing value of +4. The preferred states exhibit the minimum intrabase proton-proton repulsion interactions and are identified in Figure 6c, 6f These preferred configurations yield energy pairing values of −4. Since the G′2 0 2-C′0 2 0 duplex (Figure 6c) is a favored “relaxed” configuration compared to G′0 0 2-C′2 2 0 (Figure 6b), this would cause an enhanced availability of quantum G′2 0 2 at transcription and a corresponding increased yield of the decohered G′2 0 2 isomer at replication, which would explain the greater than expected yield, i.e., 3-fold rather than 2-fold, of G′2 0 2 → T compared to G′0 0 2 → C. This observation implies that local electric and magnetic fields and currents created by coherent enol-imine protons (Figure 4) may allow “delicate”, evolutionarily designed information processing by transcriptase measurements of genetic specificities on, e.g., G′2 0 2 and G′0 0 2. Note that quantum duplex states G′2 0 2-C′0 2 0 (Figure 6c) and *G0 2 00-*C2 0 22 (Figure 6f) are the only “preferred” configurations in Figure 6. Additionally quantum states, G′2 0 2 and *C2 0 22, are each transcribed as normal T22 0 22 and, therefore, are responsible for the 2-fold “transcription enhancement” of mutation, G′2 0 2 → T and *C2 0 22 → T [8]. Evidently this is a component of the time-dependent evolutionary scheme favoring A-T richness [8].
4. Transcriptase Measurement of Entangled Proton Bonds at G′-C′ Sites
The symmetric keto-amino → enol-imine arrangement converts the two standard keto-amino G-C hydrogen bonds into two sets of coupled two-level enol-imine proton bonds where the four coherent enol and imine protons “participate equally” in coupled quantum oscillations between the eight available sets of near symmetric electron lone-pairs, illustrated in Figure 2b to 2e. The transcriptase implements its measurements from the T-strand orientation and deciphers information from the distribution of coherent states exhibited by enol-imine proton bonds at the carbon-6 and carbon-2 side chain positions of a G′-C′ duplex (Figure 2). Quantum measurements by the transcriptase ultimately transform this information into observable biochemical instruction, e.g., G′2 0 2 → T versus G′0 0 2 → C. The fact that transcriptase measurements on coherent G′-C′ states yield decohered observable results that are in qualitative agreement with the distribution of G′-C′ states predicted by Jorgensen's [36,37] model (Figure 6) implies the transcriptase “reads”, processes and executes information derived from coupled coherent protons states within an interval, Δt ≪ 10−13 s.
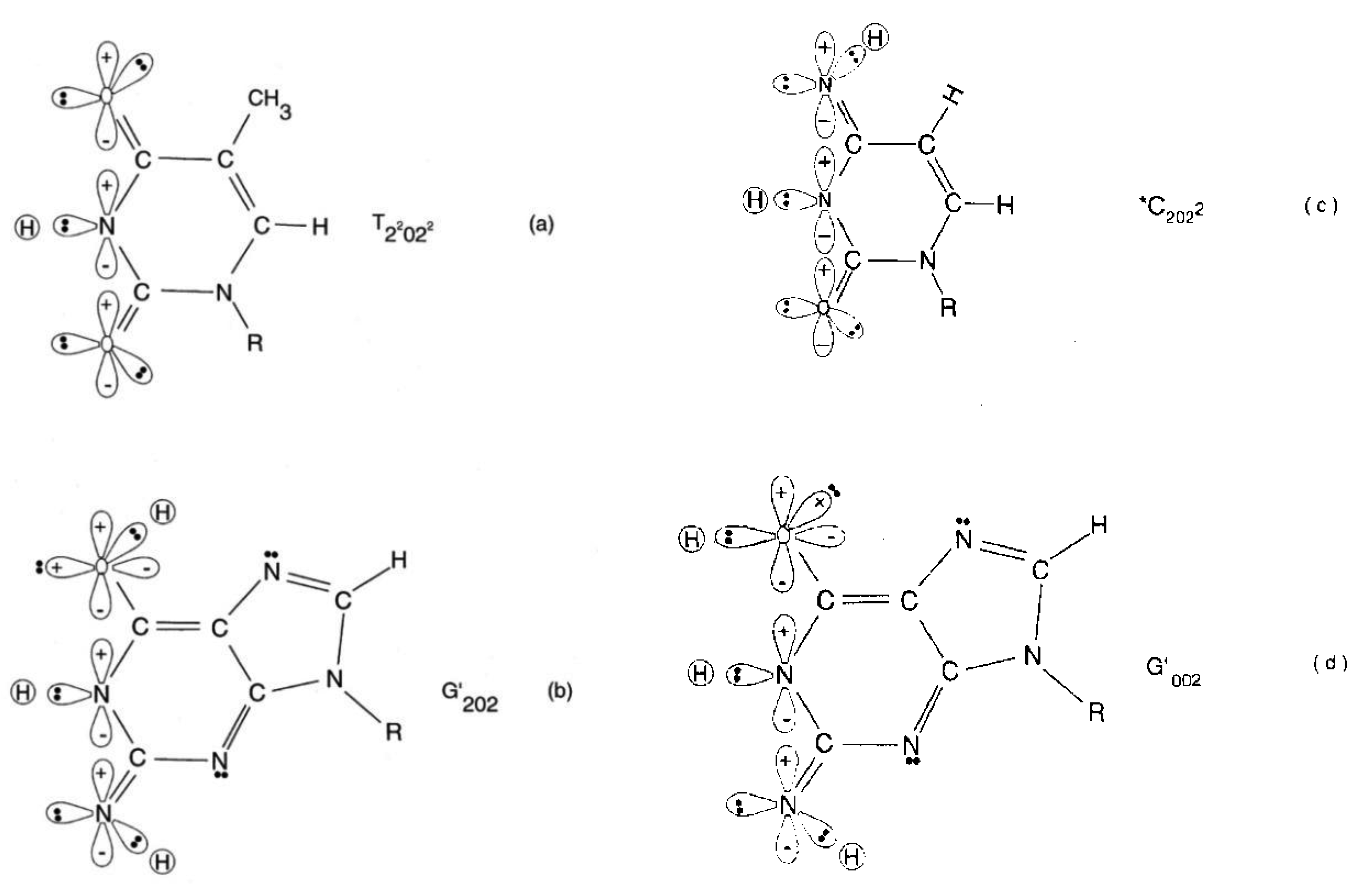
The quantum state of the enol-imine proton bond at the G′-C′ carbon-6 side chain is taken as state |+ − > when the enol proton on G′ is positioned to participate in interstrand bonding and is in state |− + > when this enol proton is “outside”, in the major or minor grove. In this notation, the second symbol in state | + − > identifies the “ −” or “+” quantum state of the coupled imine C proton in the carbon-6 side chain proton bond. Similarly, the imine-enol proton bond at the G′-C′ carbon-2 side chain is in state | + − > when the imine proton on G′ is positioned to participate in interstrand bonding and is in state | − + > when this imine proton is “outside”, in the major or minor grove. The proton bonds at the carbon-6 and carbon-2 side chains can each be described in terms of two quantum states, | + − > and | − + >. In this discussion, state | + − > is taken as | g > and state | − + > is defined as | c >. These two states obey the relation, < g | c > = δgc, and provide a computational basis for the carbon-6 and carbon-2 side chain proton bonds, hereafter identified by b6 and b2, respectively.
Coherent enol-imine proton bonds at a G′-C′ site constitute two subspaces, εx(6) and εx(2), of the combined space, εx. Other pure states of the proton bond can be expressed as a superposition, α| g > + β| c >, for some α and β where | α|2 +| β|2 = 1. The position states of proton bond b6 form a two-dimensional subspace εx(6), and likewise, the position state of proton bond b2 is defined by a ket belonging to a two-dimensional state space, εx(2). The position observables of b6 and b2 are designated by x6 and x2, respectively. In εx(6) and εx(2), the basis eigenkets of x6 and x2 are designated by | 6: g >, | 6: c> and | 2: g >, | 2: c >. The general ket of εx(6) can be written as
This yields the following ket notation as
Also the system of vectors in Equation (4) satisfy a closure relation in εx given by
A ket of εx can be constructed in terms of an arbitrary ket of εx(2) and an arbitrary ket of εx(2) given by
The components of Equation (7) in the basis of Equation (4) are the products of | χ(6) > and | ζ(2) > in the bases of εx(6) and εx(2), which were used to construct Equation (4). However, not all kets of εx can be expressed as tensor products. The most general ket of εx is an arbitrary linear combination of the basis vectors given by
Given Equation (8) describes the four-state G′-C′ (Figure 2b to 2e) superposition system just before transcriptase measurement, one can express the probability of finding the system in each of its states. For example, the probability of the system being in state G′0 0 0-C′2 2 2 as assayed by transcriptase measurement is expressed as
Similarly, the probabilities of the system being in states G′0 0 2-C′2 2 0, G′2 0 0-C′0 2 2 and G′2 0 2-C′0 2 0 are given respectively by
Observables yielded by transcriptase measurements, e.g., |< − + − +|ψ >|2 = |δ|2 and |<+ − − +|ψ >|2 = |β|2, are in qualitative agreement with the distribution of G′-C′ states predicted by Jorgensen's [36,37] model shown in Figure 6. The relative contribution of the “preferred” state, G′2 0 2-C′0 2 0, is quantified by |δ|2, which is observed as the no. of G′2 0 2 → T events. Observation shows that |δ|2 is ∼3-fold, rather than 2-fold, > |β|2, which is consistent with Figure 6. Data and Figure 6 imply that |β|2 ≈ |γ|2, which provides the relation |δ|2 = 3|β|2 = 3|γ|2. These values in the normalization expression yield |α|2 = −2/9, so .The condition, α/β = γ/δ, is not satisfied by these values for α, β, γ & δ, indicating Equation (8) cannot be expressed as a tensor product of |χ (6) > and |ζ(2) >; so, Equation (8) is the form for entangled enol-imine proton states. Since the transcriptase reads G′2 0 0-C′0 2 2 as normal G22 0 00-C00 2 22, the condition that |β|2 ≈ |γ|2 could also be determined from clonal analysis [17]. Decohered observables from transcriptase measurements yield the relative distribution of quantum duplex G′-C′ states at time of measurement, which are in qualitative agreement with Figure 6 predictions.
Consistent with an embedded microphysical subset designed to store and expresses quantum information, coherent states in duplex DNA are introduced into decoherence-free subspaces as consequences of quantum uncertainty limits on “metastable” amino DNA protons. Before decoherence, these states are measured by a transcriptase “quantum reader”. Molecular genetic data [8,14] in terms of quantum theory suggest that complementary C′-state protons and electron lone-pairs could be “ replaced by” an active transcriptase site that simulates C′-contributions in the G′-C′ duplex. This would allow the evolutionarily designed transcriptase system to identify, process and preserve the particular quantum distribution of coherent G′-states, which is ultimately decohered into non-reequilibrated enol and imine G′-isomers suitable for Topal-Fresco replication-substitution. Evolutionarily selected decohered enol and imine isomers participate in particular time-dependent base substitutions, ts,—G′2 0 2 → T, G′0 0 2 → C, *G0 2 00 → A, *C2 2 22 → T—and deletions, td, *A-*T → deletion. Consistent with observation [8,14], the quantum molecular clock [13] implies a modest evolutionary shift in A-T richness. Additionally, the quantum Darwinian evolution model, Section 5, predicts time-dependent increases in stochastic mutations, i.e., ts + td, which satisfy incidence of cancer data, Figure 7. The evolutionarily selected quantum mechanisms responsible for generating coherent G′-C′ & *G-*C states and decohered enol and imine isomers further employ a process of disallowing reequilibration before the initial round of replication. If re-equilibration were allowed, quantum contributions to the molecular clock—Σj (βj/12) t4 terms in Equation (18)—would not be allowed, which is inconsistent with observation [8,13,14]. Therefore the selected quantum processes responsible for exhibiting a time-dependent molecular clock include a “ protection mechanism” which is assumed to involve contributions by quantum entanglement states. These apparent entanglements between coherent protons and transcriptase components play a central role in forming decohered, complementary mispairs (Table 1) responsible for genotypic Topal-Fresco substitution-replication. Evolutionary pressures at the quantum level have selected effective mechanisms for implementing quantum information processing at biological temperatures. Coupled entangled enol-imine states contributed by both DNA strands would enhance quantum stability and, thus, improve the accuracy of transcriptase quantum processing. Further study of this evolved qubit system may provide insight into the dynamics of avoiding decoherence [21-25] and an improved understanding of entanglement [5,26-28] and the transition from quantum to classical.
5. Quantum Instabilities in Genetic Specificities Imply a Quantum Darwinian Evolution Model for Origin of Tumors
5.1. Polynomial Expression
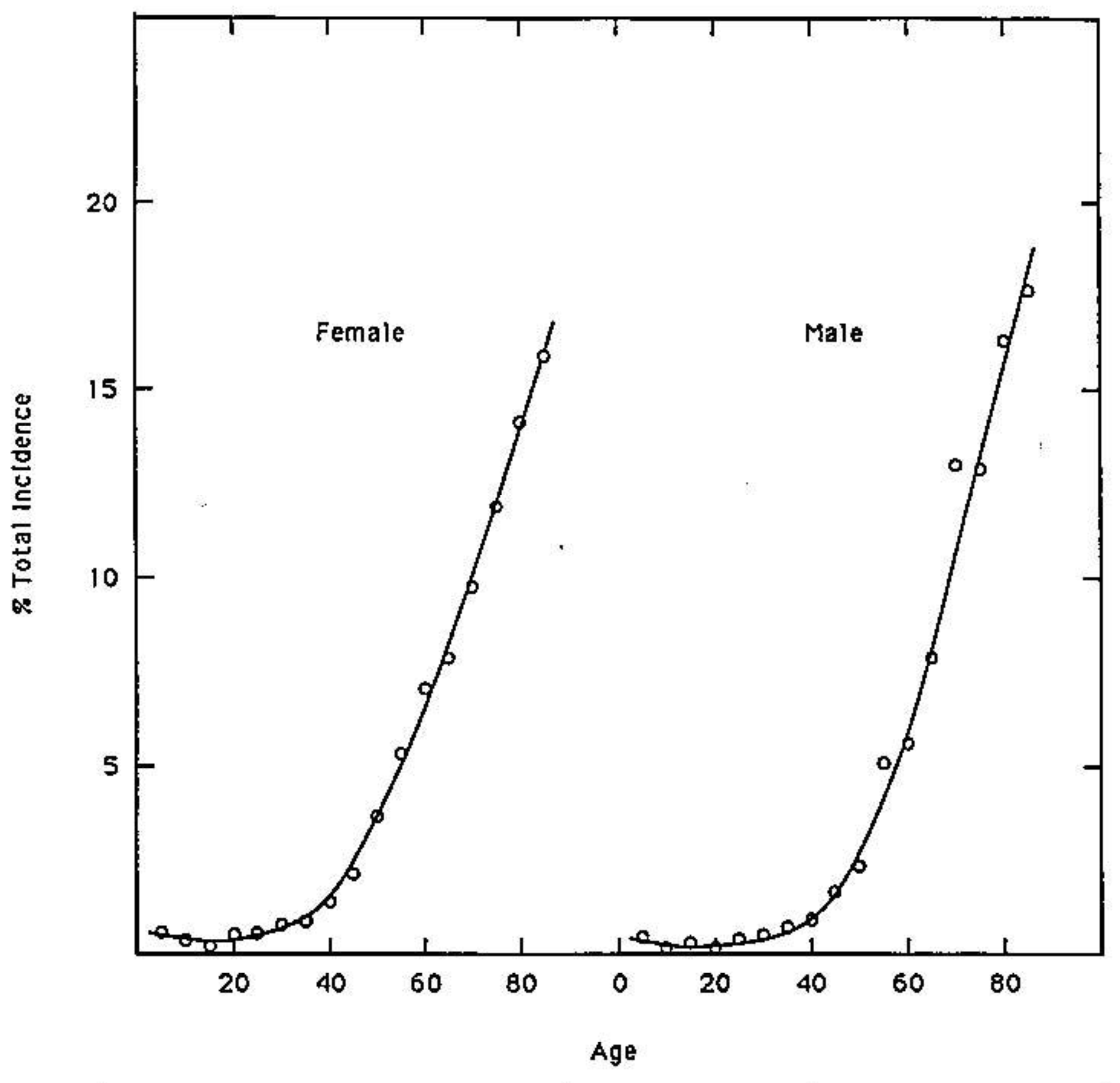
Quantum uncertainty limits [38] operating on amino DNA protons in metastable keto-amino base pairs introduce arrangements [8-13], keto-amino → enol-imine (Figure 2), consistent with evolutionary design. This implies an evolutionary origin of cancer hypothesis [39-41] where particular sensitive genes, e.g., oncogenes & tumor suppressor genes [15,42], have been selected to participate in species preservation by removing from the gene pool those genomes that have accumulated unsafe levels of ts + td, which are consequences of keto-amino → enol-imine arrangements. These genes containing sensitive “genetic domains” are referred to as “ p53-type” genes. Data in Figure 7 exhibit the average percentage total incidence of all 74 classifications of class 1 tumors (those with a single incidence peak at age > 50 year) classified by the Connecticut Tumor Registry between 1968 and 1972 [35]. These data illustrate increasing incidence of cancer in populations of advancing age. The hypothesis [39] that cancer is an inevitable part of evolution is consistent with observations [14] that multiple stochastic mutations [16,43] are responsible for the final conversion to malignancy in colorectal cancer [15]. In fact, detailed mechanisms of stochastic mutations [8-13] imply that age-related degenerative diseases, including cancers, are evolutionarily implemented as consequences of stochastic mutations revealing contents of “latent” genetic information. Expression of “latent” genetic information, e.g., K-ras or p53 containing a threshold level of stochastic mutations, can be manifested as a lethal cancer [15,42], consistent with protecting the gene pool against unsafe levels of mutation [8,34]. Since molecular genetic observations of time-dependent mutations require quantum coherence [8,18] and quantum chemical calculations identify keto-amino duplex DNA as metastable [9-13], Figure 7 data imply time-dependent genetic consequences [14,15]. In particular, a mathematical relationship is implied for phenotypic expression of cancer as a function of time-dependent alteration of genetic specificities in a normal target domain of “p53-type” genes, g. This model considers M individuals (M ≥ 100,000)—the population—who have inherited a normal target domain of “p53-type” genes. Since experimental lifetimes of metastable keto-amino states at 37 °C are ≥ ∼3000 year [9], approximate quantum methods for small times, t < ∼100 year, yield the probability, P(t), of keto-amino → enol-imine arrangements as Pρ(t) = ½ (γρ/ħ)2 t2 where γρ is the energy shift between states (see Appendix). The time derivative of biological noise, dN/dt, accumulating in the particular gene, g, can be expressed as
Here λ is the classical constant mutational load discussed by Muller [44] and β = (γ/ħ)2, which is the proportionality constant for the keto-amino → enol imine arrangement. A general expression for the total biological noise, N(t), in all M individual genes, g, in the population at age t is given by
This model assumes that target gene g can—as a consequence of accumulating an evolutionarily defined level of alterations in genetic specificities—be “converted” into a disease producing mode. The time rate of change of converted target genes, dg(t)/dt, is proportional to the total number of ts + td in the relevant genetic domain plus generation dependent mutations contained in all M genes, g(t), in the population at age t. This is given by
5.2. Model Implications and Evolutionary Consequences
Certain “class 2” tumors (e.g., bone, lymphatic leukemia, testis and Hodgkin‘s disease) exhibit high incidence peaks at age < 35 and a second peak at age > 50. Also several childhood cancers exhibit high incidence peaks at ages < 10 [35]. In situations where the inherited “p53-type” gene contained genetic sites previously populated by ts + td, the remaining “genetic space” for occupancy by ts + td would be reduced; so, high incidence peaks could be exhibited for ages < 10 or ages < 35 y. However if the “p53-type” gene were populated by ts + td to its threshold limit at time of conception, the model implies spontaneous abortion would be a consequence; so, g0 = 0 in Equation (18). This argument implies the available “genetic space”, s, associated with a “p53-type” gene satisfies the inequality, normal ≥ s ≥ threshold. Thus an inherited “p53-type” genetic domain would contain a variable “genetic space”, s, for occupancy by ts + td before achieving the threshold limit. Since mean lifetimes, τ, for the metastable state are ∼3000 year [9], at age 100 year approximately 3% of the G-C + A-T sites would be occupied by ts + td. This implies a relationship between normal and threshold. If normal is identified as 100% free of ts + td, then the threshold can be approximated by threshold = normal − 3%. The genetic space inequality can thus be rewritten as 1 ≥ s ≥ 0.97. As the available inherited genetic space, s, approaches the threshold limit in subsequent generations, smaller times are required for ts + td to populate s such that the threshold limit is achieved, s ≈ 0.97 + ε. In this situation, future generations would exhibit high incidence peaks at early ages, e.g., ages < 39 year [45]. The pre-35 high incidence peaks are considered consequences of individuals inheriting sensitive “p53-type” genes that had been previously populated by ts + td beyond the normal limit. Perturbations that introduced larger β values into Equation (18) would contribute to enhanced background “genetic noise”, responsible for additional ts + td The observed ∼70% increase in stomach cancer among white males, ages 25 to 39 year, over three decades, 1977 to 2006 [45], implies these genetic thresholds were populated by ts + td to their allowed limit at early ages. This could be a consequence of avoidable, but “additional”, external perturbations. For example, consumption of excessive carbonated beverages could cause increases in energy density of “local” DNA, thereby enhancing rates of populating a “genetic space”, s, with ts + td. Cancers that exhibit high incidence peaks for ages < 39 year can be reevaluated for their origin in terms of the particular “p53-type” gene and contributions by N0t2, λt3 and βt4 terms in Equation (18). Application of Equation (18) appears to provide an additional “tool” for assessing origins of specific cancers. This could assist in identifying and implementing “new” cancer prevention strategies, for example, including protocols for avoiding increases in energy density of DNA. Consistent with Equations (13) to (18) and Figure 7, the model implies the development of new software for predicting probabilistic times required for a particular “genetic space”, s, to become populated by ts + td to its evolutionarily allowed limit, which is manifested as phenotypic expression.
Based on observations [46,47], a restricted “genetic space”, s, inequality, 0.976 ≥ s ≥ 0.970, is inherited by the human pygmy genome. The normal human pygmy exhibits puberty at age 5, menopause at age 11 and age-related degenerative diseases at age ≥ 16, where lifespan is ≤ 26 year [46,47]. The “genetic space” quantum model implies that sensitive “genetic switches” responsible for human puberty, menopause and age-related degenerative diseases are all operated by evolutionarily selected keto-amino → enol-imine arrangements populating a particular “genetic space” to its evolutionarily defined threshold. At age 5 year, stochastic mutations would have populated a particular “genetic space” to its threshold limit which initiates puberty; so, growth in pygmy height ceases by age 7. The “compressed” pygmy lifecycle implies that the human pygmy “genetic space”, s, is (a) ∼80% occupied at conception, or (b) the “space” presents a larger cross section of metastable G-C + A-T sites, which would allow coherent states to populate the relevant space in a smaller time interval. DNA sequence evaluations of genes, e.g., p53 and K-ras, from Homo sapien and human pygmy genomes could distinguish these possibilities and provide insight into conditions responsible for time-dependent genotypic origin of cancer. When the inherited “genetic space”, s, becomes the order of s ≈ 0.970 + 2ε, evolutionary extinction is implied. The model appears to be applicable to Homo sapien and human pygmy genomes and offers an explanation for the disappearance of Neandertals after existing for ∼350,000 y [48].
6. Discussion
Consistent with experimental [8,18] and theoretical [9-14] evidence, this report implies that the classical double helix of duplex DNA contains an embedded microphysical subset of hydrogen bonded protons and electron lone pairs that (a) obeys quantum probability laws and (b) governs time-dependent specificity of DNA information. An evolutionarily designed “quantum reader”, the transcriptase, deciphers information contained within coherent states occupying this microphysical subset. Data [8,14-18] and the model [9-13] provide evidence that evolutionary pressures have selected quantum probability laws over laws of classical kinetics for (i) introducing time-dependent “point” genetic alterations, (ii) transcription of coherent states occupying decoherence-free subspaces and (iii) subsequent replication-substitution or deletion of selected decohered isomers. This provides a rationale for the selection of metastable keto-amino complementary pairs as the initial state of duplex DNA. In particular, quantum uncertainty limits operate on amino DNA protons to drive the keto-amino → enol-imine arrangement at a rate consistent with DNA evolution [8,14,16-18], thereby populating accessible enol-imine coherent states of reduced energy. Product enol-imine protons are entangled and participate in coupled quantum oscillation at frequencies of ∼ 1013 s−1 between two indistinguishable sets of electron lone-pairs. Before decoherence, genetic specificities of each superposition duplex DNA state are measured by the transcriptase within an interval, Δt ≪ 10−13 s. This quantum measurement creates an additional entanglement between coherent protons and transcriptase components, which prevents immediate reequilibration and ultimately yields an ensemble of decohered enol and imine isomers that participate in Topal-Fresco substitution-replication, i.e., G′2 0 2 → T, G′0 0 2 → C, *G0 2 00 →A & C2 0 22 → T. However, coherent states within *A-*T sites (Figure 3) are deleted. These time-dependent substitutions, ts, and deletions, td, contribute to the spectrum of stochastic mutations [15,43].
The transcriptase is a ‘quantum reader’ that can identify the relative distribution of coherent states measured at a duplex G′-C′ site. Just before transcriptase measurement, the distribution of quantum G′-C′ states is described by Equation (8), |ψ > = α|+ − + − > + β| + − − + > + γ|− + + − > + δ|− + − + >. As a result of transcriptase measurement on the G′-C′ superposition, three of the four G′-C′ states yield a corresponding decohered molecular genetic observable. For example, the probability of G′-C′ being in state G′2 0 2-C′0 2 0 is given by |<− + − +|ψ >|2 = |δ|2 where |δ|2 is determined from transcriptase measurement yielding the particular molecular genetic observable, G′2 0 2 → T. Agreement between observation and Figure 6 provides the relation, |δ|2 = 3|β|2 = 3|γ|2, which yields . Consequently, the expression for the four coupled coherent protons, Equation (8), cannot be written as a tensor product, illustrated by Equation (7), which is indicative of enol-imine proton entanglement. Evidently this entanglement originated from quantum uncertainty interactions, Δx Δpx ≥ ½ħ, evolutionarily imposed on amino (−NH2) DNA protons, which is responsible for rates of keto-amino → enol-imine arrangement. However as a consequence of the transcriptase deciphering quantum information within a G′-C′ superposition, an additional entanglement is created between coherent protons and transcriptase components. This entanglement state plays a significant role in bestowing a well defined three-dimensional structure on decohered isomers—G′, C′, *G, *C (Table 1)—which is a requirement for reproducible Topal-Fresco substitution-replication.
Since experimental lifetimes of metastable keto-amino states at 37 °C are ≥ ∼3,000 year [9], approximate quantum methods for small times, t < ∼100 year, yield the probability, P(t), of keto-amino → enol-imine arrangement as Pρ (t) = ½ (γρ /ħ)2 t2 (Appendix). This model for time-dependent alteration of genetic specificity implies a quantum Darwinian evolution model (QDEM), which expresses stochastic mutations in terms of ts + td. Data and the QDEM imply existence of an inherited genetic space, s, inequality, 1 ≥ s≥ 0.97, for Homo sapiens. When ts + td populate s such that s ≈ 0.97 + ε, an age-related degenerative disease is manifested. The QDEM allows predictive consequences of reduced energy coherent states populating “genetic space”, s, in “p53-type” genes, thereby expressing “latent” genetic information. The quantum mechanical terms in Equation (18), ∑j βjt4, express the consequences of ts + td populating sensitive genetic spaces, s, within a “p53-type” gene, which simulate data on incidence of cancer as a function of age exhibited in Figure 7. These evolutionarily acquired quantum mechanisms for operating microphysical genetic processes imply gains in evolutionary advantages. Enhanced advantages include (A) possibilities of favorable population responses to changing environmental conditions and, concomitantly, (B) mechanisms of protecting the gene pool against acquiring unsafe levels of mutation. This analysis clearly implies that phenotypic expression of the 74 class 1 tumors (Figure 7) is primarily a consequence of quantum mechanical arrangements, keto-amino → enol-imine, generating genotypic ts + td which are consistent with evolutionary design. Agreement between Equation (18) and Figure 7 implies age-related increased incidence of cancer is an example evolutionary mechanism of protecting the gene pool against acquiring unsafe levels of mutation.
Convergence of biological data and arguments from physics, chemistry and evolution support the model that age-related incidence of cancer [35] is a consequence of evolutionarily selected arrangements, keto-amino → enol-imine, populating a particular genetic space to its threshold limit, s ≈ 0.97 + ε, in a “p53-type” gene. Similar arguments are applicable to phenotypic expression of Huntington‘s disease resulting from ts + td populating an unstable (CAG)n tract to its evolutionary allowed limit [10,13]. These manifestations of quantum “genetic switches” imply that evolutionarily selected life-cycle alterations, e.g., the initiation of puberty and subsequent initiation of menopause [46], may be governed by “genetic switches” that are operated by time-dependent coherent states populating a particular “genetic space” to an evolutionarily determined threshold. Based on an accumulation of stochastic mutations, ts + td, within particular inherited genetic spaces, s, natural selection has employed quantum mechanisms to reveal “latent” genetic information which ultimately disallows further contributions to the gene pool. Compared to Homo sapiens, the life-cycle of the “normal” human pygmy is “compressed” in that puberty, menopause and onset of age-related degenerative disease are all exhibited at comparatively early ages [46,47]. This implies that ts + td populate the relevant genetic space to its “threshold limit” at early ages, thereby activating age-related “genetic switches” at relatively young ages in the human pygmy life-cycle. In this case, the genetic space, s, inequality would be approximated by 0.98 ≥ s ≥ 0.97 for the “normal” human pygmy genome. Accordingly, these human pygmy populations [46] are closer to their evolutionary extinction limit, i.e., s ≈ 0.97 + 2ε, than areHomo sapiens.
Quantum information processing exhibited by T4 phage DNA systems and by human genomes, e.g., references 10 & 13 and Figure 7 in terms of Equation (18), imply that quantum uncertainty limits on amino DNA protons have been operational since the primordial pool of primitive duplex DNA components [49]. This quantum law has been selected to drive a probabilistic yield of keto-amino → enol-imine arrangements, thereby introducing reduced energy enol-imine coherent states. However, particular decohered isomers are selected for substitution-replication or deletion. These are substitutions—G′2 0 2 → T, *C2 0 22 → T, G′0 0 2 → C, *G0 2 00 → A - and *A-*T → deletion. The fact that mutation frequencies, G′2 0 2 → T & *C2 0 22 → T, phenotypically expressed via quantum transcription—before replication—are identical to subsequent substitution frequencies, G′2 0 2 → T & *C2 0 22 → T, expressed as a consequence of Topal-Fresco replication of decohered isomers indicates that consequences of coherent states are “hard wired” into the DNA code. In these cases of the transcriptase reading quantum states G′2 0 2 and *C2 0 22 as normal T22 0 22, the transcriptase receives quantum instructions which are precisely communicated and executed for forming the particular complementary mispairs, G′2 0 2-syn-A00 2 # and *C2 0 22-A00 2 # (Table 1; Figure 5). These decohered mispairs are subsequently “replicated” to complete the prescribed substitutions, G′2 0 2 → T and *C2 0 22 → T, at the particular G′ and *C genetic sites. This apparently involves “seamless” collaboration between transcriptase and replicase systems. In the absence of entanglement, one cannot explain how ∼100% of the coherent state population identified by quantum transcription, e.g., G′2 0 2, is subsequently decohered to form the complementary mispair, G′2 0 2-syn-A00 2 # (Figure 5b), all of which participate in the G′2 0 2 → T substitution at replication [8,18]. This observation implies evolutionarily implemented quantum entanglement prevents immediate reequilibration and preserves the 3-deminsional molecular structure of particular decohered enol and imine isomers for purposes of efficient substitution-replication. Note that coherent state G′0 0 2 is not a transcription analog of any base; so, expression of the substitution G′0 0 2 → C at this G′-C′ site is a consequence of the complementary mispair, G′0 0 2-syn-G 22 2 #, completing its replication-substitution prescribed by transcriptase quantum processing. Interestingly, qualitative agreement between biologically expressed decohered data and Figure 6 suggests a field-theoretic mechanism for transcriptase quantum processing, subsequent entanglement and the observation that G′2 0 2 → T substitutions are ∼3-fold (rather than 2-fold) > G′0 0 2 → C substitutions at the particular G′-C′ genetic site. The QDEM also predicts an inaccurate molecular clock [13]. Inexactness exhibited by observable molecular clocks [14,16] is attributed to ts introducing additional initiation codons—UUG, CUG, AUG, GUG—which can manifest dynamic mutation expansion [13,34]. Additionally, DNA microsatellite contractions can be consequences of (a) ts introducing stop codons—UAA, UAG, UGA—or (b) td at *A-*T sites. The QDEM thus implies that improved models for calculating genetic distance between species could result from an inclusion of information responsible for this “clock inexactness”, i.e., include all consequences of ts + td.
Hwang and Green [14] have clearly shown that mammalian DNA exhibits time-dependent, molecular clock events, CpG → TpG substitutions, at the DNA level. The terminology, “CpG substitutions”, indicates C → T and/or G → A substitutions at a CpG site. Time-dependent CpG substitutions are the most frequent point mutation observed in the human genome and the rate is ∼15-fold greater when cytosine is methylated [16]. A consequence of a methyl group occupying carbon-5 cytosine is an increased proton-proton interaction, i.e., −NH2 - - H3C−, which would increase the probability of confining cytosine amino protons to too small of space, Δx. This would enhance rates of keto-amino → enol-imine arrangement via the asymmetric channel (Figure 1b), as observed. Although the assumed mechanism for CpG → TpG mutation is hydrolytic deamination of cytosine [14,16,48], the extensive molecular genetic investigation by Ripley [17] could not identify evidence supporting deamination of cytosine as the mechanism responsible for time-dependent CpG → TpG. Also after a CpG → TpG event, deaminated cytosine could not reacquire an −NH2 group and return to its original state, C00 2 22, in the next round of growth. However this “reequilibration recovery” of cytosine is routinely exhibited by T4 phage DNA systems that have expressed CpG → TpG [8]. Elango et al. [16] have noted that this deamination explanation for time-dependent CpG → TpG requires invoking a vague mechanism for inserting H2O between DNA strands. Since a hydrolytic deamination of cytosine mechanism would not include the βt term in Equation (13), this mechanism is inconsistent with a model that satisfies incidence of cancer data in terms of stochastic mutations, ts + td [15]. Based on evidence discussed here and the QDEM, the present report implies that most time-dependent CpG → TpG substitutions are a consequence of the asymmetric channel illustrated in Figure 1b. Also the fact that specific experimental designs are required to observe nontrivial quantum effects in biological systems [7,8] has played a role in obscuring mechanism of mutation illustrated by Equation (18).
Although cancer has been modeled in terms of classical Darwinian stochastic mutations [50], agreement between Figure 7 data and Equation (18) implies that coherent state contributions to the genotypic origin of tumors, ∑j βjt4, have been significantly underestimated [9,10,13] and, concomitantly, the role of classical stochastic mutations has apparently been over estimated. Unlike the QDEM, classical models [50] do not: (a) simulate Figure 7 data in terms of intrinsic physical properties of cells [9,10]; (b) explain molecular origins of stochastic mutations, ts + td; (c) provide internally consistent explanations for “early” cancer incidence peaks, e.g., ages < 39 [35,45]; (d) identify the evolutionary advantage of protecting the gene pool against acquiring unsafe levels of haploid stochastic mutation. The latter is a consequence of diploid “p53-type” genes manifesting age-related degenerative disease [15,42] due to an inherited “genetic space”, s, becoming populated by stochastic mutations to its threshold limit, s ≈ 0.97 + ε. The QDEM further provides testable explanations for different lifecycle manifestations exhibited by Homo sapien and human pygmy genomes, e.g., ages at puberty [46], menopause, etc. The model also predicts a modest time-dependent evolutionary shift favoring A-T richness, which may play a role in evolutionary extinction. In addition to observable transcriptase quantum processing [8,9], recent studies [51] have shown that light-harvesting by certain marine algae photosynthetic proteins involves long-lived quantum superposition states that transfer energy, thereby exhibiting nontrivial quantum phenomena by a biological system.
When viewed through the lens of quantum theory, consequences of transcriptase quantum processing not only provide insight into quantum processing and entanglements, but also identify evolutionary origins of age-related degenerative disease. This article reviews the origin of coherent states exhibited by enol-imine proton bonds in duplex DNA and outlines their role in communicating quantum information genetic specificity, which is ultimately exhibited as contributions to a quantum molecular clock. Data on enzymatic quantum measurements of genetic specificities within intervals, Δt ≪ 10−13 s, imply quantum entanglement between coherent protons and enzyme components. Transcriptase quantum processing, subsequent entanglement states and enzyme catalyzed decoherence reactions require additional theoretical refinements [52,53] to describe enzyme functions. Also, evidence of coherent states occupying decoherence-free subspaces at biological temperatures implies an opportunity for implementing carefully designed interdisciplinary experiments [7]. These recent studies [8-13,51] also identify areas in biology where quantum coherence is required for proper biological insight into microscopic molecular mechanisms and explanations of macroscopic biological consequences, Figure 7.
| ←------------------Allowable Pair Formation at Replication----------------→ | |||||||
|---|---|---|---|---|---|---|---|
| ←-------------------NORMAL ISOMERS-----→ ←------SYN-Purines----→ | |||||||
| Quantum States | G22000 | C00222 | A002# | T22022 | G222# | A002# | Transcribed Message |
| G′002 | GC → CG | U† | |||||
| G′202 | GC → TA | T22022 | |||||
| G′200 | opaque | G22000 | |||||
| G′000 | U | ||||||
| *G0200 | GC → AT | U | |||||
| *G2200 | U | ||||||
| C′220 | U | ||||||
| C′020 | U | ||||||
| C′022 | opaque | C00222 | |||||
| C′222 | U | ||||||
| *C2022 | GC → AT | T22022 | |||||
| *C0022 | U | ||||||
| *A20# | AT → GC | AT → TA | U | ||||
| *A00# | AT → CG | U | |||||
| *T0222 | AT → GC | C00222 | |||||
| *T2222 | U | ||||||
†Undefined.Transcribed messages of coherent states, decohered isomers and formation of complementary mispairs for Topal-Fresco replication. Normal tautomers (top row) and coherent quantum flip-flop states/decohered tautomers (left column) are listed in terms of the compact notation for hydrogen-bonding configurations identified in Figure 2 Legend. Consistent with Topal-Fresco [29], base pair substitution notation at the respective row-column juncture identifies decohered tautomers that will form a complementary mispair with a normal base, including syn-purines. Unsual pairs that do not exhibit mutation are identified as “opaque”. Transcribed messages obtained from a coherent quantum state are identified in the right hand column.
Acknowledgments
I thank Jacques Fresco for enlightenment on catalytic site specificities of transcriptase and replicase systems. I thank the first reviewer for identifying related studies on entanglement and uncertainty considerations. I thank the second reviewer for very useful suggestions on the manuscript, including methods for recognizing entanglement states. This investigation has benefited from informative discussions and questions by Peggy Johnson and Pam Tipton, for which the author is grateful.
Appendix
Probability of Hydrogen Bond Arrangement, keto-amino → enol-imine, Using Approximate Quantum Methods
For purposes of discussing consequences of coherent states populating duplex G′-C′ and *G-*C sites, an expression is obtained for the quantum mechanical “rate constant” associated with hydrogen bond arrangement, keto-amino → enol-imine via symmetric and asymmetric channels (Figure 2). This allows the development of a polynomial expression for time-dependent alterations (classical + quantum) in genetic specificities at a DNA base pair, which can be generalized to express an altered gene function. Time-dependence for the reactive five proton system of metastable G-C to populate complementary enol-imine states is modeled in terms of a composite proton, of mass equal two protons, in an appropriate asymmetric three-well potential illustrated in Figure A-1. Here the motion of two tunneling-exchange protons, using the symmetric and asymmetric channels (Figure 2), is simulated in terms of a composite proton model. Secondary contributions by the 2nd asymmetric pathway (unlabeled) are neglected. At t = 0 the composite proton is replicated into the metastable state | 3 > at energy E3 which, according to data [8,18] and shown in Figure A-1, is separated from the enol-imine ground state, | 1>, and hybrid state, | 2>, by approximately equal energy barriers. The relationship E1 < E2 < E3 for the ground state, hybrid state and metastable state, respectively, is displayed in Figure A-1. Enol-imine product states are designated by a general arrangement state |ρ > where the energy Eρ would equal E1 or E2 as appropriate. Time-dependence of an eigenstate, |Ψ>, is expressed by |Ψ > = |φI > exp(-i Ei t/ ħ), so |Ψ > = |φI > at t = 0 [38]. The relationship |Ψ > = Σi|i >< i|Ψ > is used to express an eigenstate |Ψ> in terms of base states | i > and amplitudes Ci as
A two-level Hamiltonian that will allow a composite proton to tunnel from the metastable state | 3> at energy E3 to an arrangement state | ρ > at energy Eρ can be written as

This can be written more succinctly as
At t = 0, the composite proton was in the metastable state |3 > at energy E3. The probability, P1(t), that the proton is in the ground state |1 > at a later time t is given by
References
- Venegas-Andraca, S.E.; Ball, J.L. Processing images in entangled quantum systems. Quantum Inf. Process 2010, 9, 1–11. [Google Scholar]
- Lanyon, B.P.; Whitfield, J.D.; Gillett, G.G.; Groggin, G.G.; Almeida, M.P.; Kassal, I.; Biamonte, J.D.; Mohseni, M.; Powell, B.J.; Barbieri, M.; et al. Toward quantum chemistry on a quantum computer. Nat. Chem. 2010, 2, 106–111. [Google Scholar]
- Ladd, T.D.; Jelezko, F.; Laflamme, R.; Nakamura, Y.; Monroe, C.; O‘Brien, J.L. Quantum computers. Nature 2010, 464, 45–53. [Google Scholar]
- Nielson, M. A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Rezakhani, A.T.; Kuo, W.J.; Hamma, A.; Lidar, D.A.; Zanardi, P. Quantum adiabatic brachistochrone. Phys. Rev. Lett. 2009, 108, 080502. [Google Scholar]
- Vedral, V. Introduction to Quantum Information Science; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Arndt, M.; Juffmann, T.; Vedral, V. Quantum physics meets biology. HFSP J. 2009, 3, 386–400. [Google Scholar]
- Cooper, W.G. Necessity of quantum coherence to account for the spectrum of time-dependent mutations exhibited by bacteriophage T4. Biochem. Genet. 2009, 47, 892–410. [Google Scholar]
- Cooper, W.G. Evidence for transcriptase quantum processing implies entanglement and decoherence of superposition proton states. Biosystems 2009, 97, 73–89. [Google Scholar]
- Cooper, W.G. Coherent states as consequences of keto-amino → enol-imine hydrogen bond arrangements driven by quantum uncertainty limits on amino DNA protons. Int. J. Quantum Chem. 2011. in press. [Google Scholar]
- Cooper, W.G. Evolutionary designed quantum information processing of coherent states in prokaryotic and eukaryotic DNA systems. In Computer Science Research and the Internet; Morris, J.E., Ed.; Nova Scientific Publishers, Inc.: Hauppauge, New York, NY, USA, 2010. [Google Scholar]
- Cooper, W.G. Transcriptase measurement of coupled entangled protons yields new proton-enzyme quantum entanglement. In Quantum Entanglement; Moran, A.M., Ed.; Nova Scientific Publishers, Inc.: Hauppauge, New York, NY, USA, 2010. [Google Scholar]
- Cooper, W.G. The molecular clock in terms of quantum information processing of coherent states, entanglement and replication of evolutionarily selected decohered isomers. Interdsci. Comput. Sci. 2011. in press. [Google Scholar]
- Hwang, D.G.; Green, P. Bayesian Markov chain Monte Carlo sequence analysis reveals varying neutral substitution patterns in mammalian evolution. Proc. Natl. Acad. Sci USA 2004, 101, 13994–14001. [Google Scholar]
- Beerenwinkel, N.; Antal, T.; Dingli, D.; Traulsen, A.; Kinzler, K.W.; Velculescu, V.E.; Vogelstein, B.; Nowak, M. A. Genetic progression and the waiting time to cancer. PLoS Comput. Biol. 2007, 3, e225. [Google Scholar]
- Elango, N.; Kim, S-H.; NICS Program; Vigoda, E.; Yi, S.V. Mutations of different molecular origins exhibit contrasting patterns of regional substitution rate variation. PLoS Comput. Biol. 2008, 4, e1000015. [Google Scholar]
- ipley, L.S. Estimation of in-vivo miscoding rates. Quantitative behavior of two classes of heat-induced DNA lesions. J. Mol. Biol. 1988, 202, 17–34. [Google Scholar]
- Cooper, W.G. T4 phage evolution data in terms of a time-dependent Topal-Fresco mechanism. Biochem. Genet. 1994, 32, 383–395. [Google Scholar]
- Löwdin, P.O. Quantum genetics and the aperiodic solid: Some aspects on the biological problems of heredity, mutations, aging and tumors in view of the quantum theory of the DNA molecule. Adv. Quantum Chem. 1965, 2, 213–359. [Google Scholar]
- Scheiner, S. Hydrogen Bonding. A Theoretical Perspective; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Bell, N.F.; Sawyer, R.F.; Volkas, R.R. Entanglement and quantal coherence: Study of two limiting cases of rapid system-bath interactions. Phys. Rev. A 2002, 65, 1–12. [Google Scholar]
- Grace, M.; Brif, C.; Rabitz, H.; Walmsley, I.L.; Kosut, R.L.; Lidar, D.A. Optimal control of quantum gates and suppression of decoherence in a system of interacting two-level particles. J. Phys. B: At. Mol. Opt. Phys. 2007, 40, S103–S125. [Google Scholar]
- Poccia, N.; Ricci, A.; Innocenti, D.; Bianconi, A. A possible mechanism for evading temperature quantum decoherence in living matter by Feshbach resonance. Int. J. Mol. Sci. 2009, 10, 2084–2106. [Google Scholar]
- Biswas, A.; Sharpiro, M.; Brumer, P. Overlapping resonances in the resistance of superposition states to decohere. J. Chem. Phys. 2010, 133, 014103. [Google Scholar]
- Zurek, W.H. Decoherence and the transition from quantum to classical. Phys. Today 1991, 44, 36–44. [Google Scholar]
- Vedral, V. Entanglements hit the big time. Nature 2003, 425, 28–29. [Google Scholar]
- Hines, A.P.; McKenzie, R.H.; Milburn, G.J. Entanglement of two-mode Bose-Einstein condensates. Phys. Rev. A 2003, 67. Art No.013609. [Google Scholar]
- Guehne, O.; Toth, G. Entanglement detection. Phys. Rep. Rev. Sect. Phys. Lett. 2009, 74, 1–75. [Google Scholar]
- Topal, M.D.; Fresco, J.R. Complementary base pairing and the origin of base substitutions. Nature 1976, 263, 285–289. [Google Scholar]
- Alberts, B.; Johnson, A.; Lewis, J.; Raff, M.; Roberts, K.; Walter, P. Molecular Biology of the Cell, 4th ed.; Garland: New York, NY, USA, 2002. [Google Scholar]
- Benzer, S. On the topography of the genetic fine structure. Proc. Natl. Acad. Sci. USA 1961, 47, 403–415. [Google Scholar]
- Baltz, R.H.; Bingham, P.M.; Drake, J.W. Heat mutagenesis in bacteriophage T4: The transition pathway. Proc. Natl. Acad. Sci. USA 1976, 73, 1269–1273. [Google Scholar]
- Bingham, P.M.; Baltz, R.H.; Ripley, L.S.; Drake, J.W. Heat mutagenesis in bacteriophage T4: The transversion pathway. Proc. Natl. Acad. Sci. USA 1976, 73, 4159–4163. [Google Scholar]
- Cooper, W.G. Evolutionary origin of expandable G-C rich triplet repeat DNA sequences. Biochem. Genet. 1995, 33, 173–181. [Google Scholar]
- Dix, D.; Cohen, P.; Flannery, J. On the role of aging in cancer incidence. J. Theoret. Biol. 1980, 83, 163–171. [Google Scholar]
- Jorgensen, W.L.; Pranata, J. The importance of secondary interactions in triply hydrogen-bonded complexes: guanine–cytosine vs uracil–diaminopyridine. J. Am. Chem. Soc. 1990, 112, 2008–2010. [Google Scholar]
- Pranata, J.; Wierschke, S.G.; Jorgensen, W.L. OPLS potential functions for nucleotide bases. Relative association constants of hydrogen bonded base pairs in chloroform. J. Am. Chem. Soc. 1991, 113, 2810–2819. [Google Scholar]
- Merzbacher, E. Quantum Mechanics, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1997. [Google Scholar]
- Feder, T. Physicists invited to apply their insights to cancer. Phys. Today 2010, 63, 27–28. [Google Scholar]
- Cooper, W.G. Roles of evolution, quantum mechanics and point mutations in origins of cancer. Cancer Biochem. Biophys. 1993, 13, 147–170. [Google Scholar]
- Cooper, W.G. Hypothesis on a causal link between EMF and an evolutionary class of cancer and spontaneous abortion. Cancer Biochem. Biophys. 1996, 15, 151–170. [Google Scholar]
- Morton, J.P.; Timpson, P.; Karim, S.A.; Ridgway, R.A.; Athineos, D.; Doyle, B.; Jamieson, N.B.; Oien, K.A.; Lowy, A.M.; Burton, V.G.; et al. Mutant p53 drives metastasis and overcomes growth arrest/senescence in pancreatic cancer. Proc. Natl. Acad. Sci. USA 2010, 107, 246–251. [Google Scholar]
- Kadenbach, B.; Munscher, C.; Frank, V.; Muller-Hocker, J.; Napiwotzki, J. Human aging is associated with stochastic somatic mutations of mitochondrial DNA. Mutation Res. 1995, 338, 161–172. [Google Scholar]
- Muller, H.J. Our load of mutations. Am. J. Hum. Genet. 1950, 2, 111–176. [Google Scholar]
- Anderson, W.F.; Camargo, M.C.; Fraumeni, J.F.; Correa, P.; Rosenberg, P.S.; Rabkin, C.S. Age-specific trends in incidence of noncardia gastric cancer in US adults. JAMA 2010, 303, 1723–1728. [Google Scholar]
- Migliano, A.B.; Vinicius, L.; Lahr, M.M. Life history trade-offs explain the evolution of human pygmies. Proc. Natl. Acad. Sci. USA 2007, 104, 20216–20219. [Google Scholar]
- Perry, G.H.; Dominy, N.J. Evolution of the human pygmy phenotype. Trends Ecol. Evolut. 2009, 24, 218–225. [Google Scholar]
- Green, R.E.; Krause, J.; Briggs, A.W.; Maricjc, T.; Stenzel, U.; Kricher, M.; Patterson, N.; Li, H.; Zhai, W.; Fritz, M.H.Y.; et al. A draft sequence of the Neandertal genome. Science 2010, 328, 710–722. [Google Scholar]
- Koonin, E.V.; Stenkevich, T.G.; Dolja, V.V. The ancient virus world and evolution of cells. Biol. Direct 2006, 1, 29. [Google Scholar]
- Little, M.P. Cancer models, genomic instability and somatic cellular Darwinian evolution. Biol. Direct 2010, 5, 19. [Google Scholar]
- Collini, E.; Wong, C.Y.; Wilk, K.E.; Curmi, P.M.G.; Burmer, P.; Scholes, G.D. Coherently wired light-harvesting in photosynthetic marine algae at ambient temperature. Nature 2010, 463, 644–648. [Google Scholar]
- Quantum Tunneling in Enzyme-Catalyzed Reactions; Allemann, R.K., Ed.; Royal Society of Chemistry: Cambridge, UK, 2009.
- Bothma, J.P.; Gilmore, J.B.; McKenzie, R.H. The role of quantum effects in proton transfer reactions inenzymes: quantum tunneling in a noisy environment. New J. Phys. 2010, 12. Art No. 055002. [Google Scholar]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Cooper, W.G. Accuracy in Biological Information Technology Involves Enzymatic Quantum Processing and Entanglement of Decohered Isomers. Information 2011, 2, 166-194. https://doi.org/10.3390/info2010166
Cooper WG. Accuracy in Biological Information Technology Involves Enzymatic Quantum Processing and Entanglement of Decohered Isomers. Information. 2011; 2(1):166-194. https://doi.org/10.3390/info2010166
Chicago/Turabian StyleCooper, Willis Grant. 2011. "Accuracy in Biological Information Technology Involves Enzymatic Quantum Processing and Entanglement of Decohered Isomers" Information 2, no. 1: 166-194. https://doi.org/10.3390/info2010166
APA StyleCooper, W. G. (2011). Accuracy in Biological Information Technology Involves Enzymatic Quantum Processing and Entanglement of Decohered Isomers. Information, 2(1), 166-194. https://doi.org/10.3390/info2010166




