A Modifiable Blockchain Based on the RE-TNG Node Selection Method
Abstract
1. Introduction
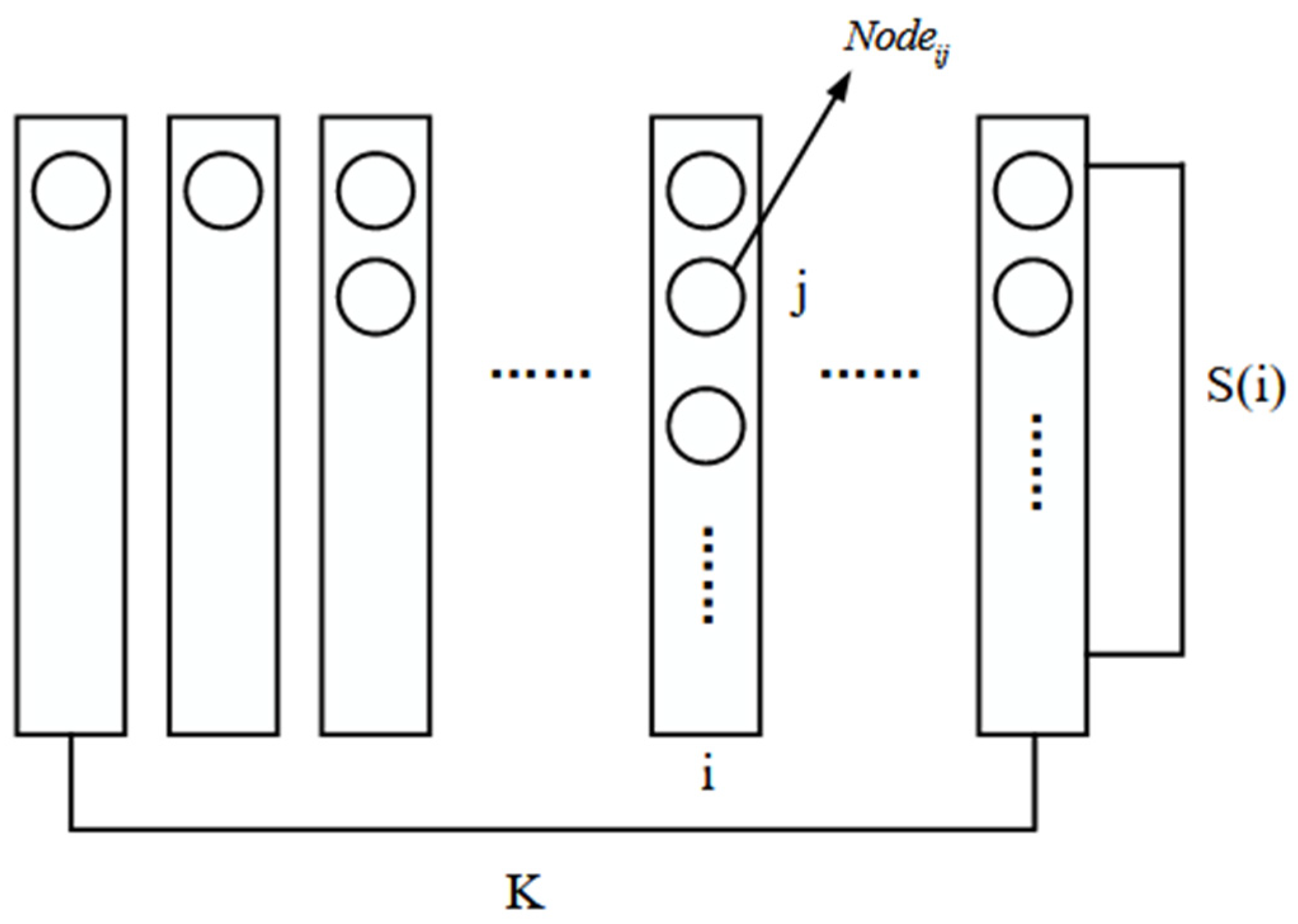
- Proposing the RE-TNG Node Selection Method: This method involves a two-stage grouping process based on reputation values. Initially, nodes are ranked by their reputation values, and the Fibonacci function is applied to perform the first grouping. Within each group, nodes are further sorted in descending order of reputation. Subsequently, a second grouping is conducted to select candidate nodes for modification and trapdoor management from the initial groups.
- The Fibonacci-based first grouping addresses the issue of reputation value accumulation prevalent in traditional reputation-based algorithms. The second grouping resolves the problem of randomly selecting modifier nodes, which often fails to ensure trustworthiness. Additionally, this method improves upon conventional modifiable blockchain schemes by limiting the voting and verification processes to nodes with high reputation scores. This reduces the influence of malicious and inactive nodes on modification security and efficiency.
- Enhancing Trapdoor Key Management with Multi-Party Collaboration: The proposed approach replaces the reliance on a single node for generating trapdoor keys in existing schemes with a multi-party collaborative key generation mechanism. Furthermore, the trapdoor recovery and redistribution processes are facilitated through secret resharing techniques. This improvement addresses the centralization issue inherent in traditional secret sharing methods that depend on authoritative nodes for trapdoor key generation and distribution.
2. Related Knowledge
2.1. Chameleon Hash
- Collision Resistance: It is computationally infeasible to find two distinct inputs and such that .
- High Sensitivity: Even a small modification in the input data , such as a single bit change, will cause a significant change in the output , resulting in a drastically different hash value.
- (1)
- . The key generation algorithm for chameleon hash functions: Given a security parameter , it outputs a public key and a private key (where is typically referred to as the trapdoor).
- (2)
- . The chameleon hash generation algorithm: Given the chameleon hash public key , arbitrary data , and a random value , the output is the hash value .
- (3)
- . The chameleon hash verification algorithm: Given the public key , arbitrary data , and the hash value , it outputs a verification result . If the hash value is correct, = 1 otherwise, = 0.
- (4)
- . The hash collision discovery algorithm: Given the trapdoor , the tuple consisting of the original data and the random value , along with the modified data , it outputs a new random value . To ensure that:
2.2. Verifiable Secret Sharing (VSS)
- (1)
- . Secret Sharing Algorithm: The secret is divided into shares , with each share distributed to a participant through a secure channel. The secret information is split into the coefficients of multiple polynomials, and participants can also compute the commitment values of their respective shares and make them public within the system.
- (1)
- . Share Verification Algorithm: When there is a need to verify the consistency of the shares, participants can exchange shares or information with each other. Using a verification algorithm (such as digital signatures or zero-knowledge proofs), the received shares are validated to ensure their correctness. Participants verify each other’s shares and ensure that they have not been tampered with or forged.
- (3)
- . Secret Reconstruction Algorithm: To recover the complete secret information, a threshold number of correct secret shares must be collected. After each participant involved in the cooperative secret recovery validates the secret’s validity using the share verification algorithm, the secret can be reconstructed using a secret reconstruction method.
2.3. Verifiable Random Functions (VRFs)
- (1)
- Key generation algorithm, .
- (2)
- Random number generation algorithm, .
- (3)
- Proof generation algorithm, .
- (4)
- Random number verification algorithm, .
3. RE-TNG Node Selection Method
3.1. Node Reputation Reward and Penalty Model
3.2. RE-TNG Node Selection Method Design
4. Design of a Modifiable Blockchain Scheme Based on the RE-TNG Node Selection Method
4.1. Scheme Definition
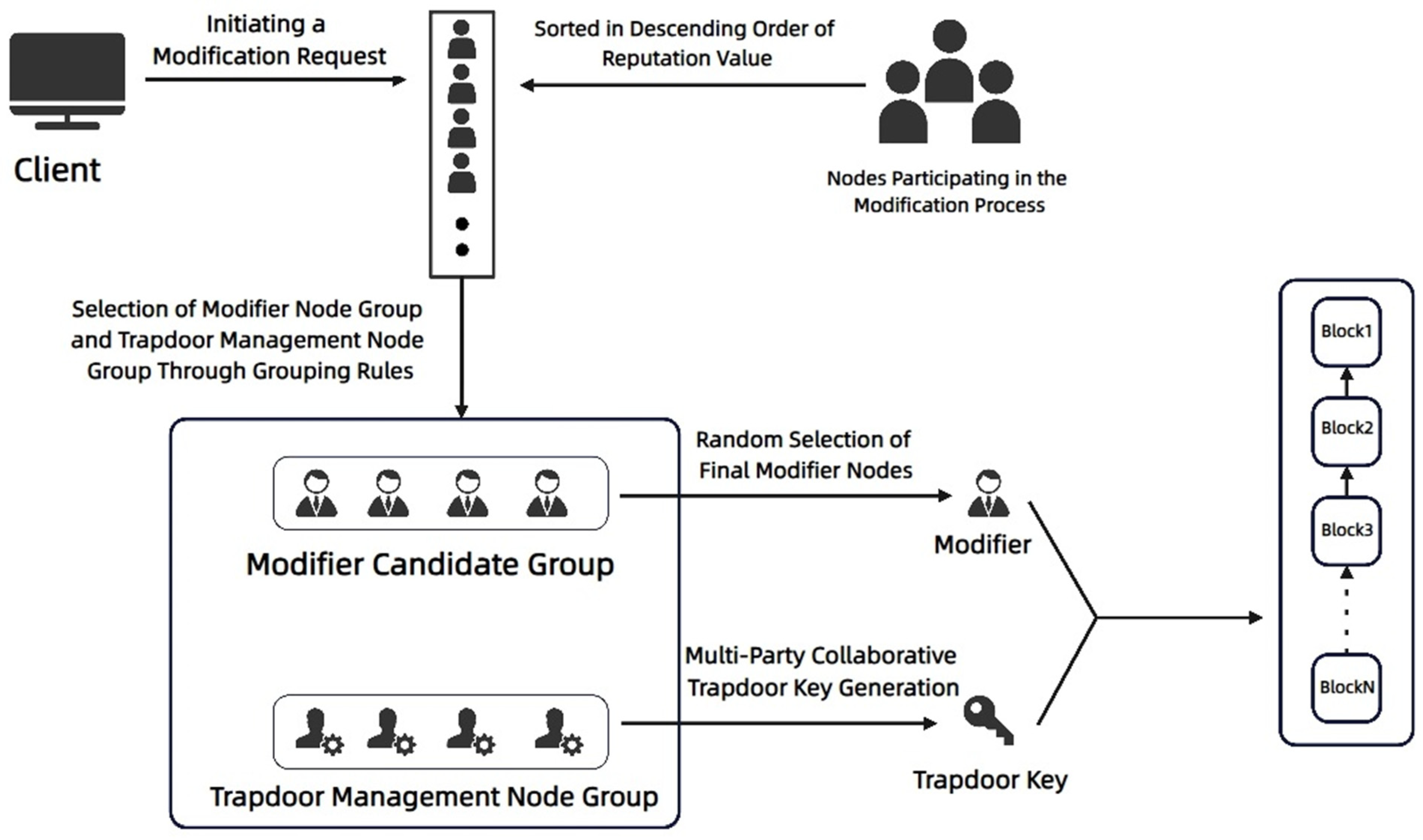
- Modifier Node Candidate Group: In the blockchain modification process, the nodes participating in the modification are first sorted based on their reputation scores. After sorting, they are grouped according to the Fibonacci function rule. The first node in each group is selected to join the modifier node candidate group. Then, the final modifier nodes are chosen through a verifiable random function (VRF), ensuring the selection process is both random and verifiable. This method ensures fairness, transparency, and prevents any manipulation in the selection of the nodes that will execute the blockchain modifications.
- Trapdoor Management Node Group: After the nodes participating in the modification process are sorted based on their reputation scores, they are grouped using the Fibonacci function rule. The second node in each group is selected to join the trapdoor management node group. This group is responsible for two main tasks: collaborative trapdoor generation and voting on the final modifier node selection.
4.1.1. Initialization Stage
4.1.2. RE-TNG Node Selection Method—Selection Stage
4.1.3. Final Modifier Node Selection Stage
4.1.4. Voting Stage
4.1.5. Trapdoor Generation Stage
| Algorithm 1: Initialization algorithm |
Input: Secure random parameter . |
| Output: . Step 1: Generate a secure random parameter . |
| Step 2: Use λ according to the predefined cryptographic function. |
| Step 3: . |
| Algorithm 2: Chameleon hash public and private key collaborative generation algorithm |
Input: . |
| Output: . , collaboratively managed by trapdoor management node group members . Step 1: Public key generation.
|
Step 2: Private key (trapdoor) generation.
|
Step 3: Public key disclosure.
|
| Algorithm 3: Trapdoor re-sharing algorithm |
Input:
|
| Output: trapdoor shares that can be distributed to trapdoor management node group members . Step 1: Secret sharing.
|
Step 2: Threshold.
|
Step 3: Trapdoor reconstruction.
|
4.1.6. Data Modification Stage
| Algorithm 4: Hash collision detection algorithm |
Input:
|
| Output: . Step 1: through collaborative calculation . |
| Step 2: . |
| Step 3: guarantees that the hash values before and after the modification remain consistent. |
| Algorithm 5: Chameleon hash verification algorithm |
Input:
. |
4.1.7. Verification Stage
| Algorithm 6: Verification algorithm |
Input:
|
4.2. Decentralized Management of Trapdoor
| Algorithm 7: Parameter initialization algorithm |
Input: Security parameter . Output: . |
| Algorithm 8: Chameleon hash public and private key collaborative generation algorithm |
Input: . Output:
where is a random integer and represents the user identity information of the node. Each node can compute an intermediate value based on this polynomial, resulting in intermediate values for the polynomial. Step 2: The nodes will distribute the i-th to node . Step 3: Node verifies the correctness of the intermediate values and calculates the output public key (where represents the chameleon hash trapdoor key, ) and the trapdoor sharing formula . The remaining nodes can obtain the shared portions of the trapdoor key through the above steps. |
| Algorithm 9: Hash algorithm |
Input: Message , random number (where is obtained from ). Output: Hash value is a traditional collision-resistant hash function) |
| Algorithm 10: Hash collision discovery algorithm |
Input:
Step 1: Compute trapdoor key share contribution; Node nin_ini . Step 2: Aggregate shares is satisfied. Step 3: Generate a new random number. , ensuring holds true. |
5. Scheme Analysis
5.1. Security Analysis
5.2. Functional Comparison
5.3. Experimental Analysis
5.3.1. Experiment Environment
5.3.2. Performance Analysis
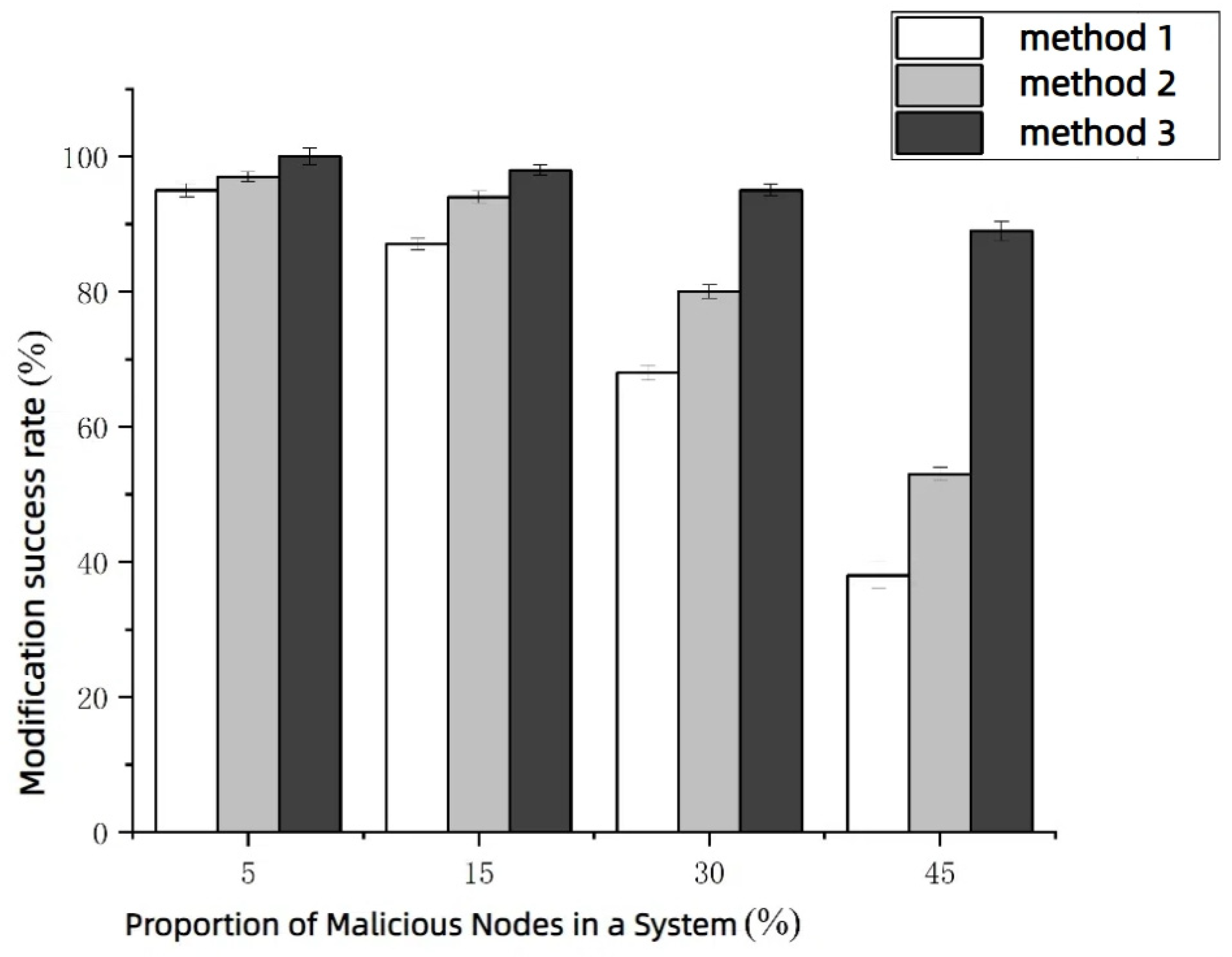
- 1.
- Success Rate of Correctly Modified Block Data with Different Numbers of Malicious Nodes
- 2.
- Modification Efficiency when Handling Multiple Modification Requests Simultaneously
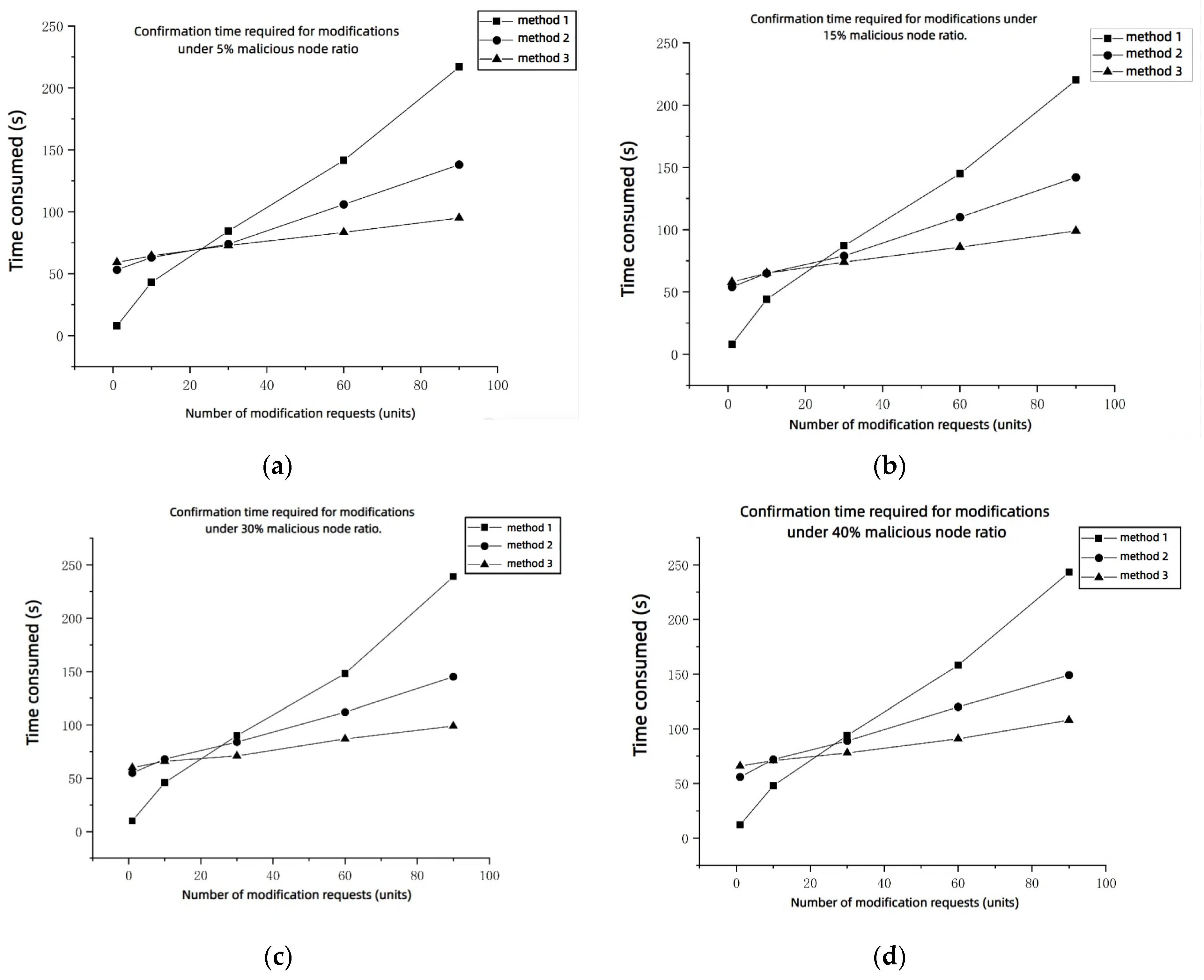
- 3.
- Confirmation Time Required for Modification under Different Proportions of Malicious Nodes
- 4.
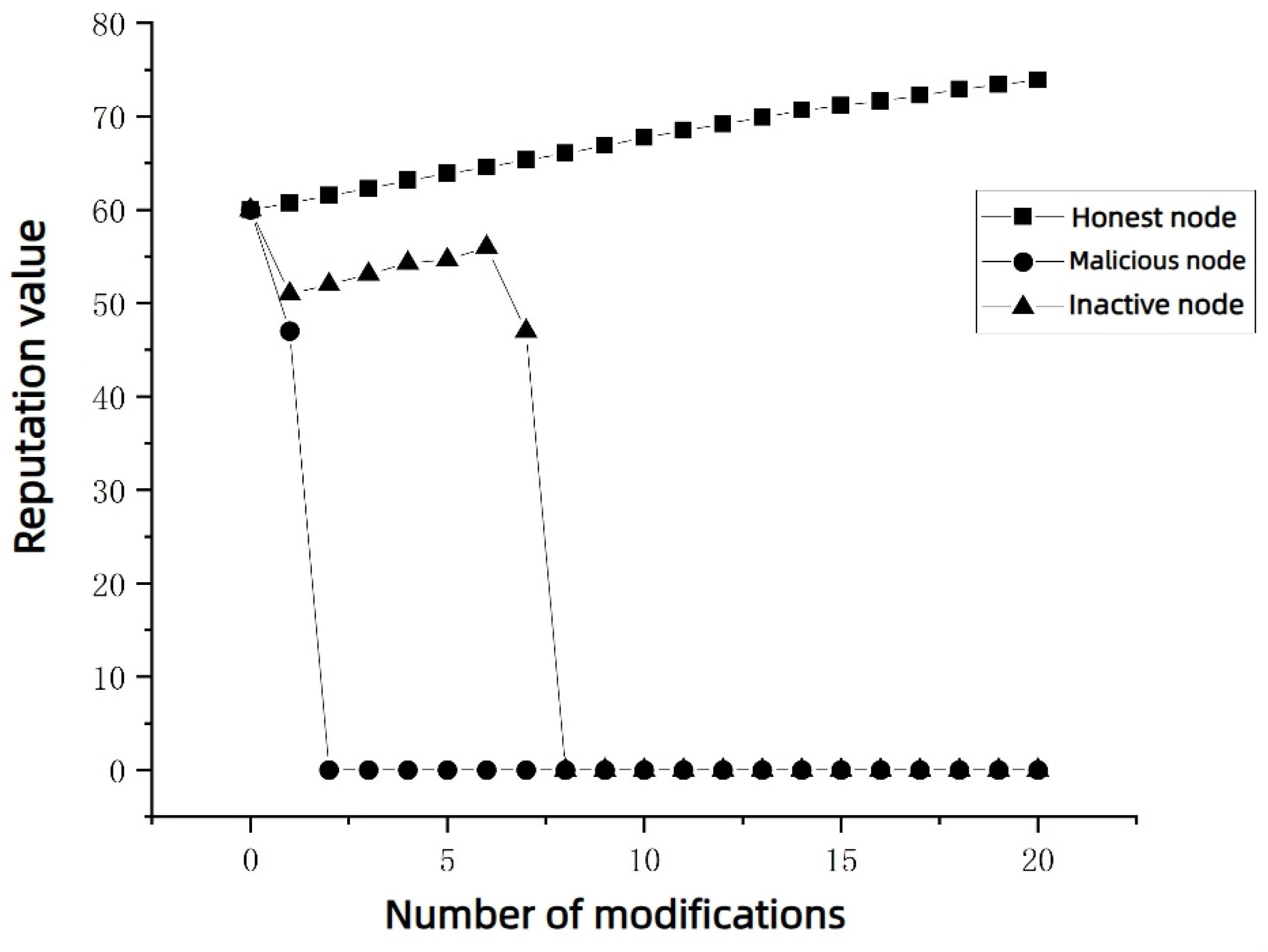
- Reputation Value Changes of Different Nodes After Multiple Modifications
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yuan, Y.; Wang, F.Y. Blockchain: The state of the art and future trends. Acta Autom. Sin. 2016, 42, 481–494. [Google Scholar]
- Liu, S.Y.; Lei, M.Y.X.; Wang, L. A review of key technologies and existing problems in blockchain research. Comput. Eng. Appl. 2022, 58, 66–82. [Google Scholar]
- Cai, X.Q.; Deng, Y.; Zhang, L. The principles and core technologies of blockchain. Chin. J. Comput. 2021, 44, 84–131. [Google Scholar]
- He, S.; Huang, X.N.; Liu, Q.B.; Yang, Y.J. Research on improvement of DPoS blockchain consensus mechanism. Appl. Res. Comput. 2021, 38, 3551–3557. [Google Scholar]
- Yuan, Y.; Wang, F.Y. Editable blockchain: Models, techniques and methods. Acta Autom. Sin. 2020, 46, 831–846. [Google Scholar]
- Krawczyk, H.; Rabin, T. Chameleon Hashing and Signatures. Cryptology ePrint Archive. 1998. Available online: http://eprint.iacr.org/1998/010 (accessed on 5 October 2023).
- Ateniese, G.; Magri, B.; Venturi, D.; Andrade, E. Redactable blockchain-or-rewriting history in bitcoin and friends. In Proceedings of the 2017 IEEE European Symposium on Security and Privacy, Paris, France, 26–28 April 2017; pp. 111–126. [Google Scholar]
- Li, P.L.; Xu, H.X.; Ma, T.J.; Mu, Y. Research on fault-correcting blockchain technology. J. Cryptologic Res. 2018, 5, 501–509. [Google Scholar]
- Ashritha, K.; Sindhu, M.; Lakhmy, K.V. Redactable blockchain using enhanced chameleon hash function. In Proceedings of the International Conference on Advanced Computing and Communication Systems, Coimbatore, India, 15–16 March 2019. [Google Scholar]
- Lyu, W.L.; Wei, S.J.; Yu, M.H.; Li, S. Research on verifiable blockchain ledger redaction method for trusted consortium. Chin. J. Comput. 2021, 44, 2016–2032. [Google Scholar]
- Gao, W.; Chen, L.Q.; Tang, C.M.; Zhang, G.; Li, F. One-time chameleon hash function and its application in redactable blockchain. J. Comput. Res. Dev. 2021, 58, 2310–2318. [Google Scholar]
- Gu, K.; Zhang, S.H.; Li, C. Blockchain ledger revision scheme based on supervisor group. Appl. Res. Comput. 2023, 40, 2266–2273. [Google Scholar]
- Chun, H.W.; Li, H.K.; Yu, S.D. Quantum resistant key-exposure free chameleon hash and applications in redactable blockchain. Inf. Sci. 2020, 548, 438–449. [Google Scholar]
- Khalili, M.; Dakhilalian, M.; Susilo, W. Efficient chameleon hash functions in the enhanced collision resistant model. Inf. Sci. 2020, 510, 155–164. [Google Scholar] [CrossRef]
- Shamir, A. How to share a secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Chor, B.; Goldwasser, S.; Micali, S.; Awerbuch, B. Verifiable secret sharing and achieving simultaneity in the presence of faults. In Proceedings of the 26th Annual Symposium on Foundations of Computer Science, Portland, OR, USA, 21–23 October 1985. [Google Scholar]
- Chen, S.M.; Wang, B.; Chen, Y.Q. Improved PBFT consensus algorithm based on node grouping reputation model. Appl. Res. Comput. 2023, 40, 2916–2921. [Google Scholar]
- Chen, R.Y.; Wang, L.W.; Zhu, R.G. PBFT consensus algorithm based on reputation value voting and random number election. Comput. Eng. 2022, 48, 42–49. [Google Scholar]
- Sun, M.; Jiao, S.X.; Wang, C.Y. Credit-based committee consensus mechanism. J. Comput. Appl. 2024, 1, 1–10. Available online: http://kns.cnki.net/kcms/detail/51.1307.TP.20240409.1659.002.html (accessed on 14 May 2024).
- Dai, B.R.; Jiang, S.M.; Li, D.W.; Li, C. Evaluation model of cross-chain notary mechanism based on improved PageRank algorithm. Comput. Eng. 2021, 47, 26–31. [Google Scholar]
- Zhao, L.; Li, B.; Zhou, Q.L.; Chen, X. Improvement and optimization of consensus algorithm based on PBFT. In Proceedings of the 4th International Conference on Communications, Information System and Computer Engineering, Piscataway, NJ, USA, 27–29 May 2022; pp. 350–356. [Google Scholar]
- Dodis, Y.; Yampolskiy, A. A verifiable random function with short proofs and keys. In International Workshop on Public Key Cryptography; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Zhao, X.; Zhang, Z.; Li, Y. An editable and accountable blockchain scheme. J. Cyber Secur. 2022, 7, 19–28. [Google Scholar] [CrossRef]
- Lai, M.X.; Du, R.Y.; Chen, J.; He, K. A Decentralized and Traceable Editable Blockchain Scheme. J. Wuhan Univ. Sci. Ed. 2024, 70, 413–420. [Google Scholar] [CrossRef]


| Level Symbols | Level Scores | Evaluation |
|---|---|---|
| Excellent Reputation Score | ||
| High Reputation Score | ||
| Normal Reputation Score | ||
| Initial Reputation Score | ||
| Low Reputation Score |
| Identity in the Previous Modification Process | Values |
|---|---|
| Nodes Not Selected for the Trapdoor Management Group and Modifier Candidate Group | 1 |
| Members of the Trapdoor Management Group | 1.1 |
| Members of the Modifier Candidate Group | 1.2 |
| Final Editors | 1.3 |
| Identity in the Previous Modification Process | Values |
|---|---|
| Inactive Nodes (Passive Nodes) | 0.9 |
| Dishonest Nodes | 1.3 |
| Variable Symbols | Definitions |
|---|---|
| Modification Request Initiator Node | |
| User Address of the Modification Request Initiator Node | |
| User Address of the Final Modifier Node | |
| Final Modifier Node | |
| A Node Participating in the Process | |
| Modifier Node Candidate Group Members | |
| Trapdoor Management Node Group Members | |
| Initial Request List | |
| Voting Request List | |
| Nodes Group Sorted by Reputation in Descending Order | |
| Random Number Generated by Algorithm | |
| Voting Opinion | |
| Number of Agreeing Votes | |
| First Node of the i-th Group | |
| Second Node of the i-th Group | |
| Proof Generated by the Algorithm | |
| Result Set Generated by the Algorithm | |
| VRF Public Key Generated by the Algorithm | |
| VRF Private Key Generated by the Algorithm |
| Scheme | Decentralized Trapdoor Management | Node Selection | Accountability | Security |
|---|---|---|---|---|
| Reference [7] | No | No | No | Low |
| Reference [8] | No | No | No | Moderate |
| Reference [24] | Yes | No | Yes | High |
| Reference [12] | No | Yes | Yes | High |
| Proposed Scheme | Yes | Yes | Yes | High |
| Hardware/Software | Model |
|---|---|
| Operating System | Windows 11, version 24H2 |
| CPU | 12th Gen Intel(R) Core(TM) i5-12400F 2.5 GHz |
| Memory | KINGBANK 16 G RAM 3200 MHZ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, R.; Li, C.; Dai, B.; Zhang, S. A Modifiable Blockchain Based on the RE-TNG Node Selection Method. Information 2025, 16, 83. https://doi.org/10.3390/info16020083
Chen R, Li C, Dai B, Zhang S. A Modifiable Blockchain Based on the RE-TNG Node Selection Method. Information. 2025; 16(2):83. https://doi.org/10.3390/info16020083
Chicago/Turabian StyleChen, Rongtao, Chao Li, Bingrong Dai, and Shaohua Zhang. 2025. "A Modifiable Blockchain Based on the RE-TNG Node Selection Method" Information 16, no. 2: 83. https://doi.org/10.3390/info16020083
APA StyleChen, R., Li, C., Dai, B., & Zhang, S. (2025). A Modifiable Blockchain Based on the RE-TNG Node Selection Method. Information, 16(2), 83. https://doi.org/10.3390/info16020083







