Graph Anomaly Detection Algorithm Based on Multi-View Heterogeneity Resistant Network
Abstract
1. Introduction
- (1)
- This paper proposes a multi-view PA scoring mechanism that introduces a new perspective for heterophilic edge detection, with theoretical proof that increasing views reduces PA score variance and enhances model stability;
- (2)
- A cross-view joint edge pruning strategy is designed to integrate structural and semantic perspectives, overcoming single-view methods’ limitations in heterophilic anomaly detection;
- (3)
- A multi-view self-distillation mechanism is introduced to exploit cross-view consistency as a regularization signal for anomaly learning.
2. Related Work
- Limited capability to suppress noise arising from strongly heterophilous connections, which often leads to unstable message propagation;
- Lack of consistent representation learning under multi-view or multimodal scenarios, resulting in incomplete anomaly characterization;
- Information conflicts and structural distortion during cross-view fusion, causing significant loss of global graph information.
3. Preliminary Knowledge
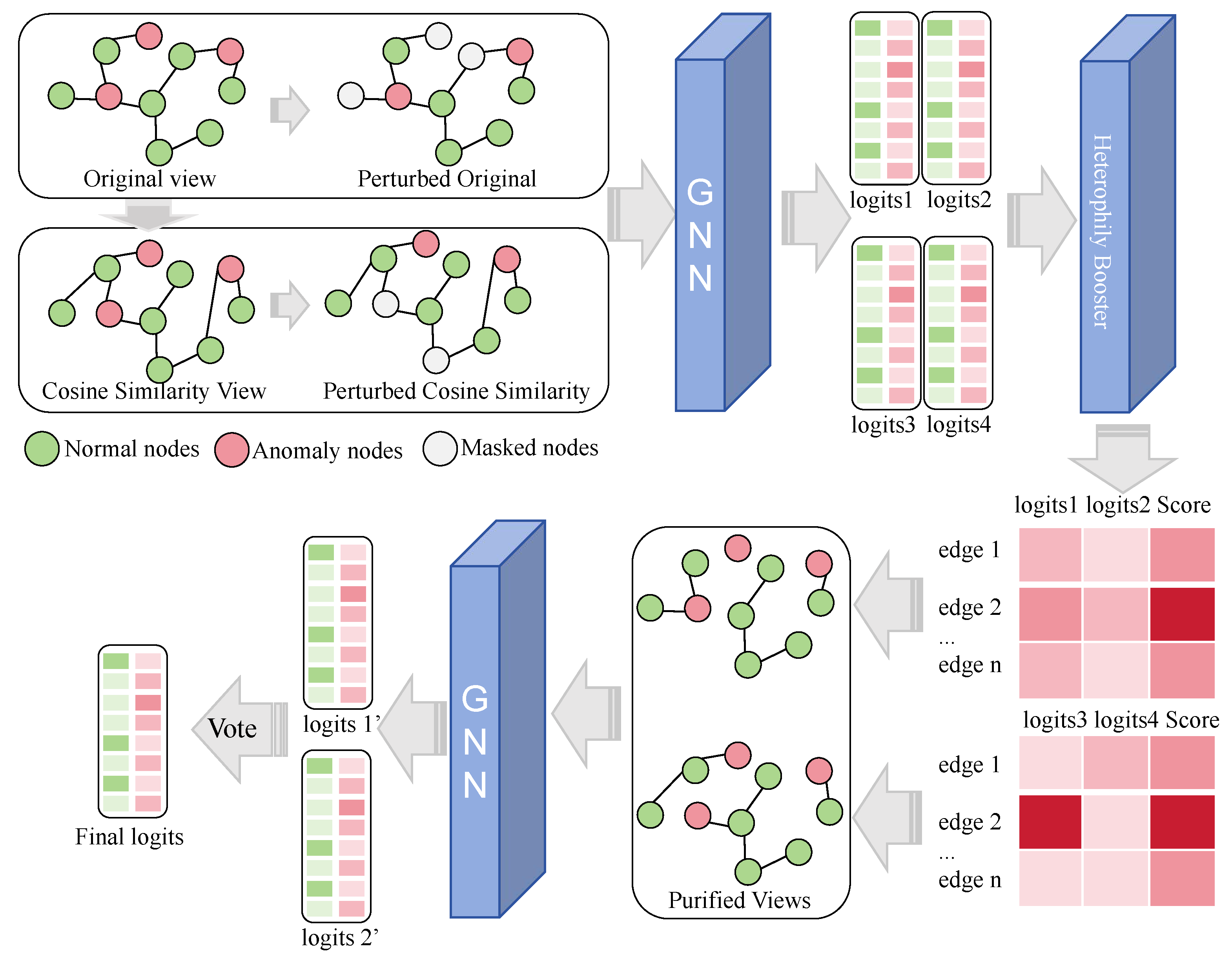
4. Implementation of MV-GHRN
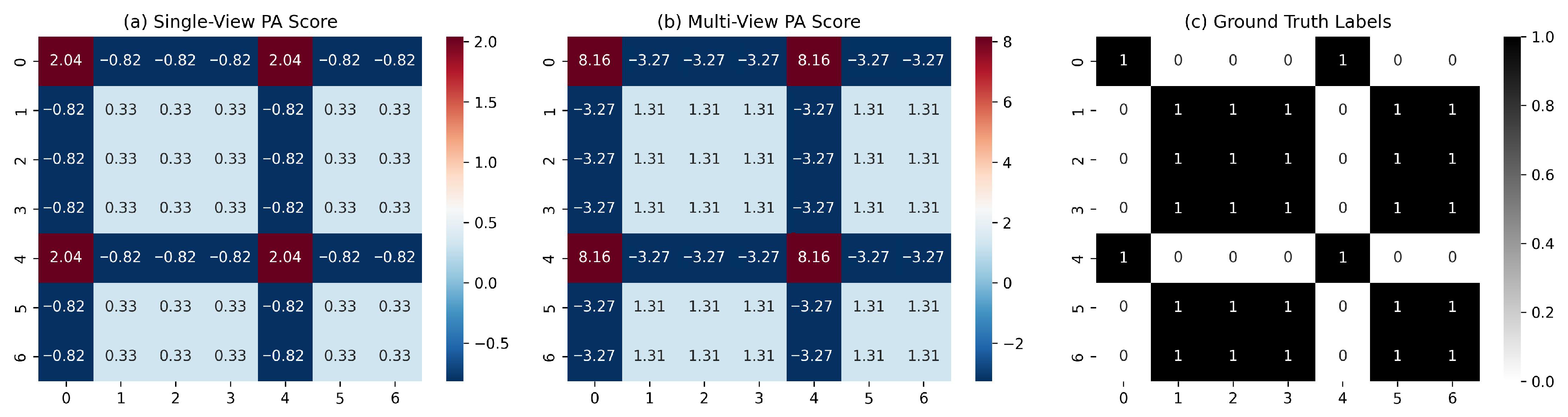
4.1. Single-View PA Scoring and Its Characteristics
4.1.1. Single-View PA Scoring
4.1.2. Prediction Error Analysis of Single-View PA Scores
4.2. Multi-View PA Scoring Theoretical Framework
4.2.1. Multi-View PA Score Definition
4.2.2. ANOVA of Multi-View PA Scores
- (1)
- Theoretically, it minimizes variance when view variances are comparable (proven by Cauchy–Schwarz inequality);
- (2)
- It avoids introducing additional hyperparameters. The variance reduction observed in Figure 2 (8.02% and 9.82% on Amazon and Yelp) validates this design choice.
4.3. Complexity Analysis
4.4. Multi-View Graph Heterogeneity-Resistant Network
5. Results
5.1. Experimental Setup
5.1.1. Dataset
5.1.2. Evaluation Metrics
5.1.3. Experimental Environment and Model Configuration
5.2. Comparative Experiments
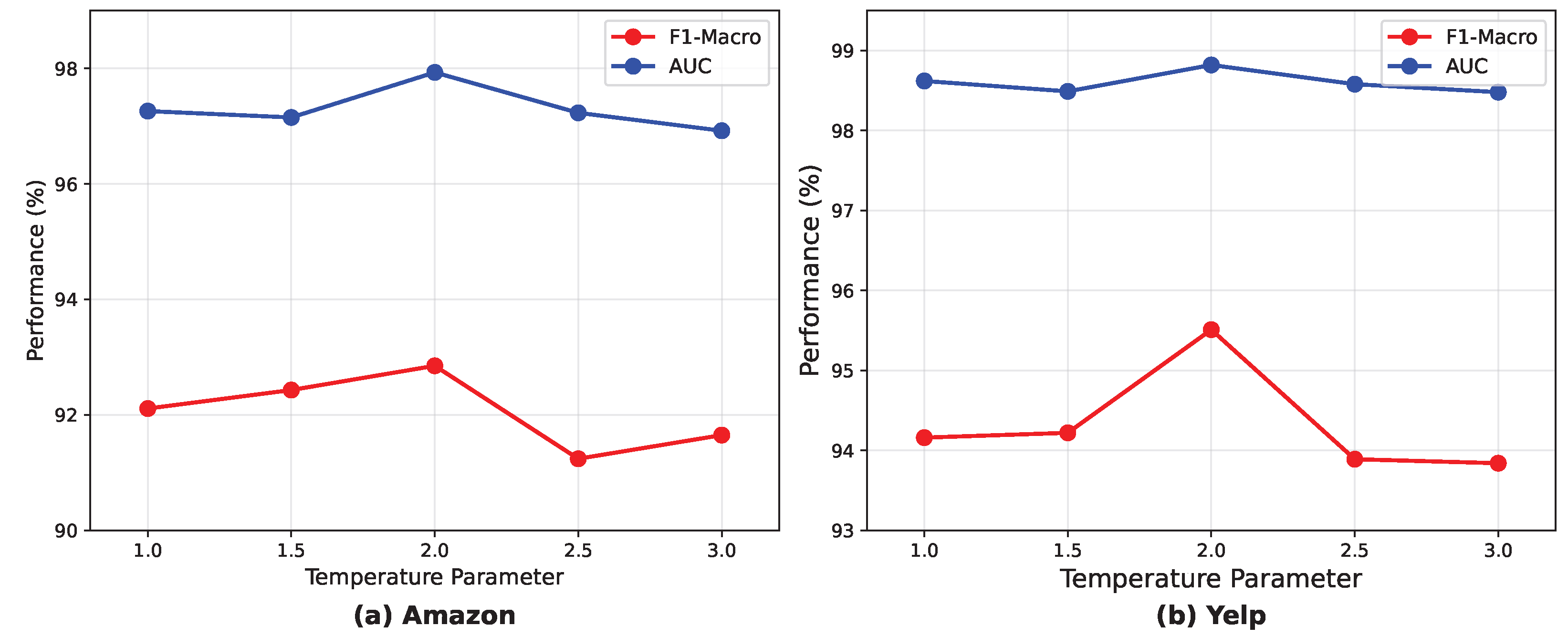
5.3. Sensitivity Analysis
5.4. Performance Evaluation Under Different Perturbation Ratios
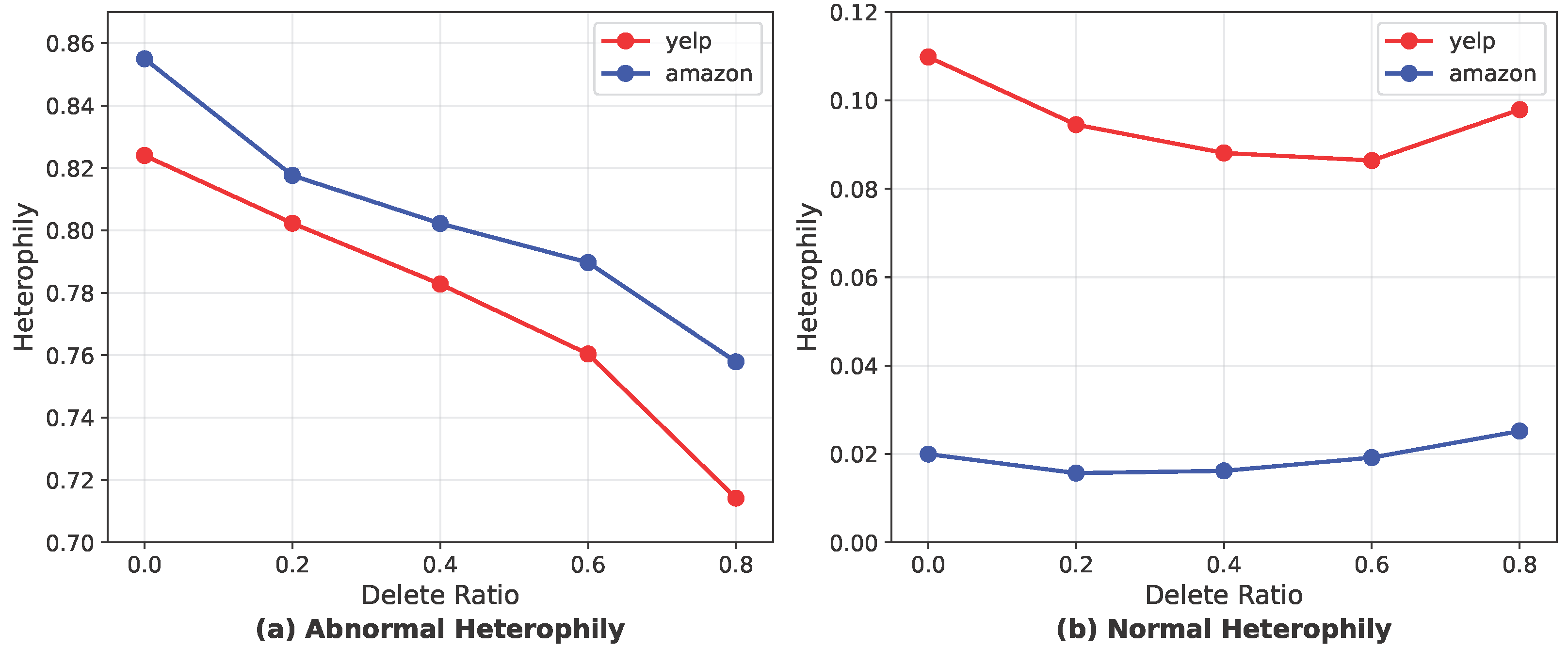
5.5. Analysis of the Impact of Edge Pruning on Heterophily
5.6. Ablation Study
5.7. Generalization to Additional Datasets
6. Conclusions
6.1. Limitations
6.2. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kipf, T.N.; Welling, M. Semi-supervised Classification with Graph Convolutional Networks. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar] [CrossRef]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph Attention Networks. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar] [CrossRef]
- Zhu, J.; Yan, Y.; Zhao, L.; Heimann, M.; Akoglu, L.; Koutra, D. Beyond Homophily in Graph Neural Networks: Current Limitations and Effective Designs. In Proceedings of the Neural Information Processing Systems, Vancouver, BC, Canada, 6–12 December 2020; pp. 7793–7804. [Google Scholar] [CrossRef]
- Zhu, J.; Rossi, R.A.; Rao, A.; Mai, T.; Lipka, N.; Ahmed, N.K.; Koutra, D. Graph Neural Networks with Heterophily. In Proceedings of the AAAI Conference on Artificial Intelligence, Menlo Park, CA, USA, 2–9 February 2021; pp. 8484–8488. [Google Scholar] [CrossRef]
- Dou, Y.; Liu, Z.; Sun, L.; Deng, Y.; Peng, H.; Yu, P.S. Enhancing Graph Neural Network-based Fraud Detectors against Camouflaged Fraudsters. In Proceedings of the ACM International Conference on Information and Knowledge Management, Virtual Event, Ireland, 19–23 October 2020; pp. 315–324. [Google Scholar] [CrossRef]
- Abed, R.A.; Hamza, E.K.; Humaidi, A.J. A Modified CNN-IDS Model for Enhancing the Efficacy of Intrusion Detection System. Meas. Sens. 2024, 35, 101299. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, X.; He, X.; Liu, Z.; Feng, H.; Zhang, Y. Addressing Heterophily in Graph Anomaly Detection: A Perspective of Graph Spectrum. In Proceedings of the ACM Web Conference 2023, Austin, TX, USA, 30 April–4 May 2023; pp. 1528–1538. [Google Scholar] [CrossRef]
- Yao, K.; Liang, J.; Liang, J.; Li, M.; Cao, F. Multi-View Graph Convolutional Networks with Attention Mechanism. Artif. Intell. 2022, 307, 103708. [Google Scholar] [CrossRef]
- Cunegatto, E.H.T.; Zinani, F.S.F.; Rigo, S.J. Multi-objective optimisation of micromixer design using genetic algorithms and multi-criteria decision-making algorithms. Int. J. Hydromechatron. 2024, 7, 224–249. [Google Scholar] [CrossRef]
- Xu, C.; Tao, D.; Xu, C. A Survey on Multi-view Learning. arXiv 2013, arXiv:1304.5634. [Google Scholar] [CrossRef]
- Jiao, Y.; Xiong, Y.; Zhang, J.; Zhang, Y.; Zhang, T.; Zhu, Y. Sub-graph Contrast for Scalable Self-Supervised Graph Representation Learning. arXiv 2020, arXiv:2009.10273. [Google Scholar]
- Lau, S.L.; Lim, J.; Chong, E.K.; Wang, X. Single-pixel image reconstruction based on block compressive sensing and convolutional neural network. Int. J. Hydromechatron. 2023, 6, 258–273. [Google Scholar] [CrossRef]
- Cui, L.; Seo, H.; Tabar, M.; Ma, F.; Wang, S.; Dong, Y. DETERRENT: Knowledge Guided Graph Attention Network for Detecting Healthcare Misinformation. In Proceedings of the ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Virtual Event, CA, USA, 6–10 July 2020; pp. 492–502. [Google Scholar] [CrossRef]
- Liu, C.; Sun, L.; Ao, X.; Yang, J.; Feng, H.; He, Q. Intention-aware Heterogeneous Graph Attention Networks for Fraud Transactions Detection. In Proceedings of the ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Singapore, 14–18 August 2021; pp. 3280–3288. [Google Scholar] [CrossRef]
- Zhao, T.; Liu, Y.; Neves, L.; Woodford, O.; Jiang, M.; Shah, N. Data Augmentation for Graph Neural Networks. In Proceedings of the AAAI Conference on Artificial Intelligence, Menlo Park, CA, USA, 2–9 February 2021; pp. 11015–11023. [Google Scholar] [CrossRef]
- Huang, M.; Liu, Y.; Ao, X.; Li, K.; Chi, J.; Feng, J.; Yang, H.; He, Q. AUC-oriented Graph Neural Network for Fraud Detection. In Proceedings of the World Wide Web Conference, Lyon, France, 25–29 April 2022; pp. 1311–1321. [Google Scholar] [CrossRef]
- Chien, E.; Peng, J.; Li, P.; Milenkovic, O. Adaptive Universal Generalized PageRank Graph Neural Network. In Proceedings of the International Conference on Learning Representations, Virtual Event, 3–7 May 2021. [Google Scholar] [CrossRef]
- Li, M.; Qiao, Y.; Lee, B. Multi-View Intrusion Detection Framework Using Deep Learning and Knowledge Graphs. Information 2025, 16, 377. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Y.; Tang, J. Detect Anomalies on Multi-View Attributed Networks. Inf. Sci. 2023, 638, 119008. [Google Scholar] [CrossRef]
- Duan, J.; Wang, S.; Zhang, P.; Zhu, E.; Hu, J.; Jin, H.; Liu, Y.; Dong, Z. Graph Anomaly Detection via Multi-Scale Contrastive Learning Networks with Augmented View. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), Washington, DC, USA, 7–14 February 2023; AAAI Press: Menlo Park, CA, USA, 2023; pp. 7459–7467. [Google Scholar] [CrossRef]
- Zhao, T.; Ni, B.; Yu, W.; Cao, J.; Mao, Z.; Liu, C. Action Sequence Augmentation for Early Graph-based Anomaly Detection. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management, Queensland, Australia, 1–5 November 2021; pp. 2668–2678. [Google Scholar] [CrossRef]
- Xu, K.; Li, C.; Tian, Y.; Sonobe, T.; Kawarabayashi, K.i.; Jegelka, S. Representation Learning on Graphs with Jumping Knowledge Networks. In Proceedings of the 35th International Conference on Machine Learning, New York, NY, USA, 10–15 July 2018; pp. 5449–5458. [Google Scholar] [CrossRef]
- Liu, Y.; Ao, X.; Qin, Z.; Chi, J.; Feng, J.; Yang, H.; He, Q. Pick and Choose: A GNN-based Imbalanced Learning Approach for Fraud Detection. In Proceedings of the 30th International World Wide Web Conference, Ljubljana, Slovenia, 19–23 April 2021; pp. 3168–3177. [Google Scholar] [CrossRef]
- Abu-El-Haija, S.; Perozzi, B.; Kapoor, A.; Alipourfard, N.; Lerman, K.; Harutyunyan, H.; Ver Steeg, G.; Galstyan, A. MixHop: Higher-Order Graph Convolutional Architectures via Sparsified Neighborhood Mixing. In Proceedings of the 36th International Conference on Machine Learning, New York, NY, USA, 9–15 June 2019; pp. 21–29. [Google Scholar] [CrossRef]
- Bo, D.; Wang, X.; Shi, C.; Shen, H. Beyond Low-frequency Information in Graph Convolutional Networks. In Proceedings of the AAAI Conference on Artificial Intelligence, Menlo Park, CA, USA, 2–9 February 2021; pp. 3950–3957. [Google Scholar] [CrossRef]
- Tang, J.; Li, J.; Gao, Z.; Li, J. Rethinking Graph Neural Networks for Anomaly Detection. In Proceedings of the 39th International Conference on Machine Learning, New York, NY, USA, 17–23 July 2022; pp. 21076–21089. [Google Scholar] [CrossRef]
- Xu, F.; Wang, N.; Wu, H.; Zhang, X.; Yu, K.; Yuan, Y.; Tang, X. Revisiting Graph-Based Fraud Detection in Sight of Heterophily and Spectrum. In Proceedings of the 38th AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; pp. 9214–9222. [Google Scholar] [CrossRef]
- Zhuo, W.; Liu, Z.; Hooi, B.; Wang, B.; He, G.; Cai, K.; Li, X. Partitioning Message Passing for Graph Fraud Detection. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024. [Google Scholar] [CrossRef]
- Tang, J.; Hua, F.; Gao, Z.; Zhao, P.; Li, J. GADBench: Revisiting and Benchmarking Supervised Graph Anomaly Detection. In Proceedings of the 36th Conference on Neural Information Processing Systems (NeurIPS 2023)—Datasets and Benchmarks Track, Red Hook, NY, USA, 10–16 December 2023. [Google Scholar]



| Dataset | Nodes | Edges | Heterophily of the Graph | Feature |
|---|---|---|---|---|
| Amazon | 11,944 | 4,398,392 | 6.87 | 25 |
| YelpChi | 45,954 | 3,846,979 | 14.53 | 32 |
| Method | YelpChi | Amazon | ||
|---|---|---|---|---|
| F1-Macro | AUC | F1-Macro | AUC | |
| GCN | 0.5157 | 0.5413 | 0.5098 | 0.5083 |
| JKNet | 0.5805 | 0.7736 | 0.8270 | 0.8970 |
| CARE-GNN | 0.5015 | 0.7300 | 0.6313 | 0.8832 |
| PC-GNN | 0.6925 | 0.8118 | 0.8367 | 0.9555 |
| H2GCN | 0.6575 | 0.8406 | 0.9213 | 0.9693 |
| MixHop | 0.6534 | 0.8796 | 0.8093 | 0.9723 |
| GPRGNN | 0.6423 | 0.8355 | 0.8059 | 0.9358 |
| BWGNN | 0.7568 | 0.8967 | 0.9204 | 0.9706 |
| GHRN | 0.7789 | 0.9073 | 0.9282 | 0.9728 |
| SEC-GFD | 0.7773 | 0.9193 | 0.9235 | 0.9823 |
| PMP | 0.8179 | 0.9397 | 0.9220 | 0.9757 |
| MV-GHRN (Ours) | 0.9551 | 0.9882 | 0.9285 | 0.9793 |
| Model | Original View | Perturbed View | Cosine Similarity View | Pruning | Amazon | |
|---|---|---|---|---|---|---|
| F1-Macro | AUC | |||||
| Base Model | ✓ | ✓ | 0.9183 | 0.9439 | ||
| Perturbation Enhancement | ✓ | ✓ | ✓ | 0.9267 | 0.9428 | |
| Similarity Fusion | ✓ | ✓ | ✓ | 0.9301 | 0.9245 | |
| Complete Model | ✓ | ✓ | ✓ | ✓ | 0.9285 | 0.9793 |
| Base Model | ✓ | 0.9194 | 0.9395 | |||
| Perturbation Enhancement | ✓ | ✓ | 0.9244 | 0.9371 | ||
| Similarity Fusion | ✓ | ✓ | 0.9164 | 0.9691 | ||
| Complete Model | ✓ | ✓ | ✓ | 0.9246 | 0.9656 | |
| Method | ||||
|---|---|---|---|---|
| F1-Macro | AUC | F1-Macro | AUC | |
| GCN | 90.36 | 96.52 | 49.15 | 60.40 |
| BWGNN | 91.08 | 97.02 | 52.92 | 65.15 |
| GHRN | 90.14 | 96.71 | 54.69 | 66.13 |
| MV-GHRN | 91.66 | 97.40 | 54.88 | 70.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.; Cui, C.; Wang, Z.; Qi, H.; Tian, Z. Graph Anomaly Detection Algorithm Based on Multi-View Heterogeneity Resistant Network. Information 2025, 16, 985. https://doi.org/10.3390/info16110985
Fan Y, Cui C, Wang Z, Qi H, Tian Z. Graph Anomaly Detection Algorithm Based on Multi-View Heterogeneity Resistant Network. Information. 2025; 16(11):985. https://doi.org/10.3390/info16110985
Chicago/Turabian StyleFan, Yangrui, Caixia Cui, Zhiqiang Wang, Hui Qi, and Zhen Tian. 2025. "Graph Anomaly Detection Algorithm Based on Multi-View Heterogeneity Resistant Network" Information 16, no. 11: 985. https://doi.org/10.3390/info16110985
APA StyleFan, Y., Cui, C., Wang, Z., Qi, H., & Tian, Z. (2025). Graph Anomaly Detection Algorithm Based on Multi-View Heterogeneity Resistant Network. Information, 16(11), 985. https://doi.org/10.3390/info16110985







