A High-Impedance Fault Feeder Detection Method for Resonant Grounded Active Distribution Systems Based on Polarity and Harmonic Wavebody Similarity

Abstract

High-impedance fault (HIF) feeder detection in resonant-grounded active distribution systems remains a challenging issue. In practice, fault currents are typically weak, and the integration of distributed generation (DG) often distorts fault signatures, significantly limiting the effectiveness of existing detection techniques. This paper presents a novel HIF feeder detection method based on the fusion of zero-sequence current (ZSC) cross-correlation polarity analysis and harmonic wavebody similarity matching. Firstly, the HIF mechanism is examined, and the impact of DG on ZSC behavior is characterized, revealing polarity differences among feeders. To suppress high-frequency interference, variational mode decomposition (VMD) is employed to extract low-frequency components indicative of ZSC polarity, which are then subjected to cross-correlation analysis and used as the primary detection indicator. When ZSCs are heavily distorted due to DG, harmonic wavebody similarity serves as a supplementary detection feature. A comprehensive detection criterion is subsequently formulated by combining both analyses. Simulation and experimental results demonstrate that under HIF conditions, the proposed method is robust against variations in fault location, fault type, and noise interference, and can accurately identify the faulty feeder. Moreover, it remains effective for arc grounding, grass grounding, and pond grounding scenarios, highlighting its strong practical applicability.

1. Introduction

Feeder fault detection in medium-voltage distribution networks remains an unresolved challenge, particularly in resonant-grounded active distribution systems [1]. In the case of single-phase-to-ground faults, the current flowing through the faulty feeder may sometimes be lower than that in healthy feeders. Furthermore, when the grounding resistance is excessively high, the fault signature becomes extremely weak, making it difficult for conventional protection schemes to distinguish the occurrence of a high-impedance fault (HIF). As a result, HIF detection has emerged as both a technical challenge and a research hotspot in recent years [2]. According to studies in the domestic and international literature, existing HIF feeder detection methods can broadly be classified into two categories: macroscopic waveform measurement methods in the time domain and conventional microscopic feature extraction methods.

Macroscopic waveform measurement approaches include grey relational analysis [3], correlation analysis [4], spatial relative distance metrics [5], cosine similarity measures [6,7], and dynamic trajectory tracking methods [8,9]. These techniques primarily analyze zero-sequence current (ZSC) characteristics of feeders in the time domain. However, as they fail to differentiate between transient and steady-state components, their detection accuracy often depends heavily on the chosen data window length. Moreover, these methods are largely limited to time-domain analysis, tending to overlook frequency-dependent features that may be critical for accurate detection. Their performance also deteriorates significantly under extreme fault conditions such as strong noise, missing data, or HIF, making it difficult to establish robust and generalizable detection criteria.

Microscopic feature extraction methods aim to detect fault signatures through advanced signal processing techniques. These include various wavelet-based approaches—such as discrete and continuous wavelet transforms [10,11], wavelet packet decomposition [12], and empirical wavelet transform [13]—as well as mode decomposition methods [14,15], mathematical morphology [16], waveform distortion metrics [17], and time–frequency analysis techniques [18]. Detection rules in this category are typically constructed based on characteristic frequency bands. Compared with macroscopic methods, microscopic feature extraction allows for deeper mining of fault-related patterns in the time, frequency, and time–frequency domains, thereby improving detection accuracy to a certain extent. Nevertheless, the effectiveness of these methods often depends on complex feature extraction procedures and expert knowledge. For instance, in wavelet-based methods [19], the choice of basis functions and decomposition levels directly impacts the quality of feature extraction and, consequently, the accuracy of the detection criterion. The advantages and disadvantages of different methods are summarized in Table 1. In addition, due to the high sampling frequencies required, most of these traditional approaches have not yet seen widespread application in practical engineering. For cases such as ground faults caused by wildfires [20], or scenarios requiring rapid tripping, the inherent complexity of feature extraction and decision-making logic prevents these methods from meeting the fast-acting response requirements of modern protection devices. Therefore, a key practical challenge lies in developing a fault feeder detection method that balances simplicity in implementation with accuracy in results, and that remains effective under adverse operating conditions such as strong noise and HIF.

Table 1. Comparative analysis of the advantages and disadvantages of different methods.

Method	Advantages	Disadvantages
Grey relational analysis	Simple computation and low sensitivity to noise	Strong dependence on reference sequence selection; threshold setting is empirical
Correlation analysis	High computational efficiency and easy implementation	Difficult to handle severely distorted signals
Spatial relative distance	Quantitatively distinguishes feeder feature differences	Highly dependent on feature selection
Cosine similarity	Insensitive to amplitude variation; suitable for fast computation	Ineffective in distinguishing weak fault features
Dynamic trajectory measurement	Capable of handling nonlinear time distortion in signals	Computationally intensive with limited real-time performance
Continuous wavelet transform	Captures transient features with high time–frequency resolution	Sensitive to noise interference
Wavelet packet transform	Suitable for quantitative feature extraction	High computational complexity and sensitive to parameter selection
Empirical wavelet transform	Strong frequency-domain adaptability	Sensitive to noise and affected by end effects
Modal decomposition	Good noise immunity and effective extraction of low-frequency features	Requires empirical parameter tuning; limited real-time performance
Mathematical morphology	Effective in detecting abrupt changes and nonlinear distortion	Difficult selection of structural elements; poor noise resistance
Waveform distortion measurement	Sensitive to HIF characteristics; simple implementation	Requires high-precision sampling
Time–frequency analysis	Suitable for non-stationary signal analysis	Limited time–frequency resolution; computationally demanding

In addition, in a distribution network with distributed generation (DG), the DG units are often neglected in the zero-sequence network after a single line-to-ground (SLG) fault, since they are usually connected to the grid through Δ/Y transformers, and the ZSC does not flow through the transformer. However, the zero-sequence network is actually connected in series with the three sequence networks at the fault point. Therefore, when an SLG fault occurs on a feeder with a connected DG unit, the DG will influence the zero-sequence component. In other words, DG should not be directly ignored in the zero-sequence network, as its connection may cause distortion in the zero-sequence current. Consequently, significant differences may exist between the zero-sequence components of networks with and without DG. With increasing DG penetration, existing fault feeder detection methods may become ineffective. To address this issue, this paper proposes a fault feeder detection method suitable for distribution networks with high DG penetration. The main contributions are summarized as follows:

• Consideration of DG interference in the detection scheme design: During an SLG fault, the three sequence networks are connected in series at the fault point, and the harmonics generated by the DG in the positive-sequence network can affect the zero-sequence component. Hence, DG cannot be neglected when analysing zero-sequence fault characteristics, and the detection scheme should be applicable to SLG fault scenarios with or without DG connection.
• Extraction of polarity features and harmonic comparison between feeders: The variational mode decomposition (VMD) algorithm is used to obtain the low-frequency intrinsic mode functions (IMFs) of the ZSCs for each feeder. The cross-correlation of IMFs is employed as the primary detection criterion. Furthermore, considering the harmonic interference caused by high DG penetration, the derivative dynamic time warping (DDTW) distance of the harmonic body derivative is introduced as an auxiliary detection criterion. Finally, a comprehensive detection scheme is established based on both the primary and auxiliary criteria.

The remainder of this paper is organized as follows: Section 2 analyzes the characteristics of the zero-sequence components during SLG faults in DG-connected distribution networks and reveals the DG-induced distortion. Section 3 presents a new fault feeder detection method that explicitly accounts for DG interference. Section 4 validates the fault analysis presented in Section 2 through simulation and field case studies. To further assess the proposed method’s detection performance, the simulation model, fault scenarios, and practical fault data are introduced, followed by comparative analyses. Finally, Section 5 concludes the study.

2. Transient Mechanism Analysis of High-Impedance Ground Fault

As shown in Figure 1, an HIF occurs on feeder 1 in a resonant-grounded active distribution network. The grounding resistance is denoted as R, and the arc suppression coil has an inductance of L_P.

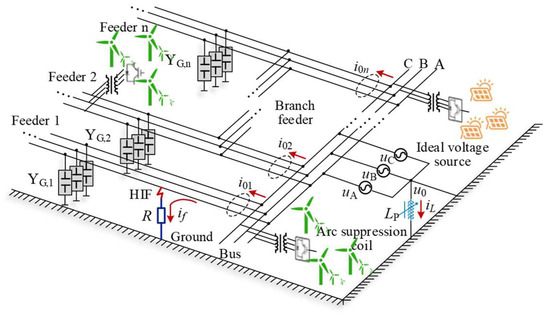
Figure 1. The single-phase-to-ground HIF model of an active distribution network.

When an HIF occurs on Feeder 1 (connected to DG), although the DG branch is open in the zero-sequence network, the current source I_DG in the positive-sequence network can still influence the ZSC on the feeder. The equivalent zero-sequence circuit is shown in Figure 2.

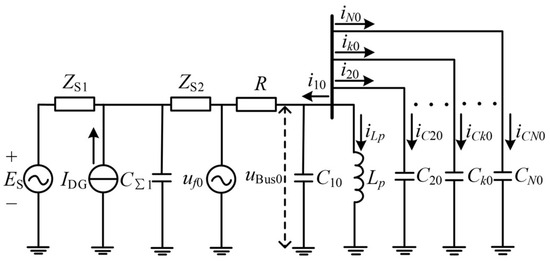
Figure 2. Equivalent circuit model under HIF on feeder 1.

Where Zs₁ and Zs₂ represent the positive and negative-sequence equivalent impedances of the source branches, respectively. C_k0 is the zero-sequence capacitance of Feeder k, and $C_{sum0}={\displaystyle {\sum }_{k=1}^n{c}_{k0}}$ denotes its capacitive zero-sequence current to ground. i_Ck0 is the ZSC flowing through Feeder k; i_Lp is the ZSC through the arc suppression coil; C_∑1 denotes the total positive-sequence capacitance of all feeders. u_f0 is the zero-sequence voltage (ZSV) at the fault point, while u_Bus0 is the busbar ZSV. The grounding resistance at the fault point is denoted as R_f. Under HIF conditions, R = 3R_f, and due to the low resonant frequency and relatively small inductance of the arc suppression coil, the inductive branch has a significant influence. The feeder inductance can be neglected, and the resonant behavior depends mainly on L_P and the distributed capacitance C_sum0.

Considering the harmonic distortion introduced by DG connections, I_DG contains multiple frequency components, leading to harmonic interference at the fault point voltage u_f0 = U₀ sin (ω₀t + φ₀) + U₁ sin (ω₁t + φ₁) + U₂ sin (ω₂t + φ₂) +···+ U_n sin (ω_nt + φ_n). U₀ sin (ω₀t + φ₀) represents the zero-sequence component generated by the source Es, where U₀, ω₀, and φ₀ are its amplitude, angular frequency, and initial phase, respectively. Similarly, U_i sin (ω_it + φ_i) are the harmonic components caused by I_DG, with U_i, ωi, and φ_i representing the amplitude, frequency, and phase of each harmonic. The equations for ZSV and ZSC are given as follows:

$$\left\{\begin{array}{l}{u}_{f0}=u_{bus0}+3R_f(-i_{10}+c_{10}{\displaystyle \frac{d{u}_{Bus0}}{dt}})\hfill \\ u_{bus0}=L_p{\displaystyle \frac{d{i}_{L_p}}{dt}}\hfill \end{array}\right.$$

(1)

$$\left\{\begin{array}{c}{i}_{k0}=c_{k0}{\displaystyle \frac{d{u}_{Bus0}}{dt}}\\ i_{10}=-i_{L_p}-{\displaystyle {\sum }_{k=2}^N{i}_{k0}}\end{array}\right.$$

(2)

In engineering practice, HIF resonance typically occurs under underdamped conditions. Applying the Laplace transform to Equations (1) and (2) and using the principle of superposition yields expressions for U_Bus0 (s), I₁₀ (s), and I_k0 (s) [21], we have

$$\left\{\begin{array}{l}{U}_{Bus0}(s)={\displaystyle {\sum }_{i=0}^n\frac{U_i}{R_f}\frac{s_i{L}_p(s_i\sin {\phi }_i+{\omega }_i\cos {\phi }_i)/\left(3L_p{C}_{sum0}\right)}{\left[s_i^2+s_i/\left(3R_f{C}_{sum0}\right)+1/\left(3L_p{C}_{sum0}\right)\right]\left(s_i^2+{\omega }_i^2\right)}}\hfill \\ I_{L_p}(s)={\displaystyle {\sum }_{i=0}^n\frac{U_i}{3R_f}\frac{(s_i\sin {\phi }_i+{\omega }_i\cos {\phi }_i)/\left(3L_p{C}_{sum0}\right)}{\left[s_i^2+s_i/\left(3R_f{C}_{sum0}\right)+1/\left(3L_p{C}_{sum0}\right)\right]\left(s_i^2+{\omega }_i^2\right)}}\hfill \\ I_{k0}(s)={\displaystyle {\sum }_{i=0}^{n}3s_i^2{L}_p{C}_{k0}{I}_{L_p}(s_i)}\hfill \\ I_{10}(s)=-{\displaystyle {\sum }_{i=0}^n\left[1+s_i^2{L}_p\left(C_{sum0}-C_{10}\right)\right]I_{L_p}(s_i)}\hfill \end{array}\right.$$

(3)

The analysis indicates that for the faulty feeder 1, harmonics are mainly concentrated in the high-frequency range. Given this, the compensation effect of the arc suppression coil becomes negligible. Both the ZSV at the busbar and the ZSC of all feeders are contaminated with DG-induced harmonics. This implies that DG integration can significantly affect the zero-sequence components after an HIF occurs. The harmonics generated by DG propagate from the faulty feeder 1 to the healthy feeder k (k = 2, …, N), resulting in opposite ZSC polarities between the faulty and non-faulty feeders.

When an HIF occurs on a feeder N not connected to DG, and assuming the effects of upstream DG and downstream loads are negligible, the equivalent zero-sequence network is shown in Figure 3.

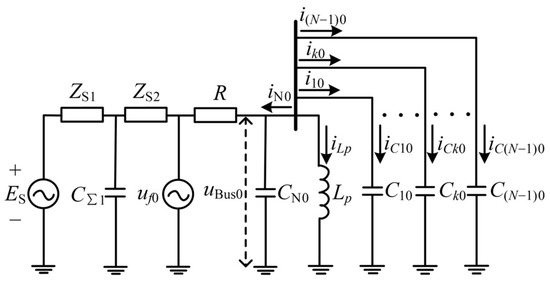
Figure 3. Equivalent circuit model under HIF on feeder N.

The ZSV and ZSC equations for this scenario are expressed as follows:

$$\left\{\begin{array}{l}{u}_{f0}=u_{bus0}+3R_f(-i_{N0}+c_{N0}{\displaystyle \frac{d{u}_{Bus0}}{dt}})\hfill \\ u_{bus0}=L_p{\displaystyle \frac{d{i}_{L_p}}{dt}}\hfill \end{array}\right.$$

(4)

$$\left\{\begin{array}{c}{i}_{k0}=c_{k0}{\displaystyle \frac{d{u}_{Bus0}}{dt}}\\ i_{N0}=-i_{L_p}-{\displaystyle {\sum }_{k=1}^{N-1}{i}_{k0}}\end{array}\right.$$

(5)

Similarly, performing a Laplace transform and applying the superposition principle yields

$$\left\{\begin{array}{l}{U}_{Bus0}(s)={\displaystyle \frac{U_0}{R_f}}{\displaystyle \frac{s{L}_p(s\sin {\phi }_0+{\omega }_0\cos {\phi }_0)/\left(3L_p{C}_{sum0}\right)}{\left[s^2+s/\left(3R_f{C}_{sum0}\right)+1/\left(3L_p{C}_{sum0}\right)\right]\left(s^2+{\omega }_0^2\right)}}\hfill \\ I_{L_p}(s)={\displaystyle \frac{U_0}{3R_f}}{\displaystyle \frac{(s\sin {\phi }_0+{\omega }_0\cos {\phi }_0)/\left(3L_p{C}_{sum0}\right)}{\left[s^2+s/\left(3R_f{C}_{sum0}\right)+1/\left(3L_p{C}_{sum0}\right)\right]\left(s^2+{\omega }_0^2\right)}}\hfill \\ I_{k0}(s)=3s^2{L}_p{C}_{k0}{I}_{L_p}(s)\hfill \\ I_{N0}(s)=-\left[1+3s^2{L}_p\left(C_{sum0}-C_{N0}\right)\right]I_{L_p}(s)\hfill \end{array}\right.$$

(6)

The analysis reveals that even for feeder N without DG, the ZSC polarities between the faulty feeder and healthy feeders remain opposite. In summary, for single-phase HIF in DG-connected distribution networks, the presence of harmonic interference in the zero-sequence components depends on which feeder experiences the fault. If the HIF occurs on a feeder connected to DG, the ZSC will be affected by harmonics. If the fault occurs on a non-DG-connected feeder, such interference is absent. Nonetheless, the opposite polarity of ZSCs between the faulty and non-faulty feeders is consistently observed. Given that harmonic disturbances persist throughout the fault duration, significant distortion may be present in the ZSC during the transient stage. In the steady state, the ZSC of the faulty feeder generally contains more harmonic energy than that of the healthy feeders. Hence, the harmonic content of the ZSC may serve as a secondary indicator, aiding in the distinction between faulty and non-faulty feeders.

3. Faulty Feeder Detection Criteria

Based on the theoretical analysis, it is evident that during the transient stage of a fault, the ZSC polarities of faulty and healthy feeders are opposite. Additionally, if the ZSC is distorted due to DG connection, the harmonic content of the faulted feeder current becomes more pronounced in the steady state than that of healthy feeders. Therefore, both characteristics can be integrated into a composite detection criterion.

• Primary criterion: In distribution networks without DG connections, the transient zero-sequence component during an HIF primarily comprises the fundamental frequency, a DC component, and oscillatory decaying components at the natural resonance frequency [22]. However, when a single-phase-to-ground fault occurs on a DG-connected feeder, the transient ZSC is significantly distorted by harmonic components. In such cases, the original transient ZSC may not clearly reflect polarity characteristics. VMD is an effective adaptive signal decomposition tool that separates the original signal into multiple intrinsic mode functions (IMFs) [23]. When the number of decomposition modes is set to 2, VMD yields a low-frequency IMF₁ representing the overall trend, and a high-frequency IMF₂ representing detailed fluctuations. To illustrate the performance of VMD, consider the synthetic fault transient signal x₁(t):

$$x_1(t)=\sin (2\pi \times 50t+{60}^{\circ })+4e^{-56t}\sin (2\pi \times 1500t+{30}^{\circ })+7.2e^{-102t}\sin (2\pi \times 315t)+e^{-5.5t}$$

(7)

The VMD decomposition result of x₁(t) is shown in Figure 4.

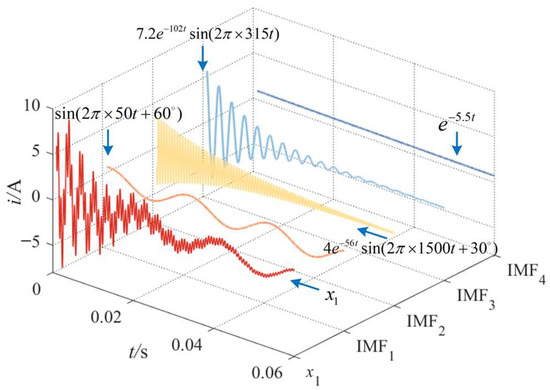
Figure 4. VMD results of example signal x₁.

IMF₁–IMF₄ accurately capture the four distinct components within x₁(t), without mode mixing, thereby verifying the effectiveness of VMD in handling transient fault signals. Additionally, using the HIF model in Figure 5a, the capability of VMD to isolate high-frequency components in a real HIF current signal x₂(t) is assessed.

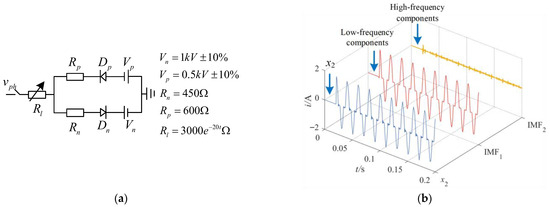
Figure 5. VMD results of HIF current signal x₂(t): (a) HIF model; (b) VMD results of signal x₂(t).

As shown in Figure 5b, IMF₁ captures the overall trend in the ZSC, accurately representing the low-frequency content of the HIF current, while IMF₂ clearly reflects high-frequency components. This confirms that the VMD algorithm is effective for isolating high-frequency components in HIF signals. To characterize the polarity between feeders, cross-correlation analysis is used to compute the correlation coefficients of the IMF₁ components of each feeder, as expressed in Equation (8):

$${\rho }_{mn}={\displaystyle \frac{{\displaystyle {\sum }_{j=1,m\ne n}^p{i}_{IMF1,m}(j)i_{IMF1,n}(j)}}{{\left({\displaystyle {\sum }_{j=1,m\ne n}^p{\left(i_{IMF1,m}(j)\right)}^2}\right)}^{1/2}{\left({\displaystyle {\sum }_{j=1,m\ne n}^p{\left(i_{IMF1,n}(j)\right)}^2}\right)}^{1/2}}}$$

(8)

where i_IMF1,m and i_IMF1,n are the IMF₁ components of ZSC for Feeders m and n, respectively; p is the total number of samples; ρ_mn denotes the correlation coefficient between the ZSC of Feeders m and n. A negative correlation indicates opposite polarities, typical between the faulty and each healthy feeder, while healthy feeders exhibit positive correlation with one another. This allows the polarity of the correlation coefficient to serve as a distinguishing indicator of the faulted feeder.

2.

Auxiliary criterion: In practice, the extracted IMF₁ may fail to reflect polarity if the original signal is significantly distorted due to DG-induced harmonics, asynchronous sampling, data corruption, or varying signal lengths. Under such conditions, relying solely on the primary criterion may lead to misjudgment. To address this, an auxiliary HIF feeder detection criterion is proposed based on harmonic waveform similarity using the DDTW algorithm [24]. DDTW is capable of capturing dynamic variations in harmonic shapes by comparing the derivatives of the harmonic waveforms between feeders. Harmonic currents introduced by DG persist during the fault steady state. By subtracting the DC component—obtained via fast Fourier transform (FFT)—from the original signal, the harmonic signal can be extracted as follows:

$$i_{n,h}(t)=i_n(t)-I_{n,l}\sin ({\omega }_{0}t+{\phi }_{n,l})$$

(9)

where i_n(t) is the original ZSC of feeder n in the steady state (defined here as post 40 ms), and I_n,l is the harmonic component. ${\omega }_0$ and ${\phi }_n^l$ are the amplitude, angular frequency, and initial phase of the n-th harmonic component. The harmonic extraction procedure is illustrated in Figure 6.

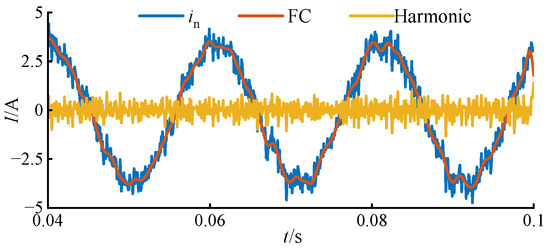
Figure 6. Zero-sequence current harmonic extraction results.

FFT effectively identifies the DC component, enabling accurate extraction of the harmonics. Figure 7 illustrates the alignment process of two arbitrary signals using both classical DTW and DDTW algorithms:

Figure 7. Algorithm alignment procedures: (a) any two signals; (b) classic DTW algorithm alignment process; (c) DDTW algorithm alignment process.

It is evident that classical DTW may lead to singularity issues and redundant alignments during harmonic comparison. In contrast, DDTW introduces slope constraints during dynamic programming, reducing misalignment. Assume that the extracted harmonic waveforms are Q = q₁, q₂, …q_i, …q_n, and C = c₁, c₂, …c_j, …c_m. A cost matrix of size n × m is constructed, where each element represents the squared difference of the derivatives between q_i and c_j, computed as d (q_i, c_j) = (D_x [q]_i − D_x [c]_j)². The estimated derivative formula is as follows:

$$D_x[q]=\left\{\begin{array}{l}{D}_q[i]={\displaystyle \frac{(q_i-q_{i-1})+((q_{i+1}-q_{i-1})/2)}{2}},1<i<m\hfill \\ D_q[0]=D_q[1]\hfill \\ D_q[m]=D_q[m-1]\hfill \end{array}\right.$$

(10)

The accumulated distance γ (i, j), representing the optimal alignment cost up to point (i, j), is defined as follows:

$$\gamma (i,j)=d(q_i,c_j)+\min \left[\gamma (i-1,j-1),\gamma (i-1,j),\gamma (i,j-1)\right]$$

(11)

where min [γ (i −1, j −1),γ (i −1, j),γ (i, j −1)] represents updating the cumulative distance from the optimal regularized path. By computing the value of min γ (i, j), the DDTW distance between harmonic waveforms is obtained. For a distribution network with n feeders, the detection matrix C_CTW is defined as follows:

$$C_{CTW}=\left[\begin{array}{lllll}1\hfill & DDT{W}_{21}\hfill & \dots \hfill & DDT{W}_{(n-1)1}\hfill & DDT{W}_{n1}\hfill \\ {\rho }_{12}\hfill & 1\hfill & \dots \hfill & DDT{W}_{(n-1)2}\hfill & DDT{W}_{n2}\hfill \\ \dots \hfill & \dots \hfill & \dots \hfill & \dots \hfill & \dots \hfill \\ {\rho }_{1(n-1)}\hfill & {\rho }_{2(n-1)}\hfill & \dots \hfill & 1\hfill & DDT{W}_{(n-1)n}\hfill \\ {\rho }_{1n}\hfill & {\rho }_{2n}\hfill & \dots \hfill & {\rho }_{(n-1)n}\hfill & 1\hfill \end{array}\right]$$

(12)

In this matrix, the lower triangular part represents the cross-correlation coefficients ρ between feeders, the diagonal elements are set to 1 (self-correlation), and the upper triangular part contains the DDTW distances between feeders. The overall HIF feeder detection procedure is shown in Figure 8.

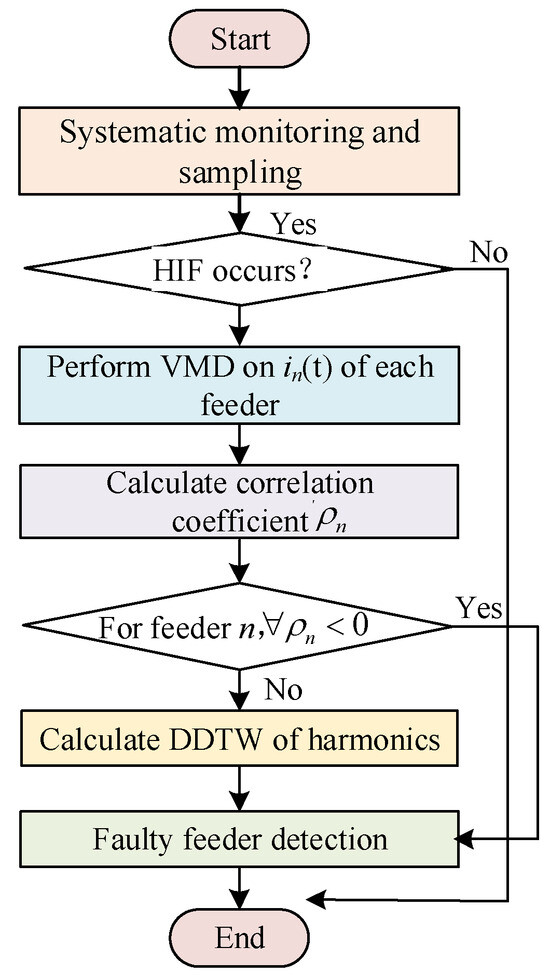
Figure 8. Flowchart of the HIF feeder detection criterion.

Specifically, when an HIF occurs, VMD is first used to compute the low-frequency IMF₁ of each feeder’s ZSC. The cross-correlation coefficients are then calculated. If a feeder exhibits a negative correlation with all others, it is identified as the faulty feeder. If all correlation coefficients are positive, the event is considered a busbar fault. Otherwise, DDTW is applied to compare harmonic waveform similarity. If a feeder has the maximum DDTW distance from all others, it is determined to be the faulted feeder.

4. Simulation Testing and Experimental Validation

To comprehensively evaluate the proposed method, tests are conducted on a resonant-grounded distribution system (radial active distribution network), an improved IEEE-34 node distribution system with an ungrounded neutral point, and real-world field experiments.

4.1. Simulation Testing

4.1.1. Radial Distribution System

A radial active distribution network, as illustrated in Figure 9, is modelled in PSCAD/EMTDC. The system parameters are listed in Table 2 and Table 3. In Figure 9, R_L and L represent the resistance and inductance of the arc suppression coil, respectively. The system neutral point is grounded via the arc suppression coil, with a compensation degree of 5%. Specifically, R_L = 3.0662 Ω and L = 325.5 mH.

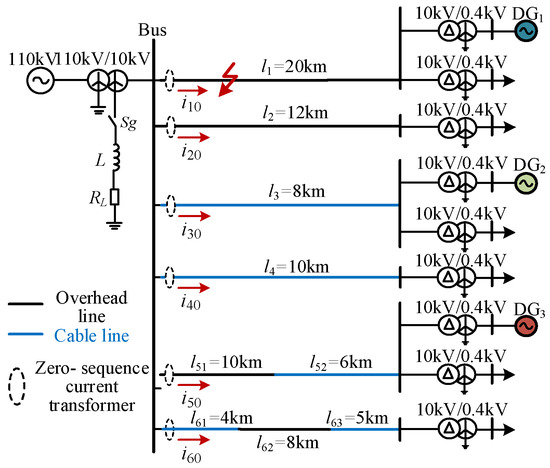
Figure 9. Structure of a radial active distribution network.

Table 2. Simulation model line parameters.

Circuit Type	Resistance (Ω·km−1)		Inductance (mH·km−1)		Grounding Capacitance (μF·km−1)
	Positive Phase	Zero Phase	Positive Phase	Zero Phase	Positive Phase	Zero Phase
Overhead line	0.178	0.25	1.21	5.54	0.015	0.012
Cable line	0.27	2.7	0.255	1.02	0.339	0.28

Table 3. Parameters of DG.

DG	Type	Capacity (MW)	Transmission Length (km)
DG1	Wind farm	4	25 km
DG2	Photovoltaic power station	0.8	12 km
DG3	Photovoltaic power station	0.3	7 km

To better align with practical engineering conditions, the sampling frequency is set to 12.8 kHz, and random noise is added during sampling. When a single-phase HIF with an initial fault angle of 60° and a fault resistance of 2 kΩ occurs at 5 km along feeder l₁, the ZSC, low-frequency IMF₁, and harmonic components of feeders l₁ to l₆ are shown in Figure 10.

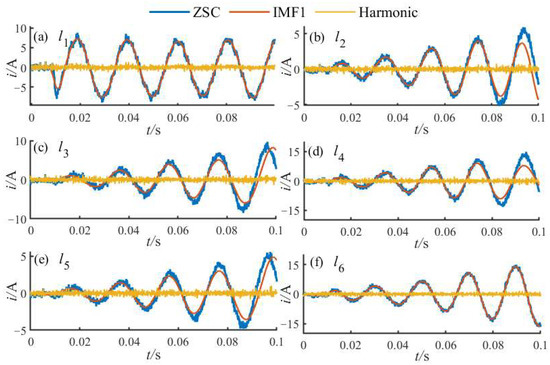
Figure 10. Current components of each feeder.

The computed detection criterion matrix C_CTW is presented in Table 4.

Table 4. The HIF detection criterion C_CTW for feeder l₁.

CCTW	DDTW1	DDTW2	DDTW3	DDTW4	DDTW5	DDTW6
ρ1	1	20.8091	15.3875	14.0662	13.5333	20.8311
ρ2	−0.6702	1	7.2124	5.7294	5.5772	12.0977
ρ3	0.2157	−0.6785	1	5.3213	4.5923	8.7427
ρ4	−0.2862	0.9997	−0.6764	1	3.9488	5.7972
ρ5	0.6591	−0.6782	0.8996	−0.6760	1	6.4779
ρ6	−0.8097	0.1456	−0.6253	0.1490	−0.6262	1

A visual representation of the C_CTW matrix is provided in Figure 11.

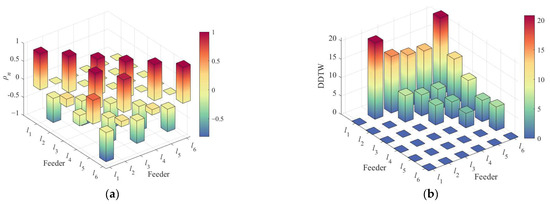
Figure 11. C_CTW graph of fault on feeder l₁: (a) correlation coefficient ρ_mn; (b) DDTW distance.

From the first column of the C_CTW matrix, it is observed that the ρ between the faulty feeder l₁ and the healthy feeders l₂, l₄, and l₆ are negative: ρ₂₁ = −0.6702, ρ₄₁ = −0.2862, and ρ₆₁ = −0.8097. However, the correlation coefficients between l₁ and feeders l₃ and l₅ are positive: ρ₃₁ = 0.2157 and ρ₅₁ = 0.6591. Furthermore, the correlation coefficients between healthy feeders l₃, l₅ and l₂, l₄, l₆ are negative, while ρ₅₃ = 8996. These results, clearly visualized in Figure 11a, indicate that feeders l₃ and l₅, which are connected to DG, are affected by harmonic interference. If only the primary detection criterion is used, it would falsely identify l₁, l₃, and l₅ as faulty, resulting in a misjudgment. Therefore, it is necessary to calculate the DDTW distances as an auxiliary criterion. As shown in Figure 11b, the DDTW distances between the faulted feeder l₁ and all healthy feeders are significantly larger than those among the healthy feeders themselves. According to the proposed detection criterion, feeder l₁ is thus correctly identified as the faulted feeder, demonstrating the method’s accuracy.

4.1.2. Modified IEEE-13 Node Distribution System

Building upon the radial active distribution network, a modified IEEE-13 node distribution system, as shown in Figure 12, is used for verification. The system operates at 4.16 kV, with DG connected at nodes 634 and 675.

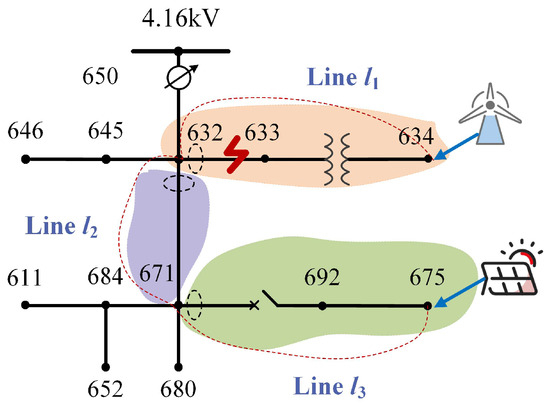
Figure 12. Improved IEEE 13-node distribution network model.

The system contains four feeders. Two HIFs are introduced: a 2 kΩ phase-A HIF at node 633 on feeder l₁, and a 4 kΩ phase-C HIF at node 684 on feeder l₄. The ZSC, low-frequency IMFs, and harmonic components of each feeder are illustrated in Figure 13.

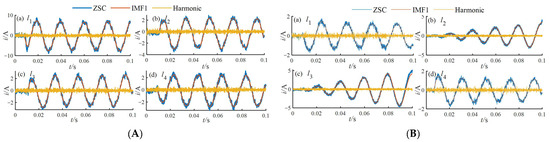
Figure 13. Current components of each faulty feeder: (A) feeder l₁; (B) feeder l₄.

The computed detection criterion matrix C_CTW is presented in Table 5 and Table 6.

Table 5. The HIF detection criterion C_CTW for feeder l₁.

CCTW	DDTW1	DDTW2	DDTW3	DDTW4
ρ1	1	11.3263	12.7901	14.3685
ρ2	−0.1136	1	0.9608	9.8719
ρ3	−0.0918	0.9895	1	10.5341
ρ4	0.8881	−0.9788	−0.9751	1

Table 6. The HIF detection criterion C_CTW for feeder l₄.

CCTW	DDTW1	DDTW2	DDTW3	DDTW4
ρ1	1	3.0576	5.4211	7.5452
ρ2	0.4403	1	3.1609	8.1371
ρ3	0.4369	0.999	1	10.4744
ρ4	−0.3598	−0.4619	−0.4708	1

A visual representation of the C_CTW matrix is provided in Figure 14.

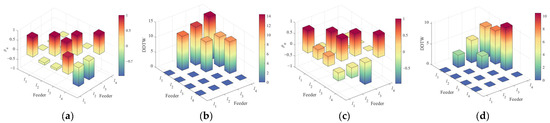
Figure 14. C_CTW graph of fault on each feeder: (a) correlation coefficient ρ_mn of feeder l₁; (b) DDTW distance of feeder l₁; (c) correlation coefficient ρ_mn of feeder l₄; (d) DDTW distance of feeder l₄.

Figure 14 presents the correlation coefficients ρ and DDTW distances between feeders. When a fault occurs on feeder l₁, the correlation values are ρ₁₂ = −0.1136 and ρ₁₃ = −0.0918 between l₁ and feeders l₂ and l₃, respectively. However, due to harmonic interference, ρ₁₄ = 0.8881 between l₁ and feeder l₄. According to the C_CTW matrix, the DDTW distances between l₁ and the healthy feeders are the highest, thus feeder l₁ is accurately identified as the faulted feeder. When a fault occurs on feeder l₄, the correlation values between l₄ and the healthy feeders are all negative: ρ₁₄ = −0.3598, ρ₂₄ = −0.4619, and ρ₃₄ = −0.4708. This indicates that the healthy feeders are unaffected by harmonics. Based on the primary detection criterion, feeder l₄ is correctly identified as the faulty feeder.

4.1.3. Modified IEEE-34 Node Distribution System

The modified IEEE-34 node distribution system, shown in Figure 15, is used for further verification. This system operates at a rated voltage of 24.9 kV, with the three-phase lines divided into five feeders. Distributed generators are connected at nodes 828, 844, 850, and 890.

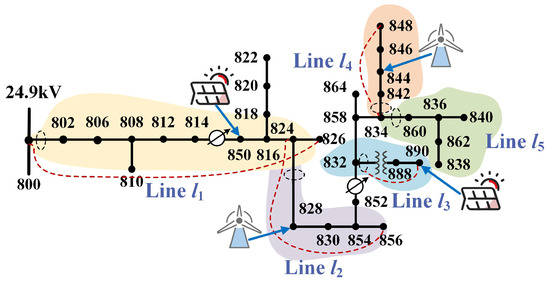
Figure 15. Improved IEEE 34-node distribution network model.

Under both resonant-grounded and ungrounded neutral configurations, two high-impedance faults are simulated: a 6 kΩ phase-B HIF at node 828 on feeder l₂, and a 3 kΩ phase-A HIF at node 836 on feeder l₅. The ZSC, low-frequency IMFs, and harmonic components of each feeder are shown in Figure 16.

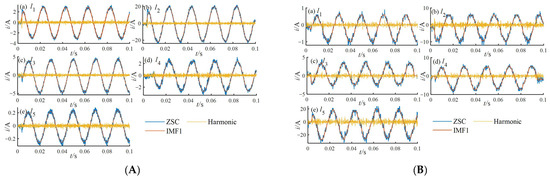
Figure 16. Current components of each faulty feeder: (A) feeder l₂; (B) feeder l₅.

The computed detection criterion matrix C_CTW is presented in Table 7 and Table 8.

Table 7. The HIF detection criterion C_CTW for feeder l₂.

CCTW	DDTW1	DDTW2	DDTW3	DDTW4	DDTW5
ρ1	1	61.4813	37.4685	41.1732	5.5420
ρ2	−0.9273	1	90.0416	98.4426	8.1651
ρ3	0.5782	−0.4296	1	50.2558	4.8783
ρ4	−0.3646	0.4028	−0.9979	1	4.2966
ρ5	0.5437	−0.3345	0.8287	−0.9954	1

Table 8. The HIF detection criterion C_CTW for feeder l₅.

CCTW	DDTW1	DDTW2	DDTW3	DDTW4	DDTW5
ρ1	1	49.2056	42.3351	44.4766	60.0965
ρ2	0.8528	1	85.4203	69.6570	92.9343
ρ3	0.4093	0.5845	1	79.1290	103.5503
ρ4	0.9546	0.1287	0.4160	1	88.0595
ρ5	−0.5381	−0.4560	−0.7532	−0.3378	1

A visual representation of the C_CTW matrix is provided in Figure 17.

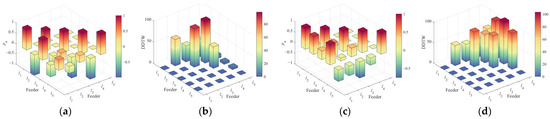
Figure 17. C_CTW graph of fault on each feeder: (a) correlation coefficient ρ_mn of feeder l₂; (b) DDTW distance of feeder l₂; (c) correlation coefficient ρ_mn of feeder l₅; (d) DDTW distance of feeder l₅.

Analysis shows that when feeder l₂ is faulted, the correlation coefficient ρ₂₄ = 0.4028 due to harmonic interference, while the correlation values between l₂ and other feeders are all negative. From the DDTW results, the DDTW distances between l₂ and the healthy feeders are the largest. Based on the detection criteria, feeder l₂ is correctly identified as the faulted feeder. When a fault occurs on feeder l₅, the correlation values with the other feeders are all negative: ρ₁₅ = −0.5381, ρ₂₅ = −0.4560, ρ₃₅ = −0.7532, and ρ₄₅ = −0.3378, while all other inter-feeder correlations are positive. This indicates that the healthy feeders are not affected by harmonics. As such, feeder l₅ is accurately identified as the faulted feeder.

4.2. Field Experiments

The field experiments were conducted in the 10 kV distribution network full-scale experimental laboratory located in Shanxi Province, and the experimental topology is illustrated in Figure 18g. Fault indicators with a sampling frequency of 12.8 kHz were installed at measurement points M₁–M₆ to record the three-phase currents and zero-sequence currents. Feeders l₁ and l₂ are indoor overhead lines with lengths of 3 km and 4 km, respectively, while feeders l₃ and l₄ are indoor cable lines with lengths of 5 km and 6 km. Feeders l₅ and l₆, with lengths of 4 km and 3.5 km, are outdoor experimental lines used to perform arc-grounding, grass-grounding, and pond-grounding fault tests.

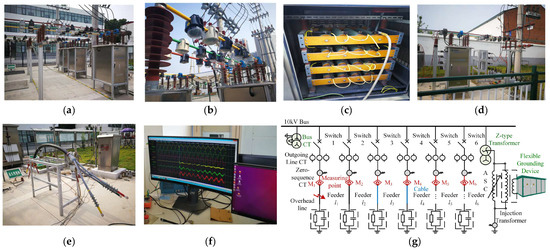
Figure 18. 10 kV distribution network experimental site and topology: (a) test control system; (b) measurement devices; (c) HIF; (d) grassland grounding; (e) arc grounding; (f) fault recording; (g) experimental topology.

The neutral grounding mode of the experimental system can be switched among low-resistance grounding, arc-suppression coil grounding, and ungrounded configurations. In addition to HIF tests, experiments involving arc-grounding, grass-grounding, and pond-grounding conditions were also conducted to verify the robustness of the proposed detection method. The experimental setups for the HIF, grass-grounding, and arc-grounding conditions are shown in Figure 18c–e.

Under ungrounded neutral conditions, a 4 kΩ phase-B HIF was applied 2 km along feeder l₁ with an initial fault angle of 30°. The three-phase currents, ZSC, low-frequency IMFs, and harmonic components of all feeders are shown in Figure 19.

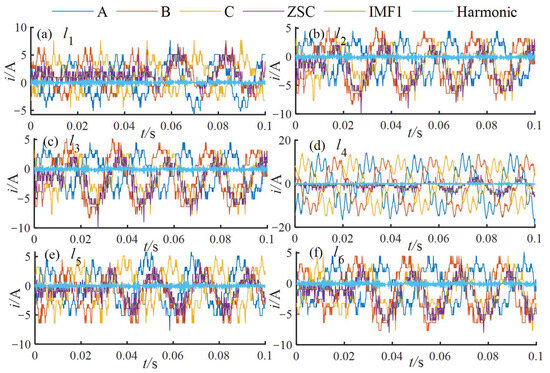
Figure 19. Current components of each feeder under HIF.

The computed detection criterion matrix C_CTW is presented in Table 9.

Table 9. The HIF detection criterion C_CTW for feeder l₁.

CCTW	DDTW1	DDTW2	DDTW3	DDTW4	DDTW5	DDTW6
ρ1	1	103.3396	109.269	82.8989	112.6667	109.2198
ρ2	−0.1228	1	55.1020	98.7480	87.8737	80.4166
ρ3	0.3927	−0.9757	1	57.7191	57.0541	52.4875
ρ4	0.4597	−0.2357	0.3441	1	98.4366	96.5652
ρ5	−0.5843	0.4561	−0.0247	−0.4112	1	86.3261
ρ6	0.7644	−0.7610	0.8024	0.2448	−0.1568	1

A visual representation of the C_CTW matrix is provided in Figure 20.

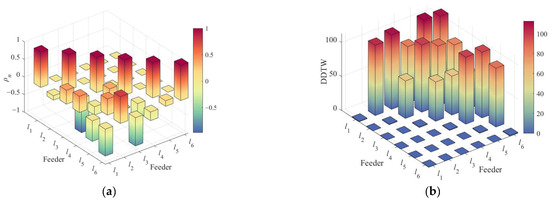
Figure 20. C_CTW graph of fault on feeder l₁: (a) correlation coefficient ρ_mn; (b) DDTW distance.

As shown in Table 8, due to harmonic interference, the correlation coefficients between feeder l₁ and other feeders are ρ₁₃ = 0.3927, ρ₁₄ = 0.4597, and ρ₁₆ = 0.7644. All other ρ between l₁ and healthy feeders are negative. Meanwhile, the DDTW distances between the faulted feeder l₁ and the healthy feeders are all the largest. Based on the auxiliary detection criterion, l₁ is accurately identified as the faulted feeder. Under the 2Ω resistance-grounded condition, a phase-A arc grounding fault was applied to feeder l₅. The corresponding three-phase currents, ZSC, low-frequency IMF, and harmonic components are shown in Figure 21.

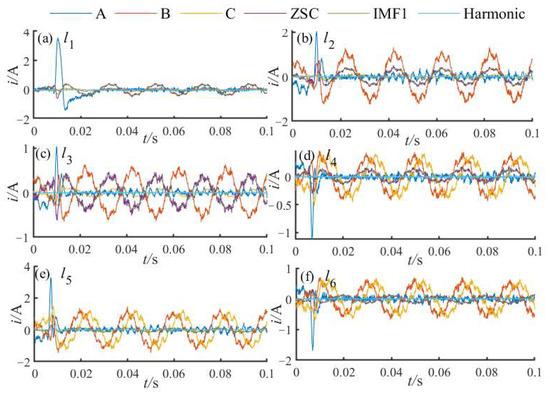
Figure 21. Current components of each feeder under arc grounding fault.

The computed detection criterion matrix C_CTW is presented in Table 10.

Table 10. The HIF detection criterion C_CTW for feeder l₅.

CCTW	DDTW1	DDTW2	DDTW3	DDTW4	DDTW5	DDTW6
ρ1	1	8.7430	10.4094	7.8901	22.4979	10.4093
ρ2	−0.3993	1	4.3695	2.7418	38.3095	5.3566
ρ3	0.7946	−0.6952	1	8.2305	16.7715	8.9006
ρ4	0.4246	−0.4248	0.2202	1	10.0241	3.6140
ρ5	−0.6203	0.3225	−0.3158	−0.7942	1	14.5088
ρ6	−0.2196	0.2210	−0.4152	−0.9886	0.2933	1

A visual representation of the C_CTW matrix is provided in Figure 22.

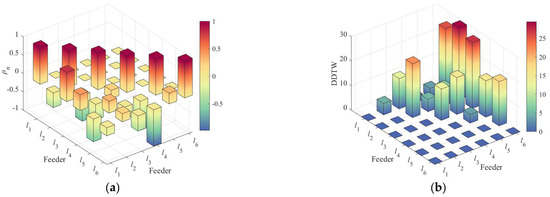
Figure 22. C_CTW graph of fault on feeder l₅: (a) Correlation coefficient ρ_mn; (b) DDTW distance.

Further analysis reveals that when feeder l₅ experiences a fault, the correlation coefficients ρ₂₅ = 0.3225 and ρ₅₆ = 0.2933 indicate that feeders l₂ and l₆ are affected by harmonic interference. The DDTW distances between the faulted feeder l₅ and the remaining feeders are all the largest, and based on the detection criterion, l₅ is correctly identified as the faulted feeder. When feeder l₆ undergoes a phase-C grassland grounding fault under arc-suppression coil grounding, the three-phase current, ZSC, low-frequency IMF, and harmonic components for all feeders are shown in Figure 23.

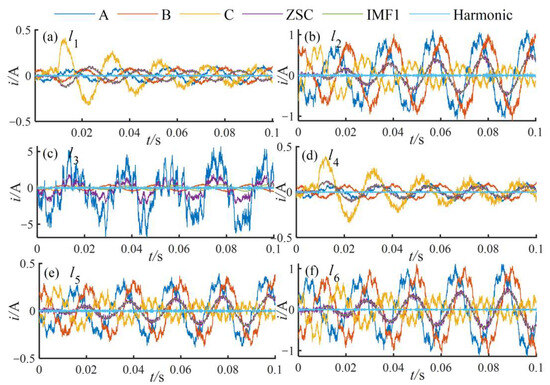
Figure 23. Current components of each feeder under the grassland grounding fault.

The computed detection criterion matrix C_CTW is presented in Table 11.

Table 11. The HIF detection criterion C_CTW for feeder l₆.

CCTW	DDTW1	DDTW2	DDTW3	DDTW4	DDTW5	DDTW6
ρ1	1	4.6898	12.4025	2.6657	3.5460	25.5125
ρ2	−0.4012	1	22.0311	5.0688	7.4278	29.4411
ρ3	−0.6825	0.6011	1	12.7987	15.0379	44.9667
ρ4	−0.9539	0.3624	0.4540	1	3.2865	14.8427
ρ5	−0.4521	0.5722	0.2453	0.1131	1	18.0890
ρ6	0.3973	−0.9942	−0.5983	−0.3613	−0.7665	1

A visual representation of the C_CTW matrix is provided in Figure 24.

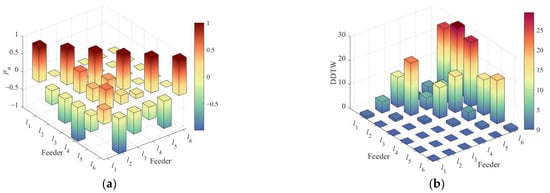
Figure 24. C_CTW graph of fault on feeder l₆: (a) correlation coefficient ρ_mn; (b) DDTW distance.

In this case, ρ₆₁ = 0.3973, while the correlation coefficients between l₆ and the other feeders are all negative, suggesting that only feeder l₁ is affected by harmonic interference. According to the DDTW values, the faulted feeder l₆ shows the largest distances from all other feeders; thus, l₆ is accurately identified as the faulted feeder. Under ungrounded neutral conditions, a phase-B pond grounding fault is introduced on feeder l₅. The corresponding three-phase current, ZSC, low-frequency IMF, and harmonic components are presented in Figure 25.

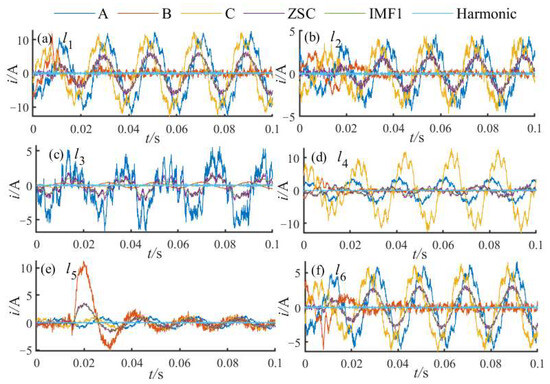
Figure 25. Current components of each feeder under the pond grounding fault.

The computed detection criterion matrix C_CTW is presented in Table 12.

Table 12. The HIF detection criterion C_CTW for feeder l₅.

CCTW	DDTW1	DDTW2	DDTW3	DDTW4	DDTW5	DDTW6
ρ1	1	95.2771	95.9331	102.0915	116.3298	91.4684
ρ2	0.2137	1	65.175	70.6606	97.5853	59.3961
ρ3	0.1348	0.4527	1	37.6901	106.8931	63.2492
ρ4	0.6283	0.2456	0.9917	1	82.2889	71.3805
ρ5	−0.1973	−0.5081	−0.2561	−0.8501	1	100.1761
ρ6	0.9831	0.3254	0.2421	0.5359	−0.3932	1

A visual representation of the C_CTW matrix is provided in Figure 26.

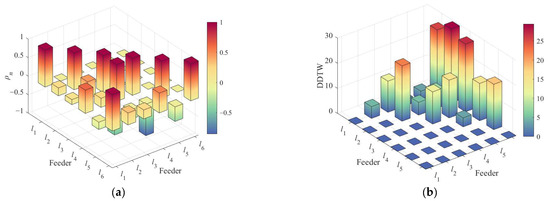
Figure 26. C_CTW graph of fault on feeder l₅: (a) correlation coefficient ρ_n; (b) DDTW distance.

The correlation coefficients in this scenario are: ρ₅₁ = −0.1973, ρ₅₂ = −0.5081, ρ₅₃ = −0.2561, ρ₅₄ = −0.8501, and ρ₅₆ = −0.3932. All ρ_mn between the faulted feeder and the others are negative, satisfying the primary detection criterion, thereby confirming l₅ as the faulted feeder. These experimental results demonstrate that the proposed method not only accurately detects HIF but also reliably identifies faulty feeders under arc-grounding, grassland-grounding, and pond-grounding conditions, exhibiting strong robustness and adaptability.

4.3. Comparison with Existing Methods

To validate the effectiveness of the proposed method, experiments were conducted in the 10 kV distribution network full-scale experimental laboratory under different conditions using the field experimental topology and measured data. Three test conditions were considered: A. grounding resistance of 2000 Ω with a signal-to-noise ratio (SNR) of 5 dB; B. grounding resistance of 3000 Ω with an SNR of 3 dB; and C. arc fault condition. Under conditions A and B, a SLG occurred on feeder l₁, whereas under condition C, an arc fault was introduced on feeder l₅. The proposed method was compared with several existing approaches, namely the first half-wave polarity method [25], the correlation analysis method [26], the maximum energy method [27], and the dynamic voltage–current characteristic method [28]. The detection results are summarized in Table 13.

Table 13. Detection results by different methods.

Method	Criteria	Scene	Detection Criteria Matrix						Result
Paper [25]	first half wave polarity	A	[+ + + + + +]						✗
		B	[+ + + − + +]						✗
		C	[− + + + + +]						✗
Paper [26]	correlation analysis (ρmax − ρmin > 0.20)	A	[0.22 −0.16 0.39 0.46 0.25 0.62]						✗
		B	[−0.23 0.20 0.28 0.35 0.76 0.45]						✗
		C	[0.19 0.57 0.19 0.43 0.34 −0.28]						✗
Paper [27]	Max (EIMFs)	A	[1640 146.0 1616 1113 1077 982]						✓
		B	[64.46 87.57 782.8 479.9 591.2 717.8]						✗
		C	[1.992 2.376 6.194 5.321 8.232 7.934]						✓
Paper [28]	The direction of the VCCP	A	[→ ← ← → → →]						✗
		B	[→ ← ← ← ← ←]						✓
		C	[← ← ← ← → ←]						✓
This paper	CCTW	A	1	104.82	110.35	104.27	111.68	108.57	✓
			−0.13	1	56.41	97.92	88.23	79.51
			0.41	−0.96	1	58.26	56.78	51.84
			0.46	−0.24	0.35	1	99.01	95.72
			−0.59	0.45	−0.03	−0.40	1	87.10
			0.77	−0.75	0.80	0.25	−0.16	1
		B	1	24.1023	15.9120	14.4501	13.1205	21.4567	✓
			−0.6620	1	7.3451	5.8123	5.6789	12.3456
			0.2245	−0.6890	1	5.2678	4.6100	8.9123
			−0.2950	0.9975	−0.6732	1	3.9344	5.8456
			0.6489	−0.6723	0.8931	−0.6725	1	6.5234
			−0.8012	0.1487	−0.6190	0.1567	−0.6289	1
		C	1	9.0148	10.7256	7.6421	22.8467	10.5384	✓
			−0.3841	1	4.5213	2.6194	38.0972	5.2846
			0.7824	−0.6895	1	8.1783	16.8237	8.9562
			0.4172	−0.4189	0.2289	1	9.9623	3.7018
			−0.6287	0.3198	−0.3112	−0.7871	1	14.6894
			−0.2263	0.2237	−0.4125	−0.9854	0.2892	1

The ← → is the detection criteria in paper [28]. ✗/✓ reprenent detection result.

Due to the minimal waveform differences in the first half-cycle between the faulted and healthy feeders, the polarity-based detection often fails—the polarity of the healthy feeder’s waveform is difficult to ascertain, leading to incorrect fault identification. According to the criterion in [26], the correlation analysis method determines the faulty feeder as the one corresponding to the minimum ρ value when the range ρ_max − ρ_min > 0.20. However, as seen in Table 13, under HIF conditions with data window lengths of 5 ms, 10 ms, and 20 ms, this method gives incorrect results. This is because the correlation method uses post-fault current waveforms within 0.25–1 cycles, which reflect macro-level features susceptible to waveform distortion. In cases where the fault occurs at the end of an overhead line and the healthy feeder is a cable, the fault current magnitude may be lower than that of the cable feeder. Under HIF conditions, this significantly distorts the initial polarity, leading to frequent misjudgment using the correlation method. The method of [25] is capable of detecting arc faults; however, it fails when the grounding resistance is excessively high or the noise level is severe. Similarly, the method presented in [26] is unable to identify the faulted feeder under high-impedance or strong-noise conditions. The proposed C_CTW criterion, which integrates the ZSC correlation coefficient and DDTW distance, captures the fault characteristics from a microscopic perspective. It reveals the intrinsic difference in the matching behavior of ZSC direction and harmonic waveform similarity between faulted and healthy feeders, thus achieving accurate detection results.

Furthermore, the computational complexity and scalability of the proposed method were analyzed. Specifically, the main operations involve VMD and correlation analysis, yielding an overall computational complexity of approximately O (N·k), where N denotes the number of sampling points and k the number of decomposition modes (N = 1280, k = 2 in the proposed). Compared with data-driven deep learning approaches, the proposed method requires significantly fewer parameters and lower computational resources, making it suitable for real-time deployment in feeder terminal units (FTUs) or distribution management systems (DMSs).

5. Conclusions

This paper addresses the issue of low detection accuracy of HIF feeders in resonant grounded active distribution systems and proposes a faulted feeder detection method based on ZSC cross-correlation polarity analysis and harmonic waveform similarity matching. The main conclusions are as follows:

• The ZSC characteristics of the distribution network with DG under HIF conditions were analyzed. The polarity differences among feeder ZSCs were revealed, leading to the conclusion that when DG is connected to the faulted feeder, the generated harmonics cause ZSC distortion.
• The VMD algorithm was employed to extract the low-frequency components of feeder ZSCs, and the cross-correlation analysis was adopted as the primary detection criterion to capture polarity features among feeders. Furthermore, when ZSC distortion is severe due to DG connection, the harmonic characteristics of ZSCs are utilized to construct an auxiliary criterion.
• Simulation and field experiments demonstrated that, under HIF conditions, the proposed detection criteria are unaffected by grounding resistance, initial fault phase angle, or strong noise interference. The method remains applicable under arc, grass, and pond grounding scenarios, accurately identifying the faulted feeder. Compared with existing methods, the proposed approach offers computational simplicity, stable performance, and strong potential for engineering applications.

Future work will focus on further enhancing the adaptability of the proposed method under multi-source integration and complex operating conditions. Deep learning techniques will be incorporated for intelligent feature extraction and parameter self-optimization. Moreover, multi-source information fusion will be explored to establish comprehensive fault detection criteria, and studies on online and embedded implementation will be conducted to promote practical deployment in active distribution systems.