Multi-Robot Navigation System Design Based on Proximal Policy Optimization Algorithm
Abstract
1. Introduction
2. Preliminary
2.1. Environment
2.2. Equipment
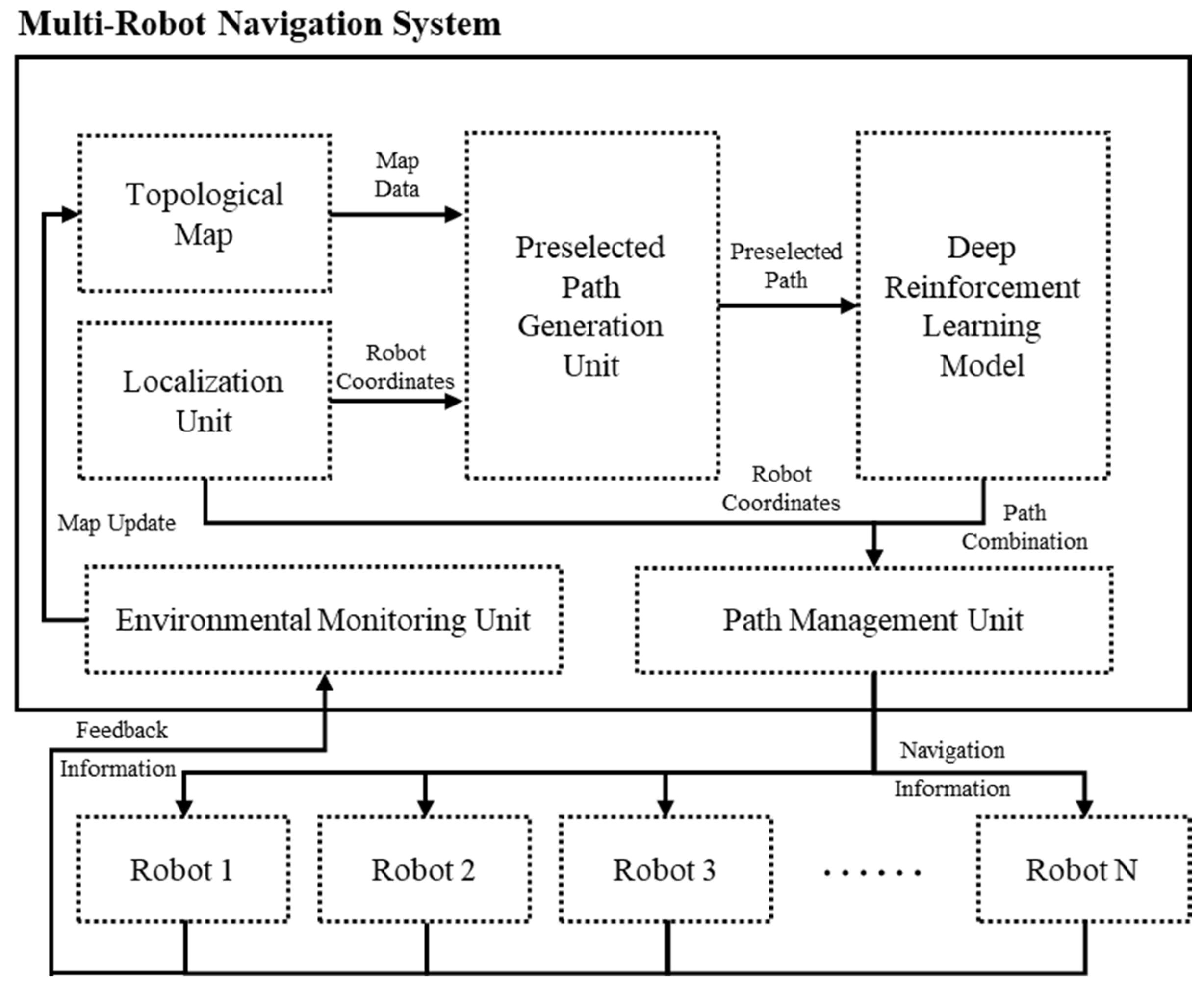
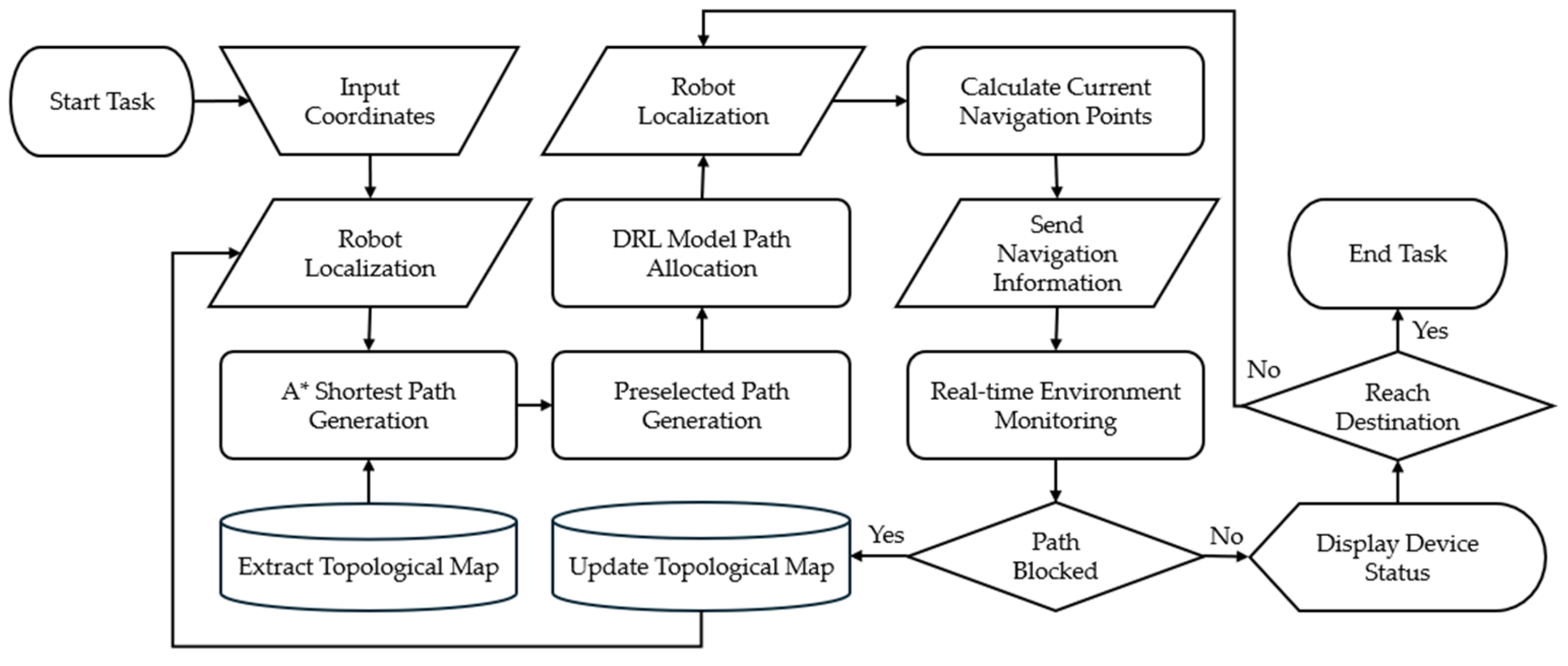
3. Multi-Robot Navigation System
3.1. System Architecture and Processes
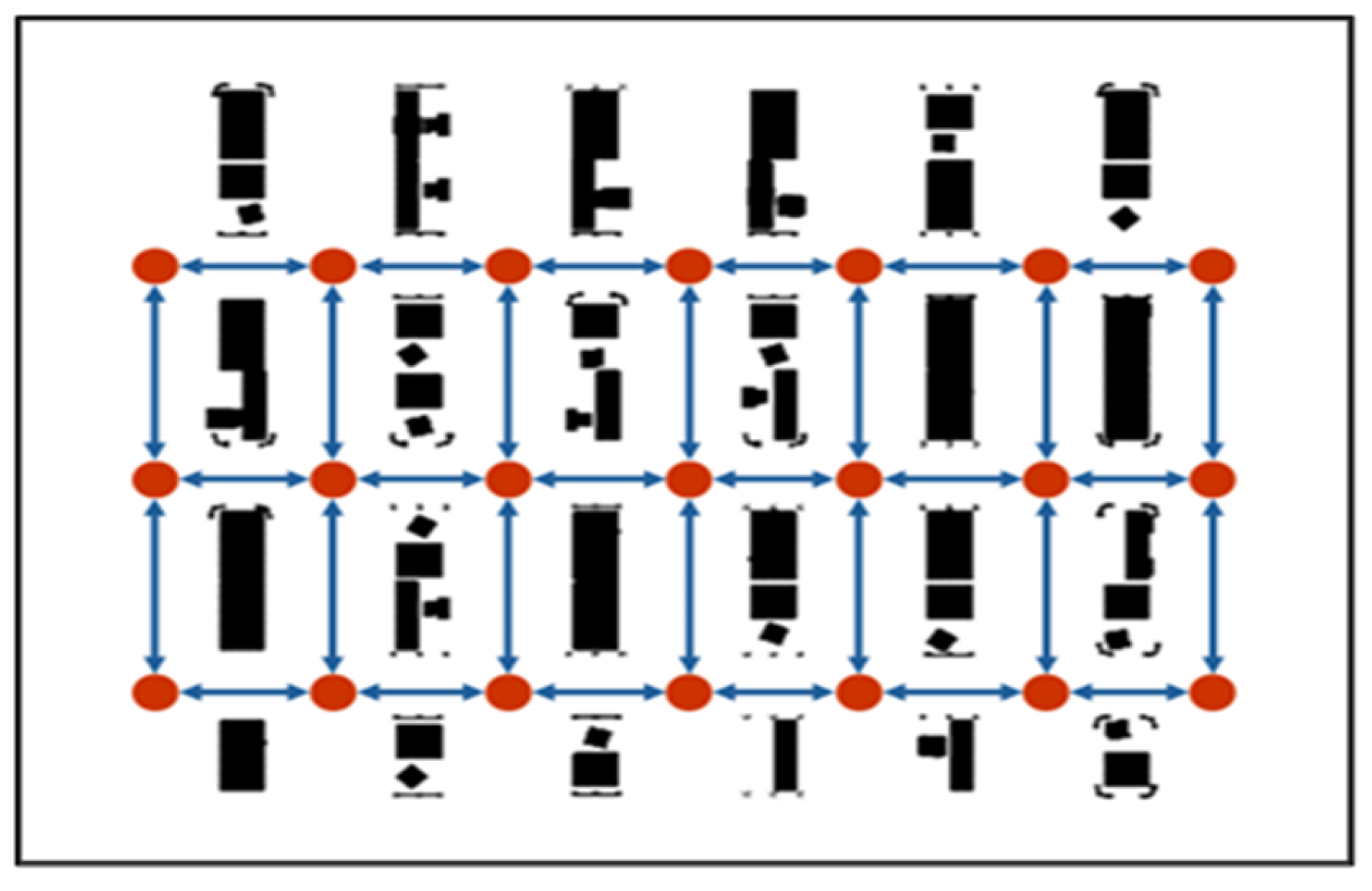
3.2. Environmental Map Representation
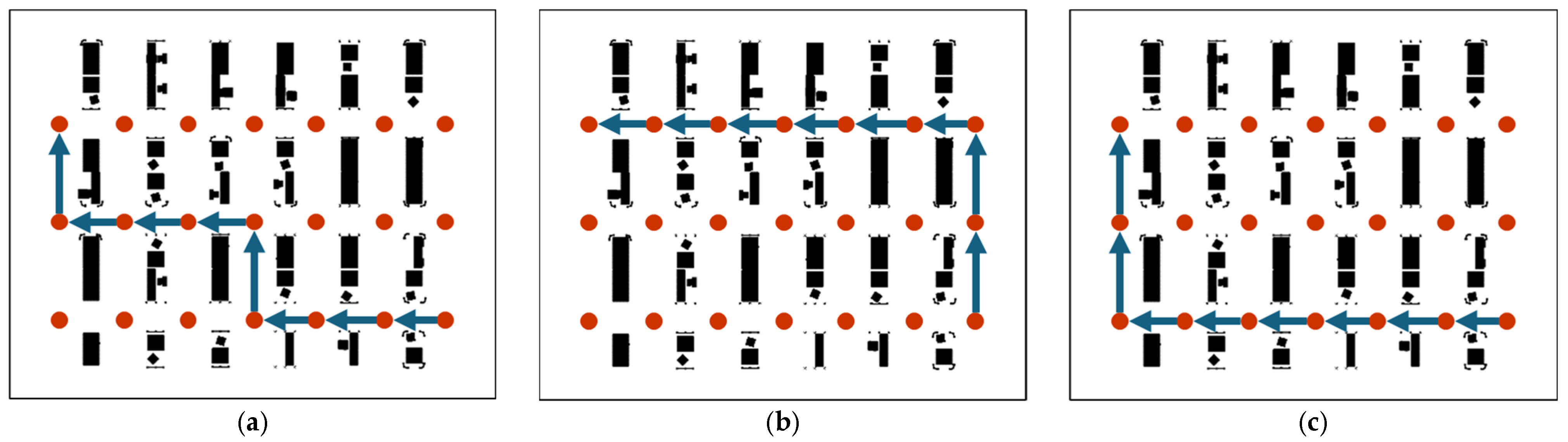
3.3. Preselected Path Generation
3.4. Deep Reinforcement Learning Model
4. Simulation Results and Discussion
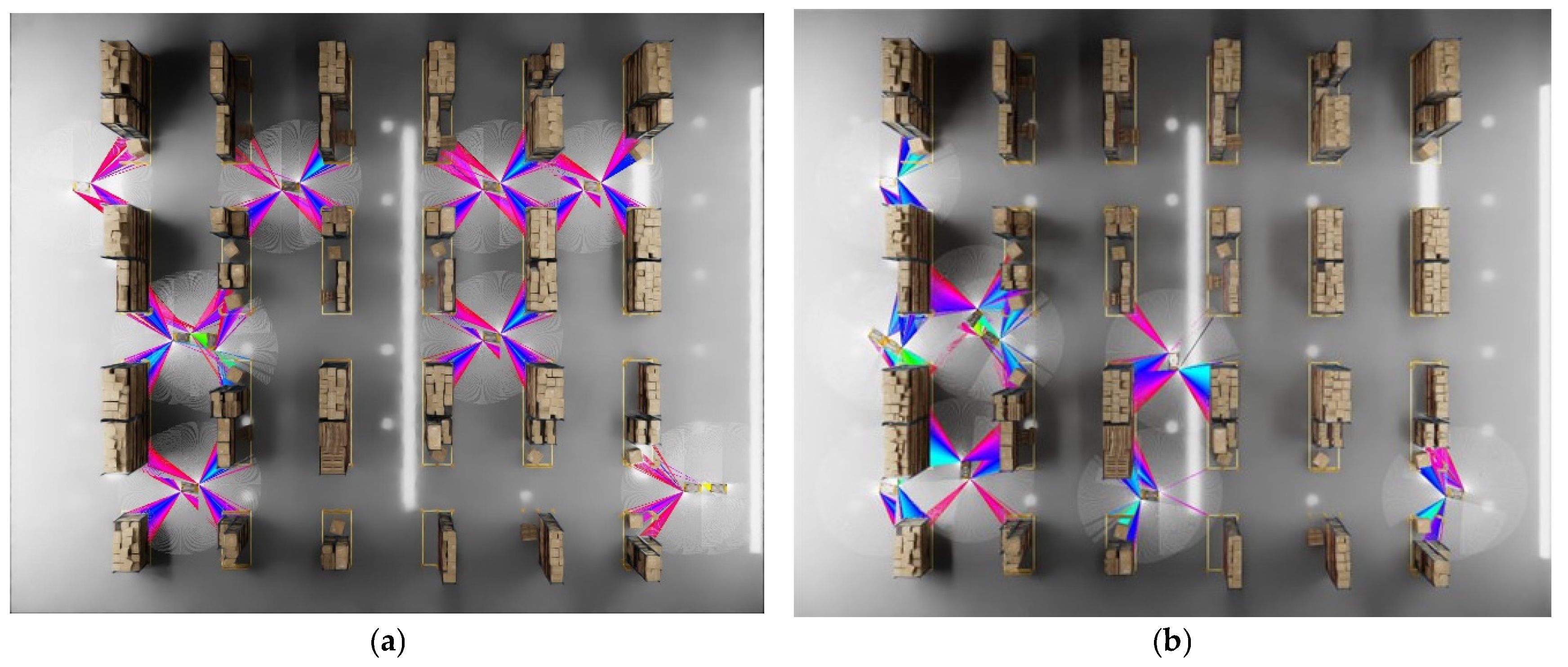
4.1. System Evaluation Experiment
4.2. Feasibility Assessment Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, K.; Zhang, T. Deep reinforcement learning based mobile robot navigation: A review. Tsinghua Sci. Technol. 2021, 26, 674–691. [Google Scholar] [CrossRef]
- Verma, J.K.; Ranga, V. Multi-robot coordination analysis, taxonomy, challenges and future scope. J. Intell. Robot. Syst. 2021, 102, 10. [Google Scholar] [CrossRef]
- Seenu, N.; RM, K.C.; Ramya, M.M.; Janardhanan, M.N. Review on state-of-the-art dynamic task allocation strategies for multiple-robot systems. Ind. Robot Int. J. Robot. Res. Appl. 2020, 47, 929–942. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Y.; Li, D.; Zhao, Q. Distributed relative localization algorithms for multi-robot networks: A survey. Sensors 2023, 23, 2399. [Google Scholar] [CrossRef] [PubMed]
- Madridano, Á.; Al-Kaff, A.; Martín, D.; De La Escalera, A. Trajectory planning for multi-robot systems: Methods and applications. Expert Syst. Appl. 2021, 173, 114660. [Google Scholar] [CrossRef]
- Fan, T.; Long, P.; Liu, W.; Pan, J. Distributed multi-robot collision avoidance via deep reinforcement learning for navigation in complex scenarios. Int. J. Robot. Res. 2020, 39, 856–892. [Google Scholar] [CrossRef]
- Olcay, E.; Schuhmann, F.; Lohmann, B. Collective navigation of a multi-robot system in an unknown environment. Robot. Auton. Syst. 2020, 132, 103604. [Google Scholar] [CrossRef]
- Expert Market Research. Logistics Market Report and Forecast 2024–2032. Available online: https://www.expertmarketresearch.com/reports/logistics-market (accessed on 30 June 2024).
- Quinlivan, J. How Amazon Deploys Robots in Its Operations Facilities. About Amazon 2023. Available online: https://www.aboutamazon.com/news/operations/how-amazon-deploys-robots-in-its-operations-facilities (accessed on 30 June 2024).
- Gao, Z.; Jiao, Y.; Yang, W.; Li, X.; Wang, Y. A Method for UWB Localization Based on CNN-SVM and Hybrid Locating Algorithm. Information 2023, 14, 46. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, X.; Zhong, H.; Xie, H.; He, W.; Tan, X.; Wang, Y. A dynamic window-based UWB-odometer fusion approach for indoor positioning. IEEE Sens. J. 2022, 23, 2922–2931. [Google Scholar] [CrossRef]
- Chatzisavvas, A.; Chatzitoulousis, P.; Ziouzios, D.; Dasygenis, M. A routing and task-allocation algorithm for robotic groups in warehouse environments. Information 2022, 13, 288. [Google Scholar] [CrossRef]
- Stern, R. Multi-agent path finding—An overview. In Artificial Intelligence; Tutorial Lectures; Osipov, G., Panov, A., Yakovlev, K., Eds.; Springer: Cham, Switzerland, 2019; pp. 96–115. [Google Scholar]
- Warita, S.; Fujita, K. Online planning for autonomous mobile robots with different objectives in warehouse commissioning task. Information 2024, 15, 130. [Google Scholar] [CrossRef]
- Meng, X.; Fang, X. A UGV Path Planning Algorithm Based on Improved A* with Improved Artificial Potential Field. Electronics 2024, 13, 972. [Google Scholar] [CrossRef]
- Wu, X.; Wu, R.; Zhang, Y.; Peng, J. Distributed Formation Control of Multi-Robot Systems with Path Navigation via Complex Laplacian. Entropy 2023, 25, 1536. [Google Scholar] [CrossRef]
- Pianpak, P.; Son, T.C.; Toups Dugas, P.O.; Yeoh, W. A distributed solver for multi-agent path finding problems. In Proceedings of the First International Conference on Distributed Artificial Intelligence, Beijing, China, 13–15 October 2019; pp. 1–7. [Google Scholar]
- Levin, M.W.; Rey, D. Conflict-point formulation of intersection control for autonomous vehicles. Transp. Res. Part C Emerg. Technol. 2017, 85, 528–547. [Google Scholar] [CrossRef]
- Motes, J.; Sandström, R.; Lee, H.; Thomas, S.; Amato, N.M. Multi-robot task and motion planning with subtask dependencies. IEEE Robot. Autom. Lett. 2020, 5, 3338–3345. [Google Scholar] [CrossRef]
- Sharon, G.; Stern, R.; Felner, A.; Sturtevant, N.R. Conflict-Based Search for Optimal Multi-Agent Pathfinding. Artif. Intell. 2015, 219, 40–66.9. [Google Scholar] [CrossRef]
- Kottinger, J.; Almagor, S.; Lahijanian, M. Conflict-based search for multi-robot motion planning with kinodynamic constraints. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 13494–13499. [Google Scholar]
- Solis, I.; Motes, J.; Sandström, R.; Amato, N.M. Representation-optimal multi-robot motion planning using conflict-based search. IEEE Robot. Autom. Lett. 2021, 6, 4608–4615. [Google Scholar] [CrossRef]
- Moldagalieva, A.; Ortiz-Haro, J.; Toussaint, M.; Hönig, W. db-CBS: Discontinuity-Bounded Conflict-Based Search for Multi-Robot Kinodynamic Motion Planning. arXiv 2023, arXiv:2309.16445. [Google Scholar] [CrossRef]
- NVIDIA Isaac Sim. Available online: https://developer.nvidia.com/isaac-sim (accessed on 9 July 2024).
- Makoviychuk, V.; Wawrzyniak, L.; Guo, Y.; Lu, M.; Storey, K.; Macklin, M.; State, G. Isaac gym: High performance GPU-based physics simulation for robot learning. arXiv 2021, arXiv:2108.10470. [Google Scholar] [CrossRef]
- OpenAI Gym. Available online: https://www.gymlibrary.dev/index.html (accessed on 9 July 2024).
- Raffin, A.; Hill, A.; Gleave, A.; Kanervisto, A.; Ernestus, M.; Dormann, N. Stable-baselines3: Reliable reinforcement learning implementations. J. Mach. Learn. Res. 2021, 22, 1–8. [Google Scholar]
- Rojas, M.; Hermosilla, G.; Yunge, D.; Farias, G. An Easy to Use Deep Reinforcement Learning Library for AI Mobile Robots in Isaac Sim. Appl. Sci. 2022, 12, 8429. [Google Scholar] [CrossRef]
- Zhou, Z.; Song, J.; Xie, X.; Shu, Z.; Ma, L.; Liu, D.; See, S. Towards building AI-CPS with NVIDIA Isaac Sim: An industrial benchmark and case study for robotics manipulation. In Proceedings of the 46th International Conference on Software Engineering: Software Engineering in Practice, Lisbon, Portugal, 14–20 April 2024; pp. 263–274. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar] [CrossRef]
- Van den Berg, J.; Lin, M.; Manocha, D. Reciprocal velocity obstacles for real-time multi-agent navigation. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation (ICRA), Pasadena, CA, USA, 19–23 May 2008; pp. 1928–1935. [Google Scholar]







| Item | Conflict-Based Search | Distributed Reinforcement Learning | Proposed Method |
|---|---|---|---|
| Method Description | Find the optimal path by detecting and resolving path conflicts | Each robot independently executes a reinforcement learning algorithm and periodically exchanges information or strategies | Effectively reduce path conflicts to reduce overall navigation time |
| Applicable Environment | Static, structured environment | Dynamic, complex environment | Dynamic, complex environment |
| Advantages | High computational efficiency | Suitable for dynamic changes and complex environments | Combining the advantages of both methods |
| Disadvantages | Not suitable for dynamic environments and computational complexity increases with the size of the area and number of robots | Require a large amount of data and training | System design is more complex |
| Item | Specification |
|---|---|
| Load Capacity | 1000 kg |
| Speed | 2.2 m/s |
| Battery Life | 8 h |
| Dimensions (L × W × H) | 1440 × 641 × 220 mm |
| Weight | 175 kg |
| Item | Start Point | Upper Bound | Lower Bound | Element Size |
|---|---|---|---|---|
| Value | (0.0, 0.0, 0.3) | (6.0, 2.0, 0.2) | (−42.0, −58.0, −0.2) | 0.05 |
| Item | Value |
|---|---|
| Environment Size | 7 × 3 |
| Number of Robots | 10 |
| Number of Candidate Paths | 3 |
| Length of Candidate Paths | 12 |
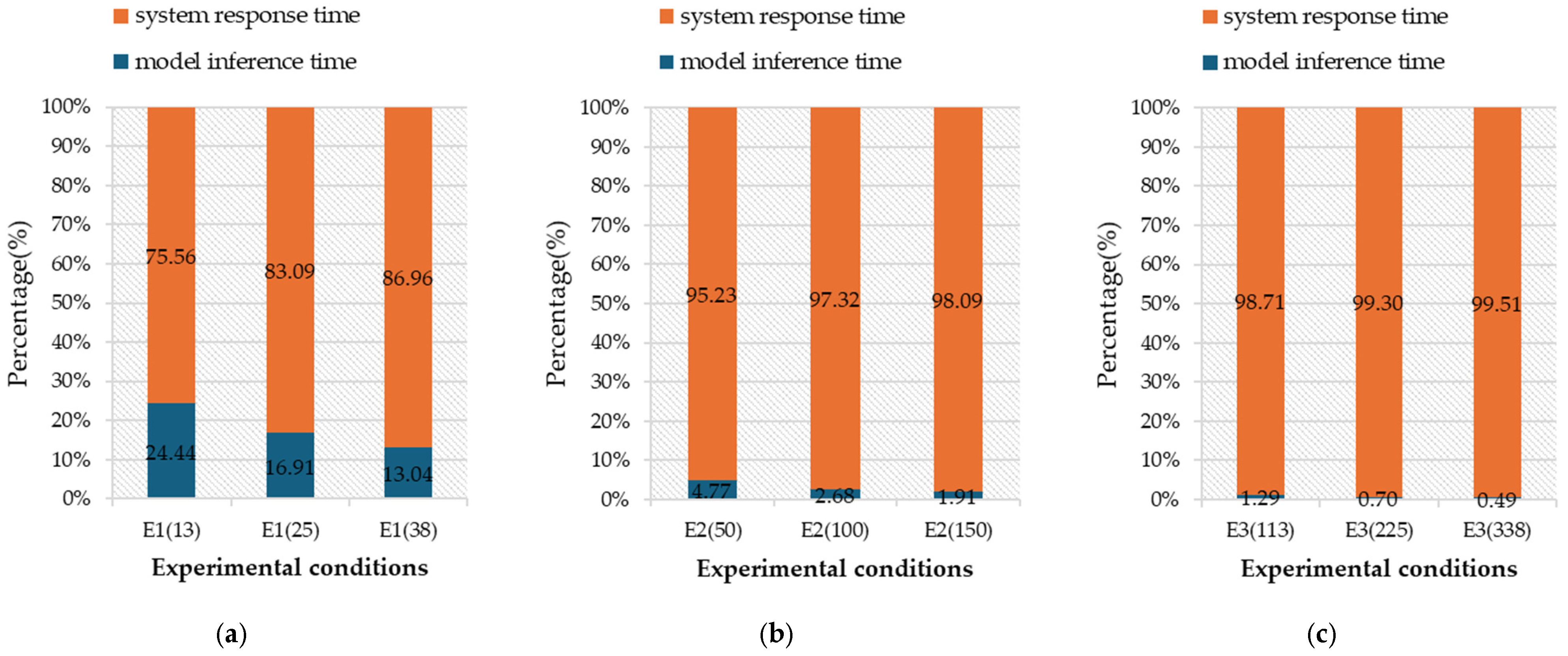
| ID | Map Size | Number of Nodes | Robot Ratio | Number of Robots |
|---|---|---|---|---|
| E1(13) | 5 × 5 | 25 | 50% | 13 |
| E1(25) | 5 × 5 | 25 | 100% | 25 |
| E1(38) | 5 × 5 | 25 | 150% | 38 |
| E2(50) | 10 × 10 | 100 | 50% | 50 |
| E2(100) | 10 × 10 | 100 | 100% | 100 |
| E2(150) | 10 × 10 | 100 | 150% | 150 |
| E3(113) | 15 × 15 | 125 | 50% | 113 |
| E3(225) | 15 × 15 | 125 | 100% | 225 |
| E3(338) | 15 × 15 | 125 | 150% | 338 |
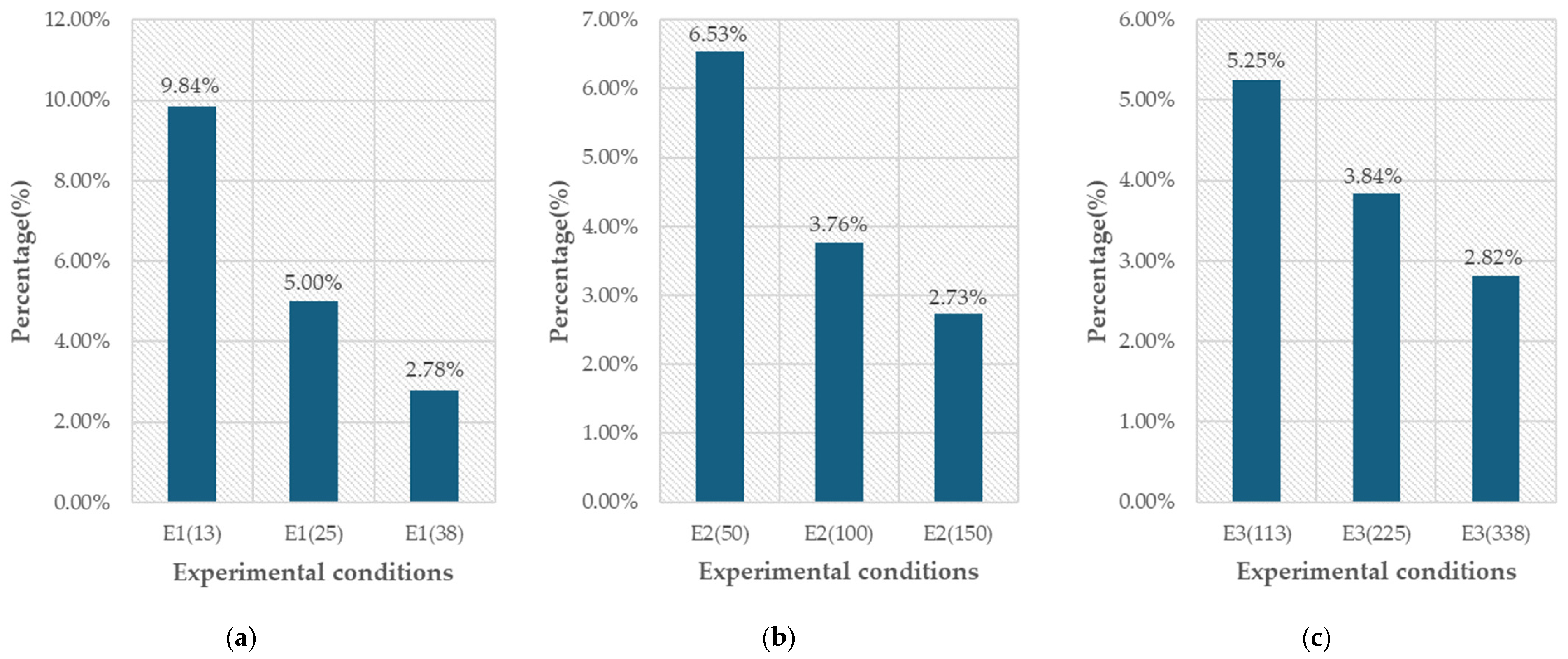
| ID | Number of Path Conflicts Using A* Method | Reduced Number of Path Conflicts | Collision Reduction Ratio | Total Navigation Time Saved by the Proposed Method (h) |
|---|---|---|---|---|
| E1(13) | 15,451 | 1520 | 9.84% | 1.27 |
| E1(25) | 49,691 | 2483 | 5.0% | 2.07 |
| E1(38) | 96,064 | 2671 | 2.78% | 2.23 |
| E2(50) | 103,857 | 6786 | 6.53% | 5.66 |
| E2(100) | 347,384 | 13,073 | 3.76% | 10.89 |
| E2(150) | 660,615 | 18,048 | 2.73% | 15.04 |
| E3(113) | 339,946 | 17,859 | 5.25% | 14.88 |
| E3(225) | 1,116,827 | 42,918 | 3.84% | 35.77 |
| E3(338) | 2,139,331 | 60,375 | 2.82% | 50.31 |
| State | Definition | Value |
|---|---|---|
| Success | No collisions occurred | 49 |
| Stopped | No collisions occurred but the task was not completed | 1 |
| Danger | Collisions occurred but the task was completed | 0 |
| Failure | Collisions occurred and the task was not completed | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wong, C.-C.; Weng, K.-D.; Yu, B.-Y. Multi-Robot Navigation System Design Based on Proximal Policy Optimization Algorithm. Information 2024, 15, 518. https://doi.org/10.3390/info15090518
Wong C-C, Weng K-D, Yu B-Y. Multi-Robot Navigation System Design Based on Proximal Policy Optimization Algorithm. Information. 2024; 15(9):518. https://doi.org/10.3390/info15090518
Chicago/Turabian StyleWong, Ching-Chang, Kun-Duo Weng, and Bo-Yun Yu. 2024. "Multi-Robot Navigation System Design Based on Proximal Policy Optimization Algorithm" Information 15, no. 9: 518. https://doi.org/10.3390/info15090518
APA StyleWong, C.-C., Weng, K.-D., & Yu, B.-Y. (2024). Multi-Robot Navigation System Design Based on Proximal Policy Optimization Algorithm. Information, 15(9), 518. https://doi.org/10.3390/info15090518







