GLIDE: Multi-Agent Deep Reinforcement Learning for Coordinated UAV Control in Dynamic Military Environments
Abstract
1. Introduction
- The coordinated UAV action control problem is formulated as a Markov Decision Process (MDP) with the action space involving accelerations of all the UAVs. Previous works use fixed-length strides for the movement of UAVs, due to which the UAVs move to a fixed distance at every timestep. In GLIDE, at each timestep, the UAVs can choose to change their acceleration. This gives freedom for the UAVs to move to any amount of distance intended per timestep. We observed that this approach also used lower parameters for training the model, since we just have three continuous values in the x, y, and z directions. The state space takes into account the global situational information and also the local situation faced by each UAV during the time of operation.
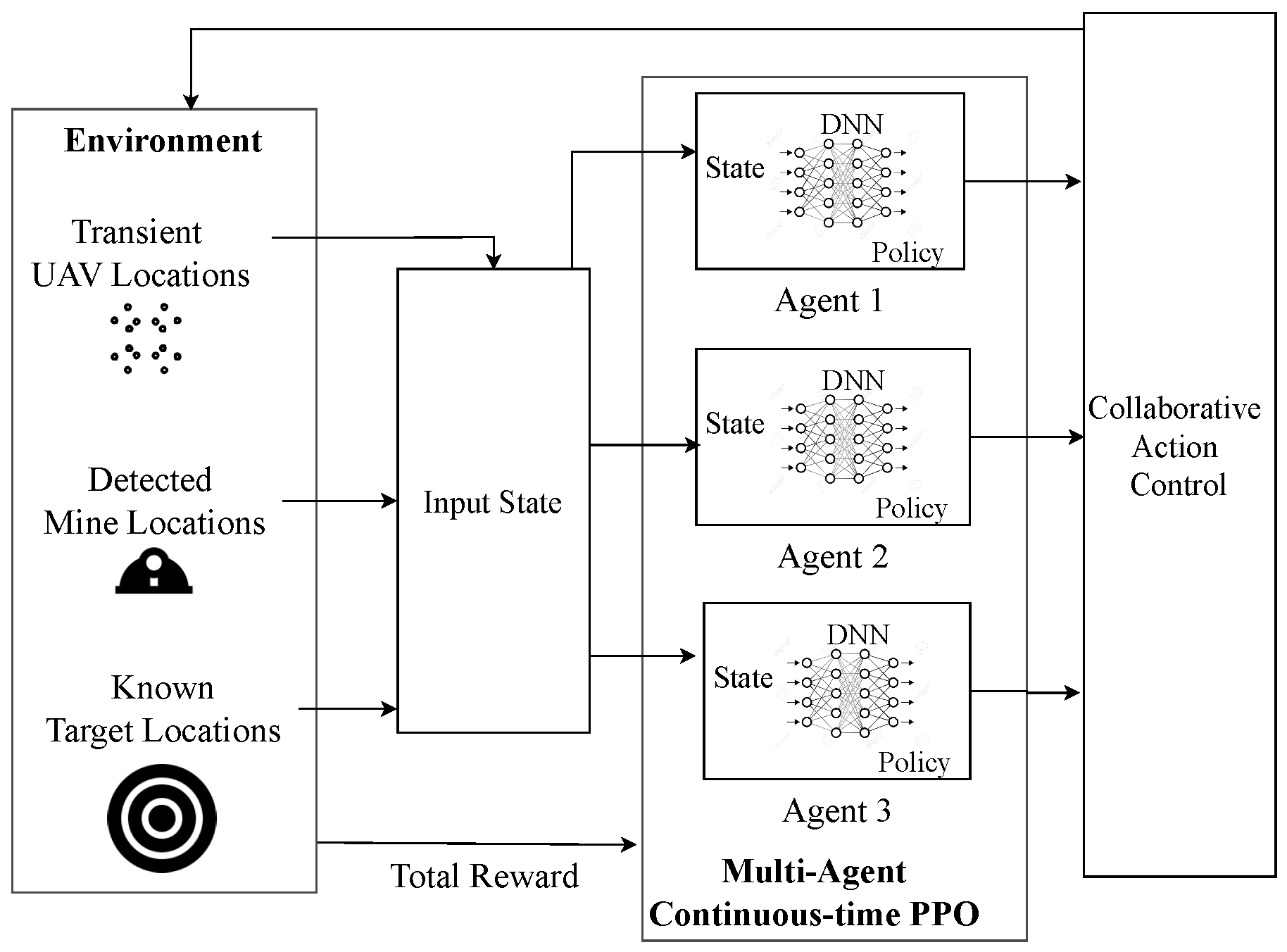
- We propose two MARL algorithms based on PPO for coordinated UAV action control, namely centralized GLIDE (C-GLIDE) and decentralized GLIDE (D-GLIDE) with a continuous action space. In C-GLIDE, the action control is performed based on the combined state space information available at the base. This keeps all the UAVs updated with global and local information. However, this slightly hampers the task-completion time, whereas D-GLIDE is based on centralized training and decentralized execution. The UAVs have access to their local data and are updated with global information once every few timesteps. This resulted in a faster task-completion time.
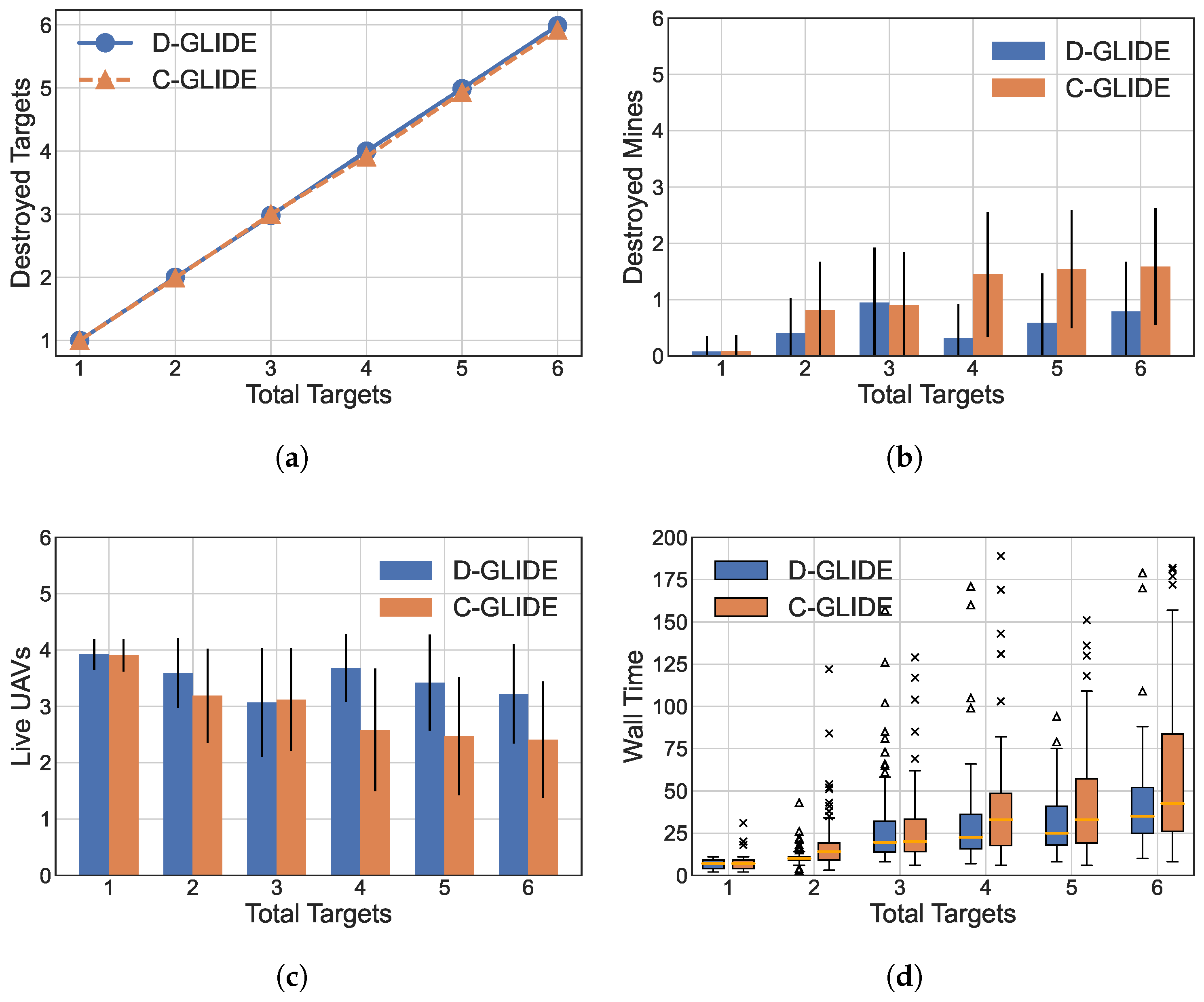
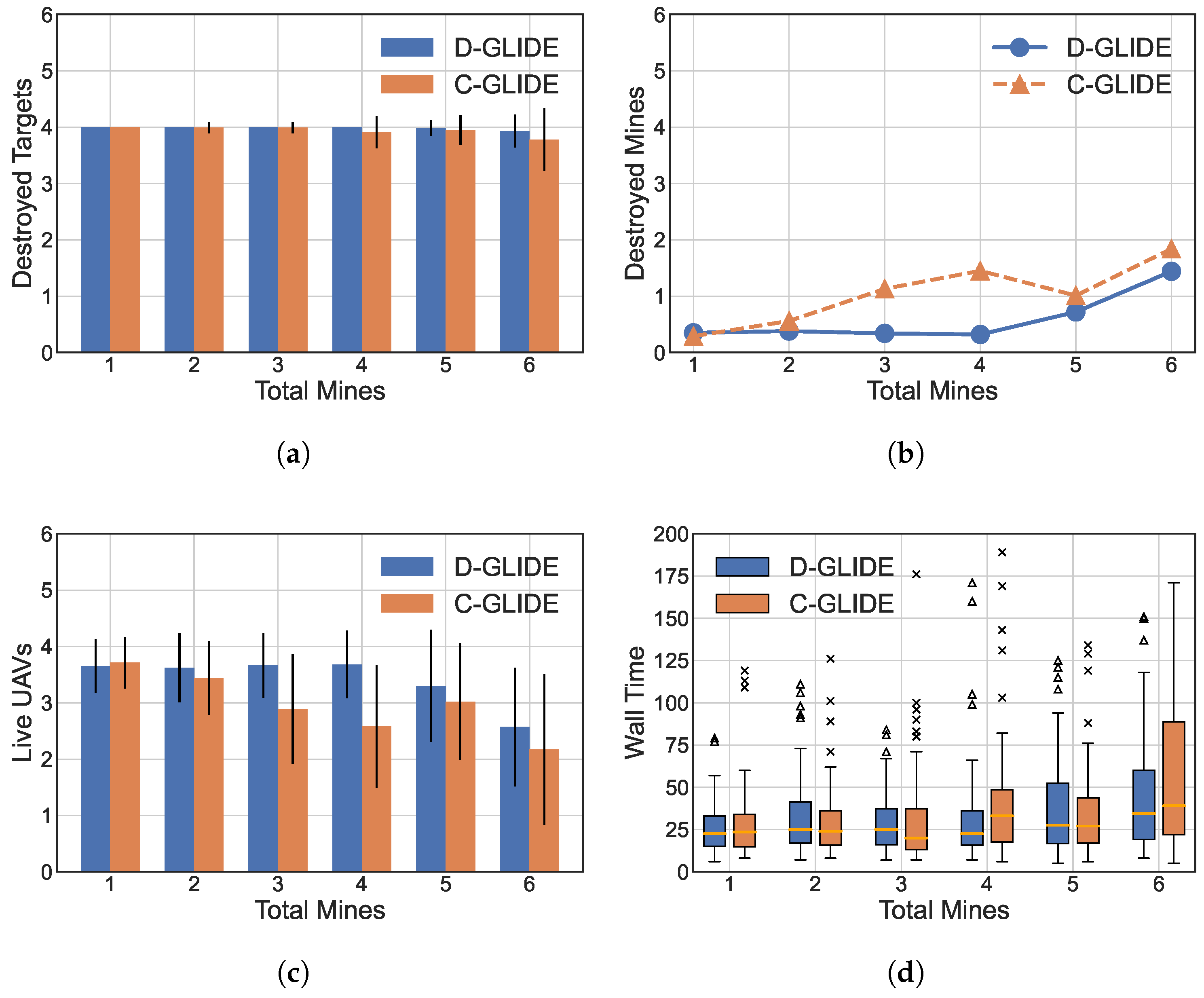
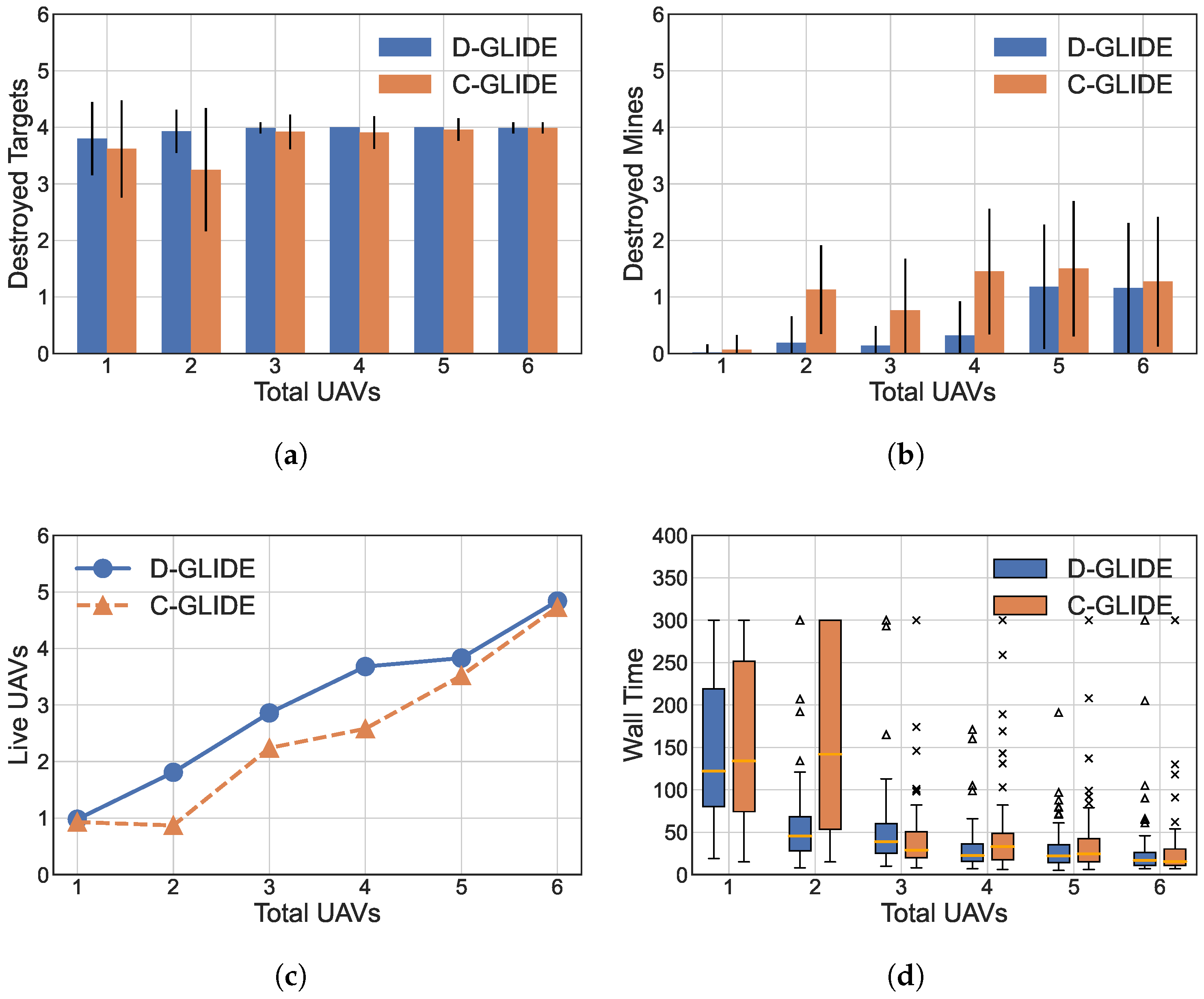
- We built a simulator for our experimentation called UAV SIM. Our experimentation results show that both these algorithms converge and have a comparable target-destruction rate and mine-discovery rate. With a low number of targets and mines, both C-GLIDE and D-GLIDE perform equally. C-GLIDE is useful for lower number of targets, mines, and UAVs. As the number of targets and mines increases to the maximum limit, D-GLIDE completes the task with up to 68% less time compared to C-GLIDE. We also observe that the target destruction rate of D-GLIDE is up to 21% and up to 42% higher, which indicates that more UAVs are alive with the same number of mines in the field compared to C-GLIDE.
2. Related Work
2.1. Path Planning and Action Control
2.2. Multi-Agent Approach for UAV Control
2.3. PPO Based MARL
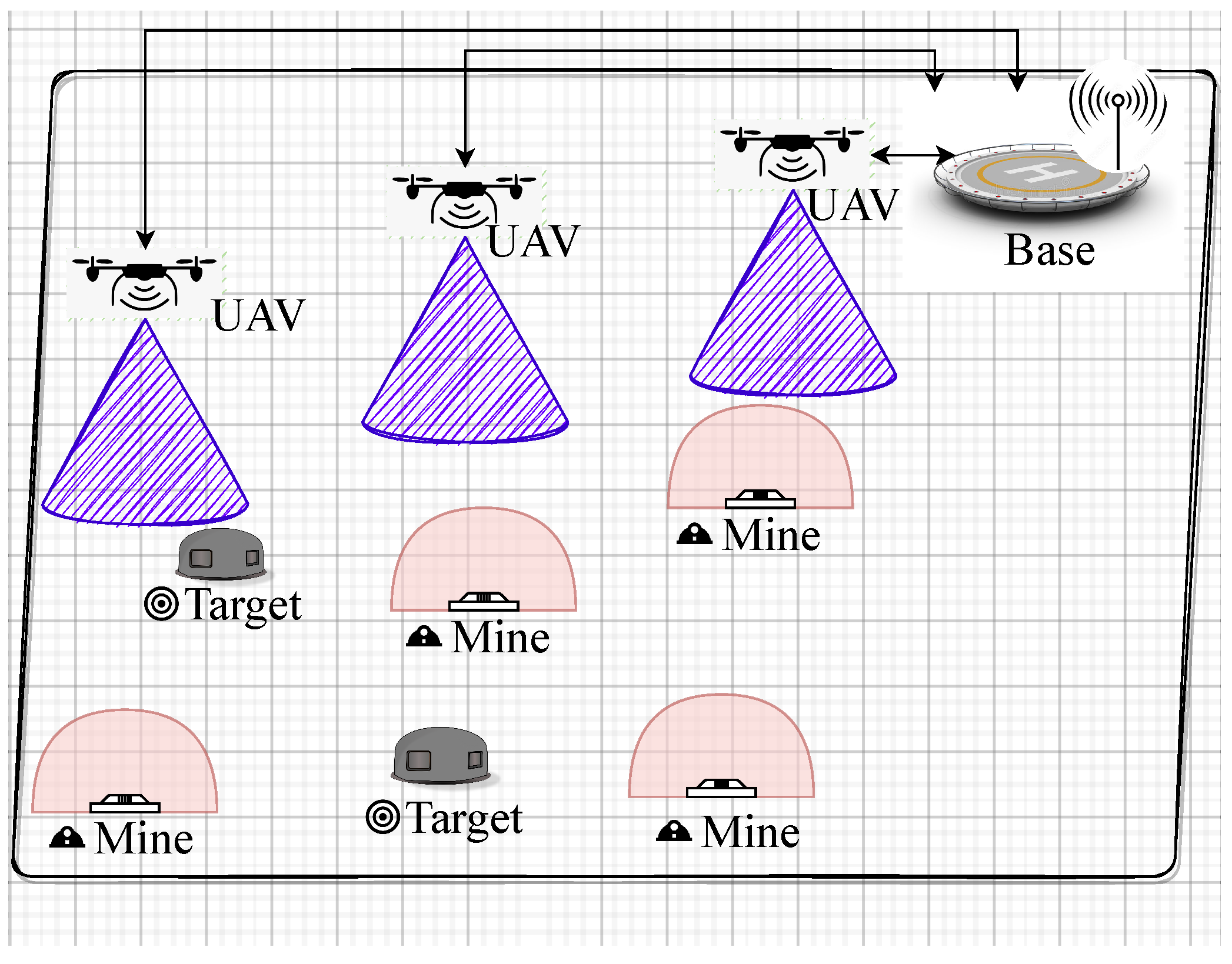
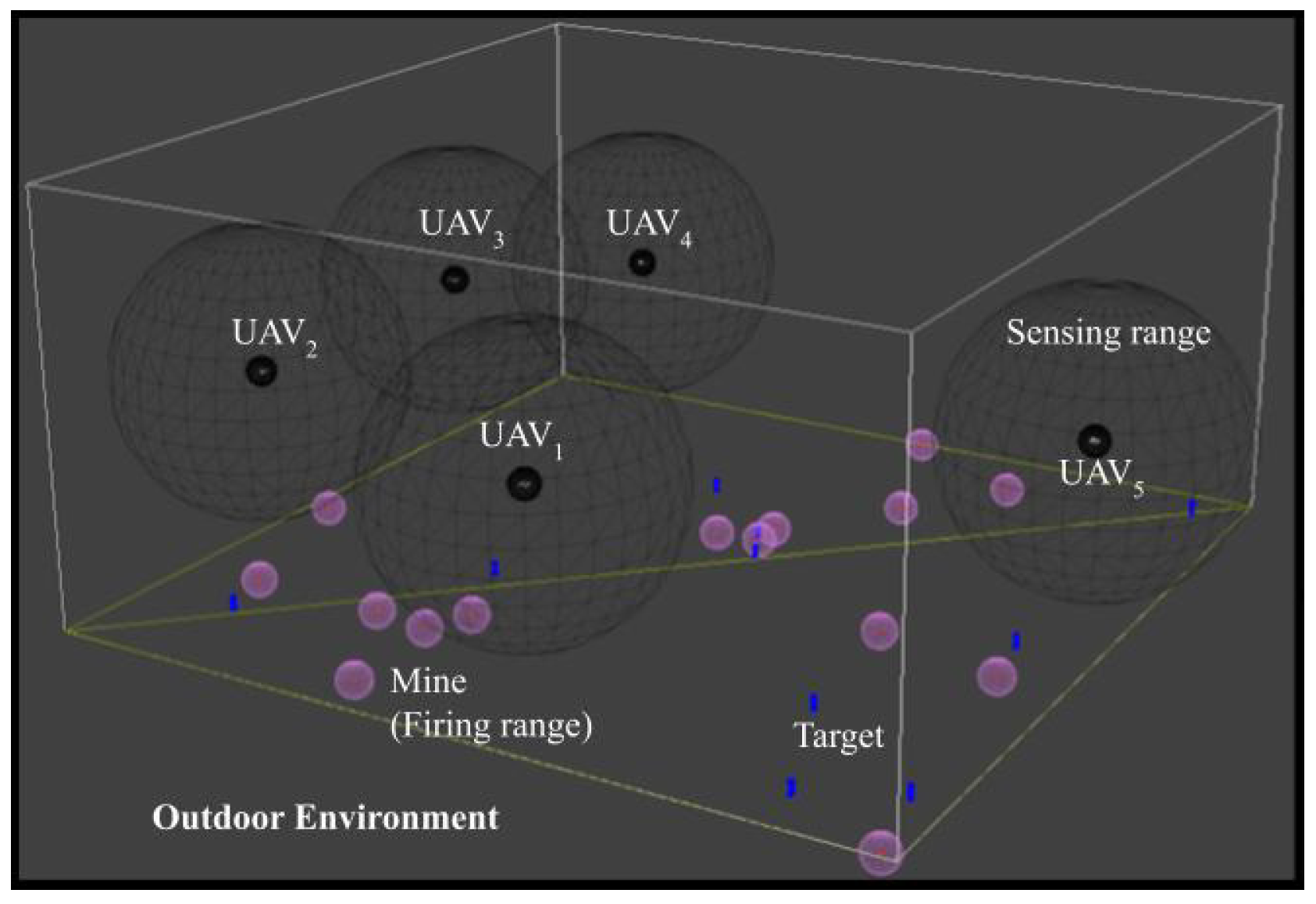
3. System Model
3.1. UAV Simulator
3.2. Markov Decision Process Model
3.2.1. State
3.2.2. Action
3.2.3. Reward Function
Proximity Based Reward
Target Destruction Reward
Mine Detection Reward
Time Based Reward
Liveliness Reward
Total Reward
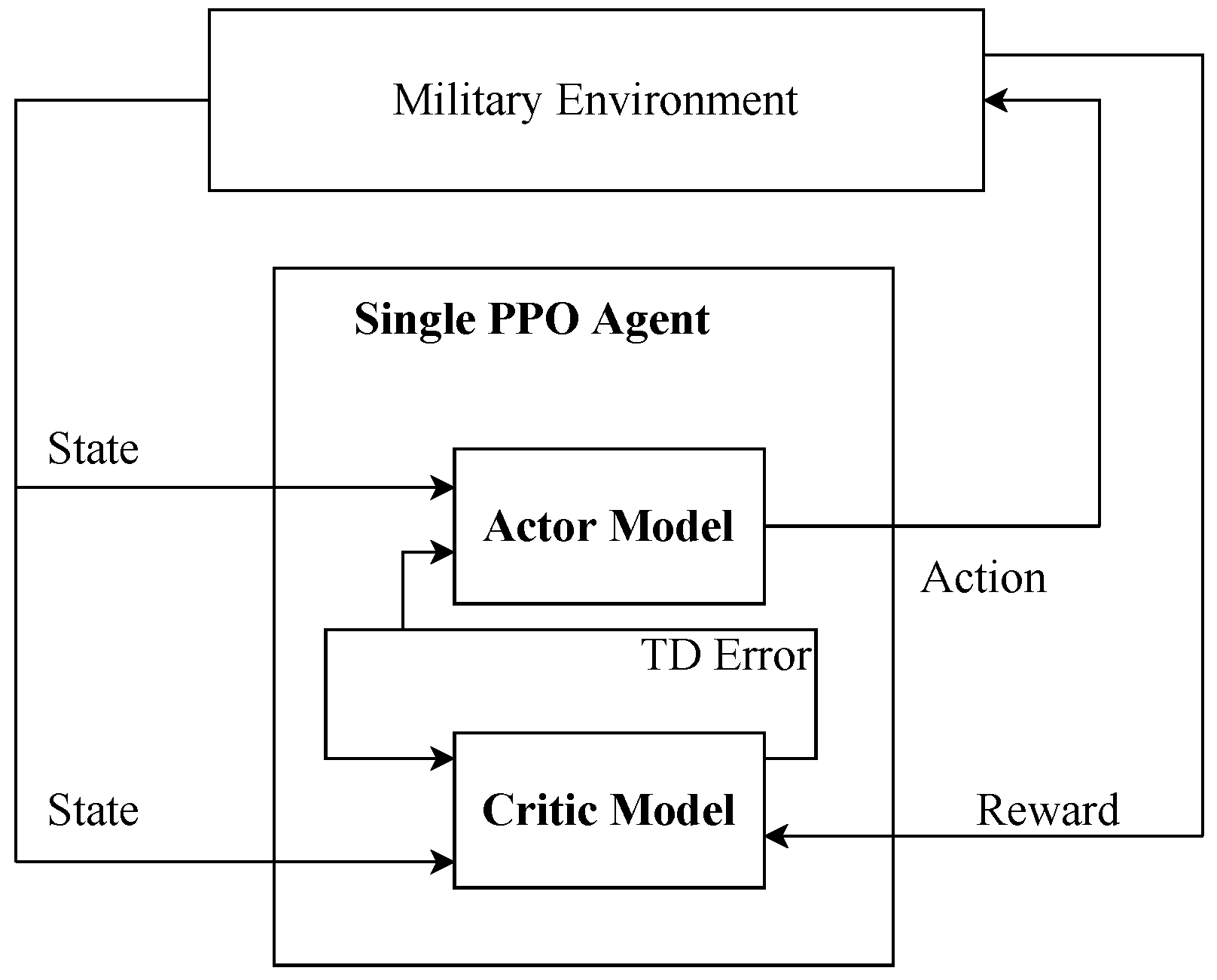
4. DRL-Based UAV Action Control
4.1. C-GLIDE
| Algorithm 1 C-GLIDE |
|
4.2. D-GLIDE
| Algorithm 2 D-GLIDE |
|
5. Results
5.1. Simulation Setting
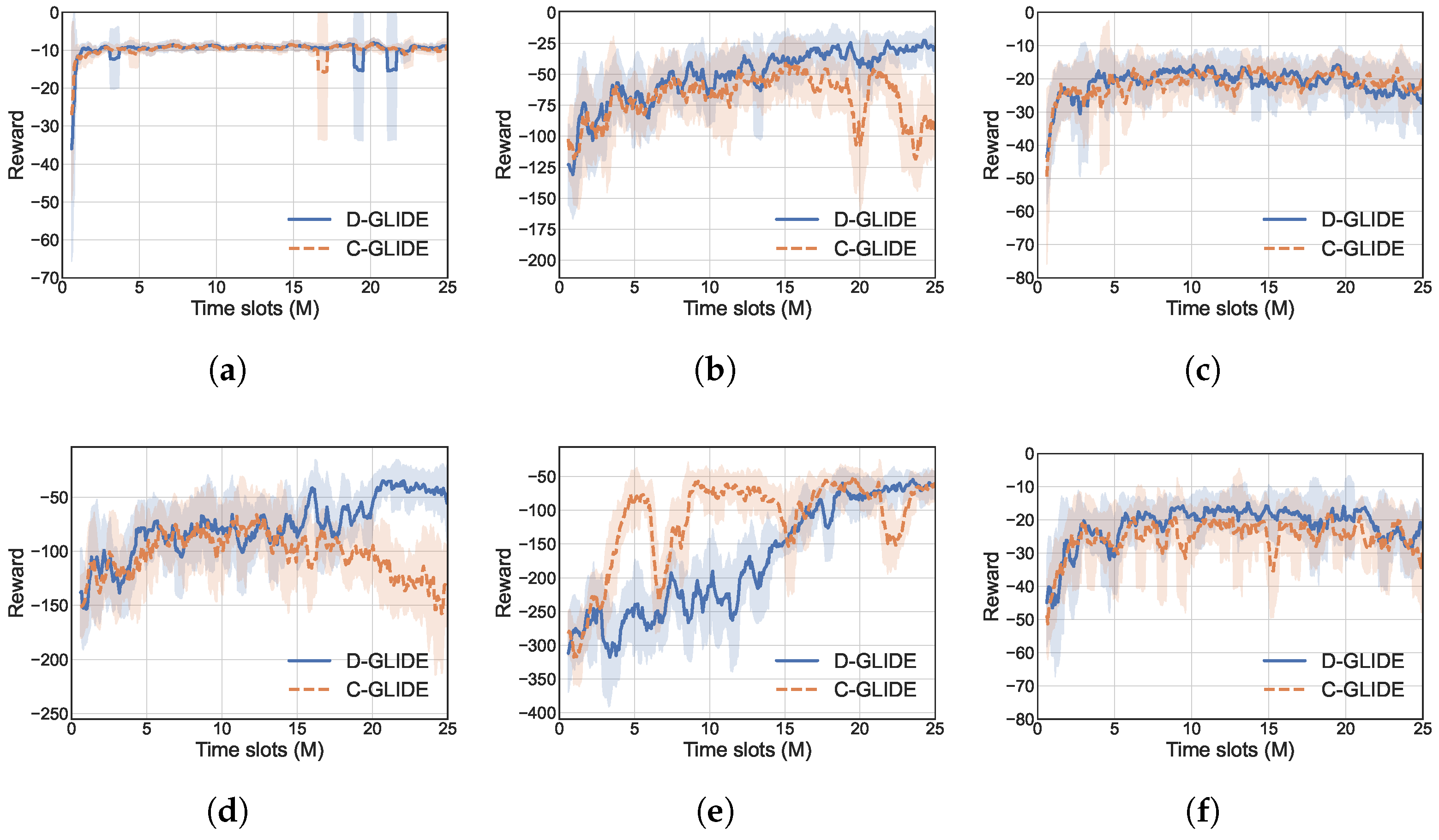
5.2. Convergence Analysis
5.3. Effectiveness Analysis
5.3.1. Increasing Targets
5.3.2. Increasing Enemy Mines
5.3.3. Increasing UAVs
5.3.4. Exploring the Area of Operation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cui, J.; Liu, Y.; Nallanathan, A. The application of multi-agent reinforcement learning in UAV networks. In Proceedings of the 2019 IEEE International Conference on Communications Workshops (ICC Workshops), Shanghai, China, 20–24 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Yan, C.; Xiang, X. A Path Planning Algorithm for UAV Based on Improved Q-Learning. In Proceedings of the 2018 2nd International Conference on Robotics and Automation Sciences (ICRAS), Wuhan, China, 23–25 June 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Pham, H.X.; La, H.M.; Feil-Seifer, D.; Nguyen, L.V. Autonomous uav navigation using reinforcement learning. arXiv 2018, arXiv:1801.05086. [Google Scholar]
- Islam, S.; Razi, A. A Path Planning Algorithm for Collective Monitoring Using Autonomous Drones. In Proceedings of the 2019 53rd Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 20–22 March 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef] [PubMed]
- Vinyals, O.; Babuschkin, I.; Czarnecki, W.M.; Mathieu, M.; Dudzik, A.; Chung, J.; Choi, D.H.; Powell, R.; Ewalds, T.; Georgiev, P.; et al. Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature 2019, 575, 350–354. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.; He, H.; Yang, P.; Lyu, F.; Wu, W.; Cheng, N.; Shen, X. Deep RL-based trajectory planning for AoI minimization in UAV-assisted IoT. In Proceedings of the 2019 11th International Conference on Wireless Communications and Signal Processing (WCSP), Xi’an, China, 23–25 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Shalev-Shwartz, S.; Shammah, S.; Shashua, A. Safe, multi-agent, reinforcement learning for autonomous driving. arXiv 2016, arXiv:1610.03295. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through Deep Reinforcement Learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, S.; Ye, F.; Jiang, T.; Li, Y. A UAV Path Planning Method Based on Deep Reinforcement Learning. In Proceedings of the 2020 IEEE USNC-CNC-URSI North American Radio Science Meeting (Joint with AP-S Symposium), Montreal, QC, Canada, 5–10 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 93–94. [Google Scholar]
- Rahim, S.; Razaq, M.M.; Chang, S.Y.; Peng, L. A reinforcement learning-based path planning for collaborative UAVs. In Proceedings of the 37th ACM/SIGAPP Symposium on Applied Computing, Virtual, 25–29 April 2022; pp. 1938–1943. [Google Scholar]
- Luong, N.C.; Hoang, D.T.; Gong, S.; Niyato, D.; Wang, P.; Liang, Y.C.; Kim, D.I. Applications of Deep Reinforcement Learning in communications and networking: A survey. IEEE Commun. Surv. Tutor. 2019, 21, 3133–3174. [Google Scholar] [CrossRef]
- Mamaghani, M.T.; Hong, Y. Intelligent Trajectory Design for Secure Full-Duplex MIMO-UAV Relaying against Active Eavesdroppers: A Model-Free Reinforcement Learning Approach. IEEE Access 2020, 9, 4447–4465. [Google Scholar] [CrossRef]
- Yijing, Z.; Zheng, Z.; Xiaoyi, Z.; Yang, L. Q learning algorithm based UAV path learning and obstacle avoidence approach. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 3397–3402. [Google Scholar]
- Nex, F.; Remondino, F. UAV for 3D mapping applications: A review. Appl. Geomat. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Schmidt, L.M.; Brosig, J.; Plinge, A.; Eskofier, B.M.; Mutschler, C. An Introduction to Multi-Agent Reinforcement Learning and Review of its Application to Autonomous Mobility. arXiv 2022, arXiv:2203.07676. [Google Scholar]
- Yan, C.; Xiang, X.; Wang, C. Towards real-time path planning through Deep Reinforcement Learning for a UAV in dynamic environments. J. Intell. Robot. Syst. 2020, 98, 297–309. [Google Scholar] [CrossRef]
- Bayerlein, H.; Theile, M.; Caccamo, M.; Gesbert, D. Multi-uav path planning for wireless data harvesting with deep reinforcement learning. IEEE Open J. Commun. Soc. 2021, 2, 1171–1187. [Google Scholar] [CrossRef]
- Li, B.; Wu, Y. Path planning for UAV ground target tracking via deep reinforcement learning. IEEE Access 2020, 8, 29064–29074. [Google Scholar] [CrossRef]
- Theile, M.; Bayerlein, H.; Nai, R.; Gesbert, D.; Caccamo, M. UAV Path Planning using Global and Local Map Information with Deep Reinforcement Learning. arXiv 2020, arXiv:2010.06917. [Google Scholar]
- Liu, Q.; Shi, L.; Sun, L.; Li, J.; Ding, M.; Shu, F. Path planning for UAV-mounted mobile edge computing with deep reinforcement learning. IEEE Trans. Veh. Technol. 2020, 69, 5723–5728. [Google Scholar] [CrossRef]
- Bayerlein, H.; Theile, M.; Caccamo, M.; Gesbert, D. UAV path planning for wireless data harvesting: A deep reinforcement learning approach. In Proceedings of the GLOBECOM 2020-2020 IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Liu, C.H.; Chen, Z.; Tang, J.; Xu, J.; Piao, C. Energy-efficient UAV control for effective and fair communication coverage: A Deep Reinforcement Learning approach. IEEE J. Sel. Areas Commun. 2018, 36, 2059–2070. [Google Scholar] [CrossRef]
- Wang, T.; Qin, R.; Chen, Y.; Snoussi, H.; Choi, C. A reinforcement learning approach for UAV target searching and tracking. Multimed. Tools Appl. 2019, 78, 4347–4364. [Google Scholar] [CrossRef]
- Zhang, B.; Mao, Z.; Liu, W.; Liu, J. Geometric reinforcement learning for path planning of UAVs. J. Intell. Robot. Syst. 2015, 77, 391–409. [Google Scholar] [CrossRef]
- Bai, X.; Lu, C.; Bao, Q.; Zhu, S.; Xia, S. An Improved PPO for Multiple Unmanned Aerial Vehicles. Proc. J. Phys. Conf. Ser. 2021, 1757, 012156. [Google Scholar] [CrossRef]
- Ates, U. Long-Term Planning with Deep Reinforcement Learning on Autonomous Drones. In Proceedings of the 2020 Innovations in Intelligent Systems and Applications Conference (ASYU), Istanbul, Turkey, 15–17 October 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Bøhn, E.; Coates, E.M.; Moe, S.; Johansen, T.A. Deep Reinforcement Learning Attitude Control of Fixed-Wing UAVs Using Proximal Policy optimization. In Proceedings of the 2019 International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 11–14 June 2019; pp. 523–533. [Google Scholar] [CrossRef]
- Mondal, W.U.; Agarwal, M.; Aggarwal, V.; Ukkusuri, S.V. On the approximation of cooperative heterogeneous multi-agent reinforcement learning (marl) using mean field control (mfc). J. Mach. Learn. Res. 2022, 23, 1–46. [Google Scholar]
- Mondal, W.U.; Aggarwal, V.; Ukkusuri, S. On the Near-Optimality of Local Policies in Large Cooperative Multi-Agent Reinforcement Learning. Trans. Mach. Learn. Res. 2022. Available online: https://openreview.net/pdf?id=t5HkgbxZp1 (accessed on 22 July 2024).
- Mondal, W.U.; Aggarwal, V.; Ukkusuri, S. Mean-Field Control Based Approximation of Multi-Agent Reinforcement Learning in Presence of a Non-decomposable Shared Global State. Trans. Mach. Learn. Res. 2023. Available online: https://openreview.net/pdf?id=ZME2nZMTvY (accessed on 22 July 2024).
- Zhou, H.; Lan, T.; Aggarwal, V. Pac: Assisted value factorization with counterfactual predictions in multi-agent reinforcement learning. Adv. Neural Inf. Process. Syst. 2022, 35, 15757–15769. [Google Scholar]
- Al-Abbasi, A.O.; Ghosh, A.; Aggarwal, V. Deeppool: Distributed model-free algorithm for ride-sharing using Deep Reinforcement Learning. IEEE Trans. Intell. Transp. Syst. 2019, 20, 4714–4727. [Google Scholar] [CrossRef]
- Singh, A.; Al-Abbasi, A.O.; Aggarwal, V. A distributed model-free algorithm for multi-hop ride-sharing using Deep Reinforcement Learning. IEEE Trans. Intell. Transp. Syst. 2021, 23, 8595–8605. [Google Scholar] [CrossRef]
- Haliem, M.; Mani, G.; Aggarwal, V.; Bhargava, B. A distributed model-free ride-sharing approach for joint matching, pricing, and dispatching using Deep Reinforcement Learning. IEEE Trans. Intell. Transp. Syst. 2021, 22, 7931–7942. [Google Scholar] [CrossRef]
- Manchella, K.; Haliem, M.; Aggarwal, V.; Bhargava, B. PassGoodPool: Joint passengers and goods fleet management with reinforcement learning aided pricing, matching, and route planning. IEEE Trans. Intell. Transp. Syst. 2021, 23, 3866–3877. [Google Scholar] [CrossRef]
- Chen, C.L.; Zhou, H.; Chen, J.; Pedramfar, M.; Aggarwal, V.; Lan, T.; Zhu, Z.; Zhou, C.; Gasser, T.; Ruiz, P.M.; et al. Two-tiered online optimization of region-wide datacenter resource allocation via Deep Reinforcement Learning. arXiv 2023, arXiv:2306.17054. [Google Scholar]
- Haydari, A.; Aggarwal, V.; Zhang, M.; Chuah, C.N. Constrained Reinforcement Learning for Fair and Environmentally Efficient Traffic Signal Controllers. J. Auton. Transp. Syst. 2024. accepted. [Google Scholar] [CrossRef]
- Hüttenrauch, M.; Šošić, A.; Neumann, G. Deep Reinforcement Learning for swarm systems. J. Mach. Learn. Res. 2019, 20, 1–31. [Google Scholar]
- Challita, U.; Saad, W.; Bettstetter, C. Deep Reinforcement Learning for interference-aware path planning of cellular-connected UAVs. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–7. [Google Scholar]
- Liu, X.; Liu, Y.; Chen, Y. Reinforcement learning in multiple-UAV networks: Deployment and movement design. IEEE Trans. Veh. Technol. 2019, 68, 8036–8049. [Google Scholar] [CrossRef]
- Chen, D.; Qi, Q.; Zhuang, Z.; Wang, J.; Liao, J.; Han, Z. Mean Field Deep Reinforcement Learning for Fair and Efficient UAV Control. IEEE Internet Things J. 2021, 8, 813–828. [Google Scholar] [CrossRef]
- Yang, Y.; Luo, R.; Li, M.; Zhou, M.; Zhang, W.; Wang, J. Mean field multi-agent reinforcement learning. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 5571–5580. [Google Scholar]
| Paper | Number of UAVs | Objective | Solution Approach | Environment | Performance |
|---|---|---|---|---|---|
| [10] | Single | Path planning | Centralized DDPG | Three-dimensional continuous environment with aerial obstacles | Reward convergence |
| [26] | Multiple | Jointly control multiple agents | Centralized PPO | Military environment | Reward convergence |
| [27] | Multiple | Drone racing competition | Decentralized PPO | Environment was created using AirSim | Task completion |
| [17] | Multiple | Path planning | Centralized D3QN combined with greedy heuristic search | Military environment developed using STAGE Scenario | Task completion |
| [18] | Multiple | Data harvesting | Centralized DQN | Urban city like structure map | Successful landing and collection ratio |
| This work, GLIDE | Multiple | Coordinated action control | Centralized and decentralized PPO | Military environment created with our simulator, UAV SIM | Task completion time and reward convergence |
| Paper | Single or Multiple UAVs | Obstacles and Mines | Assumptions | Environment | Task |
|---|---|---|---|---|---|
| [40] | Multiple | None | All the UAVs are connected to a cellular network | Ground | Finding the best path |
| [24] | Multiple | Preset obstacle areas in grid map | UAVs follow the assigned path | Ground patrol area | Target searching and tracking |
| [41] | Multiple | None | All the UAVs are connected to a cellular network | Ground based dynamic users | QoE driven UAVs assisted communications |
| This work, GLIDE | Multiple | Mines | UAVs periodically communicate with the base | Military environment created with our simulator, UAV SIM | Target destruction |
| Parameters | Value |
|---|---|
| Length l | 1000 m |
| Breadth b | 1000 m |
| Height h | 500 m |
| Height of the Target | 40 m |
| Radar range of the mine | 50 m |
| Detection range of UAV | 300 m |
| Destruction range of UAV | 100 m |
| Maximum speed of the UAV | 90 m/s |
| Maximum acceleration of the UAV | 50 m/s2 |
| Parameters | Value |
|---|---|
| Neurons in hidden layer 1 | 256 |
| Neurons in hidden layer 2 | 256 |
| Relay memory size | 3072 |
| Minibatch size | 768 |
| Learning rate | |
| Discount factor | |
| GAE parameter | |
| Activation function | ReLU |
| Clip range | |
| Optimizer | Adam |
| Epochs | 10 |
| Total episodes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gadiraju, D.S.; Karmakar, P.; Shah, V.K.; Aggarwal, V. GLIDE: Multi-Agent Deep Reinforcement Learning for Coordinated UAV Control in Dynamic Military Environments. Information 2024, 15, 477. https://doi.org/10.3390/info15080477
Gadiraju DS, Karmakar P, Shah VK, Aggarwal V. GLIDE: Multi-Agent Deep Reinforcement Learning for Coordinated UAV Control in Dynamic Military Environments. Information. 2024; 15(8):477. https://doi.org/10.3390/info15080477
Chicago/Turabian StyleGadiraju, Divija Swetha, Prasenjit Karmakar, Vijay K. Shah, and Vaneet Aggarwal. 2024. "GLIDE: Multi-Agent Deep Reinforcement Learning for Coordinated UAV Control in Dynamic Military Environments" Information 15, no. 8: 477. https://doi.org/10.3390/info15080477
APA StyleGadiraju, D. S., Karmakar, P., Shah, V. K., & Aggarwal, V. (2024). GLIDE: Multi-Agent Deep Reinforcement Learning for Coordinated UAV Control in Dynamic Military Environments. Information, 15(8), 477. https://doi.org/10.3390/info15080477







