Abstract
Memristor crossbars offer promising low-power and parallel processing capabilities, making them efficient for implementing convolutional neural networks (CNNs) in terms of delay time, area, etc. However, mapping large CNN models like ResNet-18, ResNet-34, VGG-Net, etc., onto memristor crossbars is challenging due to the line resistance problem limiting crossbar size. This necessitates partitioning full-image convolution into sub-image convolution. To do so, an optimized mapping of memristor crossbars should be considered to divide full-image convolution into multiple crossbars. With limited crossbar resources, especially in edge devices, it is crucial to optimize the crossbar allocation per layer to minimize the hardware resource in term of crossbar area, delay time, and area–delay product. This paper explores three optimization scenarios: (1) optimizing total delay time under a crossbar’s area constraint, (2) optimizing total crossbar area with a crossbar’s delay time constraint, and (3) optimizing a crossbar’s area–delay-time product without constraints. The Lagrange multiplier method is employed for the constrained cases 1 and 2. For the unconstrained case 3, a genetic algorithm (GA) is used to optimize the area–delay-time product. Simulation results demonstrate that the optimization can have significant improvements over the unoptimized results. When VGG-Net is simulated, the optimization can show about 20% reduction in delay time for case 1 and 22% area reduction for case 2. Case 3 highlights the benefits of optimizing the crossbar utilization ratio for minimizing the area–delay-time product. The proposed optimization strategies can substantially enhance the neural network’s performance of memristor crossbar-based processing-in-memory architectures, especially for resource-constrained edge computing platforms.
1. Introduction
In recent years, the proliferation of CNN has revolutionized natural language processing, computer vision, autonomous driving systems, and more [1,2,3,4,5]. However, the increasing demand for computational resources and power consumption presents significant challenges, particularly in resource-limited environments such as mobile devices and edge computing platforms [6,7,8]. To address these challenges, researchers have been exploring novel hardware architectures that can offer both computational efficiency and low power.
One promising avenue in this pursuit is the integration of memristors, a type of non-volatile memory device, into various CNN-based architectures [9,10,11,12,13]. In particular, the most important operation in CNN, the MAC (multiply and accumulation) operation, can be implemented quickly and with low power. The memristor crossbar allows for multi-row and multi-column activation, enabling a large amount of parallel computation [14,15,16,17]. This capability can markedly decrease power consumption compared to traditional GPU operations, facilitating the energy-efficient implementation of CNN. Memristor is a non-volatile device whose resistance changes according to the magnitude of voltage or current applied to the device [18,19,20,21]. This unique characteristic makes it suitable for mimicking the synaptic behavior of neurons in the human brain. Additionally, memristors can store the weights required for analog calculations in multi-bits, and are emerging as a viable alternative to Processing in Memory (PIM) computing due to their characteristics such as low power, high performance, high integration, and high reliability compared to existing digital memories such as SRAMs, DRAMs, etc.
The number of crossbars, their size, and the mapping of neural network layers to the crossbar affect all aspects such as accuracy, power consumption, latency, and hardware area. Previous research has revealed that to balance the accuracy, power, area/delay time costs for a given neural network model and application constraints, it is necessary to optimize the size and architecture of the crossbar [22,23]. In particular, the line resistance present in memristor crossbar arrays requires that the size of the crossbar array be limited [24,25,26]. Therefore, it is important to appropriately map to the crossbar by dividing a large-size input image into several small-size sub-images [24,25,26]. Also, in the case of edge AI implementation with strict restrictions on available resources, it is important to minimize the number of memristor crossbars used.
Figure 1a,b show a mapping of a convolution operation to a memristor crossbar. Figure 1a assumes a 28 × 28 MNIST image with 3 × 3 convolution kernel. The convolution operation by 3 × 3 kernel in Figure 1a can be mapped into a memristor crossbar in Figure 1b for performing convolution. To do so, the memristor crossbar in Figure 1b should be a size of 784 × 784. In Figure 1b, white memristor cells represent HRS (high-resistance state), while red memristor cells represent programmed weights. Here, let us refer to the first column in Figure 1b. The first column calculates the first convolution operation by the 3 × 3 kernel shown in Figure 1a. The nine inputs from the 28 × 28 MNIST image are applied to nine memristors of programmed weights of the 3 × 3 kernel as shown in red in Figure 1b to calculate the first convolution. The remaining 775 inputs are applied to HRS cells, thereby affecting the column current very little. Similarly, the second column in Figure 1b performs the second convolution in Figure 1a, as explained in detail in the reference [27].
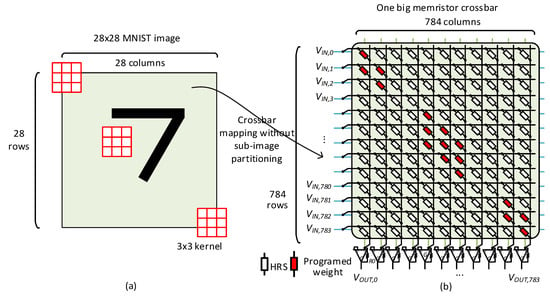
Figure 1.
Mapping of convolution operation to memristor crossbar. (a) 28 × 28 MNIST image with 3 × 3 convolution kernel. (b) Memristor crossbar performing convolution operation [22].
Figure 2a,b below show the process of performing convolution sequentially and in parallel depending on the number of memristor crossbars used in the memristor crossbar-based PIM process [27,28]. If a sub-image partitioning is not considered, to map a large-size input image to a single crossbar, the crossbar’s size should be very large. However, due to the line resistance of the memristor crossbar, if a large-sized crossbar is used, there can be cases where the sum of the line resistance of a column exceeds memristor’s LRS (low-resistance state), which can degrade MAC calculation accuracy significantly. Therefore, it is necessary to divide the large-size image into small-size sub-images and map them to the crossbars each by each [24,25,26].
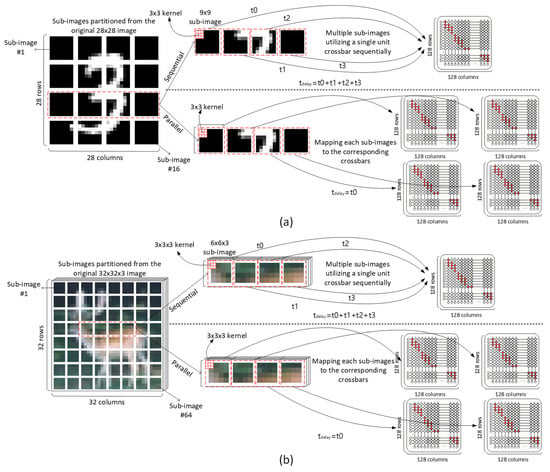
Figure 2.
Mapping from sub-images to memristor crossbars for (a) MNIST and (b) CIFAR-10 images.
In particular, Figure 2a shows the sub-images of the partitioned MNIST for mapping to the memristor crossbars. Here the upper figure indicates that sub-image convolution is performed four times sequentially using one memristor crossbar. The lower figure shows that four sub-images are mapped to four crossbars for performing sub-image convolution in parallel. In this context, the sub-image convolution process in the upper figure is performed in parallel. On the other hand, the lower figure indicates that the sub-image convolution is performed sequentially. In situations where the number of available crossbars is limited, a single crossbar must be reused by multiple sub-images in sequence. In situations where there is a sufficient number of available crossbars, each sub-image is mapped 1:1 to its corresponding crossbar. Here t0, t1, t2, and t3 mean the delay time for performing sub-image convolution. tdelay means the delay time per layer for completing the sub-image convolution in parallel or sequential process. In the upper part of Figure 2a, tdelay should be t0 + t1 + t2 + t3, because one crossbar performs four sub-image convolutions sequentially. On the other hand, tdelay in the lower part of Figure 2a is as short as t0. Here the four sub-image convolutions can be performed during the t0 at the same time.
Similarly, Figure 2b shows the sub-images of partitioned CIFAR-10. The upper and lower portions indicate the parallel and sequential sub-image convolution, respectively. Since CIFAR-10 images are three-dimensional, unlike two-dimensional MNIST images, the size of the sub-images is further diminished. The convolution process for CIFAR-10 data is the same as MNIST, but because the number of image pixels in a three-dimensional structure is much larger than the two-dimensional image, the number of crossbars needed in sub-image convolution becomes larger, as indicated in Figure 2b.
From here, the optimization of the crossbar’s area and delay time required to complete the sub-image convolution will be explained in more detail. As indicated in the upper portions of Figure 2a,b, the sub-image convolution by single crossbar can minimize memristor crossbar area, but with increased delay time. On the other hand, the sub-image convolution in the parallel process shown in the lower portions of Figure 2a,b implies that the delay time can be reduced despite large crossbar area. To explain further, when the number of crossbars is very small, the convolution operation should be processed serially, thereby increasing the delay time, as indicated in the upper portions of Figure 2a,b. If the number of crossbars is very large, the convolution operation can be processed in parallel, thereby decreasing the delay time, as shown in the lower portions of Figure 2a,b. Of course, a large number of crossbars means a large area overhead of memristor crossbars. A small number of crossbars leads to a small area of memristor crossbars for implementing CNNs. In this paper, using the optimization method, it will be shown that the crossbar’s delay time and area can be minimized under given constraints. In addition, it is also shown that the delay–area product can be optimized even without any constraint.
Applying the sub-image convolution to a very large CNN model such as ResNet-18 etc., we consider three cases of optimization in terms of crossbar area and delay time in this paper, as follows.
Case 1: Define an objective function that models the total delay time of sub-image convolution and optimize the number of crossbars per layer using the objective function, given a constraint of the total number of available crossbars used for implementing CNN.
Case 2: Define an objective function that models the total number of crossbars for sub-image convolution and optimize the number of crossbars per layer using the objective function, given a constraint of the total delay time to complete sub-image convolution.
Case 3: Define an objective function that models the product of crossbar area and delay time and optimize the number of crossbars per layer using the objective function, without any given constraint.
2. Method
The Lagrange multiplier method is one of the most well-known classic optimization algorithms, suitable for solving constrained optimization problems [29,30,31]. The Lagrange multiplier is used to create a new function by combining the objective function and constraints in an optimization problem. This new function can use partial derivatives to find the optimal solution that satisfies the constraints.
In this paper, we try to use the Lagrange multiplier method to solve the following two optimization problems with constraints. As already mentioned, case 1 involves appropriately placing the number of crossbars in each layer to optimize the total delay time of the model when the total number of crossbars is given as a constraint. Case 2 involves appropriately placing crossbars in each layer of the model to optimize the total number of crossbars when the total delay time is given as a constraint.
The following Equation (1) represents the fundamental form of the Lagrange multiplier method.
where the function denotes the Lagrangian function that combines an objective function with a constraint function. In Equation (1), the function f is an objective function of the Lagrange multiplier. The function g is the constraint function of the Lagrange multiplier. means the Lagrange multiplier. x1, x2, and xn represent variables of the objective function, and they can be optimized for the function f satisfying the constraint function g.
Equation (2) shows the process of taking the derivative for the function L.
Equation (2) can be divided into two parts of taking the derivative with respect to x1, x2, and xn and . The first part, of taking the derivative with respect to x1, x2, and xn, is shown in the following Equation (3).
The second part, of taking derivatives with respect to , is shown in the following Equation (4).
Here, is zero because f is not a function of λ. Hence Equation (4) means that the constraint should be zero.
As mentioned earlier, in this paper we consider three cases where sub-image convolution is extended to very large CNN models such as ResNet-18 to optimize the crossbar in terms of area and delay time. Case 1 and case 2 are for optimization with given constraints. Therefore, the Lagrange multiplier method is used to perform the optimization of cases 1 and 2, as follows.
Case 1: Define an objective function that models the total delay time of sub-image convolution and optimize the number of crossbars per layer using the objective function, given a constraint of the total number of available crossbars used for implementing CNN.
Equation (5) represents the objective function f1 for optimizing the total delay time in case 1, when there is a constraint on the total number of available crossbars.
In Equation (5), the objective function can be represented as the summation of the delay times of all layers in ResNet-18. Here x1, x2, and xn are the numbers of crossbars of layer #1, layer #2, and layer #n, respectively. ‘n’ is the total number of layers used in the CNN architecture. M1, M2, and Mn are the numbers of sub-image convolutions required for layer #1, layer #2, and layer #n, respectively. Thus, in Equation (5), Mi and xi are the numbers of sub-image convolutions and crossbars for layer #i, respectively. If the number of crossbars of layer #i, xi, can be used as many as Mi, the crossbar’s delay time is as short as 1. On the other hand, if the xi is as small as 1, the crossbar’s delay time of sub-image convolution for layer #i is as long as Mi/1. Each layer’s delay time can be calculated by Mi/xi for layer #i, as shown in Equation (5).
One thing to note is that the number of crossbars per layer cannot exceed the number of sub-image convolutions for the same layer, as mentioned in the condition of Equation (5). If the number of crossbars per layer is larger than the number of sub-image convolutions for the same layer, the extra crossbars cannot be involved in the sub-image convolutions. Therefore, they become useless.
Equation (6) below represents the constraint function g1 used in case 1.
calculates the total number of crossbars from layer #1 to layer #n. represents the constraint given in case 1, which means the total number of available crossbars given in case 1. Thus, the constraint function g1 can be zero if the total number of crossbars from layer #1 to layer #n is equal to the number of available crossbars given as a constraint in case 1.
Case 2: Define an objective function that models the total number of crossbars for sub-image convolution and optimize the number of crossbars per layer using the objective function, given a constraint of the total delay time to complete sub-image convolution.
Equation (7) represents the objective function f2 for optimizing the numbers of crossbars layer by layer, when there is a constraint on the total delay time to complete the sub-image convolution in case 2.
In Equation (7), x1, x2, and xn are the numbers of crossbars of layer #1, layer #2, and layer #n, respectively. ‘n’ is the total number of layers used in the CNN architecture. M1, M2, and Mn are the numbers of sub-image convolutions required for layer #1, layer #2, and layer #n, respectively.
Equation (8) indicates the total delay time constraint. Here the constraint function in case 2 is represented by g2.
To optimize the number of crossbars per layer, the total delay time for all the layers is set to in Equation (8). The number of crossbars per layer is minimized such that the total delay time for all the layers does not exceed .
Case 3: Define an objective function that models the product of the crossbar’s area and delay time and optimize the number of crossbars per layer using the objective function, without any given constraint.
Equation (9) below represents the optimization function f3 for the area–delay-time product in case 3, where the optimization is conducted solely on area–delay-time product without any constraints.
In Equation (9), x1, x2, and xn are the numbers of crossbars of layer #1, layer #2, and layer #n, respectively, to be optimized here. ‘n’ is the total number of layers used in the CNN architecture. M1, M2, and Mn are the numbers of sub-image convolutions required for layer #1, layer #2, and layer #n, respectively. Mi and xi are the numbers of sub-image convolutions and crossbars for layer #i, respectively.
As previously explained, the Lagrange multiplier method can perform the optimization with a given constraint function. Since the optimization of area–delay-time product in case 3 cannot have constraints such as area and delay time, the use of the Lagrange multiplier is not possible for case 3.
Instead of the Lagrange multiplier method, the genetic algorithm (GA) is a suitable solution for global optimization without a constraint, like case 3 [32,33,34]. GAs are powerful computational optimization techniques modeled on the principles of natural selection and genetic diversity. These algorithms mimic the process of biological evolution to enhance problem-solving capabilities, making them widely recognized and effective for solving various optimization problems.
GAs maintain a population of chromosomes, each representing potential solutions. The population evolves over successive generations. The initial population is generated randomly to ensure a diverse set of solutions. Each chromosome represents a possible solution to the problem and is evaluated using a fitness function. One of the key mechanisms of GAs is crossover (recombination). This process exchanges genetic information between parent chromosomes to create new offspring, introducing variation within the population and enabling the exploration of new solution spaces. The selection process determines which individuals will reproduce based on their fitness levels. Individuals with higher fitness scores are more likely to be selected, increasing the likelihood that optimal solutions will pass their genes to the next generation. Mutation introduces small random changes to individual chromosomes, preventing the algorithm from becoming trapped in local optima and promoting further exploration of the solution space. By balancing exploration and exploitation through crossover and mutation operations, GAs effectively find global optima in complex, multidimensional spaces.
As depicted in Figure 3a, the optimization algorithm proposed in this study works as follows. After solving the optimization problems described in cases 1, 2, and 3, the optimized numbers of x1, x2, and xn are obtained. Here ‘n’ means the number of layers. The optimized numbers of x1, x2, and xn are actually floating-point numbers, not integers. Because the number of crossbars per layer should be an integer, not a floating-point, the floating-point numbers of x1, x2, and xn should be converted to integer numbers of x1*, x2*, and xn*.
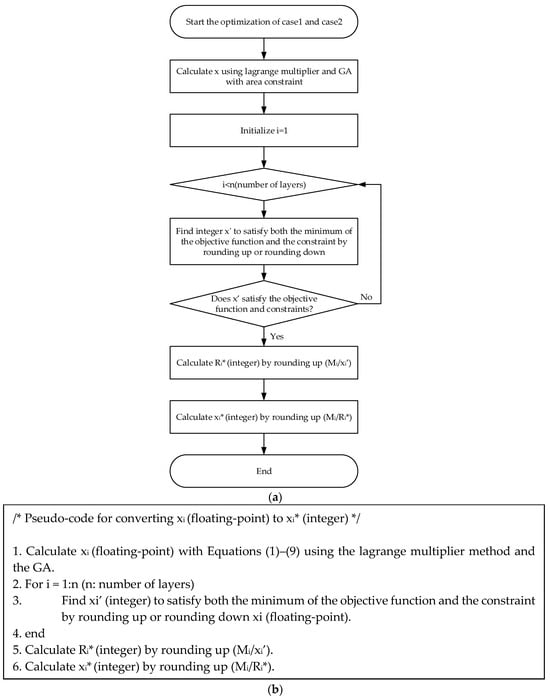
Figure 3.
(a) The flowchart for optimizing the mapping of sub-image convolutions to memristor crossbars. (b) The pseudo-code for converting the floating-point x to the integer x*.
To do so, the pseudo-code depicted in Figure 3b is used for converting the floating-point numbers of x1, x2, and xn, calculated from the Lagrange multiplier method and GA using Equations (1)–(9), to the integer numbers of x1*, x2*, and xn*. In the pseudo-code in Figure 3b, first, calculate xi (floating-point) with Equations (1)–(9) using the Lagrange multiplier method and the GA. Complete iterations for all the layers to find xi’ (integer) that satisfies both the minimum of the objective function and the constraint by rounding up or rounding down xi (floating-point). Then, calculate Ri* (integer) for layer #i by rounding up (Mi/xi’). Here, Mi and xi’ are the numbers of sub-image convolutions and crossbars for layer #i, respectively. Here Ri* (integer), calculated by rounding up (Mi/xi’), means the number of crossbar operations required to complete the sub-image convolutions for layer #i, when Mi and xi’ are given. Finally, obtain xi* (integer) by rounding up (Mi/Ri*). The xi* (integer) obtained from the pseudo-code can be regarded as the optimized number of crossbars for layer #i.
3. Results
Figure 4a shows the measurement and modeling results of a memristor cell [35,36]. In detail, Figure 4a indicates the measured butterfly curve of the memristor cell and the result of modeling it using Verilog-A. The top electrode of the memristor cell used Ta, the bottom electrode used Pt, and the memristive film used Mn2O3. The memristor cells were measured using the Keithley 4200 (Solon, OH, USA). More information about the fabricated memristors can be found in the reference [36].
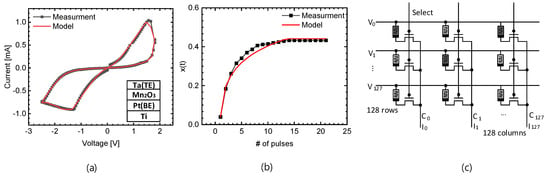
Figure 4.
(a) The measured and modeled butterfly curves of a memristor cell. (b) The measurement and the Verilog-A model of transient behavior observed in a memristor. (c) The 128 × 128 memristor crossbar [35,36].
Figure 4b shows the transient behavior of the memristor. Here, x(t) is the state variable of the memristor, and the measurement x(t) can be obtained from the below Equation (10) [35,37].
In Equation (10), I(t) means the measured memristor’s current when a voltage pulse V(t) is applied to the memristor. Parameters ‘A’ and ‘B’ are fitting parameters of the memristor’s voltage–current characteristic curve, which are A = 0.0005 and B = 2.425 in Equation (10). In Figure 4b, the model x(t) can be obtained by integrating Equation (11), which defines the dynamics of x(t) according to time.
Equation (12) defines g(V(t)). Here V(t) means a voltage applied to the memristor. ‘C’ and ‘D’ are fitting parameters used in Equation (12). Here, C = 0.00111 and D = −8 are used in Equation (11).
Figure 4c shows a memristor crossbar array with 128 × 128 cells. One weight cell consists of one select transistor and one memristor cell. In a memristor crossbar, the 1T–1R structure is essential because it helps to address sneak path currents, which can significantly affect the accuracy and reliability of the crossbar’s operations. The transistor (1T) in each cell provides the necessary isolation and control, allowing for precise read and write operations to the memristor (1R), thereby improving overall performance and functionality of the memristor crossbar array.
For a real-world circuit simulation, the memristor crossbars in Figure 4c are modeled using the Verilog-a and Equations (10)–(12). The circuit-level simulation of the memristor crossbars is performed by CADENCE SPECTRE, where the crossbar’s area and delay time for performing MAC calculation are simulated. To provide a more detailed explanation of the circuit simulation, 128 input neurons are connected to the rows of the crossbar, and 128 neurons are connected to the columns. The CMOS SPICE model used in this simulation is Generic PDK 0.18-μm technology, from CADENCE. From the CADENCE SPECTRE simulation, the delay time and power consumption of the unit memristor crossbar with 128 × 128 cells are calculated. The simulated delay time and power consumption are used in MATLAB simulation for optimizing the number of memristor crossbars per layer based on the Lagrange multiplier method and Genetic Algorithm.
Figure 5 shows the comparison of normalized delay time between the mapping without and with optimization under the normalized area constraint, as mentioned in case 1. Here the reference data represent scenarios where all layers maintain a constant ratio of Mi/xi that is not optimized at all. The simulation results in Figure 5 show that the total delay time optimized using the Lagrange multiplier method is approximately 11% less than the reference delay time, for the normalized area constraint = 0.06. As the normalized area constraint becomes larger, the delay time reduction becomes smaller, as indicated in Figure 5. When the normalized area constraint becomes almost 1, the delay time reduction becomes as small as 4%.
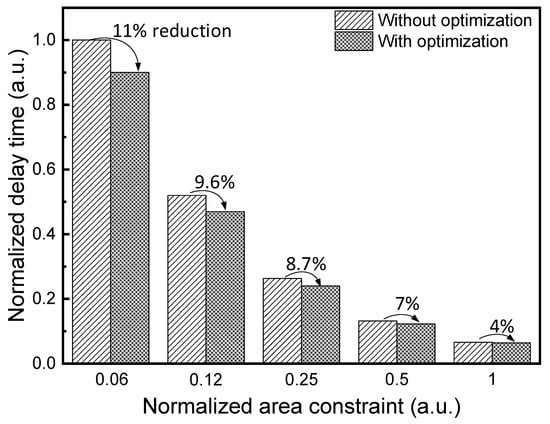
Figure 5.
Normalized delay-time comparison between the crossbar mapping without and with optimization for the normalized area constraint.
Figure 6 shows the comparison of normalized area between the crossbar mapping without and with optimization in case 2 when there is a constraint on normalized delay time. The reference data without any optimization are set by maintaining a constant Mi/xi ratio across all layers. The results of calculation through the Lagrange multiplier method are compared with the reference data without optimization in Figure 6. When the normalized delay-time constraint is 0.06, the Lagrange multiplier method can reduce the normalized crossbar’s area by 18% compared to the reference data without optimization. If the normalized delay-time constraint is 1, the normalized area reduction is still as large as 8%.
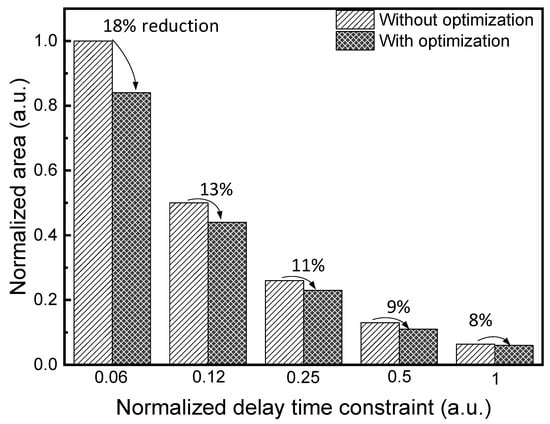
Figure 6.
Normalized area comparison between the crossbar mapping without and with optimization for the normalized delay-time constraint.
Figure 7 compares the normalized area–delay-time product between the crossbar’s mapping without and with optimization. Here the normalized area–delay-time product is optimized for each layer using the GA. As explained earlier, there is no constraint in Figure 7. The simulation results show that the optimized area–delay-time product can be improved by an average of 9% when compared to various constant Mi/xi ratios. The area–delay-time product is a crucial metric in digital systems, representing the trade-off between area and delay time. If there is enough available area, parallel computation is possible, but edge devices have limited area, which is a challenge. Therefore, minimizing the area–delay-time product is essential for maximizing the edge device’s performance by balancing area and delay time.
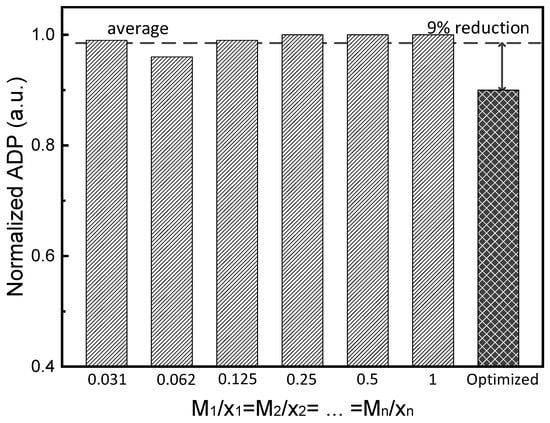
Figure 7.
Normalized area–delay-time product comparison between the crossbar mapping without and with optimization. Here, the optimization is performed without any constraint.
Finally, to ensure that the optimization method in this paper can be useful for the other convolutional neural networks, ResNet-34 and VGG-Net are considered in Table 1, in addition to ResNet-18. Table 1 compares the average reduction percentages between cases 1 and 2 in terms of normalized delay time and area for ResNet-18, ResNet-34, and VGG-Net. From Table 1, it is observed that VGG-Net shows better reduction percentages than ResNet-18 and ResNet-34 for cases 1 and 2. This is because VGG-Net has a larger difference between the maximum and minimum numbers of sub-image convolutions per layer than ResNet-18 and ResNet-34. The large difference in the numbers of sub-image convolutions per layer can lead to better optimization, and thus the average reduction percentages of delay time and area can be improved more substantially.

Table 1.
Comparison of average reduction percentages of normalized delay time and area for ResNet-18, ResNet-34, and VGG-Net.
4. Conclusions
This paper addresses the challenges of efficiently implementing convolutional neural networks (CNNs) such as ResNet-18, ResNet-34, and VGG-Net on memristor crossbars, which offer promising low-power and parallel processing capabilities. This paper investigates three optimization scenarios: (1) optimizing total delay time under an area constraint, (2) optimizing total crossbar area with a delay-time constraint, and (3) optimizing the area–delay-time product without constraints. The constrained cases 1 and 2 are addressed using the Lagrange multiplier method, while an unconstrained GA is employed for case 3’s area–delay-time product optimization.
The simulation results indicate substantial improvements due to the optimization compared to the results without optimization. For ResNet-18, case 1 shows an average reduction percentage of 8% for the normalized delay time. Case 2 shows an average reduction percentage of 11.8% for the normalized area. Case 3’s reduction percentage is as large as 9% on average for the normalized area–delay product. ResNet-34 and VGG-Net are also simulated in this paper to calculate the average reduction percentages of normalized delay time and area. These optimization strategies can be helpful to reduce the delay time and area of memristor-based neural networks, which are particularly critical for resource-constrained edge computing platforms.
Author Contributions
K.-S.M. defined the research topic. S.-M.C. contributed to the algorithm definition, the simulation, and the data analysis. R.Y., I.Y., J.M., and S.O. contributed to data analysis of the simulation result. S.-M.C. and K.-S.M. wrote the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by NRF-2021M3F3A2A01037972, RS-2024-00401234 and RS-2024-00406006, funded by NRF, Korea.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Dataset available on request from the authors.
Acknowledgments
The CAD tools were supported by IC Design Education Center (IDEC), Daejeon, Korea.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Tajbakhsh, N.; Shin, J.Y.; Gurudu, S.R.; Hurst, R.T.; Kendall, C.B.; Gotway, M.B.; Liang, J. Convolutional neural networks for medical image analysis: Full training or fine tuning? IEEE Trans. Med. Imaging 2016, 35, 1299–1312. [Google Scholar] [CrossRef] [PubMed]
- Chauhan, R.; Ghanshala, K.K.; Joshi, R.C. Convolutional neural network (CNN) for image detection and recognition. In Proceedings of the 2018 First International Conference on Secure Cyber Computing and Communication (ICSCCC), Jalandhar, India, 15–17 December 2018. [Google Scholar]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit 2018, 77, 354–377. [Google Scholar] [CrossRef]
- O’shea, K.; Nash, R. An introduction to convolutional neural networks. arXiv 2015, arXiv:1511.08458. [Google Scholar]
- Cai, E.; Juan, D.-C.; Stamoulis, D.; Marculescu, D. Neuralpower: Predict and deploy energy-efficient convolutional neural networks. In Proceedings of the Asian Conference on Machine Learning, Seoul, Republic of Korea, 15−17 November 2017. [Google Scholar]
- Rashid, N.; Demirel, B.U.; Al Faruque, M.A. AHAR: Adaptive CNN for energy-efficient human activity recognition in low-power edge devices. IEEE Internet Things J. 2022, 9, 13041–13051. [Google Scholar] [CrossRef]
- Hodak, M.; Gorkovenko, M.; Dholakia, A. Towards power efficiency in deep learning on data center hardware. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019. [Google Scholar]
- Li, Y.; Wang, Z.; Midya, R.; Xia, Q.; Yang, J.J. Review of memristor devices in neuromorphic computing: Materials sciences and device challenges. J. Phys. D Appl. Phys. 2018, 51, 503002. [Google Scholar] [CrossRef]
- Burr, G.W.; Shelby, R.M.; Sebastian, A.; Kim, S.; Kim, S.; Sidler, S.; Virwani, K.; Ishii, M.; Narayanan, P.; Fumarola, A.; et al. Neuromorphic computing using non-volatile memory. Adv. Phys. X 2016, 2, 89–124. [Google Scholar] [CrossRef]
- Huh, W.; Lee, D.; Lee, C. Memristors based on 2D materials as an artificial synapse for neuromorphic electronics. Adv. Mater. 2020, 32, 2002092. [Google Scholar] [CrossRef] [PubMed]
- Upadhyay, N.K.; Jiang, H.; Wang, Z.; Asapu, S.; Xia, Q.; Yang, J.J. Emerging memory devices for neuromorphic computing. Adv. Mater. Technol. 2019, 4, 1800589. [Google Scholar] [CrossRef]
- Sung, C.; Hwang, H.; Yoo, I.K. Perspective: A review on memristive hardware for neuromorphic computation. J. Appl. Phys. 2018, 124, 151903. [Google Scholar] [CrossRef]
- Chen, J.; Li, J.; Li, Y.; Miao, X. Multiply accumulate operations in memristor crossbar arrays for analog computing. J. Semicond. 2021, 42, 013104. [Google Scholar] [CrossRef]
- Xia, L.; Gu, P.; Li, B.; Tang, T.; Yin, X.; Huangfu, W.; Yu, S.; Cao, Y.; Wang, Y.; Yang, H. Technological exploration of RRAM crossbar array for matrix-vector multiplication. J. Comput. Sci. Technol. 2016, 31, 3–19. [Google Scholar] [CrossRef]
- Li, B.; Gu, P.; Shan, Y.; Wang, Y.; Chen, Y.; Yang, H. RRAM-based analog approximate computing. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2015, 34, 1905–1917. [Google Scholar] [CrossRef]
- Hu, M.; Graves, C.E.; Li, C.; Li, Y.; Ge, N.; Montgomery, E.; Davila, N.; Jiang, H.; Williams, R.S.; Yang, J.J.; et al. Memristor-based analog computation and neural network classification with a dot product engine. Adv. Mater. 2018, 30, 1705914. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Jiang, B.; Zhang, Z.; Ke, S.; Jin, Y.; Wen, X.; Ye, C.; Chen, X. A review of memristor: Material and structure design, device performance, applications and prospects. Sci. Technol. Adv. Mater. 2023, 24, 2162323. [Google Scholar] [CrossRef] [PubMed]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Ielmini, D. Resistive switching memories based on metal oxides: Mechanisms, reliability and scaling. Semicond. Sci. Technol. 2016, 31, 063002. [Google Scholar] [CrossRef]
- Mohammad, B.; Jaoude, M.A.; Kumar, V.; Al Homouz, D.M.; Nahla, H.A.; Al-Qutayri, M.; Christoforou, N. State of the art of metal oxide memristor devices. Nanotechnol. Rev. 2016, 5, 311–329. [Google Scholar] [CrossRef]
- Oh, S.; An, J.; Min, K. Area-Efficient Mapping of Convolutional Neural Networks to Memristor Crossbars Using Sub-Image Partitioning. Micromachines 2023, 14, 309. [Google Scholar] [CrossRef]
- Peng, X.; Liu, R.; Yu, S. Optimizing weight mapping and data flow for convolutional neural networks on RRAM based processing-in-memory architecture. In Proceedings of the 2019 IEEE International Symposium on Circuits and Systems (ISCAS), Sapporo, Japan, 26–29 May 2019. [Google Scholar]
- Murali, G.; Sun, X.; Yu, S.; Lim, S.K. Heterogeneous mixed-signal monolithic 3-D in-memory computing using resistive RAM. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2020, 29, 386–396. [Google Scholar] [CrossRef]
- Sah, M.P.; Yang, C.; Kim, H.; Muthuswamy, B.; Jevtic, J.; Chua, L. A generic model of memristors with parasitic components. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 891–898. [Google Scholar] [CrossRef]
- Nguyen, T.V.; An, J.; Min, K. Memristor-cmos hybrid neuron circuit with nonideal-effect correction related to parasitic resistance for binary-memristor-crossbar neural networks. Micromachines 2021, 12, 791. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y. The MNIST Database of Handwritten Digits. 1998. Available online: http://yann.lecun.com/exdb/mnist/ (accessed on 12 July 2024).
- Krizhevsky, A. Learning Multiple Layers of Features from Tiny Images. (Master’s Thesis, University of Toronto). Available online: https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf (accessed on 12 July 2024).
- Tran, H.G.; Ton-That, L.; Thao, N.G.M. Lagrange Multiplier-Based Optimization for Hybrid Energy Management System with Renewable Energy Sources and Electric Vehicles. Electronics 2023, 12, 4513. [Google Scholar] [CrossRef]
- Everett, H., III. Generalized Lagrange multiplier method for solving problems of optimum allocation of resources. Oper. Res. 1963, 11, 399–417. [Google Scholar] [CrossRef]
- Lagrange Multiplier. Wikipedia, The Free Encyclopedia. Available online: https://en.wikipedia.org/wiki/Lagrange_multiplier (accessed on 8 July 2024).
- Schmitt, L.M. Theory of genetic algorithms. Theor. Comput. Sci. 2001, 259, 1–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S. Genetic algorithm. In Evolutionary Algorithms and Neural Networks: Theory and Applications; 2019; pp. 43–55. Available online: https://link.springer.com/chapter/10.1007/978-3-319-93025-1_4 (accessed on 12 July 2024).
- Lambora, A.; Gupta, K.; Chopra, K. Genetic algorithm—A literature review. In Proceedings of the 2019 International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Faridabad, India, 14–16 February 2019. [Google Scholar]
- Cho, S.-M.; Oh, S.; Yoon, R.; Min, K.-S. Compact Verilog-A Model of Current-Voltage and Transient Behaviors of Memristors for Fast Circuit Simulation. J. IKEEE 2023, 27, 180–186. [Google Scholar]
- Yang, M.K.; Kim, G.H. Post-Annealing Effect on Resistive Switching Performance of a Ta/Mn2O3/Pt/Ti Stacked Device. Phys. Status Solidi (RRL)-Rapid Res. Lett. 2018, 12, 1800031. [Google Scholar] [CrossRef]
- Truong, S.N.; Van Pham, K.; Yang, W.; Shin, S.; Pedrotti, K.; Min, K.-S. New pulse amplitude modulation for fine tuning of memristor synapses. Microelectron. J. 2016, 55, 162–168. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).