Abstract
Low-current grounding systems are the main grounding method used in power distribution networks and belong to non-direct grounding systems. The most common fault in this type of system is a single-phase grounding fault, which may cause electrical fires and endanger personal safety. Due to the difficulty of troubleshooting, the selection of fault lines in low-current grounding systems has always been an important research topic in power system relay protection. This study proposes a new approach for fault identification of power lines based on the Euler transformation and deep learning. Firstly, the current signals of the distribution network are rapidly Fourier-transformed to obtain their frequencies for constructing reference signals. Then, the current signals are combined with the reference signals and transformed into images using Euler transformation in the complex plane. The images are then classified using a residual network model. The convolutional neural network in the model can automatically extract fault feature vectors, thus achieving the identification of faulty lines. The simulation was conducted based on the existing model, and extensive data training and testing were performed. The experimental results show that this method has good stability, fast convergence speed, and high accuracy. This technology can effectively accomplish fault identification in power distribution networks.
1. Introduction
Distribution networks are the final link in the electricity supply chain and play a crucial role in ensuring a stable power supply for consumers [1]. Low-current grounding systems are widely used in distribution network systems, and the network structure of these systems is becoming increasingly complex with more diverse operating conditions. As a result, distribution network systems are more prone to faults, with single-phase-to-ground (SPG) faults being the most common [2]. If SPG faults are not eliminated for a long time, it is easy for the faults to develop into two or more point grounding short circuits, which can damage equipment and even endanger personal safety. When a single-phase grounding fault occurs in the system, due to the weak fault current and severe electromagnetic interference, as well as the complex and variable fault conditions, it is difficult to accurately select the fault line. Therefore, the rapid and accurate identification of SPG faults is of great significance for maintaining the safety, stability, and reliable operation of the distribution network.
The fault selection methods for today’s power distribution network can mainly be divided into two categories: the steady-state analysis method and the transient-state analysis method [3,4]. The steady-state analysis method includes comparing the amplitude and phase of the zero-sequence current method and the injection method. In [5], an improved phase-locked loop is used to extract the fifth harmonic of the zero-sequence current signal, and fault discrimination is achieved by comparing the amplitude and phase of the fifth harmonic. However, this method is susceptible to the influence of excessive resistance and noise. The injection method is to inject signals of specific frequencies into the distribution network and detect and locate faults by tracking these signals [6]. However, this method requires expensive equipment and complex control algorithms.
To prevent excessive line currents during SPG faults, distribution networks are often equipped with arc suppression coils [7]. The compensating effect of the arc suppression coils reduces the difference in zero-sequence currents, which affects the reliability of line selection. The steady-state analysis method is not suitable for use in distribution networks with arc suppression coils. The transient-state analysis method is almost unaffected by arc suppression coils, and many researchers have devoted their efforts to studying SPG fault identification in this direction [8]. At the same time, if a large number of power electronic devices are connected, transient signals may exhibit strong randomness and non-stationarity [9]. In [10], Liu and his team applied wavelet analysis theory to fault detection from the perspective of signal processing. They extracted characteristic components of transient signals by comparing wavelet analysis with modulus maxima, achieving fault line selection. However, since wavelet transform requires the determination of appropriate basis functions in advance, if the basis functions are not suitable, the wavelet transform cannot achieve optimal results. In [11], Tao et al. proposed using the Hilbert transform to extract transient power information for fault analysis, but this method is difficult to apply in practice. In [12], the authors combine wavelet transform, singular value decomposition, Shannon entropy, and fuzzy logic to perform fault detection. However, when encountering a high-impedance ground fault in the system, the fault characteristics are weak. In [13], by combining the steady-state current and the transient current, the accuracy can be improved by establishing two coordinate detection criteria. However, this method requires strict data acquisition. If the correct or complete waveform is not captured during the transient period, accurate fault identification results will not be obtained.
To improve the accuracy and generalization ability of fault diagnosis, researchers have started to utilize deep learning algorithms, especially convolutional neural networks (CNNs), to extract fault features from signals. In [14], by adding the sampled sequences of zero-sequence current values from different lines pairwise, a fused zero-sequence current sequence is generated, which is then inputted to a one-dimensional CNN. Through the CNN, fault features are extracted to distinguish between faulty lines and normal lines. In [15], to improve the detection accuracy and reliability, the waveform of the zero-sequence voltage on the bus and the zero-sequence current on a single feedback line are directly superimposed. Then, the attention mechanism and the CNN are used to learn the voltage-current feature information, thus constructing a fault classification model. These methods employ advanced neural network algorithms, which have higher accuracy and robustness compared to traditional fault selection methods. However, these methods focus solely on the surface features of current or voltage signals, and neural networks may not fully exploit the underlying feature information. As a result, the training outcomes may suffer from overfitting.
An efficient and precise identification of fault lines in distribution networks can significantly reduce fault detection time, minimize economic losses, and enhance power safety. The paper introduces a novel approach for selecting fault lines in distribution networks based on Euler variation and the ResNet50 model to address the issue of single-phase grounding fault line selection. The key contributions of this study are as follows:
- (1)
- Using the Euler transformation principle, a one-dimensional time domain signal is transformed into a space vector ellipse (SVE). The transformed signal is better suited for training convolutional neural networks, enabling more fault-related features to be extracted and achieving accurate classification.
- (2)
- The ResNet50 neural network is utilized for automatic feature extraction from the signal converted into an image, thereby mitigating the potential interference stemming from the manual selection of fault features.
- (3)
- In contrast to the conventional fault line selection method, the proposed approach obviates the need for the meticulous processing of the original signal, streamlining the processing procedure while ensuring high accuracy and generalizability.
2. Ground Fault Analysis
To ensure the reliability of the distribution network system, a low-current grounding method is generally used at the neutral point in the system [16,17]. However, the majority of distribution networks adopt a non-grounded or grounded through an arc suppression coil (ASC) method at the neutral point. When a fault occurs, the current flowing through the fault point is small, and the line voltages between the three phases remain balanced. As a result, the distribution network can continue to operate with the fault for 1–2 h [18,19], which is why it is referred to as a low-current grounding system.
The neutral point ungrounded system, single-phase grounding fault schematic diagram is shown in Figure 1. In the figure, the phases of the bus bars in the distribution network are represented by a, b, and c, respectively. represents the ground capacitance, and and are the power supply voltage and zero-sequence current. From Figure 1, it can be seen that when a single-phase-to-ground fault occurs in phase A of line 2, the B and C phase currents of lines 1, 2, and 3 flow through two units of zero-sequence current from the busbar to the line. A phase current of line 2, on the other hand, flows through six units of zero-sequence current, from the line to the busbar. It can be observed that the zero-sequence current flowing through line 2 is the sum of the zero-sequence currents of the non-faulty lines, and it flows in the opposite direction.
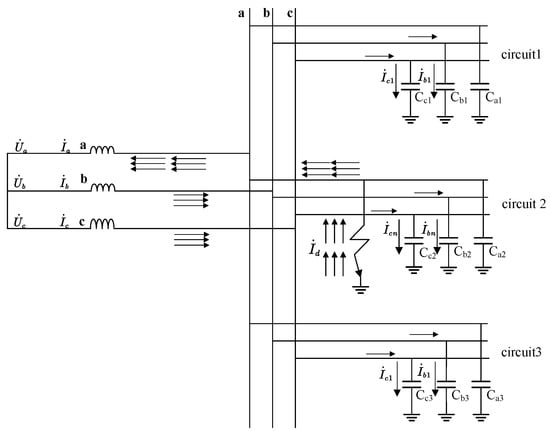
Figure 1.
Neutral point ungrounded system, single-phase grounding fault schematic diagram.
Based on the above analysis, it can be concluded that, during a ground fault, the zero-sequence current on the non-faulty line is equal to the capacitive current to the ground, with the current flowing from the busbar to the line. The zero-sequence current on the faulty line is equal to the sum of the zero-sequence currents on the non-faulty lines, with the current flowing from the line to the busbar.
Since a zero-sequence current only appears when a ground fault occurs in the circuit and is significantly different from normal current signals, most researchers have chosen zero-sequence currents as an important basis for diagnosing ground faults in power lines.
3. Signal-to-Image Conversion Method
3.1. The Theory of Space Vector Ellipses
To effectively extract the fault characteristics of the current signal in the distribution network, the zero-sequence current signal should be transformed from a one-dimensional current signal to a two-dimensional image. According to Euler’s rule, the disturbance signal and the reference signal are mapped to complex two-dimensional coordinates, resulting in an SVE graph, which allows for signal visualization [20].
First, assume that the current signal is sinusoidal. According to Euler’s rule, the signal can be represented as the sum of two vectors rotating in opposite directions with an angular frequency, which is given by
Construct a reference signal with the ideal amplitude and frequency, whose phase angle difference of with can be presented as
Then, rotate the reference signal counterclockwise by 90 degrees on the complex plane and combine and into a space vector , which is formed as
By Equation (4), it can be observed that is an elliptical vector. By transforming the time-domain signal into an elliptical shape, the characteristics of the signal can be reflected in the major axis, minor axis, and tilt angle of the ellipse. Through these parameters, the features of the signal can be identified more clearly. Figure 2 shows the time-domain signal and its corresponding SVE graph.
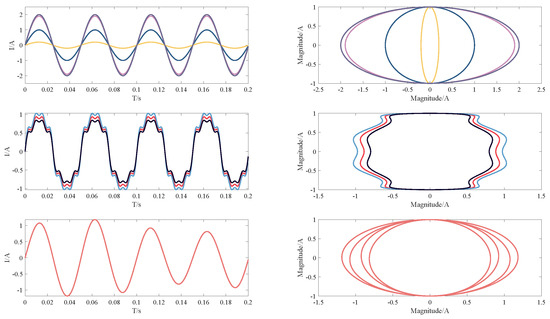
Figure 2.
Time−domain signal to space vector ellipse (left is the time−domain signal, right is the corresponding SVE).
3.2. Adaptive Space Ellipse Vector Visualization
According to the theory of SVE, a space vector ellipse can be obtained, with the reference signal a key component of this theory. However, due to the complex and variable nature of the signals in practical distribution networks, the current signal on a single line is often a combination of multiple signals with varying frequencies. Therefore, to ensure the practical application of this method, it is necessary to adaptively adjust the reference signal based on the current signal of the distribution network.
This article improves upon the theoretical basis of [20] by using a fast Fourier transform to extract the frequency of the sampled current signal from the circuit. The extracted frequency is then used to construct an ideal reference signal. The actual circuit current signal is then synthesized with the ideal reference signal to form a space vector. As time changes, the phase and amplitude of the space vector will also change. After one cycle, an irregular closed figure will be formed, which can reflect the condition of the distribution network.
Simulate a distribution network model with five lines using Simulink. At 0.02 s, a single-phase ground fault occurs, with one line simulating a low−current ground fault and the other four lines simulating normal signals. Figure 3 shows the zero-sequence current and corresponding converted SVE waveform when line 1 experiences an A-phase ground fault.
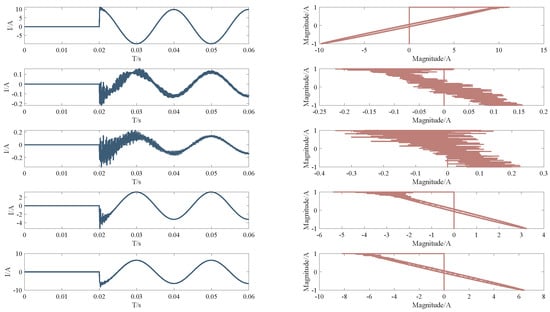
Figure 3.
Simulated current signals of five routes in the distribution network and their corresponding conversion to SVE (left: simulated signals, right: corresponding SVE).
From the graph, it can be observed that the zero-sequence current generated when a certain line experiences a ground fault can be represented in the form of an SVE diagram. The characteristics of the zero-sequence current for the faulty line and the normal line can be reflected by the inclination angle of the graph and the lengths of the major and minor axes. The features hidden in the zero-sequence current signal are represented in the form of graphical characteristics.
4. Fault Detection Model Based on ResNet50
4.1. ResNet50 Fault Selection Model
This article analyzes the characteristics of the ResNet50 network and proposes a small current grounding fault selection model based on this network, which consists of signal transformation and deep convolutional feature extraction, as shown in Figure 4.
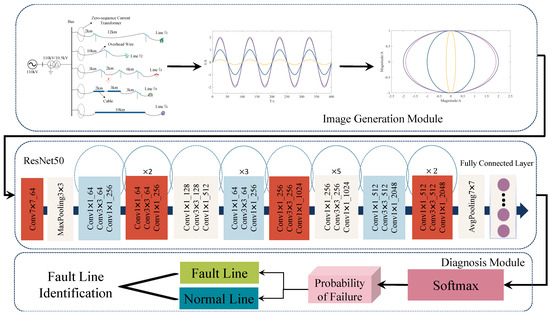
Figure 4.
Fault line selection model based on residual networks.
First, based on the rule of Euler transformation, the one-dimensional zero-sequence current time-domain signal is transformed into a two-dimensional SVE image with order m n. Then, the image is input into the pre-built ResNet50 network in the deep feature extraction layer to extract the fault information features contained in it. The fault features are output through the fully connected layer, and finally, the softmax layer is used for judgment to achieve the fault diagnosis.
4.2. Fault Data Generation
ResNet50 is a supervised neural network model, so training the ResNet50 fault selection model requires a large amount of labeled data. In this paper, a distribution network model is built using Simulink to simulate single-phase ground faults, as shown in Figure 5. The three-phase voltage sources of the distribution network model used for simulation are set to 110 kV, and five transmission lines are set up. To ensure data diversity and as close adherence to real-world scenarios as possible, the simulation model is set as a radial distribution network model. Specifically, there are three pure overhead lines (line to ), one mixed cable and overhead line (line ), and one pure cable line (line ). Due to the different lengths and types of each line, the zero-sequence currents are also different when a single-phase ground fault occurs.
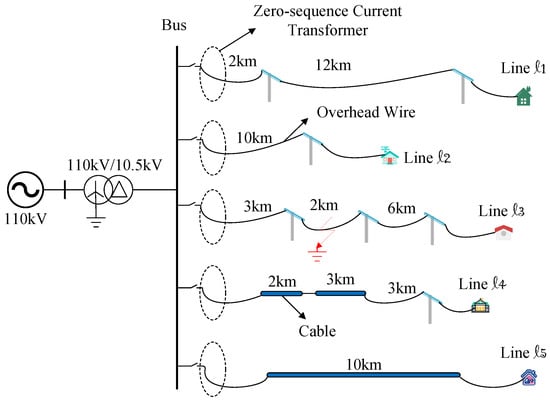
Figure 5.
Radial Distribution Network Model.
The positive-sequence and zero-sequence parameters of the overhead line in the diagram are shown in Table 1.

Table 1.
The positive-sequence and zero-sequence parameters of the overhead line.
The positive-sequence and zero-sequence parameters of the cable circuit are shown in Table 2.

Table 2.
The positive-sequence and zero-sequence parameters of the cable circuit.
Each time the simulation selects one of the transmission lines to experience a single-phase ground fault at 0.02 s, while the other four lines remain normal, it outputs a current signal dataset with a time sequence. To ensure the reliability of the obtained data and enrich the dataset, the fault resistance range is set from 0 to 100 , divided into 200 equal parts, and simulated 200 times. Among them, phase A and phase B ground faults occur 65 times each, and phase C ground faults occur 70 times. A total of 1000 datasets are obtained from the five lines, with each dataset consisting of five valid current sequences. Therefore, a total of 5000 valid current data points can be obtained, and 10% of them are randomly selected as the test set. At the same time, to improve the system’s anti-interference ability, 2000 randomly selected data points are added with noise to generate noise datasets with signal-to-noise ratios of 10 dB, 15 dB, 20 dB, and 25 dB, each containing 2000 entries. Therefore, the training set consists of 12,500 data entries, and 10% of them are randomly selected as the validation set during training. Detailed parameters are shown in Table 3.

Table 3.
Detailed parameters of the radial distribution network model.
5. Experimental Analysis
5.1. Training and Validation of ResNet50 Model
In the experiment, the pre-trained network model’s weight and bias from MATLAB were utilized for initialization. During training, the Adam optimization algorithm was employed as the optimizer, with an initial learning rate of 0.001. Additionally, a batch size of 32 was chosen to maximize the graphics card’s memory utilization. After 20 rounds of training, where each iteration was verified 50 times, it was observed that the loss function no longer exhibited a significant decrease and accuracy reached saturation. Therefore, in order to enhance classification model accuracy, minimizing cross-entropy is crucial to aligning the predicted data distribution with the real data distribution. Hence, the cross-entropy loss function is selected as the model’s loss function. The equation is shown in Equation (5)
In the equation, x represents the predicted value, y represents the true label, and C represents the total number of sample categories. The smaller the value of the loss function, the better the training effect.
The generated samples were fed into the ResNet50 model and trained for 20 rounds. The training results are shown in Figure 6. As the number of training iterations increased, the loss function gradually decreased, eventually approaching zero and remaining stable. The accuracy of the training samples also increased gradually with the number of training iterations, reaching 100%. At the same time, the accuracy of the validation set also increased gradually, eventually reaching 98.88% and stabilizing. These results indicate that the method proposed in this paper is feasible, stable, and highly accurate.
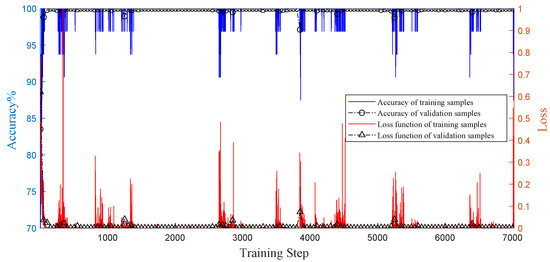
Figure 6.
Training and validation results of ResNet50.
To better verify the effectiveness of neural networks in extracting sample features and classifying them, the t-distributed stochastic neighbor embedding (t-SNE) technique was used to visualize the high-dimensional features extracted from the input layer and a fully connected output layer of the network, as shown in Figure 7. The red and blue colors in the figure represent normal samples and faulty samples, respectively. In the input layer, these samples are mixed and difficult to classify. However, after passing through the ResNet50 network, the normal and faulty samples are, respectively, clustered and gradually classified. In the fully connected output layer, they already have a high degree of discrimination, thus effectively distinguishing between normal and faulty samples.

Figure 7.
Visualization of neural network feature extraction.
The unique structure of the residual network enables it to overcome the issue of network degradation and increase the maximum number of layers. As the number of layers in the network increases, the nonlinear expression capability of the neural network also increases, allowing for the fitting of more complex feature inputs. However, with an increase in network depth comes an increase in model complexity, so it is important to select the appropriate model depth based on actual needs. Table 4 presents parameter attributes for several models. It can be observed from the table that AlexNet has the smallest depth; however, due to its rough structure and redundancies, its model size and number of parameters are large. The Vgg neural network is also excellent but has a larger model size, more training parameters, and higher training requirements. On the other hand, despite having a large depth, the residual network has a low model size and parameter count, which reduces its demand for training environments and allows it to run on edge devices.

Table 4.
Comparative analysis of network complexity.
5.2. Fault Diagnosis Testing for Different Types of Power Distribution Networks
In addition to the ungrounded system, another common structure in the distribution network is the neutral point grounded system with an arc suppression coil. By adding an arc suppression coil to the neutral point of the distribution network, it can generate an inductive current to compensate for the zero-sequence current when it passes through, thereby reducing the current flowing through the grounding point to a range where it can self-extinguish. This makes it difficult to diagnose faults using methods such as amplitude comparison. By adding an arc suppression coil to the radial distribution network model with the original neutral point ungrounded, 4500 training samples and 500 testing samples are generated. At the same time, with the development and utilization of new energy sources, distributed generation (DG) has gradually been introduced into the distribution network, making it more difficult to distinguish fault currents. To prove that the method proposed in this paper can still effectively detect fault lines in circuits with distributed generation, 4500 training samples and 500 testing samples are generated by adding distributed generation to the original simulation model. The parameters of the arc suppression coil and distributed generation are shown in Table 5.

Table 5.
Arc suppression coil and distributed power source.
Figure 8a–c, respectively, represent the confusion matrices of the ungrounded neutral point system, the neutral point system with an arc suppression coil, and the ungrounded neutral point system with distributed power sources. The rows represent the predicted output categories, while the columns represent the corresponding target categories. The main diagonal represents the number of correctly classified samples, while the off-diagonal elements represent the number of misclassified samples. The detection accuracy and error rate are displayed on the rightmost side, the recall rate and false negative rate are shown in the last row, and the overall accuracy is displayed in the bottom right corner. From the confusion matrices of the test samples, it can be observed that, regardless of the ungrounded neutral point system, the neutral point system with an arc suppression coil, or the system with distributed power sources, the diagnostic method proposed in this paper can accurately identify normal and faulty lines with high accuracy.
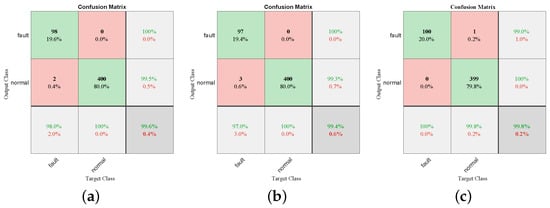
Figure 8.
Confusion matrix of different test samples. (a) Radial distribution network. (b) Radial neutral point grounded distribution network through arc suppression coil. (c) Integration of distributed power generation into the distribution grid.
5.3. Generalization Ability Test
To verify the superiority of our method, we trained and tested it using both the original zero-sequence current waveform and the waveform transformed by wavelet transform. We then changed the fault occurrence time in the simulated circuit and generated 350 new test datasets for each method to compare their general performance. From Table 6, it can be seen that the method using the time-domain current waveform and wavelet transform has similar accuracy and precision to the SVE method for the same type of fault during training. However, when testing with the changed fault occurrence time, the accuracy of the method using the time-domain current waveform dropped to 80%, and the method using wavelet transform dropped even further to 60%, while the SVE method maintained 100% accuracy. The AlexNet model is utilized for fault line classification. During the training process, the accuracy of the training set is relatively high; however, the accuracy of the validation set fluctuates around 85%, significantly lower than that of the training set. This discrepancy indicates that the model has entered an overfitting state. This suggests that the transformed waveform weakens the temporal features but highlights the fault features. The fault features extracted during training are more general, and the model has stronger generalization ability after training. Even when the fault occurrence time is changed, it still maintains a high accuracy rate.

Table 6.
Comparison of accuracy between different methods.
5.4. Noise Resistance Test
In practical distribution network lines, the current signal is susceptible to noise interference, which means that the diagnostic results will also be affected by the noise. To verify the advantages of the method proposed in this paper, the accuracy of five lines under four different signal-to-noise ratios (SNRs), 10 dB, 15 dB, 20 dB, and 25 dB, as well as the accuracy of two other line selection methods under different noise levels, were compared. The number of test samples for each case was 530, and the results are shown in Table 7. Studies [5,9] compare the amplitude and polarity of zero-sequence current signals of normal and faulty lines to achieve fault selection. This method is called amplitude comparison or polarity comparison. However, the use of these two methods is greatly affected by interference. The study [21] utilizes a data-driven approach for fault line selection, which provides a certain level of noise resistance but is still inferior to the method proposed in this paper. Additionally, the conversion of the spectrogram takes a longer time. The method in this paper converts one-dimensional zero-sequence current signals into two-dimensional images based on Euler’s rule, highlighting the characteristics of normal current signals and fault current signals. It achieves higher accuracy even in the presence of strong interference, surpassing traditional fault location methods.

Table 7.
Comparison of noise resistance in different routing methods.
6. Conclusions
This article proposes an SVE-based approach to line selection for low-current grounding faults in distribution networks using image classification methods. Unlike existing solutions, this article visualizes the zero-sequence current signal based on the theory of Euler transformation and extracts fault features using neural networks. By leveraging the powerful feature extraction capability of convolutional neural networks, hidden fault features in the data are discovered. To address the issue of neural network degradation, the ResNet50 network is chosen. The simulation experimental results demonstrate that this method can accurately identify fault lines with high precision.
To verify the effectiveness of the proposed method, modifications were made to the original ungrounded neutral system by adding arc suppression coils and distributed power sources. A grounded neutral system with arc suppression coils and a distribution network system with distributed power sources were constructed. The fault currents of both systems were sampled and tested. The results demonstrated that the proposed method had higher accuracy in diagnosing single-phase grounding faults in different distribution network systems.
To validate the generalization ability of the proposed method, the fault occurrence locations were changed, and the fault and normal current signals were resampled. The neural network model was trained using zero-sequence current diagrams and images transformed by wavelet transform. A comparison was made between the proposed method and the unchanged time-domain current diagrams and the method using wavelet transform. The results showed that the proposed method outperformed the other methods in terms of generalization ability.
To verify the noise immunity of the proposed method, noise with signal-to-noise ratios of 10 dB, 15 dB, 20 dB, and 25 dB was added to the original dataset. A comparison was made with the polarity comparison method, the amplitude comparison method, and a neural network trained using zero-sequence current diagrams. The results indicated that the proposed method had better noise immunity compared to other methods.
This paper presents a novel method for line selection in single-phase grounding faults in distribution networks. A comparative analysis with other methods demonstrates the high accuracy and robustness of the proposed method. However, due to limitations in experimental conditions, there is a lack of test data from actual samples, which hinders the ability to effectively prove the practical application of the proposed method. Future plans include increasing experimental verification using actual data to demonstrate that the method proposed in this paper can also perform effectively in real-world environments.
Author Contributions
Conceptualization, Y.S., W.G. and H.W.; methodology, W.G.; software, H.W.; validation, W.G. and H.W.; formal analysis, H.W.; investigation, H.W.; resources, Y.S., W.G. and H.W.; data curation, W.G. and H.W.; writing—original draft preparation, H.W.; writing—review and editing, W.G. and H.W.; visualization, H.W.; supervision, H.W.; project administration, Y.S. and H.W.; funding acquisition, Y.S. and W.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was sponsored by the National Natural Science Foundation of China (62373006) and the National Key R&D Program of China (2023YFC3306405).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The results/data/figures in this manuscript have not been published elsewhere, nor are they under consideration (from you or one of your Contributing Authors) by another publisher.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Mahmoud, T.; Dong, Z.; Ma, J. Integrated optimal active and reactive power control scheme for grid connected permanent magnet synchronous generator wind turbines. IET Electr. Power Appl. 2018, 12, 1751–8660. [Google Scholar] [CrossRef]
- Wei, Y.; Bao, Y.; Huang, P.; Nie, S.; Nie, S.; Han, S.; Pan, B.; Fan, R.; Wu, X. Recognition of Single-Phase-to-Ground Fault Section of Distribution Line Based Phase Current Variation. In Proceedings of the 2021 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Chengdu, China, 18–21 July 2021; pp. 1138–1144. [Google Scholar]
- Fan, B.; Yao, G.; Wang, W.; Yang, X.; Ma, H.; Yu, K.; Chao, Z.; Zeng, X. Faulty phase recognition method based on phase-to-ground voltages variation for neutral ungrounded distribution networks. Electr. Power Syst. Res. 2021, 190, 106848. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, H.; Shi, F.; Wu, Q.; Terzija, V.; Xie, W.; Fang, C. Location of Single Phase to Ground Faults in Distribution Networks Based on Synchronous Transients Energy Analysis. IEEE Trans. Smart Grid 2020, 11, 774–785. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, X.; Piao, Z. Fault line detection in neutral point ineffectively grounding power system based on phase-locked loop. IET Gener. Transm. Distrib. 2014, 8, 273–280. [Google Scholar]
- Cusido, J.; Rosero, J.; Romeral, L.; Ortega, J.A.; Garcia, A. New Techniques for Fault Detection Analysis by Injecting Additional Frequency Test. In Proceedings of the 2006 IEEE Instrumentation and Measurement Technology Conference Proceedings, Sorrento, Italy, 24–27 April 2006; pp. 2087–2090. [Google Scholar]
- Welfonder, T.; Leitloff, V.; Fenillet, R.; Vitet, S. Location strategies and evaluation of detection algorithms for earth faults in compensated MV distribution systems. IEEE Trans. Power Deliv. 2000, 15, 1121–1128. [Google Scholar] [CrossRef]
- Zhou, C.; Shu, Q.; Han, X. A single-phase earth fault location scheme for distribution feeder on the basis of the difference of zero mode traveling waves. Int. Trans. Electr. Energy Syst. 2017, 27, e2298. [Google Scholar] [CrossRef]
- Jin, T.; Zhuo, F.; Mohamed, M.A. A Novel Approach Based on CEEMDAN to Select the Faulty Feeder in Neutral Resonant Grounded Distribution Systems. IEEE Trans. Instrum. Meas. 2020, 69, 4712–4721. [Google Scholar] [CrossRef]
- Liu, H.; Liu, Q. Single-Phase Ground Fault Detection of Small Current Grounding System Base on Wavelets Analysis. In Unifying Electrical Engineering and Electronics Engineering; Springer: New York, NY, USA, 2014; pp. 257–267. [Google Scholar]
- Cui, T.; Dong, X.; Bo, Z.; Juszczyk., A. Hilbert-Transform-Based Transient/Intermittent Earth Fault Detection in Noneffectively Grounded Distribution Systems. IEEE Trans. Power Deliv. 2011, 26, 143–151. [Google Scholar] [CrossRef]
- Dehghani, M.; Khooban, M.; Niknam, T. Fast fault detection and classification based on a combination of wavelet singular entropy theory and fuzzy logic in distribution lines in the presence of distributed generations. Int. J. Electr. Power Energy Syst. 2016, 78, 455–462. [Google Scholar] [CrossRef]
- Wang, X.; Gao, J.; Wei, X.; Song, G.; Wu, L.; Liu, J.; Zeng, Z.; Kheshti, M. High Impedance Fault Detection Method Based on Variational Mode Decomposition and Teager–Kaiser Energy Operators for Distribution Network. IEEE Trans. Smart Grid 2019, 10, 6041–6054. [Google Scholar] [CrossRef]
- Gao, J.; Guo, M.; Chen, D. Fault line detection using waveform fusion and one-dimensional convolutional neural network in resonant grounding distribution systems. CSEE J. Power Energy Syst. 2021, 7, 250–260. [Google Scholar]
- Yuan, J.; Wu, T.; Hu, Y.; Jiao, Z. Faulty feeder detection based on image recognition of voltage-current waveforms in non-effectively grounded distribution networks. Int. J. Electr. Power Energy Syst. 2022, 143, 108434. [Google Scholar] [CrossRef]
- Yang, J.; Fletcher, J.E.; O’Reilly, J. Short-Circuit and Ground Fault Analyses and Location in VSC-Based DC Network Cables. IEEE Trans. Ind. Electron. 2012, 59, 3827–3837. [Google Scholar] [CrossRef]
- Li, B.; Ren, X.; Li, B. Study on the Charge Transfer Criterion for the Pole-to-Ground Fault in DC Distribution Networks. IEEE Access 2019, 7, 102386–102396. [Google Scholar] [CrossRef]
- Liu, P.; Huang, C. Detecting Single-Phase-to-Ground Fault Event and Identifying Faulty Feeder in Neutral Ineffectively Grounded Distribution System. IEEE Trans. Power Deliv. 2018, 33, 2265–2273. [Google Scholar] [CrossRef]
- Sagastabeitia, K.J.; Zamora, I.; Mazon, A.J.; Aginako, Z.; Buigues, G. Phase Asymmetry: A New Parameter for Detecting Single-Phase Earth Faults in Compensated MV Networks. IEEE Trans. Power Deliv. 2011, 26, 2251–2258. [Google Scholar] [CrossRef]
- Alam, M.R.; Bai, F.; Yan, R.; Saha, T.K. Classification and Visualization of Power Quality Disturbance-Events Using Space Vector Ellipse in Complex Plane. IEEE Trans. Power Deliv. 2021, 36, 1380–1389. [Google Scholar] [CrossRef]
- Cheng, X.; Cui, B.; Hou, S. Fault Line Selection of Distribution Network Based on Modified CEEMDAN and GoogLeNet Neural Network. IEEE Sens. J. 2022, 22, 13346–13364. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).