Clustering Offensive Strategies in Australian-Rules Football Using Social Network Analysis

Abstract

Sports teams aim to understand the tactical behaviour of their opposition to gain a competitive advantage. Prior research of tactical behaviour in team sports has predominantly focused on the relationship between key performance indicators and match outcomes. However, key performance indicators fail to capture the patterns of ball movement deployed by teams, which provide deeper insight into a team’s playing style. The purpose of this study was to quantify existing ball movement strategies in Australian-rules Football (AF) using detailed descriptions of possession types from 396 matches of the 2019 season. Ball movement patterns were measured by social network analysis for each team during offensive phases of play. K-means clustering identified four unique offensive strategies. The most successful offensive strategy, defined by the number of matches won (83/396), achieved a win/loss ratio of 1.69 and was characterised by low ball movement predictability, low reliance on well-connected athletes, and a high number of passes. This study’s insights into offensive strategy are instructional to AF coaches and high-performance support staff. The outcomes of this study can be used to support the design of tactical training and inform match-day decisions surrounding optimal offensive strategies.

1. Introduction

Understanding tactical behaviour in team sport, particularly the strategies employed during offensive phases of play, is imperative for sports teams to gain a competitive advantage over their opposition. Unsurprisingly, a substantial portion of research investigating tactical behaviour in team sport has identified Australian-rules Football (AF) teams with more kicks, time in possession, entrances into the attacking zone per shot taken at goal, and goal conversions than their opponent, being more likely to win matches [1,2]. Further, studies of the characteristics of collective team behaviours show that teams aim to occupy a larger area of space during offensive phases compared with defensive phases of play [3,4,5]. The combination of tallies of key performance indicators and characteristics of collective team behaviour, defined in industry terms as athlete spatio-temporal variables, provides a guide to ideal space occupancy and overall ball use. However, these measures fail to capture the patterns of ball movement that teams use to progress towards their scoring goals, the strategy that underpins a team’s playing style [6].

Social network analysis (commonly referred to as network analysis) is increasingly being applied to team sport contexts because its objective is to quantify connections between members of an inter-connected system. This may be social (e.g., verbal communication within a workplace) or physical (e.g., passing of a ball between team sport athletes) [7,8,9]. Ultimately, network analysis enables the identification of interaction patterns in large and inter-connected groups [10]. In the context of invasion-based team sports, where teammates continuously attempt coordinated movements to out-score their opponent, network analysis is an attractive tool for identifying hidden patterns of ball movement.

Early applications of network analysis in soccer demonstrated that teams with a greater connectivity (i.e., number of athletes involved in sequences of passes) and lower centrality (i.e., reliance on few athletes) win more matches (Table 1 for a full list of network metric definitions) [10,11,12]. Fewell et al. [13] also found that entropy (i.e., predictability of passing patterns), centrality, and connectivity are relevant components of team strategies in professional basketball. Further applications in volleyball [14], handball [15], and rugby union [16] have also established that eigenvector centrality (i.e., level of dependence on athletes that pass to and from a high number of teammates), density (i.e., the ratio of the number of possible passing connections in a team over the total number of possible passing connections), and betweenness centrality (i.e., the extent to which an athlete acts as a bridge between other athletes) influence match outcomes [17,18,19]. These key network metrics have informed investigations of changes in an athlete’s functional role [18], and adaptations to a team’s ball movement in response to changes in match status and opposition strategies [15]. Network analysis approach has been established as a useful tool for tactical insights within team sports.

The larger field sizes and free-flowing nature of AF mean that effective ball movement is integral to team success. The earliest implementation of network analysis in AF described an athlete’s influence on the final score margin [20]. Of the various network metrics, team entropy, connectivity, betweenness centrality, and disposal efficiency have been identified as having the greatest influence on match outcomes [21,22]. Taylor et al. [23] used these network metrics to show that successful passages of play initiated by kick-ins comprised fewer and less predictable passing connections, while Young [24] demonstrated the utility of network metrics, in combination with key performance indicators, to inform machine learning models capable of predicting match outcome and score margins. In combination, the application of network analysis to AF demonstrates the importance of quantifying the patterns of ball movement to understand how tactical behaviour is implemented in team sports.

Despite the demonstrated importance of understanding tactical behaviour in AF, few studies have employed network analysis to delineate the various offensive strategies deployed by teams. One study used various network metrics to derive principal components to enable practical implementation. While the derived principal components grouped similar network metrics together, aiding interpretation by performance analysts, their contributions to playing style were not investigated [25,26]. Further research examined differences in network metrics between professional AF teams and found that each team uses a unique ball movement pattern, a finding that served as the first quantification of playing styles identified using network analysis in AF [27]. However, the network metrics were averaged across an entire season, meaning that changes in playing styles within the season were not identified. Consequently, it is unclear whether each team deploys varying offensive strategies across an AF season. Further, no investigations of the relationships between the offensive strategies and match outcomes, as a determinant of strategy success, have been undertaken.

It is the aim of this study to quantify and identify the unique playing strategies employed by professional AF teams using social network analysis and k-means clustering building on previous work by Sheehan et al. [28] and Moffatt et al. [29]. Consequently, this study aims to determine whether professional AF teams use unique offensive strategies across a season of match play. This study will also rank the identified offensive strategies based on the number of matches that resulted in a win when each strategy was used.

Table 1. Network metrics’ definitions used in the k-means clustering analysis. The practical explications for each metric are presented as AF Interpretations, where the Numerical Interpretations represent the preferential values.

Network Metric	Definition	AF Interpretation	Numerical Interpretations
Betweenness Centrality	The ratio of the number of shortest paths passing through a specified node over the total number of shortest paths.	The extent to which an athlete acts as a bridge between other athletes [24].	A higher value represents a greater reliance on certain athletes to move the ball.
Closeness Centrality	The ratio of the distance between nodes over the shortest possible path between nodes.	The level of connectedness of athletes within the team’s passing structure [21].	A higher value represents a greater spread of more frequent athlete involvements.
Degree	The total number of connections a given node has.	The total number of passes received and made.	A higher value represents a greater number of successful passes made.
Density	The ratio of the number of edges over the total number of nodes.	The average ratio of passes completed in proportion to the number of athletes in the team [27].	A higher value represents a greater spread of athlete involvements.
Eigenvector Centrality	The centrality of a node based on the centrality of surrounding nodes.	The dependence of a team on few athletes that are connected to a large number of other athletes [24].	A higher value represents a team’s greater reliance on few well-connected (i.e., key) athletes.
Entropy	A measure of the predictability of the edges between nodes.	A measure of the predictability of the passing structures [23].	A higher value represents less predictable ball movement.
Transitivity	The ratio of the number of triangles out of the total number of possible triangles.	A ratio representing how many athletes are involved in a passing trio in proportion to the total number of possible trios. A trio may be used to move the ball past an opposing athlete [24].	A higher value represents a larger reliance on groups of athletes to move past opposition.

Table 1. Network metrics’ definitions used in the k-means clustering analysis. The practical explications for each metric are presented as AF Interpretations, where the Numerical Interpretations represent the preferential values.

Network Metric	Definition	AF Interpretation	Numerical Interpretations
Betweenness Centrality	The ratio of the number of shortest paths passing through a specified node over the total number of shortest paths.	The extent to which an athlete acts as a bridge between other athletes [24].	A higher value represents a greater reliance on certain athletes to move the ball.
Closeness Centrality	The ratio of the distance between nodes over the shortest possible path between nodes.	The level of connectedness of athletes within the team’s passing structure [21].	A higher value represents a greater spread of more frequent athlete involvements.
Degree	The total number of connections a given node has.	The total number of passes received and made.	A higher value represents a greater number of successful passes made.
Density	The ratio of the number of edges over the total number of nodes.	The average ratio of passes completed in proportion to the number of athletes in the team [27].	A higher value represents a greater spread of athlete involvements.
Eigenvector Centrality	The centrality of a node based on the centrality of surrounding nodes.	The dependence of a team on few athletes that are connected to a large number of other athletes [24].	A higher value represents a team’s greater reliance on few well-connected (i.e., key) athletes.
Entropy	A measure of the predictability of the edges between nodes.	A measure of the predictability of the passing structures [23].	A higher value represents less predictable ball movement.
Transitivity	The ratio of the number of triangles out of the total number of possible triangles.	A ratio representing how many athletes are involved in a passing trio in proportion to the total number of possible trios. A trio may be used to move the ball past an opposing athlete [24].	A higher value represents a larger reliance on groups of athletes to move past opposition.

2. Materials and Methods

Event data (i.e., detailed descriptions of possession types) from a single season of professional men’s AF match play were provided by the Australian Football League’s official statistics provider Champion Data. Permission to use these data for the present study was granted by the UWA Human Ethics committee (2020/ET000197). The dataset contained event data from all matches played by the 18 professional AF teams during the 2019 premiership season. Finals matches were excluded to ensure an equal balance of matches played per team. In total, 396 matches were included in the dataset. Only changes in possession between teammates, either by a handball or a kick, were considered for analysis. Additionally, scoring shots were included because the ultimate aim of all offensive strategies is to end in a scoring shot. In total, 100,737 successful changes in possession were included.

Seven selected network metrics (Table 1) are depicted based on their reported importance in previous studies [10,11,12,17,18,19,21,27]. The network metrics were calculated on a match-by-match basis for every team, including match outcome and opponents for each match ensuring a broad representation of network and ball movement descriptors. To achieve this, team-specific adjacency matrices were calculated for each individual match. Adjacency matrices tally the number of times each athlete successfully passes to each teammate. The athletes passing the ball were represented in the matrix rows, and the athletes receiving the ball were represented in the columns. This enabled the direction of the change in possession to be included, establishing bi-directional network graphs. All analyses were undertaken using the NetworkX 2.4 Python package [30].

Subsequently, k-means clustering was used to identify unique offensive strategies as a function of the calculated network metrics (Table 1). Each network metric was standardised to zero mean and unit variance using

$$z=\frac{(x-\mu )}{\sigma },$$

(1)

where x represents the network metric, z is the standard score, $\mu$ is the sample’s mean, and $\sigma$ is the sample’s standard deviation. Silhouette scores and Davies–Bouldin (DB) indices were calculated for clusters ranging from 2 to 10 to ensure the optimal number of unique strategies was adequately represented by the k-means clustering algorithm. The optimal number of unique strategies is represented by the local maximum and local minimum of the silhouette score and DB index, respectively [31,32]. The mean and standard deviation of each network metric were calculated for all clusters to provide an overview of the characteristics of the offensive strategies. Occurrence frequencies of match results for each strategy were also collated as a measure of strategy success.

3. Results

The optimal number of unique offensive strategies was determined from the local maximum of the silhouette score and the local minimum of the DB index, which was located at the fourth cluster (Figure 1).

Strategy 1 (S1) and strategy 3 (S3) were used in 132 matches (33.3%) each, while strategy 4 (S4) was used in 84 matches (21.5%), and strategy 2 (S2) was used in 47 matches (11.9%). S3 resulted in the most match wins with 83 matches (22%), whereas S1 resulted in the greatest number of match losses with 79 matches (20%). S3 also displayed the greatest win/loss ratio (1.69), followed by S4 (1.02), S2 (0.68), and S1 (0.67) (

Table 2. Total number of times that each strategy was implemented in matches that resulted in a win, loss, and both (Total).

Strategy	Wins	Losses	Win/Loss Ratio	Total
S1	53	79	0.67	132
S2	19	28	0.68	47
S3	83	49	1.69	132
S4	43	42	1.02	85

).

S1 was characterised by the lowest values for closeness centrality (−1.01 ± 0.60), degree (−0.84 ± 0.61), density (−1.03 ± 0.44), eigenvector centrality (−0.82 ± 0.58), and transitivity (−0.81 ± 0.85). In contrast, S2 was characterised by the greatest values for closeness centrality (1.53 ± 0.68), density (1.70 ± 0.76), eigenvector centrality (1.54 ± 1.00), and transitivity (1.34 ± 0.66), in addition to the second greatest value for degree (0.72 ± 0.67). S3 and S4 were similar in density (0.25 ± 0.52 and 0.28 ± 0.46), closeness centrality (0.36 ± 0.56, and 0.16 ± 0.51), and transitivity (0.30 ± 0.62 and 0.06 ± 0.75), which all lay between the associated values of S1 and S2. The degree and entropy scores for S3 (0.91 ± 0.68 and 0.89 ± 0.32) were higher than those of S4 (−0.51 ± 0.48 and −1.04 ± 0.46), while the eigenvector centrality scores for S3 (−0.27 ± 0.36) were lower than S4 (0.84 ± 0.47). The characteristics of the four offensive strategies are visually represented in Figure 2.

4. Discussion

The primary aim of this study was to quantify ball movement strategies in AF. The second aim was to determine the preferred team playing strategies and rank their success as determined by the number of matches that resulted in a win when each strategy type was adopted.

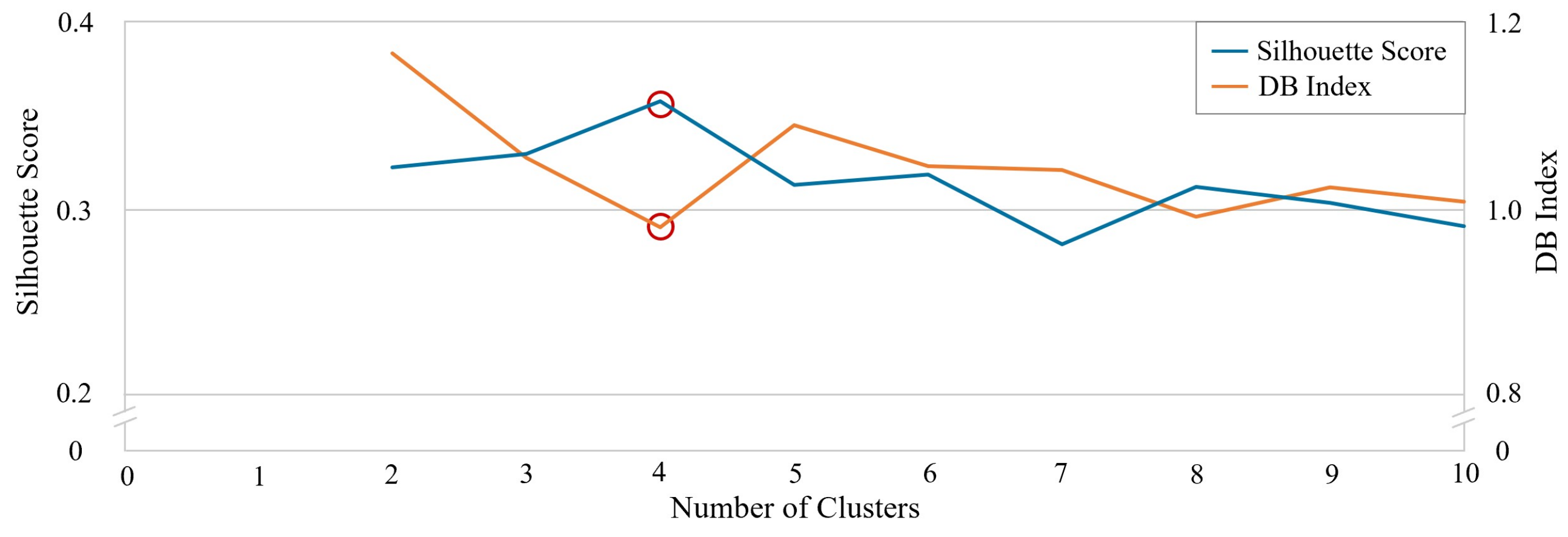
The present study identified four unique offensive strategies used by all 18 professional AF teams across the 2019 season, a finding in contrast with Young et al. [27] who reported the presence of 18 strategies. This difference is likely attributed to the current study’s methodology of calculating network metrics over a match (i.e., at a match level), instead of over the course of an entire season (i.e., at season level). It is reasonable to expect that team playing styles will change over the course of a season and adapt based on the opposition team and their expected tactical approach. The advantage of a match-level evaluation is the ability to detect the changes in playing styles throughout the season. Additionally, the current study demonstrated that all 18 professional AF teams deploy multiple strategies interchangeably across the AF season, thereby adapting their playing styles regularly. To build on these findings, future work should investigate the offensive strategies across smaller segments of a match, such as over a quarter, to capture changes in a team’s playing style during a match.

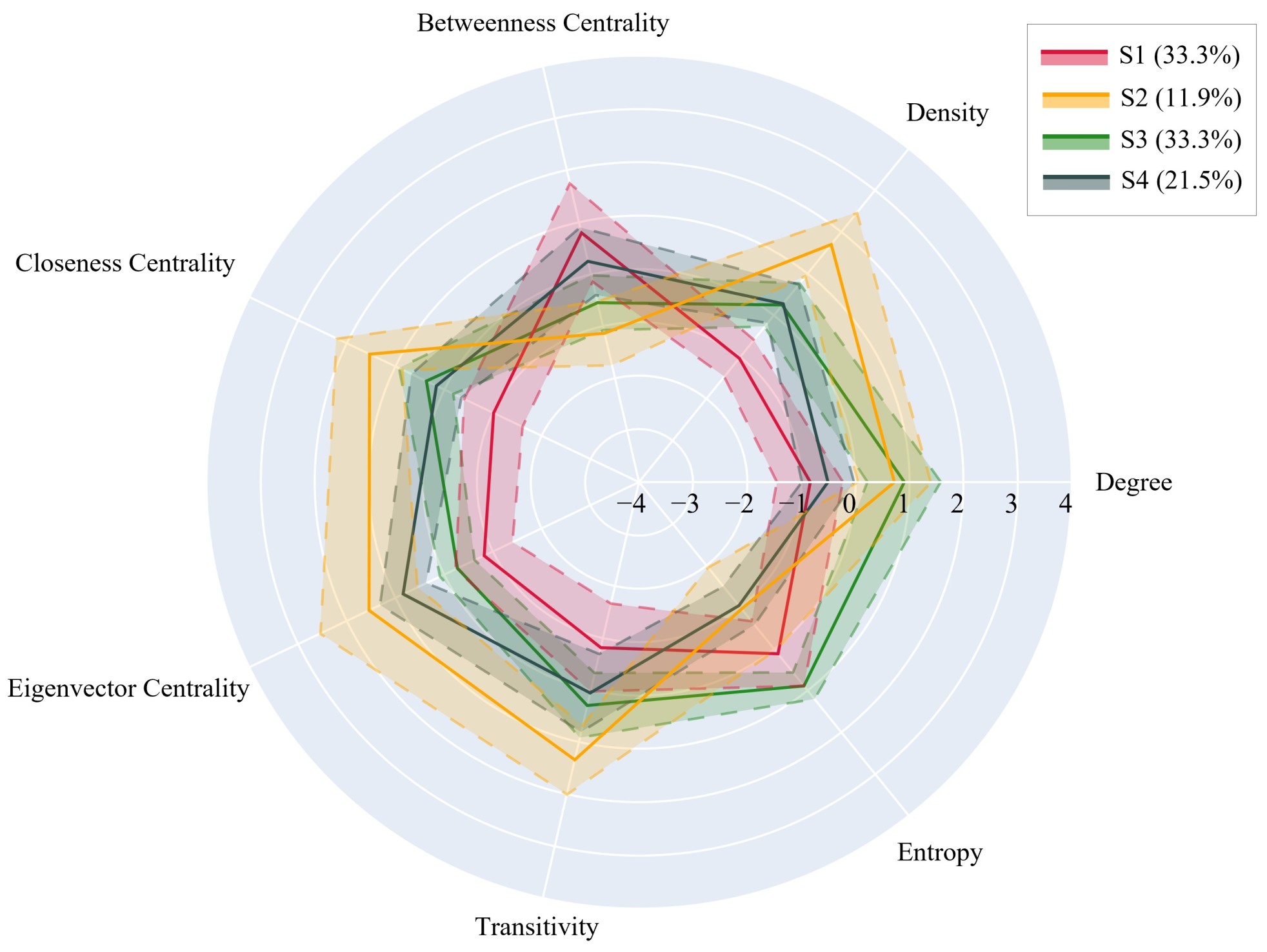
The four identified offensive strategies can be used to inform tactical training design when considered alongside practical interpretations of their characteristics (summarised in

Table 3. Characteristics of each strategy with simplified practical interpretations.

Strategy	Summary	Interpretation
S1	Greater reliance on intermediary athletes, fewer passes and spread of athlete involvements.	Run and carry
S2	Greater reliance on well-connected athletes, spread of athlete involvements, use of passing trios and ball movement predictability, less reliance on intermediary athletes.	Give X the ball
S3	Greater number of passes, less reliance on well-connected athletes and ball movement predictability.	Hot potato
S4	Greater reliance on key and intermediary athletes and ball movement predictability, moderate levels of passes and spread of athlete involvements.	Controlled movement

). S1 was the most frequently used strategy and was characterised by a lower number of overall passes and spread of athlete involvements. S1 also exhibited a greater reliance on intermediary athletes to move the ball. In the context of AF, this can be interpreted as a “run and carry” style of ball movement, where a given athlete will aim to gain territory while maintaining possession of the ball and using a less direct connection between teammates (i.e., using intermediary athletes to move the ball to the intended teammate). S3—the equally most used offensive strategy—was characterised by a greater overall number of passes, lower ball movement predictability, and less reliance on well-connected athletes. This is conducive to a “hot potato” style of play, in which athletes move the ball quickly, directly, and to the nearest available athlete. S4 was summarised as involving a greater reliance on well-connected and intermediary athletes, greater ball movement predictability, moderate number of overall passes, and a moderate spread of athlete involvements. This translates to a “controlled movement” style of play, where athletes will move the ball in a direct manner, guided by calculated and controlled decisions. S2—the least often used strategy—was characterised by a greater reliance on well-connected athletes, a greater spread of athlete involvements, a more predictable ball movement pattern, and less reliance on intermediary athletes. This is described as a “give X the ball” strategy, where athletes are tasked with getting the ball to a specific, well-connected athlete.

The identified strategies build on the outcomes of Sheehan et al. [25] and Sheehan et al. [28] by defining unique strategies comprising varying combinations of a set of network metrics. The components of passing structures within a team that were proposed previously established simplified measures of how well-connected and spread out a team’s passing is. While the proposed components simplify the practical implementation of network metrics by reducing the number of individual measures, different strategies comprising these components were not investigated. The current study assessed the various combinations of the network metrics that define unique offensive strategies to better understand the patterns of ball movement in AF.

This study also undertook the development of a success rating for each of the four identified strategies. S3 was identified as the most successful strategy as ranked by the highest win/loss ratio of 1.69. The success of this “hot potato” style of ball movement aligns with the results of previous studies, which established that teams with a greater number of athlete involvements achieve greater success [23,27]. S4 was ranked as the second most successful strategy with a win/loss ratio of 1.02, suggesting that a more direct and controlled ball movement between athletes yields great success. Interestingly, while S1 was the equally most employed strategy (alongside S3), this strategy resulted in the lowest win/loss ratio of all four strategies (0.67). This finding suggests that a “run and carry” strategy, with a reliance on intermediary athletes to pass the ball to the intended teammate, is the least robust against opposing defensive strategies. These findings can inform the design of effective tactical training scenarios. This may also be extended to the design of defensive actions to mitigate each strategy’s effectiveness. The identified strategies are limited, however, in that the current approach only considered ball movement, which is influenced by the movement of opposition athletes. To provide a more holistic descriptor of offensive strategies, future work should incorporate the movement patterns of off-ball athletes. The movement of off-ball athletes will also enable defensive strategies to be identified, which may then be used to investigate the interplay between offensive and defensive strategy adoption.

Overall, this research identified offensive strategies that are most likely to win matches. Of the four offensive strategies identified, the “run and carry” and “hot potato” offensive strategies were implemented most frequently. The greater number of passes and lower ball movement predictability characteristics of the “hot potato” strategy resulted in the most match wins. The offensive strategies identified, alongside their practical descriptions, enable coaches and athletes to make informed decisions for offensive and defensive strategy training.

5. Conclusions

This study categorised and assessed the success of unique offensive strategies in Australian-rules Football. Each of the 18 professional Australian-rules Football teams used the same four strategies interchangeably throughout the course of the 2019 Australian Football League season. A “hot potato” style of ball movement resulted in the most match wins.

Future work should focus on validating the robustness of these findings. An ablation study should be performed to analyse the influence of single network metrics on the clusters. Additionally, strategy clusters should be compared across multiple seasons to provide insights into the evolution of tactical behaviour between seasons of match play. To move towards a practical, real-time application of the developed approach, future analyses should investigate whether multiple strategies are deployed within a single match. Additionally, off-ball athlete movements should be combined into strategy identification for more holistic descriptions of offensive strategies. The off-ball movements of athletes may then be extended to defensive plays to provide insights into optimal offensive versus defensive strategy match-ups. A more in-depth analysis of the tactical strategies deployed by teams should also describe the physical demands associated with each of the identified strategies. The findings from this study advance the understanding of tactical behaviour in Australian-rules Football by providing a more robust and comprehensive analysis of the offensive strategies deployed by professional Australian-rules Football teams.