Analyzing Biomedical Datasets with Symbolic Tree Adaptive Resonance Theory
Abstract
1. Introduction
- Both a match and activation function for the Gram-ART match rule.
- Optimizations to the prototype-encoding scheme to mitigate memory complexity in grammars with large sets of terminal symbols.
- A mechanism to grow prototype tree structures when novel production rule sets are encountered.
- A supervised modification for each unsupervised START variant.
2. Background
2.1. Adaptive Resonance Theory
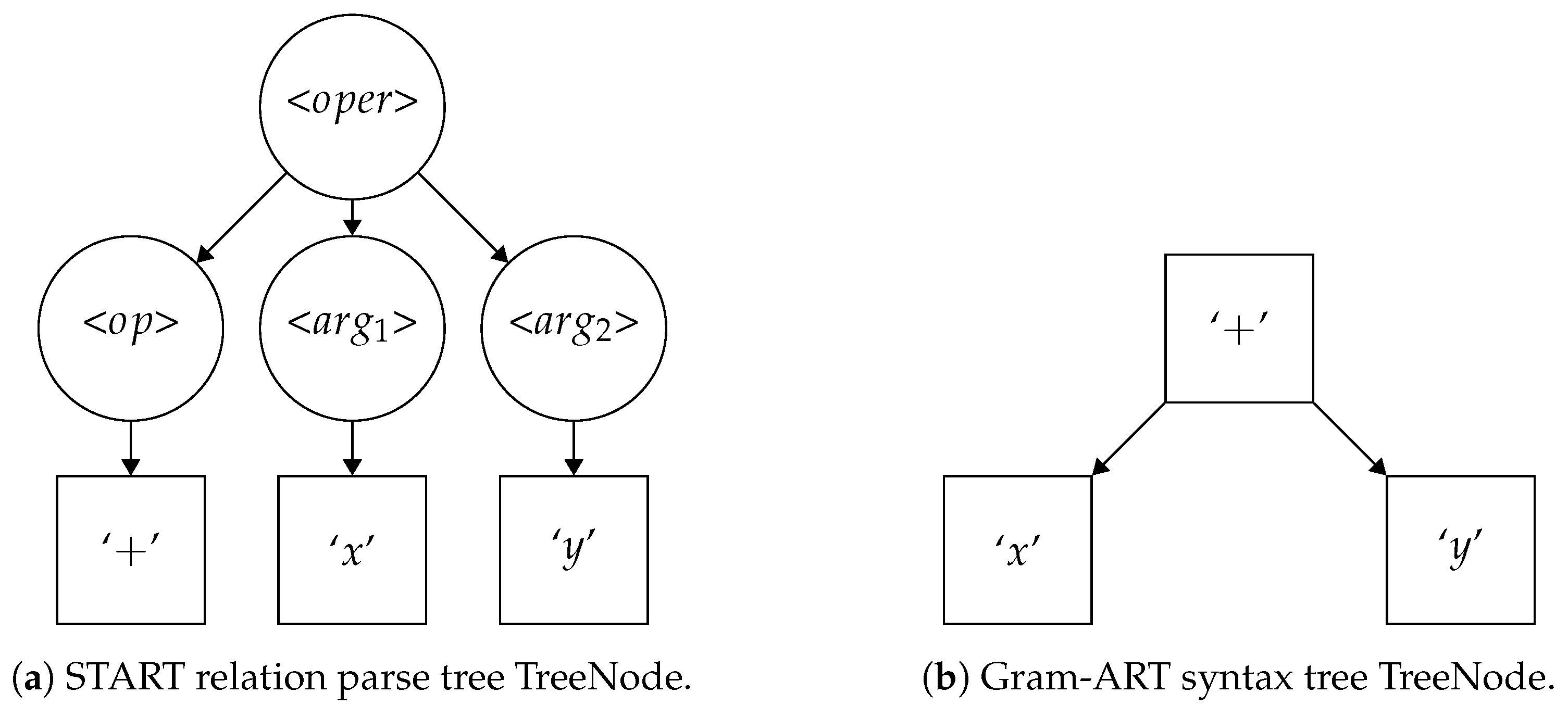
2.2. Gram-ART
3. Method
3.1. START: Symbolic Tree Adaptive Resonance Theory
3.1.1. Motivation
3.1.2. START Algorithm
| Listing 1. Formal grammar for parsing Charcot–Marie–Tooth disease–protein flat-file data. EBNF syntax is used for production rules with the exception of the regular expression symbol ‘+‘, which is used to denote one or more occurrences of the preceding symbol. Statements are composed of a series of one or more categorical attributes, all of which are listed in the non-terminal symbol <attribute>. When an attribute is missing or otherwise unknown for a CMT variant, then it is not included in the parsed syntax tree and handled accordingly by START. The production rules for two notable multi-category attributes, <> and <>, are listed to demonstrate how statements formulated from CMT disease-variant entries illustrate how a gene can be associated with multiple phenotypes and biologic processes. Other multi-category attributes are not listed for brevity. |
 |
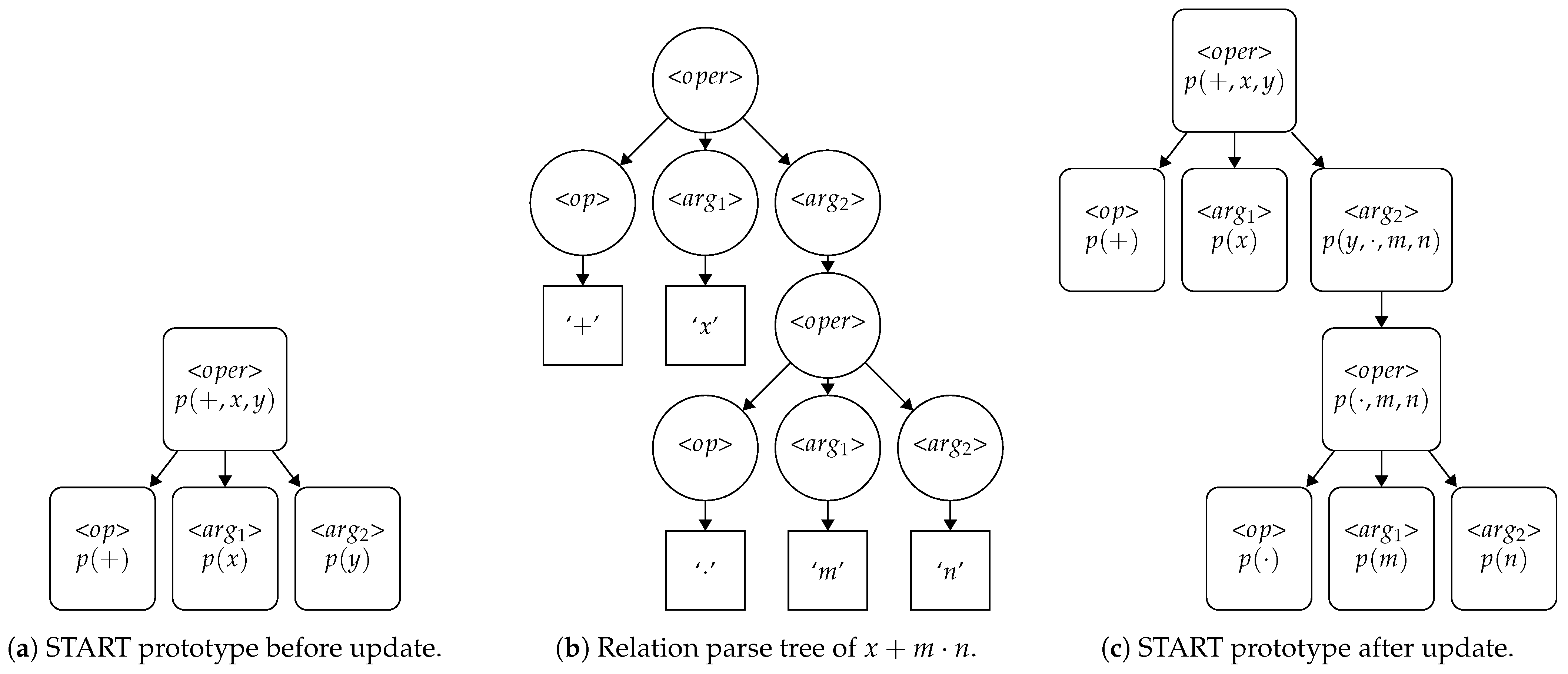
3.1.3. Derivation of the START Match Rule
3.1.4. Derivation of the Weight Update
| Algorithm 1: START algorithm. A set of symbolic statements under a formal context-free grammar are parsed into their syntax trees. Prototypes are defined as learning dynamics otherwise follow the activation, competition, match, update, and initialization rules of unsupervised ART algorithms [19]. ART dynamics notation here largely follow the elementary ART algorithm outlined in [19]. Inference during classification follows the same match rule dynamics without the instantiation of new categories; in the case of complete mismatch, either an “unknown” label or the best matching unit (the category that maximizes the match criterion) may be returned. Please see Table 1 for full notation |
 |
| Algorithm 2: Dual-Vigilance START algorithm. This algorithm combines Algorithm 1 with the dual-vigilance procedure of DVFA [25]. The vigilance test is split into a cascade of two vigilance checks for the current match candidate node. Passing the upper vigilance check updates the current category node, while passing only the lower vigilance check creates a new category node belonging to the same cluster label. Failing to pass both vigilance checks results in the instantiation of a new category node belonging to an incrementally new cluster label. Please see Table 1 for full notation |
 |
3.1.5. Dual-Vigilance and Distributed Dual-Vigilance START
- : if the current match candidate satisfies the upper vigilance threshold, then the winning category is updated according to the START weight update rules.
- : if the current match candidate only satisfies the lower vigilance threshold but not the upper, then a new category prototype is instantiated that belongs to the same cluster as the winning node.
- : if the current match candidate does not satisfy even the lower-bound vigilance threshold, then the normal mismatch procedure is followed, where a new category is instantiated belonging to an entirely new cluster.
3.1.6. Supervised Variants
3.1.7. Summary of START Variants
| Algorithm 3: Simplified supervised modification for all START variants (e.g., Simplified STARTMAP). The variation between START variants is captured in the evaluation of the vigilance test as a function ; if some node satisfies the match rule of the START variant, the sample is said to fall within the vigilance region of the prototype [19]. Complete mismatch instead occurs when no vigilance test is satisfied, and the prototype initialization procedure of the START variant is triggered. Inference after training is run through to the vigilance test procedure, reporting the supervised label mapping to the winning internal node category. In the case of complete mismatch, where no nodes satisfy the vigilance test of a supplied inference sample, either the supervised label mapping to the best matching unit (i.e., the node with the highest match value) or a custom mismatch signal may be reported depending on the desired application. Please see Table 1 for full notation |
 |
3.1.8. Comparison of START Variants
3.1.9. Comparison with Existing Methods
4. Evaluation
4.1. Software Implementation
4.2. Benchmark Datasets
4.3. Charcot–Marie–Tooth Disease Dataset
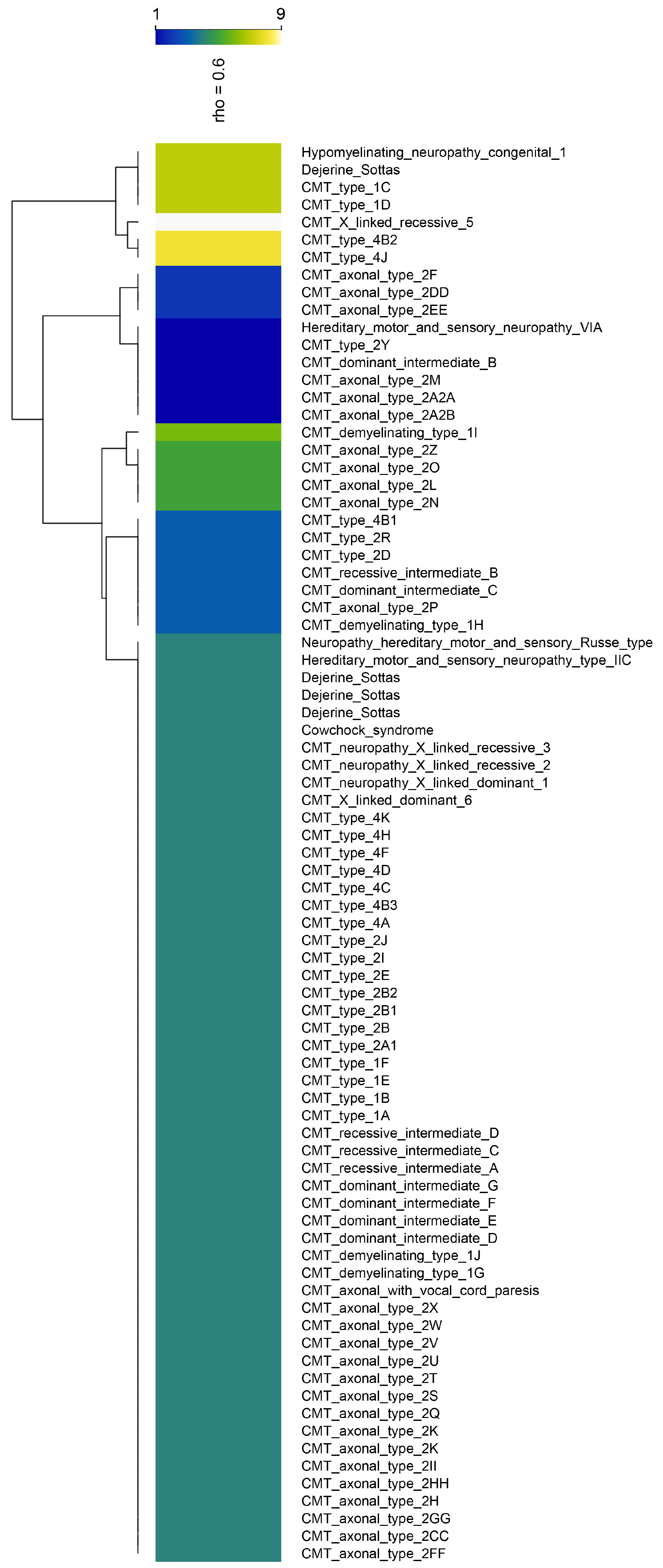
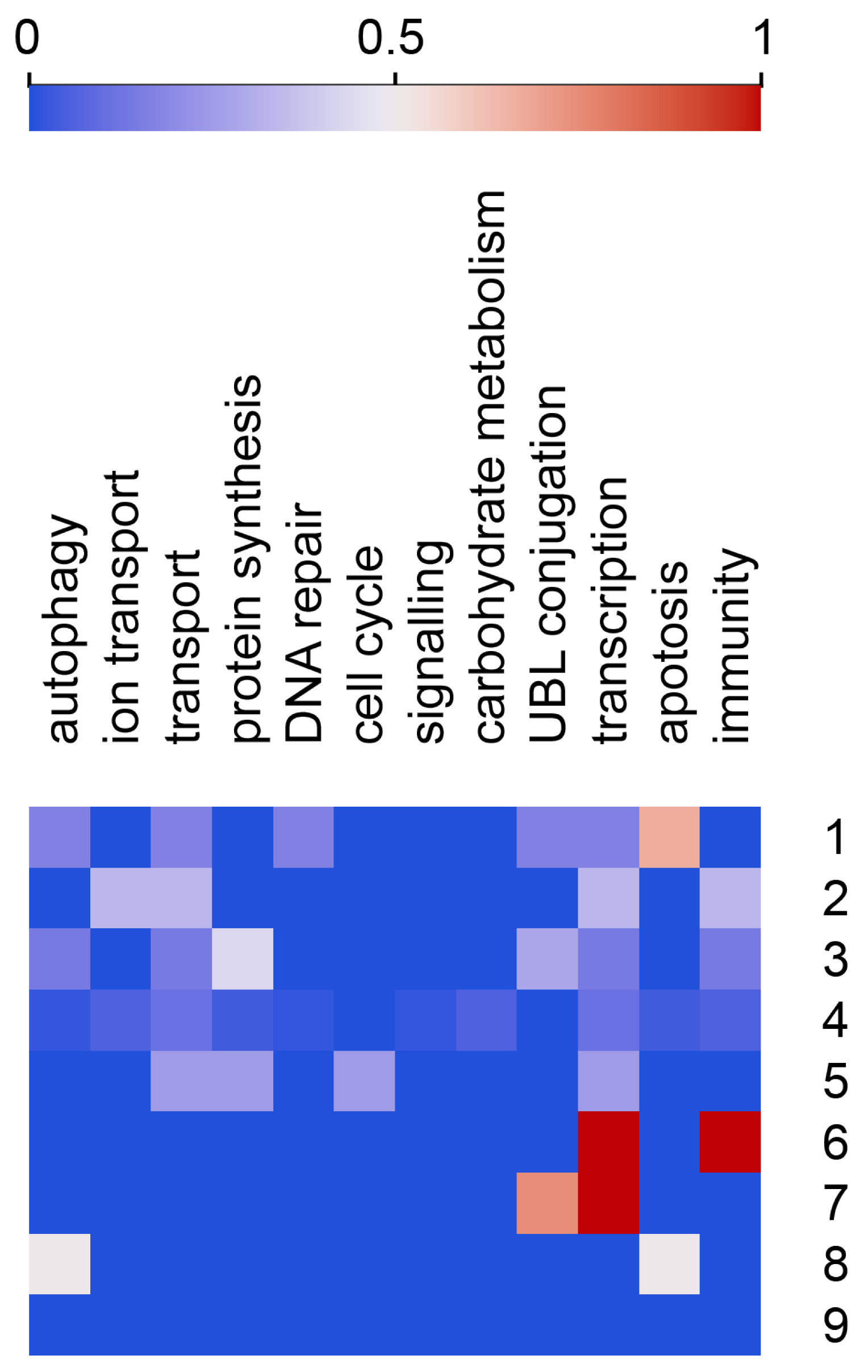
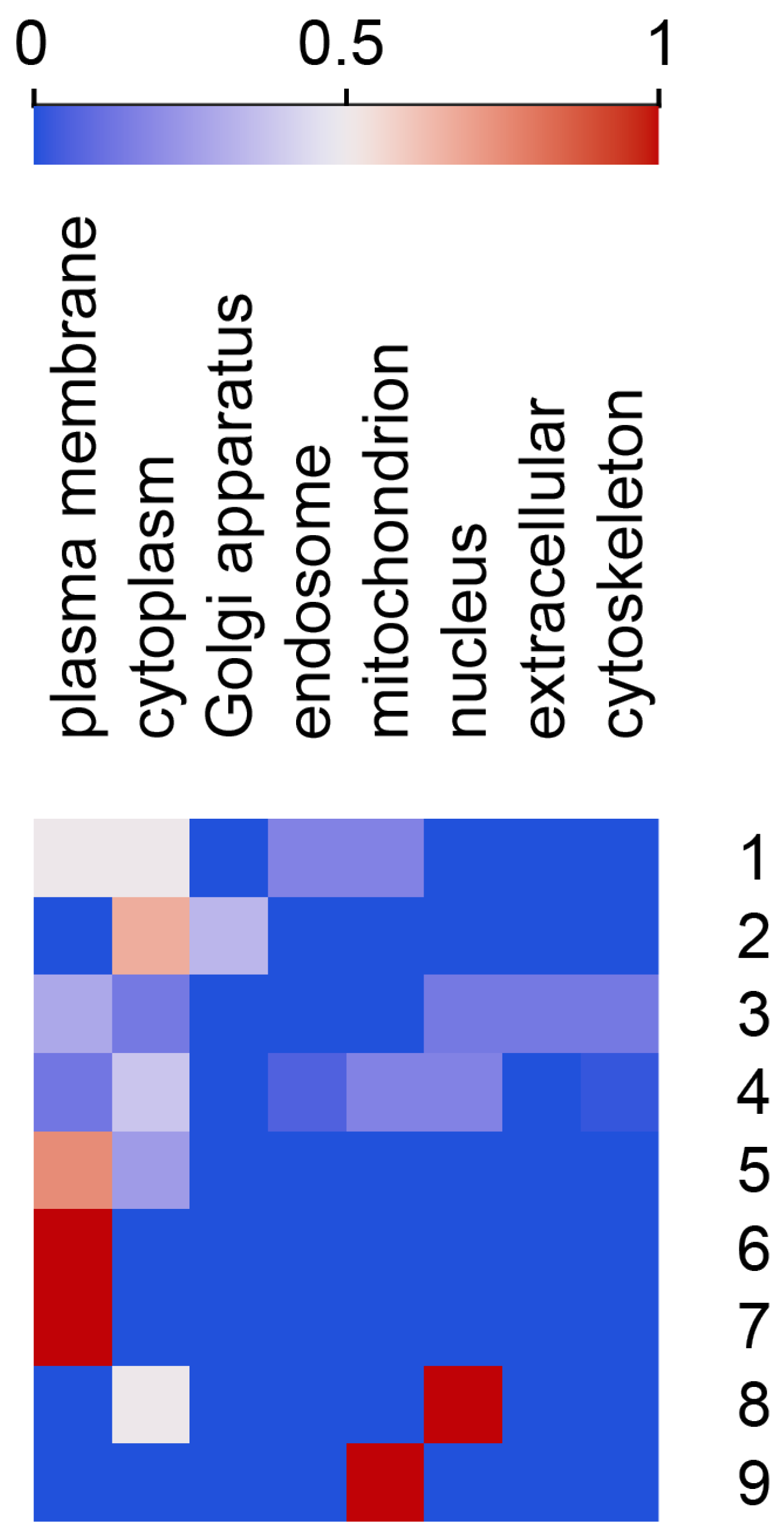
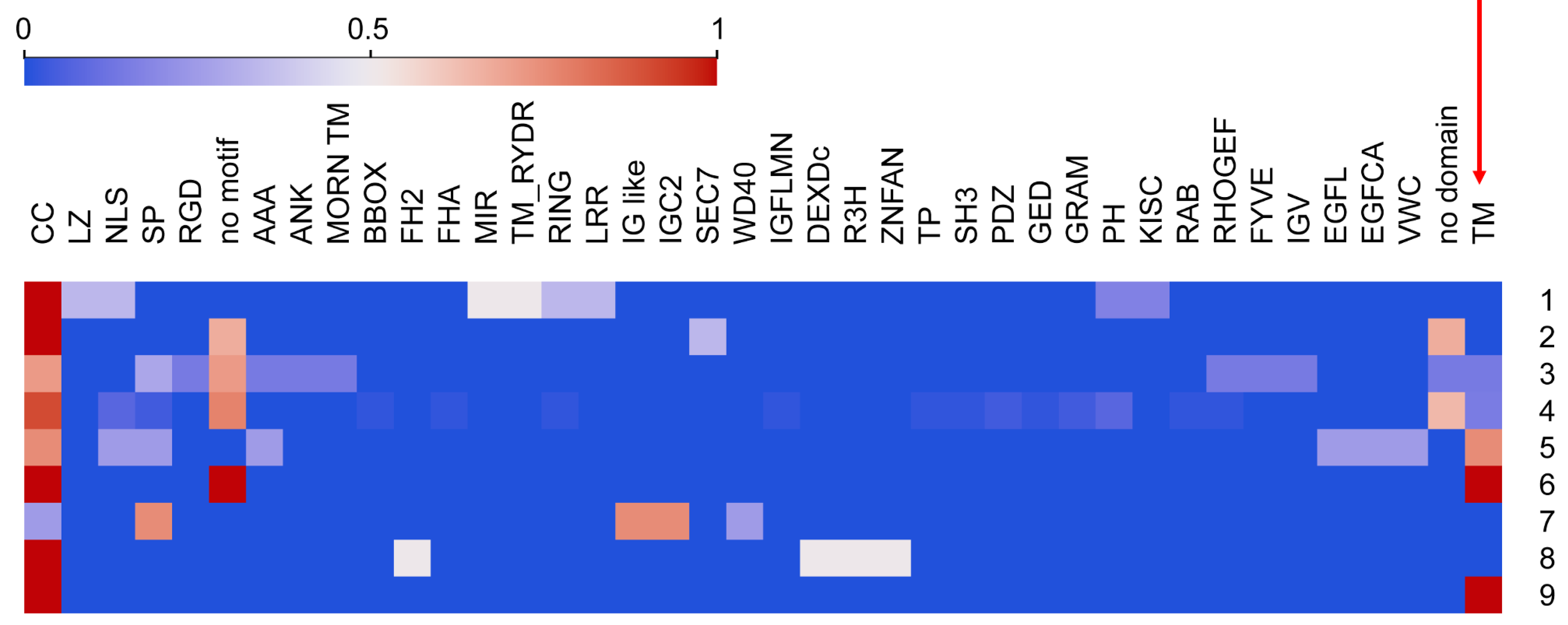
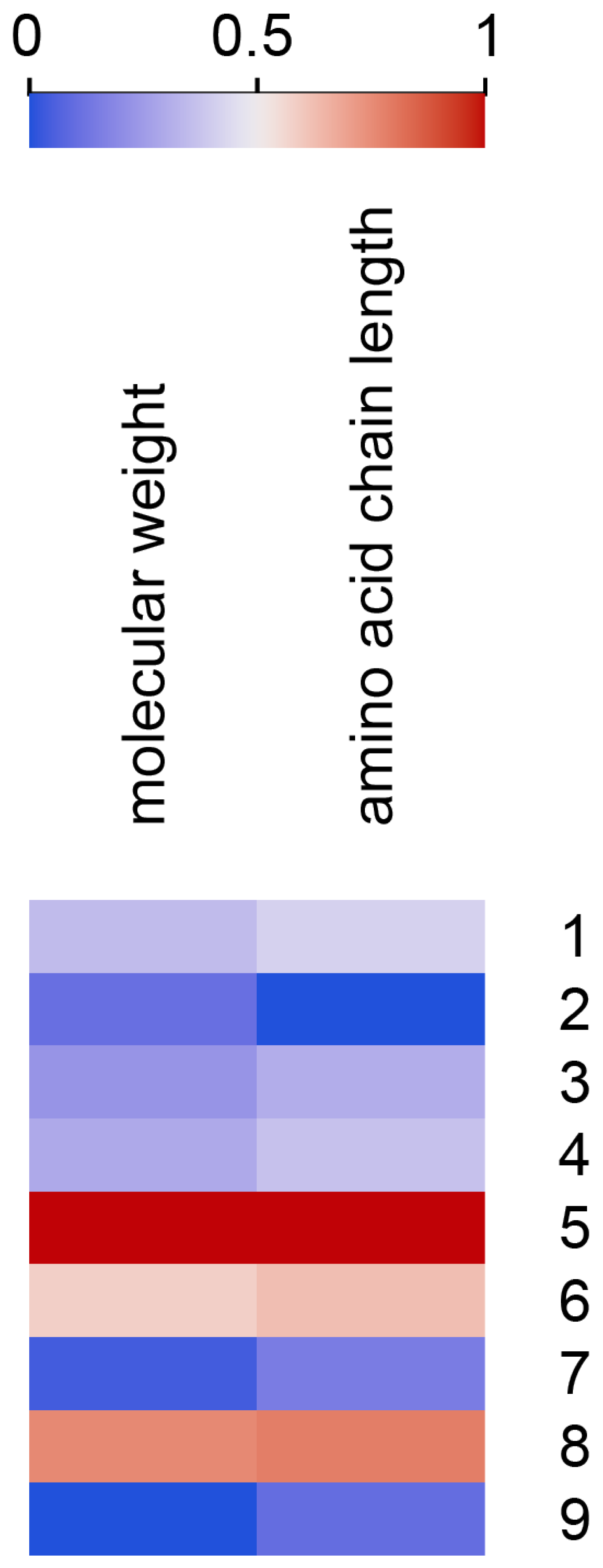
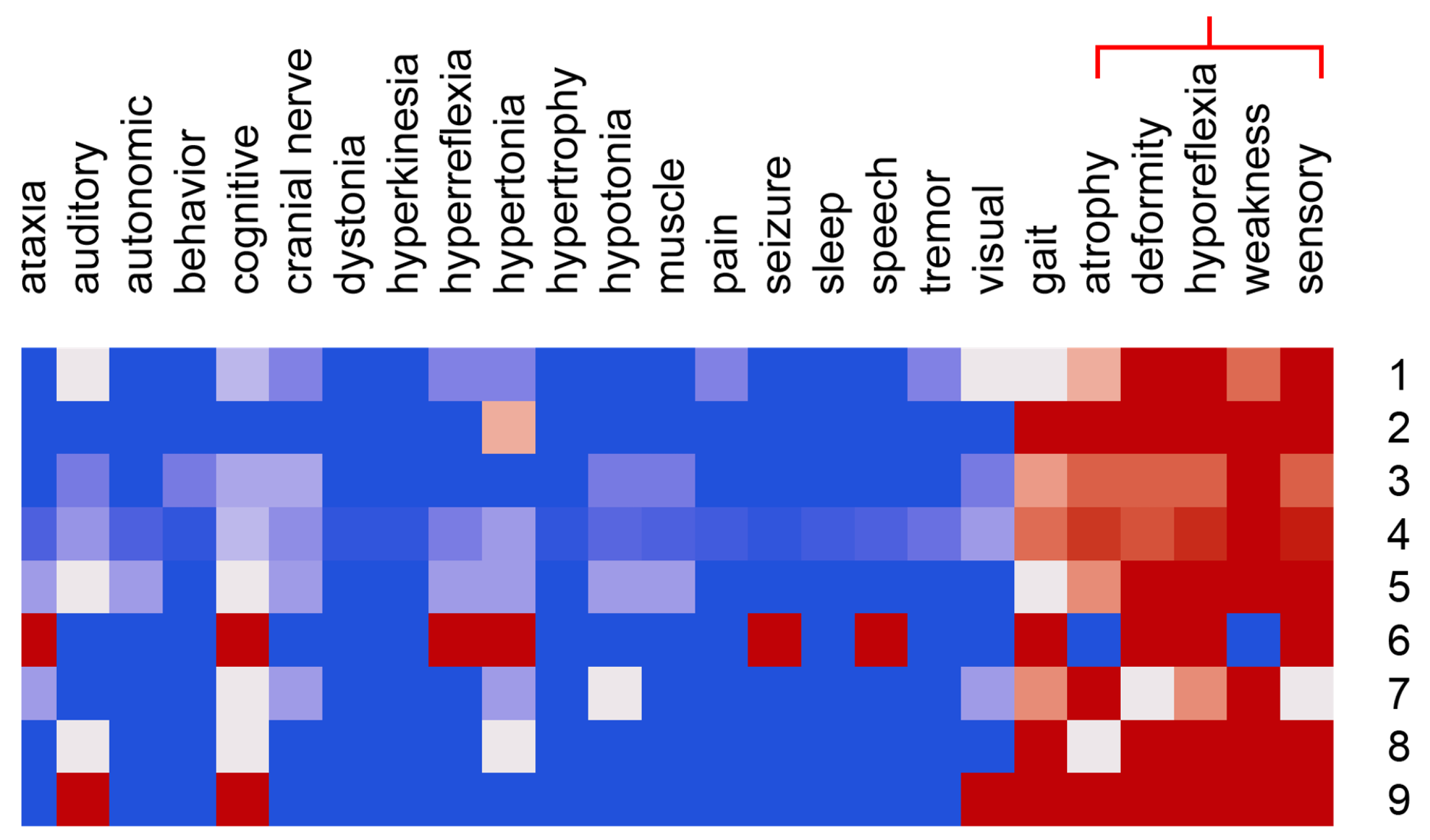
4.4. Cluster Feature Means and Heat Maps
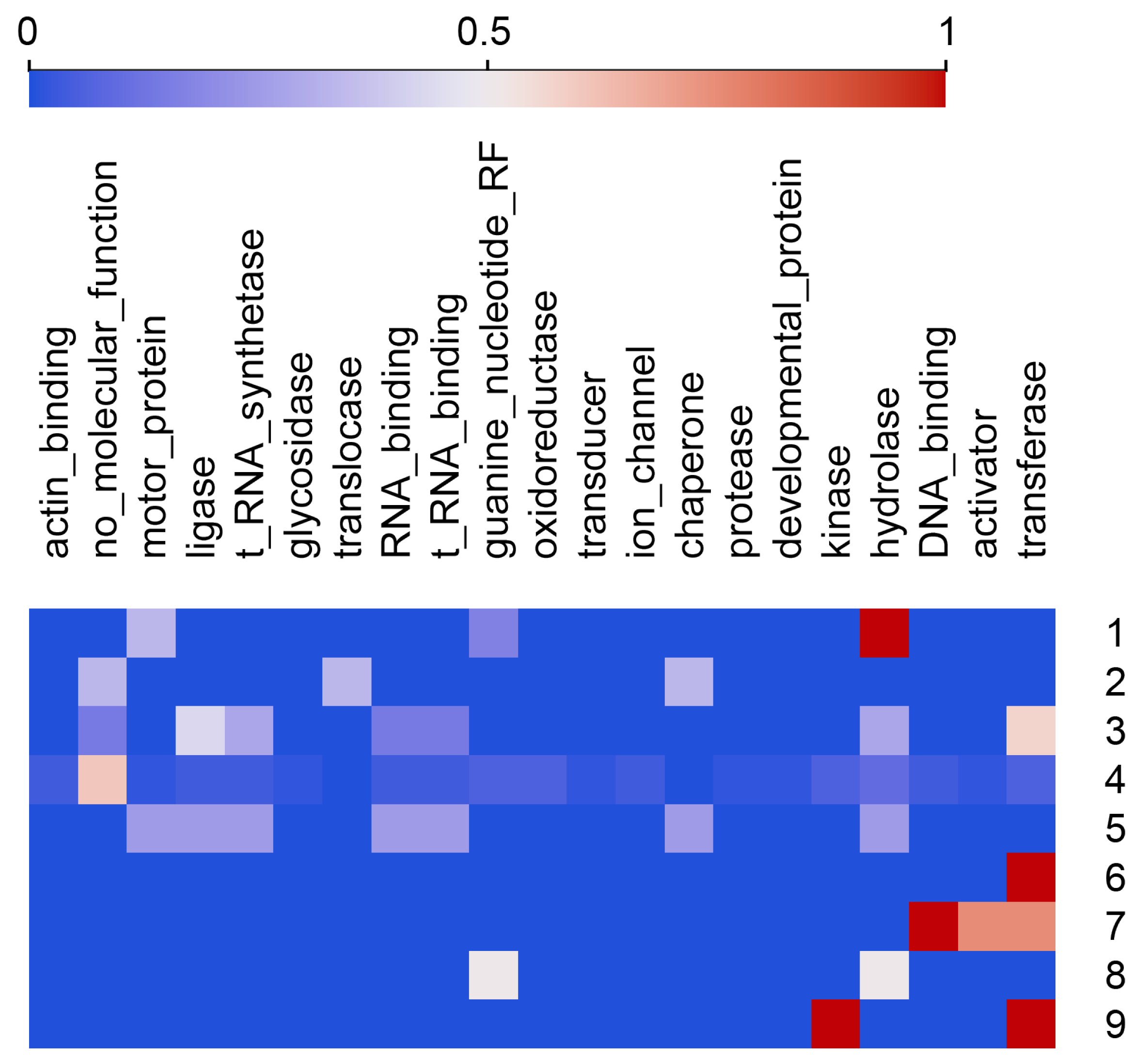
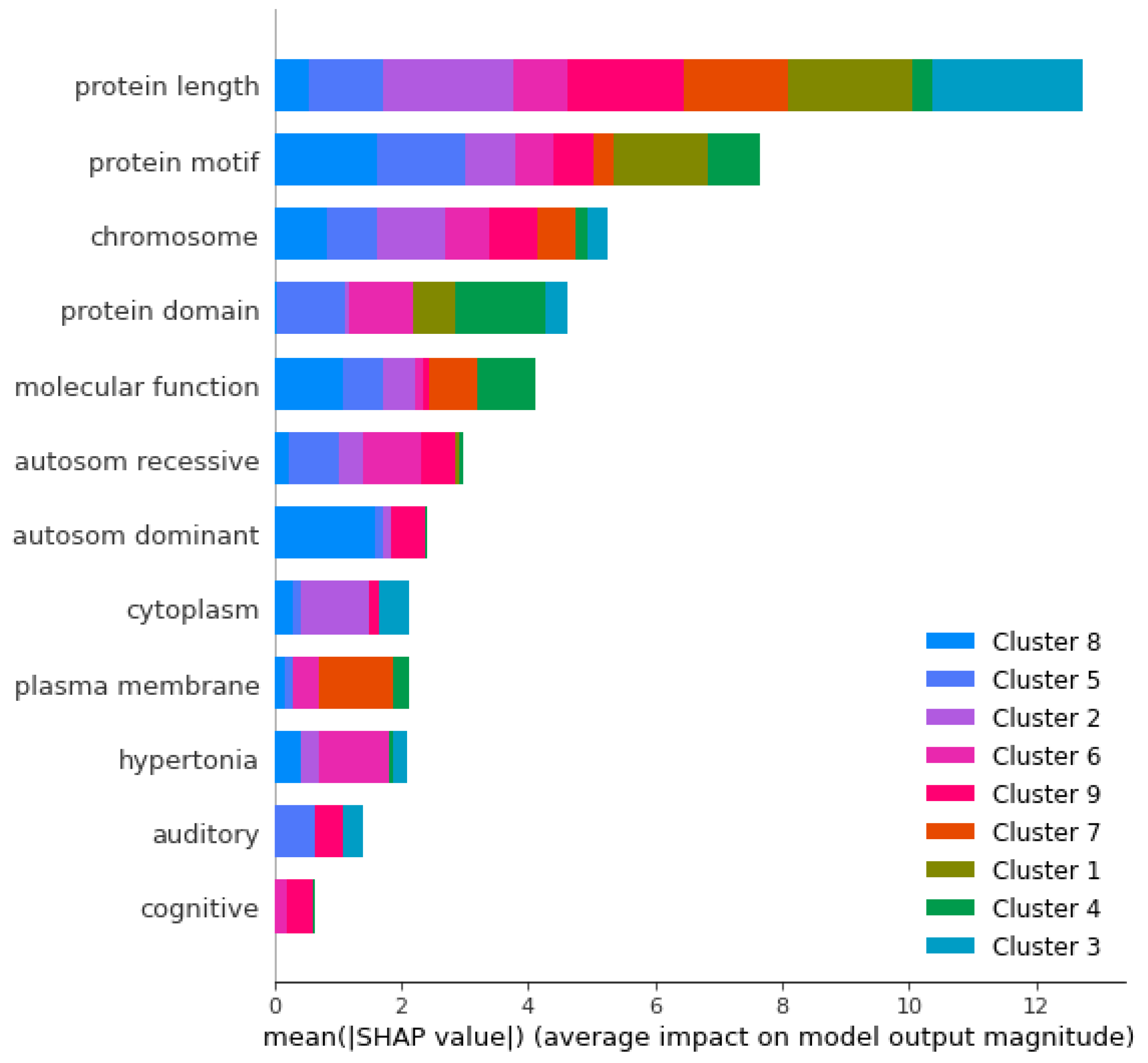
4.5. SHAP Values
5. Results
5.1. Selection of Cluster Configuration for the CMT Dataset
5.2. Cluster Characterization by Feature Composition
5.3. Identifying Features That Contributed the Most to Cluster Configuration
6. Discussion
6.1. Feasibility of Clustering Multi-Categorical Biomedical Data with START
6.2. Biological Interest and Plausibility of Derived Clusters
6.3. Limitations
6.4. Future Work
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ART | Adaptive resonance theory |
| BNF | Backus–Naur form |
| CFG | Context-free grammar |
| CMT | Charcot–Marie–Tooth disease |
| DDVFA | Distributed dual-vigilance FuzzyART |
| DDV-START | Distributed dual-vigilance symbolic tree adaptive resonance theory |
| DVFA | Dual-vigilance FuzzyART |
| DV-START | Dual-vigilance symbolic tree adaptive resonance theory |
| EBNF | Extended Backus–Naur form |
| F1 | ART Feature input layer (field 1) |
| F2 | ART Category representation layer (field 2) |
| HAC | Hierarchical agglomerative clustering |
| L2 | Lifelong learning |
| ML | Machine learning |
| PMF | Probability mass function |
| START | Symbolic tree ART |
| WTA | Winner-take-all |
Appendix A. Charcot–Marie–Tooth Dataset Grammar
References
- Robinson, P.N. Deep phenotyping for precision medicine. Hum. Mutat. 2012, 33, 777–780. [Google Scholar] [CrossRef]
- Sonawane, A.R.; Weiss, S.T.; Glass, K.; Sharma, A. Network medicine in the age of biomedical big data. Front. Genet. 2019, 10, 294. [Google Scholar] [CrossRef]
- Collins, F.S.; Varmus, H. A new initiative on precision medicine. N. Engl. J. Med. 2015, 372, 793–795. [Google Scholar] [CrossRef]
- Carrasco-Ramiro, F.; Peiró-Pastor, R.; Aguado, B. Human genomics projects and precision medicine. Gene Ther. 2017, 24, 551–561. [Google Scholar] [CrossRef]
- Phillips, C.J. Precision medicine and its imprecise history. Harv. Data Sci. Rev. 2020, 2, 1–10. [Google Scholar]
- Ginsburg, G.S.; Phillips, K.A. Precision medicine: From science to value. Health Aff. 2018, 37, 694–701. [Google Scholar] [CrossRef] [PubMed]
- Polster, A.; Cvijovic, M. Network medicine: Facilitating a new view on Complex Diseases. Front. Bioinform. 2023, 3, 47. [Google Scholar]
- Healy, M.J.; Caudell, T.P. Ontologies and worlds in category theory: Implications for neural systems. Axiomathes 2006, 16, 165–214. [Google Scholar] [CrossRef]
- Bezdek, J.C. Elementary Cluster Analysis: Four Basic Methods That (Usually) Work; River Publishers: Gistrup, Denmark, 2022. [Google Scholar]
- Xu, R.; Wunsch, D.C. Clustering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; pp. 1–21. [Google Scholar]
- Gowda, K.; Diday, E. Symbolic clustering using a new similarity measure. IEEE Trans. Syst. Man Cybern. 1992, 22, 368–378. [Google Scholar] [CrossRef]
- Chidananda Gowda, K.; Diday, E. Symbolic clustering using a new dissimilarity measure. Pattern Recognit. 1991, 24, 567–578. [Google Scholar] [CrossRef]
- Carpenter, G.A.; Grossberg, S. The ART of adaptive pattern recognition by a self-organizing neural network. Computer 1988, 21, 77–88. [Google Scholar] [CrossRef]
- Carpenter, G.A.; Grossberg, S.; Markuzon, N.; Reynolds, J.H.; Rosen, D.B. Fuzzy ARTMAP: A neural network architecture for incremental supervised learning of analog multidimensional maps. IEEE Trans. Neural Netw. 1992, 3, 698–713. [Google Scholar] [CrossRef] [PubMed]
- Tan, A.H. Adaptive resonance associative map. Neural Netw. 1995, 8, 437–446. [Google Scholar] [CrossRef]
- Subagdja, B.; Tan, A.H. iFALCON: A neural architecture for hierarchical planning. Neurocomputing 2012, 86, 124–139. [Google Scholar] [CrossRef]
- Subagdja, B.; Tan, A.H. Planning with iFALCON: Towards a neural-network-based BDI agent architecture. In Proceedings of the 2008 IEEE/WIC/ACM International Conference on Web Intelligence and Intelligent Agent Technology, Sydney, Australia, 9–12 December 2008; IEEE: Los Alamitos, CA, USA, 2008; Volume 2, pp. 231–237. [Google Scholar]
- Kim, T.; Hwang, I.; Lee, H.; Kim, H.; Choi, W.S.; Lim, J.J.; Zhang, B.T. Message passing adaptive resonance theory for online active semi-supervised learning. In Proceedings of the International Conference on Machine Learning. PMLR, Virtual, 18–24 July 2021; pp. 5519–5529. [Google Scholar]
- Brito da Silva, L.E.; Elnabarawy, I.; Wunsch, D.C. A Survey of Adaptive Resonance Theory Neural Network Models for Engineering Applications. Neural Netw. 2019, 120, 167–203. [Google Scholar] [CrossRef]
- Carpenter, G.A.; Grossberg, S.; Rosen, D.B. Fuzzy ART: Fast stable learning and categorization of analog patterns by an adaptive resonance system. Neural Netw. 1991, 4, 759–771. [Google Scholar] [CrossRef]
- Bezdek, J.C.; Keller, J.; Krisnapuram, R.; Pal, N. Fuzzy Models and Algorithms for Pattern Recognition and Image Processing; Springer Science & Business Media: New York, NY, USA, 1999; Volume 4. [Google Scholar]
- Ruspini, E.H.; Bezdek, J.C.; Keller, J.M. Fuzzy clustering: A historical perspective. IEEE Comput. Intell. Mag. 2019, 14, 45–55. [Google Scholar] [CrossRef]
- Keller, J.M.; Yager, R.R.; Tahani, H. Neural network implementation of fuzzy logic. Fuzzy Sets Syst. 1992, 45, 1–12. [Google Scholar] [CrossRef]
- Meuth, R.J. Adaptive Multi-Vehicle Mission Planning for Search Area Coverage. Ph.D. Thesis, Missouri University of Science and Technology, Rolla, MO, USA, 2007. [Google Scholar]
- Brito da Silva, L.E.; Elnabarawy, I.; Wunsch, D.C. Dual vigilance fuzzy adaptive resonance theory. Neural Netw. 2019, 109, 1–5. [Google Scholar] [CrossRef]
- Brito da Silva, L.E.; Elnabarawy, I.; Wunsch, D.C. Distributed dual vigilance fuzzy adaptive resonance theory learns online, retrieves arbitrarily-shaped clusters, and mitigates order dependence. Neural Netw. 2020, 121, 208–228. [Google Scholar] [CrossRef]
- Grossberg, S. How Does a Brain Build a Cognitive Code? Psychol. Rev. 1980, 87, 1–51. [Google Scholar] [CrossRef] [PubMed]
- Grossberg, S.; Grossberg, S. How does a brain build a cognitive code? In Studies of Mind and Brain: Neural Principles of Learning, Perception, Development, Cognition, and Motor Control; Springer: Dordrecht, The Netherlands, 1982; pp. 1–52. [Google Scholar]
- Cohen, M.A.; Grossberg, S. Absolute stability of global pattern formation and parallel memory storage by competitive neural networks. IEEE Trans. Syst. Man Cybern. 1983, SMC-13, 815–826. [Google Scholar] [CrossRef]
- Grossberg, S. Nonlinear neural networks: Principles, mechanisms, and architectures. Neural Netw. 1988, 1, 17–61. [Google Scholar] [CrossRef]
- Grossberg, S.T. Studies of Mind and Brain: Neural Principles of Learning, Perception, Development, Cognition, and Motor Control; Boston Studies in the Philosophy and History of Science Springer Dordrecht: Dordrecht, Holland, 1982; Volume 70. [Google Scholar]
- Grossberg, S.; Versace, M. Spikes, synchrony, and attentive learning by laminar thalamocortical circuits. Brain Res. 2008, 1218, 278–312. [Google Scholar] [CrossRef] [PubMed]
- Grossberg, S. Adaptive Resonance Theory: How a brain learns to consciously attend, learn, and recognize a changing world. Neural Netw. 2013, 37, 1–47. [Google Scholar] [CrossRef] [PubMed]
- Grossberg, S. The resonant brain: How attentive conscious seeing regulates action sequences that interact with attentive cognitive learning, recognition, and prediction. Atten. Percept. Psychophys. 2019, 81, 2237–2264. [Google Scholar] [CrossRef]
- Grossberg, S. Conscious Mind, Resonant Brain: How Each Brain Makes a Mind; Oxford University Press: Oxford, UK, 2021. [Google Scholar] [CrossRef]
- Carpenter, G.A.; Grossberg, S. A massively parallel architecture for a self-organizing neural pattern recognition machine. Comput. Vis. Graph. Image Process. 1987, 37, 54–115. [Google Scholar] [CrossRef]
- Carpenter, G.A.; Grossberg, S. Pattern Recognition by Self-Organizing Neural Networks; The MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Carpenter, G.; Grossberg, S. Adaptive Resonance Theory; Technical report; Boston University Center for Adaptive Systems and Department of Cognitive and Neural Systems: Boston, MA, USA, 1998. [Google Scholar]
- Petrenko, S.; Wunsch, D.C. AdaptiveResonance.jl: A Julia Implementation of Adaptive Resonance Theory (ART) Algorithms. J. Open Source Softw. 2022, 7, 3671. [Google Scholar] [CrossRef]
- Park, G.M.; Kim, J.H. Deep Adaptive Resonance Theory for learning biologically inspired episodic memory. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 5174–5180. [Google Scholar] [CrossRef]
- Carpenter, G.A. Distributed learning, recognition, and prediction by ART and ARTMAP neural networks. Neural Netw. 1997, 10, 1473–1494. [Google Scholar] [CrossRef]
- Carpenter, G.A.; Milenova, B.L.; Noeske, B.W. Distributed ARTMAP: A neural network for fast distributed supervised learning. Neural Netw. 1998, 11, 793–813. [Google Scholar] [CrossRef] [PubMed]
- Healy, M.J.; Caudell, T.P.; Smith, S.D. A neural architecture for pattern sequence verification through inferencing. IEEE Trans. Neural Netw. 1993, 4, 9–20. [Google Scholar] [CrossRef]
- Grossberg, S.; Huang, T.R. ARTSCENE: A neural system for natural scene classification. J. Vis. 2009, 9, 6. [Google Scholar] [CrossRef] [PubMed]
- Petrenko, S.; Brna, A.; Aguilar-Simon, M.; Wunsch, D. Lifelong Context Recognition via Online Deep Feature Clustering. TechRxiv 2023, 14, 1–15. [Google Scholar] [CrossRef]
- Brna, A.P.; Brown, R.C.; Connolly, P.M.; Simons, S.B.; Shimizu, R.E.; Aguilar-Simon, M. Uncertainty-based modulation for lifelong learning. Neural Netw. 2019, 120, 129–142. [Google Scholar] [CrossRef]
- Brown, R.; Brna, A.; Cook, J.; Park, S.; Aguilar-Simon, M. Uncertainty-Driven Control for a Self-Supervised Lifelong Learning Drone. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 5053–5056. [Google Scholar] [CrossRef]
- Aguilar-Simon, M.; Brna, A.; Brown, R.; Folsom, L.; Cook, J.; Park, S.; Yanoschak, A.; Shimizu, R.; Scientific, T.; Imaging, L. Adaptive Learning Through Active Neuromodulation (ALAN); Air Force Research Laboratory, Sensors Directorate: Wright-Patterson Air Force Base, OH, USA, 2022. [Google Scholar]
- Petrenko, S.; Wunsch, D.C. ClusterValidityIndices.jl: Batch and Incremental Metrics for Unsupervised Learning. J. Open Source Softw. 2022, 7, 3527. [Google Scholar] [CrossRef]
- Brito da Silva, L.E.; Rayapati, N.; Wunsch, D.C. Incremental Cluster Validity Index-Guided Online Learning for Performance and Robustness to Presentation Order. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 6686–6700. [Google Scholar] [CrossRef]
- Brito da Silva, L.E.; Rayapati, N.; Wunsch, D.C. iCVI-ARTMAP: Using Incremental Cluster Validity Indices and Adaptive Resonance Theory Reset Mechanism to Accelerate Validation and Achieve Multiprototype Unsupervised Representations. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 1–14. [Google Scholar] [CrossRef]
- Yelugam, R.; Brito da Silva, L.E.; Wunsch, D.C. TopoBARTMAP: Biclustering ARTMAP with or without Topological Methods in a Blood Cancer Case Study. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Virtual, 19–24 July 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Yelugam, R.; Brito da Silva, L.E.; Wunsch II, D.C. Topological biclustering ARTMAP for identifying within bicluster relationships. Neural Netw. 2023, 160, 34–49. [Google Scholar] [CrossRef]
- Some new indexes of cluster validity. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 1998, 28, 301–315. [CrossRef]
- Chen, Z.; Liu, B. Lifelong Machine Learning; Morgan & Claypool Publishers: San Rafael, CA, USA, 2018; pp. 1–207. [Google Scholar]
- Kudithipudi, D.; Aguilar-Simon, M.; Babb, J.; Bazhenov, M.; Blackiston, D.; Bongard, J.; Brna, A.P.; Chakravarthi Raja, S.; Cheney, N.; Clune, J.; et al. Biological underpinnings for lifelong learning machines. Nat. Mach. Intell. 2022, 4, 196–210. [Google Scholar] [CrossRef]
- Baker, M.M.; New, A.; Aguilar-Simon, M.; Al-Halah, Z.; Arnold, S.M.; Ben-Iwhiwhu, E.; Brna, A.P.; Brooks, E.; Brown, R.C.; Daniels, Z.; et al. A domain-agnostic approach for characterization of lifelong learning systems. Neural Netw. 2023, 160, 274–296. [Google Scholar] [CrossRef]
- Chomsky, N. Syntactic Structures; Mouton: Oxford, UK, 1957. [Google Scholar]
- Chomsky, N. On the Notion" Rule of Grammar"; American Mathematical Society: Providence, RI, USA, 1961. [Google Scholar]
- Wolpert, D.; Macready, W. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- ISO/IEC 14977:1996 (E); Information Technology-Syntactic Metalanguage-Extended BNF. ISO/IEC: Geneva, Switzerland, 1996.
- Hester, J.R.; Shinan, E. Lerche: Generating data file processors in Julia from EBNF grammars. J. Open Source Softw. 2021, 6, 3497. [Google Scholar] [CrossRef]
- Carpenter, G.A.; Grossberg, S.; Reynolds, J.H. ARTMAP: Supervised real-time learning and classification of nonstationary data by a self-organizing neural network. In Proceedings of the IEEE Conference on Neural Networks for Ocean Engineering, Miami, FL, USA, 9–11 December 1991; pp. 341–342. [Google Scholar] [CrossRef]
- Kasuba, T. Simplified Fuzzy ARTMAP. AI Expert 1993, 8, 19–25. [Google Scholar]
- Tan, A.H. Cascade ARTMAP: Integrating neural computation and symbolic knowledge processing. IEEE Trans. Neural Netw. 1997, 8, 237–250. [Google Scholar]
- Petrenko, S. AP6YC/OAR: V0.1.0. Zenodo, 5 January 2024. [Google Scholar] [CrossRef]
- Bezanson, J.; Edelman, A.; Karpinski, S.; Shah, V.B. Julia: A fresh approach to numerical computing. SIAM Rev. 2017, 59, 65–98. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Demšar, J.; Curk, T.; Erjavec, A.; Črt Gorup; Hočevar, T.; Milutinovič, M.; Možina, M.; Polajnar, M.; Toplak, M.; Starič, A.; et al. Orange: Data Mining Toolbox in Python. J. Mach. Learn. Res. 2013, 14, 2349–2353. [Google Scholar]
- Fisher, R.A. Iris; UCI Machine Learning Repository: Irvine, CA, USA, 1988. [Google Scholar] [CrossRef]
- Mushroom; UCI Machine Learning Repository: Irvine, CA, USA, 1987. [CrossRef]
- Lane, T. UNIX User Data; UCI Machine Learning Repository: Irvine, CA, USA, 1988. [Google Scholar] [CrossRef]
- Ilc, N. Datasets Package. Available online: https://www.researchgate.net/publication/239525861_Datasets_package (accessed on 5 January 2024).
- Fränti, P.; Sieranoja, S. K-Means Properties on Six Clustering Benchmark Datasets. Appl. Intell. 2018, 48, 4743–4759. [Google Scholar] [CrossRef]
- Ahmad, A.S.; Mayya, A.M. A new tool to predict lung cancer based on risk factors. Heliyon 2020, 6, e03402. [Google Scholar] [CrossRef] [PubMed]
- Rossor, A.M.; Polke, J.M.; Houlden, H.; Reilly, M.M. Clinical implications of genetic advances in Charcot–Marie–Tooth disease. Nat. Rev. Neurol. 2013, 9, 562–571. [Google Scholar] [CrossRef] [PubMed]
- Amberger, J.S.; Bocchini, C.A.; Scott, A.F.; Hamosh, A. OMIM.org: Leveraging knowledge across phenotype–gene relationships. Nucleic Acids Res. 2019, 47, D1038–D1043. [Google Scholar] [CrossRef]
- Köhler, S.; Gargano, M.; Matentzoglu, N.; Carmody, L.C.; Lewis-Smith, D.; Vasilevsky, N.A.; Danis, D.; Balagura, G.; Baynam, G.; Brower, A.M.; et al. The human phenotype ontology in 2021. Nucleic Acids Res. 2021, 49, D1207–D1217. [Google Scholar] [CrossRef] [PubMed]
- The UniProt Consortium. UniProt: The Universal Protein Knowledgebase in 2023. Nucleic Acids Res. 2023, 51, D523–D531. [Google Scholar] [CrossRef] [PubMed]
- Keshava Prasad, T.; Goel, R.; Kandasamy, K.; Keerthikumar, S.; Kumar, S.; Mathivanan, S.; Telikicherla, D.; Raju, R.; Shafreen, B.; Venugopal, A.; et al. Human protein reference database—2009 update. Nucleic Acids Res. 2009, 37, D767–D772. [Google Scholar] [CrossRef]
- Robinson, P.N.; Mungall, C.J.; Haendel, M. Capturing phenotypes for precision medicine. Mol. Case Stud. 2015, 1, a000372. [Google Scholar] [CrossRef]
- Gunning, D.; Stefik, M.; Choi, J.; Miller, T.; Stumpf, S.; Yang, G.Z. XAI—Explainable artificial intelligence. Sci. Robot. 2019, 4, eaay7120. [Google Scholar] [CrossRef]
- New, A.; Baker, M.; Nguyen, E.; Vallabha, G. Lifelong Learning Metrics. arXiv 2022, arXiv:2201.08278. [Google Scholar]
- Raja, S.N.; Carr, D.B.; Cohen, M.; Finnerup, N.B.; Flor, H.; Gibson, S.; Keefe, F.J.; Mogil, J.S.; Ringkamp, M.; Sluka, K.A.; et al. The revised International Association for the Study of Pain definition of pain: Concepts, challenges, and compromises. Pain 2020, 161, 1976–1982. [Google Scholar] [CrossRef]
- Hamosh, A.; Scott, A.F.; Amberger, J.S.; Bocchini, C.A.; McKusick, V.A. Online Mendelian Inheritance in Man (OMIM), a knowledgebase of human genes and genetic disorders. Nucleic Acids Res. 2005, 33, D514–D517. [Google Scholar] [CrossRef]


| : set of prototype nodes. |
| R: a single prototype node. |
| : set of prototype node indices. |
| : subset of active ART module node indices . |
| : START vigilance threshold, . |
| : dual-vigilance lower-bound vigilance threshold . |
| : dual-vigilance upper-bound vigilance threshold . |
| n: number of input dataset statements. |
| : statements parsed as syntax trees with terminal metadata. |
| : syntactic parsing algorithm taking a set of statements and a grammar and producing rooted constituency parse trees. |
| fT: activation function. |
| fM: match function. |
| fN: node initialization function. |
| fL: node weight update function. |
| fV: the vigilance test function. |
| : internal supervised category indices. |
| : set of cluster indices. |
| TreeNode |
|---|
| Symbol: GrammarSymbol |
| Children: Vector{TreeNode} |
| ProtoNode |
|---|
| Symbol: NonTerminalGrammarSymbol |
| Distribution: Dictionary{TerminalGrammarSymbol, Float} |
| InstanceCount: Dictionary{TerminalGrammarSymbol, Integer} |
| Children: Vector{ProtoNode} |
| HAC Method | |
|---|---|
| Single | |
| Complete | |
| Median | |
| Average | |
| Weighted 1 |
| Vigilance Formulation | Unsupervised | Supervised |
|---|---|---|
| Single-Vigilance | START | Simplified STARTMAP |
| Dual-Vigilance | DV-START | Simplified DV-STARTMAP |
| Distributed Dual-Vigilance | DDV-START | Simplified DDV-STARTMAP |
| Feature | Type | Format | Length | Multi-Category |
|---|---|---|---|---|
| variant name | categorical | string | variable | no |
| variant number | categorical | string | fixed | no |
| gene name | categorical | string | variable | no |
| gene number | categorical | integer | fixed | no |
| protein name | categorical | string | variable | no |
| protein number | categorical | string | fixed | no |
| protein length | numerical | integer | variable | no |
| protein weight | numerical | integer | variable | no |
| protein location | categorical | string | variable | yes |
| protein molecular function | categorical | string | variable | yes |
| protein biological process | categorical | string | variable | yes |
| protein class | categorical | string | variable | yes |
| mode of inheritance | categorical | string | variable | yes |
| phenotype | categorical | string | variable | yes |
| phenotype number | categorical | string | variable | yes |
| chromosome | categorical | string | variable | no |
| chromosome location | categorical | string | variable | no |
| chromosome location | categorical | string | variable | no |
| k | N | Process | Function | Location | Domain | Inherit | Phenotype Plus |
|---|---|---|---|---|---|---|---|
| 1 | 6 | apoptosis | hydrolase | AD | auditory, visual | ||
| 2 | 3 | cytoplasm | AD | hypertonia | |||
| 3 | 7 | protein | transferase | AD, AR | |||
| synthesis | |||||||
| 4 | 53 | plasma | TM | AD, AR | |||
| membrane | |||||||
| 5 | 4 | plasma | TM | AD | cognitive, auditory | ||
| membrane | |||||||
| 6 | 1 | immunity | transferase | plasma | AD | cognitive, ataxia, | |
| transcription | membrane | seizure, hypertonia, | |||||
| speech, hyperreflexia | |||||||
| 7 | 4 | transcription | DNA binding | plasma | AD, AR | cognitive, hypotonia | |
| membrane | |||||||
| transferase | |||||||
| 8 | 2 | autophagy | hydrolase | nucleus | AR | cognitive, auditory, | |
| apoptosis | GNRF | hypertonia | |||||
| 9 | 1 | transferase | mitochondrion | TM | XLR | cognitive, auditory |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petrenko, S.; Hier, D.B.; Bone, M.A.; Obafemi-Ajayi, T.; Timpson, E.J.; Marsh, W.E.; Speight, M.; Wunsch, D.C., II. Analyzing Biomedical Datasets with Symbolic Tree Adaptive Resonance Theory. Information 2024, 15, 125. https://doi.org/10.3390/info15030125
Petrenko S, Hier DB, Bone MA, Obafemi-Ajayi T, Timpson EJ, Marsh WE, Speight M, Wunsch DC II. Analyzing Biomedical Datasets with Symbolic Tree Adaptive Resonance Theory. Information. 2024; 15(3):125. https://doi.org/10.3390/info15030125
Chicago/Turabian StylePetrenko, Sasha, Daniel B. Hier, Mary A. Bone, Tayo Obafemi-Ajayi, Erik J. Timpson, William E. Marsh, Michael Speight, and Donald C. Wunsch, II. 2024. "Analyzing Biomedical Datasets with Symbolic Tree Adaptive Resonance Theory" Information 15, no. 3: 125. https://doi.org/10.3390/info15030125
APA StylePetrenko, S., Hier, D. B., Bone, M. A., Obafemi-Ajayi, T., Timpson, E. J., Marsh, W. E., Speight, M., & Wunsch, D. C., II. (2024). Analyzing Biomedical Datasets with Symbolic Tree Adaptive Resonance Theory. Information, 15(3), 125. https://doi.org/10.3390/info15030125







