Location Analytics of Routine Occurrences (LARO) to Identify Locations with Regularly Occurring Events with a Case Study on Traffic Accidents

Abstract

Conventional spatiotemporal methods take frequentist or density-based approaches to map event clusters over time. While these methods discern hotspots of varying continuity in space and time, their findings overlook locations of routine occurrences where the geographic context may contribute to the regularity of event occurrences. Hence, this research aims to recognize the routine occurrences of point events and relate site characteristics and situation dynamics around these locations to explain the regular occurrences. We developed an algorithm, Location Analytics of Routine Occurrences (LARO), to determine an appropriate temporal unit based on event periodicity, seek locations of routine occurrences, and geographically contextualize these locations through spatial association mining. We demonstrated LARO in a case study with over 250,000 reported traffic accidents from 2010 to 2018 in Dallas, Texas, United States. LARO identified three distinctive locations, each exhibiting varying frequencies of traffic accidents at each weekly hour. The findings indicated that locations with routine traffic accidents are surrounded by high densities of stores, restaurants, entertainment, and businesses. The timing of traffic accidents showed a strong relationship with human activities around these points of interest. Besides the LARO algorithm, this study contributes to the understanding of previously overlooked periodicity in traffic accidents, emphasizing the association between periodic human activities and the occurrence of street-level traffic accidents. The proposed LARO algorithm is applicable to occurrences of point-based events, such as crime incidents or animal sightings.

1. Introduction

Understanding the where and when of events is essential for uncovering their underlying mechanisms [1]. In geospatial information science, events can have multiple geometric dimensions, but this study specifically examined point-based events, such as traffic accidents, criminal incidents, and disease infections. A common approach for analyzing events as discrete occurrences involves studying the spatial pattern of event locations and tracking how these patterns evolve [2,3]. The geographical environment and socioeconomic characteristics at event locations generate potential explanations for the event occurrences [4]. Additionally, changes in dynamic social activities around event locations over time can indicate potential triggers for evolving spatial patterns [5].

Clustering patterns or hotspots reveal areas with a higher frequency of events. Strategies to identify hotspots in point-based events vary, but a common approach involves quantifying density or frequency within a defined spatial unit to estimate the probability distribution of these point events across space [6,7]. The frequency of traffic crashes on a length of road segments can be modeled using a Poisson distribution, as demonstrated in [8]. In contrast to segment-based research, areal unit boundaries can be administrative-based, providing the advantage of access to socio-economic data from databases of local governments [9,10]. Unlike approaches that aggregate individual events into spatial area units, alternative methods utilize disaggregated data when feasible [11]. For example, kernel density estimation (KDE) analyzes individual events rather than aggregated ones in areal units and fits a probability density function (PDF) at each event location, resulting in a grid-based output [12].

Approaches that avoid point aggregation to areal units can capture spatial continuity but may miss recurring spatial and temporal patterns. Previous studies revealed heterogeneity in traffic crash frequencies and rates linked to weather, traffic conditions, and road features [13,14]. Frequency fluctuations can be seasonal, with specific locations exhibiting high densities only during particular seasons [15]. A more detailed analysis of temporal changes in traffic accidents is based on the hourly count of traffic accidents. Kumar and Toshniwal [16] divided 26 districts into six clusters, each cluster having a similar trend in hourly counts of road accidents. Conversely, our study focused on the persistent recurring trends on an hourly scale and patterns at a micro-level spatial scale.

Researchers have for decades scrutinized features and functions in the vicinity of traffic accident locations and identified factors associated with accident occurrence. They have focused on socio-demographic factors such as population density and household income [17], vehicle-related aspects [18], road environment characteristics [13], and land use diversity [12]. Recent studies have delved into macro-level traffic crash analyses, linking crash frequencies to various zones such as traffic analysis zones (TAZs) [10], census tracts [19], and wards [20]. Some researchers have combined Points of Interest (POIs) with statistical tools to explore relationships between POIs and crash frequency in macro-level spatial units [21].

Jia [21] found positive associations between traffic crashes and residential buildings, banks, and hospitals in POIs in TAZs. Chen [22] demonstrated that incorporating POI data into classification models enhanced the true positive rate (recall) and balanced accuracy (G-mean), thereby emphasizing the positive effect of highly mixed POIs in predicting the severity of crashes. Street-level applications, like the study in [23], demonstrated the utility of POI and nighttime light (NTL) data in modeling traffic crash occurrences on different road types (i.e., expressway, arterial, local). However, these applications were primarily focused on predictive modeling and did not explore the POI-traffic collision association comprehensively. Expanding upon previous research, our study conducted a more in-depth analysis at the micro-level, exploring the connection between POIs and traffic crashes, specifically focusing on the street-level perspective. Additionally, the investigation employed association rules for different combinations of POIs and their impact on traffic accidents to uncover these intricate associations.

In recent years, the availability of POI data has significantly expanded. These data sources offer precise location information down to the building level and can detect notable changes in land-use intensity [24]. Moreover, the density of POIs commonly correlates with population density, where dense POIs correspond to high-density populations and sparse POIs indicate low-density populations, except for large shopping malls or theme parks. Studies have demonstrated a connection between higher population density and increased crash frequencies [23], and land use characteristics significantly affect crash severity [25]. Furthermore, POIs can act as both origins and destinations in human mobility, revealing visited locations of individuals and offering insights into activity patterns [26]. Many human activities, predominantly driven by social interactions or leisure, exhibit periodicities and regularities [27,28]. These crucial indicators that contribute to traffic accidents signal the associations between POIs and recurring patterns in traffic accidents.

Spatial associations should consider both reference and neighboring features. Traffic accident locations can be used as reference features to identify nearby neighboring features, including people, vehicles, roads, and environmental elements. The A-Priori algorithm distinguishes itself among association mining algorithms due to its precision and computational efficiency [29,30]. John and Shaiba [31] employed the A-Priori algorithm to identify the primary causes of traffic accidents in Dubai for a single year, focusing on the personal information and mental conditions of drivers. Their findings indicated a high frequency of accidents involving intoxicated drivers. Nidhi and Kanchana [32] established association rules between fatalities and road conditions, such as surface and lighting. Yang [33] uncovered regional disparities in associations between vehicle crashes and factors like car type, with distinctions observed across downtown, suburban, and mountainous regions. Expanding on these prior studies, this study adapted the A-Priori algorithm to ascertain the associations between POIs and locations with recurring patterns of traffic accidents.

Many studies have traditionally focused solely on the locations where events occurred to investigate their causes [31,32,34]. However, this presence-only approach is prone to sampling biases, similar to the use of presence-only data in species distribution modeling. To mitigate sample selection bias, alternative approaches consider both successful and unsuccessful movements or draw samples from participants and non-participants. Presence-only methods assess the habitat suitability, assuming that only locations with observations are habitable, whereas presence-absence methods evaluate occupied and unoccupied habitats [35]. Presence-absence methods necessitate data from non-occupied areas (absences) to establish discriminative rules for assessing habitat suitability based on a bimodal distribution of species. Research has shown that the inclusion of absence data aids in the identification of areas with low suitability that could have been mistakenly classified as suitable habitats when relying solely on the presence site [36]. In a similar vein, this study explores association rules between features for locations with no traffic accidents, sporadic traffic accidents, and routine traffic accidents.

All in all, our major contributions are as follows. (1) We introduce the LARO algorithm for identifying periodic behaviors inherent in point-based events. This enables us to understand the routine occurrence of events on street networks in terms of both location and timing. (2) Apart from the locations with routine events, we also consider locations with non-routine events and locations without events to mitigate sampling bias. (3) We examine the characteristics of geographical features in proximity to these locations to understand how the surrounding human activities influence the occurrence of events.

In summary, this study investigates the spatial event adherence to temporal cycles and examines relationships between successive events in close proximity. This study terms the phenomenon “routine occurrences” and introduces the Location Analytics of Routine Occurrences (LARO) algorithm with two objectives. The first objective is to pinpoint when and where routine occurrences take place. The second objective entails characterizing the features and functions in the proximity of these locations. This study posits that human dynamics play a role in shaping routine traffic accidents within urban environments, driven by daily, weekly, monthly, and seasonal rhythms that influence mobility patterns. These patterns, in turn, influence the spatiotemporal distribution of traffic accident risk within road networks in a city. Consequently, the locations of routine traffic accidents reflect the unique pattern of life in the city.

The subsequent sections detail the proposed LARO algorithm, its application to over 250,000 reported traffic accidents from 2010 to 2018 in Dallas, Texas, USA, and the identified locations and surrounding characteristics associated with routine occurrences. The conclusion presents fresh insights into the characteristics of POIs around traffic accident locations, highlights the contribution of LARO to the spatial analysis of point events and outlines avenues for future research.

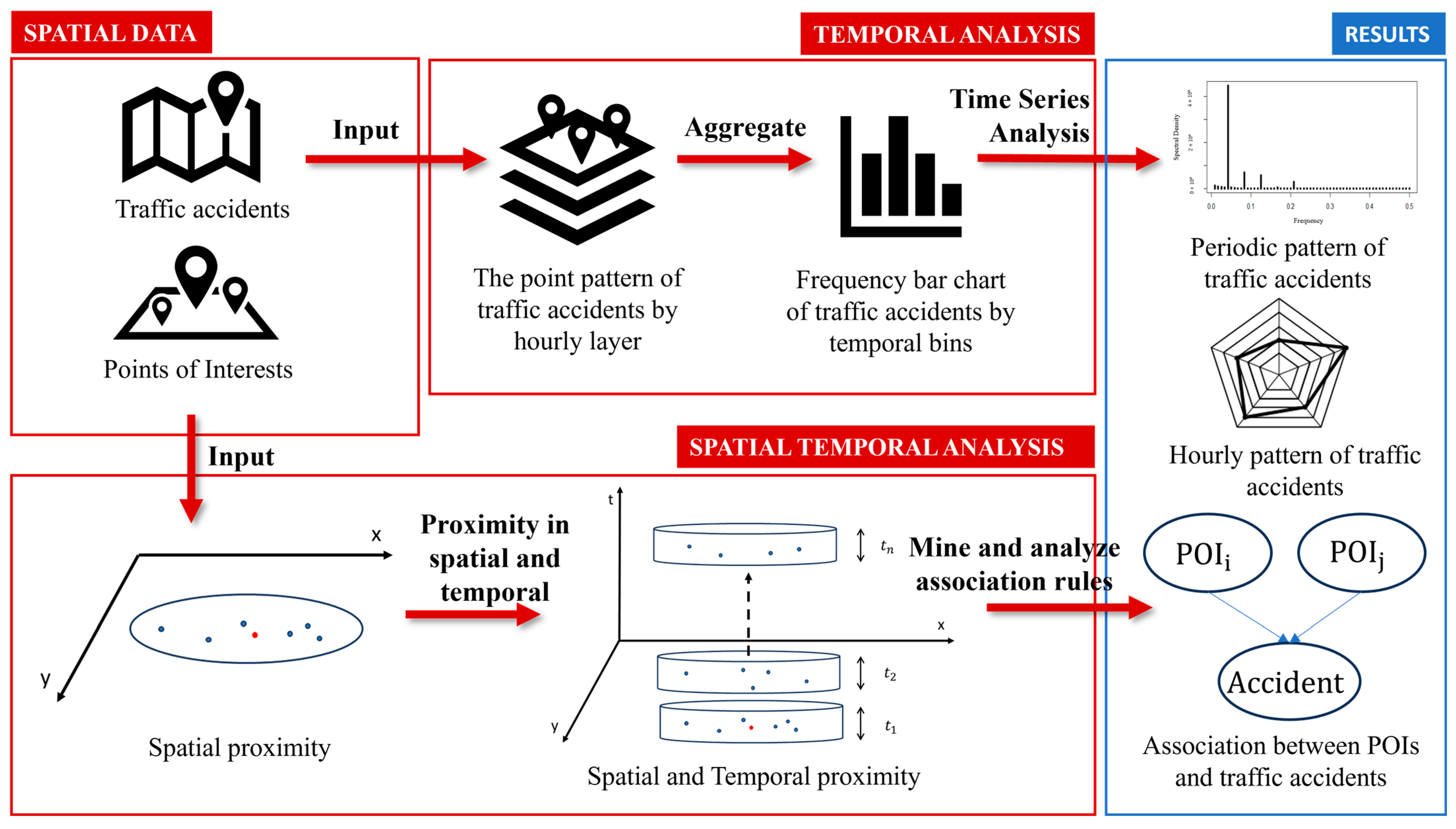
2. LARO Algorithm

The LARO algorithm aims to determine where events of interest regularly take place and to exploit site features and situational characteristics to understand why these events routinely occur at these locations. Consequently, the LARO algorithm consists of three phases: (1) identifying the temporality of event occurrences, (2) determining the locations of routine occurrences, and (3) analyzing the singular site features and situation characteristics at these locations in the context of the features and characteristics distributed across the study area. Figure 1 outlines the three phases and the specific steps in each phase.

A point event, represented as e(x_i,y_i,t_i,f_i), consisted of a spatial location (x_i,y_i), time of occurrences (t_i), and a set of features (f_i) for the $ith$ observed event. The precision of x, y, t, and f depends on their units of measurement. A point event may be georeferenced to a coordinate pair or an address. Point events may occur randomly, daily, weekly, seasonally, annually, or over longer periods. LARO assumed that the data of point events recorded locations, occurrences, and features in sufficiently fine units to differentiate individual point events.

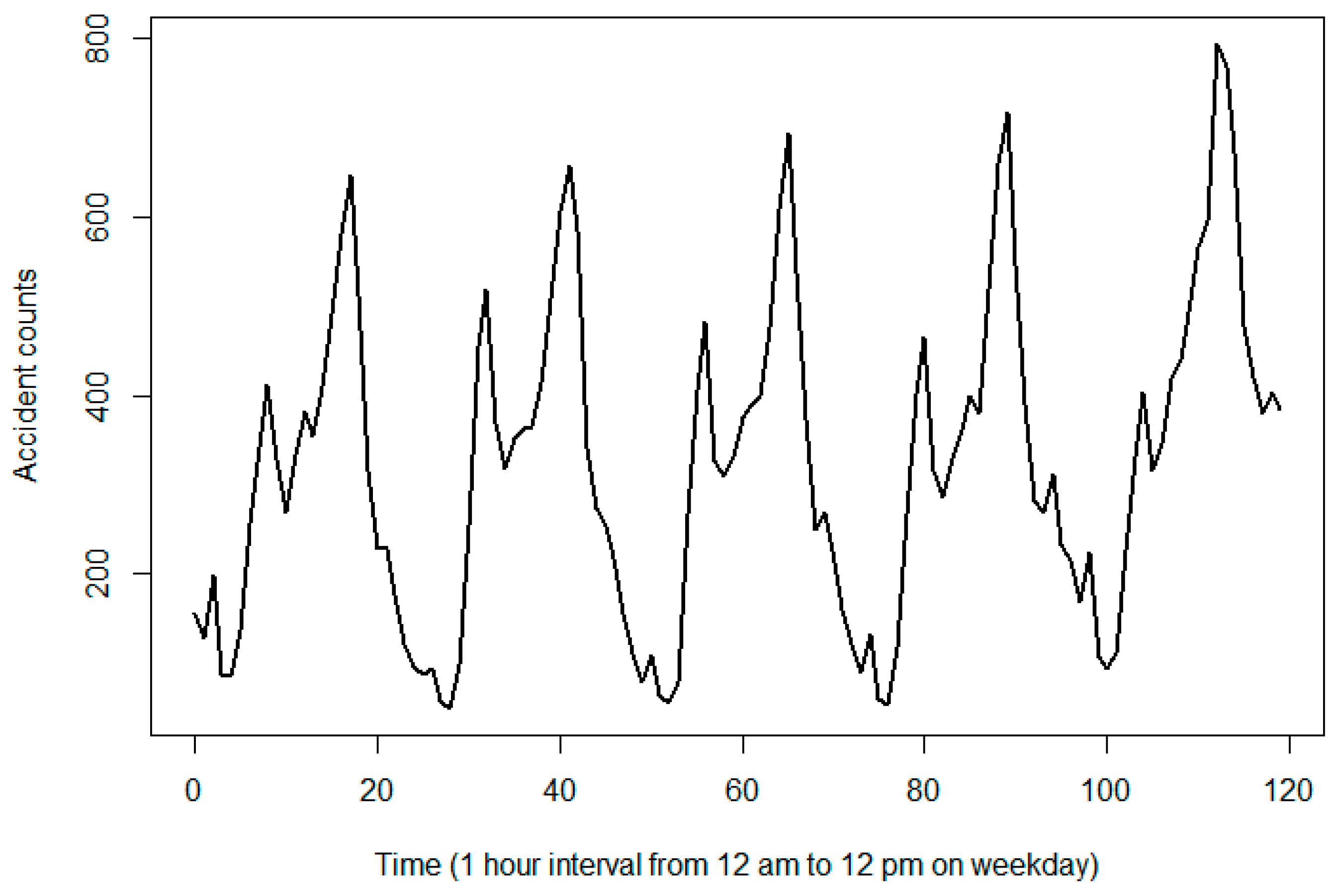
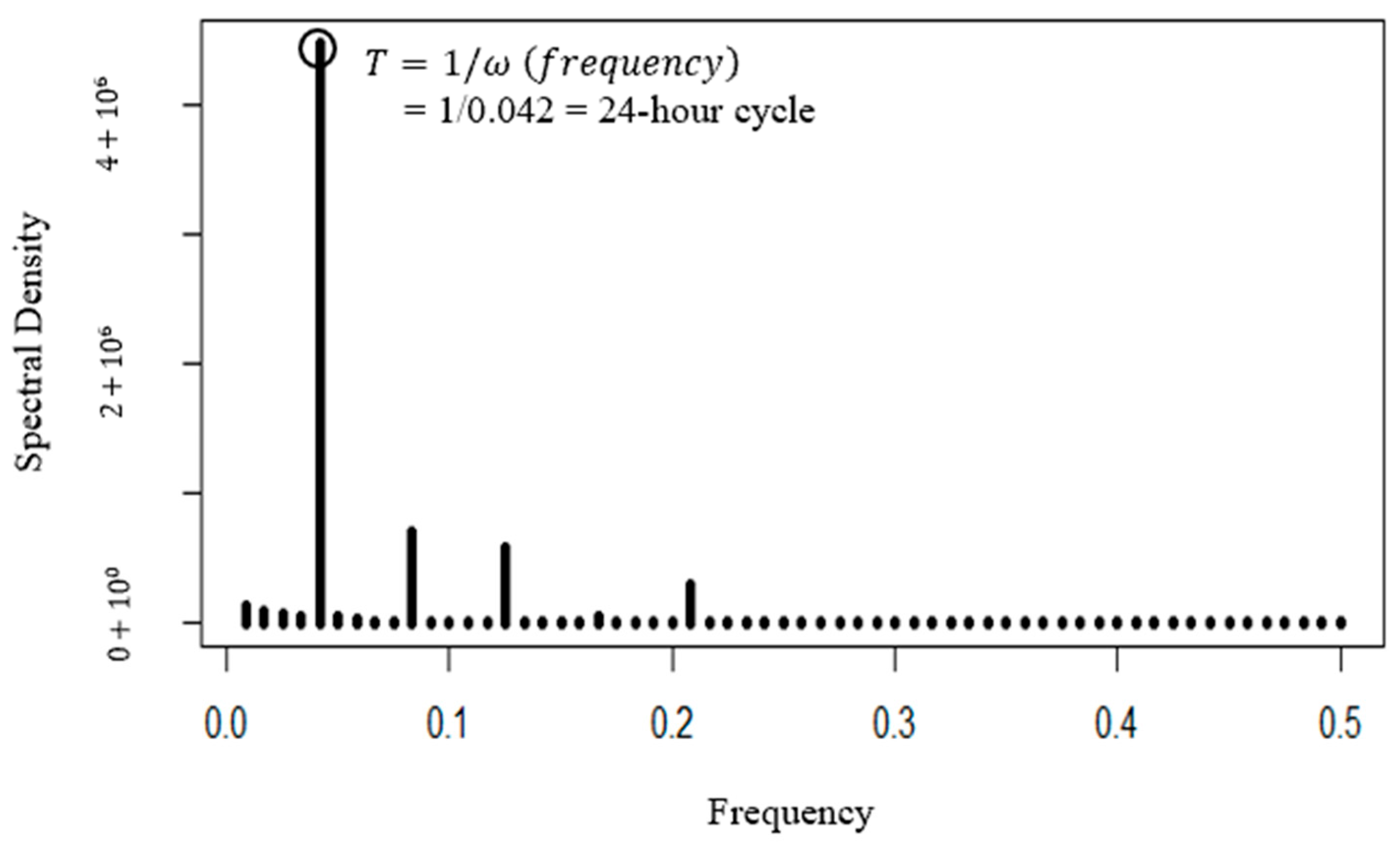
2.1. Identify the Periodicity of Routine Occurrences

LARO first exploited the periodicity of point events to identify the regular pattern on a temporal scale. Periodicity indicates temporal regularity in a recurrence interval [37]. There are two broad approaches to determining the periodicity in temporal distribution [38]. One method commonly employed to detect periodicity is spectral analysis, which involves decomposing a time series into its constituent frequency components using techniques such as the Fourier Transformation. The resulting spectrum can reveal dominant frequencies corresponding to recurring patterns or periodic behaviors within the time series [39]. The periodicity identified through spectral analysis can then be expressed as a combination of sine (or cosine) waves using a mathematical model that relates the number of events at time ‘t’ ($x_t$) to cosine and sine functions.

In the Fourier Transformation (Equation (1)), the two variables cos and sin depend on the time $t$, and the frequency $\omega . t$ refers to the time interval. The frequency $\omega$, defined as $\omega =1/T$, represents the number of complete cycles that occur in a single period ($T$). In other words, frequency determines how quickly the wave cycles repeat. Thus, $T$ represents the number of periods to complete a full cycle.

$$x_t={\beta }_0+{\beta }_1\ast cos\left(2\pi \omega t\right)-{\beta }_2\ast sin\left(2\pi \omega t\right)$$

(1)

In this study, LARO binned the point events into pre-defined temporal units—for example, the number of traffic accidents in the first hour (e.g., 0:00–0:59 a.m.) on 10 November 2020. LARO then applied the Fourier Transformation to convert the distribution of point events from a time series (i.e., a periodogram) to a frequency function (i.e., a frequency graph) (Figure 2). The spectral density for frequencies larger than 0.2 is almost equal to zero. The graph displays the dominant periodicity on the x-axis (or periods) with the highest density (or amplitude) on y-axis. The most prominent periodic components exist in the time series, which are $T$ = 24 ($\approx 1/0.042$) hour cycle (Figure 3). LARO then built a linear regression model based on the Fourier parameters to estimate the expected number of events in each time unit and determine the goodness of fit (R²), indicating the predictability of the point events based on the frequency graph and, hence, the strength of event periodicity. The first phase of the LARO algorithm examined periodicity in terms of hours of the day and days of the week based on hourly data (Algorithm 1). More temporal bins may be added for additional cycles, such as weeks of the month or months of the year.

Algorithm 1. Procedure for temporal analysis of event occurrences.

$\mathrm{Input}: E, e_i\in E$: raw point events Output: Fit the function to the frequency distribution of point events Step 1. Define temporal bins for a given period $T=\{tbi{n}_1, \dots ,tbi{n}_j\}$ Step 2. Group point events into corresponding temporal bins for each $e_i\in E$   if $e_i$ happen in $tbi{n}_j$    group $e_i$ into $tbi{n}_j$ Step 3. Calculate the frequency of point events $e_i$ in each bin $S_{cp}$$=\mathrm{aggregate}(E$$~ tbi{n}_j$, sum) Step 4. Build a periodogram to identify the dominant period in the time $\mathrm{series} \mathrm{of} \mathrm{point} \mathrm{events} (Pdm$) $Pdm$$=\mathrm{periodogram}(S_{cp}$) Step 5. Use cosine and sine waves to model the periodicity ${cos}_k=\cos (2\ast pi\ast \frac{1}{Pdm}\ast tbi{n}_j){sin}_k=\sin (2\ast pi\ast \frac{1}{Pdm}\ast tbi{n}_j)$ $\mathrm{linear}\_\mathrm{model}=\mathrm{lm}(S_{cp}$ ~ ${cos}_k+{sin}_k)$ Step 6. Use the function to predict the time series and evaluate R2 for the goodness of fit $\mathrm{result} <\text{-} \mathrm{predict}(\mathrm{linear}\_\mathrm{model}, S_{cp}$)

2.2. Identify Locations of Routine Occurrences

The first phase in LARO determined which periods have the most events and how well the events could be predicted over time. The second phase of the LARO algorithm found nearness events occurring in temporal proximity for each event (Algorithm 2). The criterion for “nearness” varies, such as being within walking distance, half of the average city block size, or 100 m, depending on the problem context. Attempting to capture spatial patterns within one hour was subject to sensitivity issues. More specifically, traffic crashes that occurred near the timeframe boundary satisfied the requirements of temporal proximity but were separated into different groups. So, we used a three-hour window to accommodate this dynamic by systematically shifting the observation window through time, capturing the evolution of spatial patterns over a short duration. We used the term $n{e}_i$ as the number of events around each focal event $e_i$. We then stored each focal event $e_i$ and its nearest event $n{e}_{t_1}, \dots , n{e}_{t_n}$ in each time window into a vector $V$; specifically, we wrote $V_i=\left(n{e}_{t_1},\dots ,n{e}_{t_n}\right)$ as the sequence of nearest events where $e_i$ was the focal event. In the end, we used Sen’s slope ($SSE$) [40], a non-parametric method for measuring temporal trends, to assess the trend of traffic accident occurrences over time. The positive value of $SSE$ indicated an increasing trend; conversely, the negative value of $SSE$ indicated a decreasing trend.

$SSE$ was calculated based on the difference between each pair of observations ($m_{ij}$) in the sample of $N$ pairs of data. The $N$ value of $m_{ij}$ was ranked from the smallest to largest, and the median of the ranked $m_{ij}$ was $SSE$. The $SSE$ reflected the temporal trend, and its value indicated the steepness of the trend.

$$m_{ij}=\frac{Y_j-Y_i}{(j-i)}$$

(2)

$$SSE=\left\{\begin{array}{c}{m}_{[\left(N+1\right)/2]} if N is odd\\ m_{\left[N/2\right]}+m_{\left[\right(N+2)/2]} if N is even\end{array}\right.$$

(3)

where $Y_i$ and $Y_j$ are the values at time $i$ and time $j$ ($j>i$).

In addressing potential sampling bias, it was imperative to consider locations with events while simultaneously considering those without events. To mitigate this bias, we identified three distinct types of locations for analysis. First, locations exhibiting routine occurrences characterized by a stable or increasing trend of larger magnitude (RO); second, locations marked by stochastic occurrences (SO), wherein traffic accidents transpire intermittently; and third, locations devoid of traffic accidents altogether (GO).

Algorithm 2. Procedure for Spatial Analysis of Event Occurrences.

Step 1. Choose a search radius for ‘spatial proximity of occurrences’ $r$: meaningful search radius for detecting nearby events Step 2. For every event location, identify events within the search radius $r$ For each $e_i$ in $tbi{n}_i$: Calculate $V_i=\left(n{e}_{t_1},\dots ,n{e}_{t_n}\right)$ Step 3. Determine the slope for each $V_i$ using Sen’s slope For each $V_i$: Calculate $SSE$

2.3. Spatial Association Mining at Locations of Routine Occurrences

The third phase of the LARO algorithm examined which POI features contribute to three different location types with the association rule mining algorithm (Algorithm 3). First, we examined the background distribution of POI based on regular grids and calculated the proportion of POI in the context of the entire study area. Second, we compared the proportion of POI around the RO, SO, and GO. Third, the A-Priori algorithm processed the associations, mined frequent site features, and pruned the rules based on pre-defined thresholds for support and confidence.

Algorithm 3. Procedures for spatial association analysis at three locations.

Step 1.$\mathrm{Analyze} \mathrm{the} \mathrm{proportion} \mathrm{of} i$th category in comparative relation to a whole at regular grid locations $F_p$$=\varnothing$ For each grid location $f_p=\frac{1}{K}{\displaystyle \sum _{o=1}^K}I$ Append $f_p$ to $F_p$ Step 2$. \mathrm{Analyze} \mathrm{the} \mathrm{associations} \mathrm{between} \mathrm{POIs} \mathrm{and} \mathrm{traffic} \mathrm{accidents}$ // Repeat step 2 for three locations (RO, SO, GO) $AssRules$ = apriori ($F_P$→ RO, SO, GO. parameter = list (sup = $sup$, conf =$conf$, target=„rules”)) Step 3. Relate the site features to situation characteristics for explanations

3. Data and Methodology

3.1. Traffic Accident Data

Traffic accident data, comprising 256,564 records, were obtained from the Texas Department of Transportation (TxDOT) for accidents in Dallas from 2010 to 2018. The traffic accident dataset contained detailed driving information, not limited to location, time, and driving environment. Alongside this, Point of Interest (POI) data, representing specific spatial features, were acquired for our study. Point of Interest (POI) data were indispensable in analyzing traffic accidents. This significance was amplified by a burgeoning literature that emphasizes the role of geographic context in comprehending event occurrences [21]. POIs extend beyond mere physical locations like business establishments and tourist landmarks; they encapsulate the essence of human activity, thus providing a richer narrative of daily patterns that potentially influence traffic dynamics [41]. We used POI data from SafeGraph due to its comprehensive technical documentation (https://docs.safegraph.com/docs/places (assessed on 20 December 2023)), which guarantees data integrity, coupled with its global reach and consistent updates, ensuring data relevance and timeliness. We categorized POI data into 13 distinct categories (

Table 1. POI categories.

General Class	# POIs	General Class	# POIs
Restaurant	7221	Entertainment	1389
Care Facility	628	Manufacturing	1494
Automotive	1566	Transportation	377
Bank	2661	Administration	2265
Education	1565	Utilities	548
Medical	7744	Business	9048
Store	8082

) and used them to capture diverse human activities that involved routine daily engagements (e.g., work, school, restaurant), social leisure (e.g., entertainment), health care needs (e.g., care facility, medical) and work-related activity (e.g., manufacturing, automotive, transportation).

3.2. Identify Locations of Routine Occurrences

3.2.1. Analyze the POI Distribution at Regular Gridded Locations in the Background

We measured the overall distribution of POI features in Dallas to foreground the uniqueness of a location with POI features. Our steps to examine the distribution of POI included: (1) creating grid points at 750-m spacing across the city of Dallas (Figure 4); (2) building a 750-m buffer around each point; (3) selecting all POIs within each buffer; and (4) calculating the proportion of POIs in individual categories within each buffer.

3.2.2. Analyze the Associations of Site Features at Three Location Types

LARO sought associations of features at locations. Uncovering these co-occurrence patterns involved three common measures: Support, Confidence, and Lift. The basic form of co-occurrence patterns discovered by the A-priori algorithm could be demonstrated as $X\to Y$. The X in our study represents POI features and Y, location types. Support was defined as the ratio in which the dataset contained certain POIs $\to$ location types. Confidence was the ratio of the dataset containing certain POIs $\to$ location types to the number of datasets containing the same POIs.

We used the quantile method to encode location buffers based on their POI frequencies into four categories from lowest (1) to highest (4) frequencies between cut-off quantile thresholds. Accordingly, the two-factor variables were converted to a single-factor variable. For example, the combined factors were formatted as hospital_level1, hospital_level2, restaurant_level3, etc. The first part of the names (i.e., hospital, restaurant) represents the corresponding POI categories, whereas the second part (i.e., level1, level2) represents the POI quantile-level. After preparation for the value of POIs, transactions were created based on three locations. The study design accounted for 2103 associations separably from RO, SO, and GO locations.

$$Support\left(X\to Y\right)=\frac{frequent\left(X\to Y\right)}{Total transactions\left\{D\right\}}$$

(4)

$$confidence \left(X\to Y \right)=\frac{frequent(X\to Y)}{transactions contain X}$$

(5)

$$lift \left(X\to Y\right)=\frac{support(X\to Y)}{support\left(X\right)\ast support\left(Y\right)}$$

(6)

4. Results

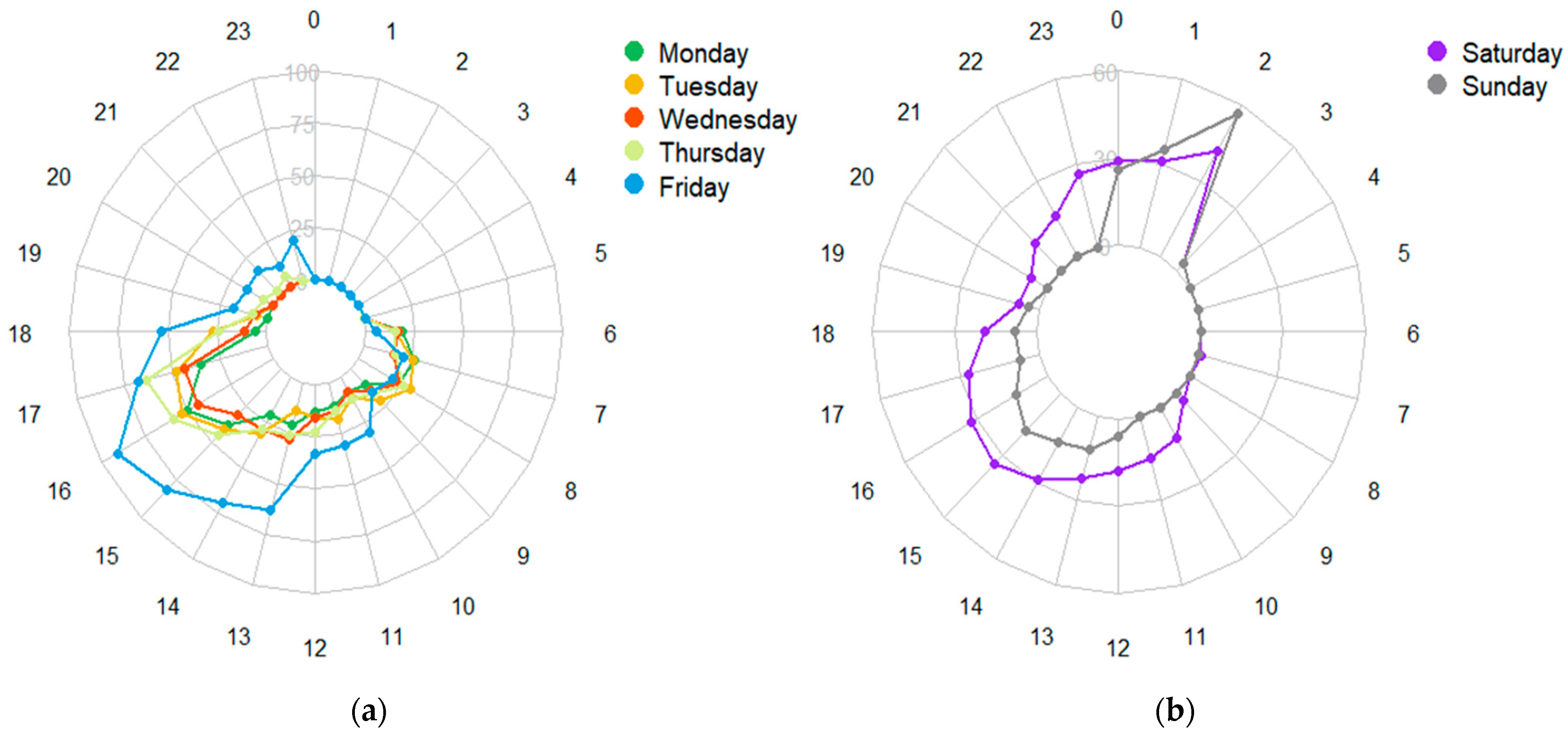
4.1. Hourly Temporal Pattern on Weekdays and Weekends

We applied a 3-h moving window with a 2-h overlap to capture the traffic accidents in nearby temporal units. For example, the temporal window for traffic accidents occurring at 8 a.m. on Monday also considers the traffic accidents occurring at 7 a.m. and 9 a.m. on Monday. In this case, this approach can avoid the sensitivity issue and consider the temporal variability of traffic crashes.

Each location had a continuity time window extending from the first period to the last period. A location is the RO location when it has a positive value of $SSE(SSE>0)$. We summarized RO locations in each weekly hour (Figure 5a,b). Figure 5a showed the temporal profiles of RO locations on weekdays and Figure 5b visualized the magnitudes of the RO locations on weekends. During weekdays, the RO locations actively occur during off-day hours, and two little spikes occur in the early morning and late night. Among the days, Friday has the highest frequency of RO locations. RO locations on weekends display a distinctive pattern; the number of RO locations increases from 9 p.m. and abruptly drops at 3 a.m., signaling the conclusion of late-night activities. The change in temporal pattern signifies the active or inactive phase of human activities. However, a more extensive moving window may provide a more comprehensive pattern that will enable policymakers to concentrate on specific time periods, such as morning, afternoon or evening.

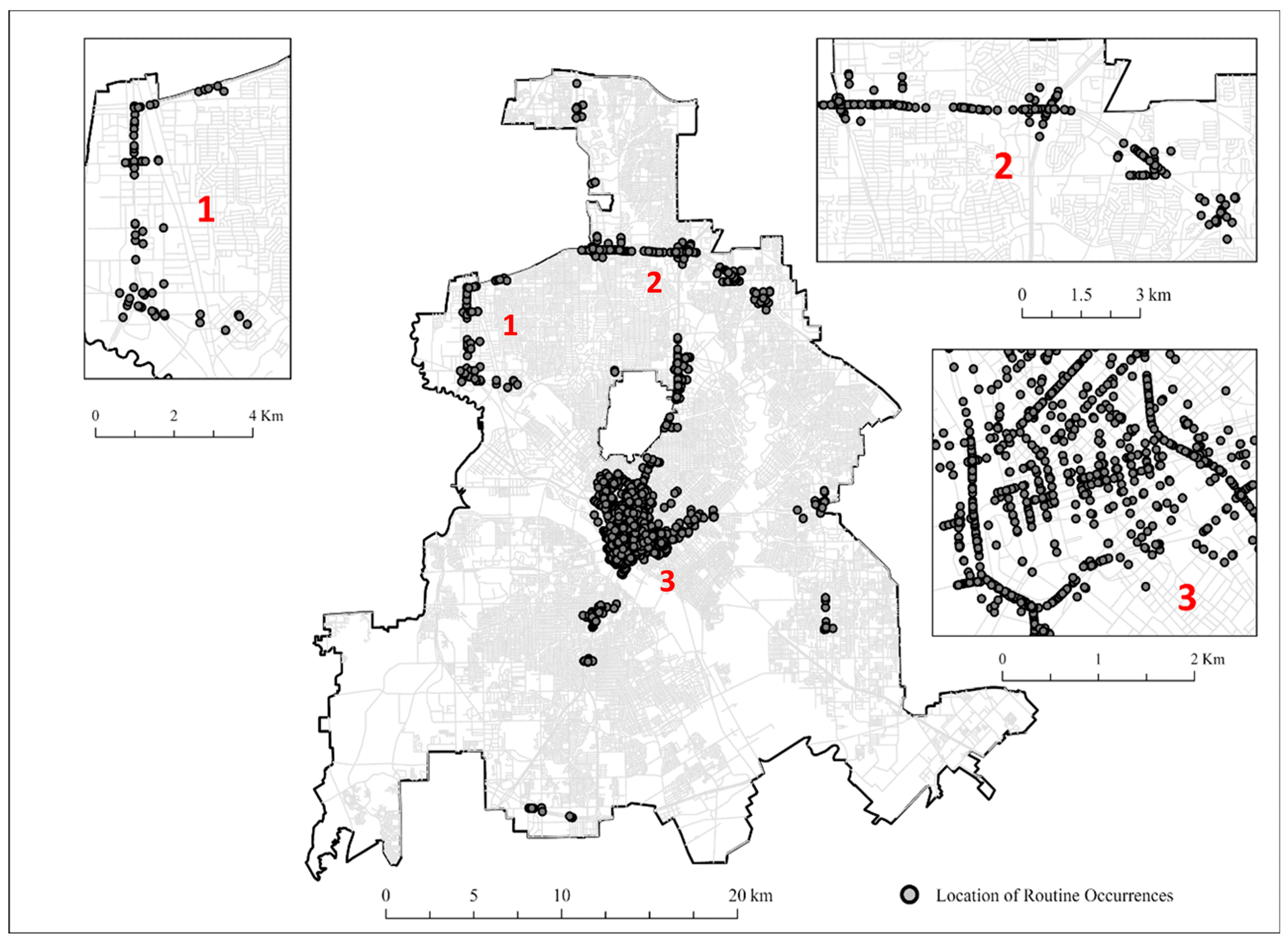
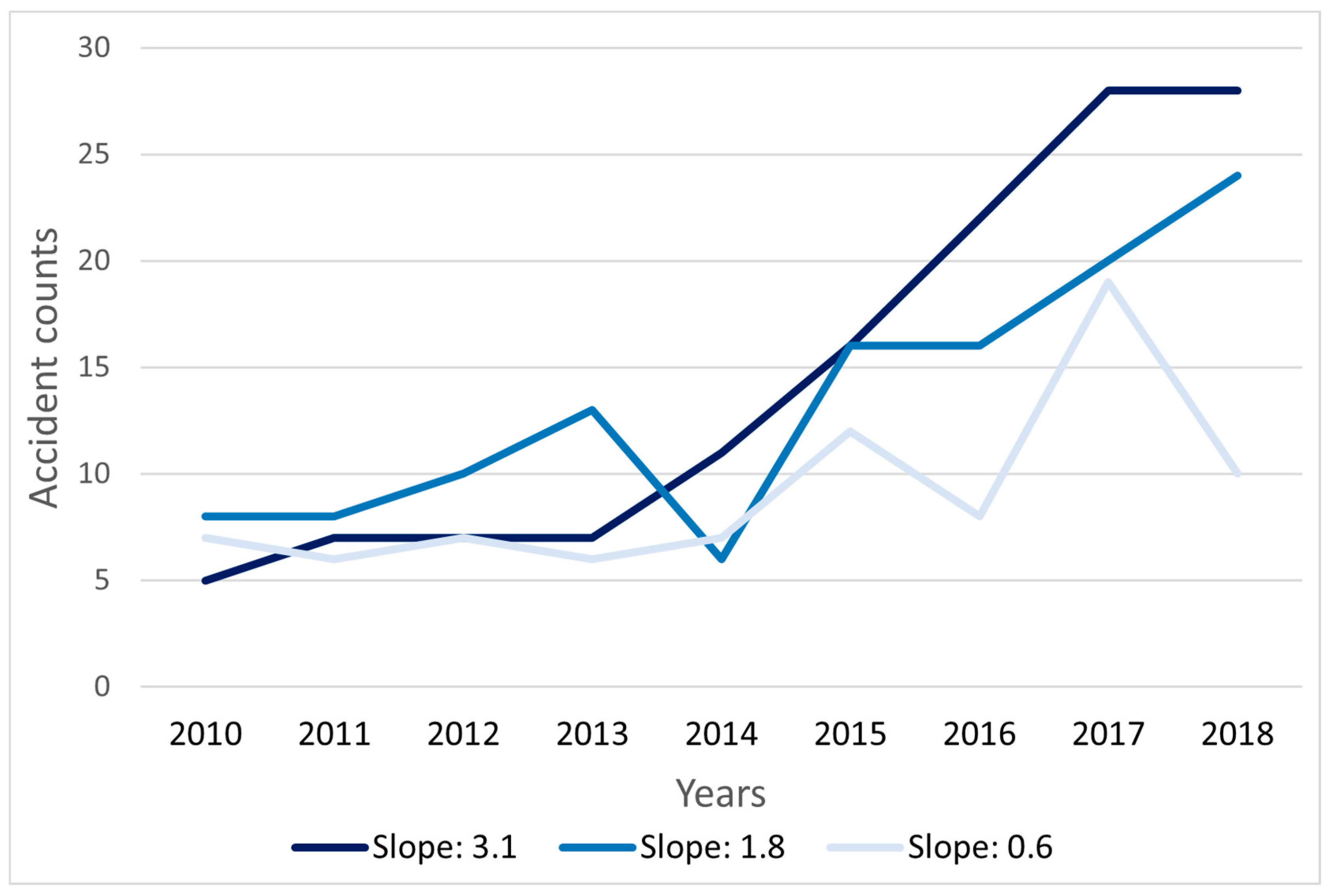
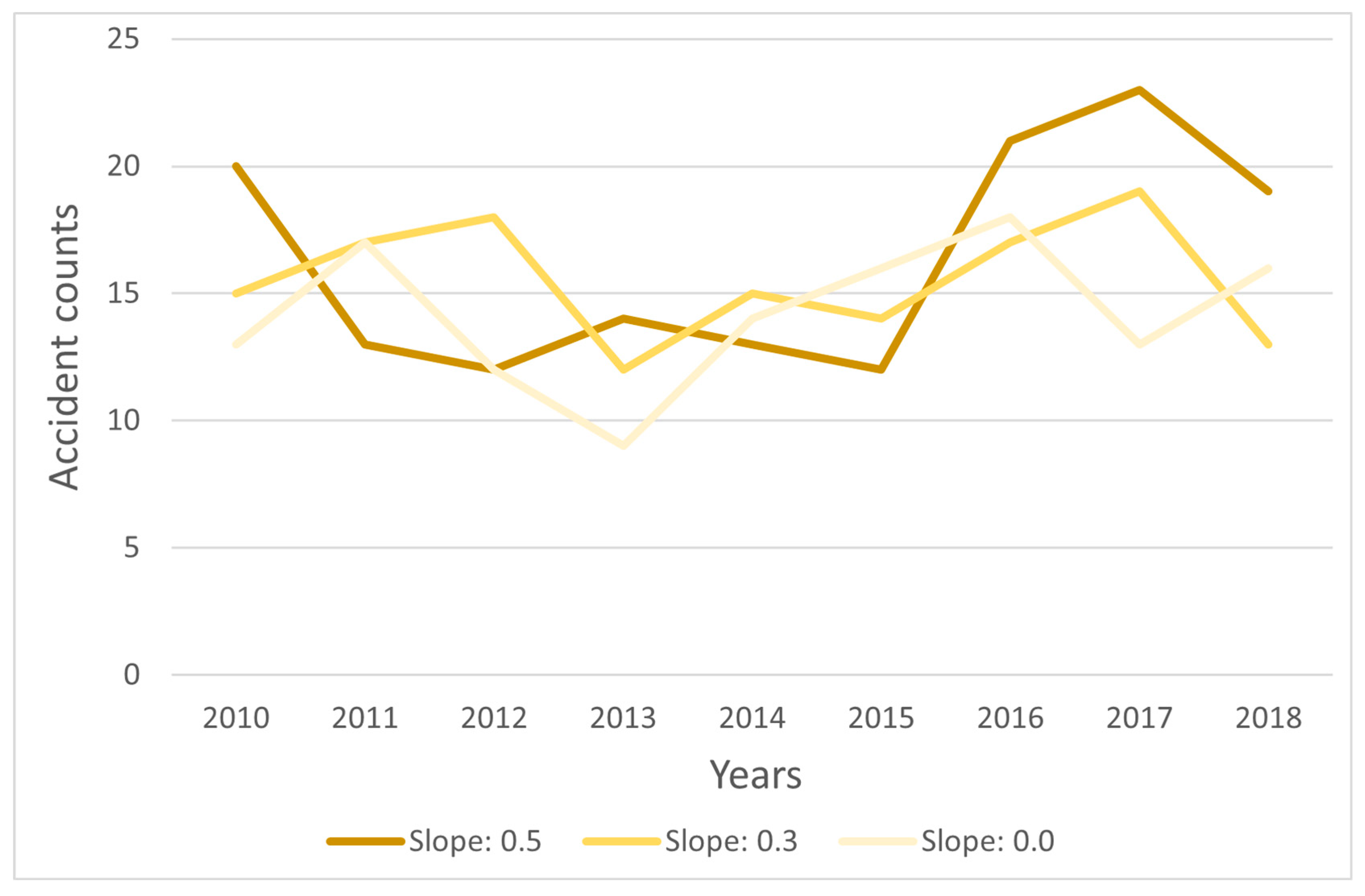
4.2. Spatial Patterns of RO Locations

For each location with continuity time windows, we used Sen’s slope to determine the location with continuous traffic accidents in a fixed time; that is, the location experiences a stable or increasing trend in a high magnitude of traffic accidents. We identified 2103 RO locations with high magnitude and a stable or increasing trend ($SSE>0$) (Figure 6). While these RO locations were distributed across the city of Dallas, they were spatially confined to street segments, intersections, and downtown. Due to the changes in traffic accidents across the different years, they had different slopes (ranging from 0 to 3.14). Cluster 1, Cluster 2, and Cluster 3 suggested high traffic accidents at a neighborhood scale. Locations in Cluster 1 had a slope from 0 to 0.6, Cluster 2 had a slope range from 0 to 1.8, and Cluster 3 had a slope from 0 to 3.1 They were similar in that some RO locations had a stable trend in traffic accidents ($SSE=0$). However, the difference was that some locations in Cluster 2 and Cluster 3 had increasing trends ($SSE=1.8 or 3.1$). Figure 7 showed the monotonic increase for the three different highest slopes in each cluster. All trends started from the lower number of traffic accidents and had a higher frequency of traffic accidents in subsequent years. The increasing slope reflected a location that has traffic accidents each hour, but more important was that the magnitude increased with the years.

Additionally, locations with lower slopes were also important since they had a stable trend of traffic accidents. Figure 8 showed the stable trend in traffic accidents that ranged from 10 to 20 in each hour across different years. In summary, the RO locations contained locations with increasing and stable trends in traffic accidents. The identification of RO is based on a fixed buffer. However, the choice of fixed buffer may not adequately consider the underlying densities of traffic accidents. To solve this issue, adaptive buffers, which vary the buffer size from one location to another, need to be applied. Once the RO locations have been identified, the characteristics in geographical environments need to be analyzed to understand the periodicity of traffic accidents. As previous studies stated, human activities exhibit periodicities and regularities because they are predominantly driven by social interactions or leisure activities. Therefore, we proceeded with an analysis of periodic relationships between human activities and traffic accidents below.

4.3. Exploratory Analysis of the Distribution of POIs

POIs represent geographic locations that attract human attention and engagement, serving as the venue for various social, cultural, and economic activities. In this study, considering the characteristics of regularities and periodicities in human activities, we explored the association between POIs and traffic accidents using the A-priori algorithm. Before proceeding to investigate association rules, it is imperative to scrutinize the underlying POI distribution to ascertain its uneven distribution (

Table 2. Summary of the proportion values of each POI category.

Variable	Min.	1st Q.	Median	Mean	3rd Q.	Max.
prop of administration	0	0.000	0.037	0.077	0.100	1.000
prop of automotive	0	0.000	0.013	0.038	0.050	1.000
prop of bank	0	0.000	0.027	0.041	0.068	0.500
prop of business	0	0.100	0.186	0.194	0.239	1.000
prop of care facility	0	0.000	0.000	0.011	0.012	0.222
prop of education	0	0.000	0.018	0.052	0.053	1.000
prop of entertainment	0	0.000	0.000	0.026	0.037	0.500
prop of manufacturing	0	0.000	0.022	0.038	0.048	0.667
prop of medical	0	0.000	0.124	0.125	0.182	1.000
prop of restaurant	0	0.000	0.125	0.130	0.193	1.000
prop of stores	0	0.053	0.143	0.151	0.207	1.000
prop of transportation	0	0.000	0.000	0.009	0.005	0.250
prop of utilities	0	0.000	0.000	0.011	0.010	1.000

). Figure 9 showed the distribution of POI composition at each location. The bar charts indicate the proportions of POI categories within individual 750-m buffers. In comparison, locations in northern Dallas had more medical facilities, locations in the west and southeast had more business, and downtown locations had more restaurants and businesses. Conversely, from the perspective of POI features, restaurants and business had higher proximity to locations in northern Dallas. The varying POI composition from one location to another asserted the potential influence of POI features on traffic accidents.

4.4. Patterns from Association Rules between POI Features and Location Types

4.4.1. Patterns for RO Locations

Our study discerned 155 rules between POI categories and Routine Occurrence (RO) locations (Figure 10). The width of the arrows corresponds to the support of the rules, ranging from 10% to 16%, indicating the proportion of transactional records that contain the POI and accident occurrence association. The saturation of the arrows represented confidence, ranging from 41% to 82%, and reflected the probability that, given the presence of specific POI types, a location will have routine traffic accidents. Lift values spanned from 1.2 to 2.4. The positive value of Lift indicated that the occurrence of the POI categories increased the likelihood of the RO occurring. For example, a Lift of 2.4 implied that the occurrence of traffic accidents was 2.4 times more likely in locations with the specified POIs compared to those without.

Among the rules derived, the association between high-frequency categories of POIs, especially those within the top quantile (level 4), and RO locations were most evident. Predominant POI categories such as Business, Store, and Restaurant, particularly at higher levels, exhibited strong ties to ROs, suggesting that areas with dense distributions of these facilities have a higher propensity for routine traffic accidents. This correlation may be attributable to the increased vehicular and pedestrian traffic these POIs attract, heightening the potential for accidents. Conversely, the education and automotive factors appeared less frequently in association with ROs.

A prominent composite of POI categories—comprising Store, Restaurant, Entertainment, and Business—emerged as more influential at RO locations. Stores in this context typically specialize in retailing a variety of goods, such as furniture, groceries, and sports equipment, and often adopt a compact distribution to leverage collective consumer draw, which in turn can increase local traffic volume. Restaurants, providing meal services at routine intervals, attract a regular flow of customers. The Entertainment category, which caters to amusement and recreational activities, sees a surge in human and vehicular presence during holidays, contributing to the incidence of traffic accidents. The Business category, serving specific clientele needs, encompasses services like travel, equipment rental, and real estate, and is instrumental in defining the traffic patterns around RO locations. These insights underline the critical role of POI distributions in shaping the spatial dynamics of traffic accidents and offer a potential framework for targeted interventions to enhance urban traffic safety.

Table 3. Top 10 association rules for three locations.

	Rules	Support	Confidence	Lift
	Location of routine occurrences (ROs)
1	Business_level4,Care_Facility_level4,Stores_level4,Utilities_level4	0.104	0.824	2.473
2	Entertainment_level4,Business_level4,Stores_level4	0.104	0.824	2.472
3	Care_Facility_level4,Stores_level4,Utilities_level4	0.104	0.823	2.470
4	Care_Facility_level4,Restaurant_level4,Stores_level4,Utilities_level4	0.104	0.823	2.469
5	Restaurant_level4,Care_Facility_level4, Utilities_level4	0.110	0.811	2.434
6	Business_level4,Care_Facility_level4,Restaurant_level4,Utilities_level4	0.108	0.810	2.430
7	Business_level4,Care_Facility_level4,Utilities_level4	0.108	0.809	2.428
8	Automotive_level4,Entertainment_level4,Restaurant_level4	0.104	0.784	2.353
9	Automotive_level4,Restaurant_level4,Utilities_level4	0.103	0.784	2.353
10	Manufacturing_level4,Restaurant_level4,Transportation_level4	0.102	0.784	2.352
	Location of stochastic occurrences (SOs)
11	Bank_level3	0.125	0.514	1.541
12	Entertainment_level3	0.141	0.510	1.530
13	Business_level3	0.125	0.507	1.520
14	Care_Facility_level3	0.130	0.502	1.505
15	Restaurant_level3	0.118	0.496	1.486
16	Manufacturing_level3	0.113	0.490	1.470
17	Stores_level3	0.122	0.488	1.463
18	Restaurant_level2	0.124	0.483	1.447
19	Automotive_level3	0.119	0.474	1.421
20	Education_level3	0.114	0.461	1.382
	Locations without traffic accidents (GOs)
21	Bank_none,Manufacturing_none,Utilities_none	0.109	0.965	2.896
22	Bank_none,Manufacturing_none,Transportation_none	0.106	0.964	2.893
23	Automotive_none,Bank_none,Transportation_none,Utilities_none	0.103	0.957	2.873
24	Care_Facility_none,Entertainment_none,Manufacturing_none, Transportation_none	0.107	0.956	2.869
25	Bank_none,Care_Facility_none,Utilities_none	0.137	0.956	2.868
26	Care_Facility_none,Entertainment_none,Manufacturing_none, Utilities_none	0.109	0.955	2.867
27	Business_level1,Care_Facility_none,Entertainment_none	0.101	0.907	2.723
28	Business_level1,Care_Facility_none,Utilities_none	0.123	0.904	2.714
29	Business_level1,Care_Facility_none,Transportation_none, Utilities_none	0.110	0.904	2.712
30	Business_level1,Transportation_none,Utilities_none	0.126	0.893	2.679

lists 10 selected rules with the highest Lift values from 155 Rules at RO locations. The first rule for RO locations is {Business_level4, Care_Facility_level4, Stores_level4, Utilities_level4 }. This rule states that locations with Business, Care Facility, Store and Utility with the highest number of POIs in each category were where traffic accidents regularly occurred. The corresponding indices that follow this rule are Support = 10.4%, Confidence = 82.4%, and Lift = 2.473. The value of Support indicates that 10.4% of RO locations have these four POI categories around them. The value of Confidence denotes that out of all locations surrounded by the four POI categories, 82.4% of them were RO locations.

To summarize the rules for RO locations, the rules indicate that public facilities categorized as Utilities (rules 1, 3, 4, 5, 6, 7, 9), Care Facility (rules 1, 3, 4, 5, 6, 7), Restaurant (rules 4, 5, 6, 8, 9, 10), Business (rules 1, 2, 6, 7), and Store (rules 1, 2, 3, 4) are highly associated with RO locations. Among them, Utilities and Care facilities are two POI types that do not exhibit fixed-time attraction or regular visitation patterns. A possible explanation for their appearance in the rules is that they co-exist with the other three POI categories. For example, Care Facility may strategically co-exist with Store or Restaurant to improve accessibility for visitors and enhance the comfort of individuals who may need to spend extended periods at care facilities. These POIs supporting human activities also cause more traffic volume. Future studies could analyze the traffic volume in proximity to these POIs to investigate whether the routine traffic accidents are influenced by recurring human events or are simply a mapping of nearby traffic flow.

4.4.2. Patterns for SO Locations and GO Locations

Locations of stochastic occurrences (SOs) were characterized as places where accidents occur intermittently. GO locations, by definition, avoid traffic accidents. Compared to the pattern at RO locations, SO locations had a lower frequency of POI categories (Figure 11). The corresponding indexes followed these rules: Support ranged from 10% to 14%, and Confidence ranged from 40% to 50%. The lower Confidence at SO locations reflects a moderate association between the presence of specific POI categories and SO locations. Rules with Entertainment_level3 had the highest Support (14%), indicating that when locations that have solely entertainment facilities, they are prone to have traffic accidents in an irregular pattern. This underlines that entertainment facilities were significant not only in the context of RO but also in SO locations, marking their broad impact on traffic safety. The absence of intricate POI combinations at SO locations indicates that varied POI types jointly influence the routine pattern of accidents at RO sites, a pattern not observed with stochastic accidents. Apart from the appeared POI categories at RO locations, Bank and Education at Level 3 appear and contribute to traffic accidents occurrence.

GO locations were characterized by no traffic crashes occurring. They did not have prominent spatial clusters like RO and SO (Figure 12). Here, we also considered POI absence, that is, when locations do not have POI around them. We denoted the POI absence as POI_none. For the rules at GO locations, most of them indicated that the GO locations are more likely to be associated with absence of POIs.

5. Conclusions

We developed the LARO algorithm to detect periodicity in space and time and demonstrated the algorithm with traffic accidents in the city of Dallas. Periodicity in traffic accidents diverges from spatial point densities as it focuses on regular patterns in traffic accidents, e.g., a location that recurrently has traffic accidents at a regular time, such as every Monday at 9 a.m. Human activities also display repetitive patterns, as human-associated activities do not occur randomly [42]. The LARO algorithm assumed that the periodicity in traffic accidents interplayed with repetitive patterns in human activities. A POI commonly serves as a venue to support human activities. The co-existence of POIs in the neighborhood of any location with regular traffic accidents can manifest potential associations between human activities and traffic accidents. The LARO algorithm includes the Fourier Transformation to identify periodicity in time by decomposing the time series into its constituent frequency components. With space-time buffering, the LARO algorithm delimited periodic traffic accidents within a spatial-temporal scale, wherein a specific location consistently experiences traffic accidents at a regular time. Also included in LARO is the A-Priori algorithm for mining association rules between two spatial features (one is the location with different frequencies of traffic accidents, and the other POI features). Significant association rules suggest the patterns in which the presence of POI features influence the presence of traffic accidents.

Our study delved into the association between Point of Interest (POI) categories and location types, leading to the identification of significant rules. POIs serve dual roles as both origins and destinations of human mobility, unveiling the locations individuals visit and providing valuable insights into their activity patterns. Among the three location types, rules for locations with routine traffic accidents revealed a strong association between the presence of entertainment, stores, restaurants, and businesses with the occurrence of regular traffic accidents, emphasizing the potential impact of these POI categories on accident likelihood. Locations with traffic accidents, but not regular ones, exhibited lower frequency and fewer combinations of POI categories, suggesting the importance of POI combinations that contribute to routine traffic accidents. Entertainment stands out as a key factor in the association rules, likely due to its role in amplifying traffic volume and pedestrian engagement. Moreover, locations without traffic accidents, characterized by the absence of traffic accidents, are associated with a distinct pattern that aligns with lower frequency or absence in POI categories. Rule comparisons from three locations help us confirm the importance of POI combinations at locations with routine traffic accidents and non-overlapping rules among the three locations.

This case study illustrated the usefulness of the proposed LARO algorithm in detecting periodicity in point-based events and contextualizing the locations of routine occurrences in nearby POIs. Additionally, crash density varies spatially and temporally, so variable periods and buffers can account for such spatial heterogeneity beyond fixed buffers [43]. Finally, further research would unveil new insights into the relationship between Points of Interest (POIs) and traffic accidents and its applicability to other urban areas. Comparison of road conditions (e.g., traffic volume) to traffic accidents could also validate whether repetitive human activities closely influence the regular occurrence of traffic accidents in urban areas or whether they are simply due to busier traffic at a specific time. LARO is applicable to point-based events, such as crime incidents, species sightings, disease cases, or social events. However, LARO cannot handle linear or areal events, such as tornado paths or wildfire burns. Future research should improve the capabilities of LARO to incorporate events of higher dimensions.