A Particle-Swarm-Optimization-Algorithm-Improved Jiles–Atherton Model for Magnetorheological Dampers Considering Magnetic Hysteresis Characteristics
Abstract
1. Introduction
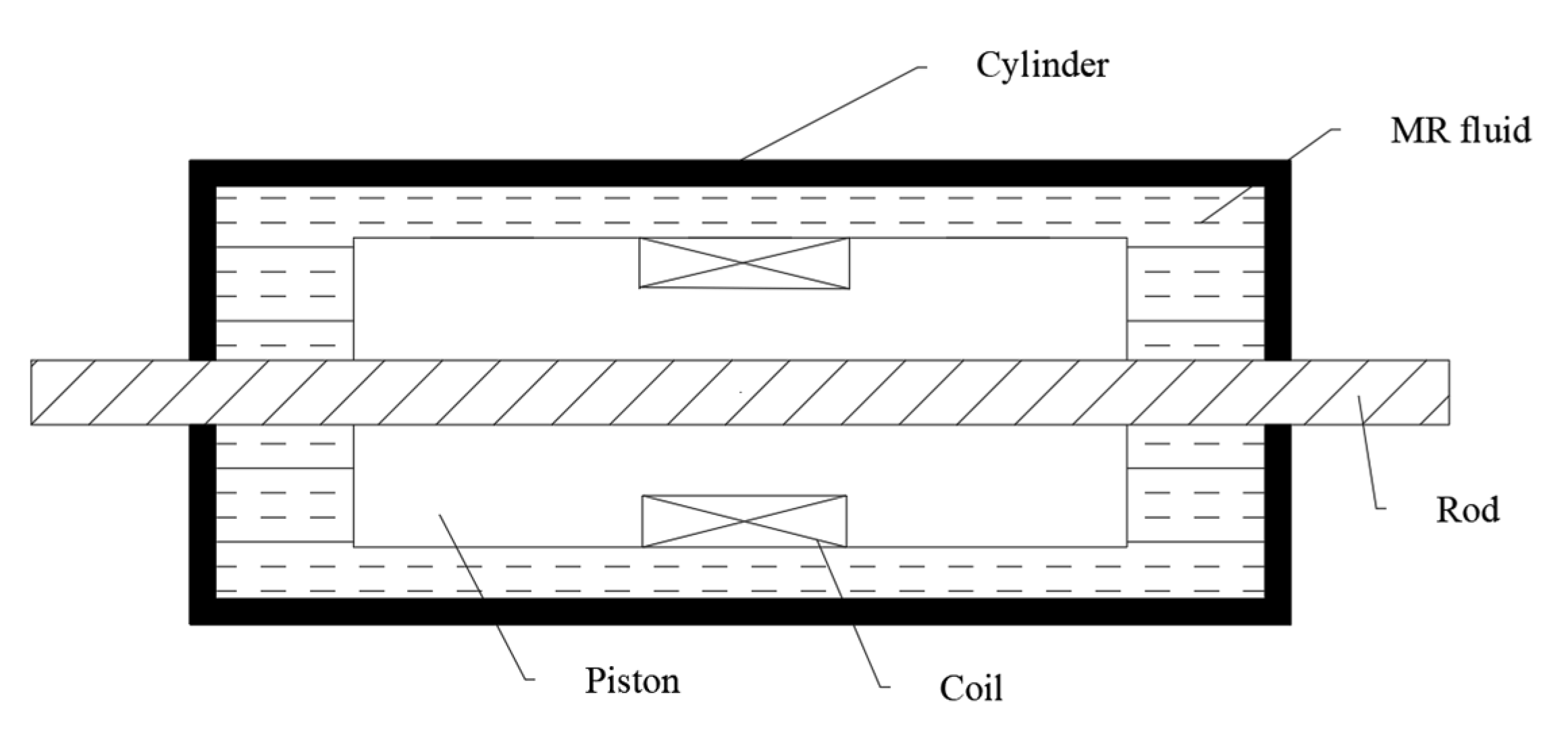
2. Mathematical Model of MR Damper
2.1. Jiles–Atherton Hysteresis Model
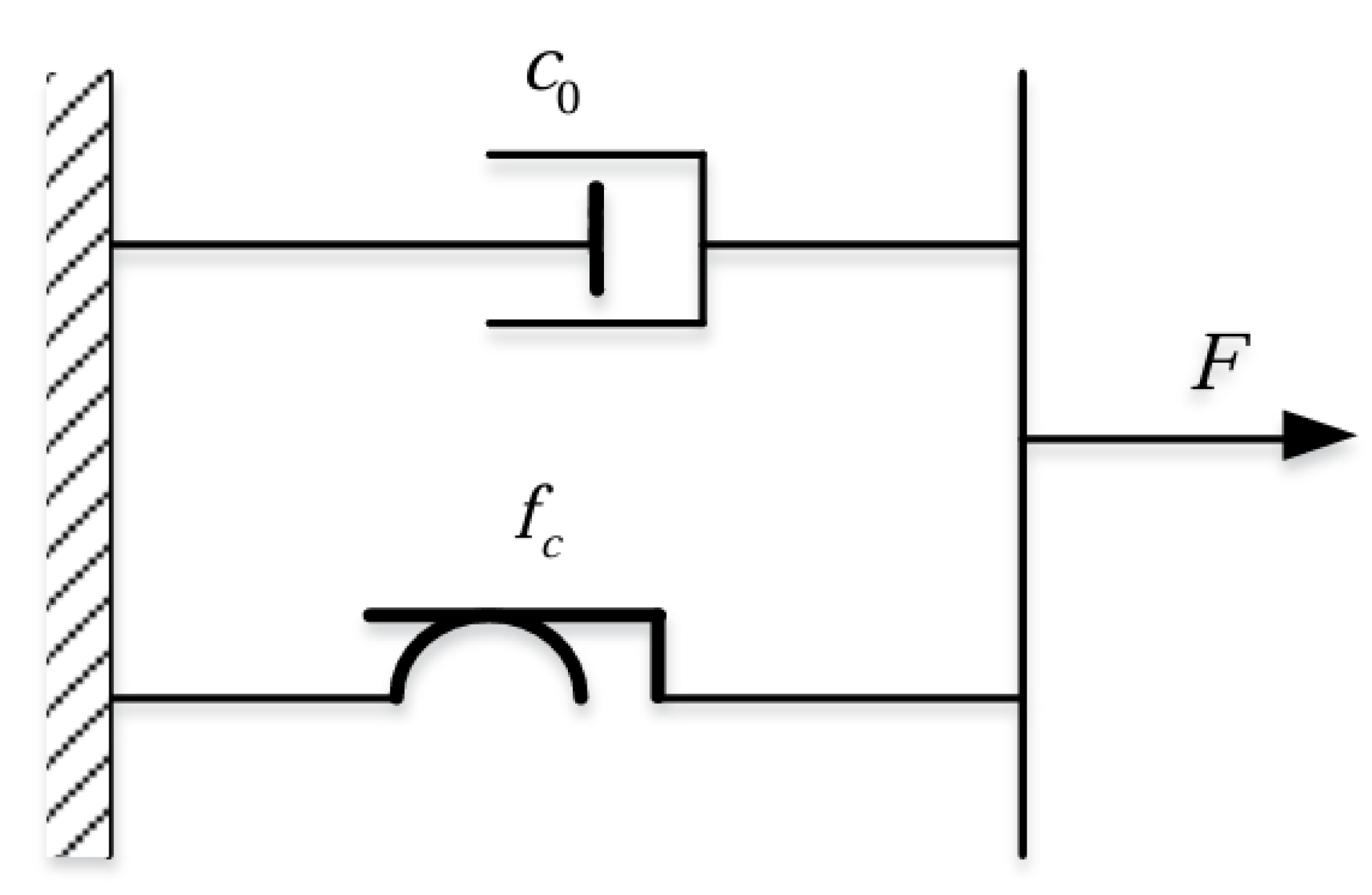
2.2. Bingham Model
3. Particle Swarm Optimization Algorithm
3.1. Classical Particle Swarm Optimization Algorithm
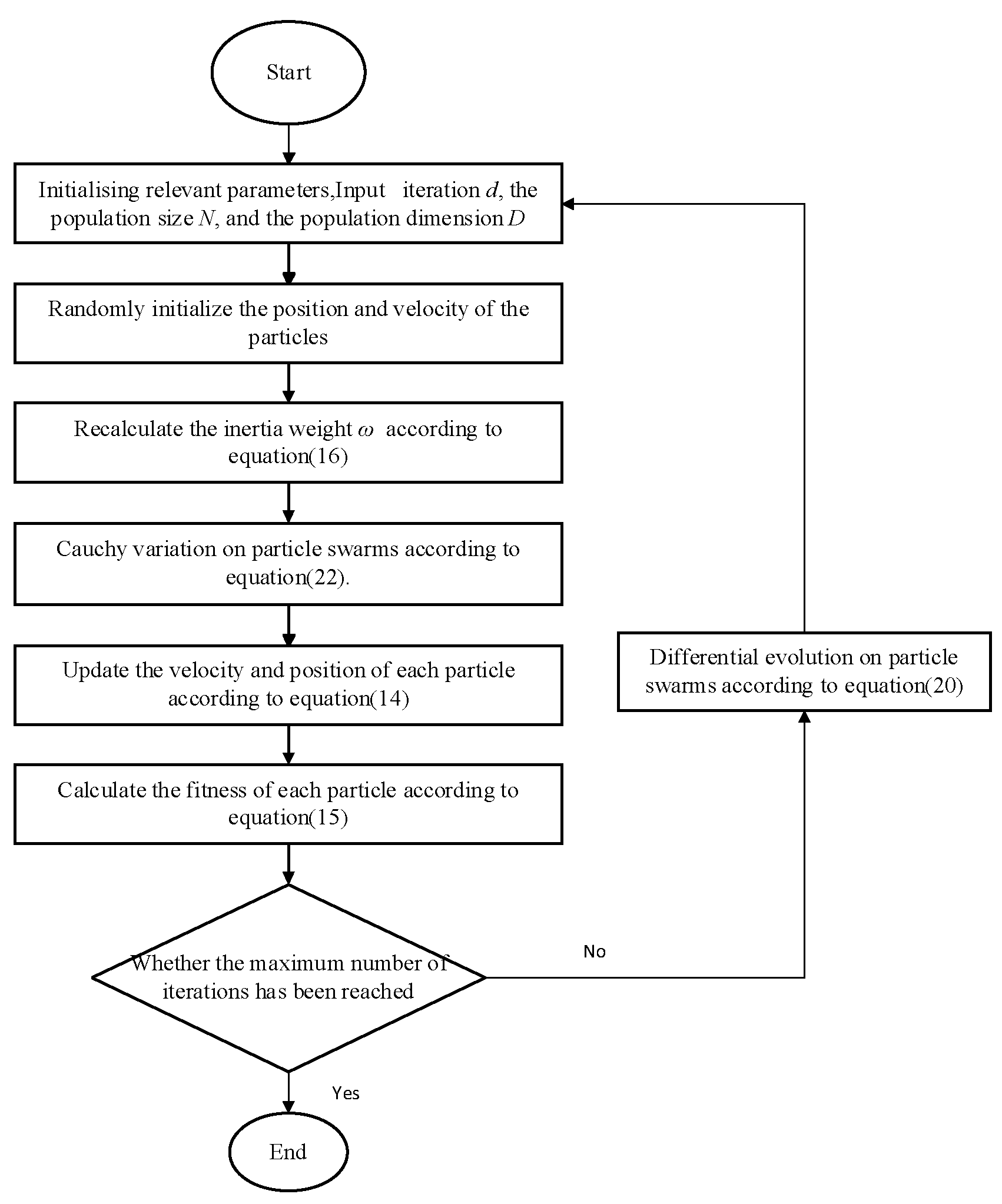
3.2. Improved Particle Swarm Optimization Algorithm
- (1)
- Weight Adaptation
- (2)
- Differential Evolution
- (a)
- Population Initialization
- (b)
- Mutation
- (c)
- Crossover
- (d)
- Selection
- (3)
- Cauchy Variation
4. Numerical Analysis
4.1. Algorithm Verification
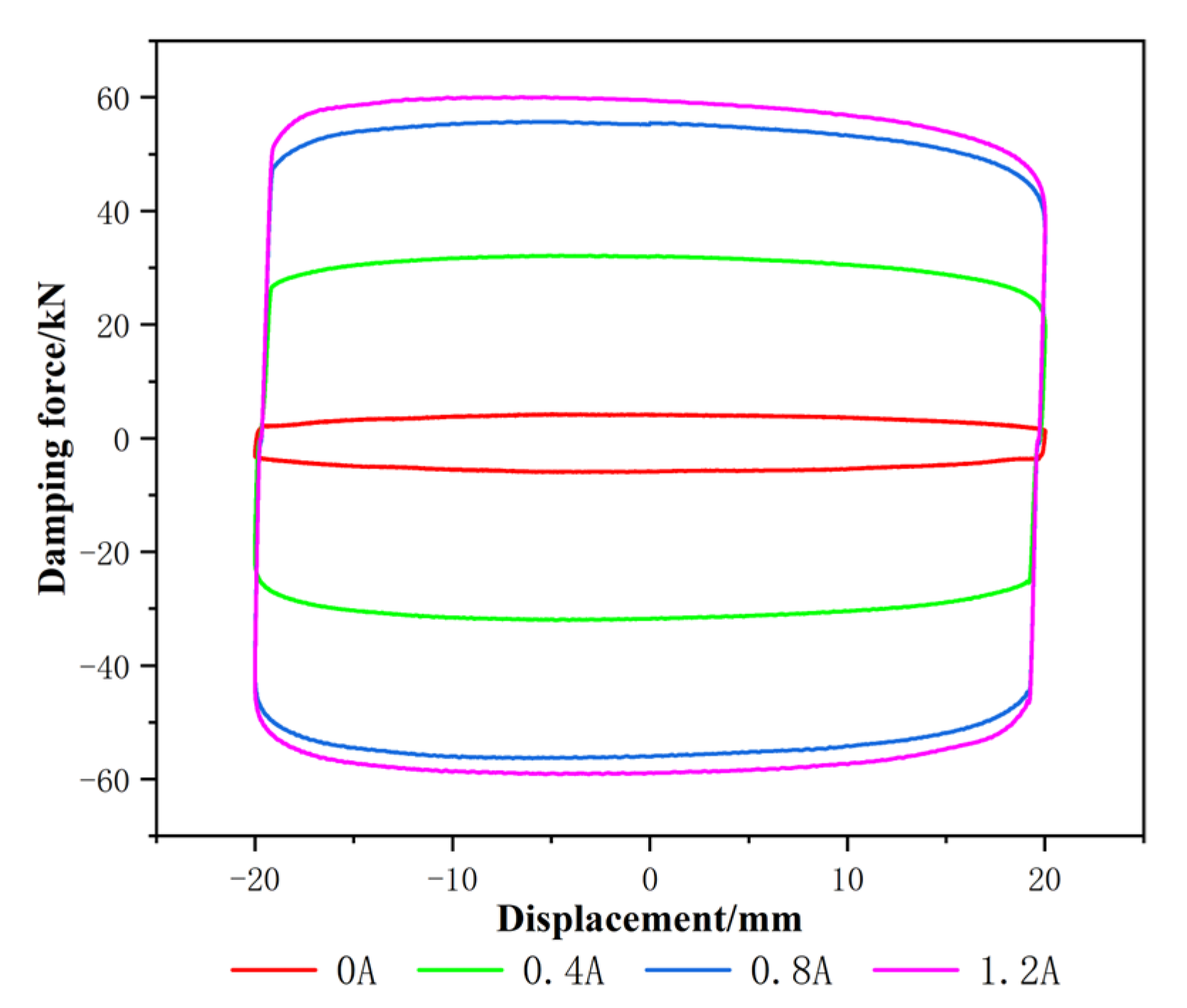
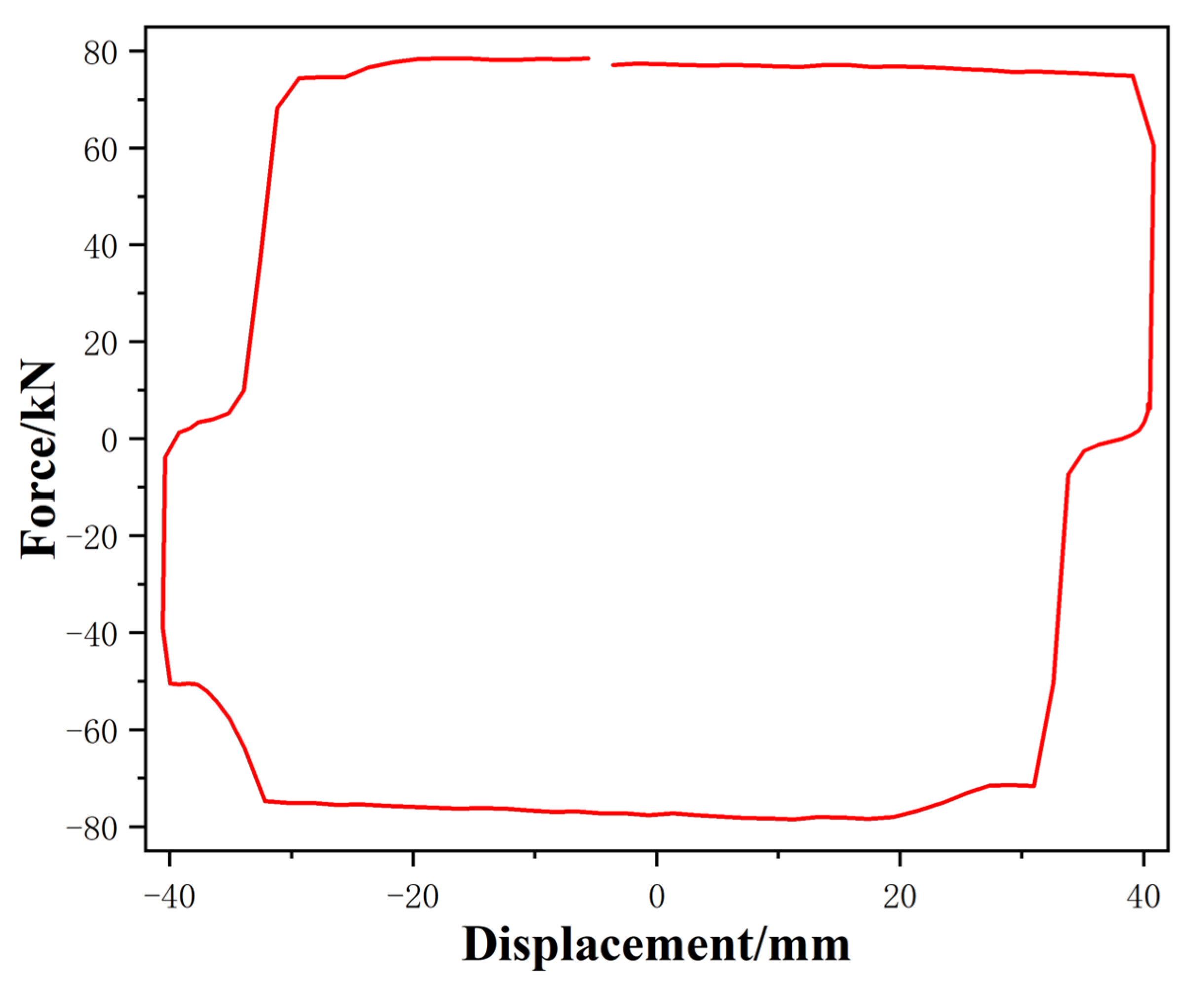
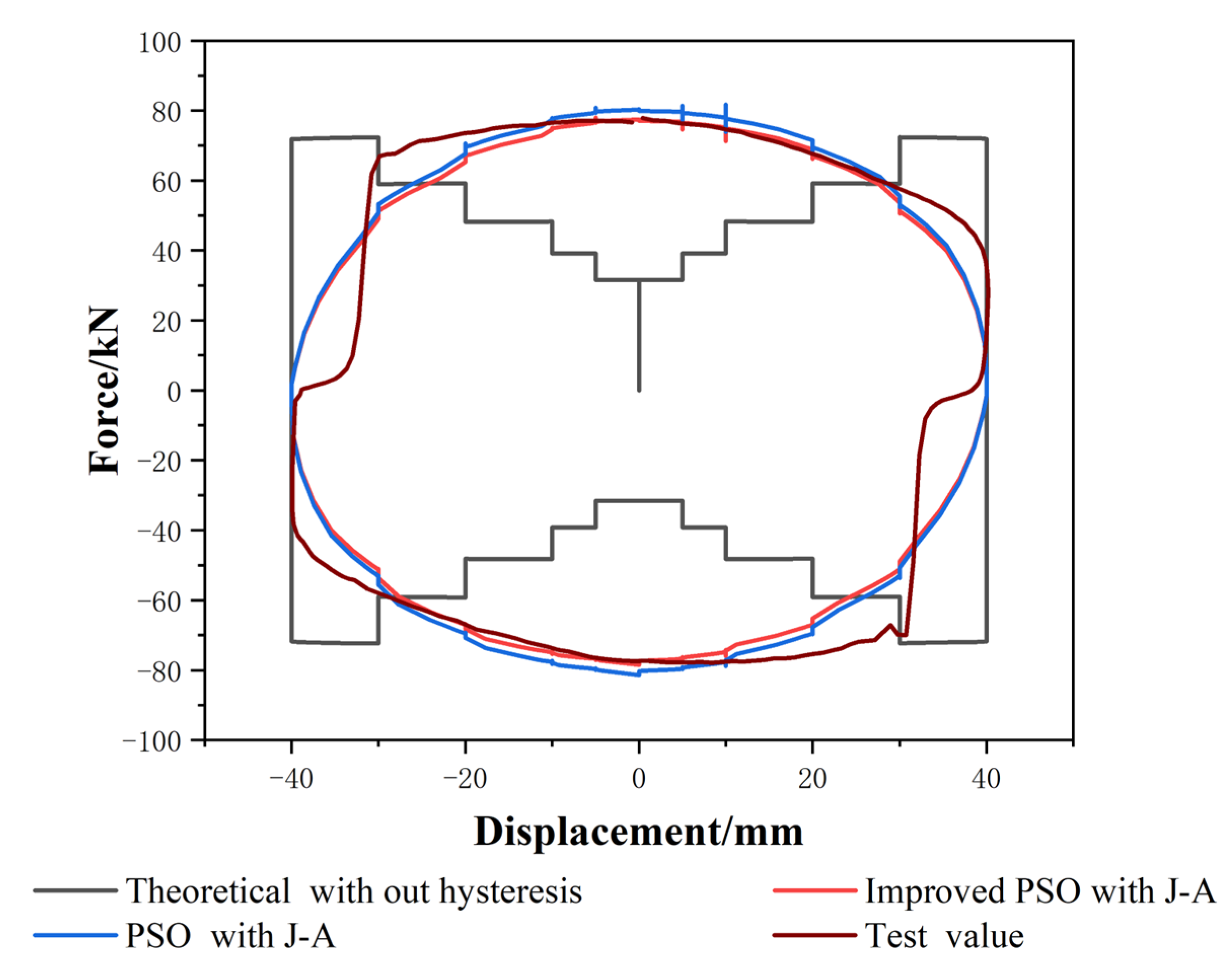
4.2. Experimental Comparison
4.3. Results and Discussions
5. Conclusions
- (1)
- The improved adaptive PSO which introduces differential evolution algorithm and Cauchy variation strategy on the basis of particle swarm effectively solves the problem that classical PSO falls easily into the local optimal solution; additionally, it solves the problem of the slow convergence of classical PSO, and improves the accuracy of identification.
- (2)
- The improved J-A model using the PSO can accurately describe the non-linear relationship between the magnetic induction and the current inside the MR damper, and can accurately predict the output force of MR dampers with magnetic hysteresis properties, providing a basis for the numerical analysis and practical engineering applications of MR dampers.
- (3)
- In this paper, the effect of hysteresis characteristics on the output damping force is most obvious at 0.5 Hz; however, when the displacement signal response is in the low-frequency band or high-frequency band greater than 1 Hz, there is a large gap between the simulation results and the experimental values, and this paper ignores the effect of the response frequency on the hysteresis characteristics, and at the same time hysteresis characteristics are not only reflected in the change of the magnetic field strength generated by the excitation coil, but also in the internal magnetic circuit of the MR damper. Hysteresis also needs to be modeled and analyzed, which is also the focus of subsequent research.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Du, X.X.; Zhang, Y.H.; Li, J.H.; Liao, C.R. Unsteady and hysteretic behavior of a magnetorheological fluid damper: Modeling, modification, and experimental verification. J. Intell. Mater. Syst. Struct. 2023, 34, 551–568. [Google Scholar] [CrossRef]
- Zhu, J.T.; Xu, Z.D.; Guo, Y.Q. Magnetoviscoelasticity parametric model of an MR elastomer vibration mitigation device. Smart Mater. Struct. 2012, 21, 075034. [Google Scholar] [CrossRef]
- Abdalaziz, M.; Sedaghati, R.; Vatandoost, H. Development of a new dynamic hysteresis model for magnetorheological dampers with annular-radial gaps considering fluid inertia and compressibility. J. Sound Vib. 2023, 561, 117826. [Google Scholar] [CrossRef]
- Wang, B.; Wang, W.J.; Li, Z.C. Sliding Mode Active Disturbance Rejection Control for Magnetorheological Impact Buffer System. Front. Mater. 2021, 8, 682215. [Google Scholar] [CrossRef]
- Aloisio, A.; Boggian, F.; Tomasi, R.; Zeng, K.N. Reliability-Based Assessment of LTF and CLT Shear Walls under In-Plane Seismic Loading Using a Modified Bouc-Wen Hysteresis Model. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2021, 7, 04021065. [Google Scholar] [CrossRef]
- Ahamed Rashid, M.M.; Ferdaus, M.M.; Yusuf, H.B.R. Modelling and performance evaluation of energy harvesting linear magnetorheological (MR) damper. J. Low Freq. Noise Vib. Act. Control 2017, 36, 177–192. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, Z.D.; Guo, Y.Q. Performance tests and microstructure-based sigmoid model for a three-coil magnetorheological damper. Struct. Control. Health Monit. 2021, 28, e2819. [Google Scholar] [CrossRef]
- Song, G.; Zhao, J.Q.; Zhou, X.Q.; de Abreu-García, J.A. Tracking control of a piezoceramic actuator with hysteresis compensation using inverse Preisach model. IEEE-ASME Trans. Mechatron. 2005, 10, 198–209. [Google Scholar] [CrossRef]
- Lacroix, L.M.; Gieraltowski, J. Magnetic hyperthermia in single-domain monodisperse FeCo nanoparticles: Evidences for Stoner-Wohlfarth behavior and large losses. J. Appl. Phys. 2009, 105, 023911. [Google Scholar] [CrossRef]
- Tannous, C.; Gieraltowski, J. The Stoner-Wohlfarth model of ferromagnetism. Eur. J. Phys. 2009, 30, 227. [Google Scholar] [CrossRef]
- Sadowski, N.; Sadowski, N.; Batistela, N.J.; Bastos, J.P.A.; Lajoie-Mazenc, M. An inverse Jiles-Atherton model to take into account hysteresis in time-stepping finite-element calculations. IEEE Trans. Magn. 2002, 38, 797–800. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, L.H.; Zhu, J.G. Core Loss Calculation Based on Finite-Element Method with Jiles-Atherton Dynamic Hysteresis Model. IEEE Trans. Magn. 2018, 54, 1300105. [Google Scholar] [CrossRef]
- Raghunathan, A.; Raghunathan, A.; Melikhov, Y.; Snyder, J.E.; Jiles, D.C. Generalized form of anhysteretic magnetization function for Jiles-Atherton theory of hysteresis. Appl. Phys. Lett. 2009, 95, 172510. [Google Scholar] [CrossRef]
- Duan, J.D.; Lei, Y.; Li, H. Research on Ferromagnetic Components J-A Model—A Review. In Proceedings of the 2018 International Conference on Power System Technology (POWERCON), Guangzhou, China, 6–9 November 2018; pp. 3288–3294. [Google Scholar]
- Zhu, R.; Fei, Q.G.; Jiang, D.; Marchesiello, S.; Anastasio, D. Identification of Nonlinear Stiffness and Damping Parameters Using a Hybrid Approach. AIAA J. 2021, 59, 4686–4695. [Google Scholar] [CrossRef]
- Leite, J.V.; Avila, S.L.; Batistela, N.J.; Carpes, W.P. Real coded genetic algorithm for Jiles-Atherton model parameters identification. IEEE Trans. Magn. 2004, 40, 888–891. [Google Scholar] [CrossRef]
- Trapanese, M. Identification of parameters of the Jiles-Atherton model by neural networks. J. Appl. Phys. 2011, 109, 07D355. [Google Scholar] [CrossRef]
- Ding, F.J.; Jia, X.D.; Hong, T.J.; Xu, Y.L. Flow Stress Prediction Model of 6061 Aluminum Alloy Sheet Based on GA-BP and PSO-BP Neural Networks. Rare Met. Mater. Eng. 2020, 49, 1840–1853. [Google Scholar]
- Chen, Z.G.; Yu, Y.; Wang, Y.X. Parameter Identification of Jiles-Atherton Model Based on Levy Whale Optimization Algorithm. IEEE Access 2022, 10, 66711–66721. [Google Scholar] [CrossRef]
- Wang, A.M.; Meng, J.J.; Xu, R.X.; Li, D.C. Parameter Identification and Linear Model of Giant Magnetostrictive Vibrator. Discret. Dyn. Nat. Soc. 2021, 2021, 6676911. [Google Scholar] [CrossRef]
- Ni, C.; Wang, D.Y.; Vinson, R.; Holmes, M. Automatic inspection machine for maize kernels based on deep convolutional neural networks. Biosyst. Eng. 2019, 178, 131–144. [Google Scholar] [CrossRef]
- Wu, Z.Q.; Hu, X.Y.; Ma, B.Y.; Hou, C.L. SOC estimation of lithium batteries based on RFF and GWO-PF. J. Metrol. 2022, 43, 8. [Google Scholar]
- Aggarwal, A.; Dimri, P.; Agarwal, A.; Bhatt, A. Self adaptive fruit fly algorithm for multiple workflow scheduling in cloud computing environment. Kybernetes 2020. ahead-of-print. [Google Scholar] [CrossRef]
- Deng, L.; Liu, S. A multi-strategy improved slime mould algorithm for global optimization and engineering design problems. Comput. Methods Appl. Mech. Eng. 2023, 404, 115764. [Google Scholar] [CrossRef]
- Wilson, P.R.; Ross, J.N.; Broen, A.D. Optimizing the Jiles-Atherton model of hysteresis by a genetic algorithm. IEEE Trans. Magn. 2001, 37, 989–993. [Google Scholar] [CrossRef]
- Guralnik, G.; Pehlevan, C. Effective potential for complex Langevin equations. Nucl. Phys. B 2009, 822, 349–366. [Google Scholar] [CrossRef]
- Xu, Z.D.; Shen, Y.P.; Guo, Y.Q. Semi-active control of structures incorporated with magnetorheological dampers using neural networks. Smart Mater. Struct. 2003, 12, 80–87. [Google Scholar] [CrossRef]
- Li, W.H.; Du, H. Design and experimental evaluation of a magnetorheological brake. Int. J. Adv. Manuf. Technol. 2003, 21, 508–515. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, Z.D.; Xu, Y.W.; Guo, Y.Q. Analysis on influence of the magnetorheological fluid microstructure on the mechanical properties of magnetorheological dampers. Smart Mater. Struct. 2020, 29, 115025. [Google Scholar] [CrossRef]
- Sun, C.L.; Xu, Z.D.; Dai, J. Testing and Mechanical Modelling of Hybrid Coated Ferromagnetic Particle-Based Magnetorheological Fluids. J. Southeast Univ. Nat. Sci. Ed. 2019, 49, 328–333. [Google Scholar]
- Li, C.H.; Liu, Y.; Zhou, A.M.; Kang, L.S. A fast particle swarm optimization algorithm with cauchy mutation and natural selection strategy. In Advances in Computation and Intelligence, Second International Symposium, ISICA 2007, Wuhan, China, 21–23 September 2007, Proceedings; Kang, L., Liu, Y., Zeng, S., Kang, L., Liu, Y., Zeng, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 334–343. [Google Scholar]
- Janakiraman, S.; Priy, M.D. Hybrid grey wolf and improved particle swarm optimization with adaptive intertial weight-based multi-dimensional learning strategy for load balancing in cloud environments. Sustain. Comput. Inform. Syst. 2023, 38, 100875. [Google Scholar] [CrossRef]
- Qin, A.K.; Huang, V.L.; Suganthan, P.N. Differential Evolution Algorithm with Strategy Adaptation for Global Numerical Optimization. IEEE Trans. Evol. Comput. 2009, 13, 398–417. [Google Scholar] [CrossRef]
- Yang, J.H.; Zhao, X.L.; Mei, J.J.; Wang, S. Total variation and high-order total variation adaptive model for restoring blurred images with Cauchy noise. Comput. Math. Appl. 2019, 77, 1255–1272. [Google Scholar] [CrossRef]
- Chwastek, K. Modelling offset minor hysteresis loops with the modified Jiles-Atherton description. J. Phys. D Appl. Physics 2009, 42, 165002. [Google Scholar] [CrossRef]


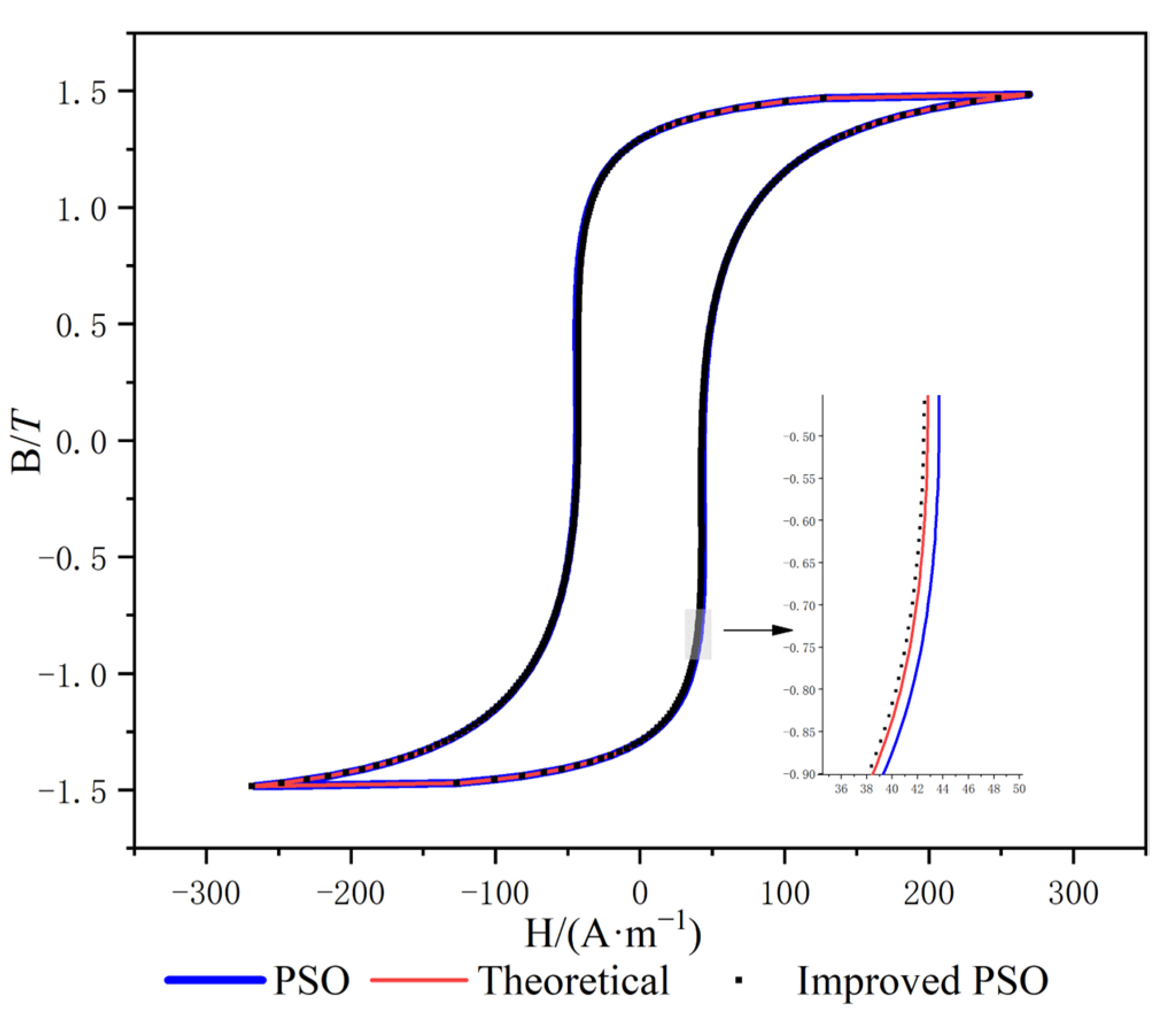

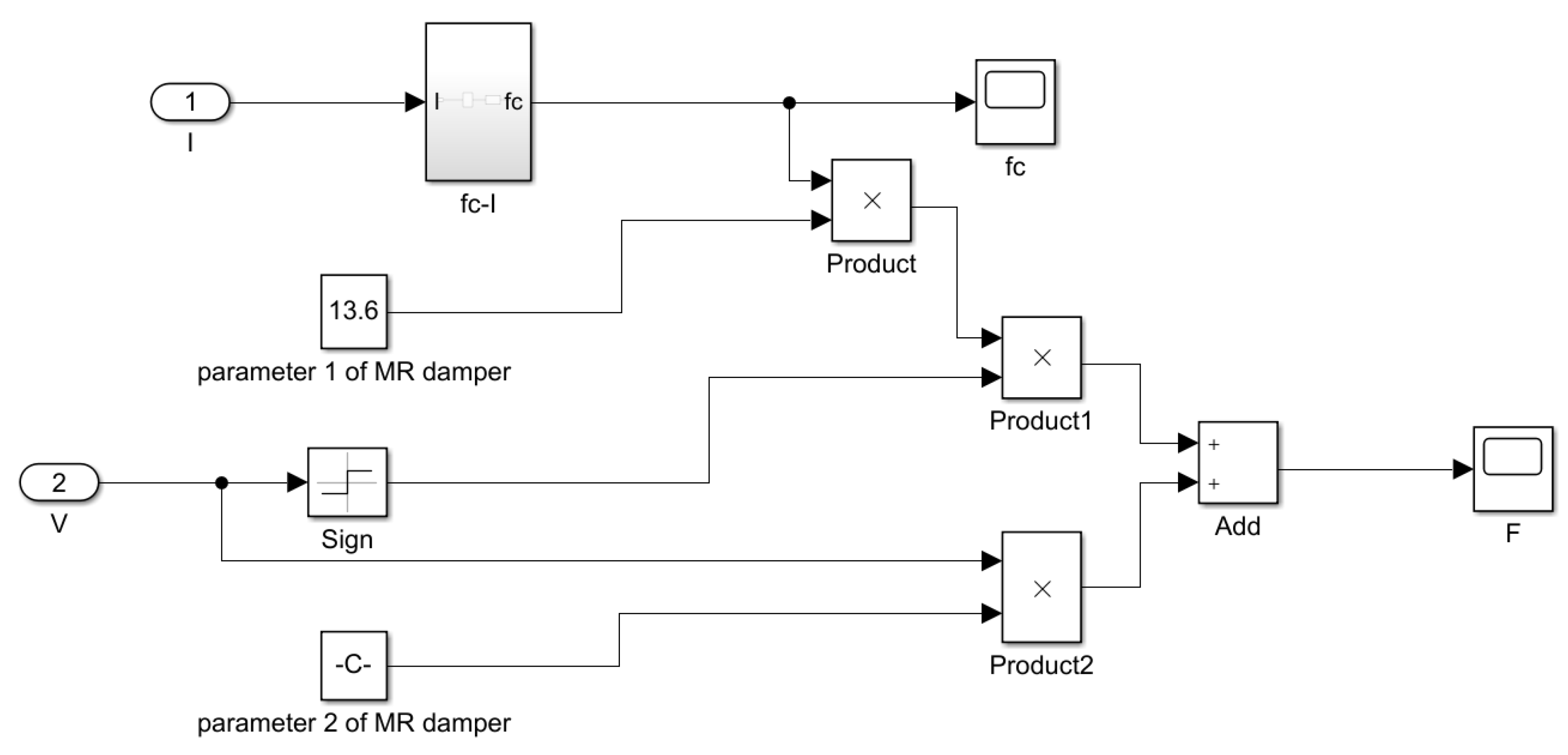
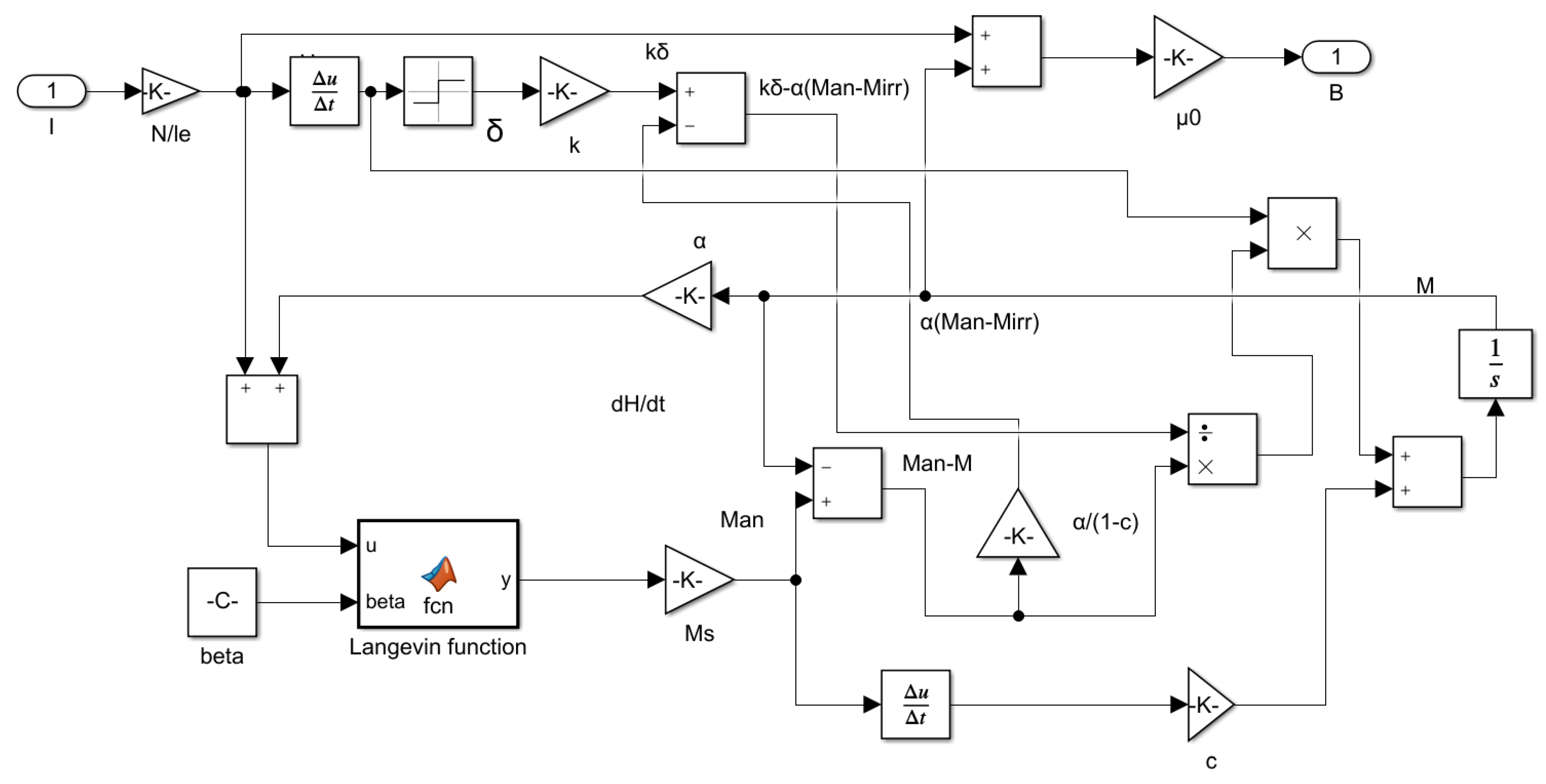

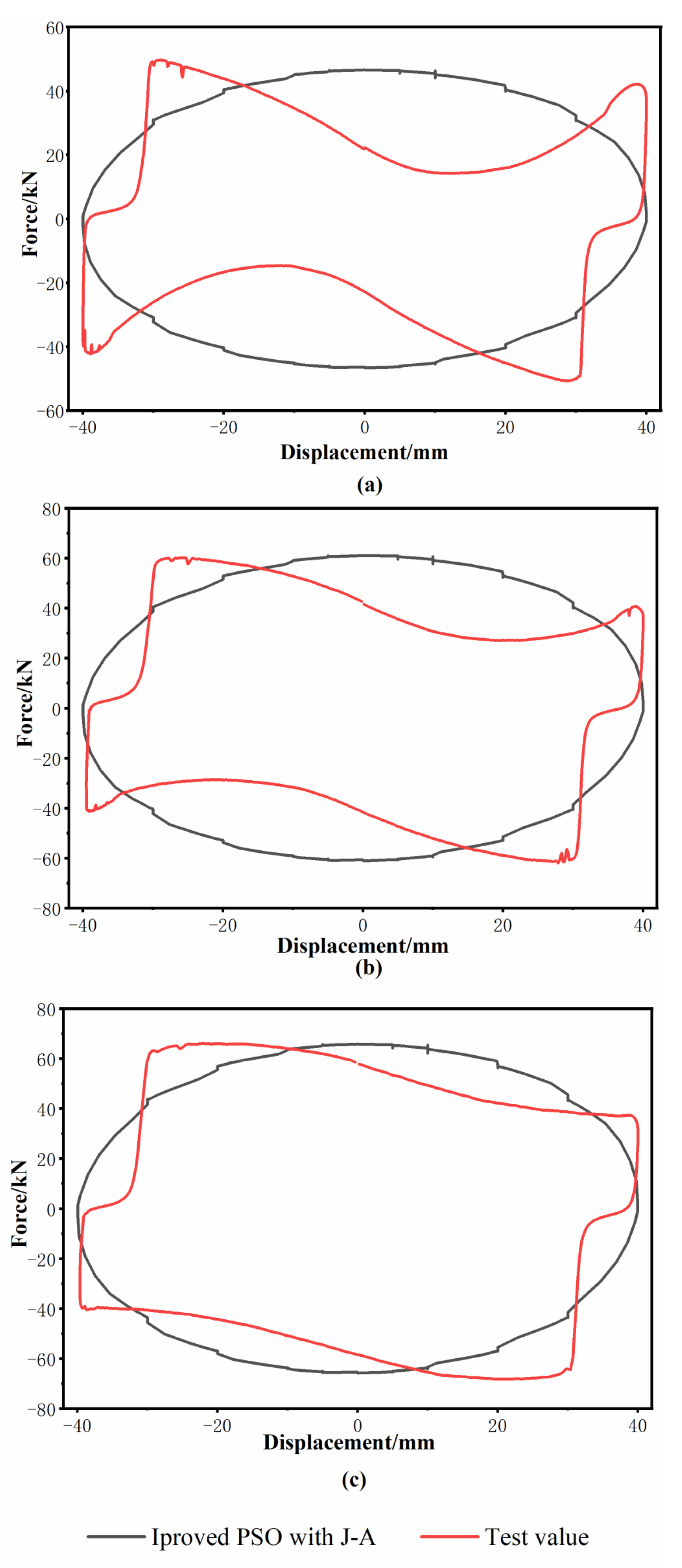
| Parameter | Theoretical Value | PSO | Improved PSO |
|---|---|---|---|
| k (A/m) | 66.6 | 70.96 | 66.51 |
| (A/m) | 25.3 | 20.03 | 25.32 |
| c (A/m) | 0.20 | 0.25 | 0.19 |
| Ms | 1.3 × 106 | 1.27 × 106 | 1.31 × 106 |
| 8.43 × 10−5 | 7.61 × 10−5 | 8.92 × 10−5 |
| Algorithm | k (A/m) | (A/m) | c (A/m) | Ms | ||
|---|---|---|---|---|---|---|
| Absolute Error | PSO | 4.36 | 5.27 | 0.05 | 3 × 104 | 8.2 × 10−6 |
| Improved PSO | 0.09 | 0.02 | 0.01 | 10,000 | 4.9 × 10−6 | |
| Relative Error (%) | PSO | 6.54 | 20.55 | 25 | 2.3 | 9.7 |
| Improved PSO | 0.13 | 0.07 | 5 | 0.7 | 5.8 |
| Cladding Thickness | Volume Fraction | Zero-Field Viscosity | |
|---|---|---|---|
| 1.5 | 0.015 | 35~45 | 2~2.5 |
| Displacement |x|(mm) | ≤5 | 5 < x ≤ 10 | 10 < x ≤ 20 | 20 < x ≤ 30 | 30 < x ≤ 40 | >40 |
|---|---|---|---|---|---|---|
| Current (A) | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.-Q.; Li, M.; Yang, Y.; Xu, Z.-D.; Xie, W.-H. A Particle-Swarm-Optimization-Algorithm-Improved Jiles–Atherton Model for Magnetorheological Dampers Considering Magnetic Hysteresis Characteristics. Information 2024, 15, 101. https://doi.org/10.3390/info15020101
Guo Y-Q, Li M, Yang Y, Xu Z-D, Xie W-H. A Particle-Swarm-Optimization-Algorithm-Improved Jiles–Atherton Model for Magnetorheological Dampers Considering Magnetic Hysteresis Characteristics. Information. 2024; 15(2):101. https://doi.org/10.3390/info15020101
Chicago/Turabian StyleGuo, Ying-Qing, Meng Li, Yang Yang, Zhao-Dong Xu, and Wen-Han Xie. 2024. "A Particle-Swarm-Optimization-Algorithm-Improved Jiles–Atherton Model for Magnetorheological Dampers Considering Magnetic Hysteresis Characteristics" Information 15, no. 2: 101. https://doi.org/10.3390/info15020101
APA StyleGuo, Y.-Q., Li, M., Yang, Y., Xu, Z.-D., & Xie, W.-H. (2024). A Particle-Swarm-Optimization-Algorithm-Improved Jiles–Atherton Model for Magnetorheological Dampers Considering Magnetic Hysteresis Characteristics. Information, 15(2), 101. https://doi.org/10.3390/info15020101








