Graph-Based Semi-Supervised Learning with Bipartite Graph for Large-Scale Data and Prediction of Unseen Data
Abstract
1. Introduction
- Many of them are not able to predict the labels of unseen data. Consequently, due to the continuous updating and creation of data in the real world through the internet and social networks, these methods are difficult to apply to real-world problems.
- The use of an affinity matrix (where n is the number of samples) makes applying these methods to large databases computationally and memory-intensive.
- Most of the existing models do not work based on weighted samples, and all samples have the same weight.
- A novel model based on graph-based semi-supervised learning is presented that uses anchor samples and can work on large-scale datasets with reasonable computational complexity.
- By leveraging principal component analysis (PCA) for dimensionality reduction during data preprocessing, the proposed model efficiently extracts key features relevant to future prediction while simultaneously reducing computational runtime.
- Similar to R-FME, the presented model can effectively handle data sampled from nonlinear manifold and provides a mapping for new data points to anticipate the labels of unseen data.
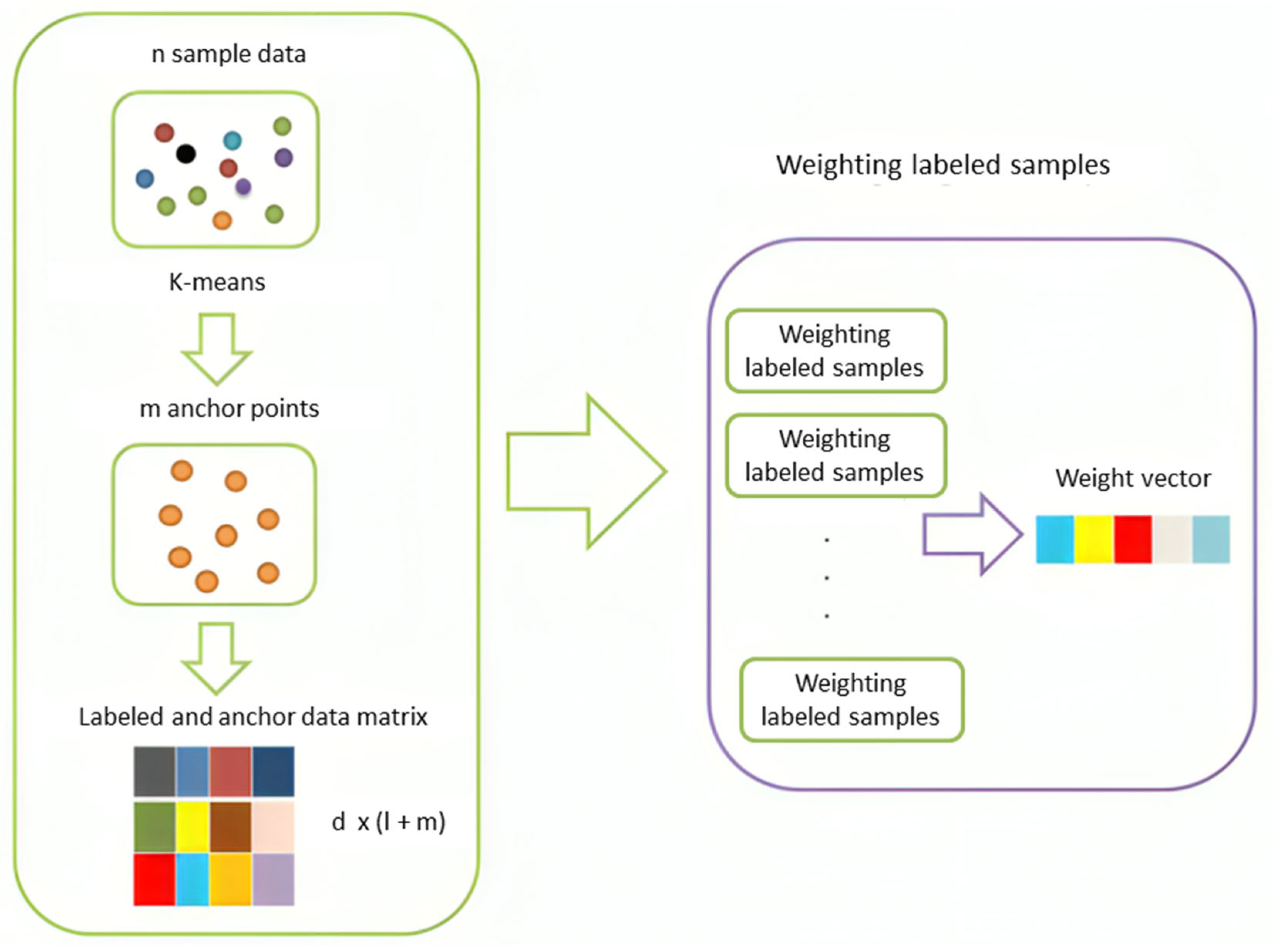
- Using anchor points, we propose a weighting scheme that calculates weights for the nodes according to their topological location.
- By weighting labeled samples, our model can reduce the effect of outliers and emphasizes samples close to decision borders, which enhance the performance of baseline methods.
2. Related Work
3. Background
3.1. Preliminaries
3.2. Review of WS3C Model
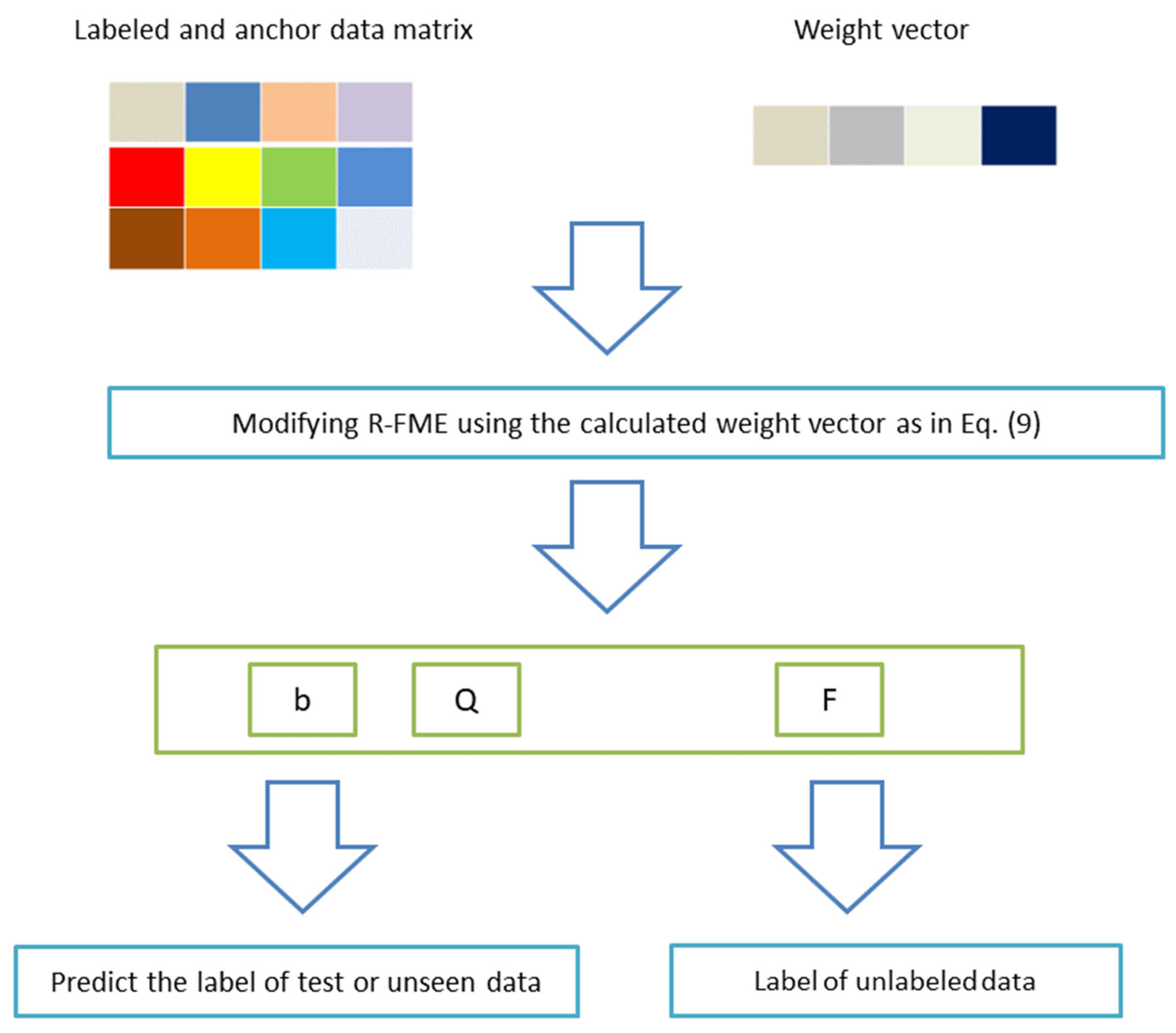
3.3. Review of R-FME
4. Proposed Model
4.1. Weighting Labeled Samples
4.2. Proposed Algorithm
5. Experiment
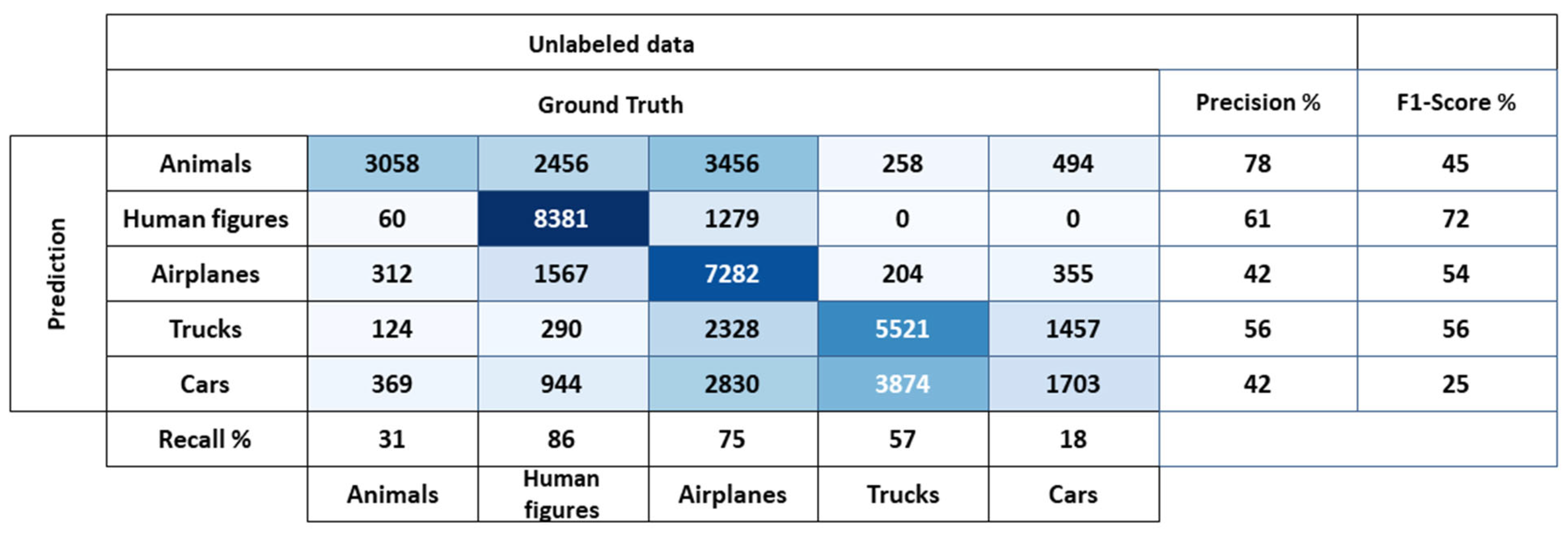
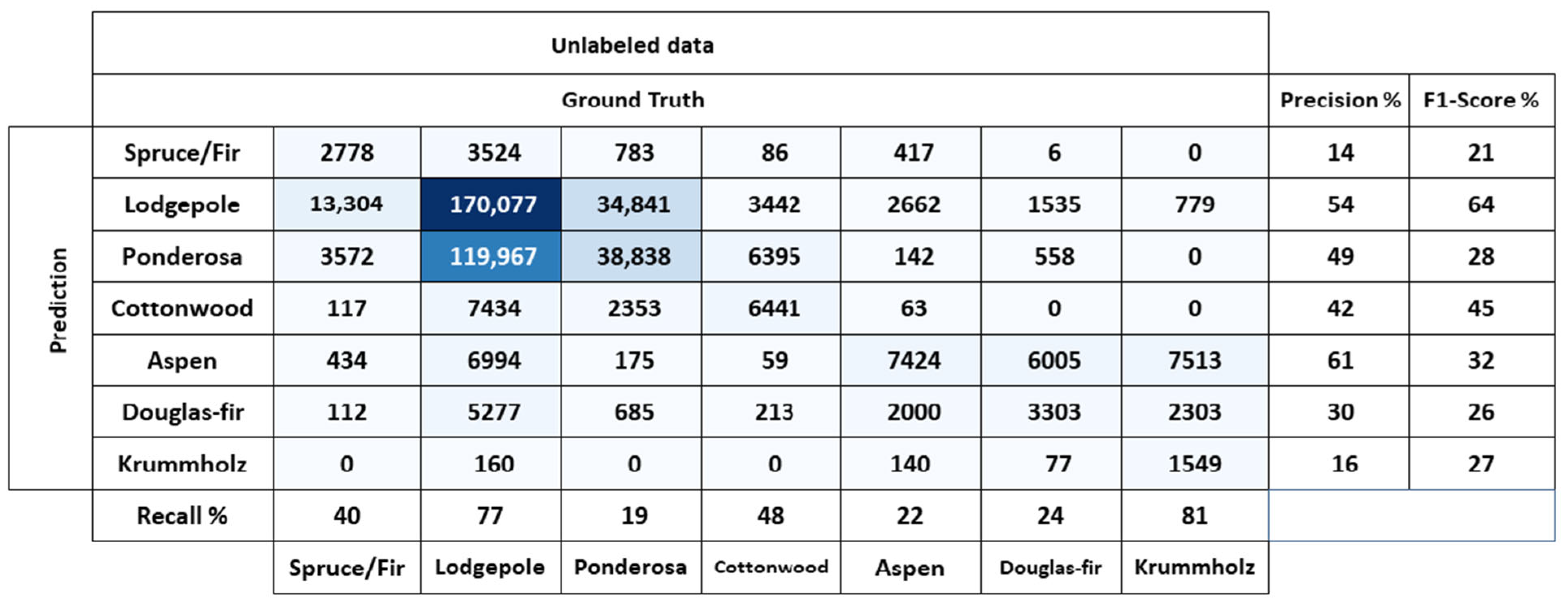
5.1. Datasets

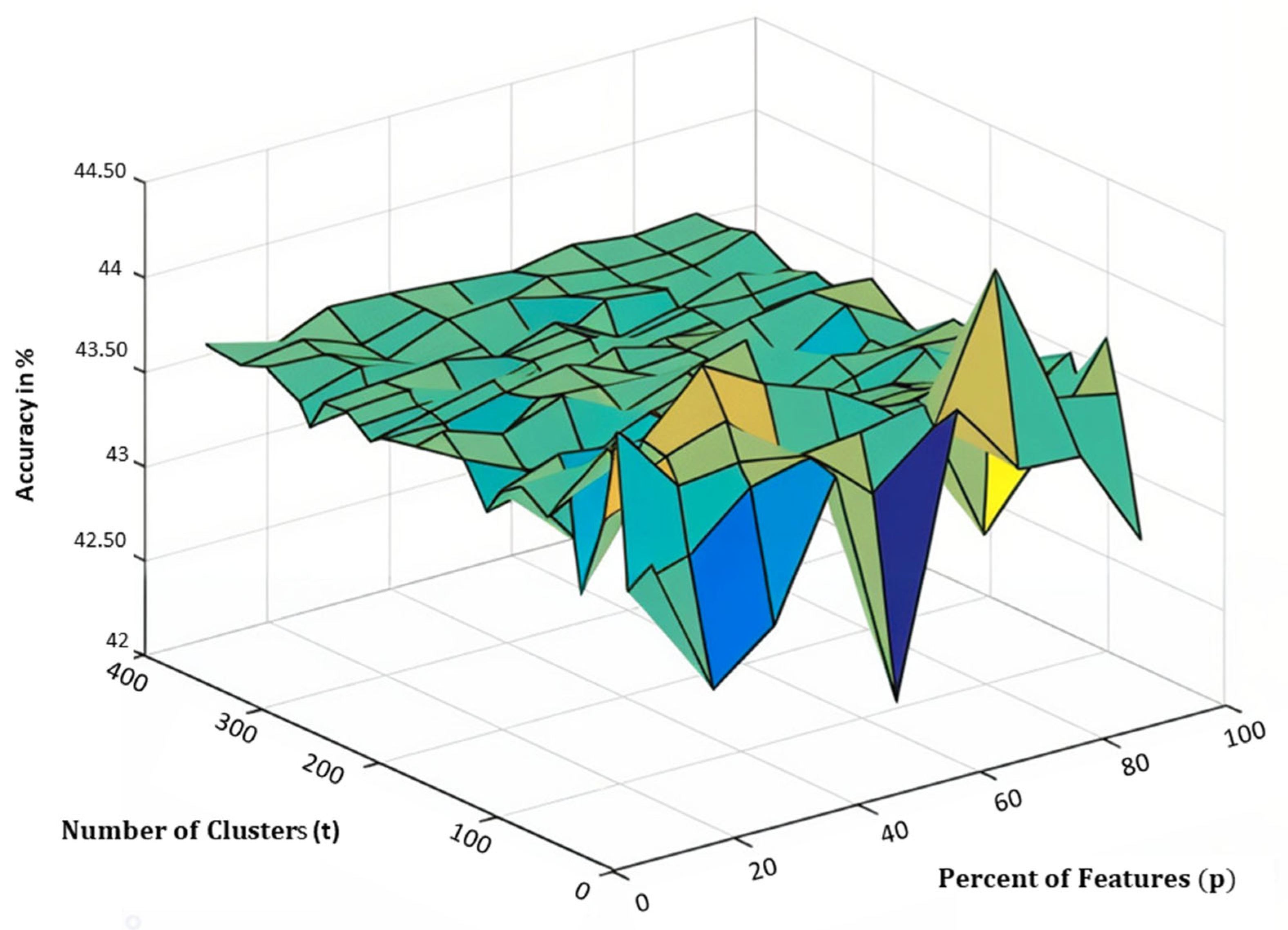
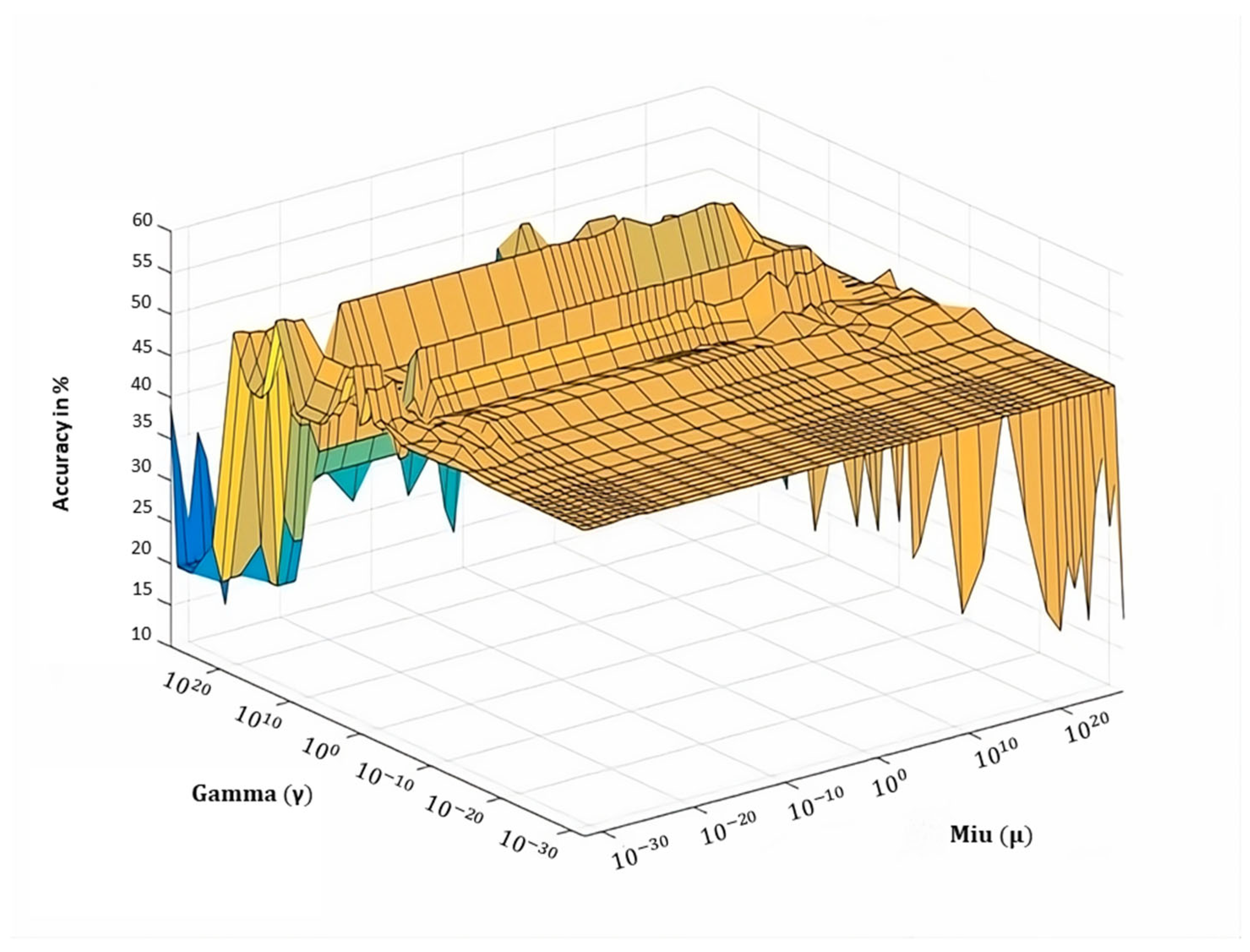
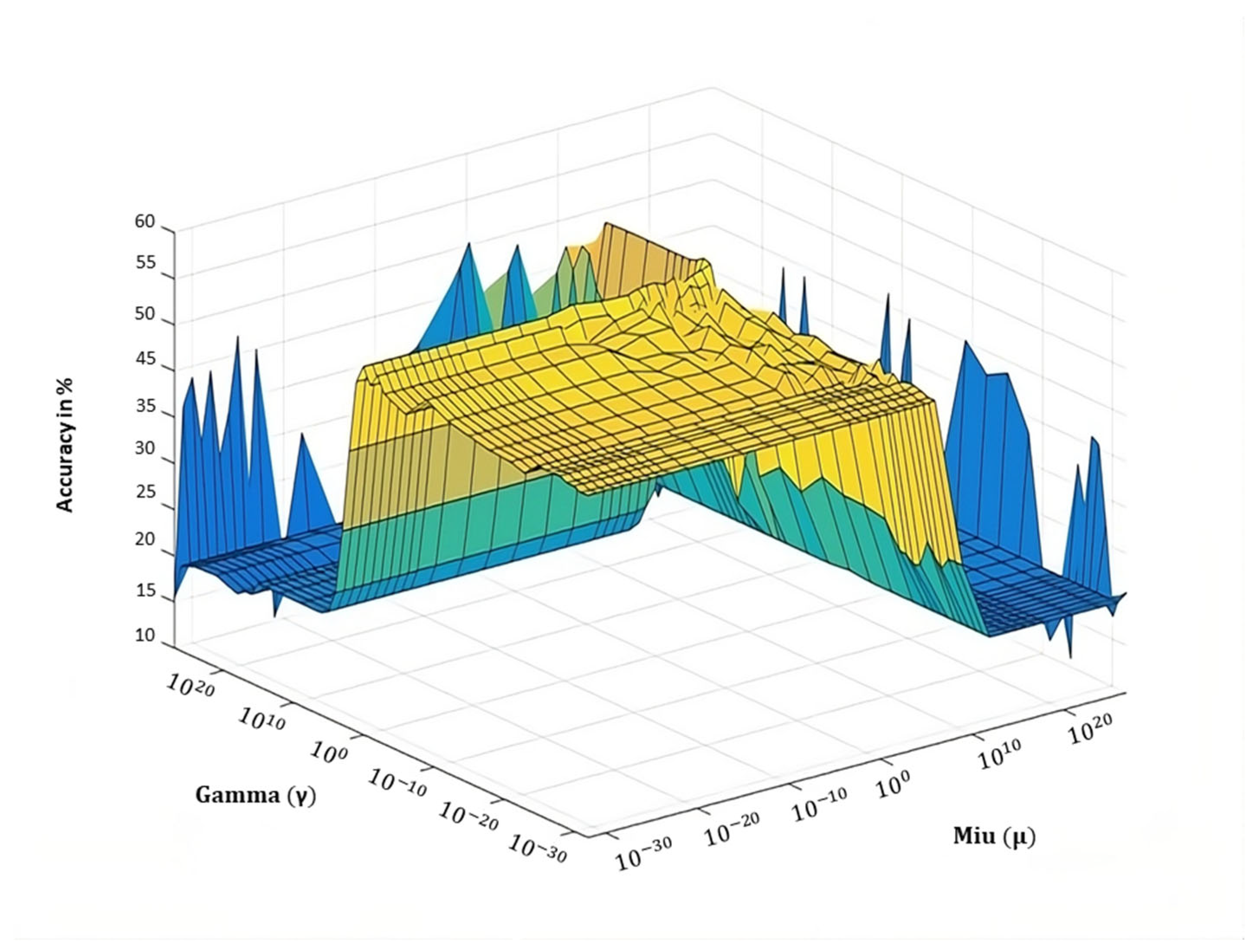
5.2. Parameter Tuning
5.3. Comparison with Other Methods
6. Conclusions
6.1. Scalability
6.2. Weighted Node Importance
6.3. Unseen Data Prediction
6.4. Performance
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, F.; Nie, F.; Wang, R.; Li, X.; Jia, W. Fast semisupervised learning with bipartite graph for large-scale data. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 626–638. [Google Scholar] [CrossRef] [PubMed]
- Cheng, L.; Pan, S.J. Semi-supervised domain adaptation on manifolds. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 2240–2249. [Google Scholar] [CrossRef] [PubMed]
- Xiang, S.; Nie, F.; Zhang, C. Semi-supervised classification via local spline regression. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2039–2053. [Google Scholar] [CrossRef]
- Joachims, T. Transductive inference for text classification using support vector machines. In Proceedings of the International Conference on Machine Learning (ICML), Bled, Slovenia, 27–30 June 1999. [Google Scholar]
- Blum, A.; Mitchell, T. Combining labeled and unlabeled data with co-training. In Proceedings of the Eleventh Annual Conference on Computational Learning Theory, Madison, WI, USA, 24–26 July 1998. [Google Scholar]
- Nie, F.; Xiang, S.; Liu, Y.; Zhang, C. A general graph-based semi-supervised learning with novel class discovery. Neural Comput. Appl. 2010, 19, 549–555. [Google Scholar] [CrossRef]
- Nie, F.; Shi, S.; Li, X. Semi-supervised learning with auto-weighting feature and adaptive graph. IEEE Trans. Knowl. Data Eng. 2019, 32, 1167–1178. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, L.; Wang, R.; Nie, F.; Li, X. Semi-supervised learning via bipartite graph construction with adaptive neighbors. IEEE Trans. Knowl. Data Eng. 2022, 35, 5257–5268. [Google Scholar] [CrossRef]
- Ziraki, N.; Dornaika, F.; Bosaghzadeh, A. Multiple-view flexible semi-supervised classification through consistent graph construction and label propagation. Neural Netw. 2022, 146, 174–180. [Google Scholar] [CrossRef] [PubMed]
- Song, Z.; Yang, X.; Xu, Z.; King, I. Graph-based semi-supervised learning: A comprehensive review. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 8174–8194. [Google Scholar] [CrossRef]
- Nie, F.; Xu, D.; Tsang, I.W.-H.; Zhang, C. Flexible manifold embedding: A framework for semi-supervised and unsupervised dimension reduction. IEEE Trans. Image Process. 2010, 19, 1921–1932. [Google Scholar] [PubMed]
- Li, Y.; Nie, F.; Huang, H.; Huang, J. Large-scale multi-view spectral clustering via bipartite graph. In Proceedings of the AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Qiu, S.; Nie, F.; Xu, X.; Qing, C.; Xu, D. Accelerating flexible manifold embedding for scalable semi-supervised learning. IEEE Trans. Circuits Syst. Video Technol. 2018, 29, 2786–2795. [Google Scholar] [CrossRef]
- Li, L.; He, H. Bipartite graph based multi-view clustering. IEEE Trans. Knowl. Data Eng. 2020, 34, 3111–3125. [Google Scholar] [CrossRef]
- Aromal, M.; Rasool, A.; Dubey, A.; Roy, B. Optimized Weighted Samples Based Semi-supervised Learning. In Proceedings of the 2021 Second International Conference on Electronics and Sustainable Communication Systems (ICESC), Coimbatore, India, 4–6 August 2021. [Google Scholar]
- Chen, X.; Yu, G.; Tan, Q.; Wang, J. Weighted samples based semi-supervised classification. Appl. Soft Comput. 2019, 79, 46–58. [Google Scholar] [CrossRef]
- Zhu, X.; Ghahramani, Z.; Lafferty, J.D. Semi-supervised learning using gaussian fields and harmonic functions. In Proceedings of the 20th International Conference on Machine Learning (ICML-03), Washington, DC, USA, 21–24 August 2003. [Google Scholar]
- Zhou, D.; Bousquet, O.; Lal, T.; Weston, J.; Schölkopf, B. Learning with local and global consistency. Adv. Neural Inf. Process. Syst. 2003, 16. [Google Scholar]
- Nie, F.; Cai, G.; Li, X. Multi-view clustering and semi-supervised classification with adaptive neighbours. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Wang, H.; Yang, Y.; Liu, B. GMC: Graph-based multi-view clustering. IEEE Trans. Knowl. Data Eng. 2019, 32, 1116–1129. [Google Scholar] [CrossRef]
- Yang, X.; Yu, W.; Wang, R.; Zhang, G.; Nie, F. Fast spectral clustering learning with hierarchical bipartite graph for large-scale data. Pattern Recognit. Lett. 2020, 130, 345–352. [Google Scholar] [CrossRef]
- Liu, W.; He, J.; Chang, S.-F. Large graph construction for scalable semi-supervised learning. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Wang, M.; Fu, W.; Hao, S.; Tao, D.; Wu, X. Scalable semi-supervised learning by efficient anchor graph regularization. IEEE Trans. Knowl. Data Eng. 2016, 28, 1864–1877. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, L.; Chan, R.; Zeng, T. Large-scale semi-supervised learning via graph structure learning over high-dense points. arXiv 2019, arXiv:1912.02233. [Google Scholar]
- Bahrami, S.; Dornaika, F.; Bosaghzadeh, A. Joint auto-weighted graph fusion and scalable semi-supervised learning. Inf. Fusion 2021, 66, 213–228. [Google Scholar] [CrossRef]
- Chen, D.; Lin, Y.; Zhao, G.; Ren, X.; Li, P.; Zhou, J.; Sun, X. Topology-imbalance learning for semi-supervised node classification. Adv. Neural Inf. Process. Syst. 2021, 34, 29885–29897. [Google Scholar]
- Sun, Q.; Li, J.; Yuan, H.; Fu, X.; Peng, H.; Ji, C.; Li, Q.; Yu, P.S. Position-aware structure learning for graph topology-imbalance by relieving under-reaching and over-squashing. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, Atlanta, GA, USA, 17–22 October 2022. [Google Scholar]
- Kim, K.-H.; Choi, S. Label propagation through minimax paths for scalable semi-supervised learning. Pattern Recognit. Lett. 2014, 45, 17–25. [Google Scholar] [CrossRef]
- Zhang, Y.-M.; Huang, K.; Geng, G.-G.; Liu, C.-L. MTC: A fast and robust graph-based transductive learning method. IEEE Trans. Neural Netw. Learn. Syst. 2014, 26, 1979–1991. [Google Scholar] [CrossRef] [PubMed]
- Sindhwani, V.; Niyogi, P.; Belkin, M.; Keerthi, S. Linear manifold regularization for large scale semi-supervised learning. In Proceedings of the 22nd ICML Workshop on Learning with Partially Classified Training Data, Bonn, Germany, 7–11 August 2005. [Google Scholar]
- Chandler, B.; Mingolla, E. Mitigation of Effects of Occlusion on Object Recognition with Deep Neural Networks through Low-Level Image Completion. Comput. Intell. Neurosci. 2016, 2016, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Pace, R.K.; Barry, R. Sparse spatial autoregressions. Stat. Probab. Lett. 1997, 33, 291–297. [Google Scholar] [CrossRef]



| Symbol | Description |
|---|---|
| n | Number of samples |
| d | Dimensionality of samples |
| Number of labeled samples | |
| Number of labeled samples per class | |
| u | Number of unlabeled samples |
| Number of anchor points | |
| Number of classes | |
| Percent of features | |
| Number of clusters | |
| r | Number of iterations |
| Balance parameters | |
| Data matrix | |
| Binary label matrix | |
| Probability matrix of samples belonging to each label | |
| Matrix of anchors | |
| Similarity matrix of data | |
| Probability matrix of sample belonging to same cluster | |
| Similarity matrix of anchors | |
| Similarity matrix of data with anchors | |
| Laplacian matrix of anchor graph | |
| Diagonal matrix | |
| Projection matrix | |
| Affinity matrix of labels and anchors | |
| Bias vector | |
| Diagonal matrix for weights of labeled data |
| Method Name | Description |
|---|---|
| GSSL | Graph-Based Semi-Supervise Learning |
| LGC [18] | Local and Global Consistency |
| FME [11] | Flexible Manifold Embedding |
| F-FME [13] | Fast Flexible Manifold Embedding |
| R-FME [13] | Reduced Flexible Manifold Embedding |
| WS3C [16] | Weighted Sample-Based Semi-Supervised Classification |
| AGR [22] | Anchor Graph Regularization |
| EAGR [23] | Efficient Anchor Graph Regularization |
| MMLP [28] | Minimax Label Propagation |
| MTC [29] | Minimum Tree Cut |
| 1NN | 1-Nearest Neighbor Classifier |
| LapRLS/L [30] | Laplacian Regularized Least Square |
Input:
|
|
| Dataset | Number of Samples | Number of Features | Number of Features after PCA |
|---|---|---|---|
| Norb | 48,600 | 9216 | 50 |
| CoverType | 581,012 | 54 | 50 |
| Norb | |||||
|---|---|---|---|---|---|
| Type | #Labeled Samples per Class | #Cluster | Percent of Features | ||
| Train | 10 | 20 | 40% | ||
| Test | 10 | 20 | 40% | ||
| Train | 8 | 320 | 60% | ||
| Test | 8 | 20 | 40% | ||
| Train | 5 | 320 | 60% | ||
| Test | 5 | 320 | 60% | ||
| Cover Type | |||||
|---|---|---|---|---|---|
| Type | #Labeled Samples per Class | #Cluster | Percent of Features | ||
| Train | 70 | 70 | 80% | ||
| Test | 70 | 70 | 80% | ||
| Train | 50 | 70 | 80% | ||
| Test | 50 | 70 | 80% | ||
| Train | 30 | 70 | 80% | ||
| Test | 30 | 70 | 80% | ||
| Dataset | Model | 5 Labeled Samples | 8 Labeled Samples | 10 Labeled Samples | |||
|---|---|---|---|---|---|---|---|
| Unlabeled | Test | Unlabeled | Test | Unlabeled | Test | ||
| Norb N = 48,600 C = 5 M = 1000 | AGR [22] | 41 ± 4.04 () | - | 48.28 ± 5.10 () | - | 52.34 ± 5.80 () | - |
| EAGR [23] | 44.79 ± 4.01 ) | - | 52.10 ± 3.85 () | - | 55.79 ± 4.31 () | - | |
| MMLP [28] | 41.61 ± 3.11 | - | 48.21 ± 3.98 | - | 52.86 ± 4.88 | - | |
| MTC [29] | 38.22 ± 3.76 | - | 41.89 ± 3.23 | - | 45.61 ± 4.01 | - | |
| 1NN | 36.68 ± 2.08 | 34.65 ± 2.36 | 41.08 ± 2.32 | 39.61 ± 2.06 | 44.65 ± 2.03 | 41.90 ± 1.80 | |
| LapRLS/L [30] | 45.23 ± 2.41 | 40.75 ± 3.75 | 49.76 ± 2.24 | 45.10 ± 3.02 | 51.9 ± 2.43 | 46.88 ± 2.89 | |
| F-FME [13] | 46.85 ± 2.54 | 41.74 ± 3.84 | 53.30 ± 3.11 | 46.36 ± 3.36 | 56.30 ± 3.25 | 47.95 ± 3.13 | |
| R-FME [13] | 50.09 ± 2.54 | 43.03 ± 3.58 | 56.40 ± 3.44 | 47.22 ± 3.21 | 59.95 ± 3.29 | 49.08 ± 2.69 | |
| Proposed Model | 53.02 ± 2.25 | 46.35 ± 2.34 | 58.59 ± 2.42 | 48.81 ± 1.58 | 60.86 ± 1.91 | 49.95 ± 2.03 | |
| Dataset | Model | 30 Labeled Samples | 50 Labeled Samples | 70 Labeled Samples | |||
|---|---|---|---|---|---|---|---|
| Unlabeled | Test | Unlabeled | Test | Unlabeled | Test | ||
| Covtype N = 464,807 C = 7 M = 1000 | AGR [22] | 44.00 ± 2.54 ( | - | 47.08 ± 2.73 () | - | 48.85 ± 2.30 () | - |
| EAGR [23] | 43.56 ± 2.4 | - | 46.35 ± 3.2 | - | 48.30 ± 2.69 | - | |
| MMLP [28] | 40.58 ± 2.55 | - | 44.54 ± 2.79 | - | 46.90 ± 1.86 | - | |
| MTC [29] | 40.50 ± 3.48 | - | 44.62 ± 3.39 | - | 48.21 ± 2.12 | - | |
| 1NN | 43.12 ± 2.26 | 43.17 ± 2.28 | 45.53 ± 1.13 | 45.61 ± 1.15 | 47.14 ± 1.60 | 47.19 ± 1.64 | |
| LapRLS/L [30] | 44.48 ± 3.27 | 44.48 ± 3.30 | 48.86 ± 2.83 | 48.97 ± 2.83 | 50.50 ± 2.23 | 50.61 ± 2.25 | |
| F-FME [13] | 48.27 ± 2.79 | 45.03 ± 6.62 | 48.86 ± 2.83 | 49.57 ± 2.98 | 51.94 ± 1.95 | 50.90 ± 2.08 | |
| R-FME [13] | 47.70 ± 3.20 | 45.88 ± 3.87 | 49.54 ± 1.78 | 50.01 ± 3.14 | 51.89 ± 2.08 | 53.36 ± 2.74 | |
| Proposed Model | 49.12 ± 2.07 | 48.86 ± 2.48 | 51.14 ± 2.20 | 51.52 ± 2.78 | 52.63 ± 1.65 | 53.97 ± 1.18 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alemi, M.; Bosaghzadeh, A.; Dornaika, F. Graph-Based Semi-Supervised Learning with Bipartite Graph for Large-Scale Data and Prediction of Unseen Data. Information 2024, 15, 591. https://doi.org/10.3390/info15100591
Alemi M, Bosaghzadeh A, Dornaika F. Graph-Based Semi-Supervised Learning with Bipartite Graph for Large-Scale Data and Prediction of Unseen Data. Information. 2024; 15(10):591. https://doi.org/10.3390/info15100591
Chicago/Turabian StyleAlemi, Mohammad, Alireza Bosaghzadeh, and Fadi Dornaika. 2024. "Graph-Based Semi-Supervised Learning with Bipartite Graph for Large-Scale Data and Prediction of Unseen Data" Information 15, no. 10: 591. https://doi.org/10.3390/info15100591
APA StyleAlemi, M., Bosaghzadeh, A., & Dornaika, F. (2024). Graph-Based Semi-Supervised Learning with Bipartite Graph for Large-Scale Data and Prediction of Unseen Data. Information, 15(10), 591. https://doi.org/10.3390/info15100591







