Abstract
At present, there is no suitable instrument available to simulate modeling the thermal performance of various areas of our states due to its complicated meteorological behavior. To accurately predict a heatwave, we studied the research gaps and current ongoing research on the prediction of heatwaves. For the accurate prediction of a heatwave, we considered two soft computing concepts, (a) Rough Set Theory (RST) and (b) Support Vector Machine (SVM). All the ongoing research on the prediction of heatwaves is based on future predictions with an error margin. All the available techniques use a particular pattern of heatwave data, and these methods do not apply to vague data. This paper used an innovative RST and SVM technique, which can be applied to vague and imprecise datasets to produce the best outcomes. RST is helpful in finding the most significant attributes that will be alarming in the future. This analysis identifies the heat wave as the most prominent characteristic among various meteorological data. SVM is responsible for the future prediction of heat waves, which includes various parameters. By further classification of heatwaves, we found that a lack of greenery will increase the heatwave in the future. Although the survey was conducted based on a sampling distribution, we expect this result to represent the population as we collected our sample in a heterogeneous environment. These outcomes are validated using a statistical method.
1. Introduction
The expected temperature increases of the last five-year period (0.750 °C–0.950 °C) from the annual report for temperature in the last decade was an all-time high, according to the report from the National Center for Environmental Information of the National Oceanic and Atmospheric Administration. A heatwave globally has significantly changed atmospheric conditions in the recent past, cumulatively increasing the probability and gravity of meteorological and abnormal atmospheric conditions [1,2]. Several researchers [3,4,5,6,7] have researched social issues using an incomplete dataset. Meehl and Claudia [3] studied the intense, frequent, and longer lasting heatwaves of the 21st century using SVM and machine learning tools. The present heat waves in North America and Europe are linked to an atmospheric circulation pattern that is being made worse by continuous greenhouse gas emissions, as shown by observations and the model used in their work. This suggests that future heatwaves in those regions will be more severe. Green et al. [4] estimated the creation of a rapid mortality surveillance system that has been a crucial element in this approach. This article examines the outcomes and timeliness of a daily mortality model that projects excess mortality using imprecise surveillance data to “nowcast” deaths in virtually real time. On 24 June 2011, the Met Office issued a heatwave alert for regions of South and East England. Anderson and Peng [5] used Monte Carlo cross-validations to predict changes in high-mortality heatwaves under various future scenarios (including climate change and population growth). These models are unique in that they use heatwave properties that are evaluated relative to a community’s temperature distribution as predictive factors, allowing for the investigation of various heat adaptation scenarios. You may contrast several adaptation scenarios by choosing unique population temperature distributions. In a parallel study, we employed the three chosen models to predict changes in high-mortality heatwaves in light of various meteorological, demographic, and adaptation scenarios. The three models have been shared on GitHub so that other researchers can utilize them. A regression-based model was created by Kim et al. [6] and was used to forecast how many people will die from heatstroke. Several statistical methods are looked at, including the zero-inflated models, the negative binomial, Poisson, and hurdle models. The zero-inflated Poisson regression model is the most appropriate statistical approach, according to the results, because zero-valued observations in the weekly heat death data occur often. In the research site and period, there were undoubtedly more heat-related deaths, and higher predicted values were also present. According to this statistical performance, disaster management and public health professionals should investigate the used models as a scientific tool for resource allocation and health risk mitigation, as well as for disseminating trustworthy weekly heatwave risk forecasts to the public. Williams et al. [7] reported that days during heatwaves were linked to higher rates of daily mortality and emergency department (ED) visits, but lower rates of overall hospital admission. To decrease the negative health effects of Perth’s extreme heat, public health initiatives will become more crucial if the current trend of rising average temperatures and an increase in the frequency of hot days persists.
Mishra et al. [8] discussed various types of classification using a rough set to increase the sustainability of the software industry. They discussed managerial policy, legal justice for government and non-government organizations, and the future and sustainability of educational institutions run by private management. Nayak et al. [9] predicted cases of cardiac arrest of certain patients from different states of Odisha considering vague data and then by using Support Vector Machine and Rough Set. Ramadan et al. [10] discussed an innovative SVM technique to forecast global solar radiation over Teheran, Iran. The SVM_rbf forecasting was compared with various soft computing methods such as ANN and AIFN. The outcomes confirmed that the SVM_rbf provided better results than all hybrid soft computing models. Das et al. [11] discussed the future and remedies for the design of a mathematical model to predict rainfall. A detailed discussion about the global medical challenges of malaria, various business establishments using rough sets applied to a vague pattern of business data, and significant results about future outcomes and their sustainability in the long run for cardiac diseases is presented. Various population parameters of different business sectors have been discussed to find the exact importance of the parameters responsible for their development. Park et al. [12] discussed the destruction and damage due to heatwaves, and they analyzed the time series dataset of the heatwave to predict the damage of heatwaves and methods to overcome these situations. Que et al. [13] used a hybrid technique using ANFIS, SVM, and ANN to estimate global solar radiation in a specific environment. The significance of solar energy and its utility in developing countries discussed by Liu et al. [14] and Besharat et al. [15] emphasized estimating solar energy using many empirical correlation techniques and various meteorological and environmental factors. The principle of the satellite-derived technique is capable of approximating cosmological energy data taken from a huge geographical region, but it is comparatively novel and may suffer from a lack of available data. Weather forecasting using Stochastic weather generators is useful for producing daily approximations from significant regulars but not for validating the model if restrained data are not present. However, because the insolation data are not easily accessible in some locations, many models based on temperature have been discussed, and several assessments and changes have since been made by Chen et al. [16] and Olatomiwa et al. [17].
Various soft computing methods have been cast off in the current time for the approximation of worldwide radiation due to sunlight, with ANFIS and ANN providing the most significant results. Mohammadi et al. [18] implemented a combination of ANFIS and SVM methods to predict worldwide solar radiation, including air temperatures in Bandar Abbas, situated in the south of Iran. Piri et al. [19] compared four sunshine periods using experiential analysis and the SVM technique to evaluate worldwide solar radiation in two different localities of Iran. Many studies [20,21,22,23,24] on soft computing have predicted different environmental and medical issues. RST is one of the best soft computing tools for analyzing vague and imprecise data, whereas heatwaves are significant meteorological data that are vague in nature. In the 1960s, the meteorological environment was different from the contemporary environment, and as such there will be no uniformity according to time series. To analyze such vagueness, this study uses RST and SVM, which classify feature selection. We have planned our work by following [25,26] to support the application of the methods to other environmental datasets.
Heatwaves are a major problem around the globe, causing phenomena such as global warming, ozone layer depression, and ultraviolet rays, which cause several health-related problems along with environmental-related issues. Early prediction of heatwaves can be helpful in resolving the above issues. In this regard, various studies are being conducted to forecast the projected rate in the future. Although numerous studies have already been conducted on this, these methods could not handle the primary data as these data are usually vague and imprecise. The data are collected randomly from various sources, i.e., from multiple sources, using statistical correlation techniques, and the vague data are regrouped into six major classes according to dissimilarity. Hence, the objective of this study is to analyze the raw data for future prediction.
2. Research Methodology
This paper uses two concepts: rough set and SVM. The datasets are taken from various regions of our state, Odisha. The seasonal data concerning heatwaves affecting our environment are described in the following Table 1. The data were collected randomly from different parts of our country. The basic concept of data collection is based on the best available sources. From the above table, it is clear that environmental hazards due to heatwaves had a uniform trend throughout India. So, we focus our attention on environmental hazards due to heatwaves. In this paper, our principal objective is to significantly identify the attributes affecting the environment. To achieve our result, we used the concept of a rough set [27] and combined it with the statistical method.

Table 1.
Change in several environmental hazards due to heatwaves in India during 2019 and 2020.
2.1. Rough Sets
In his famous work from 1982, Pawlak [28] established the idea of rough sets. It is a recognized idea that resulted from a foundational investigation into the logical characteristics of information systems. Relational databases have been mined or exploited in different ways as a source of data using rough set theory. This branch of mathematics, which deals with uncertainty, is very recent and has a close connection to abstract fuzzy theory. The rough set method may be used to find structural relationships in noisy and jumbled data. Two generalizations of classical sets that complement one another are rough sets and fuzzy sets. In contrast to fuzzy sets, rough set theory constructs its approximation using sets with many members.
Soft computing also applies fuzzy logic, chaos theory, neural networks, and machine learning in addition to rough sets. The inference of approximation ideas is the primary objective of the rough set analysis. Rough sets provide a good foundation for database knowledge discovery. This theory provides analytical techniques for finding data patterns. It may be used for a variety of tasks, including data reduction, decision rule construction, pattern extraction (including association rules and templates), feature selection and extraction, and pattern extraction. Along with the partial or total identification of data dependencies, the elimination of duplicate data, and other data-related activities, null values, missing values, dynamic data, and other difficulties are addressed.
2.1.1. Rough Set Provides Important Solutions to Data Analysis Issues
- The use of characteristics and values to describe a set of items.
- Drawing links between the characteristics.
- The elimination of extraneous qualities.
- Identifying the most important characteristics.
- Creating guidelines for decision making.
2.1.2. Rough Set Theory’s Objectives
- Inducing (learning) idea approximations is the primary objective of the rough set analysis. KDD benefits from rough setups as a good place to start. It provides analytical techniques for spotting data patterns.
- It may be applied to data reduction, decision rule construction, pattern extraction (templates, association rules), feature selection, feature extraction, pattern extraction, and pattern selection.
- Identifies complete or partial data dependencies, removes duplicated data, and proposes fixes for further issues such as null values, missing data, dynamic information, and other issues.
2.1.3. Four Basic Classes of Rough Sets
Rough set theory also includes the concepts of cores and reducts. For instance, if a non-null set , information system, and attribute superset that includes the whole set of conditional and decision attributes. the reduct. If contains the most significant features, then the S-lower approximation is the set of all R components that can be confidently classified as elements of a given specified concept. S-upper approximation set of R to be a subset of X, and containing objects that might be members of the given concept. S-upper approximation set of X contains the members of the specified concept. Using S-lower and S-upper approximation spaces with regard to R, the approximation space of R is found. Here, lower and higher approximation sets are respectively defined as and . So, we can predict the following statements:
- is roughly S—definable, if
- is roughly S—undefinable, if
- is roughly S—undefinable, if
- is roughly S—undefinable, if
Accuracy
The correctness of the rough set, which measures how much it matches the target set, is written as
where, the cardinality of . So, . It can be seen that both the approximations (upper and lower) are equal, which in turn makes the set a crisp set with respect to . Other criteria, i.e., , makes the set rough with respect to . However, if , then it can be predicted that the lower approximation is empty.
2.1.4. Attribute Dependency
Finding attribute correlations is among database analysis’s most crucial tasks. There is a list of the variables that substantially correlate with one another. If all values of characteristics from an attribute set are completely determined by values from an attribute set , then the attribute set is completely dependent on the attribute set . Dependency is extremely simply defined in crude set theory. Think about two different sets of characteristics, and . Each attribute set results in an equivalent or undetectable class structure. Let equivalence classes be induced by the two sets and respectively, and the equivalence class is derived from the equivalence class structure from the attribute set . So, we can define the dependency of the attribute set on attribute set , k, or , as
with the condition that depends totally on when k or , but for k or , T depends partially (in a degree k) on .
2.1.5. Reduct
Multiple incarnations of the same entity or invisible things are possible. Some of the features can have extraneous or superfluous portions. Only the characteristics that play a role in the indiscernibility relationship should be kept, and the approximation should be adjusted accordingly. These feature subsets are often many, with reducts being the smallest. A reduct is a sufficient group of criteria that can adequately describe the knowledge in the database on its own.
2.1.6. Core
The collection of characteristics known as the core is shared by all reducts, which is denoted by CORE(R) = ∩ (RED(R)). Important features of Core include:
- It might be empty.
- It contains qualities that must endure to prevent the collapse of the equivalence class structure.
- It consists of a group of fundamental characteristics. Necessary characteristics from the information table cannot be removed otherwise inconsistent data will come into action.
2.2. Support Vector Machine
Nowadays, most researchers are using Support Vector Machine, which is a supervised learning technique, and it is mostly used for addressing classification as well as regression problems. However, it uses machine learning classifications. SVM approaches new data to build the best line, which later can split n-dimensional space into a finite number of classes, which can be called a hyperplane. SVM generally chooses extreme vectors and respective points, which makes a hyperplane and so these types of extreme situations can be detected by using support vectors. Figure 1 describes two different categories that are classified by using a hyperplane.
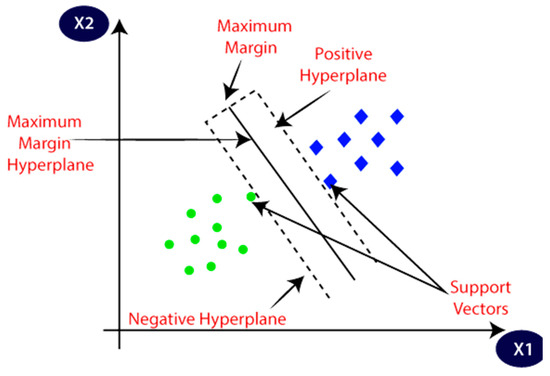
Figure 1.
Hyperplane using support vector.
2.2.1. Types of SVM
SVM comes in two varieties: i.e., (i) Linear SVM, in which data can be divided into two classes by a single straight line. It is also known as linearly separable data. (ii) Non-linear SVM, in which there is a non-linear separated dataset that cannot be categorized, and so the classifier utilized is referred to as a Non-linear SVM classifier.
2.2.2. Hyperplane and Support Vectors in the SVM Algorithm
Hyperplane: In n-dimensional space, several lines or decision borders may be utilized to separate classes, but only one line or decision boundary needs to be chosen to classify the data points. This ideal boundary is known as the hyperplane of SVM. If there are just two characteristics in the dataset, the hyperplane will be a straight line since the features of the dataset dictate its dimensions. The hyperplane only has two dimensions if there are only three properties. The biggest margin, or the greatest distance between the data points, is always selected when building a hyperplane.
Support Vectors: Support vectors are the data points or vectors that are most closely associated with the hyperplane and have a substantial influence on its location. These vectors act as supports for the hyperplane, thus the name “support vectors”. Because of this, the SVM technique aids in identifying the ideal decision boundary or area, often known as a hyperplane. The nearest line from each class is identified by the SVM algorithm. Support vectors are what we call these locations (see. In Figure 2). The margin is the distance between the vectors and the hyperplane. This margin will rise thanks to SVM. The best hyperplane is the one with the largest margin.
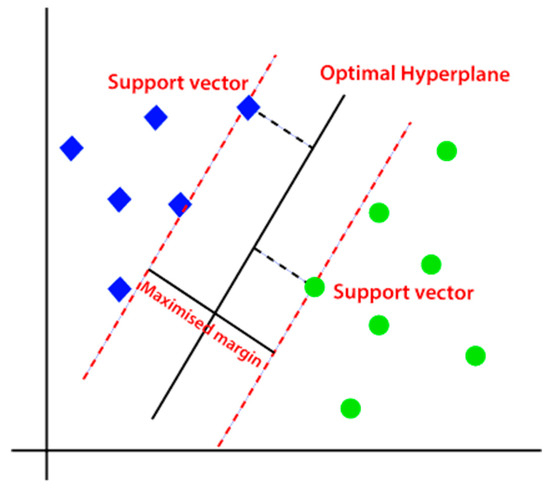
Figure 2.
SVM using support vector (optimal hyperplane).
2.2.3. Background for Data Analysis
The analytical part of this work is based on collecting data from various regions of our country. Table 1 is a time series dataset with respect to environmental hazards due to the heatwave and, for verification, whether the heatwave significantly affected the environment data in Table 2. The data are presented in the table given below.

Table 2.
Survey data related to various climates.
The conditional attributes in this case are <Cold Wave, Heavy Rainfall, Heatwave, Moderate Climate, Low Pressure>.
2.3. Further Data Analysis
We use the basic technique of a rough set to find the significant attribute that affects the environment. To achieve the result, we designed the entire Table 2 into a decision-making table similar to the rough set decision table, with the details of the rough set described in the preceding sections.
3. Working Procedure of Rough Set
The basics of a rough set are of the form <U, C, {d}> where Universal set (U), conditional attribute (C), and decision attributes ({d}). This can be represented in a table called a decision table (Table 3).

Table 3.
Rough set (initial table).
In this case, records (V <V1, V2, V3>), conditional attributes (<asx, bsx, csx>) with values <1 to 9>, and decision attributes (ds) with values <10, 11, 12>.
The decision attribute is the most significant attribute responsible for affecting the environment among the five attributes described in the above table, renamed dx. The values of the conditional attributes are <high, moderate> renamed as <bsx, csx>, and the values of the decision attributes “dsx” are significant and pointless, renamed as <1, 2>, respectively.
4. Analysis Using Rough Set Algorithm
The algorithm to find the reduct is included in the Appendix A.
To start, we considered 100,000 records initially using the statistical approach (correlation) technique, and we obtained 6 records, with dissimilar features, i.e., <VX1, VX2, VX3, VX4, VX5, VX6> for six conditional attributes <11, 22, 33, 44, 55> with their values described as High and Moderate renamed as bsx, csx as described in Table 4. The decision attribute ds to find the significant attributes is valued <1, 2>. After that Table 5 is represented for preliminary data.

Table 4.
Renaming conditional attributes.

Table 5.
Preliminary data table.
II(11) = {(rsk1, rsk2, rsk6), (rsk3, rsk4, rsk6)}, II(22) = {{rsk1, rsk2), (rsk3, rsk4, rsk5, rsk6)}, II(33) = {(rsk3, rsk4, rsk5), (rsk2, rsk3, rsk6)}, II(44) = {{rsk1, rsk2},{rsk3, rsk4, rsk5, rsk6}}, II(55) = {{rsk1, rsk2, rsk3, rsk4}, {rsk5, rsk6}}, II(11,22) = {{rsk1, rsk2}, {rsk3, rsk4, rsk5}, rsk6}, II(11,33) = {{rsk1}, {rsk2, rsk6}, {rsk3}, {rsk4, rsk5}}, II(11,44) = {{rsk1, rsk2}, {rsk2, rsk6}, {rsk3}, {rsk4, rsk5}}, II(11,55) = {{rsk1, rsk2}, {rsk3, rsk4}, {rsk5}, {rsk6}}, II(22,33) = {{rsk1}, {rsk2}, {rsk3, rsk6}, {rsk4, rsk5}}, II(22,44) = {{rsk1, rsk2}, {rsk3, rsk4, rsk5, rsk6}}, II(22,55) = {{rsk1, rsk2}, {rsk3, rsk4}, {rsk5, rsk6}}, II(33,44) = {{rsk1}, {rsk2}, {rsk3, rsk6}, {rsk4, rsk5}}, II(44,55) = {{rsk1, rsk2}, {rsk3, rsk4}, {rsk5, rsk6}}, II(11,22,33) = {{rsk1}, {rsk2}, {rsk3}, {rsk4, rsk5}, {rsk6}}, II(11,33,44) = {{rsk1}, {rsk2}, {rsk3}, {rsk4, rsk5}, {rsk6}}, II(11,44,55) = {{rsk1, rsk2}, {rsk3, rsk4}, {rsk5}, {rsk6}}, II(11,22,44) = {{rsk1, rsk2}, {rsk3, rsk4, rsk5}, {rsk6}}, II(11,22,55) = {{rsk1, rsk2}, {rsk3}, {rsk4, rsk5}, {rsk6}}, II(11,33,55) = {{rsk1}, {rsk2}, {rsk3}, {rsk4, rsk5}, {rsk6}}, II(11,44,55) = {{rsk1, rsk2}, {rsk3, rsk4}, {rsk5}, {rsk6}}, II(22,33,44) = {{rsk1}, {rsk2}, {rsk3}, {rsk4, rsk5}, {rsk6}}, II(22,33,55) = {{rsk1}, {rsk2}, {rsk3}, {rsk4}, {rsk5}, {rsk6}}, II(22,44,55) = {{rsk1, rsk2}, {rsk3, rsk4}, {rsk5, rsk6}}, II(11,22,33,44) = {{rsk1}, {rsk2}, {rsk3}, {rsk4}, {rsk5}, {rsk6}}, II(11,22,33,55) = {{rsk1}, {rsk2}, {rsk3}, {rsk4}, {rsk5}, {rsk6}}, II(11,33,44,55) = {{rsk1}, {rsk2}, {rsk3}, {rsk4}, {rsk5}, {rsk6}}, II(22,33,44,55) = {{rsk1}, {rsk2}, {rsk3}, {rsk4}, {rsk5}, {rsk6}}.
Core = {33}, as {33} = {Reduct<(1,2,3,4,5)>, as we get heatwaves that will affect the environment significantly in the future. Further, we classify the conditional attribute responsible for heatwave magnification. The calculation (Table 6) shows that in Case I, we obtained the attributes as, II(22,33,55) = {{rsk1}, {rsk2}, {rsk3}, {rsk4}, {rsk5}, {rsk6}}. In Case II we obtained II(11,22,33,44) = {{rsk1}, {rsk2}, {rsk3}, {rsk4}, {rsk5}, {rsk6}}. Case III contains II(11,22,33,55) = {{rsk1}, {rsk2}, {rsk3}, {rsk4}, {rsk5}, {rsk6}}. Case IV contains II(11,33,44,55) = {{rsk1}, {rsk2}, {rsk3}, {rsk4}, {rsk5}, {rsk6}} as reduct while Case V includes II(22,33,44,55) = {{rsk1}, {rsk2}, {rsk3}, {rsk4}, {rsk5}, {rsk6}} as expected.

Table 6.
Reduct table.
Further Analysis Using Rough Set
We consider the attributes that can be the cause of heat radiation, such as industrialization, air pollution due to motor vehicles, lack of greenery, uncontrolled wind speed, and radiation, and uses of equipment such as air conditioners and air coolers. We rename these conditional attributes (Table 7) as <1,2,3,4,5> and their values are renamed as: significant as ‘asx’ and insignificant as ‘bsx’, and decision attribute dv and its values are noteworthy and pointless as ‘csx’ and ‘dsx’. We applied the rough set concept to the data collected from various parts of our country. Initially, we collected 100,000 data points from various sources, as described in Table 2, Column 3, using the correlation technique. We divided the entire dataset into six dissimilar records, such as <AX1, AX2, AX3, AX4, AX5, AX6>.

Table 7.
Data table for heatwave.
Finding the reduct similar to the analysis performed in Section 3, we obtained the core as conditional attribute 3, i.e., lack of greenery is a major issue in incrementing a heatwave. Although there are several natural ways to preserve the greenery, advanced technology must be implemented to preserve the greenery for a long period.
5. Statistical Validation
Before employing data in a commercial function, it is necessary to validate their integrity, accuracy, and structure. A data validation process’s outputs can be used for data analytics, business intelligence, or training a machine learning model. However, the following steps have been carried out with confidence:
- We are consistent throughout and followed other datasets for confirmation.
- We have first documented the data thath have inconsistencies in the work.
- All the duplicate datasets are checked and correction was made for errors.
- Chi-square distribution is used for validation of the model.
We applied the chi-square distribution (a statistical test) to validate our claim. We prefer the chi-square distribution over another statistical test as it is a non-parametric test that does not follow any particular distribution.
H0 (Null Hypothesis):
There is no significance of the least amount of greenery (increment of a heatwave).
H1 (Alternate Hypothesis):
Lack of greenery has a strong significance on the increment of a heatwave.
- Observations: Samples are 10, 10, 15, 10, 15, 15, 5, 5, 10, 5.
- Expected samples are: 10%, 10%, 20%, 25%, 10%, 10%, 15%, 15%, 10%, 15%.
- Expected Values are: 10, 10, 20, 25, 10, 10, 15, 15, 10, 15.
tabular chi-square value as greater than so rejected the null hypothesis and accept the alternate hypothesis.
6. Concluding Remarks and Future Scope
In this major thrust to find significant attributes responsible for environmental hazards by using the rough set technique, we found that a heatwave is the conditional attribute that is mainly responsible for environmental hazards. By the further classification of heatwaves, we found that a lack of greenery will increase the heatwave in the future. Although the survey was conducted based on sampling distribution, we expect this result to represent the population as we collected our sample in a heterogeneous environment. This concept can apply to various domains such as wind speed predictions, rainfall predictions, and various meteorological phenomena. Finally, we can remark on the present study, which is about the prediction made by using vague, imprecise, and disordered datasets. Applicable to all types of environments, this deals with analyzing vague data to draw a meaningful conclusion.
Author Contributions
Conceptualization, methodology, R.D. and J.M.; validation, formal analysis, investigation, P.K.P. and M.M.B.; resources, data curation, R.D. and M.M.B.; writing—original draft preparation, writing—review, and editing, R.D. and P.K.P.; visualization, supervision, M.M.B. and P.K.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
| Algorithm A1. To find the reduct. |
| Input: |
| QPR, Conditional Attribute Set, ETM, Decision attribute set, |
| is the equivalence classes concerning R, and L is the initial equivalence class. |
| Output: R, sets with a unique feature |
| D:= { }, R: = { } |
| repeat |
| D: = R |
| ∀ y ∈ (QPR − R) |
| if RU{y} (EMT) > R(L) |
| D: = R U {y} |
| R: = D |
References
- Djalante, R. Key Assessments from the IPCC Special Report on Global Warming of 1.5 °C and the Implications for the Sendai Framework for Disaster Risk Reduction. Prog. Disaster Sci. 2019, 1, 100001. [Google Scholar] [CrossRef]
- Peduzzi, P. The Disaster Risk, Global Change, and Sustainability Nexus. Sustainability 2019, 11, 957. [Google Scholar] [CrossRef]
- Meehl, G.A.; Claudia, T. More intense, more frequent, and longer lasting heat waves in the 21st century. Science 2004, 305, 994–997. [Google Scholar] [CrossRef]
- Green, H.K.; Andrews, N.J.; Bickler, G.; Pebody, R.G. Rapid estimation of excess mortality: Nowcasting during the heatwave alert in England and Wales in June 2011. J. Epidemiol. Community Health 2012, 66, 866–868. [Google Scholar] [CrossRef] [PubMed]
- Anderson, G.B.; Oleson, K.W.; Jones, B.; Peng, R.D. Classifying heatwaves: Developing health-based models to predict high-mortality versus moderate united states heatwaves. Clim. Chang. 2018, 146, 439–453. [Google Scholar] [CrossRef]
- Kim, D.W.; Deo, R.C.; Park, S.J.; Lee, J.S.; Lee, W.S. Weekly heat wave death prediction model using zero-inflated regression approach. Theor. Appl. Climatol. 2019, 137, 823–838. [Google Scholar] [CrossRef]
- Williams, S.; Nitschke, M.; Weinstein, P.; Pisaniello, D.L.; Parton, K.A.; Bi, P. The impact of summer temperatures and heatwaves on mortality and morbidity in Perth, Australia 1994–2008. Environ. Int. 2012, 40, 33–38. [Google Scholar] [CrossRef]
- Mishra, S.; Mohmaed, A.; Pattnaik, P.K.; Muduli, K.; Ahmad, T.S.T. Soft Computing Techniques to Identify the Symptoms for COVID-19. In Advances in Data Science and Management; Springer Nature: Singapore, 2022; pp. 283–293. [Google Scholar]
- Nayak, S.K.; Pradhan, S.K.; Mishra, S.; Pradhan, S.; Pattnaik, P.K. Prediction of Cardiac Arrest Using Support Vector Machine and Rough Set. In Proceedings of the 9th IEEE International Conference on Computing for Sustainable Global Development (INDIACom), New Delhi, India, 23–25 March 2022; pp. 164–172. [Google Scholar]
- Ramedani, Z.; Omid, M.; Keyhani, A.; Shamshirband, S.; Khoshnevisan, B. Potential of Radial Basis Function Based Support Vector Regression for Global Solar Radiation Prediction. Renew. Sustain. Energy Rev. 2014, 39, 1005–1011. [Google Scholar] [CrossRef]
- Das, R.; Mishra, J.; Mishra, S.; Pattnaik, P.K. Design of Mathematical Model for the Prediction of Rainfall. J. Interdiscip. Math. 2022, 25, 587–613. [Google Scholar] [CrossRef]
- Park, M.; Jung, D.; Lee, S.; Park, S. Heatwave Damage Prediction Using Random Forest Model in Korea. Appl. Sci. 2020, 10, 8237. [Google Scholar] [CrossRef]
- Quej, V.H.; Almorox, J.; Arnaldo, J.A.; Saito, L. ANFIS, SVM and ANN Soft-Computing Techniques to Estimate Daily Global Solar Radiation in a Warm Sub-Humid Environment. J. Atmos. Sol.-Terr. Phys. 2017, 155, 62–70. [Google Scholar] [CrossRef]
- Liu, X.; Mei, X.; Li, Y.; Zhang, Y.; Wang, Q.; Jensen, J.R.; Porter, J.R. Calibration of the Ångström–Prescott Coefficients (a, b) under Different Time Scales and Their Impacts in Estimating Global Solar Radiation in the Yellow River Basin. Agric. For. Meteorol. 2009, 149, 697–710. [Google Scholar] [CrossRef]
- Besharat, F.; Dehghan, A.A.; Faghih, A.R. Empirical Models for Estimating Global Solar Radiation: A Review and Case Study. Renew. Sustain. Energy Rev. 2013, 21, 798–821. [Google Scholar] [CrossRef]
- Chen, J.-L.; Liu, H.-B.; Wu, W.; Xie, D.-T. Estimation of Monthly Solar Radiation from Measured Temperatures Using Support Vector Machines—A Case Study. Renew. Energy 2011, 36, 413–420. [Google Scholar] [CrossRef]
- Olatomiwa, L.; Mekhilef, S.; Shamshirband, S.; Mohammadi, K.; Petković, D.; Sudheer, C. A Support Vector Machine–Firefly Algorithm-Based Model for Global Solar Radiation Prediction. Sol. Energy 2015, 115, 632–644. [Google Scholar] [CrossRef]
- Khorasanizadeh, H.; Mohammadi, K. Prediction of Daily Global Solar Radiation by Day of the Year in Four Cities Located in the Sunny Regions of Iran. Energy Convers. Manag. 2013, 76, 385–392. [Google Scholar] [CrossRef]
- Piri, J.; Shamshirband, S.; Petković, D.; Tong, C.W.; ur Rehman, M.H. Prediction of the Solar Radiation on the Earth Using Support Vector Regression Technique. Infrared Phys. Technol. 2015, 68, 179–185. [Google Scholar] [CrossRef]
- Guirguis, K.; Gershunov, A.; Tardy, A.; Basu, R. The impact of recent heat waves on human health in California. J. Appl. Meteorol. Climatol. 2014, 53, 3–19. [Google Scholar] [CrossRef]
- Basu, R.; Samet, J.M. Relation between elevated ambient temperature and mortality: A review of the epidemiologic evidence. Epidemiol. Rev. 2002, 24, 190–202. [Google Scholar] [CrossRef]
- Kovats, R.S.; Hajat, S. Heat stress and public health: A critical review. Annu. Rev. Public Health 2008, 29, 41–55. [Google Scholar] [CrossRef]
- Chen, X.; Li, N.; Liu, J.; Zhang, Z.; Liu, Y. Global heat wave hazard considering humidity effects during the 21st century. Int. J. Environ. Res. Public Health 2019, 16, 1513. [Google Scholar] [CrossRef] [PubMed]
- Lemonsu, A.; Viguié, V.; Daniel, M.; Masson, V. Vulnerability to heat waves: Impact of urban expansion scenarios on urban heat island and heat stress in Paris (France). Urban Clim. 2015, 14, 86–605. [Google Scholar] [CrossRef]
- Sudha, M.; Valarmathi, B. Rainfall Forecast Analysis using Rough Set Attribute Reduction and Data Mining Methods. AGRIS On-Line Pap. Econ. Inform. 2014, 6, 145–154. [Google Scholar] [CrossRef]
- Szul, T.; Knaga, J.; Necka, K. Application of rough set theory to establish the amount of waste in households in rural areas. Ecol. Chem. Eng. S 2017, 24, 311–325. [Google Scholar] [CrossRef][Green Version]
- Pawlak, Z. Rough Sets and Flow Graphs. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; pp. 1–11. [Google Scholar]
- Pawlak, Z. Rough sets. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).