Abstract
Learning mostly involves communication and interaction that leads to new information being processed, which eventually turns into knowledge. In the digital era, these actions pass through online technologies. Formal education uses LMSs that support these actions and, at the same time, produce massive amounts of data. In a distance learning model, the assignments have an important role besides assessing the learning outcome; they also help students become actively engaged with the course and regulate their learning behavior. In this work, we leverage data retrieved from students’ online interactions to improve our understanding of the learning process. Focusing on log data, we investigate the students’ activity that occur close to and during assignment submission due dates. Additionally, their activity in relation to their academic achievements is examined and the response time in the forum communication is computed both for students and their tutors. The main findings include that students tend to procrastinate in the submission of their assignments mostly at the beginning of the course. Furthermore, the last-minute submissions are usually made late at night, which probably indicates poor management or lack of available time. Regarding forum interactions, our findings highlight that tutors tend to respond faster than students in the corresponding posts.
1. Introduction
The transition to online education has led to the creation of vast repositories of learning-related data. Educational institutions are now striving to utilize this data for evidence-based decision making in their teaching and learning strategies, as well as in the design of online courses. To achieve this goal, they are adopting and utilizing various Learning Management Systems (LMSs) in Distance Education, which offer opportunities to analyze students’ learning patterns and academic performance through extracted datasets [1,2]. Traditionally, tutors have relied on their daily interactions with the student community, drawing upon their expertise and experience to make decisions. However, in the new era of education, this knowledge and experience can be enhanced with valuable insights provided by Learning Analytics (LA).
Distance teaching and learning possess several characteristics that make it distinct from typical (face-to-face) education. In a face-to-face course, the instructor evaluates a series of information to assess the learning progress. Moreover, tutors have an organized and well-defined program, being in touch with students at a certain time schedule. However, in Distance Learning, in order to gain insight into the educational needs, tutors have to seek for additional context in the data mined. Communication between peers can be both synchronous or asynchronous, and student–student or student–tutor interactions utilize one or more technological channels [3]. Therefore, in Distance Learning, the time intervals between a message and its reply might affect the quality and effectiveness of the communication. Unlike the physical classroom, where interaction is given due to the simultaneous presence of the students and their tutor, the online learning space might be in times “lonely” or “crowded”. However, tutors are not usually aware of the online traffic in order to be available to respond in a timely manner, when students need them. These problems can be addressed by leveraging LA.
Overall, researchers conduct analyses using LMS log data in order to deeper understand the status of the students’ learning process [4], predict their learning achievement [5,6,7], and assess their levels of interaction and engagement [8,9]. Predicting learning achievement and exam performance is one of the most popular applications of LA, since it assists in identifying students at risk of failure, to provide them with additional support [10], while researchers agree that participation in discussion fora can enhance learning, there is a great need to investigate its impact on students’ course performance [11]. Considering student behavior in LMSs, this study assumes that student forum activity before or during the deadlines of final exams and written assignments might be an important factor to consider when analyzing activity logs. Behavioral patterns of both students and tutors can also be hidden in metrics of forum consumption (views) and forum contribution (posts, replies), as defined in [6], during ‘crucial’ time-frames. Despite the rich source of information on exploiting LA to predict students’ performance, identifying activity patterns in LMSs by considering exams/assignments dates, has not received much attention. Additionally, the investigation of response-time in LMS fora is significantly under researched.
Despite the fact that there have been several works introduced into the literature which highlight the supporting role of the tutors and its benefits during their interaction with the students, such as [12,13,14], the probabilistic analysis of the response time in this interaction has not received any attention. More specifically, one would be interested in answering the following question: “what is the probability of obtaining a response in a university forum within the next x minutes?”. Another interesting factor is how different academic cornerstones, such as the deadlines of assignments or dates of exams, affect the aforementioned question. Moreover, we have studied the relationship of students’ activity with their academic progress.
Conclusively, we have set the following objectives:
- Finding out whether the activity increases in the periods close to the deadlines of the written assignments or close to the dates of the final exams;
- Investigating whether there is a timely response to the posts in the forum;
- Associating the general forum activity of students with their academic progress.
To summarize, the current study seeks to explore the students’ activity in general and in relation to exams and assignments deadlines, as well as academic achievements and forum response times. This work presents an analysis of students’ log data to investigate students’ activity and the frequency of their actions, with the aim that the results would bring us closer to the design and implementation of a system of predictive analytics that would alert tutors to take action shortly after a situation occurs.
The rest of the paper is structured as follows: In Section 2, the related work is presented. In the next section we discuss the methodology of our approach. Section 4 describes the results of the analysis, followed by Section 5, where we discuss the pedagogical implications. In Section 6, the main concluding remarks are presented.
2. Related Work
Increasing amounts of important data across the board of student academic life and performance are becoming openly available, providing more resources with high potential for improving learning [15]. Many types of data contain valuable information. From simple descriptive to more elaborated methods [16,17,18,19,20,21,22], several different approaches shed light to different aspects of learning. Although self-reporting may include a sufficiently accurate insight into cognitive activities, often this insight is blurred by learners’ distorted self-perception during intensive cognitive activities [23]. Therefore, data logs can offer an initial, objective glimpse of the learning process. Further data collection and elaborated analysis methods can advance our understanding about the learning activities undertaken by the students.
A recent meta-analysis of 41 relevant studies identified an association between broad log data indicators of general online activity and learning outcomes [4]. Liz-Domínguez et al. [5] found a correlation between the raw volume of interactions with the LMS and final grade, but only for first-time students. However, this correlation is nonexistent when considering retaking students.
In [10], the authors compared the state-of-the-art supervised machine learning techniques to predict students’ performance, through log data sets. The highest accuracy score was achieved from a neural network model fed with student engagement and past performance data. The findings support that adequate data acquisition is a perquisite to ensure efficient application of LA.
The sequence of students’ actions was used in various research projects to model students’ behavior [24,25,26] and to evaluate the learning outcome and the educational design that the teaching process was based on [21]. It is known that there are certain log variables that shape whether learning has happened [27]. However, there is also the necessity to consider the reliability of log data and their connection with existing educational theories [28].
The activity of the students in the discussion fora was used for academic performance prediction by Chiu and Hew [29] along with views and post counts. Their research demonstrated greater predictive power in views count than in post counts. Crossley et al. [30] showed that students had significantly better achievement than their peers when they made at least one post of 50 words or more. Furthermore, students who produce more on-topic posts, posts that are more strongly related to other posts, or posts that are more central to conversation presented a better completion rate. Sun et al. [31] compared the forum interaction between students who participated in predefined groups and students in self-selected groups. It was found that there is a significant difference between the strength of the ties that students formed, leading to the conclusion that the course design approach is affecting students’ community structure. Chiru et al. [32] proposed a model for counting the strength of students’ connection with certain discussion topics and with other participants, called the participant–topic and the topic–topic attraction. Network representation through time reveals the evolution of students’ community and along with polarity analysis can provide insights into the social aspect of their learning behavior [33]. Hernández-García, et al. [34] highlighted the need for tailored tools for advanced and in-depth analysis that will allow the effective confrontation of the problems that commonly appear in Distance Learning.
3. Methodology
In this section, we discuss the methodology of this work. Firstly, we introduce a detailed view of our data set and we present the participants’ main features. We focus on the data set’s characteristics and then we perform our analysis based on the requirements of our research. In the next sub-section, the theoretical background related with the following analysis is briefly presented.
3.1. Description of the Data Set
Our data set is a log file that consists of 146,814 rows, where each row describes a certain action in a Moodle LMS of a postgraduate distance learning course. This particular course started in October and its duration was a whole academic year. In total, 124 participants contributed to the dataset: 111 students and 13 members of the teaching staff. The students were divided into 5 groups, each group was assigned to a tutor. Each action in the LMS might be an insertion of a topic, a reply to a topic, a view of a thread or topic, a quiz attempt, an assignment submission, a view of a module, etc.
Since the program is provided by a Distance Learning University, the courses are based on the Distance Learning methodology. Hence, the students studied from their homes in their own time, at a given pace. They had to hand in assignments, there were optional real-time sessions with their tutors and their peers and, for the final evaluation, they had to sit on face-to-face exams. Data were collected during the academic year 2020–2021. This year, the COVID-19 pandemic forced educational institutions over the world to make a transition to online teaching. However, Distance Learning Institutions kept up with the same methodology as they were offering online courses anyway. The courses were provided in Greek and the communication in the forum was in Greek as well. The course’s forum is a domain where students can discuss every issue that concerns their studies. The discussions vary from questions focused on the learning material, such as issues raised during the lectures or taken from the written assignments, to simple practical issues, such as career paths.
The majority of the rows refer to view actions and only 1% of these rows are post actions. The view actions include access to any components of the courses (viewing the initial web pages, quizzes, grade-books, or submission forms of the written assignments), the various initial web pages of the fora of each course, and the corresponding discussions. Figure 1a shows the distribution of the counts of view and post actions in each month. It is quite obvious that the activity of the LMS grows significantly towards the end of the academic year, where the students maximize their efforts to improve their grades.
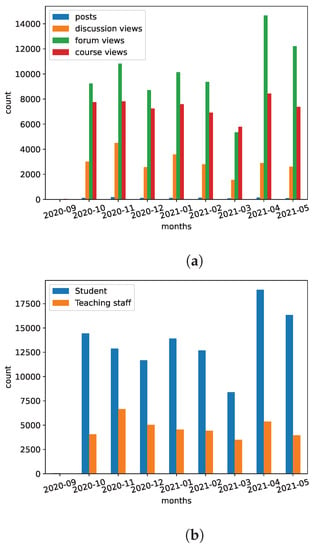
Figure 1.
The counts of view and post actions aggregated by each month. (a) Kinds of actions. (b) Roles of the users.
We have specified two major user roles; the student with 111 individuals, and the teaching staff, with 13 individuals. The student role included most of the rows, i.e., have been generated by the students, while describe actions of the teaching staff. Figure 1b illustrates the activity, in terms of the number of actions, of both roles. We have excluded the rows which referred to actions of the technical staff, which did not exhibit any particular educational interest.
For the needs of this research project, we have developed a data warehouse, where we have stored aggregated data of each user of the LMS based on the available log file. We maintain a pseudonym of each user, which is their id as given in the initial data set as well as their gender. We also maintain the counts of their view and post actions and the averages of students’ written assignments and final exams.
3.2. Theoretical Background
The series of actions, as stored in the log file, constitutes a Poisson process, where each action occurs on average times per minute. Consequently, in a period of minutes, the number of actions is a Poisson random variable with mean being equal to . The waiting times, in terms of minutes, between these actions are exponentially distributed having rate equal to . The Probability Density Function (PDF) [35] is:
where x denotes the waiting time and e is the exponential constant, whose value is approximately equal to . The reciprocal of , namely , is the theoretical mean of the distribution.
If we assume an exponentially distributed random variable X, the Cumulative Distribution Function (CDF) of X [35] evaluated at a certain waiting time x is:
Thus, the complementary of Equation (2) calculates the opposite event:
Since the rate parameters of the underlying exponential distributions in each time interval were unknown, we used the maximum likelihood estimation technique [36] for the exponential distribution to estimate the rate parameter by assuming n measurements of waiting times between the corresponding actions in the logs of the LMS:
The reciprocal of was used as the estimated average waiting time .
4. Experimental Results
For the first set of experiments, we assumed that each day of interest is divided into three-hour time intervals starting from 9:00 until 23:59. The period from midnight to 9:00 p.m. was not included due to very low activity. The purpose of doing so was to measure the elapsed amount of time, in terms of minutes, between subsequent actions, i.e., view and post actions, in the LMS, which had occurred in these time intervals. These measurements are actually the waiting times between a couple of actions, where the activity of the LMS is idle.
We considered as major cornerstones the following dates:
- The deadline of the first written assignment, 2 December 2020 (the deadline expires at 23:59);
- The deadline of the second written assignment, 20 January 2021;
- The deadline of the third written assignment, 24 February 2021;
- The deadline of the fourth written assignment, 7 April 2021;
- The deadline of the fifth written assignment, 12 May 2021;
- The date of the first exam, 6 June 2021;
- The date of the resit exam, 30 June 2021.
We derived estimate for the following:
- The fifth, third, and the day before the deadlines of each assignment;
- The dates of the deadlines of each assignment;
- The dates of the two exams.
For these dates, for each time interval, we plotted (a) the exponential distributions using the waiting times in the density function in (1) having set as the scale parameter and (b) the counts of the corresponding actions. For the rest of the manuscript, we will use and as well as and interchangeably.
4.1. Activity during the Days before the Deadlines of Each Assignment
Initially, we focused on the days immediately before the deadlines of the written assignments, namely the fifth, third, and day before. We calculated the average number of actions and the average values of for each time interval in these specific dates. We observe in Figure 2a,b that in the fifth date before each deadline during the interval 9:00–11:59 the number of actions exhibits a peak with rate . In the third day, the interval 18:00–20:59 is the busiest, where , as Figure 2c,d indicate. In contrast, as Figure 2e,f suggest, during the days just before the deadlines, the rates of actions per minute in the intervals 18:00–20:59 and 21:00–23:59 are and , with waiting times almost equal to min, respectively.
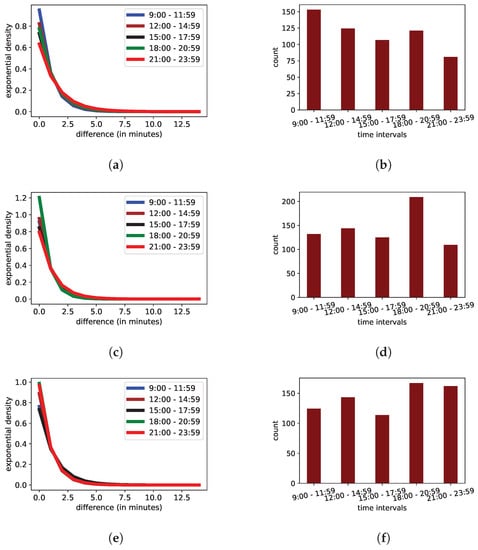
Figure 2.
The distributions calculated on certain days before the deadlines of the written assignments. (a) The exponential distributions five days before the deadlines. (b) The counts of actions five days before the deadlines. (c) The exponential distributions three days before the deadlines. (d) The counts of actions three days before the deadlines. (e) The exponential distributions one day before the deadlines. (f) The counts of actions one day before the deadlines.
Therefore, in the peaks of these dates, is around 1 action per minute, which means that the average waiting time is also , which is the empirical mean of our measurements. Thus, using the CDF in (2), the probability that an action would occur in these days within one minute from the last action received is:
whereas, using the CDF in (3), the probability of obtaining an action after two idle minutes is:
In contrast, by assuming the rate in the interval 21:00–23:59 of the fifth day, which is actions per minute, the probability to receive an action within a minute decreases:
and the probability of obtaining an action after two idle minutes increases:
In Figure 3, we present an overall picture of the counts of actions aggregated by each written assignment. The first and last assignments exhibit the two highest peaks, which refer to over 1000 actions in total, on different days. We also notice that the first two assignments follow almost the same pattern, which includes a peak in the third day, while the rest exhibit their peaks during the fifth day, and maintain lower activity during the day before the deadline.
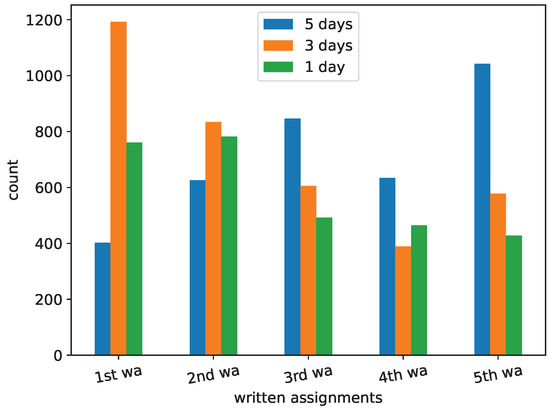
Figure 3.
The counts of actions aggregated by each assignment and certain days before the deadlines.
4.1.1. Activity during the Deadlines of Each Assignment
Figure 4a,b show the exponential distributions and the distribution of the count of actions in the deadline dates of the first three assignments, which seem to exhibit almost the same pattern. We observe a considerable increase in activity in the last two time intervals from 18:00 until midnight. The corresponding rates are and actions per minute, respectively, which yield average waiting times equal to and min, respectively. In the fourth written assignment, the increase in activity during the interval 18:00–20:59 is noteworthy, since it reaches actions per minute, as is indicated in Figure 4c. The absolute number of actions is almost 600 (Figure 4d). During the deadline date of the fifth written assignment, both time intervals from 18:00 until 23:59 exhibit high activity. However, it is apparent that the corresponding rates, waiting times, and counts are lower than these of the previous assignments (Figure 4e,f).
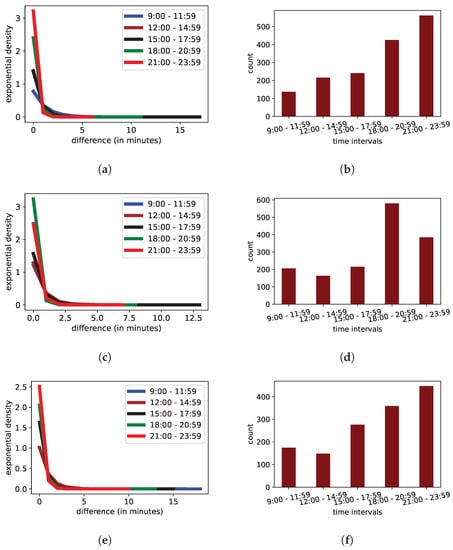
Figure 4.
The distributions during the deadline dates of the written assignments. (a) The exponential distributions of the first three written assignments. (b) The counts of actions of the first three written assignments. (c) The exponential distributions of the fourth written assignment. (d) The counts of actions of the fourth written assignment. (e) The exponential distributions of the fifth written assignment. (f) The counts of actions of the fifth written assignment.
The high rates incur higher probabilities of receiving actions. Specifically, the probability of an action occurring within a minute by assuming is:
In this case, the probability of obtaining an action after two idle minutes is negligible:
Due to this high rate of actions, the waiting times are much shorter.
4.1.2. Relationship of Students’ Activity with Their Academic Progress
We evaluated the relationship of students’ activity with their academic progress, in terms of their grades, using our own-developed data warehouse. For each student, we have stored the average of grades of their written assignments as well as the grade of their final exam into the data warehouse. Using this pair of grades, we derived the final grade for each student. These grades range from −2, which denotes violation of the rules of plagiarism, until the highest grade, namely 10. In Figure 5, we illustrate the counts of the view and post actions of the students aggregated by the intervals of their final grades. We have normalized the counts due to their great difference between the view and post actions. We observe that views scale according to the ranges; the higher the interval, the greater the number of views. More specifically, the interval exhibits an increase of more views than the lower range of , while the highest range has increase over the previous range. The distribution of the counts of posts is different. The interval has the greatest count, more posts than the range of .
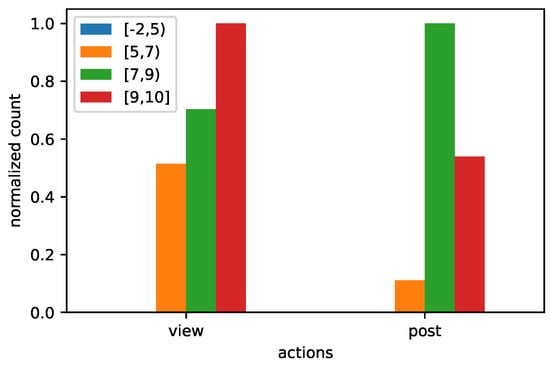
Figure 5.
The normalized counts of view and post actions aggregated by the ranges of grades of the students.
4.1.3. Elapsed Time between Posts
In this set of experiments, we investigate the elapsed time for the reaction of students or members of the teaching staff of each post. Specifically for each discussion, the so-called forum threads, we measured the waiting times between its successive posts. There are 165 discussions, where 145 and 20 are initiated by the members of the teaching staff and students, respectively. The number of the total posts is 827, where and are submitted by the members of the teaching staff and students, respectively. Figure 6 is a histogram, which illustrates these time differences, in terms of minutes. Each bin of the histogram represents a waiting time period of ten minutes. We observe that the distribution of the counts of replies follow the same distribution for both the students and members of the teaching staff. However, the majority of the replies are submitted by the members of the teaching staff; for example, during the first ten-minute period, 77 posts are submitted as replies, where the members of the teaching staff submitted the 60 of them, while the students submitted only 17.
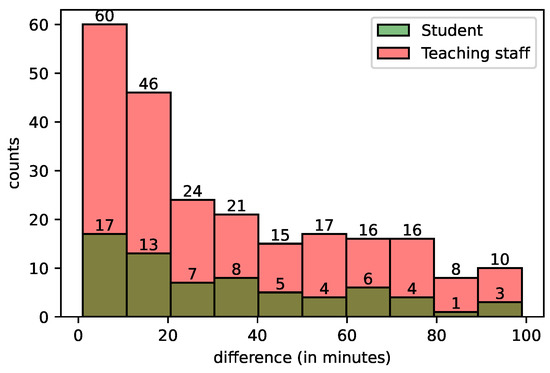
Figure 6.
The waiting times (difference) binned in 10-min intervals and the corresponding counts.
We then estimated the rate of replies, where is used as shorthand, per minute and the corresponding waiting times () using waiting times within 360 min in order to exclude late replies. The empirical mean of each for each discussion is , with an empirical standard deviation equal to . This actually means that each discussion has on average replies per minute. The empirical mean of the waiting times is min with empirical standard deviation equal to 70 min.
5. Discussion and Pedagogical Reflections
As shown in Figure 1a the number of events “forum views” is lower than the number of “course views”. This indicates that students visit the courses’ page and the majority of their action is related to the forum. It has to be noted that students are provided with printed learning material. So, they do not have to retrieve it from the online platform. The online platform mainly serves communication needs, assignments, quizzes submissions, and course planning information. On the other hand, the fact that there are more “forum views” than “discussion views” indicates that students usually check whether there is something new in the course in order to remain updated. The use of the forum for interaction, communication and information dissemination has also been stressed in the work of Onyema et al. [37] and Mtshali et al. [38]. Additionally, one of the findings in [29] was that besides commenting in the forum, viewing was one of major factors positively influencing learning.
Figure 1b shows that November was the most active month for the tutors. As was already mentioned, the data have been extracted from a postgraduate course that lasts for an academic year, starting in October. The first few weeks are mainly introductory. In November, students are preparing for the submission of the first compulsory written assignment. The results show that tutors increase their activity to support students’ efforts.
The distributions shown in Figure 4a,c,e indicate some not-so-obvious, yet explainable differences in students’ activity, which increases progressively from the due date of the first three written assignments to the final one. The graphs in Figure 4a,b show that the activity rises at night indicating an increased number of last-minute submissions. Academic procrastination is defined as delaying the academic tasks such as submitting an assignment or a term paper or last-minute preparation for the exams [39]. However, according to [40] academic procrastination is performed more frequently in online education rather than the face-to-face typical education. Thus, it is an issue of high importance, especially since students who habitually delay starting assignments have higher risk of failing their courses than students who start on time [41].
On the due date of the fourth written assignment, the maximum frequency of actions is during the afternoon and early evening. On the due date of the final written assignment, there is also a rise in last-minute submissions. This result, in combination with the information offered in Figure 3, may imply problems related to lack of time or poor time management. However, Figure 3 indicates a progressive improvement in students’ activity during the periods that a submission is pending. The “last day” actions gradually decrease and, in the three last written assignments, the peak of activity is five days before the due date, indicating a better planning strategy and time management on behalf of the students, which has been stressed as an important asset in previous research [42,43,44]. It has been found that the use of learning strategies for procrastination avoidance can influence homework timeliness, which then can affect course achievement [45], while Jones et al. [46] suggest that the earlier assignments are submitted, the higher the grades tend to be. Therefore, if faculty can help undergraduate students cultivate the habit of earlier submission of assignments, the better those students should perform in their studies.
Regarding students’ activity in relation with students’ grades (Figure 5), different approaches of forum participation can be derived. Students with the highest grades seem to closely monitor forum activity or engage in interaction, since forum views are very high in this category. However, they do not participate very actively as they exhibit lower number of forum posts. On the contrary, students that were graded between 7 and 9 do not visit the forum so often, but when they do, they usually make a post, contributing more actively in the forum community. This results is consistent with the work of [47,48], where more active students in the forum community achieved higher grades. Additionally, Cheng et al. [49] showed that students who participated in the forum tended to have better performance in the course, and that reading posts on the forum improved exam performance. Along the same lines, Voghoei et al. [50] found that the common characteristic of top students in all classes was their consistency in forum participation throughout the semester, regardless of the number of their posts.
Finally, the supporting role of the tutors as communication facilitators is confirmed in Figure 6, where we observe that a student’s post will be, most likely, resolved by a tutor. Findings from the study of Larson et al. [12] demonstrated that students desire to have engagement with their instructor in a balanced manner. This timely response by the tutors can be beneficial [13,14], especially during the beginning of an online course; however, in order to inspire students autonomy, tutors should gradually reduce their level of intervention to leave space for peer interaction.
6. Conclusions
In this work, we used log data from a Moodle LMS used in a postgraduate distance learning course to investigate the online activity during periods close to the dates of submission of written assignments. The results confirmed the importance of written assignments in the learning process, since they trigger an increase in students’ activity and their active engagement in the LMS. Additionally, their activity was shown in association with their grades. Finally, the time intervals between forum activity were investigated. The increased activity of the tutors compared with the students’ activity indicates that tutors are mainly in charge of the effectiveness of the communication, which is expected to a certain degree, since students are in their first year of a two-year, postgraduate, distance learning program and probably have not yet developed bonds of trust with their peers, nor sufficient autonomy skills. This evidence is subject to the features of the data sample that we consider and does not allow us to generalize the results. Hence, we consider it as the main limitation of this study. In the future, we plan to apply the same methodological approach to different data sets, including students of different fields and levels of studies. Additionally, we intend to expand our methodology using Machine Learning algorithms in order to extract patterns that may be hidden in the dataset, focusing mainly on the relations between online activity and students’ progress.
Author Contributions
All authors contributed equally to this manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The datasets generated and/or analyzed during the current study are available from the corresponding author upon a reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jo, I.-H.; Kim, D.; Yoon, M. Analyzing the Log Patterns of Adult Learners in LMS Using Learning Analytics. In Proceedings of the Fourth International Conference onLearning Analytics And Knowledge (LAK ’14), Indianapolis, IN, USA, 24–28 March 2014; pp. 183–187. [Google Scholar]
- Beer, C.; Clark, K.; Jones, D. Indicators of Engagement. In Ascilite Sydney; Athabasca University Press: Sydney, Australia, 2010; pp. 75–86. [Google Scholar]
- Griffiths, B. A Faculty’s approach to distance learning. Teach. Learn. Nurs. 2016, 11, 157–162. [Google Scholar]
- Klose, M.; Steger, D.; Fick, J.; Artelt, C. Decrypting log data: A meta-analysis on general online activity and learning outcome within digital learning environments. Z. Psychol. 2022, 230, 3. [Google Scholar]
- Liz-Domínguez, M.; Llamas-Nistal, M.; Caeiro-Rodríguez, M.; Mikic-Fonte, F. LMS Logs and Student Performance: The Influence of Retaking a Course. In Proceedings of the 2022 IEEE Global Engineering Education Conference (EDUCON), Tunis, Tunisia, 28–31 March 2022; pp. 1970–1974. [Google Scholar]
- Jovanović, J.; Saqr, M.J.S.; Gašević, D. Students matter the most in learning analytics: The effects of internal and instructional conditions in predicting academic success. Comput. Educ. 2021, 172. [Google Scholar]
- Hussain, M.; Hussain, S.; Zhang, W.; Zhu, W.; Theodorou, P.; Abidi, S.M.R. Mining moodle data to detect the inactive and low-performance students during the moodle course. In Proceedings of the 2nd International Conference on Big Data Research, Weihai, China, 27–29 October 2018; pp. 133–140. [Google Scholar]
- Jung, Y.; Lee, J. Learning Engagement and Persistence in Massive Open Online Courses (MOOCS). Comput. Educ. 2018, 122, 9–22. [Google Scholar]
- Wang, W.; Guo, L.H.L.; Wu, Y.J. Effects of social-interactive engagement on the dropout ratio in online learning: Insights from MOOC. Behav. Inf. Technol. 2019, 38, 621–636. [Google Scholar] [CrossRef]
- Tomasevic, N.; Gvozdenovic, N.; Vranes, S. An overview and comparison of supervised data mining techniques for student exam performance prediction. Comput. Educ. 2020, 143, 103676. [Google Scholar] [CrossRef]
- Romero, C.; López, M.I.; Luna, J.M.; Ventura, S. Predicting students’ final performance from participation in on-line discussion forums. Comput. Educ. 2013, 68, 458–472. [Google Scholar]
- Larson, E.; Aroz, J.; Nordin, E. The Goldilocks Paradox: The Need for Instructor Presence but Not Too Much in an Online Discussion Forum. J. Instr. Res. 2019, 8, 22–33. [Google Scholar] [CrossRef]
- Fernandez, R.; de Hoyos, P.; Izaguirre, N.; Artola, I.E.; Sánchez, M.A. The virtual forum as a collaborative learning tool. In Proceedings of the 16th International Technology, Education and Development Conference, Online, 7–8 March 2022; pp. 9768–9772. [Google Scholar]
- Nasir, M.K.M.; Mansor, A.Z. Discussion on online courses from the point of view of the research community. Relig. Rev. Cienc. Soc. Humanidades 2019, 4, 106–110. [Google Scholar]
- Bates, T.; Cobo, C.; Mariño, O.; Wheeler, S. Can Artificial Intelligence Transform Higher Education? Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Paxinou, E.; Sgourou, A.; Panagiotakopoulos, C.; Verykios, V. The item response theory for the assessment of users’ performance in a biology virtual laboratory. J. Open Distance Educ. Educ. Technol. 2017, 13, 107–123. [Google Scholar]
- Gkontzis, A.F.; Kotsiantis, S.; Tsoni, R.; Verykios, V.S. An effective LA approach to predict student achievement. In Proceedings of the 22nd Pan-Hellenic Conference on Informatics, Athens, Greece, 29 November–1 December 2018; pp. 76–81. [Google Scholar]
- Sakkopoulos, E.; Krasadakis, P.; Tsoni, R.; Verykios, V.S. Dynamic mobile student response system. In Proceedings of the Interactive Mobile Communication, Technologies and Learning, Thessaloniki, Greece, 31 October–1 November 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 276–288. [Google Scholar]
- Tsoni, R.; Samaras, C.; Paxinou, E.; Panagiotakopoulos, C.T.; Verykios, V.S. From Analytics to Cognition: Expanding the Reach of Data in Learning. In Proceedings of the 11th International Conference on Computer Supported Education, Heraklion, Greece, 2–4 May 2019; pp. 458–465. [Google Scholar]
- Tsoni, R.; Paxinou, E.; Stavropoulos, E.; Panagiotakopoulos, C.; Verykios, V. Looking under the hood of students’ collaboration networks in distance learning. In The Envisioning Report for Empowering Universities; EADTU: Maastricht, The Netherlands, 2019; pp. 39–41. [Google Scholar]
- Paxinou, E.; Zafeiropoulos, V.; Sypsas, A.; Kiourt, C.; Kalles, D. Assessing the impact of virtualizing physical labs. In Proceedings of the EDEN 2018 ANNUAL Conference, Exploring the Micro, Meso and Macro Navigating between dimensions in the digital learning landscape, Genova, Italy, 17–20 June 2018; pp. 151–158. [Google Scholar]
- Paxinou, E.; Kalles, D.; Panagiotakopoulos, C.T.; Verykios, V.S. Analyzing Sequence Data with Markov Chain Models in Scientific Experiments. SN Comput. Sci. 2021, 2, 385. [Google Scholar] [CrossRef] [PubMed]
- Lerche, T.; Kiel, E. Predicting student achievement in learning management systems by log data analysis. Comput. Hum. Behav. 2018, 89, 367–372. [Google Scholar] [CrossRef]
- Lan, M.; Lu, J. Assessing the Effectiveness of Self-Regulated Learning in MOOCs Using Macro-level Behavioural Sequence Data. In Proceedings of the EMOOCs-WIP, Madrid, Spain, 22–26 May 2017; pp. 1–9. [Google Scholar]
- Zhu, Y.; Li, H.; Liao, Y.; Wang, B.; Guan, Z.; Liu, H.; Cai, D. What to Do Next: Modeling User Behaviors by Time-LSTM. In Proceedings of the IJCAI, Melbourne, Australia, 19–25 August 2017; Volume 17, pp. 3602–3608. [Google Scholar]
- Mahzoon, M.J.; Maher, M.L.; Eltayeby, O.; Dou, W.; Grace, K. A sequence data model for analyzing temporal patterns of student data. J. Learn. Anal. 2018, 5, 55–74. [Google Scholar] [CrossRef]
- Winne, P.H. Cognition and metacognition within self-regulated learning. In Handbook of Self-Regulation of Learning and Performance; Routledge: London, UK, 2017; pp. 36–48. [Google Scholar]
- Winne, P.H. Construct and consequential validity for learning analytics based on trace data. Comput. Hum. Behav. 2020, 112, 106457. [Google Scholar] [CrossRef]
- Chiu, T.K.; Hew, T.K. Factors influencing peer learning and performance in MOOC asynchronous online discussion forum. Australas. J. Educ. Technol. 2018, 34. [Google Scholar] [CrossRef]
- Crossley, S.; Dascalu, M.; McNamara, D.S.; Baker, R.; Trausan-Matu, S. Predicting Success in Massive Open Online Courses (MOOCs) Using Cohesion Network Analysis; International Society of the Learning Sciences: Philadelphia, PA, USA, 2017. [Google Scholar]
- Sun, B.; Wang, M.; Guo, W. The influence of grouping/non-grouping strategies upon student interaction in online forum: A social network analysis. In Proceedings of the 2018 International Symposium on Educational Technology (ISET), Osaka, Japan, 31 July–2 August 2018; pp. 173–177. [Google Scholar]
- Chiru, C.G.; Rebedea, T.; Erbaru, A. Using PageRank for Detecting the Attraction between Participants and Topics in a Conversation. In Proceedings of the WEBIST (1), Barcelona, Spain, 3–5 April 2014; pp. 294–301. [Google Scholar]
- Tsoni, R.; Panagiotakopoulos, C.T.; Verykios, V.S. Revealing latent traits in the social behavior of distance learning students. Educ. Inf. Technol. 2022, 27, 3529–3565. [Google Scholar] [CrossRef]
- Hernández-García, Á.; Suárez-Navas, I. GraphFES: A web service and application for Moodle message board social graph extraction. In Big Data and Learning Analytics in Higher Education; Springer: Berlin/Heidelberg, Germany, 2017; pp. 167–194. [Google Scholar]
- Miller, I.; Freund, J. Probability and Statistics For Engineers; Pearson: Petaling Jaya, Malaysia, 1977. [Google Scholar]
- Fisher, R. On The Mathematical Foundations Of Theoretical Statistics. Philos. Trans. R. Soc. Lond. 1922, 222, 309–368. [Google Scholar]
- Onyema, E.M.; Deborah, E.C.; Alsayed, A.O.; Noorulhasan, Q.; Sanober, S. Online discussion forum as a tool for interactive learning and communication. Int. J. Recent Technol. Eng. 2019, 8, 4852–4859. [Google Scholar] [CrossRef]
- Mtshali, M.A.; Maistry, S.M.; Govender, D.W. Online discussion forum: A tool to support learning in business management education. S. Afr. J. Educ. 2020, 40, 1–9. [Google Scholar] [CrossRef]
- Ergene, Ö.; Kurtça, T.T. Pre-service mathematics teachers’ levels of academic procrastination and online learning readiness. Malays. Online J. Educ. Technol. 2020, 8, 52–66. [Google Scholar] [CrossRef]
- Garzón-Umerenkova, A.; Gil-Flores, J. Academic procrastination in non-traditional college students. Electron. J. Res. Educ. Psychol. 2017, 15, 510–532. [Google Scholar] [CrossRef]
- Agnihotri, L.; Baker, R.; Stalzer, S. A Procrastination Index for Online Learning Based on Assignment Start Time. In Proceedings of the 13th International Conference on Educational Data Mining (EDM 2020), Virtual, 10–13 July 2020. [Google Scholar]
- Adams, R.V.; Blair, E. Impact of time management behaviors on undergraduate engineering students’ performance. Sage Open 2019, 9, 2158244018824506. [Google Scholar] [CrossRef]
- Nesamalar, J.; Ling, T.P.; Singaram, N. Time Management Behaviour During the COVID-19 Pandemic: A Focus on Higher Education Students. Asia Pac. J. Futur. Educ. Soc. 2022, 1, 17–38. [Google Scholar]
- Xavier, M.; Meneses, J. Persistence and time challenges in an open online university: A case study of the experiences of first-year learners. Int. J. Educ. Technol. High. Educ. 2022, 19, 31. [Google Scholar] [CrossRef]
- Muljana, P.S.; Dabas, C.S.; Luo, T. Examining the relationships among self-regulated learning, homework timeliness, and course achievement: A context of female students learning quantitative topics. J. Res. Technol. Educ. 2021, 143–162. [Google Scholar] [CrossRef]
- Jones, I.S.; Blankenship, D.C. Year Two: Effect of Procrastination on Academic Performance of Undergraduate Online Students. Res. High. Educ. J. 2021, 39, 1–11. [Google Scholar]
- Tsoni, R.; Sakkopoulos, E.; Verykios, V.S. Revealing Latent Student Traits in Distance Learning Through SNA and PCA. In Handbook on Intelligent Techniques in the Educational Process; Springer: Berlin/Heidelberg, Germany, 2022; pp. 185–209. [Google Scholar]
- Nandi, D.; Hamilton, M.; Harland, J.; Warburton, G. How active are students in online discussion forums? In Proceedings of the Thirteenth Australasian Computing Education Conference, Perth, Australia, 17–20 January 2011; Volume 114, pp. 125–134. [Google Scholar]
- Cheng, C.K.; Paré, D.E.; Collimore, L.M.; Joordens, S. Assessing the effectiveness of a voluntary online discussion forum on improving students’ course performance. Comput. Educ. 2011, 56, 253–261. [Google Scholar] [CrossRef]
- Voghoei, S.; Tonekaboni, N.H.; Yazdansepas, D.; Arabnia, H.R. University online courses: Correlation between students’ participation rate and academic performance. In Proceedings of the 2019 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 5–7 December 2019; pp. 772–777. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).