Measurement of Music Aesthetics Using Deep Neural Networks and Dissonances

Abstract

In this paper, a new method that computes the aesthetics of a melody fragment is proposed, starting from dissonances. While music generated with artificial intelligence applications may be produced considerably more quickly than human-composed music, it has the drawback of not being appreciated like a human composition, being many times perceived by humans as artificial. For achieving supervised machine learning objectives of improving the quality of the great number of generated melodies, it is a challenge to ask humans to grade them. Therefore, it would be preferable if the aesthetics of artificial-intelligence-generated music is calculated by an algorithm. The proposed method in this paper is based on a neural network and a mathematical formula, which has been developed with the help of a study in which 108 students evaluated the aesthetics of several melodies. For evaluation, numerical values generated by this method were compared with ratings provided by human listeners from a second study in which 30 students participated and scores were generated by an existing different method developed by psychologists and three other methods developed by musicians. Our method achieved a Pearson correlation of 0.49 with human aesthetic scores, which is a much better result than other methods obtained. Additionally, our method made a distinction between human-composed melodies and artificial-intelligence-generated scores in the same way that human listeners did.

1. Introduction

In many domains previously dominated by humans, artificial intelligence (AI) is becoming proficient due to advances in machine learning (ML) and, especially, artificial neural networks (ANN). However, in artistic domains such as graphical arts, literature, and music, AI is not yet performing like human creators. In this paper, we will consider music our main objective, this probably being the most encountered of artistic domains in everybody’s life. Especially now, when most applications on all types of computers and mobile phones are using music, from games to background music and ringtones, it is obvious that the automatic generation of music is needed in order to satisfy demands.

For improving performances of ML and ANNs in artistic domains, an important feature that should be considered is the aesthetics of results, which is the degree to which users appreciate their beauty. Therefore, a measurement of the aesthetics of an AI painting or a piece of music is needed. There is a subfield of artificial intelligence called computational aesthetics, which has the scope to compute the value of human creative expressions such as beauty that are associated with human creativity domains such as music, poetry, or painting [1]. In most cases, mathematical formulas are proposed that try to measure the aesthetic value of human creations or of some natural patterns. In other cases, mathematical formulas are developed in conjunction with artificial intelligence algorithms such as neural networks that are trained on vast amounts of data. The validation of these formulas is usually performed by the analysis of correlations with evaluations of human experts from specific domains.

The key advantage of having an AI application that measures aesthetics is that hiring human evaluators might be expensive or problematic in various circumstances. Another advantage can be seen when evaluating large amounts of data, such as when music or images are produced automatically using artificial intelligence. In some circumstances, aesthetic computing algorithms may be more trustworthy than human evaluators, who are frequently subjective and susceptible to bias. The study of computational aesthetics may also help us better understand how people interpret beauty.

1.1. Aesthetics and Its Relation to Nature

Aesthetics is hard to define. Two descriptions might be “the philosophical study of beauty and taste” [2] and “a set of ideas or opinions about beauty or art” [3]. From these definitions, it is obvious that the analysis of aesthetics implies human subjectivity. Moreover, it depends on social and cultural contexts and on the individual taste and education in art. However, in a positivist sense, there were proposals for linking aesthetics to natural laws and for proposing mathematical measurements [4].

For a long time, many believed that there is a direct link between aesthetics and natural laws. For example, Pythagoras thought that symmetry is at the foundation of natural laws, and ancient Greeks and even Kepler discussed the music of the spheres. Moreover, the golden ratio, which characterizes natural growth processes, like in the Nautilus shell, was used in architecture and other arts for millennia [5]. However, after the scientific revolution, in recent centuries, there were very few authors [6,7,8] who that tried to find links between aesthetics, mathematics, and science. Trying to find physical connections to aesthetics is a recent component of research [9], in which physicists are employing music aesthetics to examine quantic phenomena: a pianist, for example, is playing the piano, and the produced sound waves (through air) are then transported via a BEC (Bose–Einstein condensate), by which the quantum phenomena may be studied on a larger scale since the atoms are brought to a temperature of near absolute zero, and the entire mass of atoms acts as a single atom (via entanglement and superposition). The physicists are hopeful that the pianist’s aesthetic sense may lead to the appearance of new quantic phenomena in the Bose–Einstein condensate.

Nevertheless, some physicists disagree with the idea that aesthetics may be found in all fundamental laws of nature. They state that it is wrong to believe that beauty must be present in all of nature’s laws and the mathematics that governs them, and this belief al-lowed the existence of theories that never had experimental results (the theory of strings) simply because they were too beautiful to be false. Moreover, there have been other examples in history in which this situation has occurred [10].

However, there still are arguments in favor of aesthetics as an important component of fundamental laws of nature. One of them is that human aesthetics changes with time and embraces the disagreeable. For example, in modern art, the ugly represents the negation of beauty, and its existence is important for the beauty to be able to be seen [11]. In fact, any creative work, whether it be in music, art, literature, or even in collaborative chat sessions [12], should actually contain some dissonance. For example, in stories, there should be a conflict between the hero and the antihero in order to prevent monotony. This may also be seen in music, in which dissonances can be found in many excellent compositions [13], which is the inspiration for the experiment in this paper. Monotony also inhibits the development of creativity, and modern methods of teaching students how to compose music employ a variety of techniques of engagement [14].

Another complex example of creativity in music, with major aesthetic effects, is pro-vided by polyphony, which involves the simultaneous performance of multiple voices entering in series of consonances and dissonances, in compliance to particular counterpoint principles. According to the polyphonic model of discourse [15], a similar phenomenon may be encountered in human conversations, a successful cooperation between chat participants having an intrinsic aesthetics analogous to polyphonic music [16]. The polyphonic model is a relatively new theory, having its roots in Mikhail Bakhtin’s dialogism philosophy [17], which highlighted, for example, that many characters from Fyodor Dostoevsky’s writings follow a similar theme and that the conflicts that arise between the characters appear to follow counterpoint rules [17].

As a conclusion, human aesthetics seems to be related to nature, and even if we as humans sense it, is likely that we know very little about it, and we may never know with certainty if it is a part of basic laws of nature or not, and it may even be impossible to compute [18]. A similar issue arises from the study of formal languages and neurology, in which we always run into the challenge of not being able to define the meaning of a word since it is related not only to the word itself but also to the person who is interpreting it [18]. Because Winograd ideas are rooted in Heideggerian philosophy, which states that objective and subjective reality cannot exist independently of one another [19], their implications may be found in a variety of fields impacted by Heideggerian thinking.

1.2. Music Generation Using Neural Networks

In the artificial intelligence domain, and especially in time-varying phenomena such as natural language, a major development was the idea of recurrent neural networks (RNN) [20], in which sequences of consecutive words, characters, or musical notes would be used as input, the model of the relations between them being learned by the neural network. The disadvantage of an RNN is that the longer the recursive process for a consecutive sequence of words is used, the more the gradients of the neural network will tend to diminish or explode, making the training operation useless [21]. An RNN has been used for generating music, but the results lacked more complex patterns such as rhythm or harmony, and the network was also unable to learn longer sequences of notes [22].

One solution that reduced the appearance of vanishing and exploding gradients was the invention of a new neural network design based on an RNN, which is called long short-term memory (LSTM). The inner operations of the LSTM network cell (the network part from the entire unfolded network, which represents the repetitive process that is made for each step) were replaced by gating mechanisms: the forget gate layer (which modulates the information that has to drop from the memory), the input gate layer (which modulates the information that is added to the memory), and the output gate layer (which modulates the amount of memory that will be transferred to the next step from the recursion.

Another well-known variant of LSTM is the gated recurrent unit (GRU) [23], which offers some disadvantages, in terms of learned data capability, and some advantages, in terms of the training period. The difference between them is that LSTM has one extra gating unit, which is the output gate. This enables the LSTM cell to control the amount of internal memory exposure, but it also takes extra computation, making it slower to train in comparison to the GRU. In some cases, when the network does not need to remember long sequences, the GRU outperforms LSTM because the extra gating unit of the LSTM cell is no longer an advantage [24].

The LSTM architecture has brought so far some of the best results for the purpose of generating music. Eck and Schmidhuber [25] used an architecture made of a multi-layered LSTM neural network to generate blues music, and the results were the state of the art at the time. More recent experiments were made by training an LSTM neural network combined with restricted Boltzmann machines (RNN-RBM) on a Bach music corpus [26].

The most recent research in the domain of neural networks was given by the attention mechanism and transformer neural networks [27]. The attention mechanism was initially developed to improve the already existing sequence-to-sequence models [28] that are using recursive neural networks in the domain of neural machine translation. The sequence-to-sequence models are used for mapping one sequence to another, like in the case of English-to-French translation, but language models are the tools preferred for content generation. For generating music, the transformer neural networks, which are used as language models, represent the state of the art [29]. In most recent applications, such as Magenta, music is composed by the interaction between a user and a neural network [30]. Other modern, transformer architectures are developed specifically to generate music on multiple voices with diverse instruments [31].

1.3. Methods for Aesthetic Measurement

We believe that the study of aesthetic measurement is crucial in the context of to-day’s artificially produced art. Birkhoff was the first to devise a simple formula that condensed his observations of art into a mathematical aesthetic formula [6]. The Birkhoff aesthetic measure is a score that calculates a piece of art’s aesthetic value, such as that of a painting or a melody. The score is calculated as M = O/C, where O denotes the composition’s order (coherence), and C denotes its complexity [4]. As a comment, the Birkhoff measure, even if it was used in analyzing some creations, is rather naive. For example, dissonances and polyphony (which some persons may consider to have high aesthetics) receive a small aesthetic measure due to the complexity they introduce.

In the domain of photography, the Birkhoff aesthetic measure was used as a response metric for the study of the effectiveness of techniques such as noise addition and unsharp masking [32]. Because entropy is frequently understood as a measure of disorder, the complexity of the Birkhoff measure is computed using Gibbs entropy.

For evaluating paintings, the Birkhoff aesthetic measure has also been modified to better represent the aesthetic value of a work of art. Different formulas that are based on Shannon entropy, Kolmogorov complexity, or Zurek’s physical entropy were used to compute the aesthetic measure of paintings from different artists such as Piet Mondrian, Vincent Van Gogh, or Jackson Pollock [4].

Researchers have also attempted other approaches to define aesthetic measures without using entropy. Psychologists investigating the melodic expectations of a group of people uncovered the reasoning behind a process of music expectation [33]. The group consisted of adults, 11-year-olds, and 8-year-olds. Expectations were collected and analyzed, and the findings impacted the development of a melodic aesthetic measure based on the Birkhoff formula [33].

If we consider the cases of consonance and dissonance in music, we should intro-duce the definition of a musical interval because it will be used often in the remaining sections of the paper. The difference in pitch between two successive musical notes is known as a musical interval. Even though the interval definition does not include any information regarding the difference in duration between the corresponding successive notes, the same definition is also utilized in this paper for the durations because it was also referred to as an interval of durations in the cited papers [33].

According to this concept, a normal listener assumes that after hearing an open interval, an interval that sounds unfinished, the interval would be closed very soon. Although there are three factors that contribute to the openness of an interval [33], only two of them were used in this paper in order to compute the aesthetics score.

The first factor implies that when the duration of the first note of an interval is less than the duration of the second note of the same interval, the interval is considered open. An example is when an eighth note is followed by a quarter note. The second factor indicates that an interval is considered open if the pitch of the interval’s second note is more stable than the pitch of the interval’s first note. If a pitch matches the notes do, mi, and sol from the solfege of the key to which it belongs, then it is perceived as stable. A ti note followed by a do is an example of an interval following this factor.

The opposite factors that correspond to the closure of intervals occur when the duration of the second note of an interval is less than the duration of the first note of the same interval and when the pitch of the second note of an interval is reversed to the pitch value of the first note of the interval preceding the present interval. When three notes are examined in the melodic line of a song, if the third note is a ti, the second note is a do (a sound that is regarded as stable), and the first note is also a ti, then the listener’s expectation is met. An algorithm was designed for computing aesthetics metrics for short musical fragments starting from these factors introduced by Schellenberg [34].

The Schellenberg algorithm can be used for computing the aesthetic measure of melodies. When the algorithm discovers an open interval, it checks to see if it is closed by the succeeding interval. If the next interval is closed, then the expectations of the listener have been satisfied. If all the expectations are met, the melody has a low complexity; however, if they are not met, the melody has a greater complexity [34], this being a way of computing the complexity (C) of a musical fragment. The composition’s order in the Birkhoff aesthetic measurement can be computed as O = A − C, where A represents the total amount of intervals in the melody, and C represents the previously defined complexity [34].

Research has also been conducted on measuring the aesthetics of a piece of music by determining the tonal qualities of it. In his book, A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice, Tymoczko [35] explores five aspects of music tonality:

• Conjunct melodic motion (CMM) in which the melody of a piece of music flows over small distances note by note.
• Acoustic consonance in which consonant harmonies are regarded as a point of stability in music and are favored over dissonant harmonies.
• Harmonic consistency in which the harmonies of a musical section tend to be similar in structure to one another.
• Limited macroharmony (LM) in which tonal music favors the usage of small macroharmonies (a sequence of notes that are heard over a small period of time), usually including five to eight notes.
• Centricity (CENT) in which a single note is perceived to be more dominant than the rest, and over periods of time, it begins to appear more frequently and acts as an objective for the melodic movement.

All the above aspects can be used in different ways to compute the aesthetic measure of a piece of music. Three of them have already been implemented in the music-geometry-eval python library [36] and have also been used with success in previous research [37].

Recent research [38], which analyzes the pitch histogram (or a proposed merged pitch histogram) of a melody, can provide a new perspective for the analysis of the aesthetics of a melody. This research emphasized the bell shape of the histogram of a specific class of Chinese pentatonic folk songs [39]. This kind of analysis and the bell shape of the histograms can be placed in relation to the perspective of musical aesthetics that considers natural physical laws.

1.4. Current Research Objective

This article tries to fill a methodological gap of aesthetic computing, in which music theory and human expectations are used in conjunction with modern neural networks to compute the aesthetic score of a melody.

This article’s contributions can be summarized as follows:

• Proposing a new method that computes the aesthetics of a melody fragment based on good and bad dissonance frequency (this classification is made using a neural network trained on the largest corpus of MIDI melodies that is currently available). In order to facilitate the understanding of our method, we publicly release the source code at https://github.com/razvan05/evaluated_ai_melodies (accessed on 29 May 2023).
• Realizing and presenting the results of two studies with 108 and 30 participants, in which melody fragments have been evaluated based on how aesthetically pleasant the melodies have been considered. The melodies that were used for evaluating our method have been uploaded on YouTube at https://youtu.be/uHKaeTF1PCw (accessed on 29 May 2023).
• Proposing a new mathematical formula that is used for computing the aesthetics of a melody fragment following the newly proposed method from point 1 and evaluating the formula using one of the studies from point 2.
• A comparative analysis was conducted to assess the performance of our new method in relation to two other state-of-the-art methods developed by psychologists and musicians. By comparing the results obtained from these different methodologies, we were able to gain insights into the strengths and limitations of each method, thereby highlighting the advancements and contributions offered by our novel approach.

The paper continues with a section describing the method employed to compute the aesthetics of a melody fragment using the concept of good and bad dissonance frequency. This section contains a comprehensive presentation of our proposed method, including intricate details and the methodologies employed. Additionally, it introduces two distinct human studies that were conducted to evaluate the effectiveness of our approach. Section 3 focuses on presenting the results obtained from a study introduced towards the end of Section 2, in which the entire proposed method is rigorously evaluated. This section delves into the detailed analysis and interpretation of the obtained results. Finally, Section 4 serves as the concluding section, providing a summary of the key findings and their implications. Additionally, this section presents future research directions, suggesting potential directions for further investigation and the development of the proposed method.

2. Methodology

Birkhoff’s aesthetic measure has the drawback of being too simple in some situations, as mentioned above. For example, as discussed in the second section of this paper, dissonances are exploited to generate even more enjoyable music in many great human compositions, and the Birkhoff measure is low in these cases. Even though dissonances might be associated with unnecessary complexity due to unpleasant sounds, they are employed for aesthetic enhancements in a variety of domains and not only music [13].

In music, a dissonance is the opposite impression of stability (of a consonance), which creates a sense of tension for the listener when certain combinations of notes are played simultaneously. A dissonance corresponds to two different consecutive pitches, and some examples of dissonance are the following musical intervals: major and minor seconds, tritones, and major and minor sevenths. Dissonant intervals can also be augmented or diminished, when one half step is larger or smaller than perfect or major/minor intervals. However, we did not consider augmented or diminished intervals in the research presented here. We will include them in future work. As mentioned, dissonances are very important for music in order for it to not be boring and to make it creative. Moreover, dissonances are also essential in polyphony, in general, and in any creative process, in order to achieve the necessary divergent (equivalent to dissonances) steps [12,15]. Therefore, we can consider a good dissonance is one that is adopted by human composers to improve the aesthetics of their music, whereas a bad dissonance is one that does not increase the melody’s aesthetics.

2.1. General Description of the Experiments

The Lakh MIDI dataset (LMD) [40] corpus of human compositions was employed for the research described in this paper. Almost 175,000 melodies in the MIDI format from various genres make up the corpus [41], which were collected from publicly accessible online sources and deduped according to their MD5 checksum [40]. The Lakh MIDI dataset is also the largest MIDI dataset from MIR datasets according to the ISMIR website [42]. By using the largest MIDI corpus that is currently accessible, we believe that the issues associated with training on popular music, specifically, will be reduced. Such problems will be further discussed in this section.

In the following section, Section 2.2, a comprehensive description is provided describing the methodology employed to identify the dissonances that enhance the melodic quality (good dissonances) and distinguish them from dissonances that introduce unpleasant auditory elements (bad dissonances). This section outlines the specific approach used, leveraging the Lakh MIDI dataset, to train a bidirectional GRU neural network. The network was trained using the following set of hyperparameters: a learning rate of 0.0001, a sequence length of 20, a batch size of 64, and a hidden value size of 200. The training process encompassed five epochs to ensure comprehensive model learning and convergence.

In Section 2.3, a detailed description is provided of the methodology employed to derive a mathematical formula based on the frequency of good and bad dissonances. This formula serves as the basis for computing the aesthetic score of a given melody. At this stage, a human study was conducted involving 108 students who were asked to assign aesthetic scores to five melodies. The obtained results were then compared with scores generated by multiple proposed mathematical formulas. Via this comparative analysis, the most effective formula was identified and selected for further evaluation. This evaluation, which is described in Section 2.4, encompasses the entire methodology described in the paper.

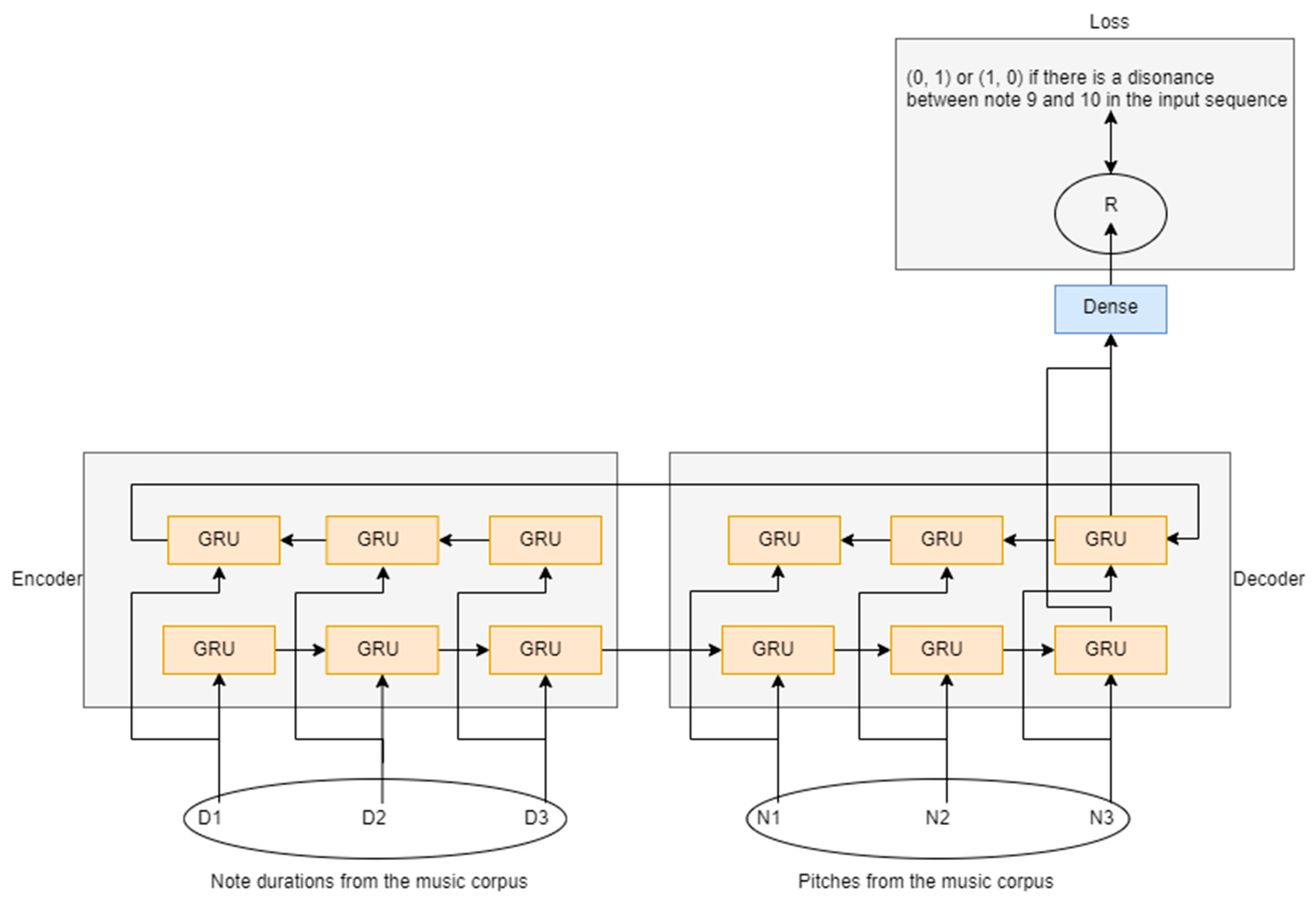
2.2. Finding the Good and Bad Dissonances

In order to determine when a dissonance improves a melody, a neural network has been trained on the entire Lakh MIDI dataset to learn the surrounding notes of any dissonance from the corpus. In this study, the dissonances from the corpus are thought to improve the melodies of which they are a part of since human composers thought to employ them in their works. Therefore, every time our neural network recognizes a dissonance, it means that the dissonance is a good dissonance, and it is counted (with the “G” variable). On the contrary, if, in a new melody that is generated by artificial intelligence, our neural network does not recognize a dissonance, it means that the dissonance is not improving the aesthetic score of the music because a human composer would not use it in his work, and the dissonance is counted (with the “B” variable).

For computing the aesthetic measure of a new melody, the neural network is used to determine if the surrounding notes of a dissonance suggest that the dissonance improves the melody (good dissonance) or, in the other case, if the dissonance reduces the aesthetics of the melody (bad dissonance). For this reason, the neural network must solve a binary classification problem.

The neural network is a sequence-to-sequence model with one bilateral GRU as the encoder and one bilateral GRU as the decoder (Figure 1). All dissonances with 10 notes to the left and 10 notes to the right have been retrieved from the original corpus (Lakh MIDI dataset). As a result of this, the length of a sequence is 20. Because the intervals without dissonances are much more frequently found in the corpus, an equal number of normal intervals are also retrieved, for which the neural network must learn that the interval has no dissonances between the middle notes. Consequently, the neural network’s input is a stack of sequences equal to the number of dissonances multiplied by two (for the intervals that are not dissonance).

All the intervals that have dissonances between the middle notes are randomly mixed with the intervals that have no dissonances in order to prevent the neural network from learning only one category instead of two if there are many intervals of the same type that may be found in a succession. Because only the dissonances must be identified in order to generate the aesthetic scores, a slightly penalized model was trained, with a weight of 1.25 for the dissonances class and 0.75 for the normal interval class.

Using the Music21 Python framework [43], the melodic lines were extracted from the Lakh MIDI dataset and divided into batches of sequences. Before being supplied into the neural network, the sequences are hot encoded. The hidden value size is 200 (which, for the current architecture, translates into a neural network with almost 1.5 million neurons), and the batch size is 64, and these values were chosen based on the results from multiple experiments (hyperparameter tuning was not used in these experiments). The neural network was trained using the Adam optimizer with a learning rate of 0.0001 and a binary crossentropy loss. The training was performed on 90% of the entire corpus for five epochs, which corresponds to the training corpus. The testing corpus is represented by 5% of the entire corpus, and the validation corpus is represented by the remaining 5% of the entire corpus. The final training precision was 91%, and the recall was 97%. In order to facilitate the understanding of our neural network, we have released the source code of the model at https://github.com/razvan05/evaluated_ai_melodies (accessed on 29 May 2023).

Because the aesthetic measure presented in this article is highly dependent on the corpus on which the neural network was trained, problems regarding a biased measure can appear. Because the neural network decides if a dissonance is good or bad, if the corpus only contained melodies from a certain genre, the aesthetic measure would give a higher aesthetic score to melodies from that genre. The same remains true if the melodies from the corpus are highly popular, and the aesthetic measure would not give a high aesthetic score to melodies that are innovative. The risk of having a biased measure is reduced by using the largest MIDI dataset from MIR datasets [42].

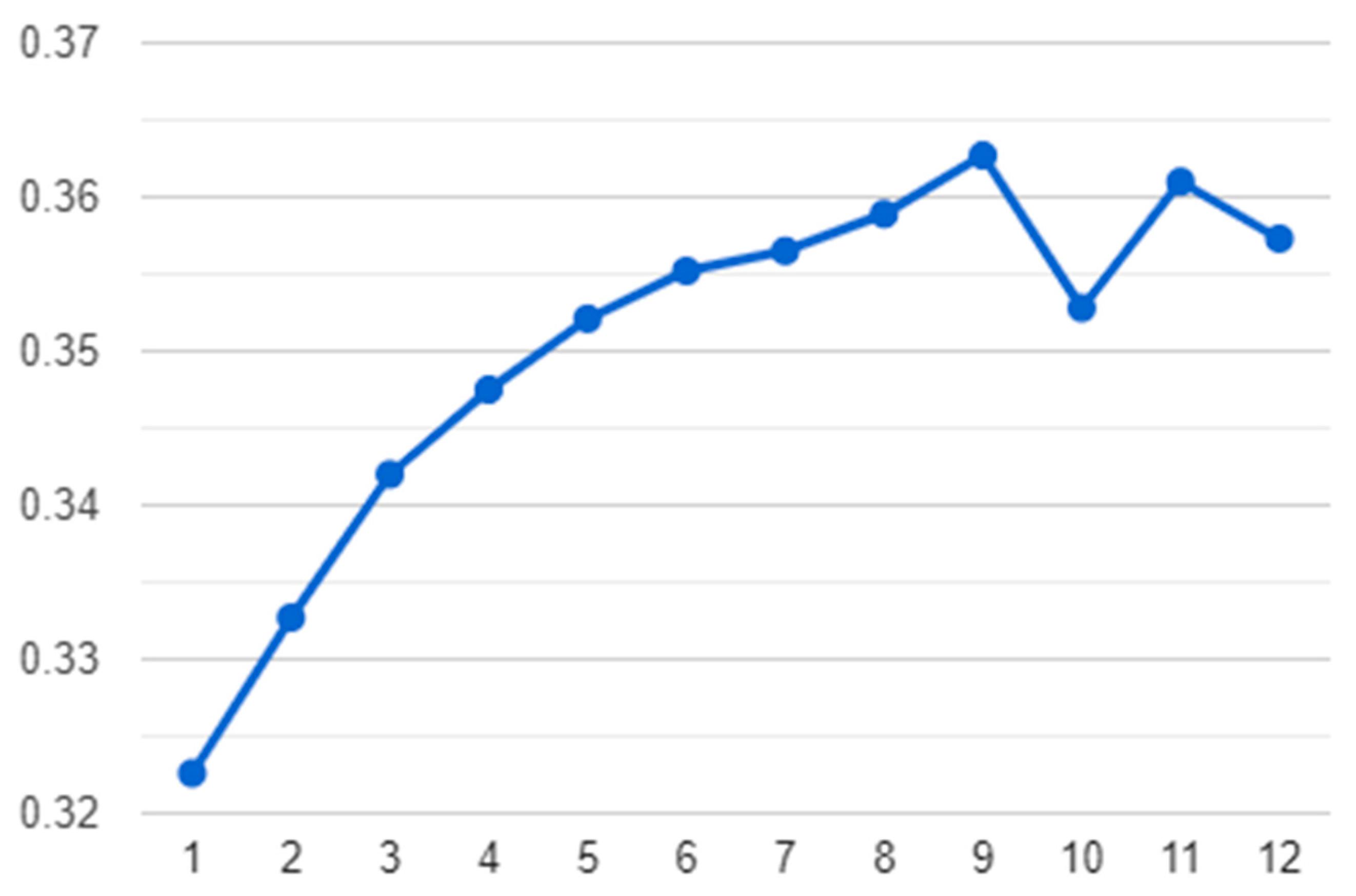
2.3. Choosing the Best Formula

In order to compute the aesthetic metric with the help of the above technique of computing the number of good and bad dissonances, seven formulas were considered because of the way they highlight the presence of dissonances that occur in considerably lesser numbers than the normal intervals in the corpus (one dissonance for every 60 normal intervals).

For evaluating the efficiency of the chosen formulas, a study was conducted at a technical university in Romania in which 108 students participated (80 male and 28 female). Students were Romanian, and most of them were aged between 22 and 25 years old. Each student was asked to complete a Google form questionnaire. At the beginning of the questionnaire, they were requested to listen to five melodies for approximately 30 s each. Following that, the students were asked to rate each melody with a mark between 1 and 5, with 1 indicating that the melody was unpleasant to hear and 5 indicating that it was a very nice melody.

The first two melodies were generated using a vision transformer neural network [44]. The neural network was trained as a language model. The melodies from the dataset are supplied to the neural network in batches of 100 melodies, and each batch is divided into 128 consecutive pitch sequences and 128 consecutive duration sequences. Each sequence is made up of 150 consecutive notes extracted from three voices (50 consecutive notes from each voice). As a result, the neural network can produce music with only three voices. The embedding size of the transformer was 256. The next three melodies were produced in a similar manner to that of previously published research [45]. In that experiment, the durations of notes from the melodies were generated by the same technique used in the MusicXML Creator platform [46], and the pitches for the same notes were generated using a GRU sequence-to-sequence neural network. For the current set of melodies, instead of a sequence-to-sequence GRU, a classic transformer was used [27].

Finally, the arithmetic mean of the students’ scores was computed and then multi-plied by 2 in order to obtain a final mark ranging from 1 to 10. The results are presented in

Table 1. Human aesthetic scores compared with the results from seven different aesthetic measure formulas. Using the numbers for G and B mentioned above, the value of the formulas can be computed.

	Melody 1	Melody 2	Melody 3	Melody 4	Melody 5
Human aesthetics score	6.88	6.62	6.29	4.12	6.18
Good dissonances (G)	167	636	52	20	20
Bad dissonances (B)	20	6	1	2	0
$\frac{\mathrm{G}}{G+B}$	8.93	9.9	9.81	9.09	10
$\frac{\mathrm{G}}{G+B^2}$	2.94	9.46	9.81	8.33	10
$\frac{\mathrm{G}}{G+2\ast B^2}$	1.72	8.98	9.62	7.14	10
$\frac{2\ast \mathrm{G}}{2\ast G+B^2}$	4.55	9.72	9.9	9.09	10
$\frac{G^2}{{(G+B)}^2}$	7.97	9.81	9.62	8.26	10
$\frac{G^2}{{(G+2\ast B)}^2}$	6.5	9.63	9.27	6.94	10
$\frac{G^2}{{(G+3\ast B)}^2}$	5.41	9.45	8.93	5.91	10

together with the number of good and bad dissonances obtained using the binary classifier constructed using a neural network. The variance and the standard deviation of the human aesthetic scores are presented in

Table 2. Variations and standard deviations for the human aesthetic scores.

	Melody 1	Melody 2	Melody 3	Melody 4	Melody 5
Variance	1.33	1.35	1.49	0.84	1.65
Standard deviation	1.15	1.16	1.22	0.91	1.28

.

In order to determine the strength of an association between the aesthetic scores provided by the students that participated in the study and the aesthetic measure scores generated by the proposed method, the Pearson correlation coefficient was computed for the results obtained for each aesthetic formula presented in Table 1. The results are specified in

Table 3. Pearson correlation coefficients between the human aesthetic scores and the current method of computing the aesthetic measure of a melody (results obtained using different formulas).

	Pearson Correlation Score		Pearson Correlation Score
$\frac{\mathrm{G}}{G+B}$	0.31	$\frac{G^2}{{(G+B)}^2}$	0.32
$\frac{\mathrm{G}}{G+B^2}$	−0.25	$\frac{G^2}{{(G+2\ast B)}^2}$	0.33
$\frac{\mathrm{G}}{G+2\ast B^2}$	−0.16	$\frac{G^2}{{(G+3\ast B)}^2}$	0.34
$\frac{2\ast \mathrm{G}}{2\ast G+B^2}$	−0.31

.

The Pearson correlation values from Table 3 indicate that the last three formulas, which have the largest correlation with the human aesthetic scores, can be generalized into a single formula using an alpha coefficient. Thus, the chosen formula is

$$\frac{G^2}{{\left(G+\alpha \times B\right)}^2}$$

(1)

where G represents good (useful) dissonances, and B represents bad dissonances.

Before testing the formula against a second study in order to find its effectiveness, the Pearson correlation was computed between the human aesthetic scores from the first study and the aesthetic scores obtained using the current formula with different alpha coefficient values. The results are displayed in Figure 2. Using these findings, the alpha coefficient for the current formula during the evaluation of the proposed aesthetic method was determined to be 9.

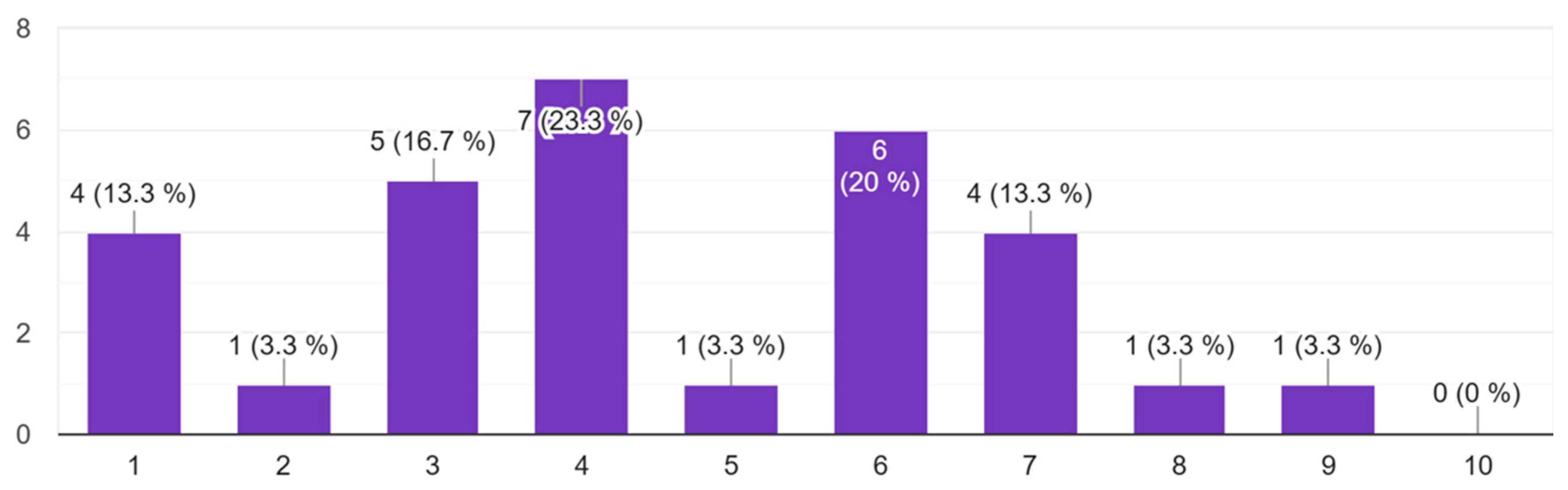
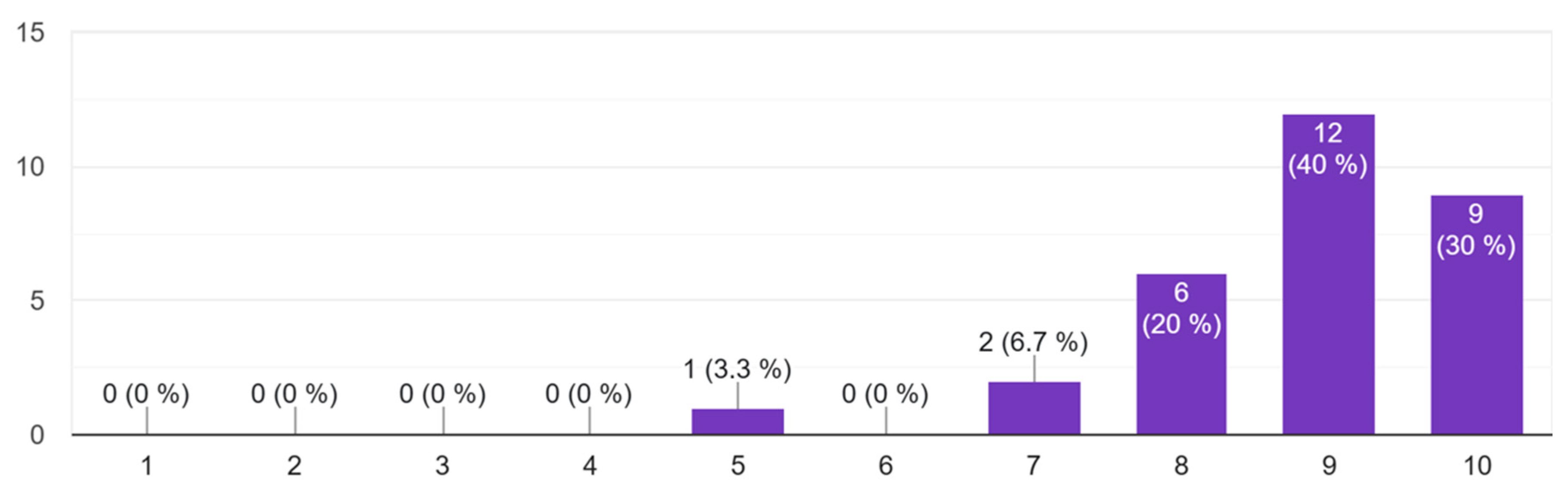
2.4. Evaluation

The second study used for the evaluation of the approach has been performed using eight melodies and a questionnaire given to students from the same technical university from Romania. The human grades were compared with the proposed aesthetic score generation method, the previously developed Schellenberg method, and the three aesthetic measures (CMM, LM, and CENT) derived from Tymoczko works [35]. The first two methods were chosen because they both rely on the Birkhoff aesthetic formula.

The number of melodies from the questionnaire was chosen based on the duration of the melodies. For a melody with a longer duration, the aesthetic measure described in this article would be more accurate because there are more dissonances in it; nevertheless, a longer duration also means that the students will need more time to complete the questionnaire. Because of this, the duration of the melodies was restricted to 30 s, which means that the questionnaire will need between 5 to 10 min to be completed if re-listening to the melodies is taken into consideration. The melodies were selected and created using the following three methodologies:

• Melodies 1, 3, 5, and 8 were all randomly selected from the testing corpus and are all human compositions. Additionally, they share the characteristic of being not popular because no references were found to them in their MIDI file;
• During prior research, melodies 2 and 7 were created by combining chat sonification with neural network pitch generation [45] with a similar method to that used for generating the last three melodies from the first study. The strategy was based on the polyphonic model theory [15] described in the Introduction;
• Melodies 4 and 6 were created using a transformer neural network that was trained on the same corpus (Lakh MIDI dataset) as the sequence-to-sequence bilateral GRU from this study. In this situation, both the durations and pitches of the notes were generated using the neural network. In order to train the transformer, the following hyperparameters were used: sine and cosine positional encoding [27], 256 embed-ding size, eight-head multi-head attention, sparse categorical crossentropy loss, and an Adam optimizer with a learning rate of 0.0001. The network was trained for a total of 10 epochs.

For evaluation, 30 computer science students completed a Google form questionnaire in which they were asked to rate each of the eight melodies on a scale of 1 to 10, with 1 indicating that the melody was not pleasant to hear and 10 indicating that it was a very nice melody. They were also informed that the questionnaire’s objective was to compare the aesthetic perception of humans with an artificially calculated aesthetic measure. The students were not stimulated with rewards if they completed the form, so only 30 from approximately 105 students in 7 classrooms who were invited to participate in the survey chose to complete the questionnaire. Finally, the arithmetic mean was calculated utilizing all the scores assigned to one melody.

3. Results and Discussion

In

Table 4. Aesthetics scores produced by different techniques.

	Melody 1	Melody 2	Melody 3	Melody 4	Melody 5	Melody 6	Melody 7	Melody 8
Human aesthetics score	5.56	3.9	7.3	5.2	6.56	4.5	4.83	8.83
Variance	3.35	2.85	2.97	4.63	3.97	4.81	4.41	1.31
Standard deviation	1.83	1.68	1.72	2.15	1.99	2.19	2.1	1.14
Schellenberg method score	2	6.08	4.22	6.04	1.76	1.81	6.58	3.33
Current method score	7.85	7.56	10	4.82	10	0.33	10	9.23
Conjunct melodic motion (CMM)	9.65	12.73	10.74	7.07	15.1	11.12	10.41	7.75
Limited macroharmony (LM)	1.71	1.64	7.03	10.02	1.04	12	1.37	5.95
Centricity (CENT)	0.03	0.13	0.02	0.03	0.07	0.07	0.06	0.05

, the following results are presented: the arithmetic mean for each melody computed using the students’ questionaire scores, the students’ scores variance and standard deviation, the Birkhoff aesthetic measure score computed using Schellenberg’s music expectation research, and the current aesthetic measure score presented in this paper.

Based on the results, the following remarks can be made:

• The first observation is that the neural network recognizes almost all the dissonances in the testing corpus because the current aesthetic measure presented in this paper gives the melodies from the testing corpus, written by human composers, a final score of almost 10.
• The second observation is that the Birkhoff measure based on human music expectation (Schellenberg method) yielded a higher score for artificial-intelligence-generated melodies (especially melodies 2, 4, and 7) than human-composed melodies (melodies 1, 3, 5, and 8), which is in contrast to the scores provided by human listeners who were able to determine which melodies were made by human composers.

The Pearson correlation coefficient has been calculated in order to determine the strength of a linear association between the aesthetics scores provided by the aesthetic measures and the human aesthetics scores. The Pearson coefficient between the human aesthetics score and the current method score is 0.49, which corresponds to a medium-to-high positive correlation between the variables. On the other side, the correlation between the human aesthetics score, the Schellenberg method score, and the three aesthetic measures (CMM, LM and CENT) derived from Tymoczko works [35] are −0.33, −0.24, 0.02, and −0.5, in which the majority of them correspond to a negative correlation.

Since the melodies were trimmed to 30 s in order for the form to be completed by as many students as possible, a more thorough evaluation will now be necessary. When the complexity and order are computed from many notes, both aesthetic measures will produce more accurate results. Additionally, students who have studied music should also be involved in filling out the survey in order to properly evaluate the approaches using human aesthetics scores. As can be seen in Figure 3 and Figure 4, the melodies generated by neural networks were not assessed for this evaluation with the same confidence as the melodies composed by humans.

The same observation can be made by looking at the variance of the student’s scores from Table 1. Melodies 4 and 6, which were generated by a transformer neural network trained on the Lakh MIDI dataset, were evaluated with the lowest degree of trust. Nevertheless, the melodies that were composed by humans and the melodies that were generated by the method that used the polyphonic model have been evaluated with more certainty. Additionally, it is important to note that the melodies that were extracted from the testing corpus (human compositions) were not popular melodies.

4. Conclusions and Future Work

The implications of dissonances in music aesthetics were addressed in the current study. From a corpus of human-composed melodies, a neural network was trained to learn the notes involving dissonances. For any new melody that does not belong to the corpus on which the neural network was trained, an aesthetic measure was computed using the assumption that, if humans used dissonances in their melodies, they used them only to increase the aesthetics of the music.

The results are satisfactory, but more investigation is required. To further understand the impact of dissonances on music aesthetics, a more thorough analysis is required, in-volving the use of several artificial-intelligence-generated melodies that are also longer in duration, which will allow a more precise measurement of the aesthetics because of the existence of multiple dissonances. Additionally, an important distinction must be made between dissonances such as augmentation and diminution intervals, which, at the current stage of the research, have not been taken into consideration.

Another factor to consider is that the present aesthetic measure only allowed for the use of dissonances. Combining multiple aesthetic measures based on distinct musical patterns, such as rhythm, is also something that has to be further researched. Another experiment that must be performed in a future study is the generation of additional aesthetic measure formulas that use the same principle of good and bad dissonances by using genetic algorithms. These algorithms will use for their fitness functions human evaluations of several melodies from the validation corpus that will be obtained from another study.

This study could also be improved by rewarding the students who complete the questionnaire. A larger number of subjects will complete the form, and the number of melodies and their durations will increase because the students will be more motivated to evaluate the aesthetics of the chosen melodies. Another improvement to the study would be to ask, for each melody in the questionnaire, whether the listener had already heard the melody in order to eliminate bias. Additionally, the students will be questioned about their cultural backgrounds, such as religion and nationality, because this factor may have a significant impact on their personal preferences.