Irradiance Non-Uniformity in LED Light Simulators
Abstract
1. Introduction
1.1. Related Work
1.2. Problem Statement
2. Methods for Irradiance Pattern Modeling of LED Sources
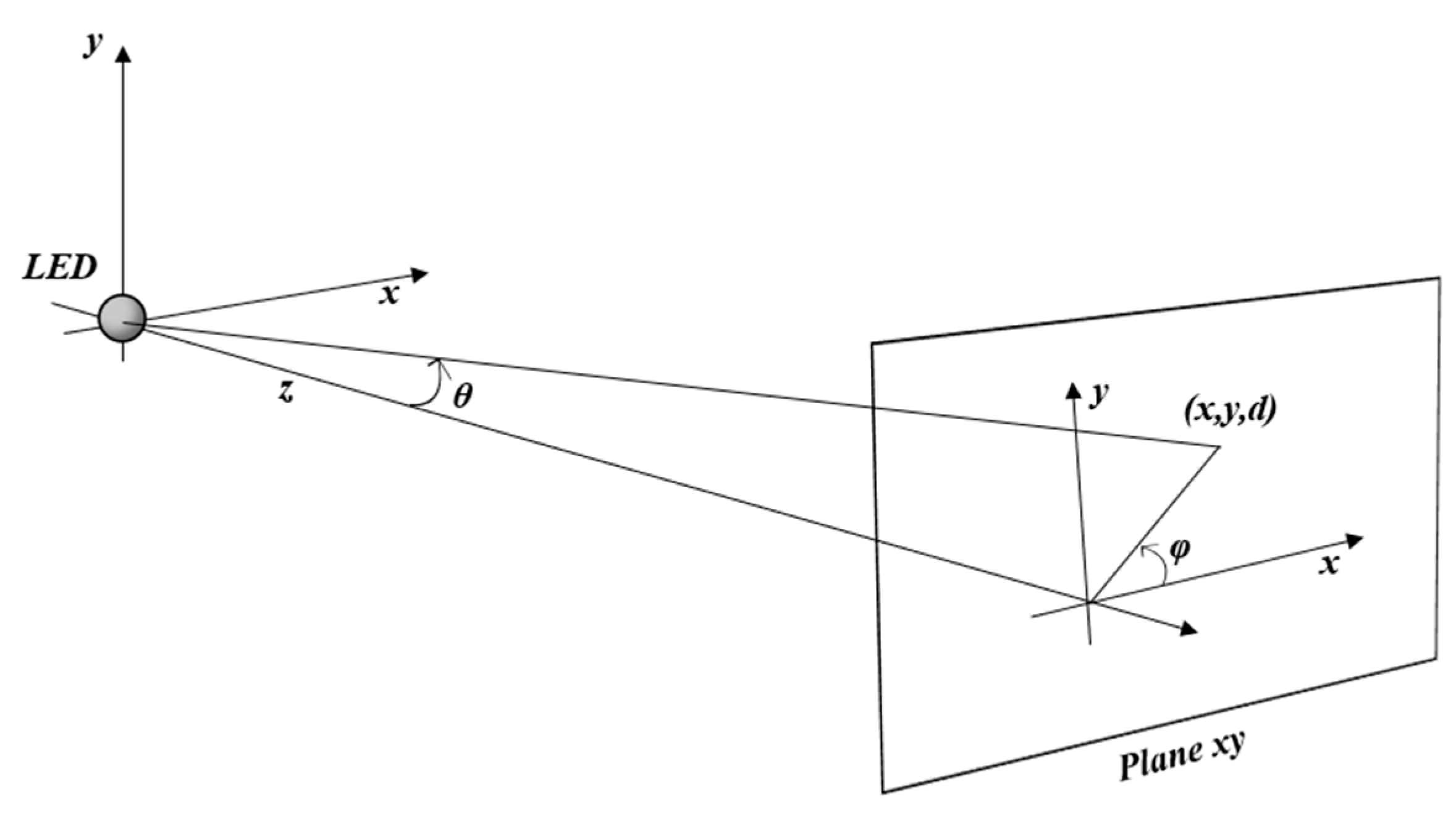
2.1. Modeling of Multisource Irradiance on a Plane
2.2. Single-Source Irradiance
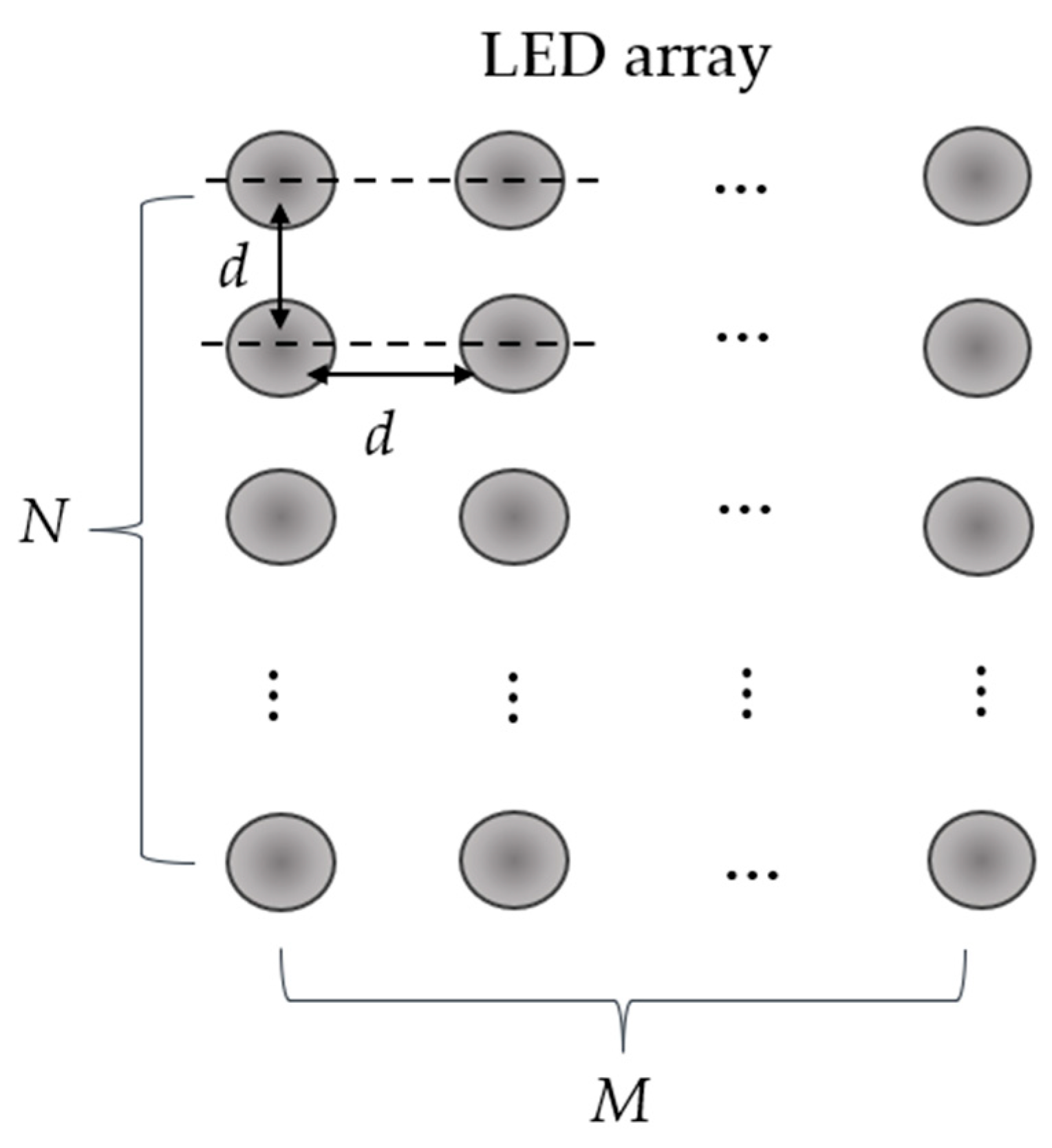
2.3. Multi-Source Irradiance
2.4. Multi-LED Light Simulator Design Guidelines
3. Experimental Implementation
3.1. Design of the Low-Cost Light Simulator Used
3.2. The Software Model
4. Discussion
4.1. Evaluation
4.1.1. Uniformity of Illumination Distribution
4.1.2. Non-Uniformity
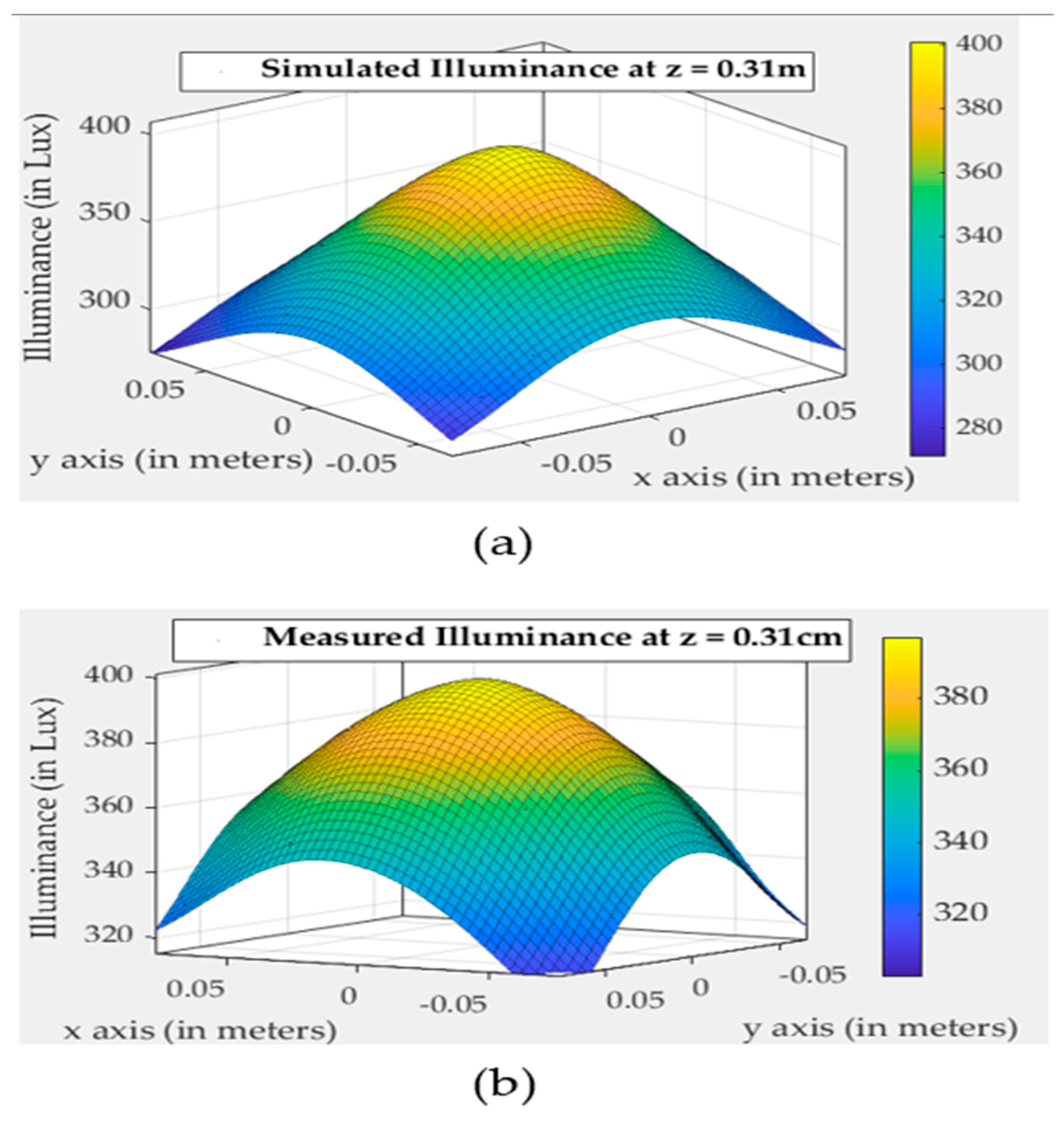
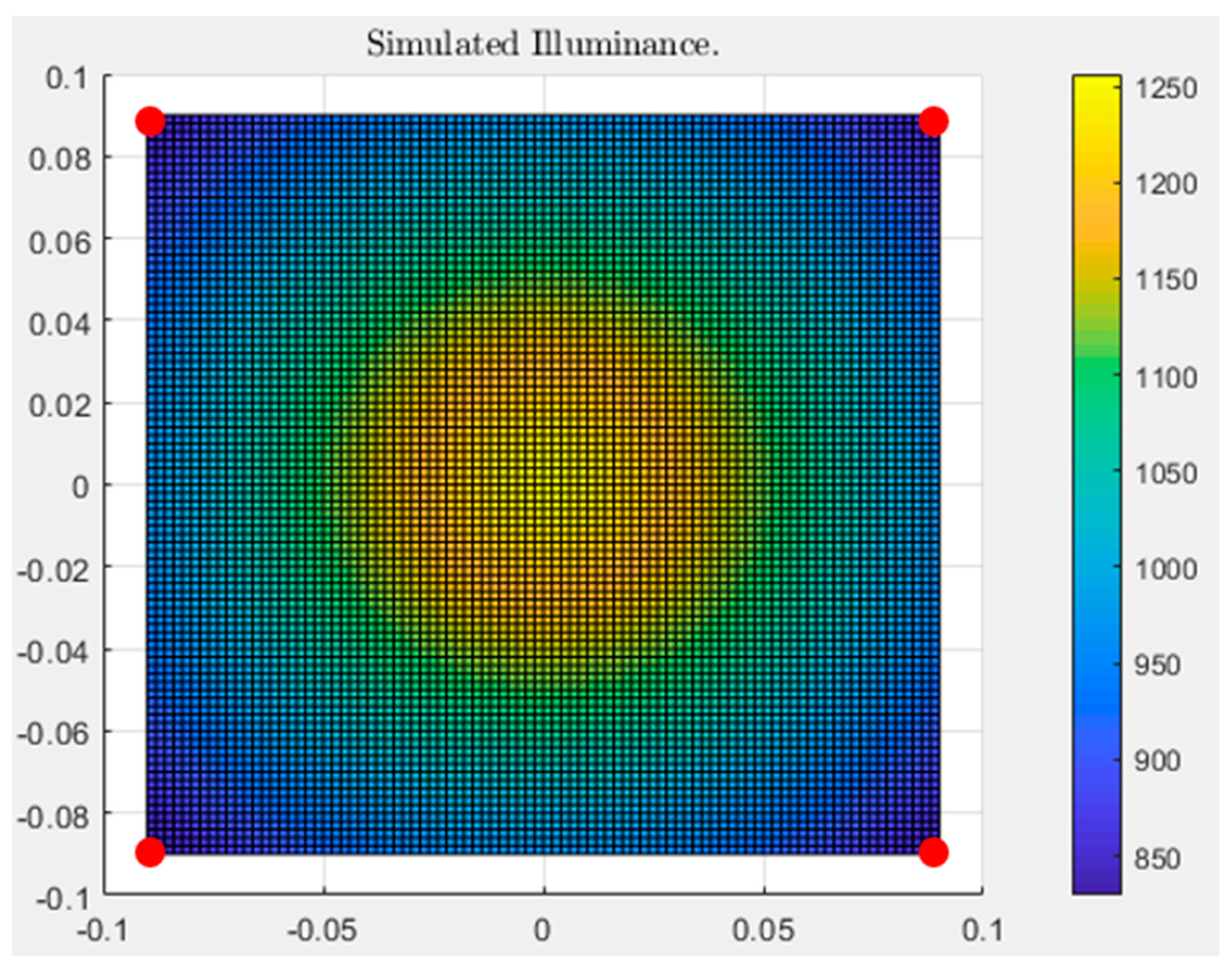
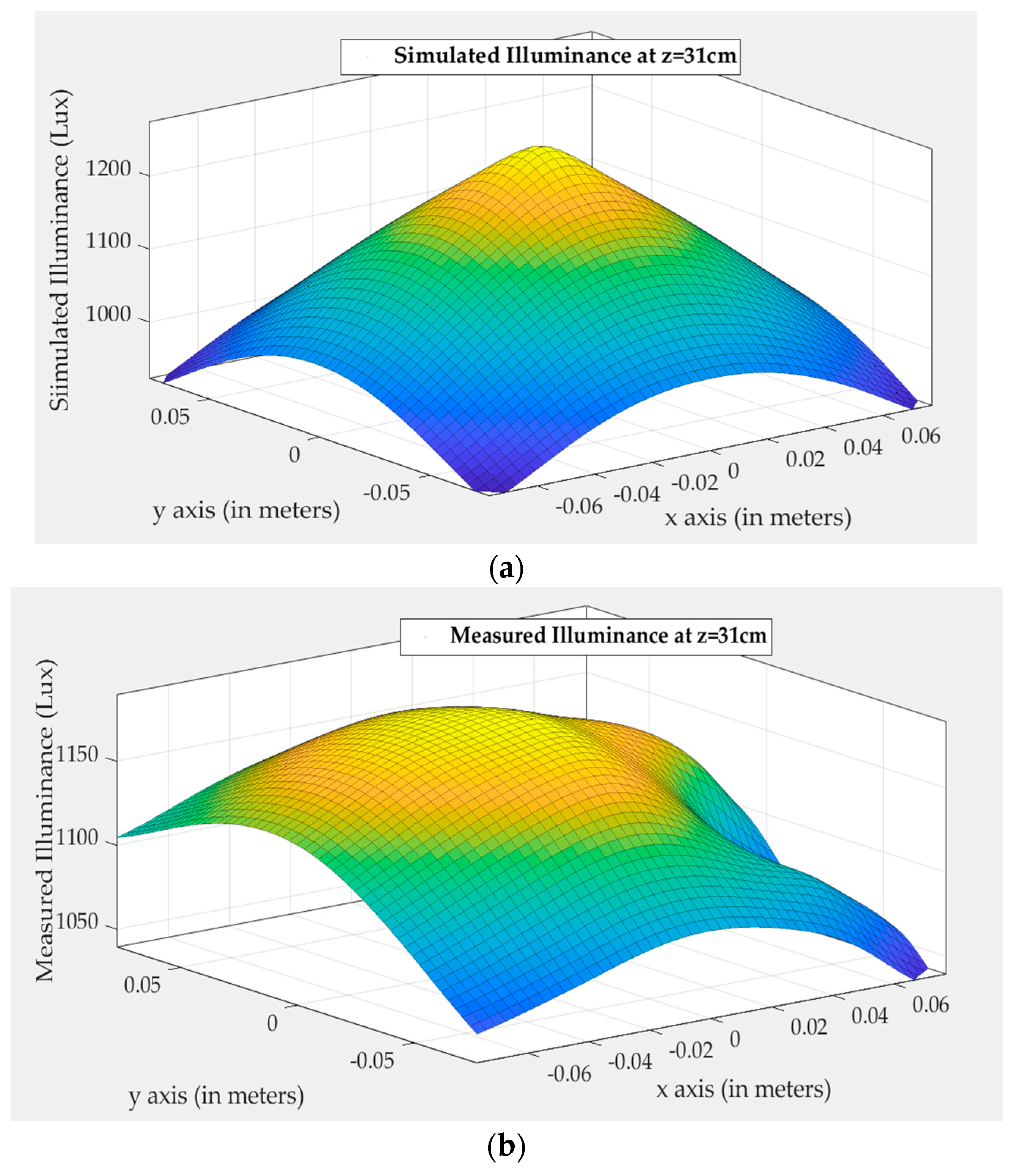
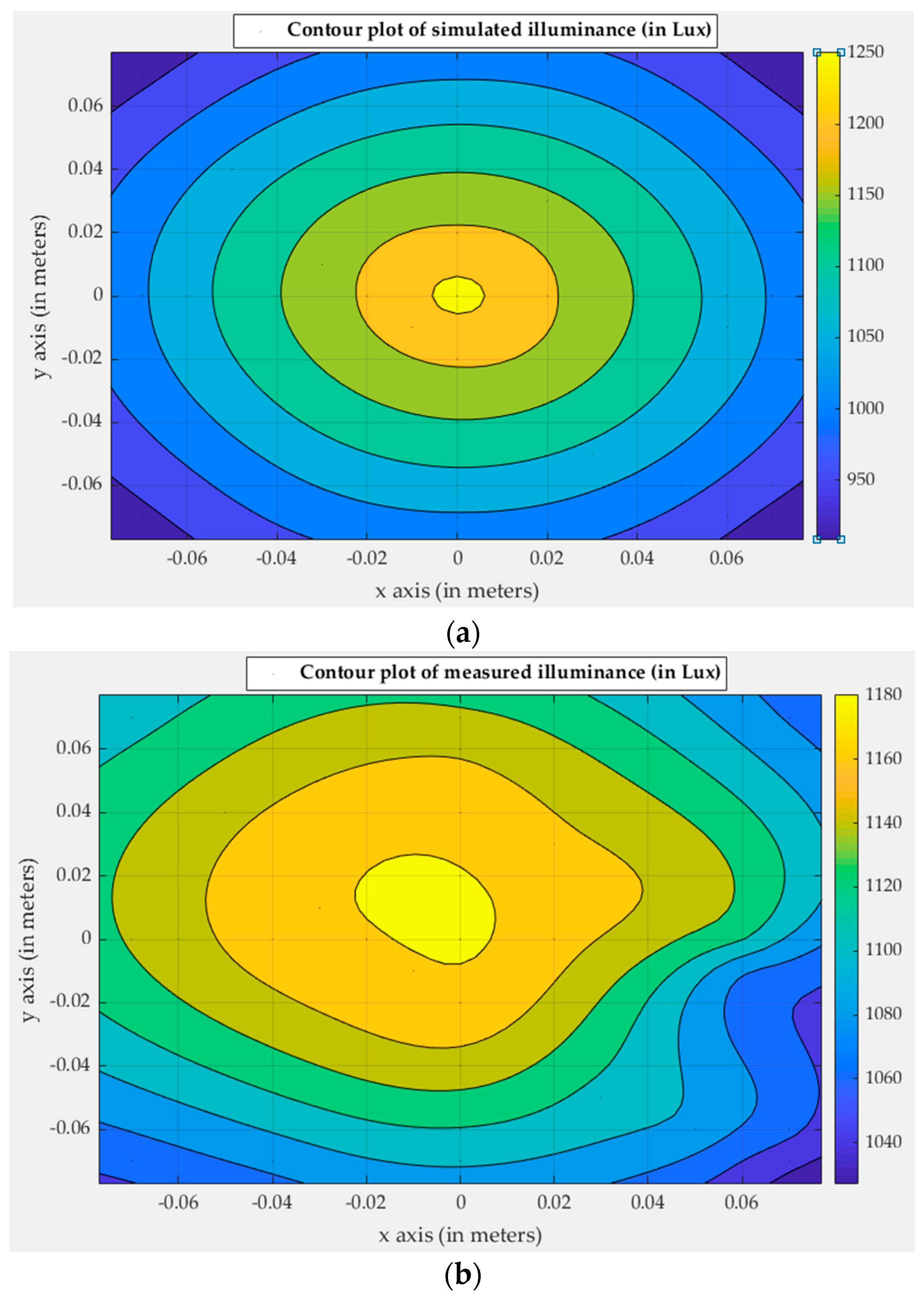
4.2. Simulations vs. Measurements
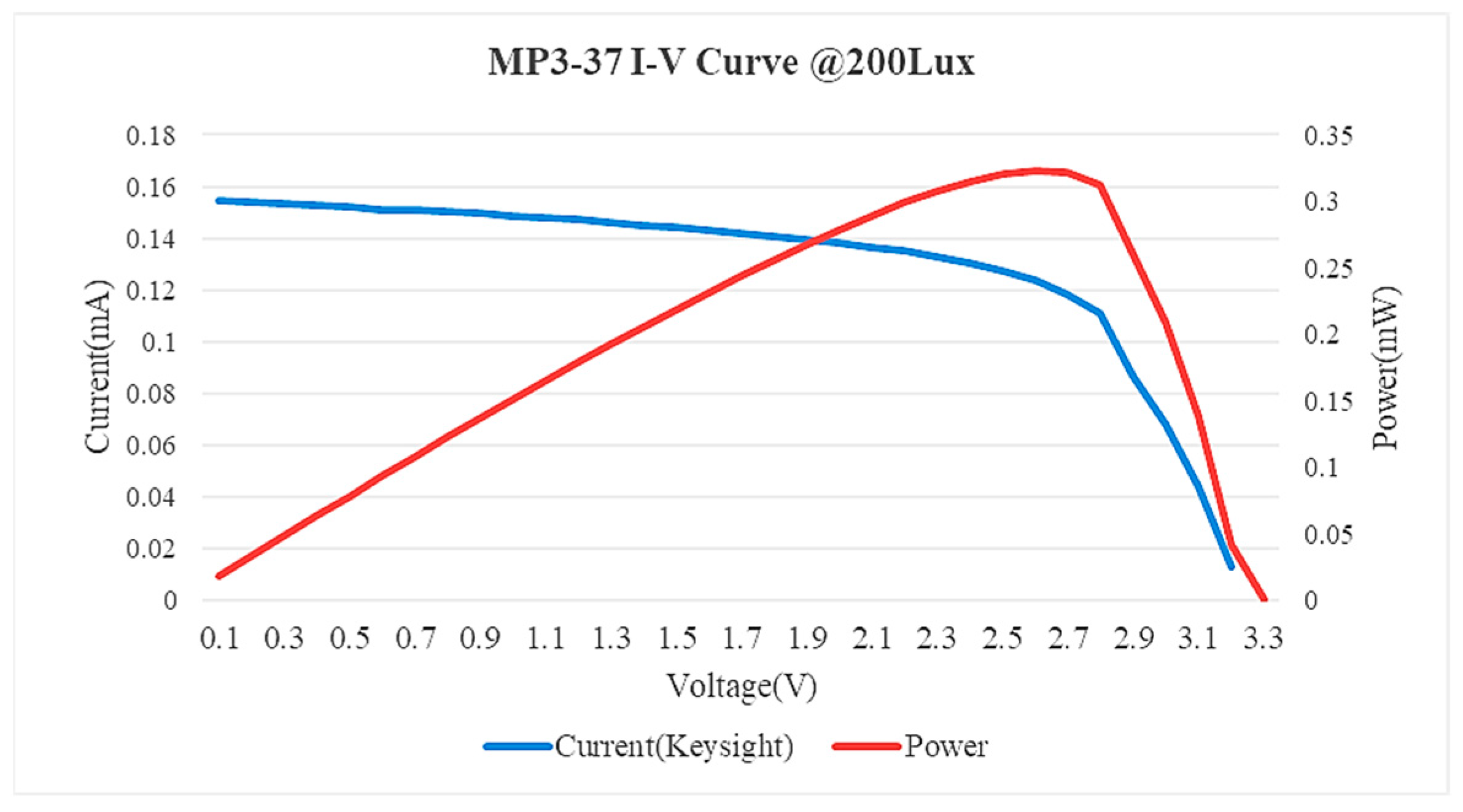
4.2.1. Single LED Measurements
4.2.2. Multi-LED Measurements
Square LED Topology
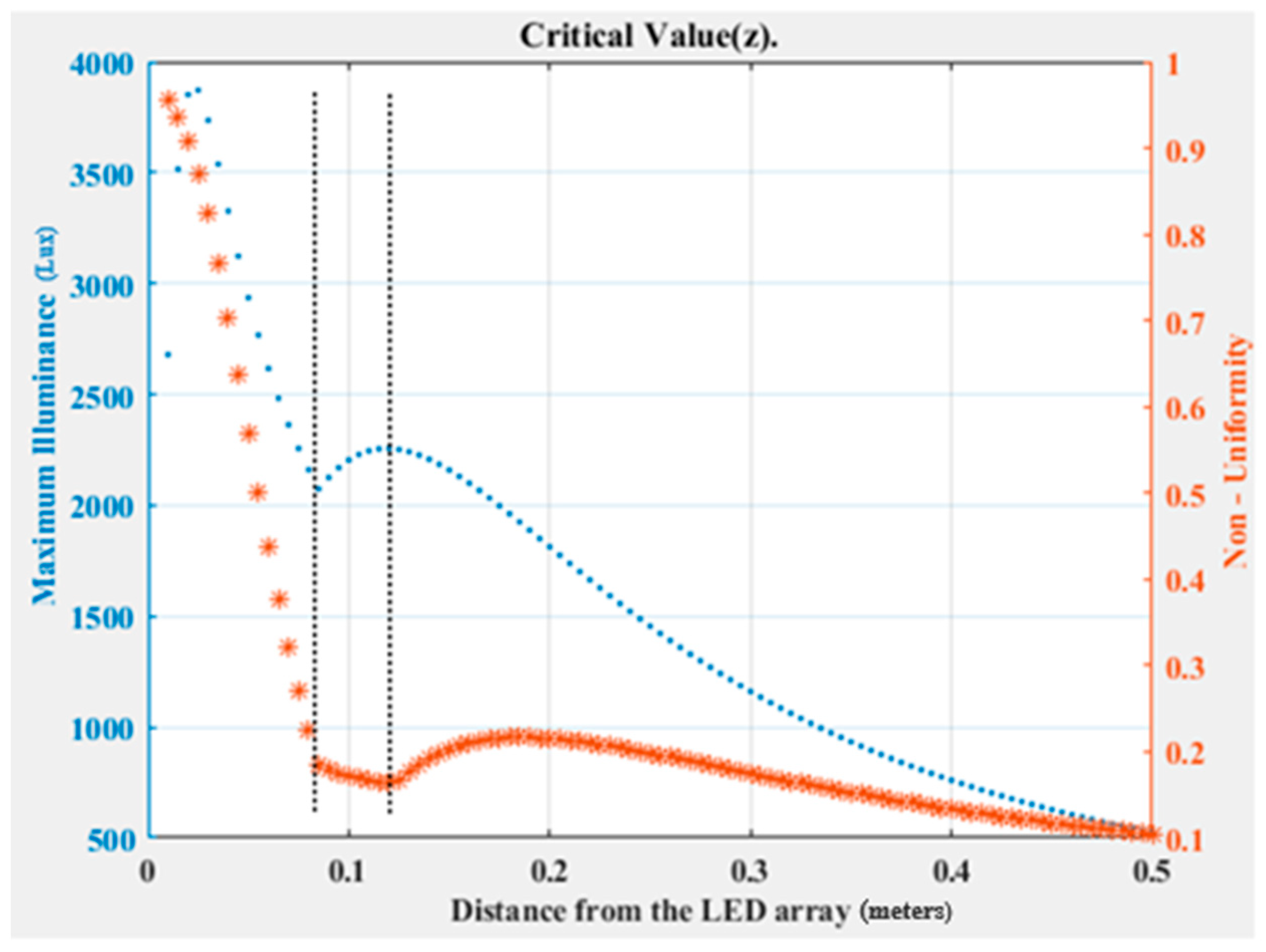
4.3. Multi-LED Light Simulator Design Guidelines’ Test
- ▪
- First Case: Analysis of a Two × Two Light-Emitting Diode (LED) Array
- ▪
- Second Case: Analysis of a Four × Four Light-Emitting Diode (LED) Array.
- ▪
- Third Case: Analysis of a Six × Six Light-Emitting Diode (LED) Array
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviation
| Abbreviation | Definition | Unit |
| RES | Renewable energy source | - |
| IoT | Internet of Things | - |
| PV cells | Photovoltaic cells | - |
| LED | Light-emitting diode | - |
| SRC | Standardized reporting condition | - |
| FWHM | Full width at half maximum | - |
| θ | Polar angle | rad |
| φ | Azimuth angle | rad |
| I(θ,φ) | Radiant intensity | W/sr |
| Ee | Irradiance | W/m2 |
| Ev | Illuminance | Lux |
| m | Position-dependent constant value for LED emission region | - |
| d | Distance | m |
| sup | Supremum | |
| inf | Infimum | |
| U | Uniformity | |
| NU | Non-uniformity |
References
- Madeti, S.R.; Singh, S.N. Monitoring System for Photovoltaic Plants: A Review. Renew. Sustain. Energy Rev. 2017, 67, 1180–1207. [Google Scholar] [CrossRef]
- Rahman, M.M.; Selvaraj, J.; Rahim, N.A.; Hasanuzzaman, M. Global Modern Monitoring Systems for PV Based Power Generation: A Review. Renew. Sustain. Energy Rev. 2018, 82, 4142–4158. [Google Scholar] [CrossRef]
- Al-Fuqaha, A.; Guizani, M.; Mohammadi, M.; Aledhari, M.; Ayyash, M. Internet of Things: A Survey on Enabling Technologies, Protocols, and Applications. IEEE Commun. Surv. Tutor. 2015, 17, 2347–2376. [Google Scholar] [CrossRef]
- Zanella, A.; Bui, N.; Castellani, A.; Vangelista, L.; Zorzi, M. Internet of Things for Smart Cities. IEEE Internet Things J. 2014, 1, 22–32. [Google Scholar] [CrossRef]
- Xu, L.D.; He, W.; Li, S. Internet of Things in Industries: A Survey. IEEE Trans. Ind. Inform. 2014, 10, 2233–2243. [Google Scholar] [CrossRef]
- Tellawar, M.; Chamat, N. An Exclusive Review on IoT Based Solar Photovoltaic Remote Monitoring and Controlling Unit. Int. Res. J. Eng. Technol. (IRJET) 2019, 6, 1520–1525. [Google Scholar]
- Narendra, N.; Harshitha, P.; Layana Shree, N.; Sushmitha, M.; Harshavardana, D. SOLAR PANEL ANALYSIS USING IOT AND IMAGE PROCESSING. Int. Res. J. Eng. Technol. (IRJET) 2021, 8, 1452–1455. [Google Scholar]
- Best Research-Cell Efficiency Chart. Available online: https://www.nrel.gov/pv/cell-efficiency.html (accessed on 24 May 2023).
- Bouclé, J.; Ribeiro Dos Santos, D.; Julien-Vergonjanne, A. Doing More with Ambient Light: Harvesting Indoor Energy and Data Using Emerging Solar Cells. Solar 2023, 3, 161–183. [Google Scholar] [CrossRef]
- PowerFilm, S. Electronic Component Solar Panels, MP3-37. Available online: https://www.powerfilmsolar.com/products/electronic-component-solar-panels/classic-application-series/mp3-37 (accessed on 24 May 2023).
- IEC 60904-1:2006|IEC Webstore|Water Management, Smart City, Rural Electrification, Solar Power, Solar Panel, Photovoltaic, PV, LVDC. Available online: https://webstore.iec.ch/publication/3872 (accessed on 24 May 2023).
- Solar Simulator|Low Price, Class AAA, Small Area. Available online: https://www.ossila.com/en-eu/products/solar-simulator (accessed on 24 May 2023).
- López-Fraguas, E.; Sánchez-Pena, J.M.; Vergaz, R. A Low-Cost LED-Based Solar Simulator. IEEE Trans. Instrum. Meas. 2019, 68, 4913–4923. [Google Scholar] [CrossRef]
- Moria, H. Radiation Distribution Uniformization by Optimized Halogen Lamps Arrangement for a Solar Simulator. J. Sci. Eng. Res. 2016, 3, 29–34. [Google Scholar]
- Irwan, Y.M.; Leow, W.Z.; Irwanto, M.; Fareq, M.; Amelia, A.R.; Gomesh, N.; Safwati, I. Indoor Test Performance of PV Panel through Water Cooling Method. Energy Procedia 2015, 79, 604–611. [Google Scholar] [CrossRef]
- Elgendy, M.A.; Sundaram, V.M.; Surati, B.U. Design and Construction of a Low Cost Photovoltaic Generator for Laboratory Investigations. In Proceedings of the 2013 International Conference on Clean Electrical Power (ICCEP), Alghero, Italy, 11–13 June 2013; pp. 79–83. [Google Scholar]
- Landrock, C.; Omrane, B.; Aristizabal, J.; Kaminska, B.; Menon, C. An Improved Light Source Using Filtered Tungsten Lamps as an Affordable Solar Simulator for Testing of Photovoltaic Cells. In Proceedings of the 2011 IEEE 17th International Mixed-Signals, Sensors and Systems Test Workshop, Santa Barbara, CA, USA, 16–18 May 2011; pp. 153–158. [Google Scholar]
- Yandri, E. Uniformity Characteristic and Calibration of Simple Low Cost Compact Halogen Solar Simulator for Indoor Experiments. Int. J. Low-Carbon Technol. 2018, 13, 218–230. [Google Scholar] [CrossRef]
- Li, G.; Xuan, Q.; Pei, G.; Su, Y.; Ji, J. Effect of Non-Uniform Illumination and Temperature Distribution on Concentrating Solar Cell—A Review. Energy 2018, 144, 1119–1136. [Google Scholar] [CrossRef]
- Moreno, I. Configurations of LED Arrays for Uniform Illumination. In Proceedings of the 5th Iberoamerican Meeting on Optics and 8th Latin American Meeting on Optics, Lasers, and Their Applications; SPIE: Porlamar, Venezuela, 2004; Volume 5622, pp. 713–718. [Google Scholar]
- Naskari, V.; Doumenis, G.; Koutsos, C.; Masklavanos, I. Design and Implementation of an Indoors Light Simulator. In Proceedings of the 2022 7th South-East Europe Design Automation, Computer Engineering, Computer Networks and Social Media Conference (SEEDA-CECNSM), Ioannina, Greece, 23–25 September 2022; pp. 1–6. [Google Scholar]
- Naskari, V. Modeling of Artificial Light Pv Cell Evaluation System; University of Ioannina: Arta, Greece, 2022. [Google Scholar]
- Moreno, I.; Avendaño-Alejo, M.; Tzonchev, R.I. Designing Light-Emitting Diode Arrays for Uniform near-Field Irradiance. Appl. Opt. 2006, 45, 2265–2272. [Google Scholar] [CrossRef] [PubMed]
- Κουτσός, Χ.; Σκαλτσώνης, Λ. Σχεδίαση και ανάπτυξη συστήματος αξιολόγησης επιδόσεων Φ/Β στοιχείων; Bsc, University of Ioannina: Arta, Greece, 2021. [Google Scholar]
- Luminus SST-20-WxH High Power SST Product Datasheet 2021. Available online: https://download.luminus.com/datasheets/Luminus_SST-20-WxH_Datasheet.pdf (accessed on 23 May 2023).
- Nasiri, A.; Zabalawi, S.A.; Mandic, G. Indoor Power Harvesting Using Photovoltaic Cells for Low-Power Applications. IEEE Trans. Ind. Electron. 2009, 56, 4502–4509. [Google Scholar] [CrossRef]
- Shao, H.; Tsui, C.-Y.; Ki, W.-H. The Design of a Micro Power Management System for Applications Using Photovoltaic Cells With the Maximum Output Power Control. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2009, 17, 1138–1142. [Google Scholar] [CrossRef]
- LedsMaster LED Lighting. What is Light Uniformity? How to Calculate Lux Level Lighting Uniformity. 2019. Available online: https://www.ledsmaster.com/what-is-light-uniformity-how-to-calculate-lux-level-lighting-uniformity.html (accessed on 23 May 2023).
- He, Y.; Xiong, L.; Meng, H.; Zhang, J.; Liu, D.; Zhang, J. Analysis of Non-Uniformity of Irradiance Measurement Uncertainties of a Pulsed Solar Simulator. In Proceedings of the Optical Metrology and Inspection for Industrial Applications II; SPIE: Beijing, China, 2012; Volume 8563, pp. 273–277. [Google Scholar]




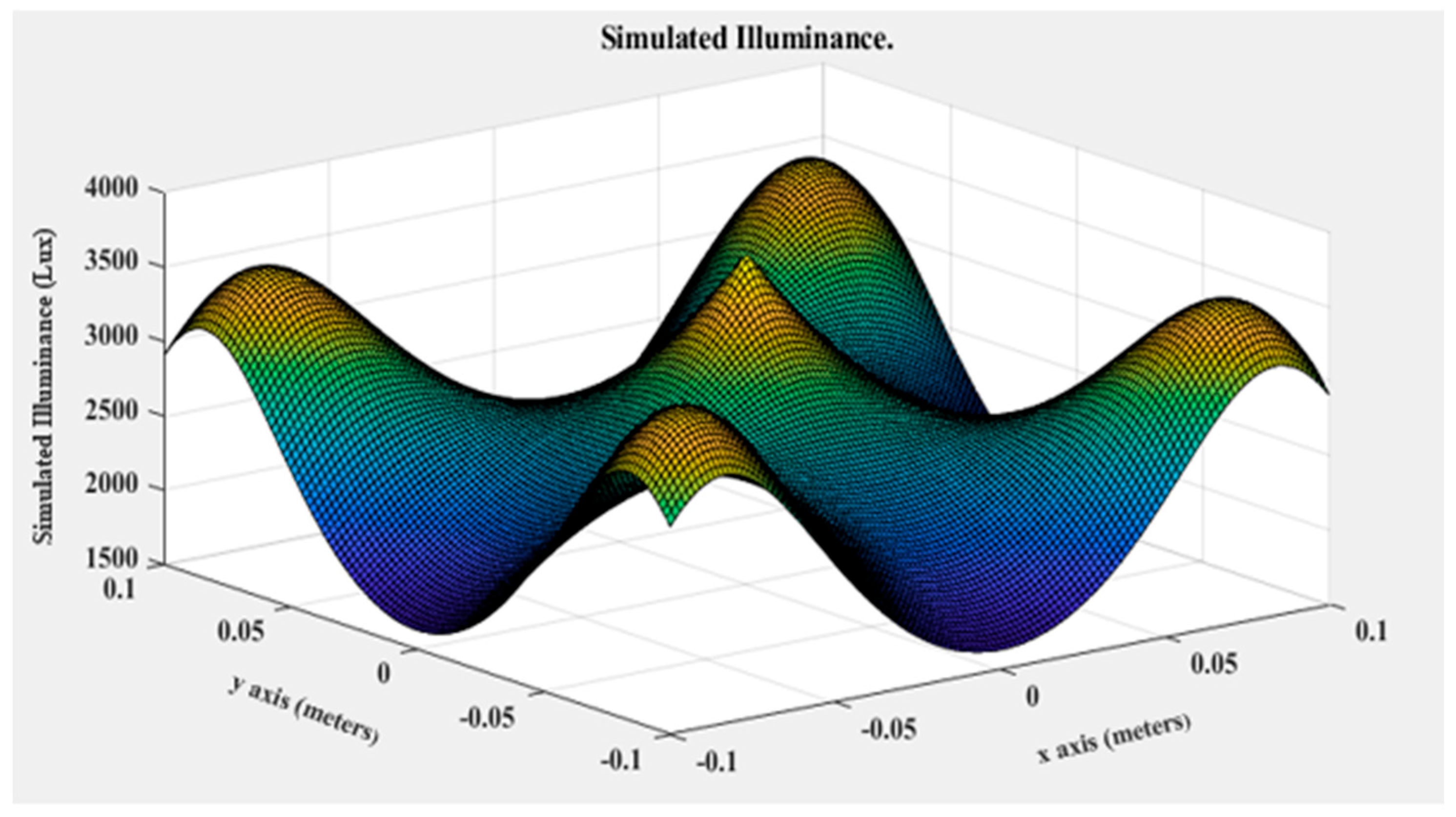
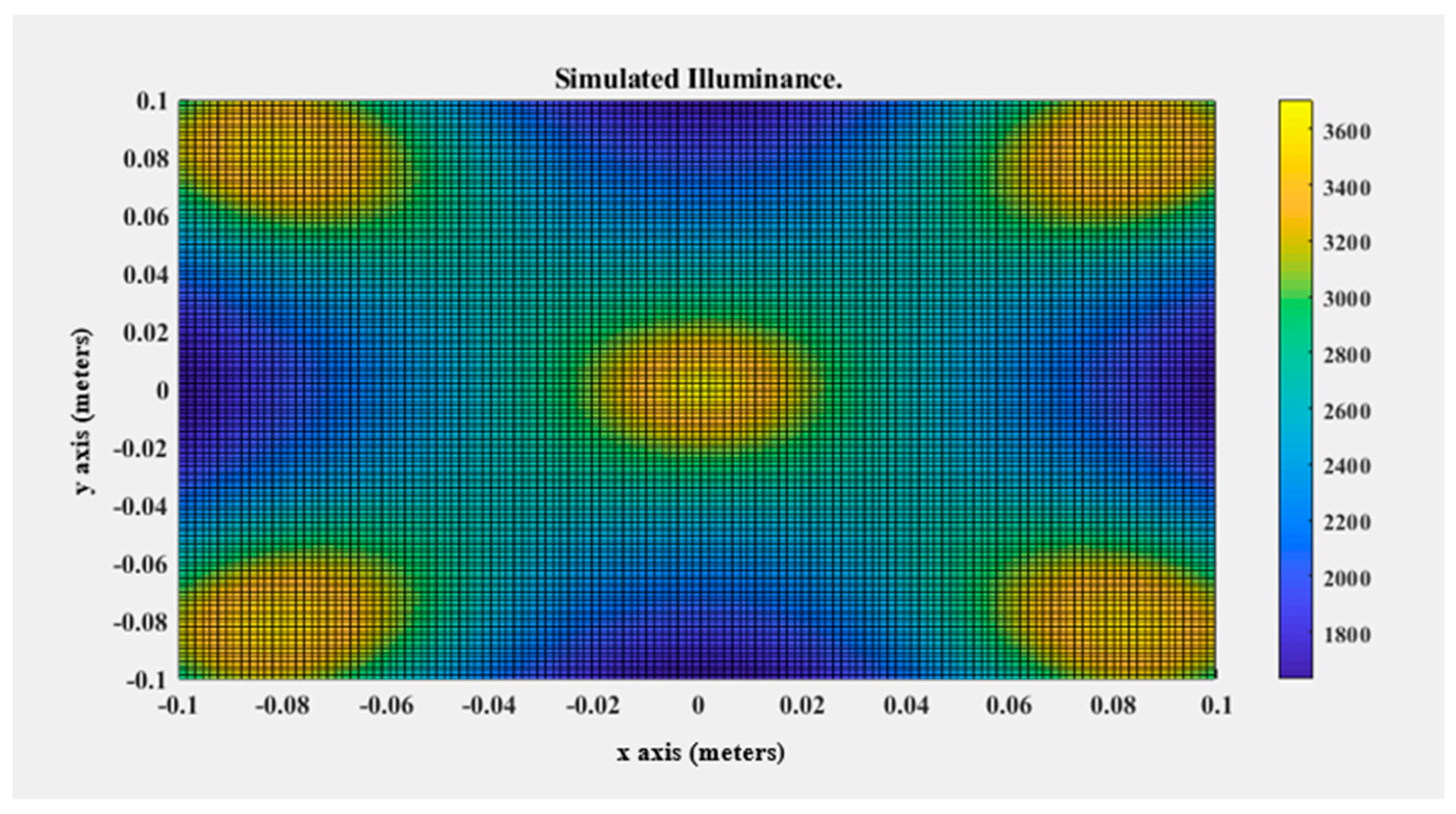
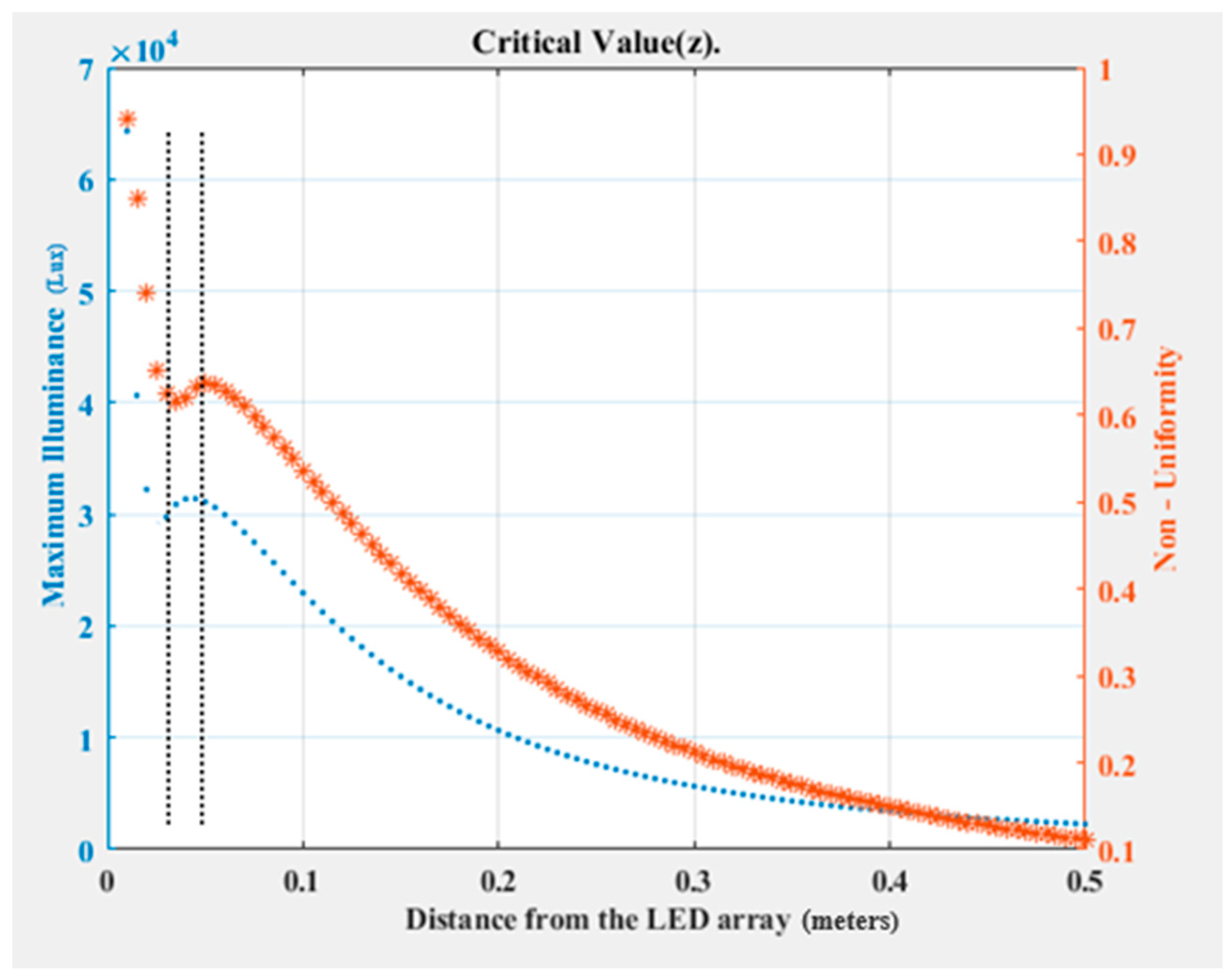
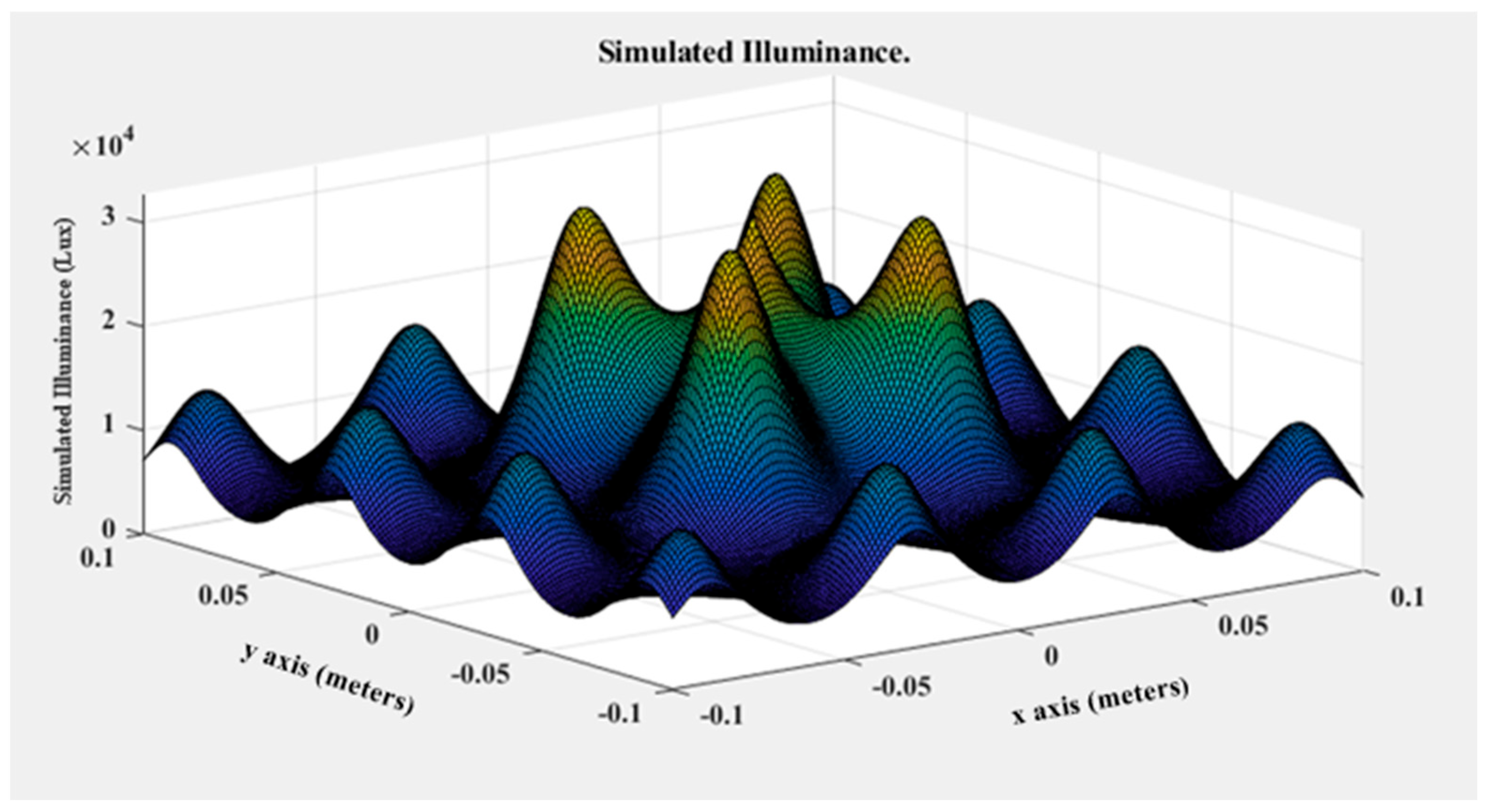


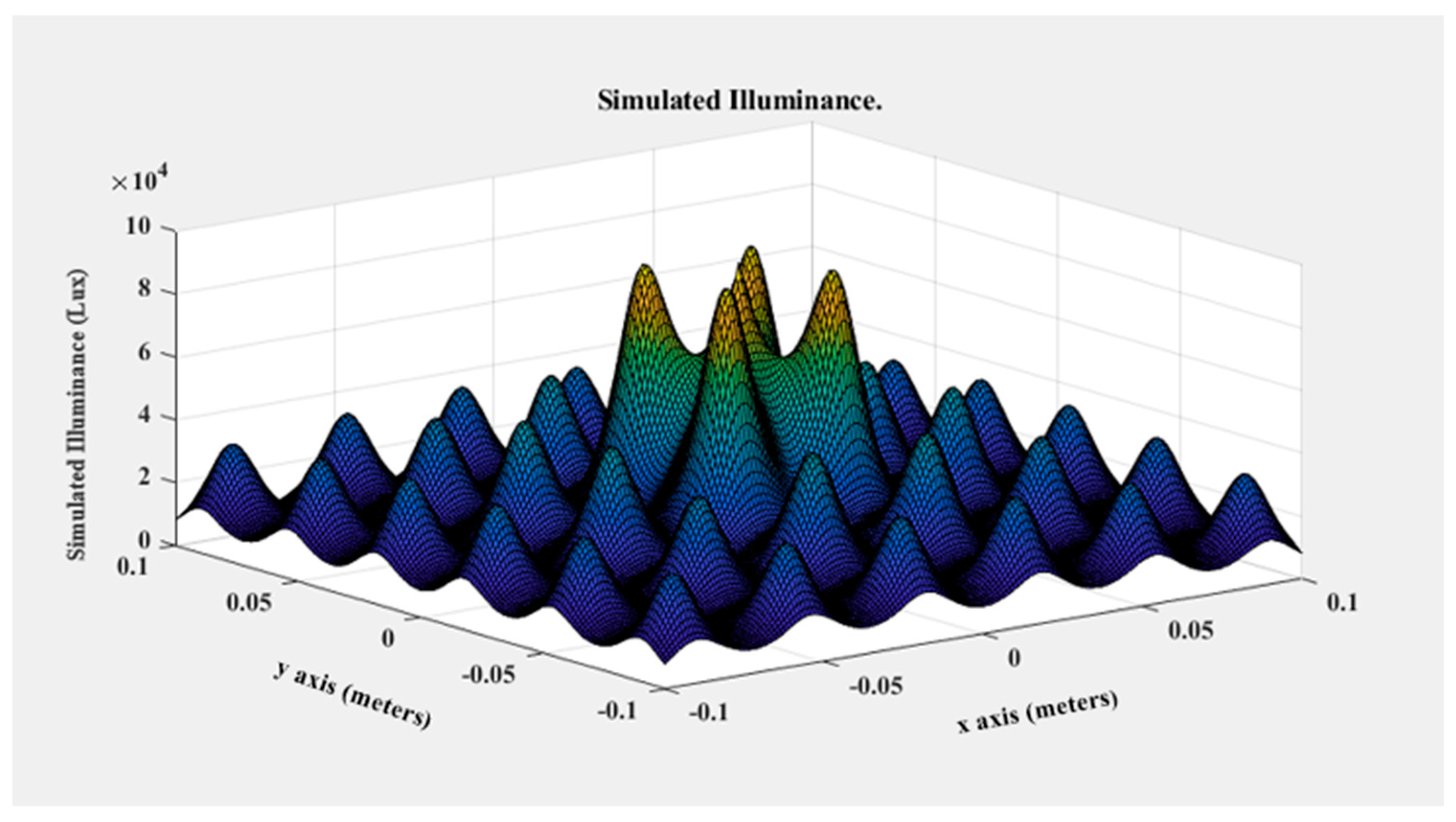
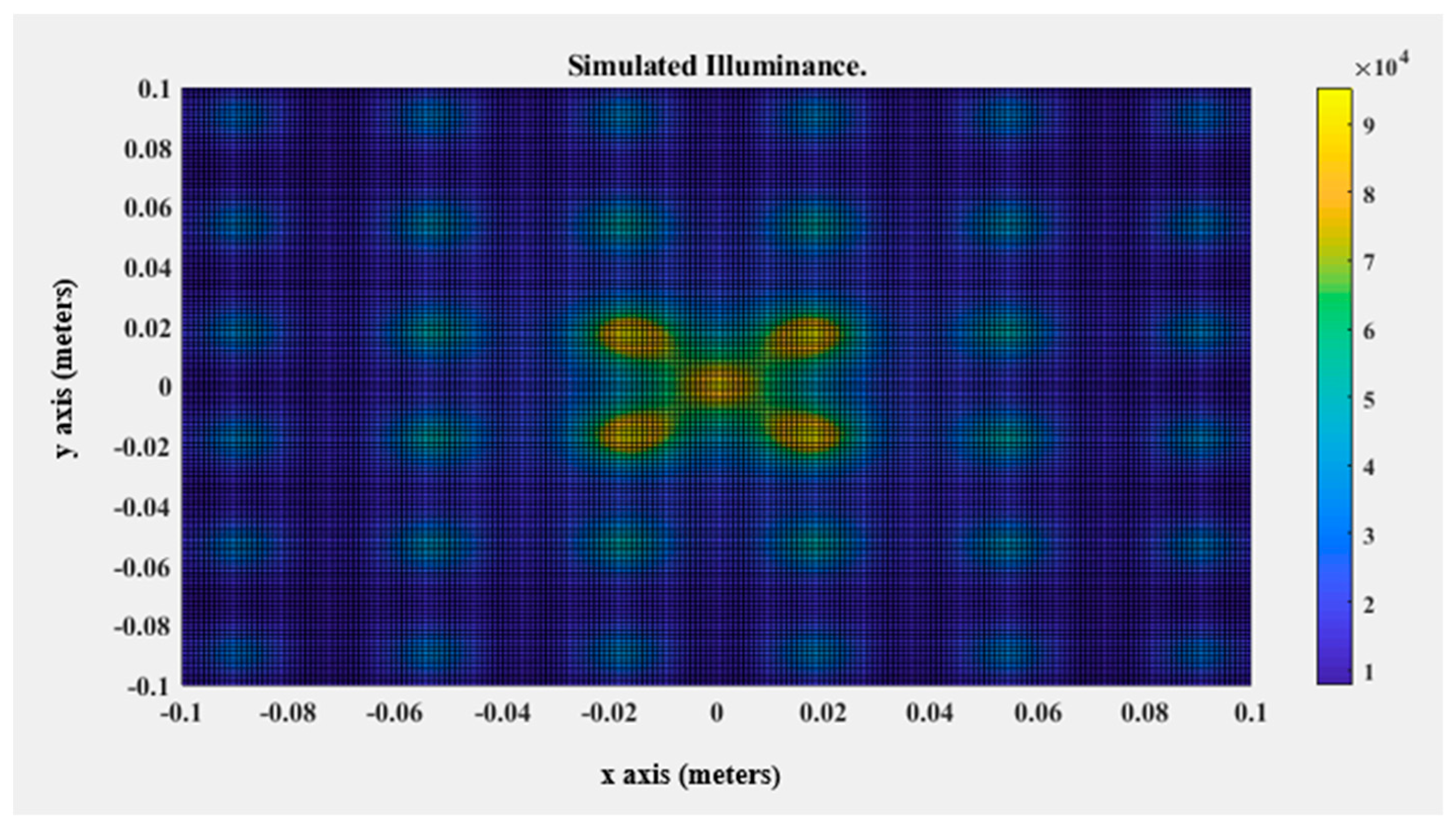
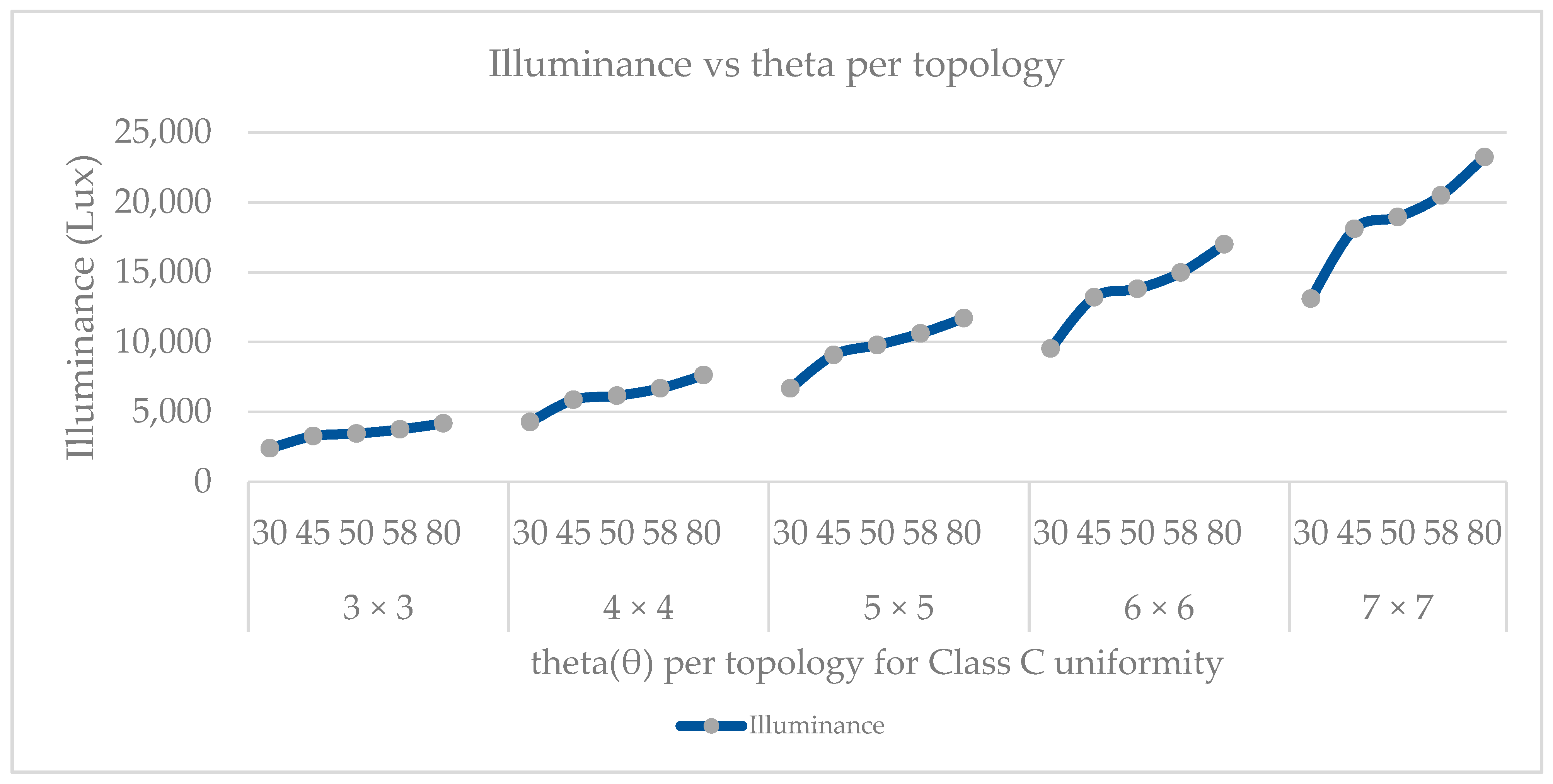
| Name | Spatial Non-Uniformity (Class) | Target Size Square (Side cm) | Working Distance (cm) | Price (USD) | Lamp Wattage (W) |
|---|---|---|---|---|---|
| Sciencetech SF-300-A | Class AAA | <5.5 × 5.5 | 10–13 | 6850 | 300 |
| Sciencetech PSS2 | Class AAA | >50 × 50 | 7.5 | 90,000 | - |
| WaveLabs Sinus-70 | Class A+ | 5.1 × 5.1 | 38 | - | 270 |
| G2V Pico DIR-BASE | Class AAA | 2.5 × 2.5 | 7 | - | 220 |
| Oriel SOL-UV-6 | Class AAA | 15.2 × 15.2 | 15.24 | - | 1600 |
| Dimensions of Illuminated Surface (m) | Height (m) | LED Array’s Dimensions (m) | Radiometric Flux (mW) | |||
| φe | 442 | |||||
| x-axis | [−0.07, 0.07] | z-axis | x-axis | [−0.09, 0.09] | Viewing Angle (degrees) | |
| y-axis | [−0.07, 0.07] | 0.31 | y-axis | [−0.09, 0.09] | 2 ϑ/2 | 120 |
| Topology | Distance between LEDs (m) | Z0 (m) |
|---|---|---|
| 2 × 2 | 0.18 | 0.078 |
| 4 × 4 | 0.06 | 0.031 |
| 6 × 6 | 0.036 | 0.019 |
| Topology | Interval of Distance from LED Array—Height (m) | Interval of Non-Uniformity | Interval of Max-Illuminance (lux) |
|---|---|---|---|
| 2 × 2 | [0.078, 0.121] | [0.162, 0.181] | [2080, 2270] |
| 4 × 4 | [0.023, 0.048] | [0.62, 0.63] | [32,900, 30,800] |
| 6 × 6 | [0.012, 0.041] | [0.71, 0.735] | [81,500, 83,000] |
| Topology | Distance from LED Array—Height (cm) | Selected Centered Test Plane (cm) | Non-Uniformity of the Selected Test Plane (%) | Maximum Illuminance (lux) |
|---|---|---|---|---|
| 2 × 2 | 12.1 | 12 × 12 | 18.26 | 2270 |
| 3 × 3 | 9 | 7 × 7 | 17.59 | 12,380 |
| 4 × 4 | 4.8 | 4 × 4 | 17.29 | 30,800 |
| 5 × 5 | 4.55 | 3.3 × 3.3 | 17.25 | 71,260 |
| 6 × 6 | 4.1 | 3 × 3 | 17.12 | 83,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naskari, V.; Doumenis, G.; Masklavanos, I. Irradiance Non-Uniformity in LED Light Simulators. Information 2023, 14, 316. https://doi.org/10.3390/info14060316
Naskari V, Doumenis G, Masklavanos I. Irradiance Non-Uniformity in LED Light Simulators. Information. 2023; 14(6):316. https://doi.org/10.3390/info14060316
Chicago/Turabian StyleNaskari, Vasiliki, Gregory Doumenis, and Ioannis Masklavanos. 2023. "Irradiance Non-Uniformity in LED Light Simulators" Information 14, no. 6: 316. https://doi.org/10.3390/info14060316
APA StyleNaskari, V., Doumenis, G., & Masklavanos, I. (2023). Irradiance Non-Uniformity in LED Light Simulators. Information, 14(6), 316. https://doi.org/10.3390/info14060316






