Abstract
With the rapid development of mobile positioning technologies, location-based services (LBSs) have become more widely used. The amount of user location information collected and applied has increased, and if these datasets are directly released, attackers may infer other unknown locations through partial background knowledge in their possession. To solve this problem, a privacy-preserving method for trajectory data publication based on local preferential anonymity (LPA) is proposed. First, the method considers suppression, splitting, and dummy trajectory adding as candidate techniques. Second, a local preferential (LP) function based on the analysis of location loss and anonymity gain is designed to effectively select an anonymity technique for each anonymous operation. Theoretical analysis and experimental results show that the proposed method can effectively protect the privacy of trajectory data and improve the utility of anonymous datasets.
1. Introduction
With the rapid development of modern device awareness systems and mobile positioning technologies, such as global positioning systems (GPSs) and radio frequency identification devices (RFID), access to location-based services (LBSs) is becoming increasingly used [1,2]. While enjoying convenient services, users leave their location records, which constitute the trajectory data. Many trajectories are released and used for various applications, such as urban planning, advertisement placement, and shop bidding [3,4,5]. However, the direct publication and application of trajectory data may lead to the leakage of users’ information [6,7]. Attackers can infer other unknown locations or identify users’ full trajectory based on some of the background knowledge they own [8].
For example, an electronic card company provides payment services for two chain stores A and B and stores user transaction records. Chain stores A and B store transaction records of users consuming at their stores, and the transaction records generated in physical locations may contain some important spatiotemporal information (e.g., the user in a specific location at a certain time). After preprocessing, the transaction records in some chain stores can be presented as the type of trajectory in Table 1. As shown in Table 1, assume that Alice generates the record , which represents that she consumes at stores and of A and store of B, respectively. Considering a publication of the transaction records by the company for analysis purposes, A can be regarded as an attacker who owns and tracks all the locations ; he owns the partial record of Alice and can infer that Alice has visited in addition to and . This is because only the record goes through and then through , so it can be determined that the complete record of Alice is . In this case, the user’s consumption preferences and other information may be leaked, resulting in a breach of user privacy.

Table 1.
An example of trajectory set T.
To achieve the safe publication of trajectory data in the above scenarios, existing works usually anonymize the trajectory dataset before publication [8,9,10,11]. Specifically, the data holder processes the trajectory dataset to be published when the background knowledge mastered by attackers is known to prevent the attackers from inferring user information. Under the premise of meeting users’ privacy requirements, such methods continuously process trajectory sequences to reduce the probability of unknown location information being inferred. This data processing can be divided into two steps. The first step is to identify the privacy threats; in other words, all the problematic sequences in the dataset should be found. The second step is to eliminate those privacy threats by processing some trajectory sequences. The algorithms [8] based on suppression and splitting can effectively achieve privacy preservation, but the time consumption for identifying privacy threats is relatively large, and the utility of the anonymous dataset after suppression is not very great. Two new tree-based structure [9,10] were proposed to optimize time performance. However, similar to the above methods, these methods are also implemented based on suppression. Due to the implementation characteristics of suppression, a large amount of information loss also often occurs.
The above methods can effectively achieve safe publication of trajectory data while meeting users’ privacy requirements. However, the methods are implemented based on suppression to eliminate privacy threats, which may lead to large information loss [9,10,11]. Specifically, the global suppression and local suppression algorithms are implemented to calculate the anonymity gain value and then delete some specific locations directly. Therefore, anonymous datasets usually lose many locations, and the number of lost locations gradually increases with an increasing dataset size. This characteristic may result in the excessive loss of information in the anonymous dataset, which is not conducive to analysis and application of the data after publication.
To improve the above problem, in other words, to realize the safe publication of trajectory data and improve the utility of trajectory data after publication, we propose a privacy-preserving method for trajectory data publication based on local preferential anonymity (LPA). We adopt a tree-based storage structure [10] and a simplified calculation method to extract problematic nodes; consider suppression, splitting, and dummy trajectory adding as candidate techniques; and select a specific technique based on the analysis of location loss and anonymity gain.
The main contributions of this paper are as follows:
- (1)
- We propose a privacy-preserving method based on LPA, which implements suppression, splitting, and dummy trajectory adding based on the trajectory projection tree.
- (2)
- We design a local preferential (LP) function based on the analysis of location loss and anonymity gain to select the final technique. Selecting an appropriate technique for problematic nodes can effectively achieve privacy preservation and reduce information loss in the process of privacy preservation.
- (3)
- We conduct theoretical analysis and a set of experiments to show the feasibility of privacy preservation. Experimental results show that compared with existing methods, the LPA algorithm can effectively achieve privacy preservation while reducing the information loss of anonymous datasets.
2. Related Work
When trajectory datasets are published, user privacy has increasingly attracted attention from all walks of life. Researchers have done much work on privacy preservation of trajectory data and have proposed many privacy-preserving methods [1,7]. In this section, we investigate the existing work in this field. The methods for anonymizing locations can be divided into the following categories.
2.1. Dummy Trajectory
The method based on dummy trajectory adds synthetic dummy trajectories according to the characteristics of the original trajectory to reduce the probability that the real trajectory is inferred. Luper et al. [12] applied the dummy trajectory technique to trajectory data publication. Effectively generating dummy trajectories is a main problem. On the one hand, the dummy trajectory should be similar to the motion pattern of the real trajectory. The trajectory synthesis method proposed by Lei et al. [13] is widely used. When synthesizing spatiotemporal trajectory data, some spatiotemporal points are selected from the real trajectory, and these spatiotemporal points are rotated at the centre. Wu et al. [14] considered the gravity movement model to generate a dummy trajectory and proposed a method to protect trajectory data in continuous LBS and trajectory publication. Considering the spatiotemporal constraints of geographical environment of the users, Lu et al. [15] proposed a trajectory privacy protection method based on dummy trajectory; this method hides the real trajectories by dummy trajectories and can effectively protect user privacy. On the other hand, it is necessary to avoid adding too many dummy trajectories.
However, existing works rarely apply dummy trajectory to privacy protection for location sequences such as our work. The method proposed in this paper is applied to the environment where the attackers have already mastered some background knowledge, and the dummy trajectory is used to reduce the availability of background knowledge.
2.2. Clustering and Partition
The method based on clustering and partitioning divides the original trajectory dataset into small groups and then performs anonymization in each group to make the trajectories within each group indistinguishable. These methods are mostly used for spatiotemporal trajectories.Samarati [16] and Sweeney [17] implemented privacy protection based on k-anonymity, which deal the data so that each record has at least the exact same quasi-identifier attrib-ute value as the other k-1 records in the same group. Abul et al. [18] proposed (k, δ)-anonymity based on k-anonymity, proposed the never walk alone (NWA) algorithm, and proposed achieving k-anonymity through trajectory clustering. Domingo-Ferrer et al. [19,20] pointed out that the NWA algorithm may still leak privacy, and they proposed the SwapLocations algorithm to classify trajectories by general microaggregation and then replace the locations in the clusters. This method may also lose much information. Dong et al. [21] proposed a trajectory privacy preservation method based on frequent paths, which applied the concept of frequent paths to trajectory privacy preservation for the first time. They first found frequent paths to divide candidate groups and then selected representative trajectories in the candidate groups. This method can effectively achieve privacy protection but does not consider the different privacy requirements of users. Considering users’ privacy requirements, Kopanaki et al. [22] proposed personalized privacy parameters based on the research of Domingo-Ferrer et al. [19] and proposed trajectory division in the preprocessing stage. To further improve the utility of anonymous datasets, Chen et al. [23] considered multiple factors of spatiotemporal trajectories and proposed a method of privacy preservation for trajectory data publication based on 3D cell division to improve the problem of excessive information loss. The method divides cells in the trajectory preprocessing stage and performs suppression or location exchange within each cell for anonymity, which improves data utility.
Unlike our work, the above methods are often used for spatiotemporal trajectory data publication, and the partitioning of trajectories is implemented in the preprocessing stage. The advantage of trajectory division is that no locations are lost. Terrovitis et al. [8] proposed a method of splitting trajectories. The trajectories are split in the anonymous stage, and a trajectory may be split into two trajectories in their method, which can achieve effective anonymity and reduce the loss of locations. However, it may not work very well if only the splitting is implemented in trajectory anonymity, because splitting trajectories may affect the behavioral pattern of the users.
2.3. Generalization and Suppression
The privacy-preserving methods for location sequences are mostly based on generalization and suppression. Generalization is utilized to replace the content of information with a more ambiguous concept and generalize the locations on the trajectory to an enlarged area, which causes the locations in this area to be indistinguishable. Suppression selectively deletes specific sensitive locations before releasing trajectory data to achieve trajectory privacy preservation. Nergiz et al. [24] first proposed a generalization-based privacy preservation method for trajectory data publication, which introduced k-anonymity into the generalization-based method to achieve anonymity. Then, Yarovoy et al. [25] proposed a spatial generalization-based k-anonymity approach to anonymously publish moving object databases. Terrovitis et al. [26] defined a km-anonymity model, which is a new version of k-anonymity and is mainly used to protect privacy in the publication of set-valued data. To effectively protect data utility, Poulis et al. [27] applied km-anonymity to trajectory data and developed three anonymity algorithms based on a priori principles. Terrovitis et al. [28] proposed a method to suppress partial location information to achieve privacy preservation. To solve the problem of inferring unknown locations through partial information by attackers, they used partial trajectory knowledge as the quasi-identifier of the remaining locations and transformed the trajectory database into a safe counterpart.
For the above problem, Terrovitis et al. [8] continued applying suppression and splitting to develop four algorithms. Among those four algorithms, they proposed two algorithms based on suppression and , which delete specific locations according to different selection methods. The proposed algorithms can effectively achieve privacy protection, but there are still some problems in the processing. One is the linear storage of the original trajectory and the idea of the greedy algorithm, which result in a large amount of computation time. The other is the large information loss of the anonymous dataset. Lin et al. [10] proposed four algorithms based on suppression, which were implemented on tree structures. They proposed a method of anonymity gain measurement, which was optimized in terms of the performance of computation time. Although the performance of computation time is significantly improved, the information loss is basically the same as that of the algorithms [8]. In addition, the global suppression algorithm based on the tree structure cannot perform the correct update operation in some cases.
To reduce information loss of the anonymous dataset, we adopt a tree-based storage structure [10] to store the original data and implement suppression, splitting, and dummy trajectory adding based on the tree structure, which transforms processing of the privacy problems into problematic nodes. We consider suppression, splitting, and dummy trajectory adding as candidate techniques and design an LP function based on location loss and anonymity gain to select the final anonymity technique.
3. Preliminaries
To address the problem of privacy preservation for trajectory data publication, some specific locations in the dataset to be published should be processed, and a corresponding safe dataset with minimal information loss and good privacy preservation will be obtained. In this section, we introduce some basic definitions and formulas that will be used throughout this paper, and the storage structure used in our method will also be described.
3.1. Problem Definition
We proposed a privacy protection method for trajectory data publication in this paper. In our method, it should be noted that the trajectories studied in our work are sematic trajectories and are unidirectional. In other words, there are no repeated locations in a trajectory, The relevant definitions of the trajectory data are introduced as follows.
Let be a location of special interest on a map (e.g., hospital, bank, or store). Then, is a set of locations denoted by .
Definition 1 (Trajectory).
A trajectory is defined as an ordered list of locations, , where L, . The length of a trajectory denoted as , which represents the number of locations in . The set of trajectories is presented as
Example 1.
Table 1 shows eight trajectories, which are defined on the set of locations , and . The length of trajectory is
Definition 2 (Subtrajectory).
Given two trajectories defined on the set of locations L, denoted as and , we say that is a subtrajectory of , denoted as , if and only if and there is a mapping that , , …, , holds.
Example 2.
To achieve the safe publication of trajectory data, we anonymize the trajectory dataset before publication [8,9,10,11]. Therefore, we need to infer the partial information of trajectory owned by potential attackers Adv, which is called the background knowledge.
Definition 3 (Background Knowledge).
For a set of trajectories defined on , an attacker A in Adv owns a set of locations , and is called the background knowledge owned by A. Attacker A can track any user visiting the locations in .
In this paper, we assume that any attacker owns background knowledge and that the background knowledge mastered by any two attackers is not shared. In other words, for any attacker A, B and , . If our method is applied to the situation where attackers are sharing background knowledge, the trajectory data publisher needs to regroup attackers according to the disjointed background knowledge.
Example 3.
Definition 4 (Trajectory Projection).
Let A be an attacker owning , and there is a trajectory . The trajectory projection of attacker A is denoted as and is a subtrajectory of trajectory . In other words, all locations in belong to and trajectory .
The set of trajectory projections of all trajectories about attacker A is denoted as =.
Example 4.

In Table 1, the trajectory projections of to attackers A and B areand, respectively. The trajectory projection set of all trajectoriesis, as shown in Table 2.

Table 2.
Trajectory projection set of T.
The attacker A may be able to infer the trajectories that contain the trajectory projection; we say that the set of these trajectories is a trajectory projection support set.
Definition 5 (Trajectory Projection Support Set).
Let be a trajectory dataset to be published, and let be a trajectory in . If , we say that supports a trajectory projection . The trajectory projection support set of in about is denoted as , =. represents a set of trajectories, and each trajectory in supports a trajectory projection .
Example 5.
In Table 1, if , the trajectory projection support set of is . It also represents that the attacker A may be able to infer that is the trajectory projection of either of or .
For these scenarios, A can also infer that may be associated with . Let be a trajectory set that contains all trajectories in and a location , denoted as .
Definition 6 (Inference Probability).
The inference probability is denoted by, which represents the probability of associating a location to trajectory projection , and calculated as Equation (1):
Example 6.
After Example 5, . The inference probability of associating to trajectory projection is =.
Definition 7 (Problematic Pair).
Letbe a probability threshold defined by the user, which represents the user’s privacy requirements. If , then the pair is a problematic pair, and is defined as problematic. Moreover, the number of problems of is , and the total number of problems is denoted as N.
A trajectory dataset is called unsafe if it has at least one problematic pair. The aim of our work is to eliminate all problems.
Definition 8 (Problem Definition).
Given a trajectory dataset T, a user’s privacy requirements threshold, and a set of potential attackers Adv, construct a corresponding safe dataset to T, with minimum information loss.
3.2. Trajectory Projection Tree
In the existing trajectory privacy preservation methods, some storage structures were proposed in the trajectory preprocessing stage, such as linear structures [8], graph structures [21,29] and tree structures [9,10]. In this paper, we choose the tree structure (TP-tree) [10] to store the original trajectory dataset T. The reason is that the tree-based storage structure can simplify the calculation of inference probability and reduce the computational cost.
Example 7.

With Table 1 as the original trajectory dataset T and attackers set as the inputs, let us execute the TP-treeConstruction algorithm [10]to construct a TP-tree corresponding to T. The TP-tree of Table 1is shown in Figure 1. The details of the TP-tree are introduced as follows:

Figure 1.
The TP-tree in Table 1. The -level nodes of the TP-tree correspond to projection trajectories, and the -level nodes correspond to locations that may be inferred.
Fisrtly, obtain the trajectory projections of different attackers; the trajectory projections are inserted as -level nodes. For trajectory , the trajectory projections of A and B are and , respectively. The -level nodes and should be inserted into the TP-tree.
Secondly, for each attacker’s trajectory projection, all locations in the trajectory but not in the trajectory projection are the locations that may be inferred. For the tree node , the location in but not in may be inferred by A, so the -level node of the -level node should be generated. Similarly, for the tree node , the locations and in but not in may be inferred by B, and the -level nodes and of the -level node should be generated.
It should be noted that in order to facilitate writing, only the trajectory projection and location representation contained in the node are written in the subsequent description of the node. For example, the -level node can be written as .
3.3. Anonymity Gain Measurement
When processing location sequences, the trajectories will be changed, and the total number of problems N may also be changed. Taking both aspects into consideration, a set of gain measurement formulas for suppression and splitting were proposed [8]. To measure the change in N, is defined as Equation (2):
where N () represents the number of problems before (after) anonymity.
Let and () be the trajectory projections owned by an attacker A. When at least one of and is problematic, we use to unify ; in other words, the locations in but not in must be deleted from and the original trajectories that contain . To measure the information loss, the ploss of suppression is defined as Equation (3):
where () represents the trajectory before (after) suppression and () represents the length of trajectory (). The anonymity gain measurement of suppression is defined as , which is shown as Equation (4):
where S represents the set of trajectories that are affected by the change in suppression, .
Let be the splitting location in a trajectory . Trajectory is split into two subtrajectories () from location . The ploss of splitting is defined as Equation (5):
where () represents the trajectory before (after) splitting, and () represents the length of the trajectory (). Therefore, the anonymity gain measurement of splitting is defined as , shown as Equation (6):
where S represents the set of trajectories affected by the change in splitting, .
For a problematic trajectory projection , a dummy trajectory identical to will be generated and defined as . Therefore, the ploss of the dummy trajectory is defined as Equation (7):
where () represents the trajectory before (after) adding the dummy trajectory, and () represents the length of trajectory (). However, there is no original trajectory that corresponds to , so the values of must be 1. The anonymity gain measurement of the dummy trajectory is defined as , shown as Equation (8):
4. Methods
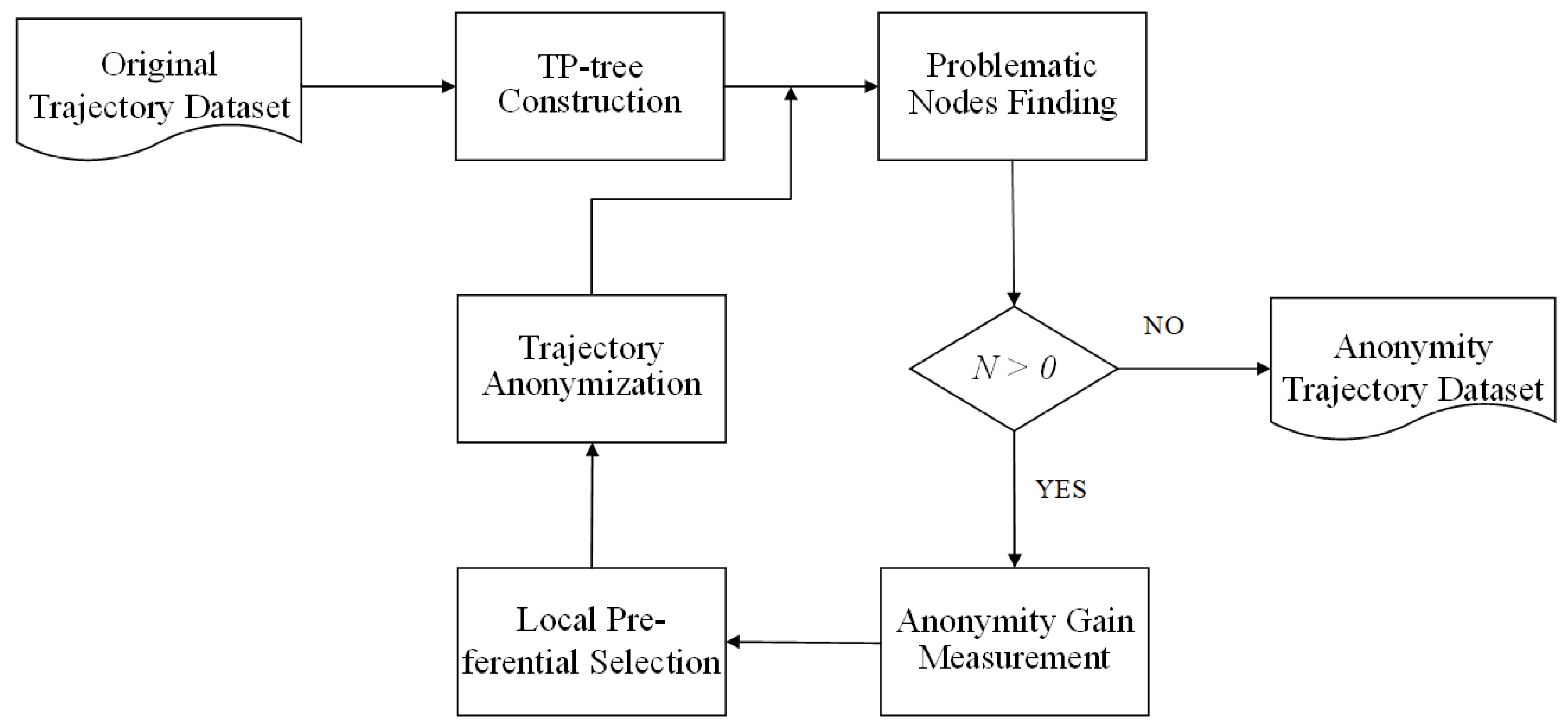
In this section, we propose a privacy-preserving method based on LPA to protect the privacy of trajectory publication. An overview of the proposed algorithm is shown in Figure 2. First, we construct the TP-tree [10] to store the original trajectory dataset T. Then, we use the problematic nodes finding (PNF) algorithm to obtain the set of problematic nodes P in the TP-tree and the total number of the problems N. Afterwards, we measure the anonymity gain of each anonymity technique and obtain the anonymity gains , , and . Then, the LP algorithm is used to select a specific technique to process the problematic nodes. The proposed method is described in detail in the rest of this section.
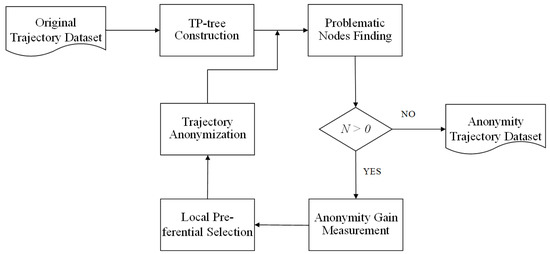
Figure 2.
Overview of the proposed methods (LPA). N is the total number of problems.
Definition 9 (Problematic Node).
The problematic node is the -level node containing the problem in the TP-tree, which needs to be eliminated. The tree node of TP-tree containing is a problematic node if and only if is problematic.
4.1. Problematic Nodes Finding
Based on the TP-tree constructed in the preprocessing stage, we use the PNF algorithm to identify the privacy threats of the trajectory dataset. Then, we find all problematic nodes in the tree under the user’s privacy requirements. The PNF algorithm is depicted as Algorithm 1.
| Algorithm 1: Problematic_Nodes_Finding (PNF) |
| Input: TP-tree, user’s privacy requirements threshold |
| Output: Problematic pairs set Q, problematic nodes set P, |
| the total number of problems N |
|
Algorithm 1 takes the TP-tree and user’s privacy requirements threshold as the inputs and returns the set of problematic pairs Q, the set of problematic nodes P, and the total number of problems N. After initialization, the algorithm scans all the -level nodes Sec and the corresponding child nodes Thi of Sec and obtains the trajectory number of Thi and Sec, denoted as and (Lines 2 to 5), respectively. Then, this algorithm calculates and checks whether is greater than . If is greater than , is inserted into set Q. Moreover, if Sec is not in set P, Sec is inserted into set P. Finally, the of Thi is accumulated into the total number of problems N (Lines 6 to 11).
Example 8.

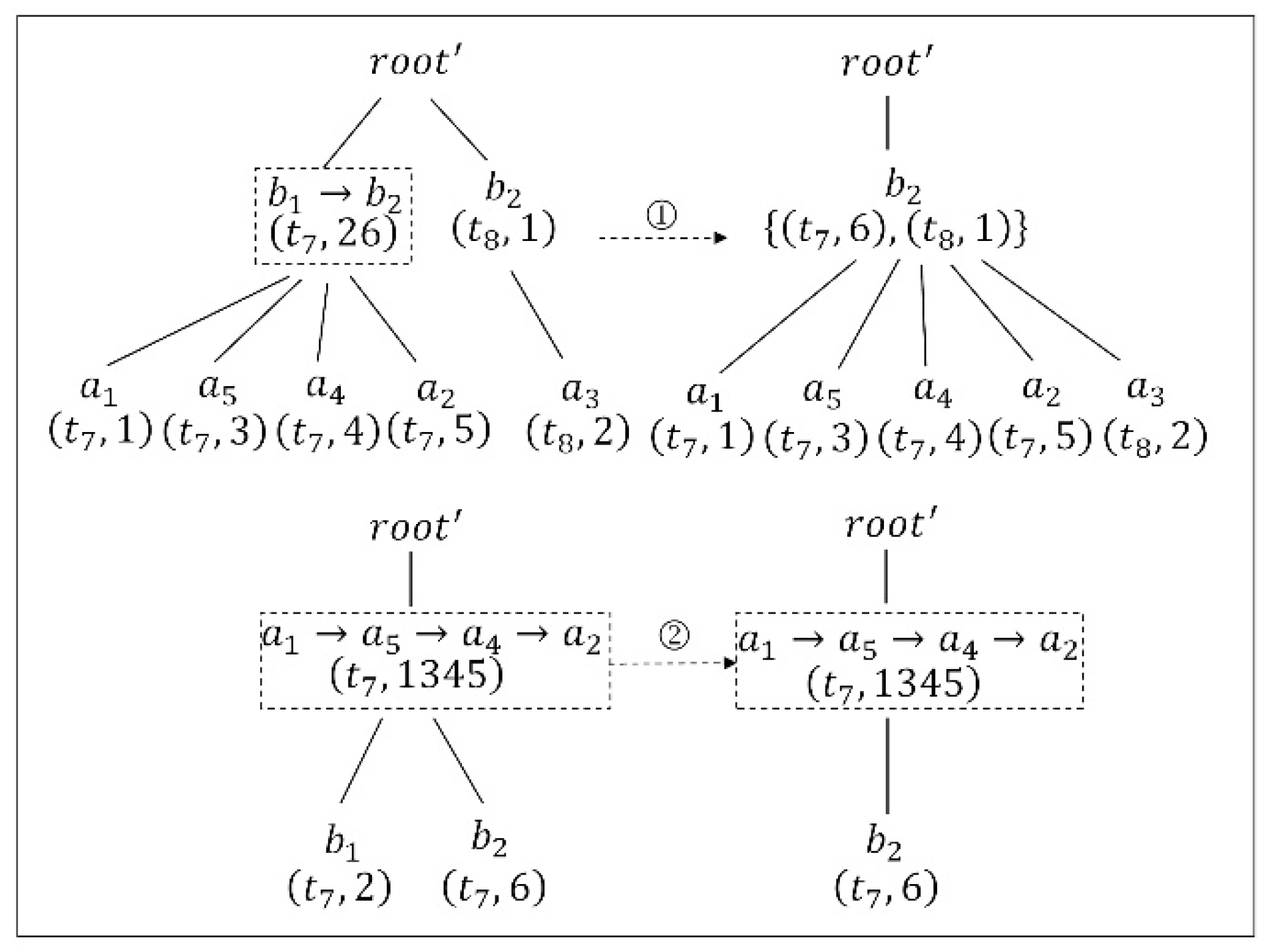
After constructing the TP-tree of T, Algorithm 1 is executed to find the problematic nodes of the TP-tree. In our example, the user’s privacy requirements threshold is defined as 0.5. After executing Algorithm 1, as Figure 3demonstrates the problematic nodes are shown in the dotted box, the problematic set ,and the total number of problems N is 16.

Figure 3.
Problematic nodes in Table 1. Problematic nodes are marked with dotted boxes.
4.2. Anonymity Gain Measurment
For a problematic node, we calculate the anonymity gain when applying suppression (), splitting ( and the dummy trajectory (). Then, we select the final technique and obtain an array denoted as FinalGain, which is a row of PreGain. The PreGain array is shown in Table 3, where each column of the PreGain array corresponds to the trajectory projection contained in problematic node that needs to be processed, the trajectory ID contained in the node, the final operation, the relevant operation information, and the anonymity gain.

Table 3.
Array of PreGain.
4.2.1. Suppression
We introduce the operation of suppression based on the TP-tree. For a problematic node, we first find two nodes of the same attacker from the level of the TP-tree to form a node pair . Notably, is the subtrajectory of . The idea of suppression is to use to unify . In other words, the locations that exist in but not in are deleted. The details of the tree updating are described in Example 9.
Example 9.
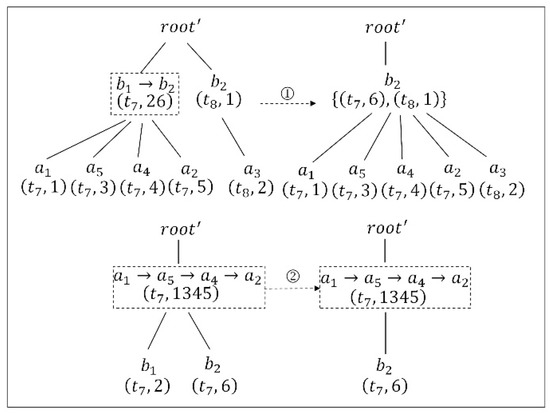
Considering the problematic node , suppression based on the TP-tree is used, and the anonymity gain is obtained. The first step is to find the node pair that includes , in which is the only node pair. Therefore, we use to unify , and the location must be removed from . As shown in the first step of Figure 4, the location and its location.id are deleted from the -level node , and then the remaining and its child nodes are inserted into the -level node and its child nodes, respectively. We can see from the second step in Figure 4 that node also includes ; therefore, child node and its location.id must also be deleted. Afterwards, the problem number N is 10, the length of trajectory becomes 5, and the anonymity gain is 1.12.

Figure 4.
Updating of the TP-tree by using suppression. The number ① represents the location was removed from -level node , and updated the remaining nodes, and ② represents -level node and also be deleted.
4.2.2. Splitting
We design the splitting operation based on the TP-tree. The idea of the intuitive splitting technique is to directly divide a trajectory into two trajectories from the splitting location. The splitting location is selected based on the trajectory projection contained in the problematic node, and all the locations in the trajectory projection contained in the problematic node can be defined as the splitting location . The location is an indivisible location if and only if is the last location of the original trajectory. For a problematic node there may be several cases of splitting, so selecting the final splitting location requires calculating the splitting anonymity gain of all potential locations except the indivisible one and then selecting the best one as the final splitting anonymity gain. The details of the TP-tree changes are described in Example 10.
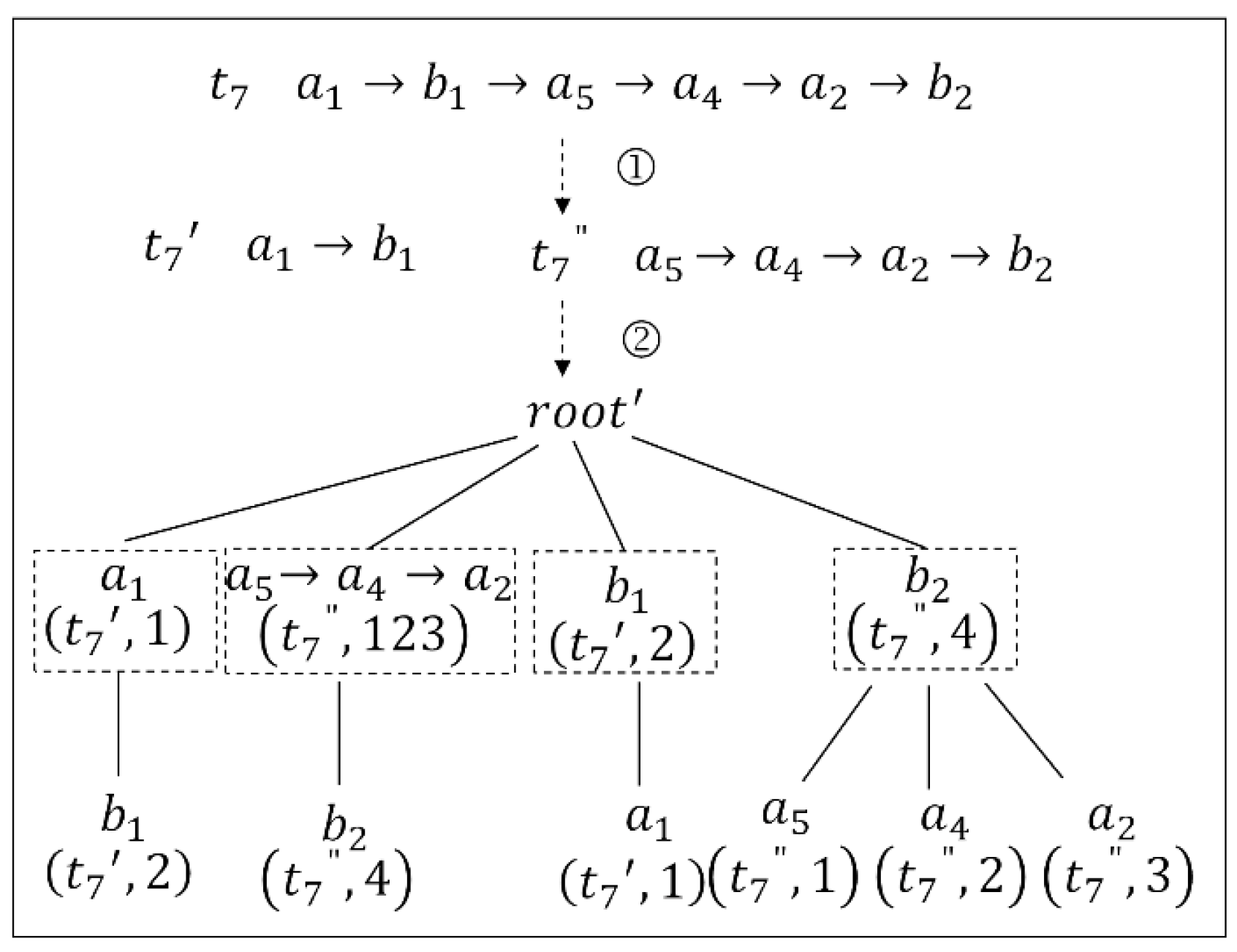
Example 10.
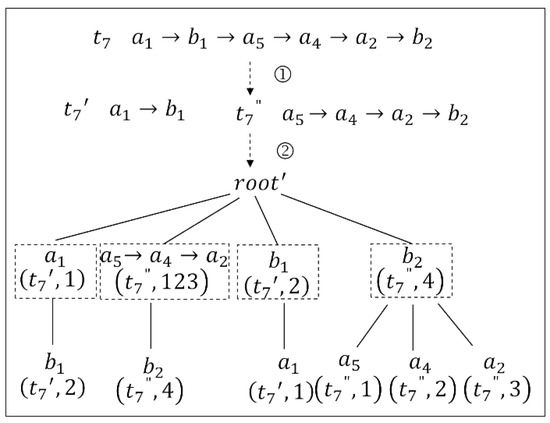
Considering the problematic node , splitting based on the TP-tree is used, and the anonymity gain is obtained. The local change in the tree is shown in Figure 5. First, the trajectories that are involved in the problematic node are found. Moreover, the trajectory involved is, and the splitting location is or , where is an indivisible location. Thus, is split from to obtain and . Then, we construct a new TP-tree* about the trajectory and , delete all node information of in the original TP-tree, and merge the TP-tree* of the trajectory and into the original TP-tree. After splitting, the number of problems N is 12; the length of is 6; the length of the trajectory and are 2 and 4, respectively; and the is 0.47.

Figure 5.
Updating of the TP-tree by using splitting. The number ① represents is split from to obtain and , and ② represents the construction of a new TP-tree* about the trajectory and .
4.2.3. Dummy Trajectory
The key to the dummy trajectory based on the TP-tree is adding dummy trajectories; in this paper, we add a dummy trajectory based on the trajectory projection contained in the problematic node. In other words, a dummy trajectory similar to the trajectory protection contained in problematic node is added to the TP-tree. The details of the TP-tree changes are described in Example 11.
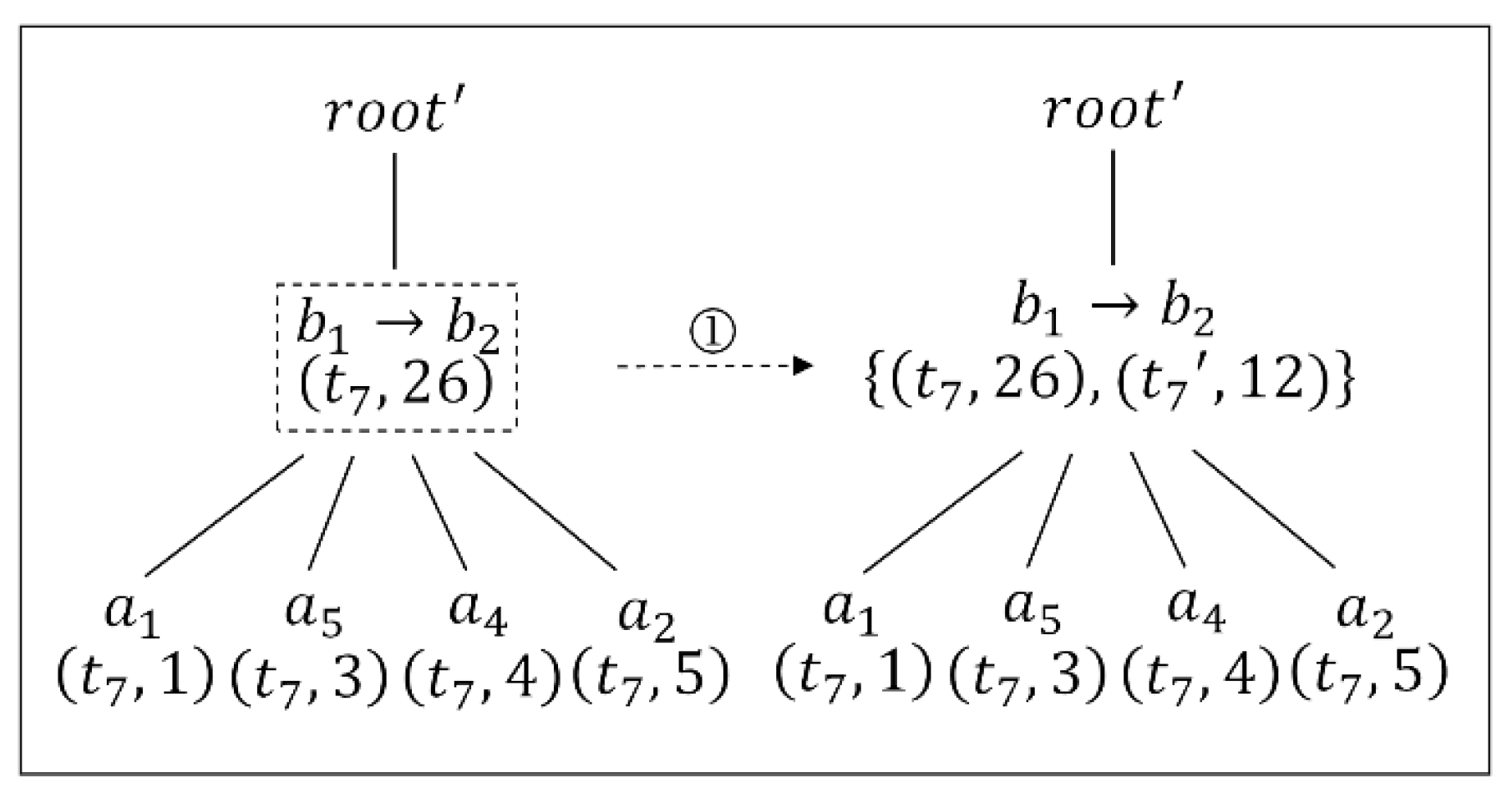
Example 11.
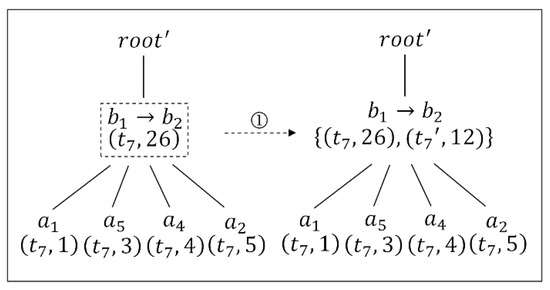
Considering the problematic node , the dummy trajectory based on the TP-tree is used, and the anonymity gain is obtained. A dummy trajectory is added to the TP-tree, and Figure 6shows the local change of the tree by using the dummy trajectory. Afterwards, the problem number N is 12, and is 0.25.

Figure 6.
Updating of the TP-tree by using a dummy trajectory. The number ① represents a dummy trajectory is added.
4.3. Local Preferential Seclection
We consider suppression, splitting, and dummy trajectory adding as candidate techniques to achieve privacy preservation based on the tree structure, solving problematic nodes step by step. To select the final technique for a specific problematic node, we propose an LP function based on the analysis of location loss and the anonymity gain.
Let and be the first and second anonymity gains, respectively. The suppression is the final selection if one of the following conditions holds:
- (1)
- and Del.loc = 1;
- (2)
- and
In other cases, the operation that corresponds to must be finally selected.
Analysis. In this paper, we consider suppression, splitting, and dummy trajectory adding as candidate techniques. However, suppression will quickly delete several locations once to reduce the number of problems, which results in the algorithm tending towards suppression. Additionally, many locations may be deleted. Therefore, we construct an LP function to change this trend to protect privacy and reduce information loss. We define the operation as the best operation if and only if the number of locations lost is 1 and the anonymity gain of the suppression is largest. We set the value of to the same as the user’s privacy requirements threshold.
The LP algorithm is shown as Algorithm 2. The LP algorithm takes a problematic node c, the user’s privacy requirements threshold , and the TP-tree as the inputs. The LP algorithm returns an array FinGain, shown as Table 3. Initially, for a problematic node c, the LP algorithm calculates the anonymity gain of suppression . The node pair is set as the maximum anonymity gain (Lines 2 to 4). Then, the LP algorithm scans all the -level nodes of the TP-tree, finds all the trajectories that the problematic node contained, and calculates the splitting anonymity gain of all trajectories at each splitting location. By letting be the gain, is largest (Lines 5 to 7). Finally, the LP algorithm adds the same dummy trajectory as trajectory projection and calculates the anonymity gain of dummy trajectory (Line 8). Afterwards, the LP algorithm selects the final operation for the problematic node and returns FinGain (Lines 9 to 17).
| Algorithm 2: Local_Preferential (LP) |
| Input: Pending problematic node c, user’s privacy requirements threshold , TP-tree |
| Output: Array of final operation FinGain |
|
4.4. Trajectory Anonymization
In this subsection, we introduce our algorithm of privacy preservation for trajectory data publication based on LPA. The algorithm iteratively solves the problematic nodes of the TP-tree until the trajectory dataset release is met. The LPA algorithm is shown as Algorithm 3.
Algorithm 3 takes an original trajectory dataset T, a set of attackers Adv, and a user’s privacy requirements threshold as the inputs and returns a safe trajectory dataset . Initially, the LPA algorithm constructs the TP-tree [10] (Line 1) and then calls the PNF algorithm to obtain the set of problematic nodes P and the total number of problems N (Line 2). If there are problematic nodes in the TP-tree (, c is set to be a problematic node, and the LPA algorithm continues to select the final operation according to the LP algorithm (Line 5). Afterwards, the returned final operation and related information are used to solve the problematic node c and update the TP-tree. Specifically, if the final operation is suppression, the corresponding node updates of are merged into (Lines 6 to 11). If the final operation is splitting, the LPA algorithm finds all the trajectories that are involved in the problematic node and constructs a dataset . All node information about the trajectory must be deleted from the original TP-tree. After that, each trajectory is split from the splitting location l, and a new dataset is reconstructed. Finally, the TP-tree* of the dataset is merged to the TP-tree (Lines 13 to 18). If the final operation is to add a dummy trajectory, then the same dummy trajectory as the problematic node is added and merged into the TP-tree (Lines 20 to 21). After the above step, the new number of problems N is calculated, and the LPA algorithm iteratively eliminates the number of problems until N is 0. Then, the corresponding safe trajectory dataset is obtained.
| Algorithm 3: Local_Preferential_Anonymity (LPA) |
| Input: Original trajectory dataset T, attackers set Adv, user’s privacy requirements threshold |
| Output: A corresponding safe dataset |
|
Example 12.
According to the LP function, the final operation for the problematic node is suppression.
4.5. Algorithms Anlysis
4.5.1. Trajectory Privacy Preservation Capability
Consider an original trajectory dataset T, and let be the anonymized trajectory dataset of T.
Theorem 1.
The LPA algorithm can derive a corresponding safe dataset of the original trajectory datasetT.
Proof.
To derive a corresponding safe dataset of trajectory dataset T, there are no problem pairs in and no problematic nodes in the final TP-tree, and the number of problems N is 0. In our method, the LPA algorithm first constructs a TP-tree of T, so each entire trajectory will be stored in the tree. Then LPA calls the PNF algorithm to find the problematic nodes P in the TP-tree. Afterwards, the LPA algorithm selects the anonymity operation for each problematic node based on the LP algorithm and then solves the problematic node one by one until P is empty and N is 0. □
For example, for the original dataset in Table 1, after executing the LPA algorithm, we obtain a dataset , as shown in Table 4. Then, we execute the PNF algorithm for identification; the problem pairs set Q and the problematic nodes set P are empty, and the number of problems N is 0. Therefore, is a safe dataset.

Table 4.
A corresponding safe dataset of T.
4.5.2. Complexity Analysis
In order to present the results of algorithm complexity more clearly, let Adv be a set of potential attackers, be the maximum number of different projections about trajectory dataset T to an attacker, and be the maximum number of different locations contained in the trajectories to a projection. N is the total number of problems.
The cost of the TPtreeConstruction algorithm depends on inserting the trajectories in T into TP-tree. When considering an attacker and a trajectory, the cost of inserting all locations into the tree is . Therefore, the cost of inserting all locations of all trajectories of all attackers is . The most expensive cost of algorithm PNF depends on scanning the -level node and the corresponding -level nodes of each -level node at the same time. The worst case is the maximum number of -level projection nodes, as the cost of algorithm PNF is .
Algorithm LP mainly measures the anonymous gains of suppression, splitting, and dummy trajectory adding for a problematic node in the problematic node set of the TP-tree and selects the best value in the FinGain array. The expensive cost of suppression involves to scanning the -level nodes of the TP-tree once, finding all the trajectory projection pairs, and then scanning the TP-tree again for the calculation. The cost is .
The cost of splitting involves scanning the trajectories contained in the problematic node and the corresponding trajectory projection of the problematic node, and then the different locations of this trajectory projection are analyzed, with the cost of .The cost of dummy trajectory adding involves scanning the TP-tree for calculation, and the time requirement is . In total, the cost of algorithm LP is .
The time cost of algorithm LPA is mainly dependent on the total number of problems N in the TP-tree and the call to the above algorithms. The worst case is that all problems N need to be iterated, and the cost is .
Discussion.
Time performance analysis of the proposed algorithm LPA and the compared algorithms [8,10].
The storage structures of and [8] are arrays to store the trajectory dataset and the set of trajectory projection, so each calculation of the inference probability needs to traverse the trajectory projection set first and then the trajectory dataset, which results in lower time performance. In order to solve this problem, the tree-based storage structure is adopted in the algorithms and [10], which avoids wasting time in traversing the trajectory dataset in the calculation process of inference probability and verifies the significant improvement of time performance through a number of experiments. In our method, the tree-based storage structure [10] is also be applied to store the trajectory dataset, so the time performance of the problematic node finding is better than that of algorithm and and is similar to the algorithm and . In the stage of solving the problematic nodes, we consider three candidate technologies for a specific node, which takes more time than the algorithm and , but its traversal performance is still better than the algorithm and because of the storage structure. However, although the time performance of the algorithm LPA is worse than that of the algorithms and , the data utility of the anonymous dataset constructed by the LPA algorithm is significantly better than that of the comparison algorithm. The detailed analysis of data utility will be introduced in Section 5.
5. Experiment
The LPA algorithm was implemented in Python 3, and other algorithms were implemented in Java. All experiments were tested on a PC with an AMD Ryzen 7 at 2.90 GHz with 16 GB of RAM. We compared our algorithm with the algorithm and [8]; both algorithms apply global and local suppression. The and [10], which are based on suppression and pruning techniques, are also compared. Our experiment is mainly aimed at measuring the data utility of the anonymous dataset; the programming language of the algorithm will not affect the final result of the data.
5.1. Dataset
We use the City80K [30,31] dataset in our experiments. City80K contains 80,000 trajectories. After trajectory preprocessing, the data form shown in Table 1 will be obtained. In this paper, only the location information that the user signs in with was used.
5.2. Metrics
The key to measuring the performance of the trajectory privacy preservation algorithm is to evaluate the quality of anonymous trajectory datasets, which mainly include information that remains from anonymous datasets and the utility of anonymous datasets. We focus on the changes in the trajectory dataset before and after anonymity. The measuring utilities are as follows.
Average trajectory remaining ratio. The first metric measures the remaining ratio of locations of each trajectory. We define as the trajectory remaining ratio of trajectory and calculate it as Equation (9):
We compare each trajectory step by step and find the average trajectory remaining ratio for the anonymous dataset, denoted as TR(avg). The higher the value is, the better the effect will be. The formula for calculating TR(avg) is in Equation (10):
Average location appearance ratio. We use the average location appearance ratio to measure changes in the number of locations before and after anonymity, denoted as AR(avg), and we calculate the change in the number of appearances of the location in the original trajectory dataset and the anonymous dataset. For each location in the trajectory dataset, we define AR(l) as the number of appearances of l in the anonymity dataset and the original trajectory dataset ratio. The formulas are shown in Equations (11) and (12):
where the value of AR(avg) is between 0 and 1; the higher the value is, the better the effect.
Frequent sequential pattern remaining ratio. In general, if there are more frequent sequential patterns that are preserved after anonymity, then the better the data utility will be. We use the Prefixspan algorithm to obtain frequent sequential patterns in the original dataset and the anonymity dataset. Then, we calculate the average percentage of frequent sequential patterns of the original dataset observed in the safe counterpart, denoted as FSP(avg).
5.3. Result and Analysis
Considering the parameter settings of the compared algorithms, we set the experimental parameters as follows:
- (1)
- The user’s privacy requirements threshold . is 0.5 by default, and the range varies from 0.4 to 0.7.
- (2)
- The average length of a trajectory denoted by . is 6 by default, and the range varies from 4 to 7.
- (3)
- The size of the trajectory dataset denoted by . is 300 by default, and the range varies between 150 and 400.
Since our algorithm has a certain randomness in the order of processing and the selection of problematic node c, each group of experiments is run ten times and the results are averaged.
5.3.1. Average Trajectory Remaining Ratio
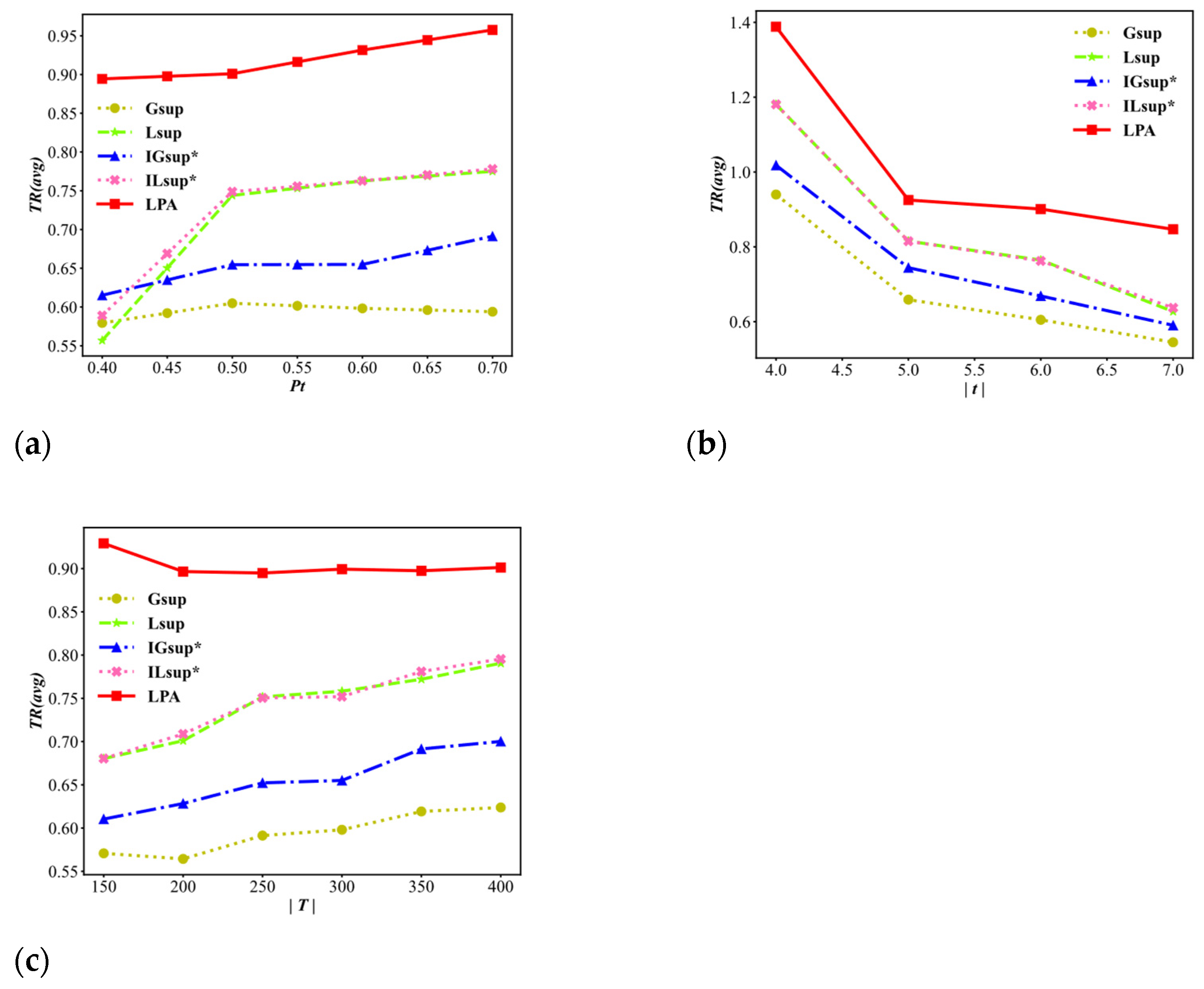
Figure 7 shows the average trajectory remaining ratio TR(avg) for the variable of the user’s privacy requirements threshold , the average length of a trajectory , and the size of the trajectory dataset .
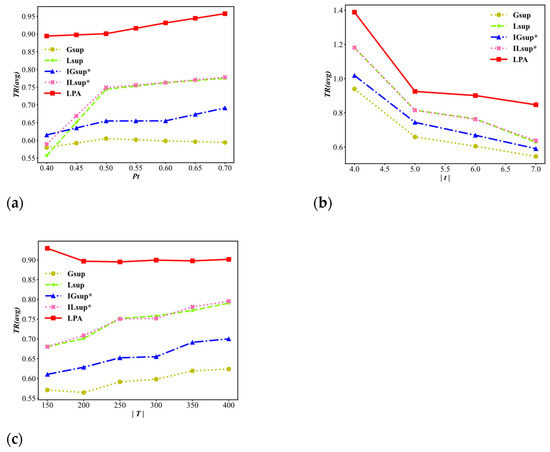
Figure 7.
Average trajectory remaining ratio TR(avg) (higher is better). (a) Varying . (b) Varying (avg). (c) Varying .
As shown in Figure 7a, the highest TR(avg) value is always achieved by the LPA algorithm, which is much better than , , and . The trend of the LPA algorithm initially decreases and then increases because the LP function is used in the LPA algorithm, which can balance the use of the three techniques with certain randomness. In Figure 7b, the TR(avg) values decrease as increase. This occurs because if the trajectory is larger, the locations of a trajectory that are owned by the attackers will also be larger, which results in an increase in the number of problems N. We can see that the values of TR(avg) of the LPA algorithm are on average 0.32 and 0.25 higher than that of and , respectively, and 0.16 higher than and . Figure 7c presents the result when the value of increases. The TR(avg) values of the LPA algorithm fluctuate within the range of approximately 0.88 to 0.93. Additionally, the TR(avg) values are always much higher than the other algorithms, which indicates that the scalability of our algorithm is better than that of the other algorithms. The main reason for this result occurring is that the LP function used in the LPA balances the selection of the three techniques.
5.3.2. Average Location Appearance Ratio
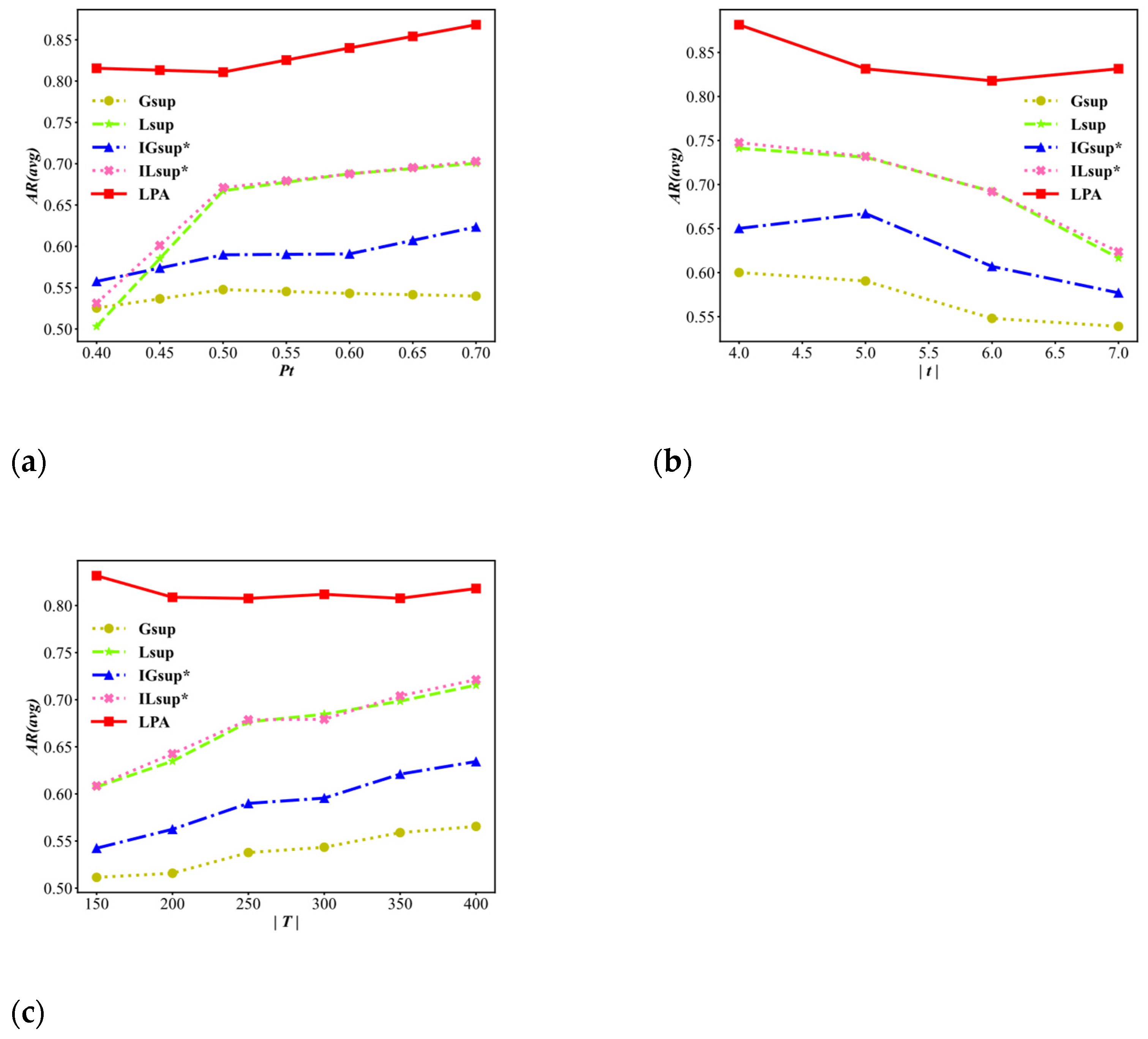
Figure 8 shows the average location appearance ratio AR(avg) for the user’s privacy requirements threshold , the average length of a trajectory , and the size of the trajectory dataset .
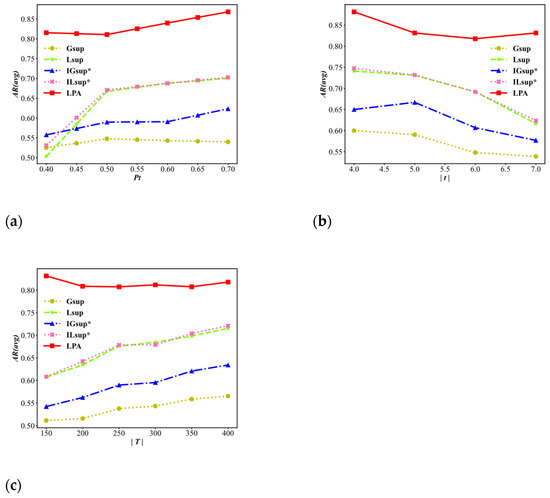
Figure 8.
Average location appearance ratio AR(avg) (higher is better). (a) Varying . (b) Varying (avg). (c) Varying .
As shown in Figure 8a, with the increase of , the AR(avg) values of all algorithms show an upwards trend, and the AR(avg) values of the LPA algorithm are always significantly higher than those of the others. In Figure 8b with the increase of , the AR(avg) values of the four algorithms gradually decrease, but the AR(avg) values of the LPA algorithm take 6 as the critical point and show a trend of first decreasing and then increasing. Moreover, the AR(avg) value of the LPA algorithm is always higher than that of the other algorithms. Figure 8c shows that as increases, the AR(avg) values of the LPA algorithm fluctuate within the range of approximately 0.80 and are always higher than those of the other four algorithms. The reason for this phenomenon is that the LPA algorithm considers three techniques as candidate techniques, and the application of the LP function reduces the frequency of the suppression and reduces the information loss of anonymity processing.
5.3.3. Frequent Sequential Pattern Mining
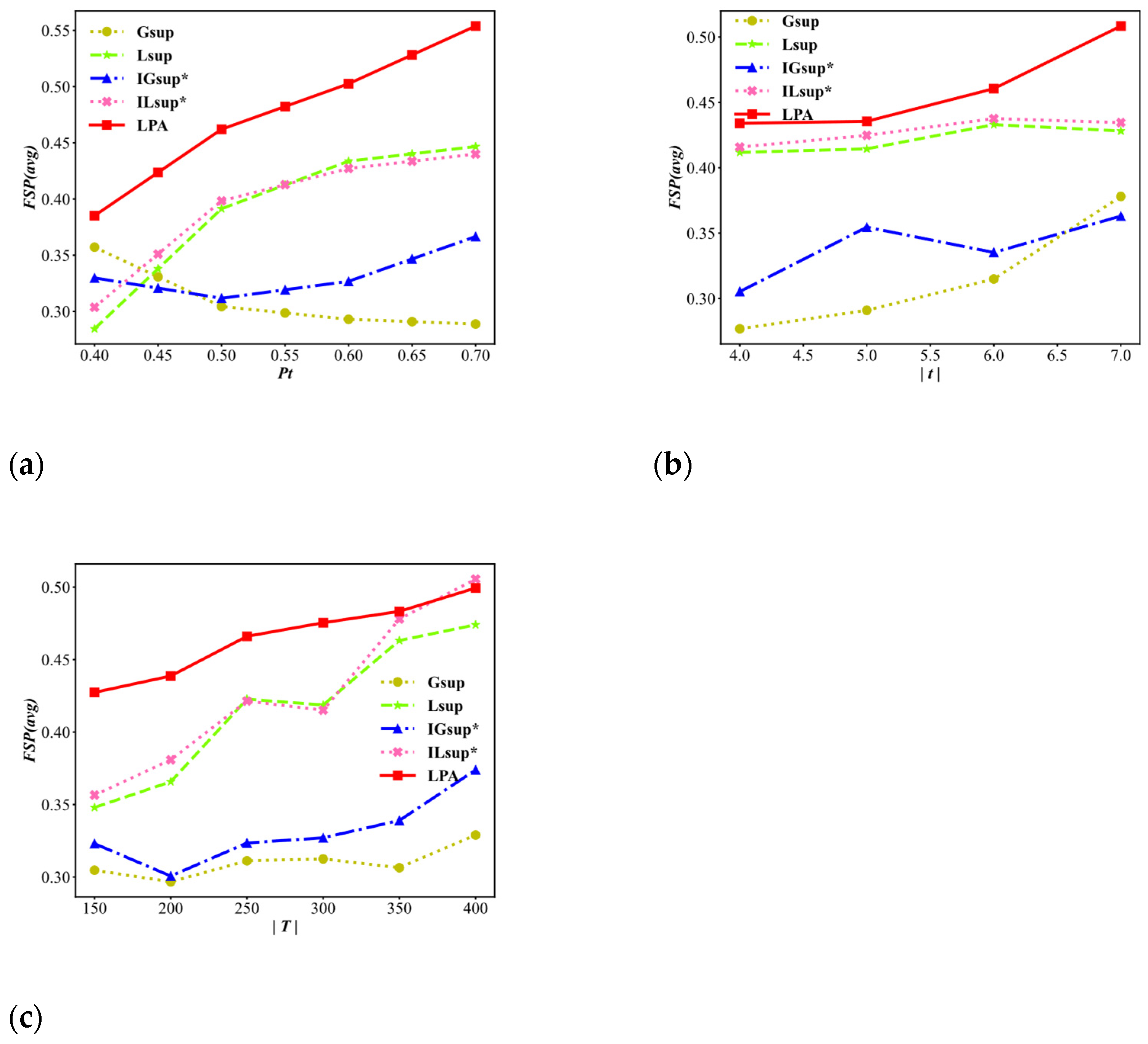
We present the average frequent sequential pattern remaining ratio FSP(avg) for the variable of the user’s privacy requirements threshold , the average length of a trajectory , and the size of the trajectory dataset . In our experiments, the frequent pattern threshold is defined as 2. The results are shown in Figure 9. For each parameter change, the LPA algorithm has the highest FSP(avg) values.
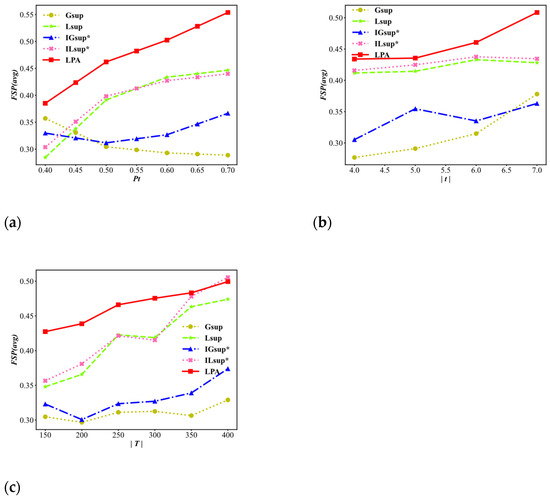
Figure 9.
Average published frequent sequential pattern remaining ratio FSP(avg) (higher is better). (a) Varying . (b) Varying (avg). (c) Varying .
As shown in Figure 9a, for LPA, , and , the general trend is that the FSP(avg) values increase as increases, while the trends of and have no obvious upwards motion. Furthermore, the FSP(avg) values of the LPA algorithm are significantly better than those of the other algorithms because the LP function of the LPA algorithm gradually processes the problematic nodes and merges the nodes, which improves the FSP(avg). In Figure 9b, the FSP(avg) values gradually increase with an increasing , and the FSP(avg) value of the LPA algorithm is always higher than that of the other algorithms. The reason for this result is that the longer the average trajectory length is, the higher the number of problems. Similar to the data in the previous two experimental results, Figure 9c shows that as increases, the FSP(avg) values show an overall upwards trend, and the values of LPA are overall higher than those of the other algorithms. It can be concluded that the overall performance of FSP(avg) in LPA is better than that of the other algorithms.
To summarize, compared with the other algorithms [8,10], the performance of the LPA algorithm is better in terms of data utility. Additionally, this result indicates that the LPA algorithm achieves higher data utility in anonymity and effectively balances the data utility and privacy preservation.
6. Discussion
We mainly focus on the research of privacy protection methods of trajectory data publishing by trajectory data processing. The data type is semantic location (such as user transaction data). Considering potential attackers, we can further infer the unknown location of users that may be inferred by attackers through identifying the privacy threats. A new privacy protection method is proposed to solve the problem of privacy disclosure in the analysis and reuse of such data. We conducted an experimental evaluation on the public dataset, and the experimental results show that our method can effectively achieve trajectory privacy protection, reduce information loss, and improve the data utility. The preprocessing part and storage structure of the tree in the first stage can reduce the running time of identifying the privacy threats, which has been proved in other work [10]. In the second stage, we consider the mixed use of multiple technologies to improve the utility of anonymous data. At the same time, this method can be further extended to a data-type privacy protection method with different types of sensitive attributes in semantic location, which is the next research content.
7. Conclusions
In this paper, we proposed a novel privacy-preserving method for trajectory data publication based on LPA, which is used to defend against attackers and infer other unknown locations through partial background knowledge in their possession. We designed the operation of splitting and dummy trajectory based on the tree structure and considered suppression, splitting, and dummy trajectory adding as candidate techniques. Then, we proposed an LP function based on the analysis of location loss and anonymity gain to select the final operation for each problematic node. The empirical results illustrated that the LPA algorithm reduces information loss and improves data utility to a certain extent. There is also room for improvement in the selection function, and we will continue to study this problem and consider the relevance of different types of sensitive attributes in semantic location in our ongoing work.
8. Patent
A patent of the same name has been applied for the relevant research content of this manuscript (No. CN202210178099.9), which entered the substantive examination stage on 27 May 2022.
Author Contributions
Conceptualization, X.Z. and Y.L.; methodology, X.Z.; validation, X.Z., L.X. and Z.L.; investigation, L.X. and Z.L.; resources, Q.Y.; data curation, X.Z.; writing—original draft preparation, X.Z.; writing—review and editing, Y.L. and Q.Y.; visualization, Z.L.; supervision, Y.L.; project administration, Y.L.; funding acquisition, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 62272006 and the University Collaborative Innovation Project of Anhui Province, grant number GXXT-2019-040. The APC was funded by the National Natural Science Foundation of China, grant number 62272006.
Data Availability Statement
We are sorry that the raw/processed data required to reproduce these findings cannot be shared at this time as the data also forms part of an ongoing study. However, if the paper is accepted for publication, the data and code in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mendes, R.; Vilela, J.P. Privacy-preserving Data Mining: Methods, Metrics, and Applications. IEEE Access 2017, 5, 10562–10582. [Google Scholar] [CrossRef]
- Naji, H.A.; Wu, C.; Zhang, H. Understanding the impact of human mobility patterns on taxi drivers’ profitability using clustering techniques: A case study in Wuhan, China. Information 2017, 8, 67. [Google Scholar] [CrossRef]
- Wang, W.; Mu, Q.; Pu, Y.; Man, D.; Yang, W.; Du, X. Sensitive Labels Matching Privacy Protection in Multi-Social Networks. In Proceedings of the ICC 2020–2020 IEEE International Conference on Communications, Dublin, Ireland, 7–11 June 2020; pp. 1–7. [Google Scholar]
- Chen, L.; Xu, Y.; Xie, F.; Huang, M.; Zheng, Z. Data Poisoning Attacks on Neighborhood-Based Recommender Systems. Trans. Emerg. Telecommun. Technol. 2021, 32, e3872. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, R.; Wu, D.; Wang, H.; Song, H.; Ma, X. Local Trajectory Privacy Protection in 5G Enabled Industrial Intelligent Logistics. IEEE Trans. Ind. Inform. 2021, 18, 2868–2876. [Google Scholar] [CrossRef]
- Fung, B.C.; Wang, K.; Chen, R.; Yu, P.S. Privacy-preserving Data Publishing: A Survey of Recent Developments. ACM Comput. Surv. 2010, 42, 1–53. [Google Scholar] [CrossRef]
- Jin, F.; Hua, W.; Francia, M.; Chao, P.; Orlowska, M.; Zhou, X. A Survey and Experimental Study on Privacy-Preserving Trajectory Data Publishing. IEEE Trans. Knowl. Data Eng. 2022, 1. [Google Scholar] [CrossRef]
- Terrovitis, M.; Poulis, G.; Mamoulis, N.; Skiadopoulos, S. Local Suppression and Splitting Techniques for Privacy Preserving Publication of Trajectories. IEEE Trans. Knowl. Data Eng. 2017, 29, 1466–1479. [Google Scholar] [CrossRef]
- Hassan, M.Y.; Saha, U.; Mohammed, N.; Durocher, S.; Miller, A. Efficient Privacy-Preserving Approaches for Trajectory Datasets. In Proceedings of the IEEE International Conference on Dependable, Autonomic and Secure Computing, International Conference on Pervasive Intelligence and Computing, International Conference on Cloud and Big Data Computing, International Conference on Cyber Science and Technology Congress, Calgary, AB, Canada, 17–22 August 2020; pp. 612–619. [Google Scholar]
- Lin, C.Y. Suppression Techniques for Privacy-preserving Trajectory Data Publishing. Knowl.-Based Syst. 2020, 206, 106354. [Google Scholar] [CrossRef]
- Lin, C.Y.; Wang, Y.C.; Fu, W.T.; Chen, Y.S.; Chien, K.C.; Lin, B.Y. Efficiently Preserving Privacy on Large Trajectory Datasets. In Proceedings of the IEEE Third International Conference on Data Science in Cyberspace, Guangzhou, China, 18–21 June 2018; pp. 358–364. [Google Scholar]
- Luper, D.; Cameron, D.; Miller, J.; Arabnia, H.R. Spatial and Temporal Target Association Through Semantic Analysis and GPS Data Mining. In Proceedings of the 2007 International Conference on Information & Knowledge Engineering, Las Vegas, Nevada, USA, 25–28 June 2007; pp. 25–28. [Google Scholar]
- Lei, P.R.; Peng, W.C.; Su, I.J.; Chang, C.P. Dummy-based Schemes for Protecting Movement Trajectories. J. Inf. Sci. Eng. 2012, 28, 335–350. [Google Scholar]
- Wu, Q.; Liu, H.; Zhang, C.; Fan, Q.; Li, Z.; Wang, K. Trajectory Protection Schemes Based on A Gravity Mobility Model in IoT. Electronics 2019, 8, 148. [Google Scholar] [CrossRef]
- Liu, X.; Chen, J.; Xia, X.; Zong, C.; Zhu, R.; Li, J. Dummy-Based Trajectory Privacy Protection Against Exposure Location Attacks. In Proceedings of the International Conference on Web Information Systems and Applications, Qingdao, China, 20–22 September 2019; pp. 368–381. [Google Scholar]
- Samarati, P. Protecting Respondents Identities in Microdata Release. IEEE Trans. Knowl. Data Eng. 2001, 13, 1010–1027. [Google Scholar] [CrossRef]
- Sweeney, L. k-anonymity: A Model for Protecting Privacy. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2002, 10, 557–570. [Google Scholar] [CrossRef]
- Abul, O.; Bonchi, F.; Nanni, M. Never walk alone: Uncertainty for Anonymity in Moving Objects Databases. In Proceedings of the IEEE 24th International Conference on Data Engineering, Cancun, Mexico, 7–12 April 2008; pp. 376–385. [Google Scholar]
- Domingo-Ferrer, J.; Trujillo-Rasua, R. Microaggregation-and Permutation-Based Anonymization of Movement Data. Inf. Sci. 2012, 208, 55–80. [Google Scholar] [CrossRef]
- Trujillo-Rasua, R.; Domingo-Ferrer, J. On the Privacy Offered by (k, δ)-Anonymity. Inf. Syst. 2013, 38, 491–494. [Google Scholar] [CrossRef]
- Dong, Y.; Pi, D. Novel Privacy-Preserving Algorithm Based on Frequent Path for Trajectory Data Publishing. Knowl.-Based Syst. 2018, 148, 55–65. [Google Scholar] [CrossRef]
- Kopanaki, D.; Pelekis, N.; Kopanakis, I.; Theodoridis, Y. Who Cares about Others’ privacy: Personalized Anonymization of Moving Object Trajectories. In Proceedings of the 19th International Conference on Extending Database Technology: Advances in Database Technology, Bordeaux, France, 15–18 March 2016. [Google Scholar]
- Chen, C.; Luo, Y.; Yu, Q.; Hu, G. TPPG: Privacy-Preserving Trajectory Data Publication Based on 3D-Grid Partition. Intell. Data Anal. 2019, 23, 503–533. [Google Scholar] [CrossRef]
- Nergiz, M.E.; Atzori, M.; Saygin, Y. Towards Trajectory Anonymization: A Generalization-Based Approach. In Proceedings of the SIGSPATIAL ACM GIS 2008 International Workshop on Security and Privacy in GIS and LBS, Irvine, CA, USA, 4–7 November 2008; Volume 2, pp. 52–61. [Google Scholar] [CrossRef]
- Yarovoy, R.; Bonchi, F.; Lakshmanan, L.V.; Wang, W.H. Anonymizing Moving Objects: How to Hide a Mob in A Crowd? In Proceedings of the 12th International Conference on Extending Database Technology: Advances in Database Technology, Saint Petersburg, Russia, 24–26 March 2009; pp. 72–83. [Google Scholar]
- Terrovitis, M.; Mamoulis, N.; Kalnis, P. Local and Global Recoding Methods for Anonymizing Set-valued Data. VLDB J. 2011, 20, 83–106. [Google Scholar] [CrossRef]
- Poulis, G.; Skiadopoulos, S.; Loukidis, G.; Gkoulalas Divanis, A. Apriori-based Algorithms for km-anonymizing Trajectory Data. Trans. Data Priv. 2014, 7, 165–194. [Google Scholar] [CrossRef]
- Terrovitis, M.; Mamoulis, N. Privacy preservation in the publication of trajectories. In Proceedings of the 9th International Conference on Mobile Data Management, Beijing, China, 27-30 April 2008; pp. 65–72. [Google Scholar]
- Yao, L.; Chen, Z.; Hu, H.; Wu, G.; Wu, B. Privacy Preservation for Trajectory Publication Based on Differential Privacy. ACM Trans. Intell. Syst. Technol. 2022, 13, 1–21. [Google Scholar] [CrossRef]
- Chen, R.; Fung, B.C.; Mohammed, N.; Desai, B.C.; Wang, K. Privacy-preserving Trajectory Data Publishing by Local Suppression. Inf. Sci. 2013, 231, 83–97. [Google Scholar] [CrossRef]
- Komishani, E.G.; Abadi, M.; Deldar, F. PPTD: Preserving Personalized Privacy in Trajectory Data Publishing by Sensitive Attribute Generalization and Trajectory Local Suppression. Knowl.-Based Syst. 2016, 94, 43–59. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).