Sufficient Networks for Computing Support of Graph Patterns
Abstract
1. Introduction
2. Definitions
2.1. Graphs and Networks
- Graphs and are isomorphic, denoted by , if there exists a bijection such that if and only if ;
- A graph is called a subgraph of a graph if and , written as ;
- A graph H is a proper subgraph of a graph G if it is a subgraph of G but it is not equal to G, denoted by ;
- A subgraph isomorphism from a graph H to a graph G exists if H is isomorphic to a subgraph of G, denoted by ;
- If a graph H is isomorphic to a proper subgraph of a graph G, we denote it by .
- A graph G is disconnected if there exists a partition of its nodes such that there are no edges with one end in and another in , and it is connected otherwise;
- A node subset U is a node-cut (or cut) if removal of U and edges incident to the nodes in U results in a disconnected graph;
- A node-cut of minimal size is called a minimal node-cut or simply a min-cut.
- The size of a flow is the total weight of paths exiting the source or entering the sink;
- A flow of maximal size is called a maximal flow (or max-flow);
- A flow is called integer if it assumes an integer value on all edges—such a flow is a collection of paths with one end in the source and another in the sink; for a path P its segment bounded by nodes is denoted by ;
- An integer flow is node-disjoint if its paths have no common nodes except for the source and the sink.
2.2. Patterns and Support Measures
2.3. Properties of Valid Support Measures
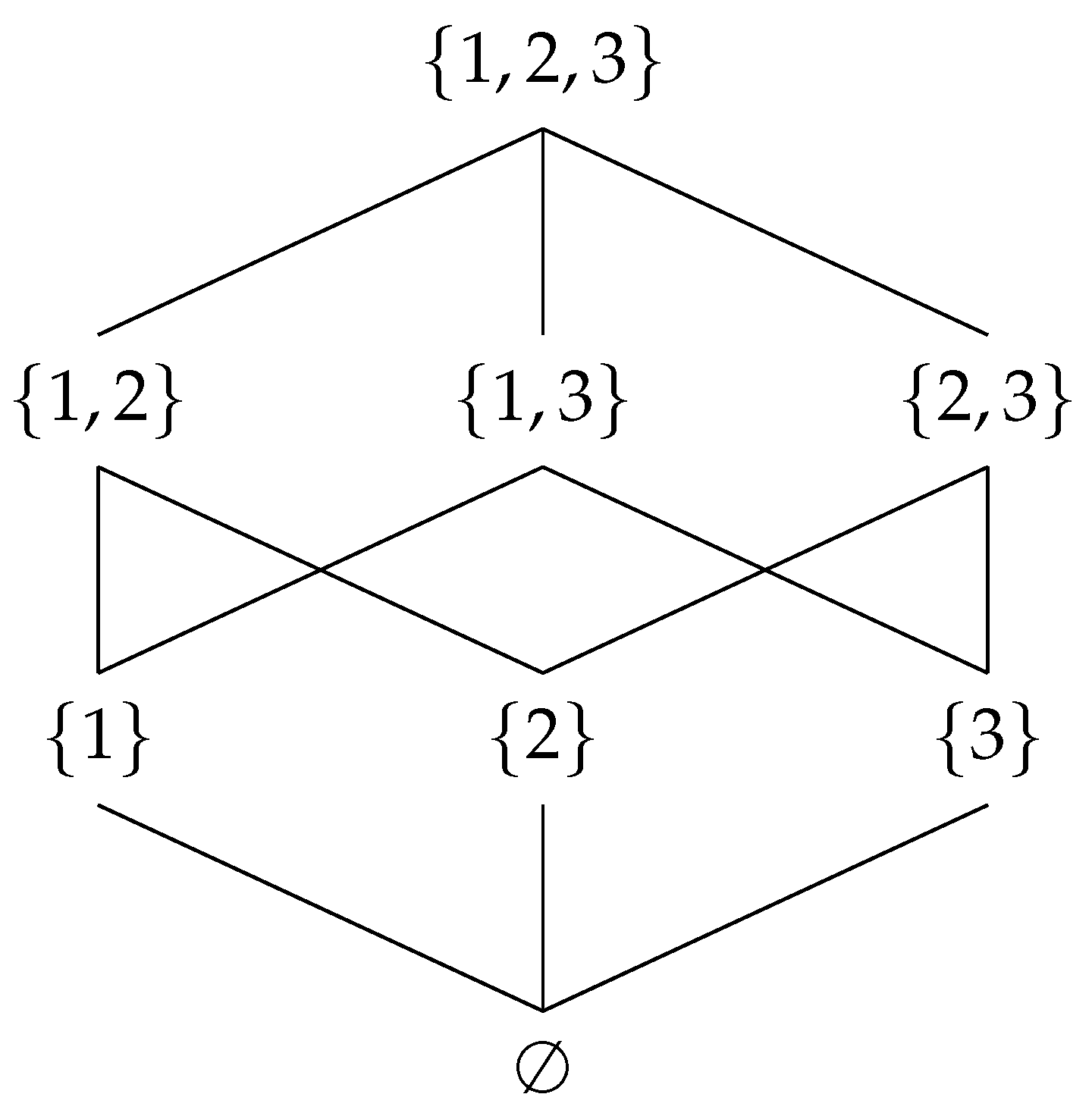
- The nodes of this network are instances of all the patterns in G, including the empty instance ⊥ and G itself.
- The empty instance is the bottom element of the diagram, and G is the top element.
- The edges of the network are defined by the Hasse diagram of the partially ordered set implied by the subgraph relation on pattern instances.
- All edge weights are set to 1.
- The empty instance ⊥ is considered to be a subgraph of all the nodes in V.
3. Sufficient Instance Networks
3.1. Definition
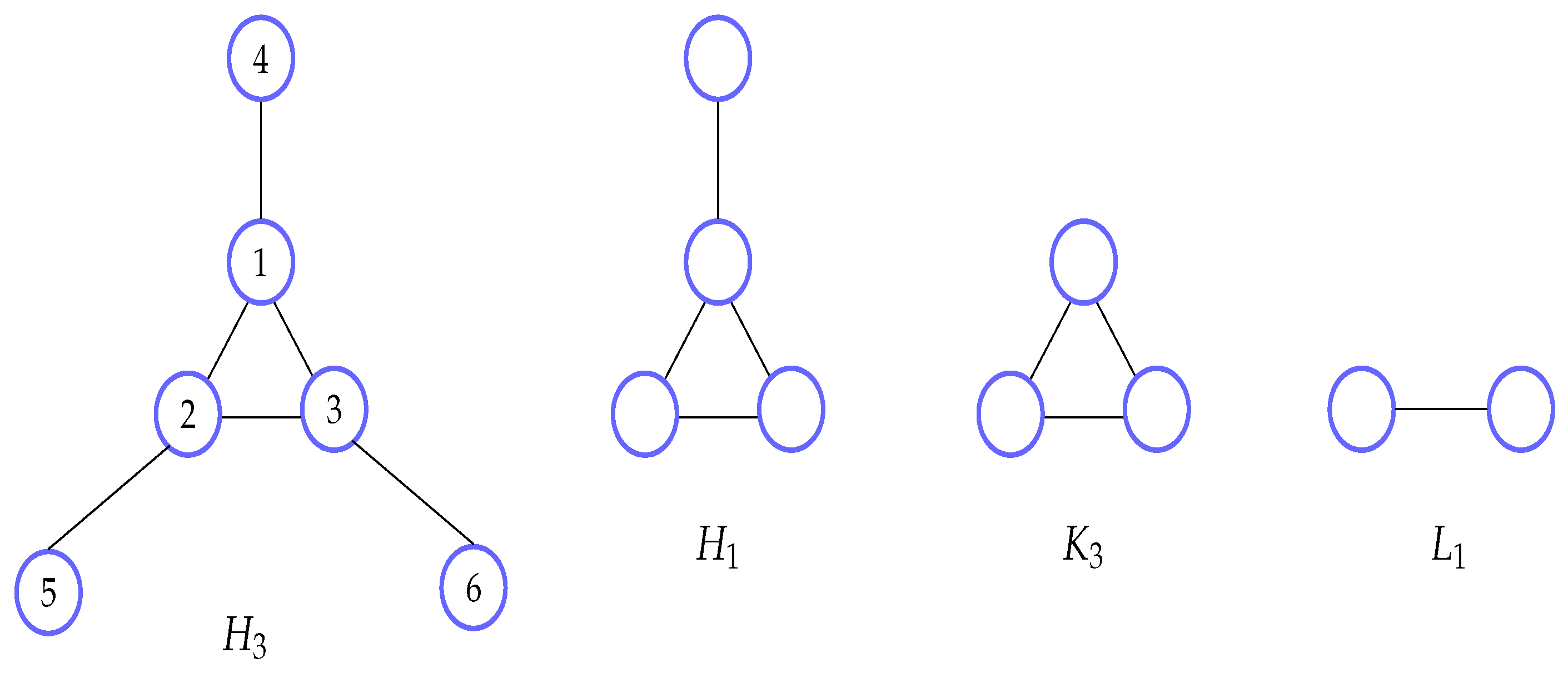
3.2. Examples of Insufficient Sub-Networks
3.3. Sufficient Networks
4. Intersection Networks
Sufficiency
- Case 1: if C contains nodes, instances of p and instances of patterns in , it exists in network as well and then as well because there is no flow of size S or bigger in .
- Case 2: otherwise, C contains instances of patterns . Then, every instance of in C is a subgraph of a different instance of p, denoted by . If this is not the case then lies in an intersection of two instances of p and we have contrary to our assumption. Let us replace in C every such instance by the instance of p and have case 1.
| Algorithm 1 Computing maximal support measures from |
|
5. Experimental Evaluation
5.1. Graph Types and Objectives of Experiments
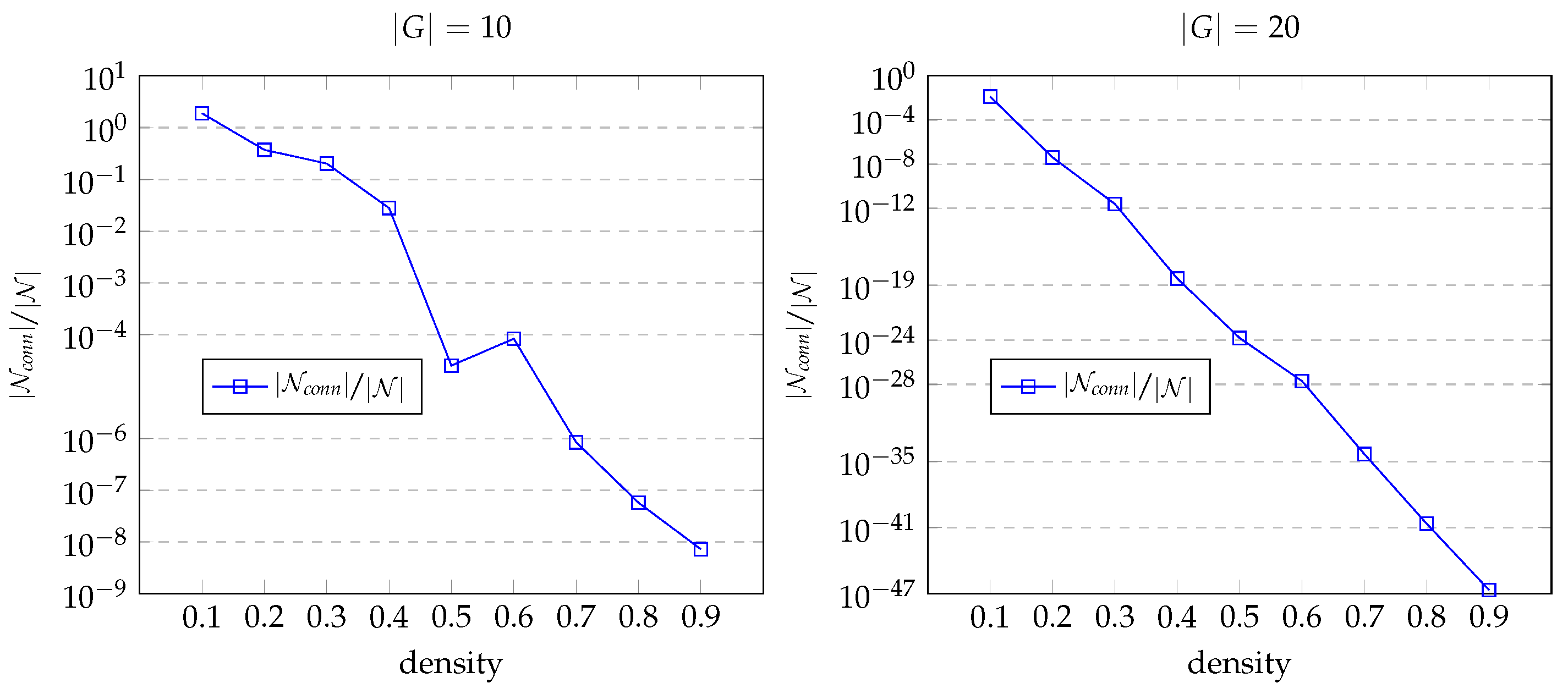
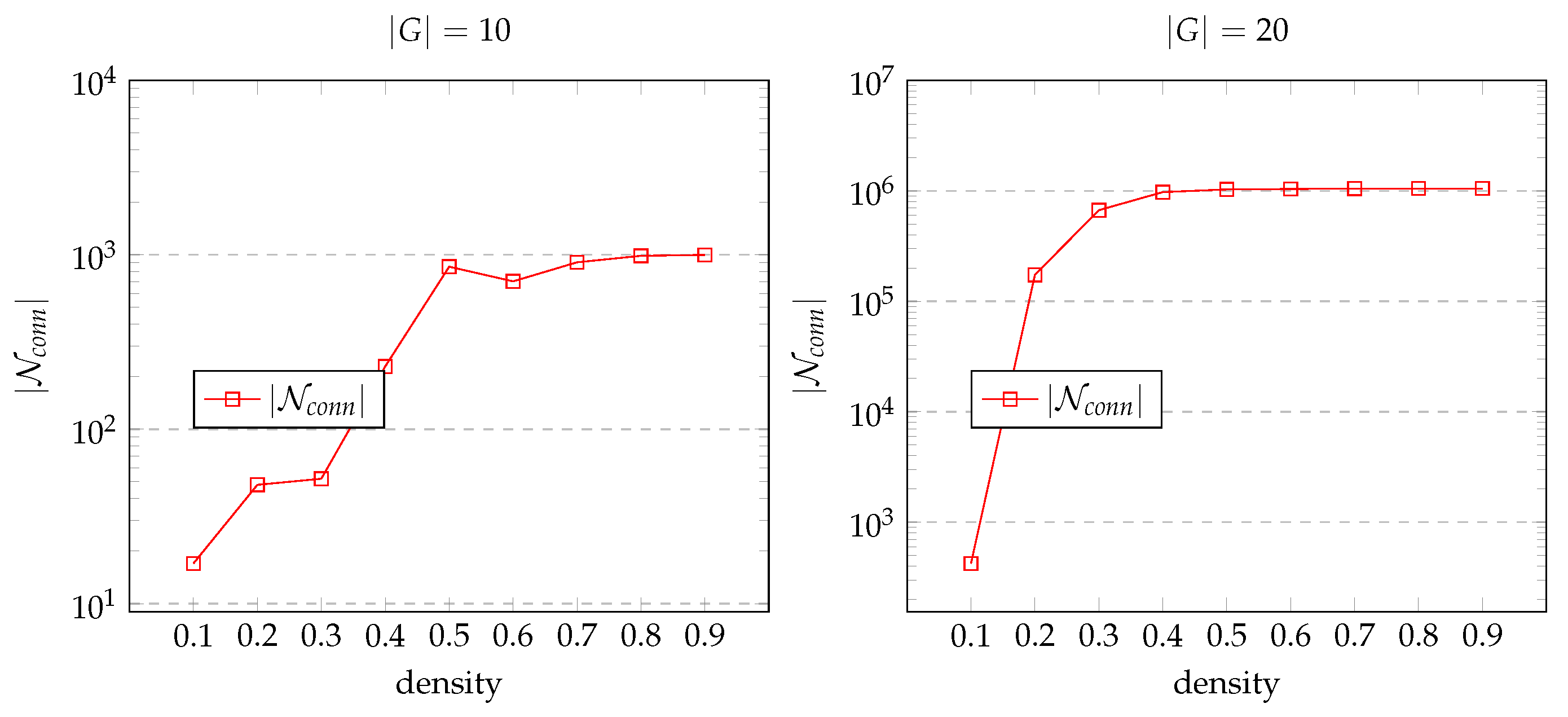
- To study whether or not using instead of decreases the network size;
- To evaluate the effect of graph density on network size when using ;
- To study how the use of an intersection network for a specific pattern affects the network size.
5.2. Software and Hardware Setup
5.3. Evaluation Results
6. Extensions and Limitations
- Directed graphs.In this case, patterns and their instances are directed graphs as well, and the instance network is defined in the same way as for the undirected graphs. Therefore, Theorem 2 holds for directed graphs as well, and all the results in this paper apply to them.
- Edge and node labeled graphs.Node and edge labels affect how instances of graph patterns are found in the database graphs because subgraph isomorphism has to take label matching into account. However, the rest of the results are not affected. Table 4 shows some experimental evaluations I performed for this type of graph.
- Multi-graphs and graphs with integer edge weights.An integer edge weight w is equivalent to replacing that edge with w edges between its incident nodes. In both cases, the subgraph isomorphism test for pattern instances is affected, because of the number of edges between a pair of nodes taken into account. The rest of the results hold for these graph types.
- Graphs with real edge weights.This case is equivalent to the previous one.
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Barbier, G.; Liu, H. Data mining in social media. In Social Network Data Analytics; Springer: Berlin/Heidelberg, Germany, 2011; pp. 327–352. [Google Scholar]
- Kurshan, E.; Shen, H. Graph computing for financial crime and fraud detection: Trends, challenges and outlook. Int. J. Semant. Comput. 2020, 14, 565–589. [Google Scholar] [CrossRef]
- Pourhabibi, T.; Ong, K.L.; Kam, B.H.; Boo, Y.L. Fraud detection: A systematic literature review of graph-based anomaly detection approaches. Decis. Support Syst. 2020, 133, 113303. [Google Scholar] [CrossRef]
- Kutty, S.; Nayak, R.; Chen, L. A people-to-people matching system using graph mining techniques. World Wide Web 2014, 17, 311–349. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Asemi, A.; Nezarat, A.; Ko, A. Developing a mathematical model of the co-author recommender system using graph mining techniques and big data applications. J. Big Data 2021, 8, 1–15. [Google Scholar] [CrossRef]
- Shin, Y.; Yoon, Y. Incorporating dynamicity of transportation network with multi-weight traffic graph convolutional network for traffic forecasting. IEEE Trans. Intell. Transp. Syst. 2020, 23, 2082–2092. [Google Scholar] [CrossRef]
- Ay, F.; Gülsoy, G.; Kahveci, T. Mining Biological Networks for Similar Patterns. In Data Mining: Foundations and Intelligent Paradigms; Springer: Berlin/Heidelberg, Germany, 2012; pp. 63–99. [Google Scholar]
- Durmaz, A.; Henderson, T.A.; Bebek, G. Frequent Subgraph Mining of Functional Interaction Patterns Across Multiple Cancers. In Proceedings of the BIOCOMPUTING 2021: Proceedings of the Pacific Symposium, Fairmont Orchid, HI, USA, 5–7 January 2020; pp. 261–272. [Google Scholar]
- Mihalcea, R.; Tarau, P. Textrank: Bringing order into text. In Proceedings of the 2004 Conference on Empirical Methods in Natural Language Processing, Barcelona, Spain, 25–26 July 2004; pp. 404–411. [Google Scholar]
- Jiang, C.; Coenen, F.; Sanderson, R.; Zito, M. Text classification using graph mining-based feature extraction. In Research and Development in Intelligent Systems XXVI; Springer: Berlin/Heidelberg, Germany, 2010; pp. 21–34. [Google Scholar]
- Liu, J.B.; Raza, Z.; Javaid, M. Zagreb connection numbers for cellular neural networks. Discret. Dyn. Nat. Soc. 2020, 2020, 8038304. [Google Scholar] [CrossRef]
- Majeed, A.; Rauf, I. Graph theory: A comprehensive survey about graph theory applications in computer science and social networks. Inventions 2020, 5, 10. [Google Scholar] [CrossRef]
- Kenyeres, M.; Kenyeres, J. Distributed Mechanism for Detecting Average Consensus with Maximum-Degree Weights in Bipartite Regular Graphs. Mathematics 2021, 9, 3020. [Google Scholar] [CrossRef]
- Krasanakis, E.; Symeonidis, A. Fast library recommendation in software dependency graphs with symmetric partially absorbing random walks. Future Internet 2022, 14, 124. [Google Scholar] [CrossRef]
- Jalali, M.; Tsotsalas, M.; Wöll, C. MOFSocialNet: Exploiting Metal-Organic Framework Relationships via Social Network Analysis. Nanomaterials 2022, 12, 704. [Google Scholar] [CrossRef]
- Li, P.; Chen, P.; Zhang, D. Cross-modal feature representation learning and label graph mining in a residual multi-attentional CNN-LSTM network for multi-label aerial scene classification. Remote Sens. 2022, 14, 2424. [Google Scholar] [CrossRef]
- Singh, M. Using natural language processing and graph mining to explore inter-related requirements in software artefacts. ACM Sigsoft Softw. Eng. Notes 2022, 44, 37–42. [Google Scholar] [CrossRef]
- Nijssen, S.; Kok, J.N. Frequent graph mining and its application to molecular databases. In Proceedings of the 2004 IEEE International Conference on Systems, Man and Cybernetics (IEEE Cat. No. 04CH37583), The Hague, The Netherlands, 10–13 October 2004; Volume 5, pp. 4571–4577. [Google Scholar]
- Takigawa, I.; Mamitsuka, H. Graph mining: Procedure, application to drug discovery and recent advances. Drug Discov. Today 2013, 18, 50–57. [Google Scholar] [CrossRef]
- Hoory, S.; Linial, N.; Wigderson, A. Expander graphs and their applications. Bull. Am. Math. Soc. 2006, 43, 439–561. [Google Scholar] [CrossRef]
- Vanetik, N.; Shimony, S.E.; Gudes, E. Support measures for graph data. Data Min. Knowl. Discov. 2006, 13, 243–260. [Google Scholar] [CrossRef]
- Bringmann, B.; Nijssen, S. What is frequent in a single graph? In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Osaka, Japan, 20–23 May 2008; pp. 858–863. [Google Scholar]
- Fiedler, M.; Borgelt, C. Subgraph support in a single large graph. In Proceedings of the Seventh IEEE International Conference on Data Mining Workshops (ICDMW 2007), Omaha, NE, USA, 28–31 October 2007; pp. 399–404. [Google Scholar]
- Wang, Y.; Guo, Z.C.; Ramon, J. Learning from networked examples. In Proceedings of the International Conference on Algorithmic Learning Theory, Kyoto, Japan, 15–17 October 2017; pp. 641–666. [Google Scholar]
- Meng, J.; Tu, Y.c. Flexible and Feasible Support Measures for Mining Frequent Patterns in Large Labeled Graphs. In Proceedings of the 2017 ACM International Conference on Management of Data, Chicago, IL, USA, 14–19 May 2017; pp. 391–402. [Google Scholar]
- Meng, J.; Tu, Y.C.; Pitaksirianan, N. A New Polynomial-time Support Measure for Counting Frequent Patterns in Graphs. In Proceedings of the 31st International Conference on Scientific and Statistical Database Management, Santa Cruz, CA, USA, 23–25 July 2019; pp. 214–217. [Google Scholar]
- Vanetik, N. Graph support measures and flows. Soc. Netw. Anal. Min. 2022, 12, 1–9. [Google Scholar]
- Yan, D.; Chen, H.; Cheng, J.; Özsu, M.T.; Zhang, Q.; Lui, J. G-thinker: Big graph mining made easier and faster. arXiv 2017, arXiv:1709.03110. [Google Scholar]
- Koutra, D. The power of summarization in graph mining and learning: Smaller data, faster methods, more interpretability. Proc. VLDB Endow. 2021, 14, 3416. [Google Scholar] [CrossRef]
- Shin, K.; Eliassi-Rad, T.; Faloutsos, C. Corescope: Graph mining using k-core analysis—patterns, anomalies and algorithms. In Proceedings of the 2016 IEEE 16th international conference on data mining (ICDM), Barcelona, Spain, 12–15 December 2016; pp. 469–478. [Google Scholar]
- Mawhirter, D.; Reinehr, S.; Holmes, C.; Liu, T.; Wu, B. Graphzero: Breaking symmetry for efficient graph mining. arXiv 2019, arXiv:1911.12877. [Google Scholar]
- Rao, G.; Chen, J.; Yik, J.; Qian, X. Intersectx: An efficient accelerator for graph mining. arXiv 2020, arXiv:2012.10848. [Google Scholar]
- Teixeira, C.H.; Fonseca, A.J.; Serafini, M.; Siganos, G.; Zaki, M.J.; Aboulnaga, A. Arabesque: A system for distributed graph mining. In Proceedings of the 25th Symposium on Operating Systems Principles, Monterey, CA, USA, 4–7 October 2015; pp. 425–440. [Google Scholar]
- Talukder, N.; Zaki, M.J. A distributed approach for graph mining in massive networks. Data Min. Knowl. Discov. 2016, 30, 1024–1052. [Google Scholar] [CrossRef]
- Buehrer, G.; Parthasarathy, S.; Chen, Y.K. Adaptive parallel graph mining for CMP architectures. In Proceedings of the Sixth International Conference on Data Mining (ICDM’06), Hong Kong, China, 18–22 December 2006; pp. 97–106. [Google Scholar]
- Menger, K. Zur allgemeinen kurventheorie. Fundam. Math. 1927, 10, 96–115. [Google Scholar] [CrossRef]
- Huan, J.; Wang, W.; Prins, J.; Yang, J. Spin: Mining maximal frequent subgraphs from graph databases. In Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Seattle, WA, USA, 22–25 August 2004; pp. 581–586. [Google Scholar]
- Li, X.L.; Foo, C.S.; Tan, S.H.; Ng, S.K. Interaction graph mining for protein complexes using local clique merging. Genome Inform. 2005, 16, 260–269. [Google Scholar] [PubMed]
- Falkowski, T.; Barth, A.; Spiliopoulou, M. Studying community dynamics with an incremental graph mining algorithm. AMCIS 2008 Proc. 2008, 29. [Google Scholar]
- Kuramochi, M.; Karypis, G. An efficient algorithm for discovering frequent subgraphs. IEEE Trans. Knowl. Data Eng. 2004, 16, 1038–1051. [Google Scholar] [CrossRef]
- Yan, X.; Han, J. gSpan: Graph-based substructure pattern mining. In Proceedings of the 2002 IEEE International Conference on Data Mining, Maebashi City, Japan, 9–12 December 2002; pp. 721–724. [Google Scholar]
- Bisong, E. Building Machine Learning and Deep Learning Models on Google Cloud Platform: A Comprehensive Guide for Beginners; Apress: New York, NY, USA, 2019. [Google Scholar]
- Hagberg, A.; Swart, P.; S Chult, D. Exploring Network Structure, Dynamics, and Function Using NetworkX; Technical Report; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2008. [Google Scholar]



| Graph | Nodes | Edges | Ratio | ||
|---|---|---|---|---|---|
| Erdős–Rényi | 10 | 20 | 576 | ||
| Erdős–Rényi | 11 | 26 | 1496 | ||
| Erdős–Rényi | 12 | 30 | 3066 | ||
| Erdős–Rényi | 13 | 34 | 6265 | ||
| Erdős–Rényi | 14 | 41 | 13,561 | ||
| Erdős–Rényi | 15 | 56 | 30,517 | ||
| Erdős–Rényi | 16 | 55 | 57,956 | ||
| Erdős–Rényi | 17 | 68 | 121,646 | ||
| Erdős–Rényi | 18 | 74 | 247,486 | ||
| Erdős–Rényi | 19 | 85 | 497,709 | ||
| Erdős–Rényi | 20 | 102 | 1,031,828 | ||
| 10 | 45 | 1023 | |||
| 11 | 55 | 2047 | |||
| 12 | 66 | 4095 | |||
| 13 | 78 | 8191 | |||
| 14 | 91 | 16,383 | |||
| 15 | 105 | 32,767 | |||
| 16 | 120 | 65,535 | |||
| 17 | 136 | 131,071 | |||
| 18 | 153 | 262,143 | |||
| 19 | 171 | 524,287 | |||
| 20 | 190 | 1,048,575 | |||
| 10 | 25 | 971 | |||
| 12 | 36 | 3981 | |||
| 14 | 49 | 16,143 | |||
| 16 | 64 | 65,041 | |||
| 18 | 81 | 261,139 | |||
| 20 | 100 | 1,046,549 |
| # of Graph | # of Graph | # of Pattern | # of Pattern | Size of | # of Pattern |
|---|---|---|---|---|---|
| Nodes | Edges | Nodes | Edges | Instances | |
| 25 | 141 | 5 | 6 | 2752 | |
| 25 | 141 | 6 | 4 | 3032 | |
| 25 | 141 | 7 | 9 | 1693 | |
| 25 | 141 | 8 | 16 | 136 | |
| 25 | 141 | 9 | 23 | 1 | |
| 25 | 141 | 10 | 17 | 2 | |
| 25 | 141 | 11 | 26 | 0 | |
| 25 | 141 | 12 | 32 | 0 | |
| 25 | 141 | 13 | 38 | 0 | |
| 25 | 141 | 14 | 45 | 0 | |
| 30 | 225 | 5 | 6 | 9141 | |
| 30 | 225 | 6 | 8 | 13,144 | |
| 30 | 225 | 7 | 11 | 1339 | |
| 30 | 225 | 8 | 14 | 933 | |
| 30 | 225 | 9 | 18 | 85 | |
| 30 | 225 | 10 | 26 | 1 | |
| 30 | 225 | 11 | 28 | 0 | |
| 30 | 225 | 12 | 32 | 0 | |
| 30 | 225 | 13 | 43 | 0 | |
| 30 | 225 | 14 | 50 | 0 |
| # of Graph | # of Graph | # of Pattern | # of Pattern | Size of | Size of | Ratio |
|---|---|---|---|---|---|---|
| Nodes | Edges | Nodes | Edges | |||
| 25 | 150 | 5 | 7 | 3139 | ||
| 25 | 150 | 6 | 6 | 3648 | ||
| 25 | 150 | 7 | 13 | 1297 | ||
| 25 | 150 | 8 | 16 | 181 | ||
| 25 | 150 | 9 | 15 | 44 | ||
| 25 | 150 | 10 | 25 | 27 | ||
| 25 | 150 | 11 | 28 | 27 | ||
| 25 | 150 | 12 | 33 | 27 | ||
| 25 | 150 | 13 | 42 | 27 | ||
| 25 | 150 | 14 | 56 | 27 | ||
| 30 | 224 | 5 | 2 | 1542 | ||
| 30 | 224 | 6 | 8 | 7135 | ||
| 30 | 224 | 7 | 9 | 2223 | ||
| 30 | 224 | 8 | 11 | 320 | ||
| 30 | 224 | 9 | 23 | 137 | ||
| 30 | 224 | 10 | 19 | 32 | ||
| 30 | 224 | 11 | 21 | 32 | ||
| 30 | 224 | 12 | 38 | 32 | ||
| 30 | 224 | 13 | 32 | 32 | ||
| 30 | 224 | 14 | 50 | 32 |
| # of | # of Graph | # of Graph | # of Pattern | # of Pattern | Size of | Size of | Ratio |
|---|---|---|---|---|---|---|---|
| Labels | Nodes | Edges | Nodes | Edges | |||
| 1 | 25 | 149 | 5 | 3 | 1644 | ||
| 2 | 25 | 157 | 5 | 6 | 277 | ||
| 3 | 25 | 140 | 5 | 3 | 53 | ||
| 4 | 25 | 148 | 5 | 6 | 38 | ||
| 5 | 25 | 149 | 5 | 8 | 27 | ||
| 1 | 30 | 217 | 5 | 5 | 8380 | ||
| 2 | 30 | 217 | 5 | 2 | 56 | ||
| 3 | 30 | 224 | 5 | 5 | 40 | ||
| 4 | 30 | 230 | 5 | 4 | 36 | ||
| 5 | 30 | 234 | 5 | 6 | 32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vanetik, N. Sufficient Networks for Computing Support of Graph Patterns. Information 2023, 14, 143. https://doi.org/10.3390/info14030143
Vanetik N. Sufficient Networks for Computing Support of Graph Patterns. Information. 2023; 14(3):143. https://doi.org/10.3390/info14030143
Chicago/Turabian StyleVanetik, Natalia. 2023. "Sufficient Networks for Computing Support of Graph Patterns" Information 14, no. 3: 143. https://doi.org/10.3390/info14030143
APA StyleVanetik, N. (2023). Sufficient Networks for Computing Support of Graph Patterns. Information, 14(3), 143. https://doi.org/10.3390/info14030143








