Using Deep-Learning for 5G End-to-End Delay Estimation Based on Gaussian Mixture Models
Abstract
:1. Introduction
- A methodology to label 5G E2E delay data according to the GMM parameters obtained with the EM algorithm for different amounts of observed values to be used in the estimation;
- The description of an estimation methodology that uses the 5G E2E labeled data in a deep learning model capable of computing the GMM parameters;
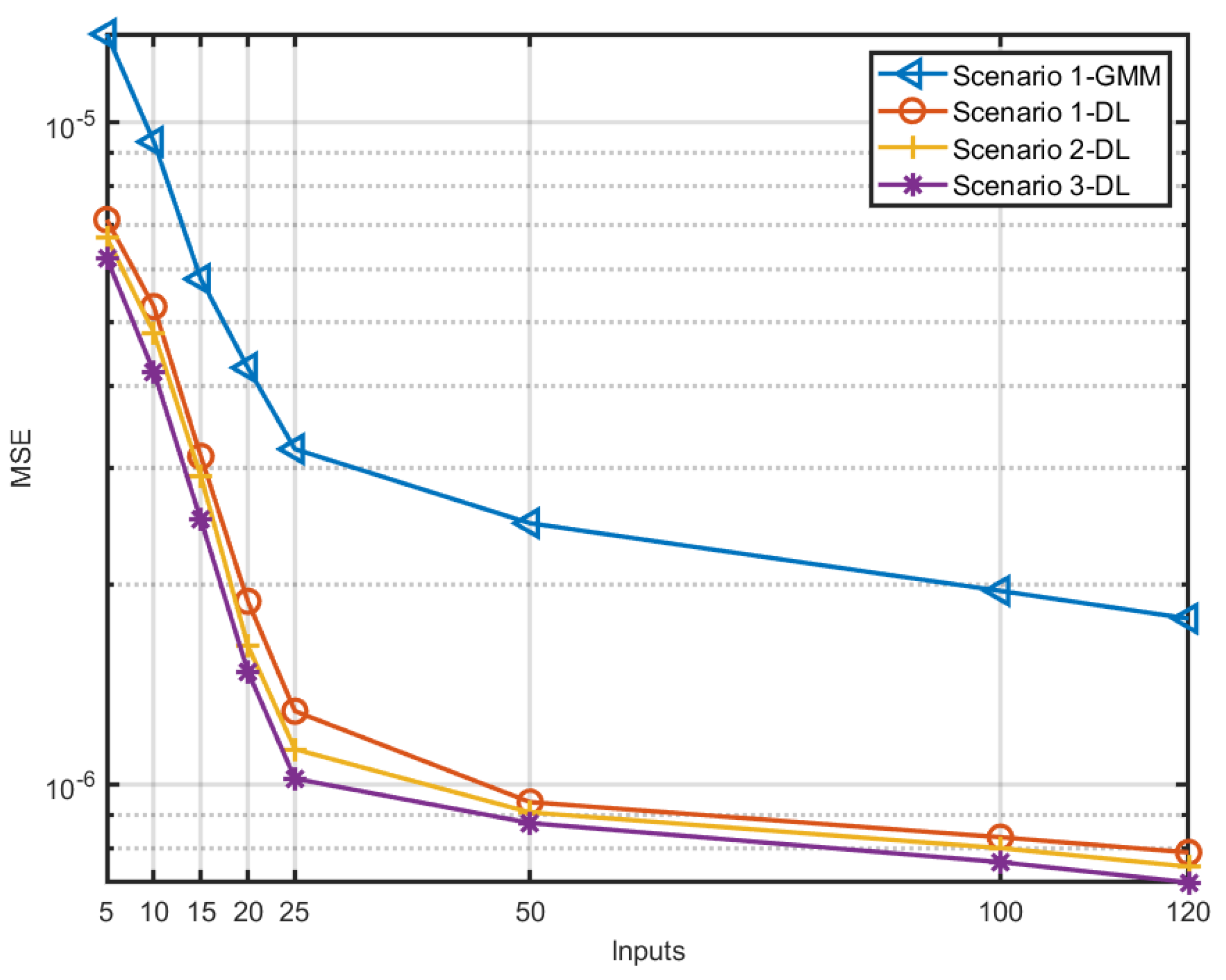
- The evaluation of the proposed estimation methodology in terms of accuracy and computation time and its comparison with the estimation approach in [8] that adopts the EM algorithm only.
2. Literature Review
- Statistical modeling approaches different from queuing models have also been proposed for predicting E2E delay in 5G networks [8,20,21]. These approaches typically use statistical techniques such as regression analysis, time-series analysis, and probabilistic modeling to estimate the relation between network parameters and delay performance;
- Network simulation: Network simulation tools such as ns-3 and OPNET have been used to simulate and analyze the performance of 5G networks. These tools allow researchers to model the network architecture, traffic patterns, and other key parameters, and analyze the impact on end-to-end delay performance;
- Various deep learning (DL) models have been adopted for E2E delay estimation [22]. These models capture the complex temporal dependencies and non-linear relationships present in the network data. The models are trained on large-scale datasets comprising network measurements, traffic patterns, network topology, and other relevant features.
3. System Model
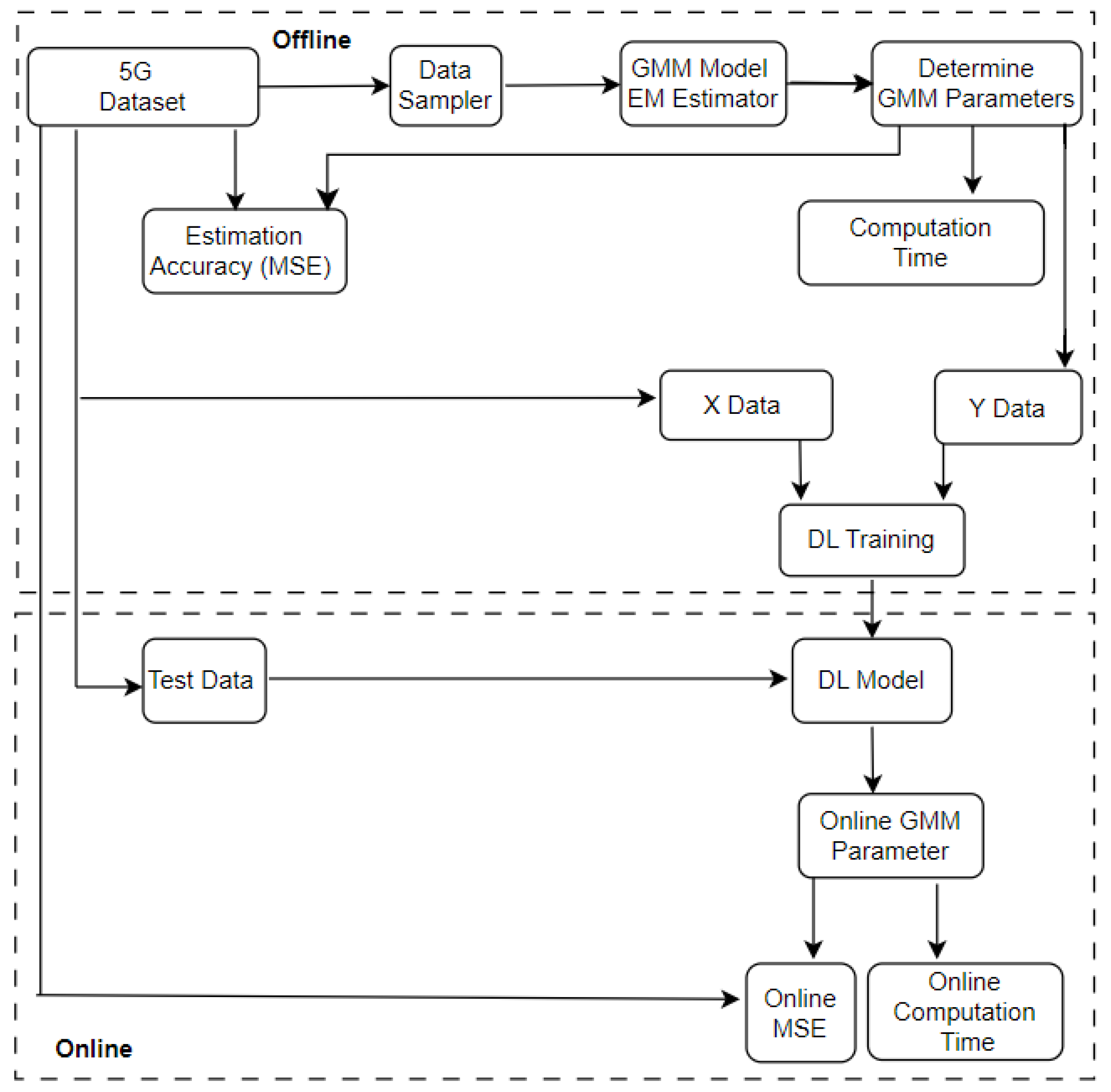
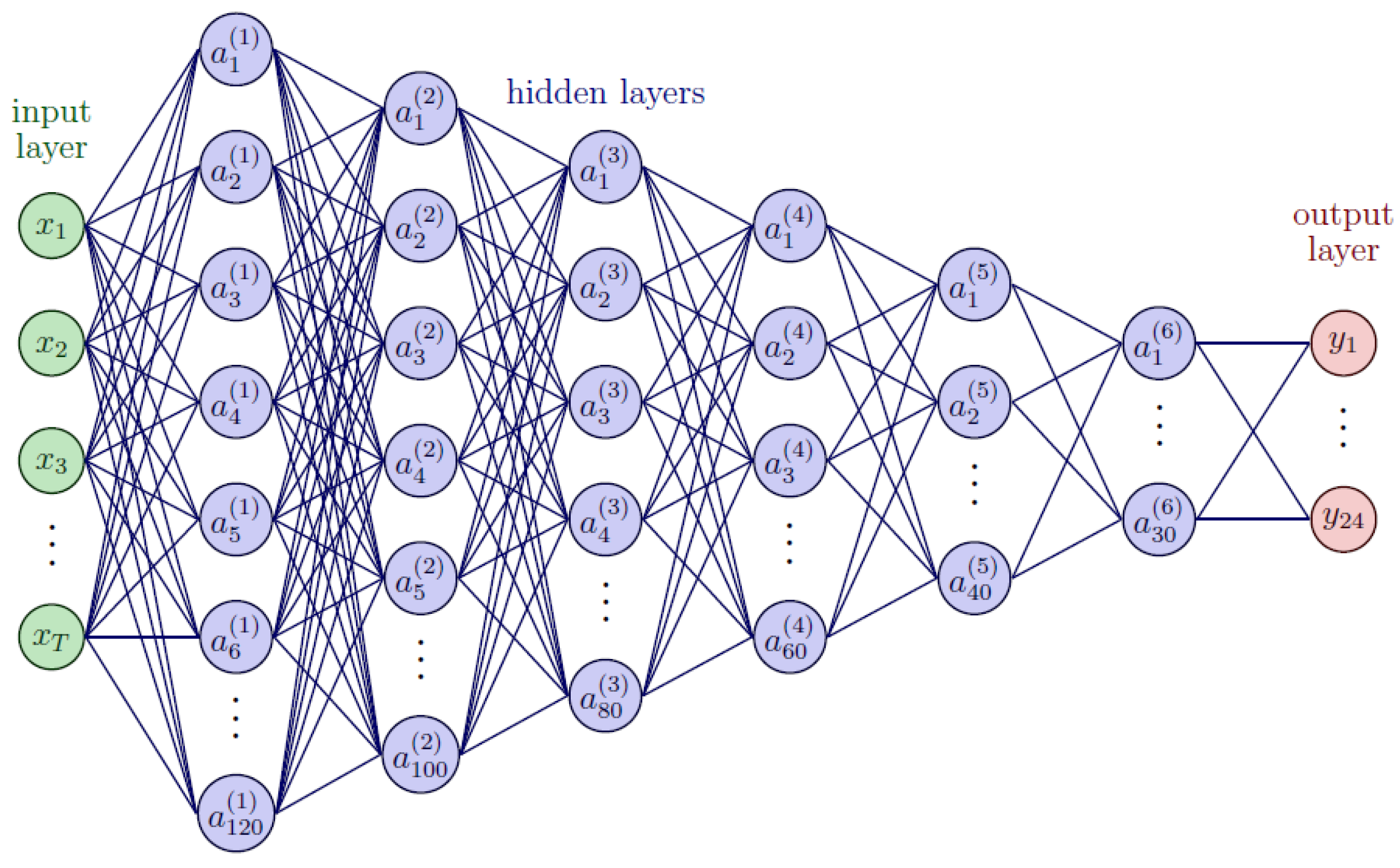
4. Estimation Methodology
5. Performance Evaluation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pržulj, N.; Malod-Dognin, N. Network Analytics in the Age of Big Data. Science 2016, 353, 123–124. [Google Scholar] [CrossRef] [PubMed]
- Pandey, K.; Arya, R. Robust Distributed Power Control with Resource Allocation in D2D Communication Network for 5G-IoT Communication System. Int. J. Comput. Netw. Inf. Secur. 2022, 14, 73–81. [Google Scholar] [CrossRef]
- Oleiwi, S.S.; Mohammed, G.N.; Al_barazanchi, I. Mitigation of Packet Loss with End-to-End Delay in Wireless Body Area Network Applications. Int. J. Electr. Comput. Eng. 2022, 12, 460. [Google Scholar] [CrossRef]
- Afolabi, I.; Taleb, T.; Samdanis, K.; Ksentini, A.; Flinck, H. Network Slicing and Softwarization: A Survey on Principles, Enabling Technologies, and Solutions. IEEE Commun. Surv. Tutor. 2018, 20, 2429–2453. [Google Scholar] [CrossRef]
- Ye, Q.; Zhuang, W.; Li, X.; Rao, J. End-to-End Delay Modeling for Embedded VNF Chains in 5G Core Networks. IEEE Internet Things J. 2019, 6, 692–704. [Google Scholar] [CrossRef]
- Banavalikar, B.G. Quality of Service (QoS) for Multi-Tenant-Aware Overlay Virtual Networks. US Patent 10,177,936, 1 October 2015. [Google Scholar]
- Reynolds, D.A. Gaussian Mixture Models. Encycl. Biom. 2009, 741, 659–663. [Google Scholar]
- Fadhil, D.; Oliveira, R. Estimation of 5G Core and RAN End-to-End Delay through Gaussian Mixture Models. Computers 2022, 11, 184. [Google Scholar] [CrossRef]
- Yuan, X.; Wu, M.; Wang, Z.; Zhu, Y.; Ma, M.; Guo, J.; Zhang, Z.L.; Zhu, W. Understanding 5G performance for real-world services: A content provider’s perspective. In Proceedings of the ACM SIGCOMM 2022 Conference, Amsterdam, The Netherlands, 22–26 August 2022; pp. 101–113. [Google Scholar]
- Chinchilla-Romero, L.; Prados-Garzon, J.; Ameigeiras, P.; Muñoz, P.; Lopez-Soler, J.M. 5G infrastructure network slicing: E2E mean delay model and effectiveness assessment to reduce downtimes in industry 4.0. Sensors 2021, 22, 229. [Google Scholar] [CrossRef] [PubMed]
- Maroufi, M.; Abdolee, R.; Tazekand, B.M.; Mortezavi, S.A. Lightweight Blockchain-Based Architecture for 5G Enabled IoT. IEEE Access 2023, 11, 60223–60239. [Google Scholar] [CrossRef]
- Herrera-Garcia, A.; Fortes, S.; Baena, E.; Mendoza, J.; Baena, C.; Barco, R. Modeling of Key Quality Indicators for End-to-End Network Management: Preparing for 5G. IEEE Veh. Technol. Mag. 2019, 14, 76–84. [Google Scholar] [CrossRef]
- Gupta, A.; Jha, R.K. A Survey of 5G Network: Architecture and Emerging Technologies. IEEE Access 2015, 3, 1206–1232. [Google Scholar] [CrossRef]
- Liu, J.; Wan, J.; Jia, D.; Zeng, B.; Li, D.; Hsu, C.H.; Chen, H. High-Efficiency Urban Traffic Management in Context-Aware Computing and 5G Communication. IEEE Commun. Mag. 2017, 55, 34–40. [Google Scholar] [CrossRef]
- Xu, Y.; Gui, G.; Gacanin, H.; Adachi, F. A survey on resource allocation for 5G heterogeneous networks: Current research, future trends, and challenges. IEEE Commun. Surv. Tutor. 2021, 23, 668–695. [Google Scholar] [CrossRef]
- Zhang, Z.; Chai, X.; Long, K.; Vasilakos, A.V.; Hanzo, L. Full duplex techniques for 5G networks: Self-interference cancellation, protocol design, and relay selection. IEEE Commun. Mag. 2015, 53, 128–137. [Google Scholar] [CrossRef]
- Diez, L.; Alba, A.M.; Kellerer, W.; Aguero, R. Flexible Functional Split and Fronthaul Delay: A Queuing-Based Model. IEEE Access 2021, 9, 151049–151066. [Google Scholar] [CrossRef]
- Fadhil, D.; Oliveira, R. A Novel Packet End-to-End Delay Estimation Method for Heterogeneous Networks. IEEE Access 2022, 10, 71387–71397. [Google Scholar] [CrossRef]
- Adamuz-Hinojosa, O.; Sciancalepore, V.; Ameigeiras, P.; Lopez-Soler, J.M.; Costa-Pérez, X. A Stochastic Network Calculus (SNC)-Based Model for Planning B5G uRLLC RAN Slices. IEEE Trans. Wirel. Commun. 2023, 22, 1250–1265. [Google Scholar] [CrossRef]
- Ahmed, A.H.; Hicks, S.; Riegler, M.A.; Elmokashfi, A. Predicting High Delays in Mobile Broadband Networks. IEEE Access 2021, 9, 168999–169013. [Google Scholar] [CrossRef]
- Fadhil, D.; Oliveira, R. Characterization of the End-to-End Delay in Heterogeneous Networks. In Proceedings of the 12th International Conference on Network of the Future (NoF), Coimbra, Portugal, 6–8 October 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Ge, Z.; Hou, J.; Nayak, A. GNN-based End-to-end Delay Prediction in Software Defined Networking. In Proceedings of the 2022 18th International Conference on Distributed Computing in Sensor Systems (DCOSS), Los Angeles, CA, USA, 30 May–1 June 2022; IEEE Computer Society: Los Alamitos, CA, USA, 2022; pp. 372–378. [Google Scholar] [CrossRef]
- Rischke, J.; Sossalla, P.; Itting, S.; Fitzek, F.H.P.; Reisslein, M. 5G Campus Networks: A First Measurement Study. IEEE Access 2021, 9, 121786–121803. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]

| Datasets | W | ||
|---|---|---|---|
| Scenario 1 | 0.1368 | 0.0040 | 0.0188 |
| 0.1505 | 0.0071 | 0.0476 | |
| 0.1895 | 0.0085 | 0.1464 | |
| 0.2067 | 0.0304 | 0.2358 | |
| 0.2343 | 0.0072 | 0.1490 | |
| 0.2558 | 0.0109 | 0.2210 | |
| 0.2906 | 0.0100 | 0.1498 | |
| 0.2912 | 0.0027 | 0.0316 | |
| Scenario 2 | 0.1407 | 0.0068 | 0.0740 |
| 0.1814 | 0.0065 | 0.2063 | |
| 0.1625 | 0.0201 | 0.1109 | |
| 0.1972 | 0.0049 | 0.0737 | |
| 0.2281 | 0.0126 | 0.3851 | |
| 0.2435 | 0.0044 | 0.0199 | |
| 0.2606 | 0.0011 | 0.0144 | |
| 0.2706 | 0.0147 | 0.1157 | |
| Scenario 3 | 0.0476 | 0.0015 | 0.0214 |
| 0.1231 | 0.0081 | 0.2412 | |
| 0.1449 | 0.0129 | 0.1539 | |
| 0.0695 | 0.0119 | 0.1921 | |
| 0.1941 | 0.0083 | 0.1313 | |
| 0.1830 | 0.0017 | 0.0523 | |
| 0.2420 | 0.0255 | 0.1627 | |
| 0.2789 | 0.0028 | 0.0452 |
| Scenarios | Topology | Delay Type | Stream Direction | Packet Size [Bytes] | Packet Rate [Packets/s] |
|---|---|---|---|---|---|
| Scenario 1 | NSA | Core | Download | 1024 | 10 |
| Scenario 2 | NSA | Core | Download | 1024 | 100 |
| Scenario 3 | NSA | Core | Download | 1024 | 1000 |
| Scenarios | T = 5 | T = 10 | T = 15 | T = 20 | T = 25 | T = 50 | T = 100 | T = 120 |
|---|---|---|---|---|---|---|---|---|
| Scenario 1-GMM | ||||||||
| Scenario 1-DL | ||||||||
| Scenario 2-DL | ||||||||
| Scenario 3-DL |
| Scenarios | T = 5 | T = 10 | T = 15 | T = 20 | T = 25 | T = 50 | T = 100 | T = 120 |
|---|---|---|---|---|---|---|---|---|
| Scenario 1-GMM | ||||||||
| Scenario 1-DL | ||||||||
| Scenario 2-DL | ||||||||
| Scenario 3-DL |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fadhil, D.; Oliveira, R. Using Deep-Learning for 5G End-to-End Delay Estimation Based on Gaussian Mixture Models. Information 2023, 14, 648. https://doi.org/10.3390/info14120648
Fadhil D, Oliveira R. Using Deep-Learning for 5G End-to-End Delay Estimation Based on Gaussian Mixture Models. Information. 2023; 14(12):648. https://doi.org/10.3390/info14120648
Chicago/Turabian StyleFadhil, Diyar, and Rodolfo Oliveira. 2023. "Using Deep-Learning for 5G End-to-End Delay Estimation Based on Gaussian Mixture Models" Information 14, no. 12: 648. https://doi.org/10.3390/info14120648
APA StyleFadhil, D., & Oliveira, R. (2023). Using Deep-Learning for 5G End-to-End Delay Estimation Based on Gaussian Mixture Models. Information, 14(12), 648. https://doi.org/10.3390/info14120648







