Abstract
Thanks to the success of deep learning, deep hashing has recently evolved as a leading method for large-scale image retrieval. Most existing hashing methods use the last layer to extract semantic information from the input image. However, these methods have deficiencies because semantic features extracted from the last layer lack local information, which might impact the global system’s performance. To this end, a Deep Feature Pyramid Hashing DFPH is proposed in this study, which can fully utilize images’ multi-level visual and semantic information. Our architecture applies a new feature pyramid network designed for deep hashing to the VGG-19 model, so the model becomes able to learn the hash codes from various feature scales and then fuse them to create final binary hash codes. The experimental results performed on two widely used image retrieval datasets demonstrate the superiority of our method.
1. Introduction
A vast amount of data, including images and videos, is produced daily as a result of social media’s fast growth. There have been many methods suggested to retrieve them effectively [1,2]. Approximate nearest neighbor (ANN) search [3] has recently drawn more and more interest due to its low computing cost and high retrieval accuracy. Among several ANN search techniques, the hashing [4] method is one of the more promising techniques to learn compact binary codes for high-dimensional input data and retrieve it at the Hamming Space.
For decades, several hashing techniques have been studied and proposed. Due to the tremendous success of deep learning, deep neural networks have been used in hashing algorithms for end-to-end learning hash codes and feature representations [5,6,7,8]. These techniques have attained cutting-edge retrieval performance, demonstrating the importance of concurrently generating similarity-preserving representations and reducing quantization error while transforming the representations into hash codes [6,9,10,11].
However, most of the existing deep hashing methods [12,13,14,15] used the top-layer feature to learn binary codes while disregarding down-layer features. The lower ConvLayer is generally responsible for extracting the image’s visual details, including its edge, color and texture information [16]. Meanwhile, this visual information is combined in the middle layers to discover ingrained patterns. The top layer is concerned with using semantic information to produce discriminated representation [17].
Furthermore, recent research in Feature pyramids [18,19], which boost the performance by utilizing different ConvLayer in the convolutional network, has demonstrated the superiority of learning local features in a vast number of visual tasks, such as object detection [20] and image segmentation [21]. As for deep hashing, it is still full of challenges in encoding the feature pyramids into efficient binary codes.
Some of the earlier techniques functioned by feeding the network to take an image pyramid as the input (various sizes of the input image). Doing this improves the feature extraction process but increases the processing time and is not as efficient.
Even though Feature Pyramid Network (FPN) was created for object detection, we offer a novel model that uses FPN for deep hashing in this work. Using FPN makes extracting the input image’s multi-level visual and semantic information easier. More specifically, an FPN creates a hierarchy of bottom-up and top-down feature maps with lateral connections of features produced from the network at various scales. We learn hash codes from these feature scales, which we fuse to obtain the final hash codes. The main contributions of this work can be summarized as follows:
- A Deep Feature Pyramid Hashing is proposed in this work which can fully exploit the multi-level visual and semantic information of images. Our architecture applies a new feature pyramid network designed for deep hashing to the VGG-19 model. Thus, the model becomes able to learn binary hash codes from various feature scales and then fuse them to obtain the final hash codes.
- To the best of our knowledge, the proposed DFPH is the first feature pyramid network-based method which generates hash codes from multiple feature scales for image retrieval.
2. Related Works
Thanks to their small storage capacity and quick processing speed, hashing methods have recently become widespread in image retrieval [22,23]. The primary goal of hashing is to convert high-dimensional input data into low-dimensional hash codes, with the Hamming distance reduced in similar pairs and maximizing in dissimilar pairs.
Existing hashing methods can be divided into supervised methods [24,25] and unsupervised methods [26,27,28,29,30], depending on whether or not supervised data are used. Unsupervised hashing approaches [31,32,33,34] aim to learn the hash functions with unlabeled training samples, which convert input images into binary code. LSH [35] has been the most representative of the approaches. However, several other unsupervised hashing methods, such as SH [32], and ITQ [33], have been used in subsequent studies.
Unlike unsupervised hashing methods, supervised hashing techniques take supervised information from the labeled input data to learn hash code, which outperforms unsupervised approaches in terms of accuracy. Supervised Hashing with Kernels (KSH) [36] is a suggested supervised hashing method for generating a nonlinear hash function in kernel space. Unlike previous hashing approaches, Minimal Loss Hashing (MLH) [37] uses structured SVM to develop an objective function for hash function learning. Supervised Discrete Hashing (SDH) [27] provides high-quality hash codes without relaxing by reformulating the goal function.
With the rapid advancement of deep neural networks, several deep hashing algorithms [10,38,39,40,41,42,43,44] have recently been presented. Deep hashing can outperform approaches based on hand-crafted features because of the rich feature representations offered by deep neural networks. Pairwise and triplet-wise similarity preservation are the most prevalent ways of utilizing the relationship between labeled data when it comes to the utilization of label information.
CNNH [38] learns the hashing codes using features obtained from CNN. However, the hash function and feature representation are learned independently. There are many literature researching the hashing algorithm that the hash function and feature representation are learned independently [45,46]. Moreover, in this case, the learning hash function cannot provide feedback to a feature representation learning. Deep Pairwise-supervised Hashing (DPSH) [10] uses the Bayesian framework to create a relationship between hash codes and pairwise labels and then optimizes the relationship to learn hash functions. HashGAN [39] uses Wasserstein GAN to increase training data by exploiting pairwise similarity (dissimilarity) information, and hash codes are generated inside a Bayesian framework. In order to learn the hashing functions, Zhuang et al. [40] developed a binary CNN classifier that uses triplet-based loss for maintain semantic links. Deep Triplet Quantization (DTQ) [41] combines triplet quantization strategy in a supervised deep learning framework to enable optimization of quantization and feature learning simultaneously. Supervised Learning of Semantics-Preserving Hash (SSDH) [42] involves building hash functions as a new fully connected layer (FC Layers), and the hash codes are learned by optimizing the cost function-specified classification error. Wang et al. [43] provided a general framework for distance-preserving linear hashing containing a deep hashing approach. In this approach, the features of the fully connected layer (FC Layers) were used for the learning hashing. Similarity-Adaptive Deep Hashing (SADH), invented by Shen et al. [44], is a two-step hashing algorithm. The fully connected layer (FC Layers) output representations aid in updating the similarity graph matrix and are then used to improve the hash code optimization process.
The approaches above use one type of feature, mostly features from the last FC layer (high-level features). However, different types of features need to be extracted to create a more complete description. Many methods have been proposed for multi-level image retrieval. Lin et al. proposed a DDH [47] method for image retrieving. The authors combine end-to-end learning, divide-and-encode, and hash code learning into a single framework. Specifically, the stack of conv-pool (convolution pooling) layers was then used to acquire multi-scale features. By combining the third pooling layer’s and fourth Conv layer’s outputs. In [48], Yang et al. proposed a Feature Pyramid Hashing (FPH) as a two-pyramids (vertical and horizontal) image hashing architecture to learn the subtle appearance details and the semantic information for fine-grained image retrieval. Ng et al. [49] developed a novel multi-level supervised hashing (MLSH) technique for image retrieval. The authors built and trained the tables individually, utilizing different levels of features (semantic and structural).
3. Proposed Method
This section will detail the suggested Deep Feature Pyramid Hashing for Image Retrieval. We begin by presenting the problem definition for learning hash codes. Then, we introduce the model architecture. Finally, we give our proposed method’s objective function.
3.1. Problem Definition
Let denote the training dataset with N image samples, and d features sizes. Let represent the ground truth labels of the training dataset X, where K is the number of classes.
Let be the matrix to denote the pair-wise labels for training samples, with , where the element represents that and samples are semantically similar, represents that and samples are not semantically similar. The goal of deep hashing techniques with pair-wise labels is to learn a nonlinear deep hash function , which can encode each sample into binary codes , L is the length of hash codes.
3.2. Model Architecture
Feature pyramid network (FPN) was proposed by Lin [19] as a feature extractor design. FPN generates multiple feature map layers (multi-scale feature maps) with better-quality information than the regular feature pyramid.
Figure 1 shows the network’s architecture of the proposed deep hashing for image retrieval. The bottom-up hierarchy uses VGG-19 to construct the bottom-up hierarchy. Specifically, we use the feature output of the last convolutional layer in each convolutional block . We denote the output of these last convolutional layers as for , and outputs, respectively. We omit conv1 and conv2 into the pyramid due to its large memory footprint. Table 1 details the convolutional layers’ parameters and feature sizes of different convolutional blocks.
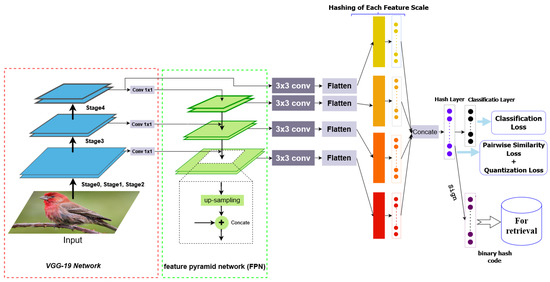
Figure 1.
This figure shows our proposed model: Deep Feature Pyramid Hashing (DFPH), which uses VGG19 as the backbone and uses the feature pyramid network (FPN) and the created layers for hashing.

Table 1.
Details of the feature extraction network. Note that we use the features of the layers marked by ‘‘#’’. For simplicity, we omit ReLU and Batch Normalization layers.
As we go down the top-down path, we upsample the previous layer using bilinear interpolation. Moreover, we apply a 1 × 1 convolution filter (reduce C3, C4, and C5 channels) to the corresponding feature maps in the bottom-up pathway. Then, we add them element-wise.
FPN extracts four final features (multi-scale feature maps). The bottom and upper layers are selected to exploit spatial resolution and semantic information because the spatial resolution decreases as we go up in the layers.
For the obtained features, we fuse them using a convolutional layer to obtain a fused feature and apply dropout layers (to avoid overfitting). After that, we attach the hashing layer on this final set of feature maps to produce the first hashing codes. Note that we use the Relu activation function for the first hashing layers.
At the end of the architecture, we concatenated the four hashing layers. Then, we connected this layer to the final hashing layer and connected the latter with the classification layer (the sum of neurons equals the sum of classes of the dataset). With running this procedure, the network utilizes different hashing results based on various scale features. As a result, the network could retrieve the images better.
3.3. Objective Function
To learn similarity-preserving hash codes, we develop the following loss functions: pairwise similarity loss, pairwise quantization loss, and classification loss. All of them are merged to train our model.
Pairwise Similarity Loss. We perform our deep hashing model by preserving similarities as possible of all pairwise images in the Hamming space. The pairwise similarity is computed using the inner product. The inner product for two binary codes, and , is formulated as follows:
Given that all of the points’ binary codes are , we can formulate the likelihood of the pairwise labels as:
where , and
Based on the equation above, we can infer that the larger the inner product , the smaller the corresponding , and the larger . This also implies that the hash codes and are considered as similar when , and vice versa.
By taking the negative log-likelihood of the observed pairwise labels in S, we can obtain the following optimization problem:
The above formula (optimization problem) makes the Hamming distance between two similar (dissimilar) points to be as small (large) as possible, which is precisely what pairwise similarity-based hashing techniques aim to achieve.
Pairwise Quantization Loss. Discrete hash codes are utilized in real-world applications to determine similarity. However, discrete hash coding in CNN is challenging to optimize. Therefore, the continuous form of hash coding is used to prevent gradient disappearance during the back-propagation phase. We define the output of the hash layer as and make .
Hence, quantization loss is introduced to minimize the gap between continuous and discrete hash codes. The second objective is defined as:
where Q is the size of the mini-batch.
Classification Loss. To achieve robust representations of multi-scale features during training of deep network, we apply the classification loss to find the classification of the classes. The classification loss can be expressed as follows:
where is the ground-truth label, is the softmax output of the training sample, which belongs to the class.
To sum up, the total loss function can be achieved by combining pairwise similarity loss, pairwise quantization loss, and classification loss:
where , are hyper parameters that control importance of the J2 and J3 terms. The final objective function in Equation (5) is convex and can be optimized by the Adam algorithm [50]. At the training phase, J1 makes similar binary codes as close as possible and places dissimilar binary codes as far away as possible. J2 quantization loss is introduced to minimize the gap between continuous and discrete hash codes. J3 can use semantic supervision to direct how discrete hash codes are learned and add more semantic information to the hash codes that are created to improve hash code discrimination.
4. Experiments
We verify the effectiveness of our method on two public datasets: CIFAR-10 and NUS-WIDE. We first present these datasets in brief and then explore experimental settings. Evaluation metrics and baselines are given in Section 4.3. In the last section, we show the results with validations and comparisons to various state-of-the-art hashing methods.
4.1. Datasets
CIFAR-10 [51] database contains 60,000 images composed of 10 categories, each image with the size of 32 × 32. Following to [52], we randomly selected 100 images per class as the queries (1000 testings) and the rest images as the database. Furthermore, we randomly sampled 500 images per category (5000 images) from the retrieval database as the training set.
NUS-WIDE [53] is a multi-label database that contains nearly 270,000 color images collected from Flickr, and is composed of 81 labels. We randomly selected 2100 images from the 21 most frequent concepts as the query set, while the rest as the database, and randomly selected 10,000 images from the database as a training dataset.
4.2. Experimental Settings
Our implementation of DFPH is based on the Pytorch framework, which is based on the Torch library. We adopt a VGG-19-convolutional network, pretrained on ImageNet [54]. In all experiments, we used the Adam algorithm [50] to train our network (learning rate ). For the hyper-parameter of the loss function, alpha is set to 0.01 and beta to 0.1.
4.3. Evaluation Metrics and Baselines
To evaluate the retrieval performance of different approaches, we use four evaluation metrics: (1) Mean Average Precision (MAP); (2) Precision–Recall curves (PR); (3) Precision curves with respect to the number of top returned results (P@N); (4) and Precision within Hamming radius 2 (P@H ≤ 2). We compare the proposed DFPH with several of traditional or state-of-the-art hashing techniques, including five shallow unsupervised methods, i.e., LSH [3], SGH [55], SH [32], PCAH [56], ITQ [33], and two shallow supervised hashing methods, i.e., SDH [27], KSH [36], and eight deep supervised hashing methods, i.e., CNNH [38], DPH [57], DNNH [7], DHN [6], DCH [58], LRH [52], HashNet [9], DHDW [59]. For the multi-label NUS-WIDE and CIFAR-10 data-sets, if two samples share the same semantic labels, they are similar. Otherwise, they are not similar.
4.4. Results
The MAP results for all techniques on CIFAR-10 and NUS-WIDE datasets with various hash code lengths are presented in Table 2 and Table 3. The tables show that the proposed method substantially outperforms all compared techniques. Specifically, compared to SDH, the best shallow hashing method, DFPH achieves absolute increases of 49.8% and 24.4% in average mAP scores on CIFAR-10 and NUS-WIDE datasets, respectively. However, we can see that the performance of deep hashing is better than traditional hashing methods, mainly due to its ability to create more robust representations of features. For deep hashing methods, compared to the second-best hashing method LRH, the average mAP of our method was increased by 11.5% and 8.3% on CIFAR-10 and NUS-WIDE, respectively.

Table 2.
Mean Average Precision (MAP) of Hamming ranking for different number of bits on CIFAR-10.

Table 3.
The MAP of DFPH and other hashing methods on NUS-WIDE dataset, MAP are calculated within the top 5000 returned images.
Figure 2a and Figure 3a show the retrieval performance in terms of precision curves (P@H = 2). The proposed model significantly outperforms other methods. The precision curves show that the proposed DFPH method still has the best precision rate when the code length increases.
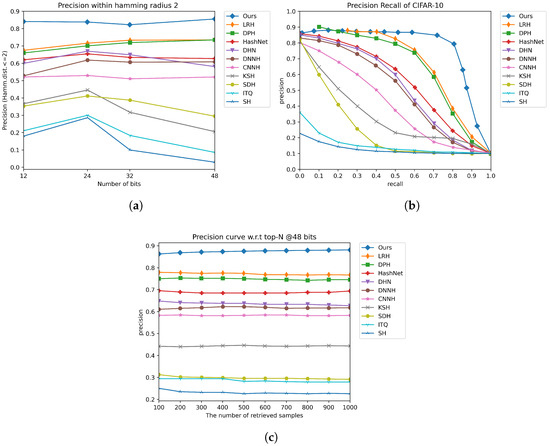
Figure 2.
The comparison results on the CIFAR-10 dataset under three evaluation metrics. (a) Precision within hamming radius 2. (b) Precision recall curve on 48 bits. (c) Precision curve w.r.t top-N @48 bits.
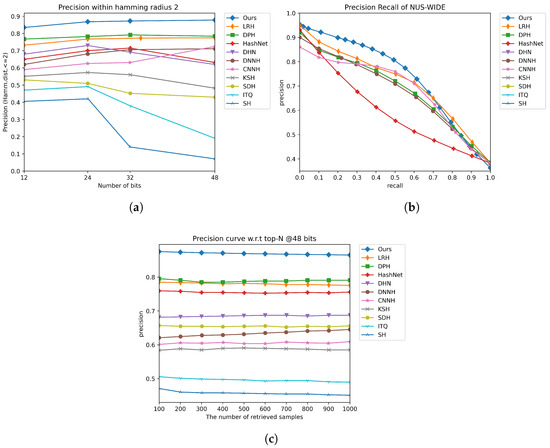
Figure 3.
The comparison results on the NUS-WIDE dataset under three evaluation metrics. (a) Precision within hamming radius 2. (b) Precision Recall Curve on 48 bits. (c) Precision curve w.r.t top-N @48 bits.
We further demonstrate the efficiency of our method by comparing its precision–recall and precision with respect to top returned samples with other methods in Figure 2b,c and Figure 3b,c, respectively. From Figure 2c and Figure 3c, it can be seen that the proposed DFPH method achieves the best precision with 48 bits when the number of return samples is from 100 to 1000. From Figure 2b and Figure 3b, our DFPH achieves substantially high precision at a low recall level, which is required for precision-first retrieval, and widely used in practical systems. Generally speaking, our method DFPH has better performance than the compared methods.
Moreover, the retrieval accuracy for CIFAR-10 dataset is shown for different categories of images as illustrated in Figure 4. For this example, we have proved that we can remove the irrelevant images by using our DFPH approach. Figure 4 shows the top 20 retrieved images from CIFAR-10 dataset by DFPH with 48-bit hash codes. The first column shows the query images, the retrieval results of DFPH are shown in other columns.

Figure 4.
Top 20 retrieved results from CIFAR-10 dataset by DFPH with 48-bit hash codes. The first column shows the query images, the retrieval results of DFPH are shown at other columns.
4.5. Ablation Studies
- (1)
- Using various fundamental feature extractors: We replace VGG19 with VGG13 and VGG16, and Table 4 details their performance on the CIFAR-10 dataset. The table shows that employing deeper networks can enhance image retrieval performance. We thus employ VGG19 as our fundamental feature extractor.
 Table 4. Mean Average Precision (MAP) of Hamming ranking for different number of bits using VGG13, VGG16 and VGG19 as the fundamental feature extractors on CIFAR-10 dataset. The best results are highlighted with bold.
Table 4. Mean Average Precision (MAP) of Hamming ranking for different number of bits using VGG13, VGG16 and VGG19 as the fundamental feature extractors on CIFAR-10 dataset. The best results are highlighted with bold. - (2)
- Pyramid representations efficiency: We compare our DFPH method with its variants to further explore the effect of different scale features on performance. We use the single-scale map of C4 and C5 (Conv 4; Conv 5) and remove the top-down pathway. With this modification, the 3 × 3 convolutions connections followed by 1 × 1 convolutions are attached to the bottom-up pyramid.Table 5 shows the retrieval performance of single-level and multi-level features on CIFAR-10. It can be seen that using a feature from ‘Conv 5’ achieves the most significant average mAP score of 76.5%, while that from ‘Conv 4’ only achieves 58%. Moreover, our DFPH has achieved the average mAP scores of 82.75%, 6.25% higher than simply using single-level features. The hash codes achieve the best performance when all scale features are.
 Table 5. Mean Average Precision (MAP) of Hamming ranking of different scales for different number of bits on CIFAR-10.In Figure 5, we display the precision–recall curves of DFPH in the case of various scale features. Our DFPH retains over 80% precision and nearly identical precision–recall curves at hash bits 12, 24, 36, and 48. DFPH achieves superior precision and recall with the same hash code length compared to single-level features. The binary hash codes perform best when all feature scales are used. It proves that high-level characteristics are more effective in carrying information when creating hash codes. While low-level features can contribute supplementary information to the high-level features information, low-level features cannot entirely take the place of high-level characteristics. The information contained in each scale’s features is essential. It further demonstrates how well DFPH makes use of all scales’ features.
Table 5. Mean Average Precision (MAP) of Hamming ranking of different scales for different number of bits on CIFAR-10.In Figure 5, we display the precision–recall curves of DFPH in the case of various scale features. Our DFPH retains over 80% precision and nearly identical precision–recall curves at hash bits 12, 24, 36, and 48. DFPH achieves superior precision and recall with the same hash code length compared to single-level features. The binary hash codes perform best when all feature scales are used. It proves that high-level characteristics are more effective in carrying information when creating hash codes. While low-level features can contribute supplementary information to the high-level features information, low-level features cannot entirely take the place of high-level characteristics. The information contained in each scale’s features is essential. It further demonstrates how well DFPH makes use of all scales’ features.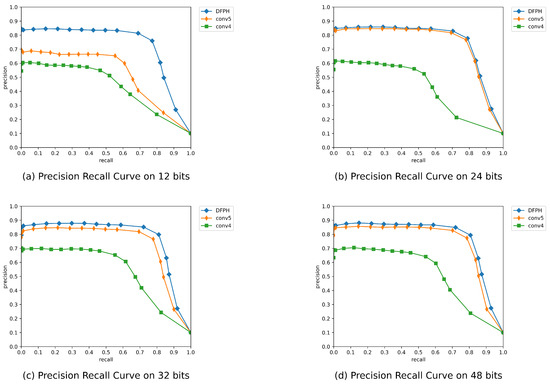 Figure 5. Precision–recall curve of different scales features on CIFAR-10 with hash bits 12, 24, 32 and 48.
Figure 5. Precision–recall curve of different scales features on CIFAR-10 with hash bits 12, 24, 32 and 48. - (3)
- Ablation studies of the objective function: We evaluate the impact of Pairwise Quantization Loss and Classification Loss constraints, which reflects the effects of hash coding and classification on CIFAR-10. The experimental configuration is based on the proposed DFPH method, where and are the relevant parameters for and . The model is designated DFPH-J3 when and DFPH-J2 when . As seen in Table 6, if and are not 0, then each term of the suggested loss function constrains the creation of hash codes, and our method has achieved a improvement. and make nearly identical enhancements. The primary reason is that for the whole model, and play a role in reducing quantization error and semantic preservation, respectively. The performance of our model as a whole may decrease if one of them is eliminated.
 Table 6. MAP values of different variants of our objective function for CIFAR-10 data set.
Table 6. MAP values of different variants of our objective function for CIFAR-10 data set.
4.6. Parameter Sensitivity Analysis
To analyze the influence of hyper-parameters and on retrieval performance, we conducted experiments to determine the impact of the choice of and on retrieval performance. We tested the and from to with a multiplicative step-size ten on the CIFAR-10 dataset in the case of code. In Figure 6, we display the changes in mAP curves of DFPH concerning the variation of and . We can see that MAP initially increases with the increase of and , while the performances progressively stabilize after reaching their peak. Additionally, we can always obtain satisfactory performance in a large range of and , which shows that our method is not sensitive to parameters and and accordingly proves the robustness of our method.
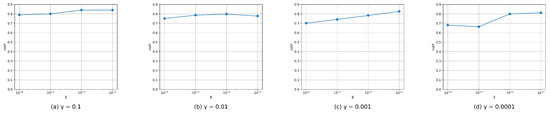
Figure 6.
Parameter sensitivity analysis on CIFAR-10 dataset with 48-bit of the proposed DFPH.
5. Conclusions and Future Work
In this paper, we developed an end-to-end multi-scale deep Hashing method for large-scale image retrieval. Our architecture applies a new feature hierarchy network designed for deep hashing to generate multi-scale features. In addition, efficient binary codes are generated by learning hash codes from different feature scales and then combining them to create final binary hash codes. The experimental results on two image retrieval datasets demonstrated that our method outperforms other state-of-the-art hashing methods. This multi-level visual and semantic information can also be very useful in a non-hashing system such as detection and segmentation. In this case, to increase the detection performance of multi-scale information, we can add a novel Multi-Scale Image Fusion layer to the backbone network. In future work, it is interesting to apply our proposed framework to medical image data sets. Since medical images contain objects at different scales, especially as many of them are very small, using our method helps to increase retrieval performance.
Author Contributions
Conceptualization, A.R.; methodology, K.B.; software, A.R.; validation, K.B. and A.R.; formal analysis, A.R. and K.B.; investigation, K.B.; writing–original draft preparation, A.R. and K.B.; writing–review and editing, K.B. and A.R.; visualization, A.R.; supervision, K.B.; project administration, K.B.; funding acquisition, K.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Publicly available datasets were analyzed in this study. These data can be found here: http://www.cs.toronto.edu/~kriz/cifar.html https://paperswithcode.com/datasets (all accessed on 18 June 2021).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DFPH | Deep Feature Pyramid Hashing for efficient Image Retrieval |
| CBIR | Content-Based Image Retrieval |
| FPN | Feature Pyramid Network |
| CNN | Convolutional Neural Network |
| DCNN | Deep Convolutional Neural Network |
References
- Belloulata, K.; Belhallouche, L.; Belalia, A.; Kpalma, K. Region Based Image Retrieval using Shape-Adaptive DCT. In Proceedings of the ChinaSIP-14 (2nd IEEE China Summit and International Conference on Signal and Information Processing), Xi’an, China, 9–13 July 2014; pp. 470–474. [Google Scholar]
- Belalia, A.; Belloulata, K.; Kpalma, K. Region-based image retrieval in the compressed domain using shape-adaptive DCT. Multimed. Tools Appl. 2016, 75, 10175–10199. [Google Scholar] [CrossRef]
- Gionis, A.; Indyk, P.; Motwani, R. Similarity search in high dimensions via hashing. In Proceedings of the VlDB, Edinburgh, UK, 7–10 September 1999; Volume 99, pp. 518–529. [Google Scholar]
- Wang, J.; Zhang, T.; Song, J.; Sebe, N.; Shen, H.T. A survey on learning to hash. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 769–790. [Google Scholar] [CrossRef] [PubMed]
- Erin Liong, V.; Lu, J.; Wang, G.; Moulin, P.; Zhou, J. Deep hashing for compact binary codes learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 2475–2483. [Google Scholar]
- Zhu, H.; Long, M.; Wang, J.; Cao, Y. Deep hashing network for efficient similarity retrieval. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. [Google Scholar]
- Lai, H.; Pan, Y.; Liu, Y.; Yan, S. Simultaneous feature learning and hash coding with deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3270–3278. [Google Scholar]
- Cakir, F.; He, K.; Bargal, S.A.; Sclaroff, S. Hashing with mutual information. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 2424–2437. [Google Scholar] [CrossRef] [PubMed]
- Cao, Z.; Long, M.; Wang, J.; Yu, P.S. Hashnet: Deep learning to hash by continuation. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 5608–5617. [Google Scholar]
- Li, W.J.; Wang, S.; Kang, W.C. Feature learning based deep supervised hashing with pairwise labels. arXiv 2015, arXiv:1511.03855. [Google Scholar]
- Liu, H.; Wang, R.; Shan, S.; Chen, X. Deep supervised hashing for fast image retrieval. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2064–2072. [Google Scholar]
- Gordo, A.; Almazán, J.; Revaud, J.; Larlus, D. Deep image retrieval: Learning global representations for image search. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 241–257. [Google Scholar]
- Jiang, Q.Y.; Li, W.J. Asymmetric deep supervised hashing. In Proceedings of the AAAI Conference on Artificial Intelligence, Edmonton, AB, Canada, 13–17 November 2018; Volume 32. [Google Scholar]
- Shen, F.; Gao, X.; Liu, L.; Yang, Y.; Shen, H.T. Deep asymmetric pairwise hashing. In Proceedings of the 25th ACM International Conference on Multimedia, Mountain View, CA, USA, 23–27 October 2017; pp. 1522–1530. [Google Scholar]
- Yang, W.; Wang, L.; Cheng, S.; Li, Y.; Du, A. Deep Hash with Improved Dual Attention for Image Retrieval. Information 2021, 12, 285. [Google Scholar] [CrossRef]
- Monowar, M.; Hamid, M.; Ohi, A.; Alassafi, M.; Mridha, M. AutoRet: A Self-Supervised Spatial Recurrent Network for Content-Based Image Retrieval. Sensors 2022, 22, 2188. [Google Scholar] [CrossRef]
- Jardim, S.; António, J.; Mora, C.; Almeida, A. A Novel Trademark Image Retrieval System Based on Multi-Feature Extraction and Deep Networks. J. Imaging 2022, 8, 238. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Z.; Peng, Y.; Zhang, Z.; Yu, G.; Sun, J. Cascaded pyramid network for multi-person pose estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7103–7112. [Google Scholar]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Wang, W.; Zhao, S.; Shen, J.; Hoi, S.C.; Borji, A. Salient object detection with pyramid attention and salient edges. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 1448–1457. [Google Scholar]
- Ye, L.; Rochan, M.; Liu, Z.; Wang, Y. Cross-modal self-attention network for referring image segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 10502–10511. [Google Scholar]
- Jin, Z.; Li, C.; Lin, Y.; Cai, D. Density sensitive hashing. IEEE Trans. Cybern. 2013, 44, 1362–1371. [Google Scholar] [CrossRef]
- Andoni, A.; Indyk, P. Near-optimal hashing algorithms for near neighbor problem in high dimension. Commun. ACM 2008, 51, 117–122. [Google Scholar] [CrossRef]
- Kulis, B.; Darrell, T. Learning to hash with binary reconstructive embeddings. Adv. Neural Inf. Process. Syst. 2009, 22, 1. [Google Scholar]
- Liu, H.; Ji, R.; Wu, Y.; Liu, W. Towards optimal binary code learning via ordinal embedding. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Wang, J.; Wang, J.; Yu, N.; Li, S. Order preserving hashing for approximate nearest neighbor search. In Proceedings of the 21st ACM International Conference on Multimedia, Barcelona, Spain, 21–25 October 2013; pp. 133–142. [Google Scholar]
- Shen, F.; Shen, C.; Liu, W.; Tao Shen, H. Supervised discrete hashing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 37–45. [Google Scholar]
- Salakhutdinov, R.; Hinton, G. Semantic hashing. Int. J. Approx. Reason. 2009, 50, 969–978. [Google Scholar] [CrossRef]
- Zhang, S.; Li, J.; Jiang, M.; Yuan, P.; Zhang, B. Scalable discrete supervised multimedia hash learning with clustering. IEEE Trans. Circuits Syst. Video Technol. 2017, 28, 2716–2729. [Google Scholar] [CrossRef]
- Lin, M.; Ji, R.; Liu, H.; Sun, X.; Wu, Y.; Wu, Y. Towards optimal discrete online hashing with balanced similarity. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27–28 January 2019; Volume 33, pp. 8722–8729. [Google Scholar]
- Jegou, H.; Douze, M.; Schmid, C. Product quantization for nearest neighbor search. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 117–128. [Google Scholar] [CrossRef]
- Weiss, Y.; Torralba, A.; Fergus, R. Spectral hashing. Adv. Neural Inf. Process. Syst. 2008, 21, 1. [Google Scholar]
- Gong, Y.; Lazebnik, S.; Gordo, A.; Perronnin, F. Iterative quantization: A procrustean approach to learning binary codes for large-scale image retrieval. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 2916–2929. [Google Scholar] [CrossRef]
- Liu, W.; Wang, J.; Kumar, S.; Chang, S.F. Hashing with graphs. In Proceedings of the ICML, Bellevue, WA, USA, 28 June–2 July 2011. [Google Scholar]
- Datar, M.; Immorlica, N.; Indyk, P.; Mirrokni, V.S. Locality-sensitive hashing scheme based on p-stable distributions. In Proceedings of the Twentieth Annual Symposium on Computational Geometry, Brooklyn, NY, USA, 8–11 June 2004; pp. 253–262. [Google Scholar]
- Liu, W.; Wang, J.; Ji, R.; Jiang, Y.G.; Chang, S.F. Supervised hashing with kernels. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2074–2081. [Google Scholar]
- Norouzi, M.; Fleet, D.J. Minimal loss hashing for compact binary codes. In Proceedings of the ICML, Bellevue, WA, USA, 28 June–2 July 2011. [Google Scholar]
- Xia, R.; Pan, Y.; Lai, H.; Liu, C.; Yan, S. Supervised hashing for image retrieval via image representation learning. In Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence, Quebec City, QC, Canada, 27–31 July 2014. [Google Scholar]
- Cao, Y.; Liu, B.; Long, M.; Wang, J. Hashgan: Deep learning to hash with pair conditional wasserstein gan. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1287–1296. [Google Scholar]
- Zhuang, B.; Lin, G.; Shen, C.; Reid, I. Fast training of triplet-based deep binary embedding networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5955–5964. [Google Scholar]
- Liu, B.; Cao, Y.; Long, M.; Wang, J.; Wang, J. Deep triplet quantization. In Proceedings of the 26th ACM International Conference on Multimedia, Seoul, Republic of Korea, 22–26 October 2018; pp. 755–763. [Google Scholar]
- Yang, H.F.; Lin, K.; Chen, C.S. Supervised learning of semantics-preserving hash via deep convolutional neural networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 437–451. [Google Scholar] [CrossRef]
- Wang, M.; Zhou, W.; Tian, Q.; Li, H. A general framework for linear distance preserving hashing. IEEE Trans. Image Process. 2017, 27, 907–922. [Google Scholar] [CrossRef]
- Shen, F.; Xu, Y.; Liu, L.; Yang, Y.; Huang, Z.; Shen, H.T. Unsupervised deep hashing with similarity-adaptive and discrete optimization. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 3034–3044. [Google Scholar] [CrossRef]
- Fang, Y.; Li, P.; Zhang, J.; Ren, P. Cohesion Intensive Hash Code Book Co-construction for Efficiently Localizing Sketch Depicted Scenes. IEEE Trans. Geo-Sci. Remote Sens. 2022, 60, 1–16. [Google Scholar]
- Jiang, Q.Y.; Li, W.J. Discrete latent factor model for cross-modal hashing. IEEE Trans. Image Process. 2019, 28, 3490–3501. [Google Scholar] [CrossRef]
- Lin, J.; Li, Z.; Tang, J. Discriminative Deep Hashing for Scalable Face Image Retrieval. In Proceedings of the IJCAI, Melbourne, Australia, 19–25 August 2017; pp. 2266–2272. [Google Scholar]
- Yang, Y.; Geng, L.; Lai, H.; Pan, Y.; Yin, J. Feature pyramid hashing. In Proceedings of the 2019 on International Conference on Multimedia Retrieval, Ottawa, ON, Canada, 10–13 June 2019; pp. 114–122. [Google Scholar]
- Ng, W.W.; Li, J.; Tian, X.; Wang, H.; Kwong, S.; Wallace, J. Multi-level supervised hashing with deep features for efficient image retrieval. Neurocomputing 2020, 399, 171–182. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images. 2009. Available online: https://www.cs.utoronto.ca/~kriz/learning-features-2009-TR.pdf (accessed on 2 August 2022).
- Bai, J.; Li, Z.; Ni, B.; Wang, M.; Yang, X.; Hu, C.; Gao, W. Loopy residual hashing: Filling the quantization gap for image retrieval. IEEE Trans. Multimed. 2019, 22, 215–228. [Google Scholar] [CrossRef]
- Chua, T.S.; Tang, J.; Hong, R.; Li, H.; Luo, Z.; Zheng, Y. Nus-wide: A real-world web image database from national university of singapore. In Proceedings of the ACM International Conference on Image and Video Retrieval, Santorini Island, Greece, 8–10 July 2009; pp. 1–9. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Jiang, Q.Y.; Li, W.J. Scalable graph hashing with feature transformation. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015. [Google Scholar]
- Wang, J.; Kumar, S.; Chang, S.F. Semi-supervised hashing for large-scale search. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2393–2406. [Google Scholar] [CrossRef]
- Bai, J.; Ni, B.; Wang, M.; Li, Z.; Cheng, S.; Yang, X.; Hu, C.; Gao, W. Deep progressive hashing for image retrieval. IEEE Trans. Multimed. 2019, 21, 3178–3193. [Google Scholar] [CrossRef]
- Cao, Y.; Long, M.; Liu, B.; Wang, J. Deep cauchy hashing for hamming space retrieval. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1229–1237. [Google Scholar]
- Sun, Y.; Yu, S. Deep Supervised Hashing with Dynamic Weighting Scheme. In Proceedings of the 2020 5th IEEE International Conference on Big Data Analytics (ICBDA), Xiamen, China, 8–11 May 2020; pp. 57–62. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).