Abstract
Traditional screening approaches identify students who might be at risk for academic problems based on how they perform on a single screening measure. However, using multiple screening measures may improve accuracy when identifying at-risk students. The advent of machine learning algorithms has allowed researchers to consider using advanced predictive models to identify at-risk students. The purpose of this study is to investigate if machine learning algorithms can strengthen the accuracy of predictions made from progress monitoring data to classify students as at risk for low mathematics performance. This study used a sample of first-grade students who completed a series of computerized formative assessments (Star Math, Star Reading, and Star Early Literacy) during the 2016–2017 (n = 45,478) and 2017–2018 (n = 45,501) school years. Predictive models using two machine learning algorithms (i.e., Random Forest and LogitBoost) were constructed to identify students at risk for low mathematics performance. The classification results were evaluated using evaluation metrics of accuracy, sensitivity, specificity, , and Matthews correlation coefficient. Across the five metrics, a multi-measure screening procedure involving mathematics, reading, and early literacy scores generally outperformed single-measure approaches relying solely on mathematics scores. These findings suggest that educators may be able to use a cluster of measures administered once at the beginning of the school year to screen their first grade for at-risk math performance.
1. Introduction
The purpose of a screening assessment is to identify potential problems (e.g., learning difficulties) accurately [1]. The problems that can be identified from screening assessments used in schools can vary considerably—spanning the domains of cognitive abilities, social–emotional functioning, and academic achievement, to name a few. The practice of using screening measures to identify educational needs early is considered a key component to implementing a multi-tiered system for identifying and supporting students’ instructional needs. Typically, schools collect information using evidence-based screening measures three times a year [2]. The timing of the screening assessments tends to follow the same schedule in all schools, with assessments being administered to students at the beginning, midpoint, and end of the school year. This data collection schedule is usually referred to as fall, winter, and spring benchmark assessments. The consequence associated with the interpretation of screening data typically involves some type of change to curriculum, instruction, or intervention planning. The over-arching goal, essentially, is to identify problems before they become more significant. Thus, the key to achieving this goal is to be able to accurately predict academic performance later in the school year.
The common saying “the best predictor of future behavior is past behavior” has been used in many contexts and is often considered to hold true [3]. Within the context of education, despite the temptation to use other variables (e.g., cognitive abilities) to explain a particular outcome (e.g., academic achievement), the variable with the greatest predictive power will likely be the one that is most closely related to the target outcome. That is, instead of attempting to explain academic performance from a number of related influences (e.g., cognitive abilities, demographic variables, school-related factors), we should focus on predicting academic achievement from academic measures because the direct link is more likely to produce the most useful information [4]. Following this rationale, we would expect the best predictor of mathematics performance to be a general measure of mathematics achievement or of relevant skills or sub-skills. In addition, especially in later grades, the assessment of core academic areas tends to involve more overlap between reading, writing, and mathematics skills. For example, research suggested that reading ability and linguistic skills may contribute significantly to mathematics performance [5,6].
Given the strong connection among core academic areas, some researchers have suggested that using multiple screening measures systematically (typically referred to as multivariate screening) may be an effective and efficient way to identify students who are at risk for learning difficulties [7,8,9]. The primary goal of multivariate screening is to gather information from multiple measures and thereby increase the accuracy of prediction for identifying “students at risk” while reducing the number of students incorrectly identified as at risk. Similarly, a tiered form of multivariate screening, gated screening, has also been used in this context [8]. In gated screening, educators use a screening measure to identify students who are “potentially at risk” and then collect more information for this group of students using another screening measure. In other words, each screening measure is expected to bring unique information about students’ academic performance, leading to more refined and accurate predictions of their potential to be at risk for poor academic performance.
In this study, we aim to extend the current gated screening framework by harnessing information collected from multiple screening measures focusing on different academic areas. Specifically, we posit that screening measures for reading and early literacy could contribute to the prediction of students at risk in mathematics because these screening measures can provide unique information about at-risk students beyond the information obtained from a screening measure used for evaluating mathematics performance. Furthermore, we utilize machine learning algorithms to enhance the predictive power of the proposed approach. To demonstrate the proposed gated screening approach for mathematics and evaluate its accuracy, we use real data from a large sample of students who participated in the Star assessments (i.e., Star Math, Star Reading, and Star Early Literacy). In the following sections, we first explain gated screening and important concepts related to gated screening (e.g., classification accuracy); then, we describe the methodological approach of our study, and present our findings.
1.1. Gated Screening Approaches
Gated screening began to appear in the educational assessment literature over 10 years ago and, at the time, the approach was referred to as multi-stage assessment or multi-gate screening [10]. Gated screening generally implies that multiple types of measures be used across contexts to optimize the quality of the data that are produced for decision making. For example, early on, researchers suggested that using teacher ratings in addition to educational assessment data may be more useful in identifying struggling learners than using these measures in isolation [11]. Glover and Albers [10] identified “the appropriateness of the measured construct and content, the timing and frequency of administration, the suitability of the informant, and the representativeness of the normative sample” (p. 125) as important considerations for gated screening assessments.
Although validity and reliability will always be central to the assessment process, the psychometric properties of assessments available in schools have changed dramatically over the past 10 years. The increased sophistication that has resulted from rigorous development processes, which includes the use of advanced measurement and statistical techniques, has led researchers to focus more on the efficiency and effectiveness of assessment practices that are used in schools [12]. In other words, the focus in the literature has shifted away from the psychometric properties of tests and has focused more on developing efficient assessment practices that lead to effective decisions regarding student needs and supports. For example, researchers have examined the potential of using only educational data that are readily available in schools. This includes attempts at maximizing the predictions of end-of-year achievement levels from data collected early in the school year [13]. In particular, they appear to focus on benchmark data [7] and state assessment performance [14].
Recently, researchers have begun to use these approaches more systematically by applying them within gated screening frameworks. To gather evidence to support the use of gated screening approaches in schools, researchers appear to specifically be focusing on: (a) differentiating between using screening measures simultaneously or sequentially (e.g., [8]); (b) the classification accuracy of screening measures (e.g., [7,13,15,16]); and (c) the feasibility and practical utility of using predictive models (e.g., [7,17,18]). Furthermore, there are studies employing machine learning approaches to students who are at risk of adverse academic outcomes. For example, researchers harnessed predictive models using machine learning algorithms for the detection of students at risk of not graduating high school on time or dropping out of high school (e.g., [19,20,21]) and for the prediction of low academic performance (e.g., [22,23]). Despite their promising results for identifying at-risk students with a high degree of accuracy, the scope of these studies has been limited to middle and high school levels.
1.2. Classification Accuracy
The classification accuracy of an assessment refers to its ability to discriminate between two distinct groups (“classification accuracy” is often referred to as diagnostic accuracy; however, for the purposes of this research, it seemed more appropriate to use classification accuracy to describe the results because the categorical variables defined and used in this study do not refer to the identification or diagnosis of a disability or disorder). In the context of educational screening assessments, classification accuracy refers to the ability to discriminate between students who are at risk for academic difficulties (i.e., in need of additional instructional supports) and students who are not at risk for academic difficulties (i.e., demonstrating adequate growth in response to general classroom instruction). Ideally, a screening measure would discriminate between these two groups with perfect classification accuracy. Perfect classification accuracy refers to correctly identifying all the students who are at risk (true positives) and all students who are not at risk for academic difficulties (true negatives). However, in practice, it is highly unlikely that any screening measure will have perfect classification accuracy. Consequently, the sensitivity and specificity of the screening measure are typically evaluated to determine if the classification accuracy of the measures is strong enough to make good decisions.
Sensitivity and specificity have a direct influence on the efficiency and effectiveness of the instructional supports that are provided to students. For example, if a measure does not have a high degree of sensitivity, many students who are in fact in need of additional instructional supports (i.e., at risk for academic difficulties) will be identified as not at risk for academic difficulty (i.e., FN: false negative), and therefore, they will not be provided with the additional instructional supports. Similarly, if a measure does not have a high degree of specificity, many students who are not in need of additional instructional supports (i.e., not at risk for academic difficulties) will be identified as at risk for academic difficulty (i.e., FP: false positive) and therefore will be provided additional supports unnecessarily. It is, therefore, not surprising that the accuracy of the prediction (i.e., classification accuracy) of an assessment is extremely important, and it should be optimized to: (a) avoid squandering resources by delivering additional supports unnecessarily and (b) identifying as many struggling learners as possible.
To be able to determine the classification accuracy of a screening measure, a cut score needs to be used to be able to compare the accuracy of the classifications. Defining students as at risk can be challenging, given the implications of assigning this status to students. For example, if a student is identified as at risk, there may be an implied responsibility to provide additional instructional supports to that student. On the other hand, if a student is identified as at risk, but they do not require supplemental instructional supports to grow academically, then additional educational resources would be provided unnecessarily. Thus, the assignment of an appropriate cut score involves two important considerations—A statistical one and a practical one. A value greater than 0.75 is the recommended minimum standard when evaluating the sensitivity and specificity of screening measures [10]. However, the parameters used by other researchers tend to provide a more nuanced interpretation of classification accuracy statistics. These parameters and their associated descriptors are ≥0.70, acceptable and ≥0.80, optimal [24,25].
To be able to attain this target, researchers can modify cut scores to find a balance between sensitivity and specificity. However, research should not lose sight of what the cut scores represent—whether or not a student is at risk for later difficulties. This process is more important when selecting an appropriate cut score for an outcome than a predictor. In other words, a student’s actual at-risk status (as opposed to their predicted at-risk status) should be clearly defined and not be altered to increase the sensitivity or specificity of a screening approach. With this in mind, researchers will attempt to find a balance between the optimal sensitivity and specificity that is generated from their predictors. Some researchers “consider the outcome of an FP to be twice as costly as the outcome of an FN” ([8], p. 159). This is not surprising considering the resources that would be wasted if a high number of students not at risk for academic difficulties were provided additional instructional supports. Van Norman and colleagues [8], however, did note that “the cost of FNs within a gated screening framework should not be ignored” (p. 159), which emphasizes the need for balance between sensitivity and specificity.
1.3. Current Study
The purpose of the current study was to develop an effective screening procedure that can identify students in need of targeted instructional supports. To achieve this goal, a number of different methodologies and approaches to screening for academic difficulties was considered. Predictive models with various machine learning algorithms were developed to classify at-risk students in mathematics based on scores from computerized adaptive assessments focusing on mathematics, reading, and early literacy (i.e., Star Math, Star Reading, and Star Early Literacy). The following research questions will be addressed:
- What is the difference in classification accuracy outcomes between single-measure and multi-measure (e.g., gated) screening frameworks?
- To what extent does the cut-score parameter influence the classification accuracy of the screening approach used to identify at-risk students?
2. Methods
2.1. Sample
This study used a sample of first-grade students ( years, years) in the United States who participated in a series of computerized formative assessments (Star Math, Star Reading, and Star Early Literacy) during the 2016–2017 (n = 45,478) and 2017–2018 (n = 45,501) academic years. Each student participated in the Star assessments multiple times during a school year based on their teacher’s test administration decisions (e.g., at the beginning of the school year, later in the first semester, earlier in the second semester, and before the second semester ends). The sample was divided into two groups by school year to provide separate results that could be reviewed for consistency. In other words, completing the analysis by year allowed for greater confidence in the results, assuming that they would be consistent across academic years.
2.2. Measures
The Star assessments are computerized-adaptive formative assessments used for both screening and progress monitoring purposes in K–12 classrooms [26,27,28]. Students are typically administered several Star assessments, starting from early fall until the end of the spring term. The following sections briefly describe each Star assessment used in the current study.
2.2.1. Star Early Literacy
The purpose of the Star Early Literacy assessment is to inform classroom instruction in the areas that are foundational to developing reading skills. Star Early Literacy was developed to be used regularly so teachers could receive ongoing feedback about the growth in skill development for each of their students. The early literacy skills that are incorporated into this measure are subsumed under three categories: (a) Word Knowledge and Skills; (b) Comprehension Strategies and Constructing Meaning; and (c) Numbers and Operations. Forty-one sub-skills are defined under these three over-arching categories. Star Early Literacy is a fixed-length computer adaptive test that administers 27 items for an average completion time of less than 10 min. Strong evidence of reliability and validity is described in detail in the Star Early Literacy technical manual [28].
2.2.2. Star Reading
Star Reading was designed as a standards-based test that includes items that were developed from five blueprint domains, ten skill sets, thirty-six general skills, and more than 470 discrete skills [26]. This highly structured design was developed intentionally to align with national and state curriculum standards in reading, which includes an alignment with the Common Core State Standards [26]. The purpose of the Star Reading assessment is to provide meaningful information to teachers to inform their classroom instruction. It can also provide information about the likelihood that a student will progress well in response to classroom instruction throughout the year and perform well on the state test at the end of the school year. This latter purpose is essentially describing Star Reading as a screening measure.
Currently, Star Reading has two components—a brief measure of reading comprehension used for progress monitoring and a more comprehensive version that can be used to assess student achievement or as a screening measure to predict students’ need for additional instructional supports later in the school year. The version of Star Reading used to assess reading achievement comprehensively is a fixed-length computerized adaptive test that administers 34 items to students to identify their current reading level within an average administration time of approximately 20 min. Star Reading can be administered to students with a sight-word vocabulary of at least 100 words from kindergarten to grade 12. Strong evidence of reliability and validity are described in detail in the Star Reading technical manual [26].
2.2.3. Star Math
The purpose of the Star Math assessment is to provide mathematics achievement data to inform classroom instruction. It was developed to include four broad domains of mathematics: (a) Numbers and Operations; (b) Algebra; (c) Geometry and Measurement; and (d) Data Analysis, Statistics and Probability [27]. To ensure that specific skills are assessed to best inform targeted instruction, 790 individual skills subsumed under 54 skill sets are included within one of the four broad domains [27]. The inclusion of a wide range of mathematics skills allows Star Math to be administered to students from kindergarten to grade 12.
The overall structure and functioning of Star Math are quite similar to Star Reading. Star Math also has two versions available—A brief measure of mathematical ability that produces progress monitoring data and a comprehensive measure of mathematics achievement. The purpose of the latter is to inform instruction and to predict students’ needs for additional instructional supports later in the school year. Again, much like Star Reading, the version of Star Math used to assess mathematics achievement comprehensively is a fixed-length computerized adaptive test that administers 34 items to students to identify their current mathematics level within an average administration time of approximately 20 min. Strong evidence of reliability and validity is described in detail in the Star Math technical manual [27].
2.3. Data Analysis
To classify at-risk students in mathematics, we followed two methodological approaches: a single-stage prediction and a gated screening approach that involved either a standard or mixed framework. The following sections describe these approaches in more detail. For all analyses, the outcome variable was held constant. The criterion used for end-of-year performance in mathematics was set at the 25th percentile. The 25th percentile was selected as the outcome variable for two reasons. First, from a normative perspective, the 25th percentile typically represents the division between typical (i.e., average) performance and below average performance on norm-referenced measures of academic achievement (e.g., Wechsler Individual Achievement Test, Third Edition [29]).
Second, students performing at or below the 25th percentile are considered by some to be “low achieving”, which suggests that additional educational supports are needed to help these students demonstrate adequate growth in academic domains [30]. Due to scaled score conversions only being available for the first month of each school year, we used the 25th percentile score from the following year as the end-of-year criterion. For example, in order to identify the first-grade students who might be at risk for learning difficulties in mathematics, we first found the Star Math scale score corresponding to the 25th percentile in Grade 2 using the Star Math technical manual. Then, the first-grade students whose last Star Math score for that school year was less than this scaled score was identified as “at risk”, whereas the remaining students were identified as “not at risk”. This binary variable was used as the dependent variable in the classification analysis.
2.3.1. Single-Stage Screening
In the single-stage screening, we built two models (Model 0 and Model 1) to examine the predictive power of Star assessment scores from the first half of the fall semester (i.e., August, September, or October) in the classification of students at risk for learning difficulties in mathematics. In Model 0, we used students’ first Star assessment score (as a continuous predictor) and the administration time of the first Star Math (i.e., month) to predict the binary dependent variable (i.e., 1 = “at risk” and 0 = “not at risk”). In Model 1, in addition to the predictors in Model 0, we also included the first Star Reading and Star Early Literacy scores and the administration times of the first Star Reading and Star Early Literacy. Model 0 represents the traditional screening approach based on a single measure, while Model 1 mimics the gated screening approach by using multiple measures but concurrently rather than sequentially. Hence, Model 1 can be considered a single-stage screening approach.
For each model, we used the Logitboost and Random Forest (RF) classification algorithms to run the analysis using the caret package [31] in R [32]. In machine learning, a boosting procedure applies a classification algorithm repeatedly to reweighted versions of a training dataset and then takes a weighted majority vote of the sequence of resulting classifications [33]. The Logitboost algorithm aims to improve the accuracy of traditional logistic regression by performing additive logistic regressions based on maximum Bernoulli likelihood as a criterion. The goal of traditional logistic regression is to learn a function that estimates the probability of falling into one of the two exclusive categories, given a set of predictors. In the context of classification of at-risk students, a logistic regression model would have the following form:
where the probability of being at risk (i.e., ) is predicted based on k number of predictors, e refers to the exponential function, and . The logistic regression function aims to learn the ideal set of parameters (i.e., ) from the training dataset to make accurate predictions for the test dataset. The Logitboost algorithm employs a sequential approach for updating the prediction model as:
where is a pre-specified function to adjust the predictions over M sequences. The task is to learn the parameters and from the training dataset to adjust the prediction accuracy.
The RF algorithm [34] is another widely studied method in machine learning. This algorithm is often considered a “standard classification method”, competing with other popular machine learning algorithms such as logistic regression [35]. As an ensemble learning method, the RF algorithm draws random, bootstrap samples from the original data, builds classification models in the form of a tree structure (i.e., decision trees), and then aggregates all decision trees to reduce the overall variance before making a prediction. The main advantage of the RF algorithm over decision trees is its ability to add randomness to the predictive model by searching for the best feature (i.e., predictor) among a random subset of features. This approach results in a wider diversity in the model and thereby generalizes over the data more accurately. To implement the RF algorithm, we followed the same model set up where the dependent variable was the classification of at-risk students (i.e., 1 = “at risk” and 0 = “not at risk”) and the predictors were students’ first Star assessment score and the administration time of the first Star Math (Model 0) and additional predictors, including the first Star Reading and Star Early Literacy scores and the administration times of these assessments (Model 1). For both the Logitboost and RF algorithms, once we obtained a prediction model based on the training dataset (70% of the full dataset), we applied the model to the test dataset (30% of the full dataset) to obtain classifications of students at risk in mathematics.
In the model training process for both algorithms, we applied the undersampling, oversampling, and ROSE techniques [36,37] due to the strong class imbalance problem (i.e., having much fewer number of at-risk students compared with those who were not at risk). The proportion of at-risk students was 17% and 18% in the 2016–2017 and 2017–2018 datasets. Undersampling randomly subset both classes (i.e., 1 = “at risk” and 0 = “not at risk”) in the training dataset so that the class frequencies could match the least prevalent class (i.e., students at risk for learning difficulties in mathematics). Oversampling took a random sample of the minority class (i.e., 1 = “at risk”) with replacement so that it became the same size as the majority class (i.e., 0 = “not at risk”). The ROSE method created a sample of synthetic data by downsampling the majority class (i.e., 0 = “not at risk”) and synthesized new data points in the minority class (i.e., 1 = “at risk”). This process yielded a synthetic and balanced sample of the two classes (see Menardi and Torelli [36] for further details on the ROSE method).
2.3.2. Gated Screening
In the standard gated screening analysis, we first predicted students at risk for learning difficulties in mathematics based on their first Star Math score in a school year. The criterion for the identification of these students was that their first Star Math score must be higher than the Star Math scores corresponding to the 30th, 40th, or 50th percentiles. This process resulted in a categorical flag (i.e., 0 = not at risk or 1 = at risk) for each percentile cut-off value. Second, we reviewed the scores from other Star assessments for students who were identified as “at risk” based on the initial flag and created a second flag if the students were also “at risk” based on the 30th, 40th, and 50th percentiles of the other Star assessments (i.e., Star Reading and Star Early Literacy). The students who were flagged in both rounds were considered being “at risk”, whereas the remaining students were considered being “not at risk”. For example, if a student’s Star Math score is below the scale score corresponding to the 30th percentile in Star Math, then the student receives an initial “at risk” flag. Next, if the student’s score in either Star Reading or Star Early Literacy is also below the scale scores corresponding to the 30th percentile for those assessments, then the student’s “at risk” flag is confirmed. Other students who are not flagged after the two rounds of screening are considered being “not at risk”. Using the standard gated screening approach, we examined if the students were correctly identified as being “at risk” at the end of the school year based on whether their last Star Math score was above the scale score for the 25th percentile in Grade 2.
The mixed gated screening approach also consisted of two stages. The first stage involved the identification of the students who were “not at risk”, which was based on their first Star Math score in a school year. We again used the scale scores corresponding to the 30th, 40th, and 50th percentiles to identify students who were above these cut-off values and then temporarily removed these students from the training dataset. Then, in the second stage, we used the remaining students (i.e., the sample of students who were identified as being “at risk” in the first stage) and applied the Logitboost and RF algorithms to predict whether they would still be identified as being “at risk” based on their last Star Math score (i.e., whether or not their scores were above the scale score corresponding to the 25th percentile of the next grade level). Using the training dataset, the classification based on the final Star Math score was predicted based on the first Star Reading and Star Early Literacy scores and the administration times of these assessments. The prediction algorithm from the training dataset was then applied to the test dataset to make predictions and evaluate the outcomes. Students in the test dataset who were flagged either based on their first Star Math score or by the machine learning model were considered “at-risk” students. All single-stage and gated screening methods were applied to student data from the 2016–2017 and 2017–2018 academic years. Figure 1 depicts the single-stage and mixed gated screening procedures involving a binary classification model based on machine learning.
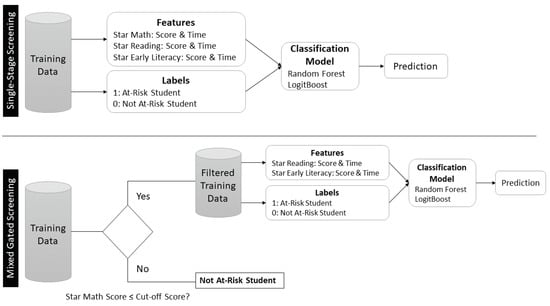
Figure 1.
Single-stage and mixed gated screening procedures.
2.3.3. Evaluation Criteria
The results of both the single-stage and mixed gated screening approaches were evaluated based on the following metrics:
where is the proportion of true positive classifications, is the proportion of false positive classifications, is the proportion of true negative classifications, is the proportion of false negative classifications, and MCC is the Matthews correlation coefficient. Among these metrics, sensitivity, specificity, and accuracy have been widely used by educational researchers for identifying at-risk students, whereas the score and MCC metrics have been less prevalent in the literature despite their higher robustness for handling highly imbalanced classes [38]. Unlike the other evaluation metrics that range from 0 to 1, MCC ranges between −1 and 1 where −1 represents perfect misclassification, 0 represents no agreement through a random guess classifier, and 1 represents perfect classification.
3. Results
The findings from single-stage and gated screening methods (i.e., standard and mixed) for the 2016–2017 and 2017–2018 academic years are presented in Table 1 and Table 2. All single-stage screening methods using oversampling yielded sensitivity, specificity, and accuracy values exceeding the acceptable threshold of 0.70, except for Model 1 with the RF algorithm. Although this model produced lower sensitivity in the 2016–2017 (0.685) and 2017–2018 (0.678) datasets, its specificity and accuracy were much higher than those observed for the single-stage screening methods. Compared to the oversampling results, the single-stage screening with undersampling yielded much higher values of sensitivity, specificity, and accuracy across both academic years. All evaluation values exceeded the acceptable threshold of 0.70 or the optimal threshold of 0.8, except for the specificity of Model 1 with the LogitBoost algorithm for the 2017–2018 dataset (see Table 2).

Table 1.
Sensitivity, Specificity, and Accuracy Results for the 2016–2017 School Year.

Table 2.
Sensitivity, Specificity, and Accuracy Results for the 2017–2018 School Year.
The single-stage screening methods with the ROSE approach generally yielded less accurate results than the single-stage screening methods with the oversampling and undersampling methods. This particular method produced optimal sensitivity values (≥0.80) across both academic years, except for Model 0 (only Star Math as a predictor) with the RF algorithm; however, the same method yielded relatively lower sensitivity and accuracy values (either optimal or below the optimal value of 0.70). It should be also noted that unlike the lower specificity and accuracy values, the sensitivity values produced by the single-stage screening methods with the ROSE approach were the highest value across all single-stage screening methods.
Among the three standard gated screening methods, the 50% threshold model using the Star Math score corresponding to the 50th percentile as a cut-off score was the only one that produced sensitivity, specificity, and accuracy values higher than the acceptable threshold of 0.70 for both academic years (see Table 1 and Table 2). Although the other two models with 30% and 40% thresholds yielded optimal specificity and accuracy values above 0.80, they produced lower levels of sensitivity. This finding suggests that those two models would accurately identify students whose academic performance levels in mathematics are acceptable but fail to detect students at risk in mathematics. Therefore, the standard gated screening models with 30% and 40% thresholds may not be useful to school-based professionals (e.g., school psychologists) who aim to proactively identify students at risk in mathematics and providing them with individualized support.
Compared with the standard gated screening methods, the mixed gated screening methods involving a standard gated screening based on Star Math in the first stage and a predictive model based on Star Reading and Star Early Literacy in the second stage generally yielded more accurate results. This finding highlights the value of using reading-related measures in identifying students at risk in mathematics. However, the mixed gated screening methods yielded inconsistent results in exceeding acceptable and optimal thresholds of sensitivity, specificity, and accuracy. For example, during the 2016–2017 academic year, the mixed gated screening method with oversampling could not meet the acceptable or optimal values, regardless of the prediction algorithm (RF or LogitBoost) and the cut-off score for Stage 1 (30%, 40%, or 50%). However, the mixed gated screening with oversampling yielded relatively better results for the 2017–2018 academic year. Similarly, the results for the mixed gated screening using the ROSE approach produced different results across the two academic years. These findings suggest that the composition of the student at risk in mathematics and those who perform reasonably in mathematics might be slightly different between the two academic years.
Unlike the mixed gated screening methods with either oversampling or ROSE, mixed gated screening using undersampling yielded relatively more consistent results across the two academic years. The models using the 30% and 40% thresholds with undersampling could generally achieve the acceptable threshold of 0.70 for the sensitivity, specificity, and accuracy values. For the RF algorithm, the mixed gated screening using the 30% and 40% thresholds in the first stage exceeded the acceptable threshold of 0.70; whereas for the LogitBoost algorithm, only the 30% threshold could exceed the acceptable threshold. Using the 50% threshold in the first stage seemed to improve the sensitivity significantly (i.e., beyond the optimal threshold of 0.80) while decreasing specificity and accuracy for both the RF and LogitBoost algorithms (see Table 1 and Table 2). Furthermore, although the overall performance of the RF and LogitBoost algorithms was not the same, the differences in terms of the evaluation metrics (i.e., sensitivity, specificity, and accuracy) were mostly negligible.
Table 3 presents the scores and MCC results for the 2016–2017 and 2017–2018 school years. As explained earlier, scores and MCC tend to be more reliable metrics for evaluating binary classifications results on imbalanced datasets. The results presented in Table 3 show that the scores were above 0.70 and the MCC values were above 0.40 for all screening methods, except for a few cases (e.g., the standard gated screening with the 30% threshold). Generally, the single-stage screening methods with either oversampling or undersampling seemed to yield higher values of and MCC, compared with the other screening methods. Specifically, single-stage screening based on Model 1 (i.e., Star Math, Star Reading, and Star Early Literacy as predictors) with the LogitBoost algorithm and undersampling was the best performing screening method in the 2016–2017 dataset, while the same method with oversampling was the best performing screening method in the 2017–2018 dataset. The standard gated screening method with the 50% threshold also yielded comparable results. Similar to the findings presented in Table 1 and Table 2, the mixed gated screening methods produced inconsistent results across the two evaluation metrics and the two school years. The only consistent pattern for the mixed gated screening was the positive impact of using the 40% threshold, which seemed to improve both and MCC. Overall, these findings are aligned with the conclusions drawn based on the sensitivity, specificity, and accuracy metrics.

Table 3.
Scores and MCC Results for the 2016–2017 and 2017–2018 School Years.
Overall, the screening methods that produced the greatest balance between the five evaluation metrics (i.e., sensitivity, specificity, accuracy, , and MCC) were single-stage screening with either oversampling or undersampling. Furthermore, the RF algorithm generally yielded better results in terms of balancing sensitivity, specificity and accuracy compared to the LogitBoost algorithm; however, the LogitBoost algorithm generally outperformed the RF algorithm based on the and MCC metrics. In terms of the sampling method, oversampling (for RF) and undersampling (for LogitBoost) seemed to be more reasonable options. Regardless of the screening method, the ROSE approach appeared to enhance sensitivity at the expense of specificity. Compared to the single-stage screening approaches, the gated screening approaches (both standard and mixed gated) performed relatively less accurately. Especially the mixed gated screening methods yielded inconsistent results across different algorithms, prediction models, and sampling strategies. However, the standard gated screening approach with the 50% threshold seemed to be a reliable and consistent option for detecting students at risk in mathematics when there is no secondary measure (e.g., Star Reading or Star Early Literacy) available to measure students’ reading skills.
4. Discussion
The use of the same measures for the purpose of both screening and progress monitoring has the potential to contribute to an efficient assessment system that is able to identify students who are at risk for academic difficulties. If this dual purpose is possible, then the data would be able to identify students who are struggling early in the school year, which would allow educators to implement supports before the difficulties become even more significant. This focus on prevention, rather than intervention, represents the future of educational assessment and interventions in schools [12]. To be able to achieve both efficiency and effectiveness in a school-based assessment system, strong empirical evidence must exist for each identified purpose [39]. Star assessments are well established as having strong psychometric properties. Moreover, considerable evidence in support of their use as progress monitoring measures has also been documented in the literature (e.g., [40,41,42]). The purpose of this study was to extend the existing evidence to identify an optimal methodology that could maximize the potential of using multiple Star assessment scores to produce highly accurate screening data for students at risk for mathematics difficulties later in the school year.
4.1. Screening for Mathematics Difficulties
The established relationship between mathematics performance and reading skills [5] led us to consider if using multiple measures from different content areas (e.g., reading and early literacy) could produce greater accuracy in identifying students who are at risk for mathematics difficulties in their early elementary years (e.g., grades 1 and 2). In addition, Van Norman et al. [8] showed that measures with the potential to explain unique variance in the outcome variable were more likely to improve the diagnostic accuracy of the screening approach. When considering the single-stage screening method results, several combinations of algorithms and sampling methods produced better sensitivity, specificity, or accuracy when multiple measures were used. For example, our study showed that the RF and LogitBoost algorithms combined with an undersampling approach led to improvements across all evaluation metrics when Star Math, Star Reading, and Star Early Literacy were used together. These findings further support the use of multiple measures, from a variety of core curricular areas, as being beneficial to increasing the quality of predictions made from screeners.
4.1.1. Single vs. Gated Screening Approaches
In this study, the gated screening results were somewhat surprising, since they did not necessarily lead to significant improvements over the single-stage approaches when various evaluation metrics were considered concurrently. However, the results were more nuanced than those reported by Van Norman et al. [9], who described a consistent reduction in sensitivity across all grade levels when comparing gated screening and single measure approaches. Specifically, the gated screening approaches applied in this study were able to produce some particularly strong results when only a single evaluation metric was considered. For example, the mixed gated approach with a LogitBoost algorithm and a 50% prediction model threshold produced a sensitivity value of 0.930—A value that significantly exceeded any of the other approaches from the single-stage methods. Nonetheless, the results of this study suggest that many approaches to single- or multi-stage screening can produce acceptable levels of sensitivity, specificity, and accuracy. Thus, the primary consideration when selecting a methodology could be whether a balanced level of the evaluation metrics is optimal for the purpose of screening or if one or two of the evaluation metrics should be weighed more than another.
4.1.2. Weighing Evaluation Metrics
It could be argued that for the purpose of screening, minimizing the occurrence of false negatives (i.e., not providing additional supports to students who are in fact at risk) is a greater priority than minimizing the occurrence of false positives (i.e., providing additional supports to students who may not necessarily need them). If this is the case, then the sensitivity metric could be prioritized in the selection of an approaching screening approach. Using this logic, a gated screening approach using the LogitBoost algorithm would likely be an optimal choice. It could, however, also be argued that the accuracy, , and MCC metrics provide guidance as to the approach that provides the greatest balance between students who are in fact at risk for mathematics difficulties versus those that are not, given their ability to consider both true positives and true negatives. In this case, a single-stage or gated screening approach could be taken. Of note, the multi-measure model (i.e., Model 1) within the single-stage screening approach generally produced stronger accuracy than the single-measure approach.
Although the results of this study were perhaps not as clear as we had hoped in identifying a single, optimal approach to implementing an efficient screening process for mathematics difficulties, the results were similar to other studies that took different approaches. For example, Klingbeil et al. [43] used likelihood ratios to evaluate the utility of fall and winter MAP math assessments for the purpose of identifying at-risk math learners. A computerized summative statewide assessment was used as the criterion measure. Their results showed similar or slightly better evaluation metrics than those reported in the current study. Thus, this comparison leads to additional considerations as different approaches to screening at-risk learners are weighed. Specifically, the data or broader assessment practices within a school, district, or state may lead administrators to select one approach over another. In other words, a school with Star assessments covering core content areas may opt to take the approach to screening described in this study. Conversely, a school that is using the MAP math assessment with periodic benchmark assessments (i.e., fall and winter) may opt to simply use those data for the additional purpose of screening for at-risk learners. In addition to data availability within their current assessment practices, school administrators may also want to consider the difference in administration time and how the measures they select meet their over-arching assessment needs.
4.1.3. The Influence of Cut-Score Parameters
By comparing multiple approaches to generating screening results, the results of this study also allowed us to evaluate the influence of cut-score parameters on the classification accuracy of the screening approach used to identify at-risk students in mathematics. The results of previous research examining evaluation metrics between cut scores suggested that specificity values are consistently higher than sensitivity values [44]. However, this trend was not consistently observed in our results. Instead, a more restrictive (i.e., lower) threshold for the cut-score parameter leads to a more balanced outcome across the five evaluation metrics. Thus, similar to the conclusions drawn from the discussion comparing single and gated screening methods, priorities with respect to the purpose of the screening could be considered to select an appropriate threshold. For example, a less restrictive (i.e., higher) prediction model threshold tended to produce stronger sensitivity while reducing the values for the other two evaluation metrics. Thus, if sensitivity were to be prioritized, a higher threshold parameter could be set.
4.2. Limitations and Future Directions
The results of this study should be considered in light of several limitations. First, this study included three measures—Star Math, Star Reading, and Star Early Literacy—in the prediction model. The inclusion of these three measures is somewhat unique to early grade levels, given that Star Early Literacy is not likely to yield useful information at higher grade levels when most students have progressed significantly with respect to their reading skills. Second, the relationship between reading and mathematical skills is likely to change over time, as the math curriculum includes more word-based problems [6]. Thus, the current study is limited to only applying to screening for at-risk math learners at grade 1. Third, this study used Star Math scores as the end-of-year criterion when identifying students at risk for low math performance. However, the results of other measures of mathematics (e.g., statewide assessment programs) could be used as the end-of-year criteria to further validate the findings of this study.
There are three directions for future research that may further improve the quality of the screening approaches generated from this research. First, the screening framework for mathematics could potentially be improved by creating subscores within the Star Early Literacy assessment that better account for the math skills from that measure that set the foundation for later math skills. Second, to increase the strength and quality of the prediction for end-of-year performance in mathematics, a number of additional predictors (e.g., demographic characteristics and other cognitive measures) could be incorporated into the assessment systems used by schools. If additional predictors were to be identified, they should incorporate a different aspect of the desired outcome, as the ones included in the current analysis capture the core aspects of reading and mathematics very well. However, the increased effectiveness of using additional predictors may come at too great of a cost when considering the high-quality information that is already generated from the efficient screening framework presented using only Star assessments. Third, this study used supervised machine learning models for binary classification of students at risk in mathematics and those who are not. Future studies can utilize supervised anomaly detection using machine learning and deep learning algorithms (see Ángela Fernández et al. [45] for a review of different algorithms) to identify abnormal patterns (e.g., students who perform significantly worse than their peers). Fourth, depending on the outcomes of the screening procedure, students could be more or less frequently tested based on their academic growth in mathematics throughout the academic year. Previous research showed that students’ assessment schedules can be personalized in core subject areas based on their learning progress estimated from Star assessment scores [46,47,48]. Future research can investigate the relationship between screening results and students’ academic growth throughout the academic year by following a personalized assessment schedule for students.
5. Conclusions
This study fills a practical gap in education to support the development of more sophisticated predictive models for screening approaches. The screening methods introduced in this study can be used by researchers to design more effective screening procedures based on multiple academic measures and test their efficacy based on multiple evaluation metrics (e.g., sensitivity, specificity, accuracy, , and MCC). In addition, the results of this study provide an important opportunity for educators to leverage available data to identify students who are at risk for low mathematics performance.
Author Contributions
Conceptualization, O.B. and D.C.C.; methodology, O.B.; software, O.B.; validation, O.B. and D.C.C.; formal analysis, O.B.; investigation, O.B., D.C.C. and S.N.Y.-E.; data curation, O.B.; writing—original draft preparation, O.B., D.C.C. and S.N.Y.-E.; writing—review and editing, O.B., D.C.C. and S.N.Y.-E.; supervision, O.B.; project administration, O.B. and D.C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data analyzed in this study were obtained from Renaissance, Inc., the following restrictions apply: all data are solely owned and licensed by Renaissance, Inc., and thus, it cannot be discussed or shared by the researchers in any form or format. Requests to access these datasets should be directed to Eric Stickney, eric.stickney@renaissance.com.
Conflicts of Interest
O.B. and D.C.C. were paid consultants for Renaissance, Inc. during the design and implementation of the project that resulted in this manuscript. S.N.Y.-E. declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FN | False negative classifications |
| FP | False positive classifications |
| MCC | Matthews correlation coefficient |
| RF | Random Forest algorithm |
| TN | True negative classifications |
| TP | True positive classifications |
References
- Christ, T.J.; Nelson, P.M. Developing and evaluating screening systems: Practical and psychometric considerations. In Universal Screening in Educational Settings: Evidence-Based Decision Making for Schools; Kettler, R.J., Glover, T.A., Albers, C.A., Feeney-Kettler, K.A., Eds.; American Psychological Association: Washington DC, USA, 2014; pp. 79–110. [Google Scholar] [CrossRef]
- Mellard, D.F.; McKnight, M.; Woods, K. Response to intervention screening and progress-monitoring practices in 41 local schools. Learn. Disabil. Res. Pract. 2009, 24, 186–195. [Google Scholar] [CrossRef]
- Franklin, K. The Best Predictor of Future Behavior Is … Past Behavior. 2013. Available online: https://www.psychologytoday.com/us/blog/witness/201301/the-best-predictor-future-behavior-is-past-behavior (accessed on 15 March 2022).
- Cormier, D.C.; Bulut, O.; Niileksela, C.R.; Singh, D.; Funamoto, A.; Schneider, J. Revisiting the relationship between CHC abilities and academic achievement. Presented at the Annual Conference of the National Association of School Psychologists, New Orleans, LA, USA, 17–20 February 2016. [Google Scholar]
- Cormier, D.C.; Yeo, S.; Christ, T.J.; Offrey, L.D.; Pratt, K. An examination of the relationship between computation, problem solving, and reading. Exceptionality 2016, 24, 225–240. [Google Scholar] [CrossRef]
- Kan, A.; Bulut, O.; Cormier, D.C. The impact of item stem format on the dimensional structure of mathematics assessments. Educ. Assess. 2019, 24, 13–32. [Google Scholar] [CrossRef]
- Compton, D.L.; Fuchs, D.; Fuchs, L.S.; Bouton, B.; Gilbert, J.K.; Barquero, L.A.; Cho, E.; Crouch, R.C. Selecting at-risk first-grade readers for early intervention: Eliminating false positives and exploring the promise of a two-stage gated screening process. J. Educ. Psychol. 2010, 102, 327. [Google Scholar] [CrossRef]
- Van Norman, E.R.; Nelson, P.M.; Klingbeil, D.A.; Cormier, D.C.; Lekwa, A.J. Gated screening frameworks for academic concerns: The influence of redundant information on diagnostic accuracy outcomes. Contemp. Sch. Psychol. 2019, 23, 152–162. [Google Scholar] [CrossRef]
- Van Norman, E.R.; Nelson, P.M.; Klingbeil, D.A. Single measure and gated screening approaches for identifying students at-risk for academic problems: Implications for sensitivity and specificity. Sch. Psychol. Q. 2017, 32, 405. [Google Scholar] [CrossRef]
- Glover, T.A.; Albers, C.A. Considerations for evaluating universal screening assessments. J. Sch. Psychol. 2007, 45, 117–135. [Google Scholar] [CrossRef]
- Elliott, S.N.; Huai, N.; Roach, A.T. Universal and early screening for educational difficulties: Current and future approaches. J. Sch. Psychol. 2007, 45, 137–161. [Google Scholar] [CrossRef]
- Fuchs, D.; Fuchs, L.S.; Compton, D.L. Smart RTI: A next-generation approach to multilevel prevention. Except. Child. 2012, 78, 263–279. [Google Scholar] [CrossRef]
- Catts, H.W.; Petscher, Y.; Schatschneider, C.; Sittner Bridges, M.; Mendoza, K. Floor effects associated with universal screening and their impact on the early identification of reading disabilities. J. Learn. Disabil. 2009, 42, 163–176. [Google Scholar] [CrossRef]
- Johnson, E.S.; Jenkins, J.R.; Petscher, Y. Improving the accuracy of a direct route screening process. Assess. Eff. Interv. 2010, 35, 131–140. [Google Scholar] [CrossRef]
- Catts, H.W.; Nielsen, D.C.; Bridges, M.S.; Liu, Y.S.; Bontempo, D.E. Early identification of reading disabilities within an RTI framework. J. Learn. Disabil. 2015, 48, 281–297. [Google Scholar] [CrossRef] [PubMed]
- Nelson, P.M.; Van Norman, E.R.; Lackner, S.K. A comparison of methods to screen middle school students for reading and math difficulties. Sch. Psychol. Rev. 2016, 45, 327–342. [Google Scholar] [CrossRef]
- Klingbeil, D.A.; Van Norman, E.R.; Nelson, P.M.; Birr, C. Interval likelihood ratios: Applications for gated screening in schools. J. Sch. Psychol. 2019, 76, 107–123. [Google Scholar] [CrossRef]
- Poulsen, M.; Nielsen, A.M.V.; Juul, H.; Elbro, C. Early identification of reading difficulties: A screening strategy that adjusts the sensitivity to the level of prediction accuracy. Dyslexia 2017, 23, 251–267. [Google Scholar] [CrossRef] [PubMed]
- Aguiar, E.; Lakkaraju, H.; Bhanpuri, N.; Miller, D.; Yuhas, B.; Addison, K.L. Who, when, and why: A machine learning approach to prioritizing students at risk of not graduating high school on time. In Proceedings of the Fifth International Conference on Learning Analytics And Knowledge, Poughkeepsie, NY, USA, 16–20 March 2015; pp. 93–102. [Google Scholar] [CrossRef]
- Lakkaraju, H.; Aguiar, E.; Shan, C.; Miller, D.; Bhanpuri, N.; Ghani, R.; Addison, K.L. A machine learning framework to identify students at risk of adverse academic outcomes. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, NSW, Australia, 10–13 August 2015; pp. 1909–1918. [Google Scholar] [CrossRef]
- Márquez-Vera, C.; Cano, A.; Romero, C.; Noaman, A.Y.M.; Mousa Fardoun, H.; Ventura, S. Early dropout prediction using data mining: A case study with high school students. Expert Syst. 2016, 33, 107–124. [Google Scholar] [CrossRef]
- Hamsa, H.; Indiradevi, S.; Kizhakkethottam, J.J. Student academic performance prediction model using decision tree and fuzzy genetic algorithm. Procedia Technol. 2016, 25, 326–332. [Google Scholar] [CrossRef]
- Tamhane, A.; Ikbal, S.; Sengupta, B.; Duggirala, M.; Appleton, J. Predicting student risks through longitudinal analysis. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 1544–1552. [Google Scholar] [CrossRef]
- Hintze, J.M.; Silberglitt, B. A longitudinal examination of the diagnostic accuracy and predictive validity of R-CBM and high-stakes testing. Sch. Psychol. Rev. 2005, 34, 372–386. [Google Scholar] [CrossRef]
- Kilgus, S.P.; Chafouleas, S.M.; Riley-Tillman, T.C. Development and initial validation of the Social and Academic Behavior Risk Screener for elementary grades. Sch. Psychol. Q. 2013, 28, 210. [Google Scholar] [CrossRef]
- Renaissance. Star Assessments™ for Reading Technical Manual; Technical Report; Renaissance: Wisconsin Rapids, WI, USA, 2018. [Google Scholar]
- Renaissance. Star Assessments™ for Math Technical Manual; Technical Report; Renaissance: Wisconsin Rapids, WI, USA, 2018. [Google Scholar]
- Renaissance. Star Early Literacy™ for Early Literacy Technical Manual; Technical Report; Renaissance: Wisconsin Rapids, WI, USA, 2018. [Google Scholar]
- Dumont, R.; Willis, J.O.; Veizel, K.; Zibulsky, J. Wechsler Individual Achievement Test–Third Edition. In Encyclopedia of Special Education: A Reference for the Education of Children, Adolescents, and Adults with Disabilities and Other Exceptional Individuals; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Fletcher, J.M.; Barth, A.E.; Stuebing, K.K. A response to intervention (RTI) approach to SLD identification. In Essentials of Specific Learning Disability Identification; Flanagan, D.P., Alfonso, V.C., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011; pp. 115–144. [Google Scholar]
- Kuhn, M. caret: Classification and Regression Training. R Package Version 6.0-90. 2021. Available online: https://cran.r-project.org/web/packages/caret/index.html (accessed on 5 March 2022).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting (with discussion and a rejoinder by the authors). Ann. Stat. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Couronné, R.; Probst, P.; Boulesteix, A.L. Random forest versus logistic regression: A large-scale benchmark experiment. BMC Bioinform. 2018, 19, 270. [Google Scholar] [CrossRef] [PubMed]
- Menardi, G.; Torelli, N. Training and assessing classification rules with imbalanced data. Data Min. Knowl. Discov. 2014, 28, 92–122. [Google Scholar] [CrossRef]
- Lunardon, N.; Menardi, G.; Torelli, N. ROSE: A Package for Binary Imbalanced Learning. R Journal 2014, 6, 79–89. [Google Scholar] [CrossRef]
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 6. [Google Scholar] [CrossRef]
- American Educational Research Association; American Psychological Association; National Council on Measurement in Education. Standards for Educational and Psychological Testing; American Educational Research Association: Washington, DC, USA, 2014. [Google Scholar]
- Bulut, O.; Cormier, D.C. Validity evidence for progress monitoring with Star Reading: Slope estimates, administration frequency, and number of data points. Front. Educ. 2018, 3. [Google Scholar] [CrossRef]
- Lambert, R.; Algozzine, B.; McGee, J. Effects of progress monitoring on math performance of at-risk students. Br. J. Educ. Soc. Behav. Sci. 2014, 4, 527–540. [Google Scholar] [CrossRef][Green Version]
- Shapiro, E.S.; Dennis, M.S.; Fu, Q. Comparing computer adaptive and curriculum-based measures of math in progress monitoring. Sch. Psychol. Q. 2015, 30, 470. [Google Scholar] [CrossRef]
- Klingbeil, D.A.; Van Norman, E.R.; Nelson, P.M. Using interval likelihood ratios in gated screening: A direct replication study. Assess. Eff. Interv. 2021, 47, 14–25. [Google Scholar] [CrossRef]
- Turner, M.I.; Van Norman, E.R.; Hojnoski, R.L. An Independent Evaluation of the Diagnostic Accuracy of a Computer Adaptive Test to Predict Proficiency on an End of Year High-Stakes Assessment. J. Psychoeduc. Assess. 2022. [Google Scholar] [CrossRef]
- Fernández, Á.; Bella, J.; Dorronsoro, J.R. Supervised outlier detection for classification and regression. Neurocomputing 2022, 486, 77–92. [Google Scholar] [CrossRef]
- Bulut, O.; Cormier, D.C.; Shin, J. An intelligent recommender system for personalized test administration scheduling with computerized formative assessments. Front. Educ. 2020, 5, 182. [Google Scholar] [CrossRef]
- Bulut, O.; Shin, J.; Cormier, D.C. Learning analytics and computerized formative Assessments: An application of Dijkstra’s shortest path algorithm for personalized test scheduling. Mathematics 2022, 10, 2230. [Google Scholar] [CrossRef]
- Shin, J.; Bulut, O. Building an intelligent recommendation system for personalized test scheduling in computerized assessments: A reinforcement learning approach. Behav. Res. Methods 2022, 54, 216–232. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).