Automatic Identification of Similar Pull-Requests in GitHub’s Repositories Using Machine Learning

Abstract

Context: In a social coding platform such as GitHub, a pull-request mechanism is frequently used by contributors to submit their code changes to reviewers of a given repository. In general, these code changes are either to add a new feature or to fix an existing bug. However, this mechanism is distributed and allows different contributors to submit unintentionally similar pull-requests that perform similar development activities. Similar pull-requests may be submitted to review in parallel time by different reviewers. This will cause redundant reviewing time and efforts. Moreover, it will complicate the collaboration process. Objective: Therefore, it is useful to assign similar pull-requests to the same reviewer to be able to decide which pull-request to choose in effective time and effort. In this article, we propose to group similar pull-requests together into clusters so that each cluster is assigned to the same reviewer or the same reviewing team. This proposal allows saving reviewing efforts and time. Method: To do so, we first extract descriptive textual information from pull-requests content to link similar pull-requests together. Then, we employ the extracted information to find similarities among pull-requests. Finally, machine learning algorithms (K-Means clustering and agglomeration hierarchical clustering algorithms) are used to group similar pull-requests together. Results: To validate our proposal, we have applied it to twenty popular repositories from public dataset. The experimental results show that the proposed approach achieved promising results according to the well-known metrics in this subject: precision and recall. Furthermore, it helps to save the reviewer time and effort. Conclusion: According to the obtained results, the K-Means algorithm achieves 94% and 91% average precision and recall values over all considered repositories, respectively, while agglomeration hierarchical clustering performs 93% and 98% average precision and recall values over all considered repositories, respectively. Moreover, the proposed approach saves reviewing time and effort on average between (67% and 91%) by K-Means algorithm and between (67% and 83%) by agglomeration hierarchical clustering algorithm.

1. Introduction

In a social coding platforms such as GitHub, contributors (developers) frequently use Pull-Request (PR) mechanisms to submit their code changes to reviewers or owners of a given software project (repository) [1,2].These changes include development activities (e.g., adding new functional features) [3,4], fixing errors in an existing project [5] or for improvements (in terms of performance, usability, reliability, and so on). The contributors are volunteers, who are distributed geographically around the world, and they implicitly collaborate together to work on a repository [1]. Indeed, each contributor independently clones or forks the original repository and makes their changes to that fork [6]. These changes could be useful to merge to the original repository. Therefore, the contributor creates a PR to package and submit their changes to core reviewers of the original repository. The content of these submitted PRs passes through several rounds of code reviews and discussions. At last, the core reviewers decide which PRs should be merged to the upstream repository (original repository) while other PRs are rejected [7]. The PR mechanism is useful to keep the contributors up to date about the changes made to the original repository and to manage these changes. In open-source projects, it speeds up the growth of repositories through distributed development. For example, Rails (https://github.com/rails/rails/pulls) repository has more than 26,557 PRs.

Although the PR mechanism is useful in GitHub, it has own drawbacks. The nature of parallel and distributed development using PR mechanism allows many contributors to submit PRs that perform similar or same development activities [8]. Generally, similar PRs can be completely duplicated or partially duplicated (some common changed lines of code) or PRs having common keywords in their titles and descriptions with common changed files. In this work clusters of duplicate PRs can be treated as clusters of similar PRs as the duplication is a similarity form (i.e., 100% similarity). Similar PRs are common in popular repositories that attract a number of contributors around the world. Unfortunately, each contributor works without any coordination with others and GitHub platform does not support such coordination activity [6]. This leads to redundant development activities. Consequently, this yields a waste of time and effort spent on development (by contributors) and on reviewing (by core reviewers). Moreover, the contributor updates the PR content in several reviewing rounds based on the reviewer’s feedback before the reviewer discovers that the PR is duplicated (fully or partially) or similar to other PR assigned to the different reviewers or teams.

In addition, the GitHub policy for managing the PRs review aggravates the problem of missing the synchronization among development activities submitted by contributors. In GitHub, there are two algorithms to automatically assign PRs to reviewers. The first one is “the round-robin algorithm chooses reviewers based on who’s received the least recent review request, focusing on alternating between all members of the team regardless of the number of outstanding reviews they currently have” (https://docs.github.com/en/github/setting-up-and-managing-organizations-and-teams/managing-code-review-assignment-for-your-team). The second one is “the load balance algorithm chooses reviewers based on each member’s total number of recent review requests and considers the number of outstanding reviews for each member. The load balance algorithm tries to ensure that each team member reviews an equal number of PRs in any 30 day period” (https://docs.github.com/en/github/setting-up-and-managing-organizations-and-teams/managing-code-review-assignment-for-your-team). Following these algorithms, a group of similar PRs (e.g., n-PR) will be assigned to n reviewers and the reviewing efforts will be redundant n times especially when these PRs are assigned to plain reviewers. However, when such a cluster is assigned to one team or reviewer, the reviewing effort and time of (n-1) reviewers will be saved and the updating efforts and time by contributors will be reduced as well. Clustering similar PRs together and then submitting them to reviewers as clusters have the following benefits: (1) help to detect duplicated parts (duplication in parts of code changes) among PRs, (2) help to expedite code changes reviewing, and thus lead to low latency for processing PRs, (3) mitigate the limitation of heuristic-duplicate PRs detection techniques.

Existing works related to the research problem addressed in this article take two directions. The first direction refers to the research works interested in detecting duplicate PRs [1,5,8,9]. However, this research direction considers only duplicate PRs in pairs and does not take into account the similar PRs as a group. Moreover, most of these works depended on heuristics (e.g., submission times for PRs) to detect duplicated PRs which that means not all duplicated PRs are detected and removed before assigning them to reviewers. The second direction refers to the research works interested in recommending proper reviewers for PRs in GitHub [7,10,11,12,13]. The limitation of this research direction is that the recommending process does not pay attention to cluster similar PRs together before assigning PRs to reviewers. In other words, although the recommending process depends on some relevancy (textual similarity or reviewer history) between PRs and reviewers, there is no guarantee that a group of similar PRs will be assigned to the same team or reviewer.

In this article, we propose an automatic approach to group open similar PRs together for a given repository. We first extract textual information from PRs to link similar PRs together. Then, the extracted information is used to find similarities among PRs. Finally, the textual similarity helps machine learning (ML) algorithms to group similar PRs together. The proposed approach employs supervised and unsupervised ML algorithms. The former is K-mean clustering [14]. The later agglomeration hierarchical clustering (AHC) [15]. To evaluate the superiority and effectiveness of our proposal, we have applied it to twenty popular GitHub’s repositories. These repositories are included in a public dataset (https://github.com/whystar/MSR2018-DupPR/blob/master/dup_prs.md). We evaluate the effectiveness in different scenarios: (i) in case of the number of PRs is more than or equal to the number of reviewers, (ii) in case of the number PRs is less than the number of reviewers. The experimental results show that the proposed approach achieved promising results according to the well-known metrics in this subject: Precision and Recall. Furthermore, the experimental results show that the proposed approach is efficient to save the time and efforts of reviewers. As a summary, our proposal makes the following contributions:

• An automatic approach to cluster similar PRs together using two supervised and unsupervised ML algorithms considering the number of reviewers or repository’s owner preferences.
• An empirical evaluation for our proposal using twenty popular repositories from different domains and sizes.

The remainder of this article is structured as follows. Firstly, we provide basics about PR mechanism and development in GitHub in Section 2. Then, we present existing research works close to our research topic in Section 3. Next, the proposed approach is detailed in Section 4. In Section 5, the experimental results are discussed and evaluated. Finally, we conclude the article in Section 6.

2. Background

2.1. Pull-Request Mechanism

Managing changes in software development can be challenging in terms of continuous, parallel, and distributed development [16]. GitHub implements a model to manage these changes called pull-request (PR) [17]. PR lets other contributors know, discuss and review the potential changes before these changes are accepted (merged) or refused in a repository on GitHub.

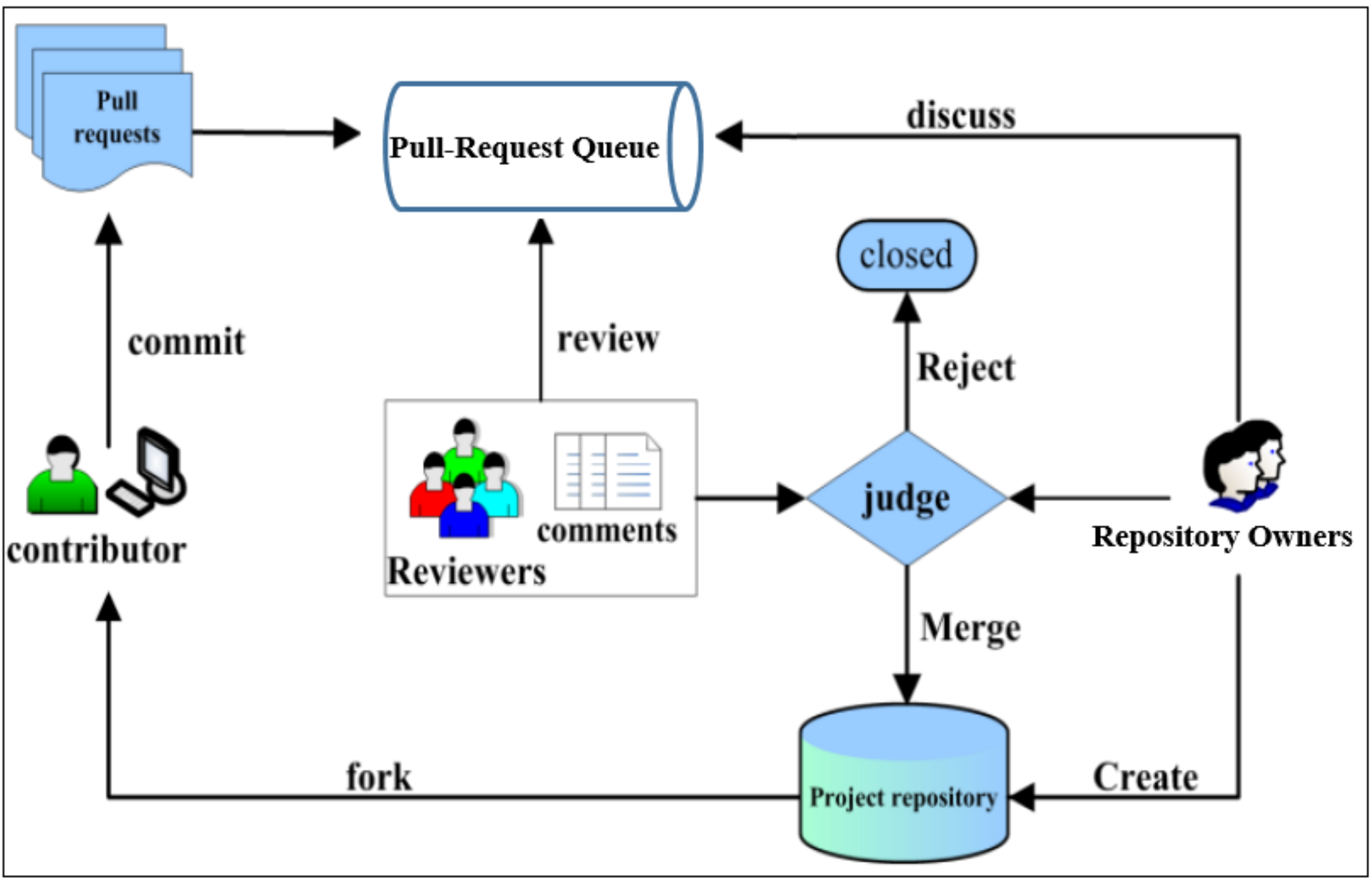
A common PR flow is depicted in Figure 1. When contributors need to add new features or fix existing bugs in the main repository. First of all, rather than contributes to the original repository, the contributors fork the repository and create a branch to keep changes organized and separated from the original repository. Then, the contributors can safely add their changes (commits) and test them in their own branch. Changes or commits could be created, edited, renamed, moved, or deleted files. When the changes are ready, the contributors open a PR of all of their changes (commits) to review and discuss them with other team members. PRs let contributors show their changes and additional information (e.g., build and test results) with other team members, so they can review and discuss these changes before accept, give some comments, or reject them. If the reviewer gives comments, then the contributor handles these comments and updates the PR. After that, the reviewing process will be repeated to discuss the updates. Finally, when changes are approved, the changes are merged into the main repository [17].

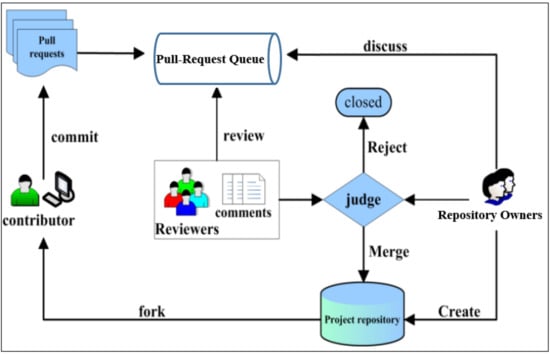
Figure 1. An overview of pull-request mechanism in GitHub [18].

2.2. Similar Pull-Requests

PRs that are aiming to contribute congruous features or fix congruous bugs in the same GitHub repository are called similar PRs [19]. Similar PRs may be submitted to review in parallel time by different reviewers. This will cause redundant reviewing time and efforts. Moreover, it will complicate the collaboration process. Therefore, it is useful to assign similar PRs to the same reviewer to be able to decide which the PR is more suitable on effective time and effort.

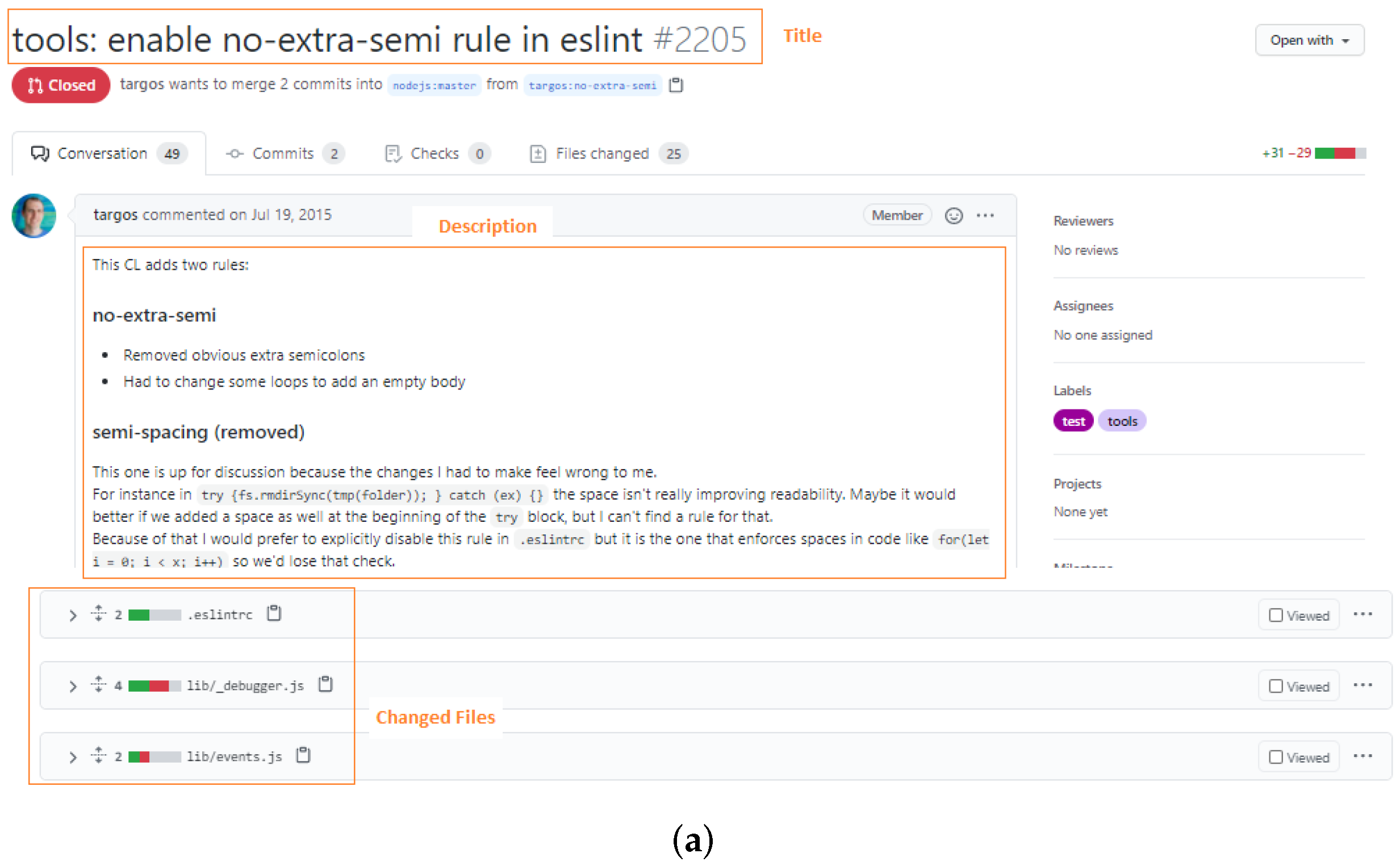
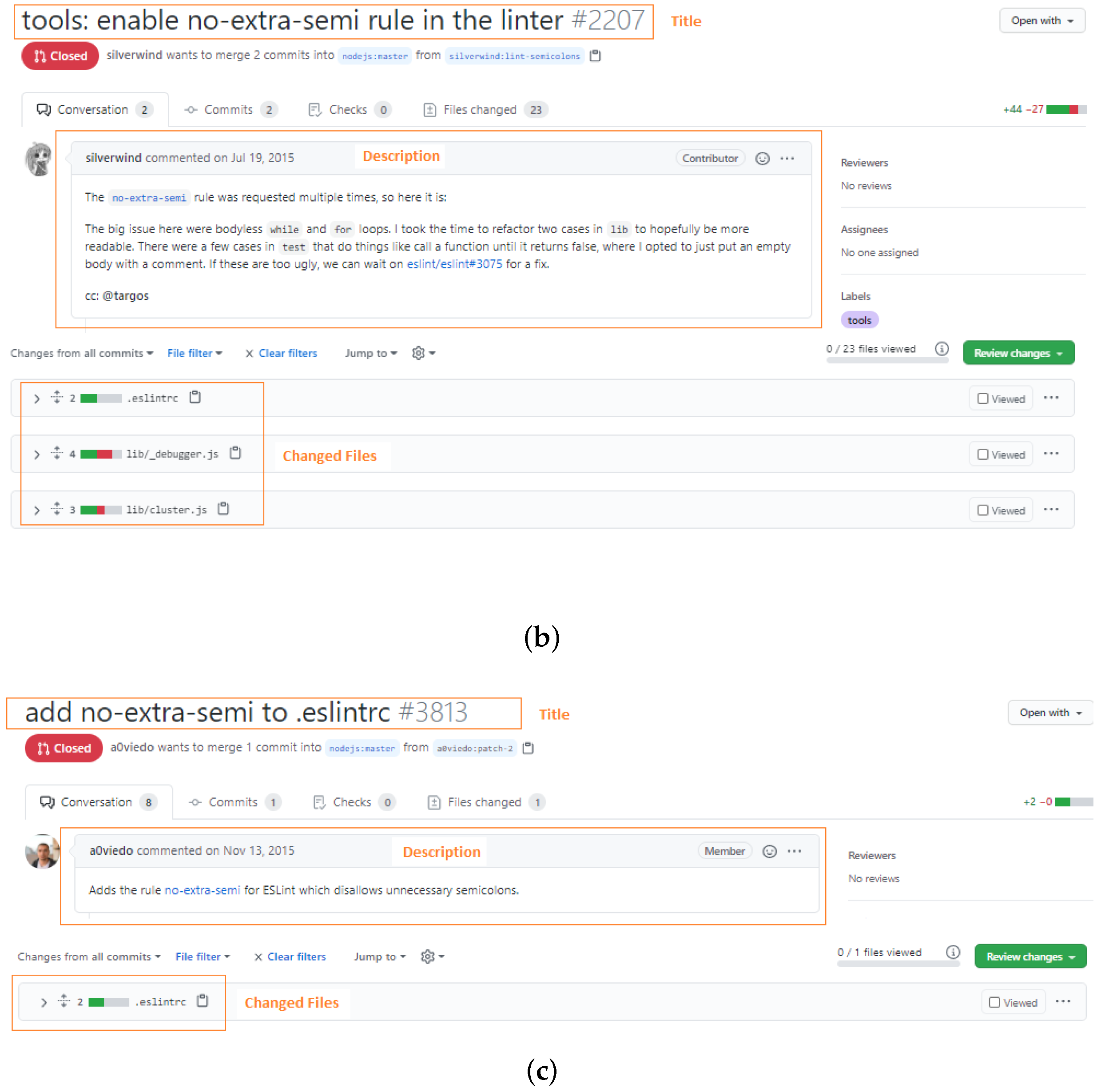
When contributors create a new PR, they should provide a title of the PR, a description that describes in details the contributions in the PR, and commits that contain the contributions [20]. Reviewers can detect similar PRs after examining these PR contents. Figure 2 shows three similar PRs located in nodejs/node (https://github.com/nodejs/node) repository on GitHub. All of them aimed to contribute a congruous feature by different contributors. From the figure, we can recognize that the three PRs are similar by the titles and descriptions of these PRs. Therefore, in this paper, we propose a machine learning technique that can automatically detect and group similar PRs before reviewing and assign them to the same reviewers.

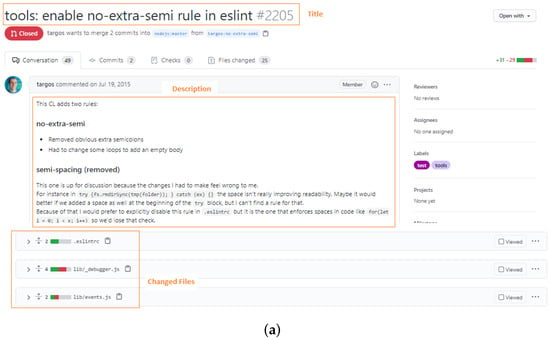
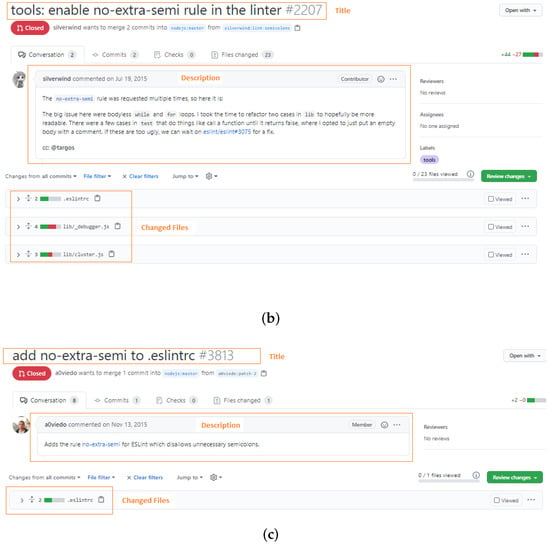
Figure 2. Three similar pull-requests of nodejs/node in GitHub. (a) https://github.com/nodejs/node/pull/2205, (b) https://github.com/nodejs/node/pull/2207, (c) https://github.com/nodejs/node/pull/3813.

3. Related Work

In this section, we present the most recent and relevant research works on this subject. We divide these research works into three categories: (i) detecting duplicate pull-requests, (ii) recommending code reviewers for pull-requests, (iii) detecting duplicate bug reports.

3.1. Detecting Duplicate Pull-Requests

Although few studies detect duplicate PRs in social coding platforms, these studies are classified into two branches [5]:

• Pull-request retrieval: retrieving a ranked list of PRs for a given new PR.
• Pull-request classification: assigning a label (duplicated or not duplicated) for a given new PR using a ML algorithm.

There are only two works In the first branch. Li et al. [9] suggest a method to detect duplicate PRs. For a new coming PR, their method computes the textual similarity between the new PR and the existing PRs. The textual information included in this textual similarity is the title and description of PRs. Based on this similarity, a ranked top-k PRs are retrieved for this new PR by average the title and description similarities. These top-k PRs may include duplicate PRs with the new PR. The experimental results showed that (55.3–71.0%) of the duplicate PRs are found when both title and description similarities are used in a combination.

In [21], Li et al. have proposed an approach to improve their previous work [9] to detect duplicate PRs in GitHub. Their approach combines textual similarity (title and description similarities) and change similarity (changed files and changed lines of code) to retrieve a top-k ranked list of PRs that are the most similar to the new coming PR. This list represents candidate duplicate PRs. The experimental results show that the combined similarities achieved best performance instead of using each similarity separately. The combined similarities help to identify 83% of the duplicate PRs compared with 54.8% using only textual similarity and 78.2% only change similarity.

The main concern in works of Li et al.( [9,21]) is how to adjust the similarity threshold or top-k items in order to retrieve only similar PRs and only those PRs. Moreover, the proposed approach in [21] depends on historical PRs to weigh four types of similarities. These historical PRs are not always available, especially, in small and medium repositories.

Similarly, also there are only two existing works in the second branch. Ren et al. [8] suggest an approach to improve Li et al.’s work [9] by considering other factors besides the textual information that can be extracted from both the title and description of PRs. These factors are five clues (change description, patch content, changed files list, changed lines of code, reference to issue tracker) with nine features. Their approach assigns a label (duplicate or not duplicate) to new coming PR instead of retrieving a ranked list of PRs. First, they manually checked 45 pairs of duplicate PRs to identify these features that help to find that a pair of PRs might be duplicated. Secondly, they measure these features. Finally, a machine learning algorithm (called AdaBoost [22]) is used to decide whether a pair of PRs are duplicate using these features set. The experimental results showed that Ren et al.’s work outperformed Li et al.’s work by (16–21%) in terms of the Recall metric.

Wang et al. [5] proposed an approach to improve the work of Ren et al. by considering the creation time of PRs in combination with the nine features identified by Ren et al. They assume that when the creation times of two PRs are close to each other, they are most likely to be duplicated. Firstly, they extract ten features from the training dataset used by Ren et al. The values of these features are used to train the AdaBoost classifier. Finally, for new coming PR, the classifier decides whether this new PR duplicate with other existing one. The experiments showed that Wang et al. improve the performance of Ren et al.’s work by 14.36% and 11.93% in terms of F1-score metric.

The common concern among the second branch approaches is that they detect duplicate PRs in pairs (i.e., detecting the top-1 PR that is the most similar one to the incoming PR). However, similar PRs (including duplicate PRs) can be exist as groups. Even if we set the similarity threshold lower, we will encounter the problem how to aggregate and weigh nine features as authors stated "Since it is not obvious how to aggregate and weigh the features, we use machine learning to train a model." [8].

3.2. Detecting Duplicate Bug Reports

In the literature, researchers proposed different approaches to detect duplicate bug reports. In [23], Runeson et al. proposed an approach to detect duplicate bug reports using natural language processing (NLP). The results show that their approach can detect 2/3 of duplicate bug reports using NLP techniques. In [24], Wang et al. proposed to combine natural language information and execution information of new-arrive bug report. Their approach compares the natural language information and execution information for new incoming bug report with those existing reports. Then, a list of suggested duplicate reports are returned to examine by a reviewer. The evaluation show that about (67–93%) of duplicate bug reports are detected compared to (43–72%) using natural language information alone. In [25], Sun et al. proposed a function (called retrieval function) to measure the similarity between two bug reports. This similarity includes textual similarity and non-textual similarity such as, version, component, etc. Recently in [26], He et al. have proposed an approach to detect duplicate reports in pair using convolutional neural network (CNN). They proposed to build a single representation for each pair of bug reports through dual-channel matrix. This matrix is fed to CNN model to find semantic relationship between bug reports. Then, their approach decide whether a pair of bug reports are duplicate or not based on the association features. The results show that their approach achieves high accuracy observing a range of [94.29–96.85%].

3.3. Recommending Code Reviewers for PRs

For improving the quality of code reviewing in social coding (e.g., GitHub), many techniques are proposed to recommend relevant reviewers for opened PRs. In [27], Lipcak et al. make a large-scale study on these techniques and structure them into four categories based on the features and algorithms that they use: (1) heuristic-based techniques, (2) social network-based techniques, (3) machine learning-based techniques, and (4) hybrid techniques. All these techniques do not cluster similar PRs together and do not assign PRs as clusters to the reviewer but they assign each PR individually to reviewers. These techniques are as follows:

3.3.1. Heuristic-Based Techniques

The techniques of this category rely on historical data and heuristics to recommend proper reviewers for opened PRs. In [28], Balachandran proposed a recommendation technique called ReviewBot. This technique is based on the assumption that the reviewer who in the past reviewed the same lines of code changes in the emerging PR should review this emerging PR. In [29], Thongtanunam et al. proposed a recommender technique called RevFinder based on the similarity between files path of previously PR and files of emerging PR. In [30], Xia et al. proposed a technique called TIE to improve the RevFinder technique by combining textual content of code review (PR) and similarity of file paths. CHREV [31] and WRC [32] are two recommender techniques based on the reviewers’ expertise (past reviewing). COREECT [33] is another heuristic recommender. The idea behind this recommender is that if a previous PR employed a similar technology or library to the emerging PR, the reviewer of this previous PR should review the emerging one. Recently, Chueshev et al. [34] have proposed an approach to expand the number of reviewers from appropriate contributors. For a given new PR, their approach finds relevant reviewers based on past reviews and suggests new reviewers whose development history similar to found reviewers.

3.3.2. Social Network-Based Techniques

The techniques in this category consider the social network between contributors as an important factor to suggest suitable reviewer for new PR. Yu et al. in [10,35] used a type of social network called Comment Network (CN). This network is built only among contributors and based on the contributors’ comments on PRs. The idea behind using this type of network is the relevant reviewer can be identified from the number of comments he has posted. A reviewer who has common interests to the originator of new PR is a relevant candidate to the new PR. In [7], Liao et al. proposed a recommender technique by building a social network consisting of collaborators and PRs (called collaborator-PR network).

3.3.3. Machine Learning-Based Techniques

Machine learning-based techniques refer to the use of ML algorithms to recommend proper reviewers by building a learning model based on the training dataset [36,37,38,39,40,41]. There is one typical approach in this category proposed by Jeong et al. [42]. This approach uses a Bayesian network classifier and processes a set of patch features (e.g., patch content and patch meta-data) to predict suitable reviewers and accept patches (PRs).

3.3.4. Hybrid Techniques

Each recommender system in this category uses a different combination of algorithms. These systems include the following work: [10,12,43,44]. For example, Xia et al. [12] proposed a recommender system that combines neighborhood methods and latent factor models to capture implicit relations among contributors in CN.

4. The Proposed Approach

In this section, we present the proposed approach. In the beginning, we provide a holistic view of the approach. Then, we detail the approach steps in the coming subsections.

4.1. Holistic View of the Proposed Approach

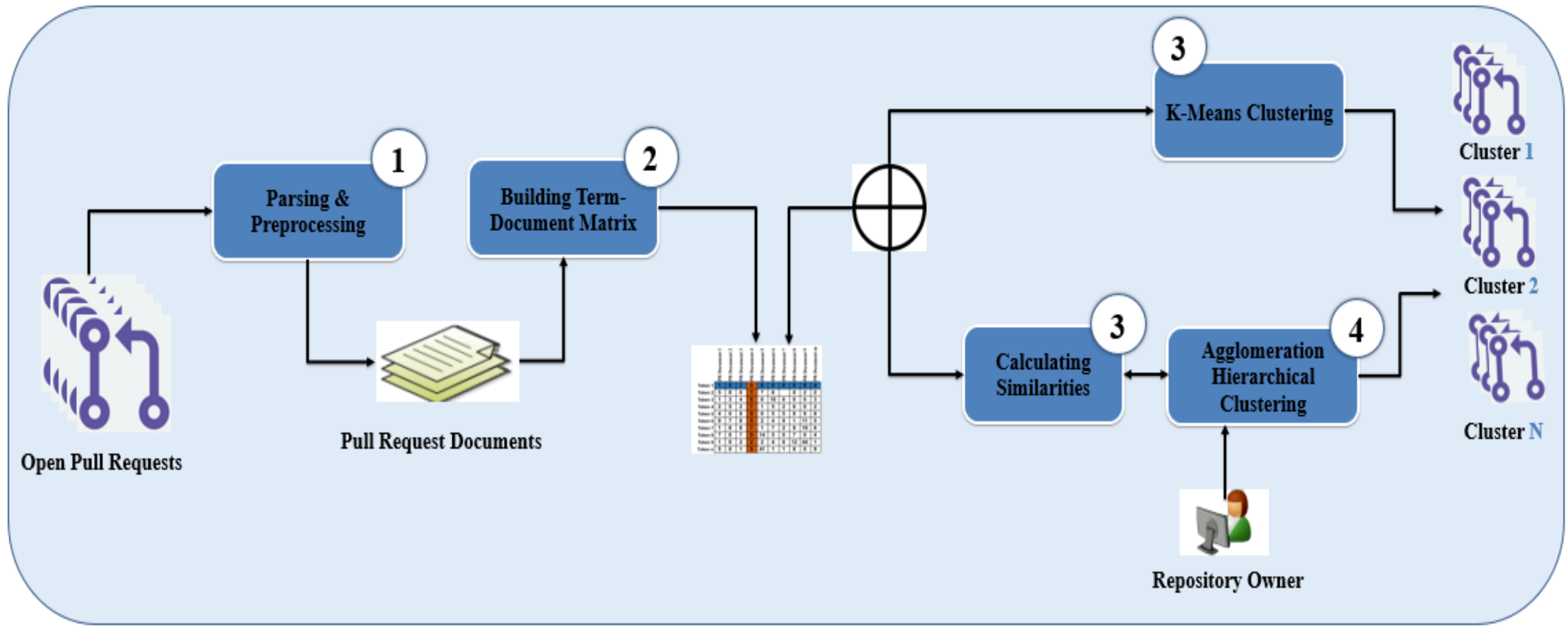
Figure 3 shows a holistic view of the proposed approach. As shown, the approach takes, as input, open PRs and follows four main steps to produce clusters of similar PRs, as output. In the first step, we extract and process PRs information. For each PR, we extract the title, description, and changed file(s). In the second step, PRs and its information is transformed into multi-dimensional vectors. In the third step, the similar PRs are grouped using only one clustering algorithm, either the k-mean clustering algorithm or agglomeration hierarchical clustering (AHC) algorithm. The proposed approach takes into account the number of PRs against the number of reviewers (NRs) in the repository under consideration to decide which clustering algorithm should be employed. In the case of NRs is less than or equal to the number of PRs, the K-means clustering algorithm is used with K equal to NRs, otherwise, the AHC algorithm is used. If the AHC is adopted, we compute textual similarity between PRs vectors using cosine similarity. The proposed approach allows to repository manager to control the number of identified clusters based on reasons in their mind (e.g., number of available reviewing teams). This is achieved by calibrating a distance threshold that specifies the maximum distance required to identify the recommended number of clusters by the manager. If we decrease the threshold value, more clusters will be result and vice versa.

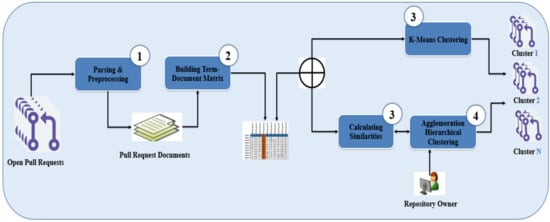
Figure 3. A holistic view of the proposed approach.

The rationale behind using k-means when NRs are less than or equal to the number of PRs is to form clusters of similar PRs instead of creating random clusters where, in this case, for sure each reviewer will receive more than one PR (many-to-one relation). In the literature, many different machine learning algorithms are addressing the clustering task but we need an algorithm that aware predefined number of clusters. Therefore, we adopt K-means such that we can adjust the k value as NRs. In the case of NRs greater than the number of PRs, it is impossible to use k-means clustering because the number of clusters (NRs) will be greater than the number of instances (PRs). We investigated the results of different clustering algorithms without a predefined number of clusters. We noticed that the best results obtained using AHC, therefore, we adopted it.

4.2. Parsing and Preprocessing Pull-Requests

Each PR in the GitHub project must have a title, description, and list of changed files. In this step, we parse open PRs of a given repository to extract these three pieces of information using GitHub GraphQL API (https://docs.github.com/en/graphql/overview/about-the-graphql-api). This information includes implicit useful information about PRs objectives and context. The description may include a code snippet to exactly refer to and detail the buggy code. Figure 2 shows three similar PRs with similar titles and descriptions. Furthermore, each PR provides a list of changed files where a developer made their contribution or change. We consider that if two or more PRs share the same file paths, they have a high chance to be related and work on the same functionality or tackle the same issue. For example, Figure 2 shows three PRs changed the file eslintrc.

The standard preprocessing tasks in natural language processing (NLP) are applied to manipulate the extracted information from each PR (title, description and changed files list). These tasks are [23,45]: removing punctuation marks and special characters, tokenization, stemming, and stop words removal. In the first task, we remove numbers, all punctuation marks, brackets, parenthesis, and other special characters. An appropriate regular expression has been used to perform such a cleaning task. In the second task, we convert textual sentences into stream of tokens. We applied here different tokenization strategies. The text of title and description is split into many tokens while the path of each changed file is treat a single token. This helps to find similarity between changed file paths.

Tokens are written in different grammatical forms. Therefore, in task three, we convert each token into ground form called stem or root. This is achieved by help of Porter algorithm [46]. During this task, the affixes in each token are removed and remain only the stem of the token (“helps” to “help”, “fixed” to “fix”, “was” to “be”). Finally, stop words (like, the, that, when, etc.) in PRs information are removed. Such words do not carry any useful information specific to each PR, and thus not help to compute similarity among them. This is because that they have similar occurrences in PRs text and most of these words are conjunctions articles and pronouns. We use NLTK’s list (http://www.nltk.org/) that includes most of stop words in English language to perform this final preprocessing task.

4.3. Building Term-Document Matrix

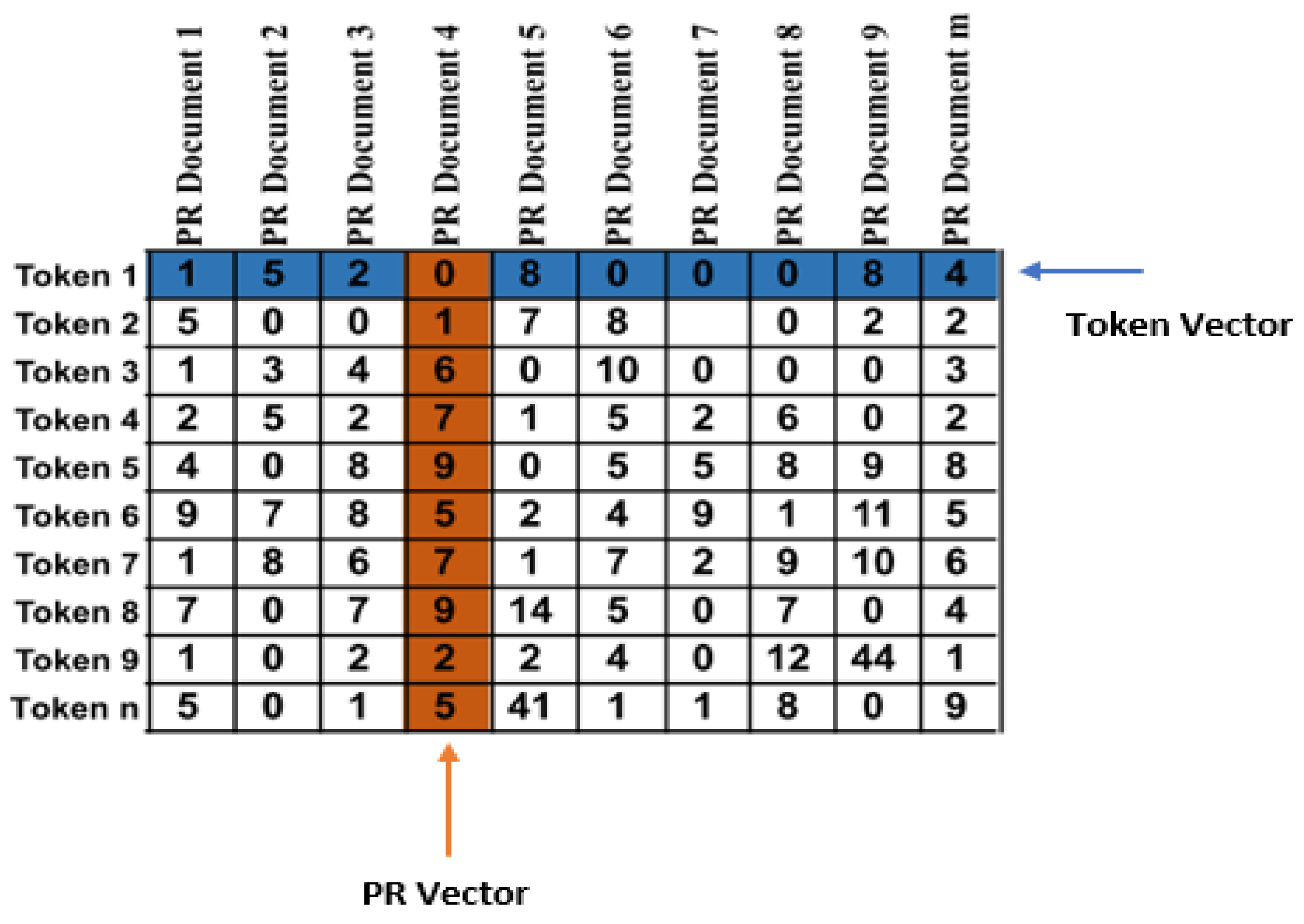
In this step, PRs and its information is transformed into multi-dimensional vectors such that each dimension represent a token in a corpus formed from all extracted PRs information while vector correspond to a PR from the corpus. We convert this corpus of PRs into a 2D matrix by counting token occurrences in documents. This matrix is well-known as a term-document matrix. Figure 4 is an example of a term-document matrix. Then, we apply the well-known weighting technique called Term Frequency Inverse Document Frequency (TF-IDF) [47] to produce TF-IDF matrix. This weighting technique gives importance to each token in a PR document or vector. Tokens appear frequently in a document but not frequently within-corpus take a higher weight as these tokens better represent the document content. For example, in Figure 2, the tokens “no-extra-semi” appear frequently in three PRs while they disappear in other PRs so these tokens are assumed to receive a higher TF-IDF weight.

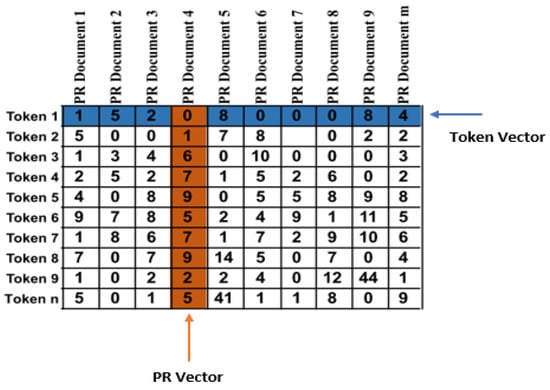
Figure 4. Term-document matrix.

4.4. Calculating Similarities among Pull-Requests

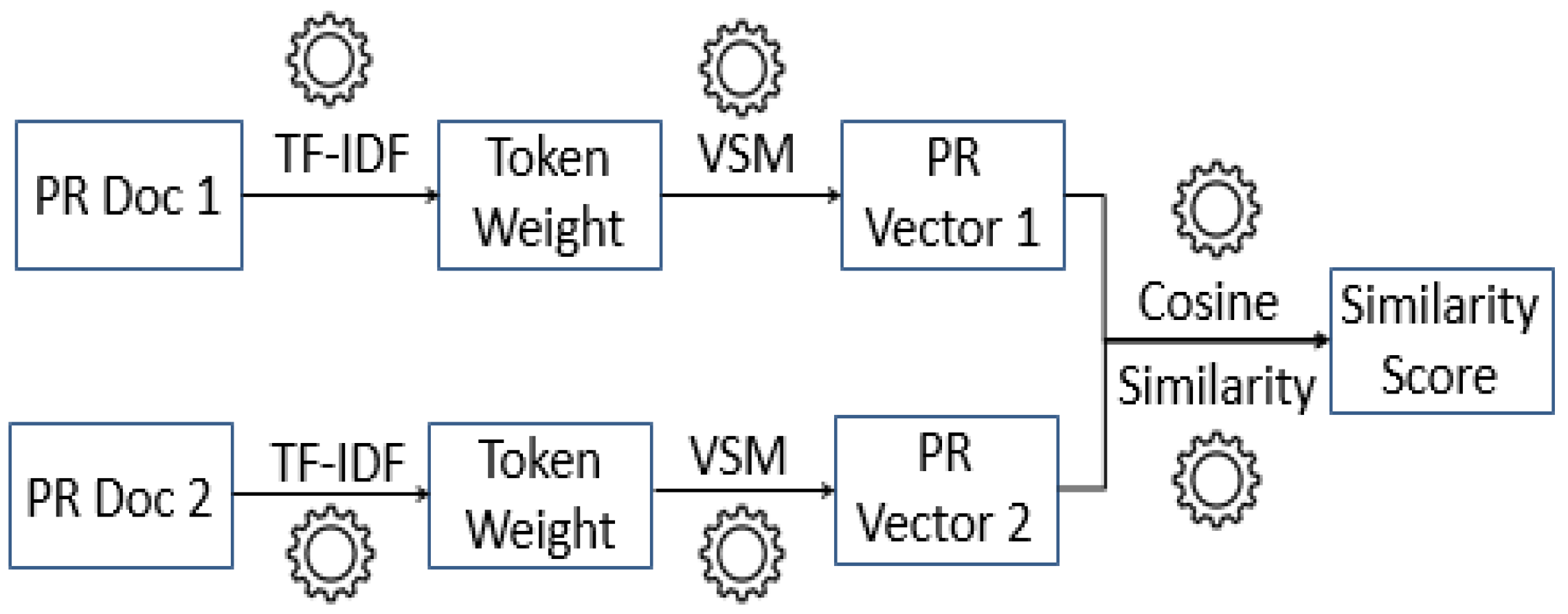
In this step, we calculate textual similarities among open PRs to help AHC algorithm to cluster similar PRs into groups. To do so, we apply Vector Space Model (VSM) to compute the similarity between two PR documents. VSM is a standard technique in Information Retrieval (IR) field and NLP. It has been proved to perform textual similarity task on software artifacts [48,49]. Finally, we use cosine similarity to measure the similarity between each PR document and other PR documents (see Figure 5).

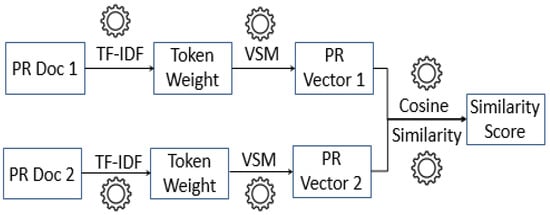
Figure 5. Standard steps to compute similarity using VSM [8].

4.5. Clustering-Based Agglomeration Hierarchical Algorithm

As mentioned earlier, when NRs are greater than the number of PRs, the AHC algorithm is applied to find clusters of similar PRs. The conventional application of AHC involves starting from singleton clusters so that each cluster consists of only one object. Then, recursively each pair of clusters with minimal distance is merged. Eventually, all clusters are merged to constitute a large cluster. Such successive merging forms a tree-like presentation called dendrogram. This hierarchy is cut based on some criterion to result in desired sub-clusters. In this step, we adapt AHC to support our goal into two phases.

4.5.1. Building Dendrogram Tree

AHC algorithm builds a structure of nested clusters. This structure is called a dendrogram. In this phase of AHC, we build a dendrogram tree from a forest of singleton clusters. Each PR vector with TF-IDF weights represents a singleton cluster. To do so, the Algorithm 1 is proposed. The algorithm takes, as input, this forest of PR vectors and produces, as output, a dendrogram tree. The algorithm relies on a series of binary merging. In each iteration, a pair of clusters ‘v’ and ‘t’ with a higher cosine similarity score are merged into a single new cluster ‘z’. Then, this pair is removed from the forest and the new cluster ‘z’ is added to the forest. This process stops when only one cluster remains in the forest. This cluster becomes the root and represents the dendrogram.

Algorithm 1 BuildingDendrogramTree

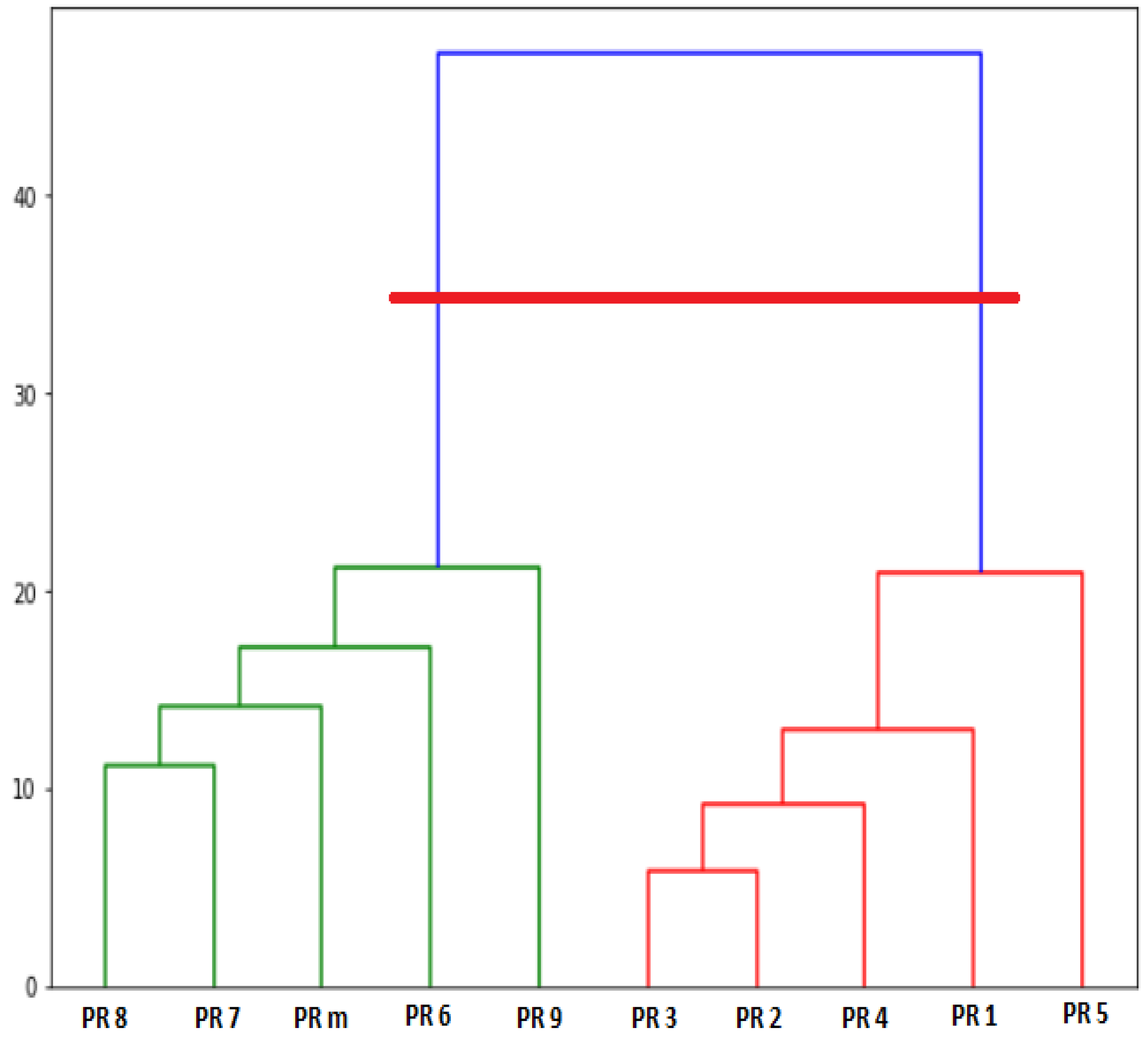
Figure 6 shows an example of a dendrogram tree. Y-axis represents distance scale (cosine similarity) while X-axis represents PR vectors. As shown, the initial forest which is individual PR vectors is at the lowest level. At the highest level, all PR vectors belong to the same cluster. The internal nodes represent new clusters resulting by merging the clusters that appear as their children in the tree. The vertical height in the dendrogram between PR vectors or between merged PR vectors shows the cosine similarity.

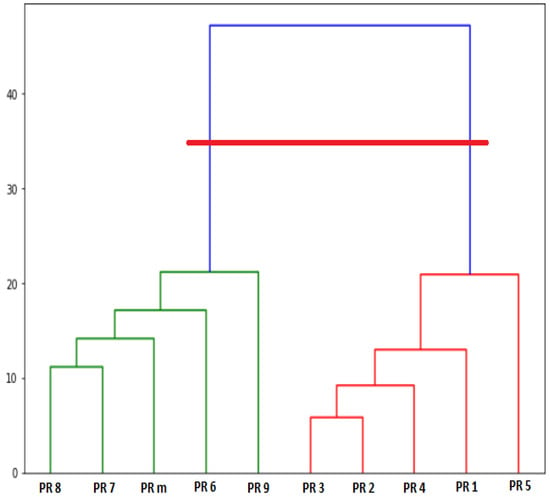
Figure 6. An example of dendrogram tree.

4.5.2. Identifying Candidate PR Clusters

In this second phase of AHC, we split the dendrogram tree based on a distance threshold fed by the repository owner. This distance threshold is the same as acceptable cosine similarity among PRs clusters. This allows identifying the number of PR clusters depending on the splitting point. When this point moves from top to down, the number of identified clusters increases and vice versa. Therefore, the splitting point is controlled by the repository owner as it adjusts the distance threshold. We propose Algorithm 2 based on a Depth-First Search (DFS) algorithm to split the dendrogram tree into a set of candidate PR clusters. The algorithm takes two inputs: the dendrogram (dendgr) tree and the Distance Threshold (DT). The main idea behind this algorithm is to compute the cosine similarity between the left and right nodes (clusters) of a parent starting from the root. Each node (cluster of PRs) is treated as a single vector. If the similarity value less than the DT, the algorithm goes down further to the next immediate sons. Otherwise, the parent node is identified as a cluster, added to an accumulator (prClusters) and the algorithm goes to the next node in the stack (pile). As the traversal proceeds, the PR clusters are identified.

In Figure 6, the horizontal line is the DT value. In case of the DT value is too small, the algorithm returns all PRs as singleton clusters. In case of the DT value is too large, the algorithm returns a single cluster including all PRs. Figure 6 shows an example to picture out how the Algorithm 2 driven by DT identifies PR cluster. The DT line passes to vertical lines, therefore, the number of identified clusters is two: a cluster of {PR8, PR7, PRm, PR6, PR9} and a cluster of {PR3, PR2, PR4, PR1, PR5}.

4.6. Clustering-Based K-Means Algorithm

In the case where the Number of Reviewers (NRs) is less than the number of open PRs, we use the K-means clustering algorithm in step 3. K-means algorithm is a simple and widely used clustering technique. It divides a space of objects into K non-overlap partitions or clusters where K is a predefined number of clusters determined by the user. Each cluster has a centroid (center) and each member object in the cluster has the minimum distance to the centroid and far from other centroids in other clusters. The standard K-means algorithm uses Euclidean distance to compute the distance between each object and the centroid [50].

Algorithm 2 Identifying PR Clusters

We propose Algorithm 3, that employs the standard application of the K-means algorithm to support our goal in this step. The algorithm takes two inputs: TF-IDF matrix of PRs vectors and NRs which represents the K value. As output, the algorithm produces K of PRs clusters (K-Clusters). The algorithm starts by randomly selecting K of PRs vectors as centroids of the K cluster. Then, each PR vector is assigned to a cluster with a minimum distance to its centroid. The tokens of each PR vector are considered as features to compute Euclidean distance between each PR vector and centroid [51]. Then, in each cluster, the mean of clustered PR vectors are computed and used as a new centroid. Next, PR vectors are reassigned in clusters, and centroids are recalculated in an iterative process. Finally, the algorithm stops when no change occurs on K-clusters membership.

Algorithm 3 Identifying K PR-Clusters

5. Experimental Results and Evaluation

In this section, we validate our proposed approach. Firstly, this validation task starts by suggesting Research Questions (RQs) with their evaluation procedures to demonstrate the effectiveness and integrity of the proposed approach. Next, we show case studies that have been used to apply the proposed approach. Then, we evaluate the experimental results and answer the research questions. Finally, we list the threats that may decrease the proposed approach effectiveness.

5.1. Investigation Research Questions and Evaluation Procedure

We derive three RQs from the literature review and at the same time to reflect the importance of our features to discover similar PRs in groups. These RQs are as follows:

-

RQ1: To what extent the proposed approach does identify relevant PRs clusters?

-

RQ2: How much efforts could the proposed approach save for reviewers?

-

RQ3: To what extent the proposed is effective when it is compared to the most recent and relevant works in the subject?

We address the first research question (RQ1) by considering a measure for the relevancy of the PRs clusters. The relevancy here means that each PR in a cluster is related and textually similar to other PRs in the same cluster. For that, we adopt two widely used measures in Information Retrieval (IR) discipline. These measures are: Precision and Recall [52]. Both metrics have values in a range between 0 and 1. The ideal value for Precision and Recall is 1. For each identified PRs cluster, we adopted the following protocol to address the RQ1:

-

We find a match between an identified cluster (i.e., their PRs) with all already existed actual PRs clusters of a given repository of interest. Suppose that Z is an identified cluster. The cluster that maximizes the matching with Z cluster in terms of PRs is called actual cluster. Such actual clusters (ACs) represent ground truth clusters for the evaluation purpose.

-

We use the following equations to compute the precision and recall values for each PR cluster against their actual cluster:

$$\begin{array}{c}\hfill Precision=\frac{|\{AC\_CLUSTER\}\bigcap \{IDE\_CLUSTER\}|}{|\{IDE\_CLUSTER\}|}\end{array}$$

(1)

$$\begin{array}{c}\hfill Recall=\frac{|\{AC\_CLUSTER\}\bigcap \{IDE\_CLUSTER\}|}{|\{AC\_CLUSTER\}|}\end{array}$$

(2)

In these equations, AC_CLUSTER and IDE_CLUSTER represent the PRs of actual and identified clusters, respectively. When the precision value of an identified cluster is equal to 1, this means that all PRs of that cluster are relevant but it may miss other relevant PRs. Furthermore, when the recall value of the obtained cluster is equal to 1, this means that the obtained cluster includes all relevant PRs supposed to have but with other irrelevant PRs. Therefore, to evaluate the relevancy of the identified PR clusters, these metrics should be used together to know to what extent the proposed approach identifies PRs clusters that include all relevant PRs and only those PRs.

The second research question focuses on the reviewers efforts spent in PRs reviewing. Therefore to address RQ2, we propose a metric to measure the saved reviewing effort (SRE) percent (see Equation (3)). In this metric, IDE_CLUSTER refers to each identified cluster of PRs. For example, suppose that an identified cluster consists of 10 PRs and this cluster is assigned to one reviewer. Then SRE value for this cluster is 90% (1-(1/10). However, if PRs of this cluster are assigned to different reviewers, of course, the SRE value will be degraded. This research question is in the course of reducing the lost efforts in reviewing PRs.

$$SRE=1-\frac{1}{|IDE\_CLUSTER|}\times 100\%$$

(3)

The third research question analyzes the efficiency of the proposed approach against the most recent and relevant works. These works take two branches: (I) pull-request retrieval [9,21], and (II) pull-request classification [5,8]. To address this research question, we perform qualitative analysis as we see in the subsequent subsection.

As a summary, the experimental results are mainly assessed by precision, recall, and SRE metrics. These metrics work in harmony with each other. precision and recall are used at the level of each identified cluster to evaluate the relevancy of each cluster of PRs while SRE metric is used at the project level to evaluate the percent of saved reviewing efforts by submitting similar PRs as a cluster to the same reviewer.

5.2. Dataset

To evaluate our approach, we should apply it on a ground truth dataset. Unfortunately, in this subject, there is no benchmark to support our evaluation task. Furthermore, there are no GitHub repositories with predefined similar PRs clusters in each repository. Therefore, we experiment the proposed approach on repositories with clusters of duplicate PRs as each duplicate cluster is also a similar cluster with 100% similarity.

We have applied the proposed approach on a public dataset of duplicate PRs, called DupPR (https://github.com/whystar/MSR2018-DupPR), established by Yu et al. [53]. The dataset includes 2323 pairs of duplicate PRs extracted from 26 popular software projects in GitHub. Moreover, these pairs were automatically identified and then manually verified. Most duplicate PRs in DupPR are in pairs. It is unrealistic to evaluate the effectiveness of the proposed approach on clusters of two duplicate PRs while similar PRs clusters consisting of three or more similar PRs. Therefore, our experimental evaluation process excludes binary clusters in DupPR and considers other duplicate clusters with three or more PRs as ground truth data in the evaluation of this study. After excluding the binary PRs, the number of repositories that are included in the evaluation process is 20 repositories while 6 repositories are excluded.

Table 1 shows statistical information about GitHub repositories used in our evaluation process. It includes, for each repository, the total number of duplicate PRs (#PRs), number, and size of clusters of duplicate PRs (#Clusters). As shown in this table, the number of repositories that are considered in the evaluation process is 20 repositories with 86 cluster. In our evaluation process, we refer to these clusters as actual clusters (ACs).

Table 1. Statistical information about the repositories of interest with their duplicate PRs.

Repository Name	#PRs	#Clusters (ACs)	NRs	Cluster Size
				Min	Max	Avg
angular/angular.js	31	8	15	3	5	3.75
facebook/react	15	4	2374	3	6	3.75
twbs/bootstrap	47	14	16	3	5	3.35
symfony/symfony	33	9	23	3	7	3.66
rails/rails	25	8	50	3	4	3.13
joomla/joomla-cms	19	6	24	3	4	3.17
ansible/ansible	18	6	63	3	3	3
nodejs/node	15	5	113	3	3	3
cocos2d/cocos2d-x	3	1	10	3	3	3
rust-lang/rust	9	3	179	3	3	3
ceph/ceph	9	3	213	3	3	3
zendframework/zf2	9	3	15	3	3	3
django/django	3	1	50	3	3	3
pydata/pandas	3	1	49	3	3	3
elastic/elasticsearch	6	2	1800	3	3	3
JuliaLang/julia	3	1	98	3	3	3
scikit-learn/scikit-learn	3	1	34	3	3	3
kubernetes/kubernetes	13	4	1208	3	4	3.25
docker/docker	7	2	56	3	4	3.5
symfony/symfony-docs	19	5	9	3	5	3.8

5.3. Results Analysis

To empirically answer our research questions, we apply the proposed approach on 20 GitHub repository shown in Table 1. Below, we answer each research question separately based on the obtained experimental results.

5.3.1. Identifying Relevant PRs Clusters (RQ1)

Using k-means clustering algorithm. As stated before, the K-means clustering algorithm is used when the number of reviewers (NRs) is less than the number of PRs (#PRs). Therefore, among existing repositories in Table 1, we select only the repositories that meet this constraint. Table 2 shows these selected repositories with the Precision and Recall values obtained by applying the K-means algorithm with K equal to NRs. We did not compute the Precision values for the repository with NRs less than the number of actual duplicate clusters (#AC). This is because that the number of identified clusters will be less than the number of actual clusters. Meaning that two or more of the actual clusters supposed to be identified are merged, and thus Precision values are degraded. Therefore, in this case, it is fair to exclude Precision values. In contrast, we did not compute the recall values for repositories with NRs greater than the number of actual duplicate clusters (#AC). This is because that one or more of the actual clusters supposed to be identified are split to identify the number of clusters equal to the number of reviewers. Meaning that recall values of these identified clusters are degraded. Therefore, in this case, it is fair to exclude Recall values. The results displayed in Table 2 shows that precision values for other repositories are high with an average in a range (73–98%).

Table 2. Precision and Recall values of the identified clusters using k-mean clustering when (NRs < #PRs).

Repository Name	#PRs	#AC	NRs	Precision				Recall
				Min	Max	Avg	StDev	Min	Max	Avg	StDev
angular/angular.js	31	8	15	0.50	1.0	0.91	0.18	$---$	$---$	$---$	$---$
twbs/bootstrap	47	14	16	0.22	1.0	0.73	0.29	$---$	$---$	$---$	$---$
symfony/symfony	33	9	23	0.50	1.0	0.93	0.16	$---$	$---$	$---$	$---$
symfony/symfony-docs	19	5	9	0.67	1.0	0.93	0.13	$---$	$---$	$---$	$---$

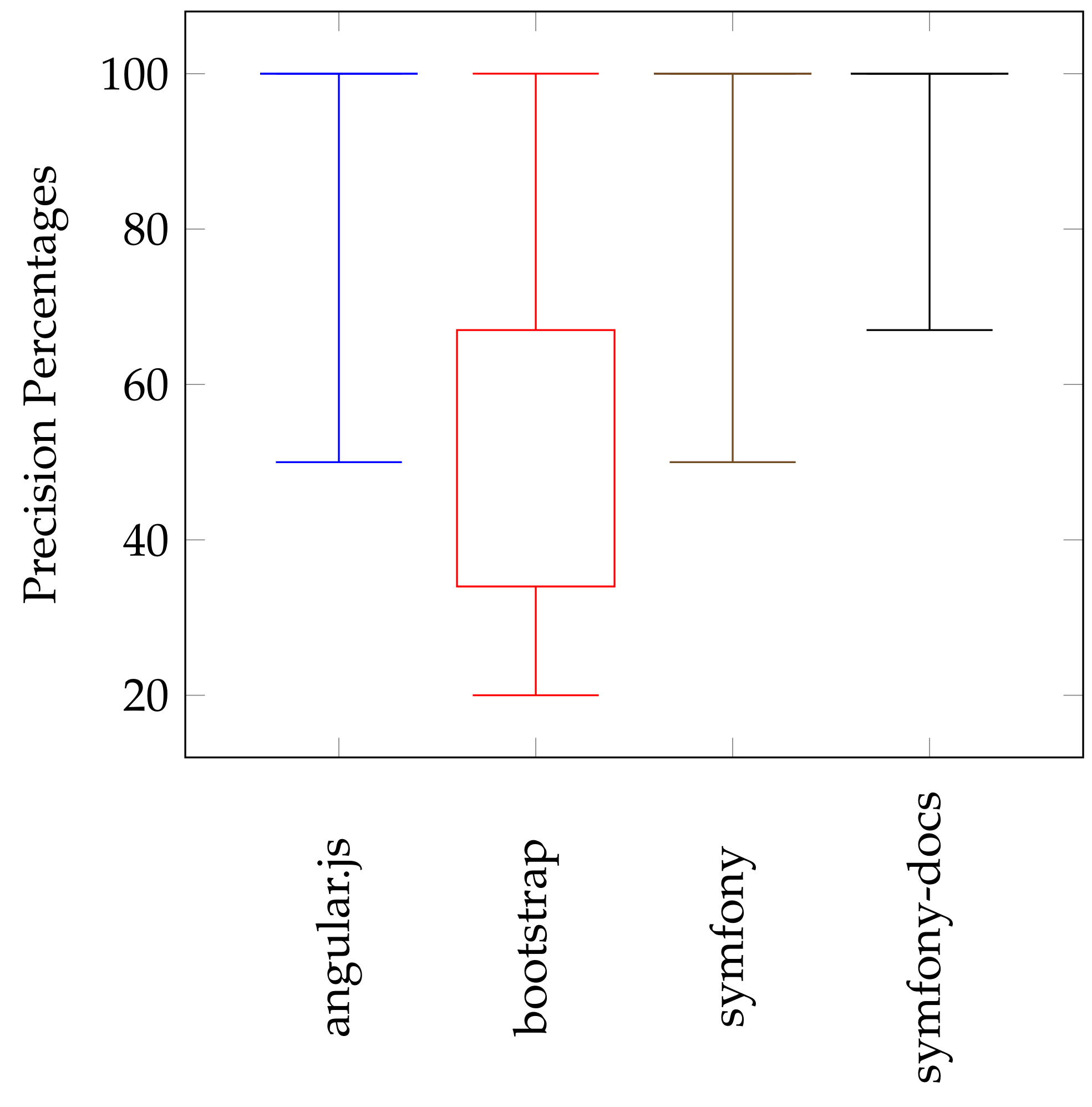
To easily understand the obtained results, we visualize the distribution of precision and recall values using a well-known statistical diagram called Boxplot. This diagram is built around a set of important values which we use to clarify the results: minimum, maximum, median, lower quartile (Q1), and upper quartile (Q3). Figure 7 shows the distribution of Precision (P) values of identified clusters using the K-means clustering algorithm. As shown, the distribution of these values confirms the results mentioned above. In angular.js repository, the minimum precision value is far from the box’s angular.js. In other words, more than 75% of precision values are equal to 100% (maximum = Q3 = median = Q1). For bootstrap repository, the maximum Precision value is far from the box’s bootstrap, and 50% of precision values in a range between 34% and 67%. This degradation in precision values due to that many PRs in the bootstrap repository with empty descriptions. For both symfony and joomla-cms repositories, minimum Precision values are far from the their boxes with tight boxes. Besides, more than 75% of precision values are equal to 100% (maximum = Q3 = median = Q1).

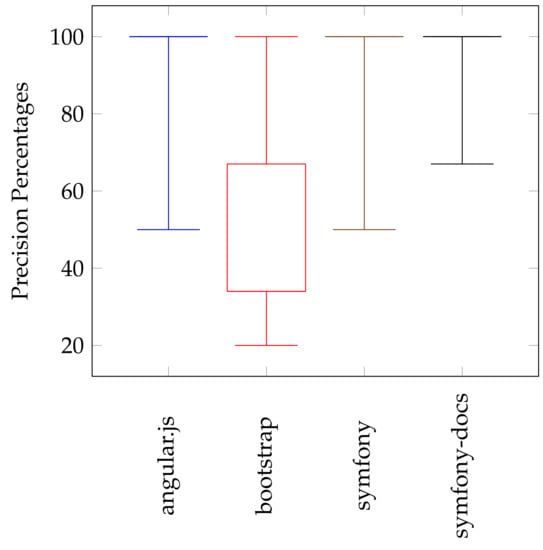
Figure 7. Precision values distribution of the identified clusters using K-means clustering algorithm.

In fact, to asses the effectiveness of the K-means algorithm for identifying clusters of similar PRs, both precision and recall values should be calculated of identified clusters. To do so, we assume that number of reviewers is equal to the number of actual clusters in all repositories under consideration. Of course, this is not the real case but it is necessary to evaluate the results of using the K-means algorithm in such identification process. Table 3 shows the results of the K-means algorithm with K value equal to the number of actual clusters. According to the results, Precision values are high with an average between 70% and 100%, and with a maximum value 100% in all repositories. Besides, the recall values in most of the repositories are high with an average between 68% and 100%, and with a maximum value 100% in all repositories. However, the average Recall value of clusters identified from twbs/bootstrap is low (52%) as many PRs in this repository with empty descriptions. We argue that this is the reason behind the degradation of the recall value.

Table 3. Precision and Recall values of identified clusters considering using k-means clustering when (k = #ACs).

Repository Name	#ACs	K	Precision				Recall
			Min	Max	Avg	StDev	Min	Max	Avg	StDev
angular/angular.js	8	8	0.60	1.0	0.92	0.14	0.40	1.0	0.88	0.22
facebook/react	4	4	1.0	1.0	1.0	0.0	1.0	1.0	1.0	0.0
twbs/bootstrap	14	14	0.22	1.0	0.70	0.29	0.20	1.0	0.52	0.24
symfony/symfony	9	9	0.38	1.0	0.87	0.22	0.33	1.0	0.68	0.27
symfony/symfony-docs	5	5	0.67	1.0	0.87	0.16	0.67	1.0	0.87	0.16
rails/rails	8	8	0.50	1.0	0.80	0.21	0.25	1.0	0.75	0.23
joomla/joomla-cms	6	6	0.50	1.0	0.78	0.22	0.33	1.0	0.78	0.24
ansible/ansible	6	6	0.67	1.0	0.89	0.15	0.67	1.0	0.89	0.15
nodejs/node	5	5	0.60	1.0	0.92	0.16	0.34	1.0	0.87	0.26
cocos2d/cocos2d-x	1	1	1.0	1.0	1.0	0.0	1.0	1.0	1.0	0.0
rust-lang/rust	3	3	1.0	1.0	1.0	0.0	1.0	1.0	1.0	0.0
ceph/ceph	3	3	1.0	1.0	1.0	0.0	1.0	1.0	1.0	0.0
zendframework/zf2	3	3	1.0	1.0	1.0	0.0	1.0	1.0	1.0	0.0
django/django	1	1	1.0	1.0	1.0	0.0	1.0	1.0	1.0	0.0
pydata/pandas	1	1	1.0	1.0	1.0	0.0	1.0	1.0	1.0	0.0
elastic/elasticsearch	2	2	1.0	1.0	1.0	0.0	1.0	1.0	1.0	0.0
JuliaLang/julia	1	1	1.0	1.0	1.0	0.0	1.0	1.0	1.0	0.0
scikit-learn/scikit-learn	1	1	1.0	1.0	1.0	0.0	1.0	1.0	1.0	0.0
kubernetes/kubernetes	4	4	1.0	1.0	1.0	0.0	1.0	1.0	1.0	0.0
docker/docker	2	2	1.0	1.0	1.0	0.0	1.0	1.0	1.0	0.0

Using AHC algorithm. As mentioned before, the AHC algorithm is used when the number of reviewers is greater than the number of PRs. Therefore, among existing repositories in Table 1, we select the repositories that meet this constraint to apply the AHC algorithm. Table 4 shows the precision and recall values obtained using the AHC algorithm. As shown, average Precision values take a high range between 70% and 100% except the average precision value for joomla/joomla-cms repository as it equals to 60%. This is because different vocabulary is used in the title and description of some PRs. Additionally, as shown in this table, recall values are high with an average between 85% and 100%. Besides, max precision and recall values in all repositories are equal to 100%. It is noteworthy that in case of the number of identified clusters is equal to the number of actual clusters, the AHC algorithm achieves 100% for both precision and recall (see facebook/react repository and others). We can also see that when the number of identified clusters is less than the number of actual clusters, recall values are equal to 100% in most repositories with high average precision Values. This is because one or more of the actual clusters that should be identified have merged during the identification process. Consequently, this increases the recall values at the expense of small degradation in the precision values.

Table 4. Precision and Recall values of the identified clusters using AHC when (NRs > #PRs).

Repository Name	#PRs	#ACs	#ICs	NRs	Precision				Recall
					Min	Max	Avg	StdDev	Min	Max	Avg	StdDev
facebook/react	15	4	4	2374	1.0	1.0	1.0	0.0	1.0	1.0	1.0	0.0
rails/rails	25	8	6	50	0.50	1.0	0.70	0.24	0.50	1.0	0.87	0.20
ansible/ansible	18	6	4	63	0.50	1.0	0.72	0.18	1.0	1.0	1.0	0.0
nodejs/node	15	5	4	113	0.50	1.0	0.88	0.21	1.0	1.0	1.0	0.0
joomla/joomla-cms	19	6	4	24	0.40	1.0	0.60	0.23	0.70	1.0	0.85	0.16
cocos2d/cocos2d-x	3	1	1	10	1.0	1.0	1.0	0.0	1.0	1.0	1.0	0.0
rust-lang/rust	9	3	3	179	1.0	1.0	1.0	0.0	1.0	1.0	1.0	0.0
ceph/ceph	9	3	3	213	1.0	1.0	1.0	0.0	1.0	1.0	1.0	0.0
zendframework/zf2	9	3	3	15	1.0	1.0	1.0	0.0	1.0	1.0	1.0	0.0
django/django	3	1	1	50	1.0	1.0	1.0	0.0	1.0	1.0	1.0	0.0
pydata/pandas	3	1	1	49	1.0	1.0	1.0	0.0	1.0	1.0	1.0	0.0
elastic/elasticsearch	6	2	2	1800	1.0	1.0	1.0	0.0	1.0	1.0	1.0	0.0
JuliaLang/julia	3	1	1	98	1.0	1.0	1.0	0.0	1.0	1.0	1.0	0.0
scikit-learn/scikit-learn	3	1	1	34	1.0	1.0	1.0	0.0	1.0	1.0	1.0	0.0
kubernetes/kubernetes	13	4	4	1208	1.0	1.0	1.0	0.0	1.0	1.0	1.0	0.0
docker/docker	7	2	2	56	1.0	1.0	1.0	0.0	1.0	1.0	1.0	0.0

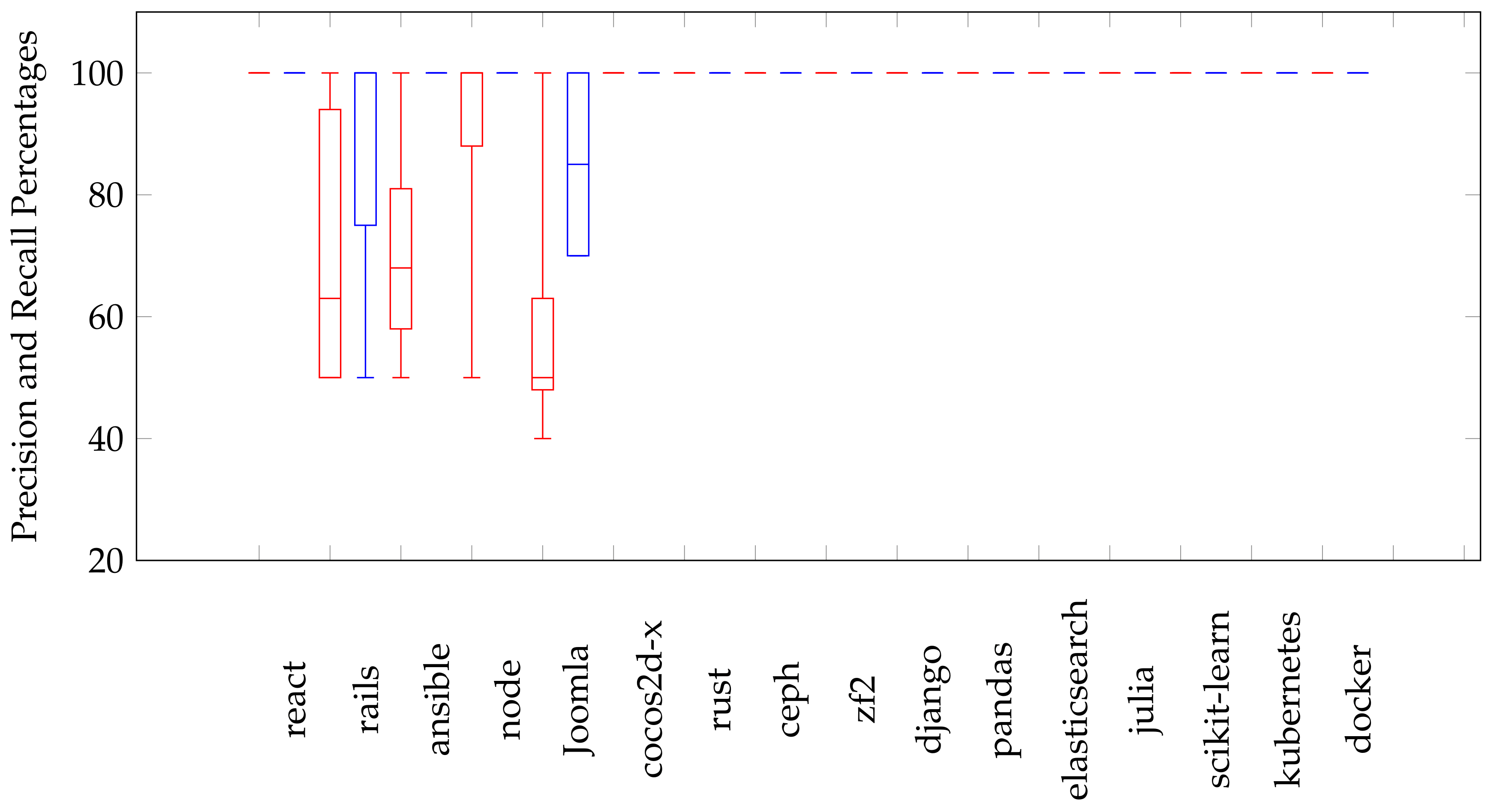
The Boxplots in Figure 8 visualize the distribution of precision and recall values of identified clusters using the AHC algorithm. In this figure, Precision and Recall values for each repository are displayed as pairs of red and blue boxes, repectively. Firstly, for the react repository, Boxplots for precision and recall values are identical singular points (i.e., minimum = Q1 = median = Q3 = maximum). These points are equal to 100% Precision and Recall because the number of identified clusters is equal to the number of actual clusters. For the rails repository, maximum precision value is near from the box’s rails, and all precision values are in a range of (50–100%) with minimum = Q1. Additionally, the minimum recall value is far from the box, and 75% of Recall values are in a range (75–100%) with (median = Q3 = maximum). For ansible repository, the maximum precision value is far from the box, and 50% of recall values are in a range between 58% and 81%. This mild degradation in precision is due to that identified clusters include PRs with a large number of changed files while the number of common changed’s ansible files among them is small. Recall values in ansible’s Boxplot are identical singular points and they are equal to 100% (i.e., minimum = Q1 = median = Q3 = maximum). For the node repository, the minimum Precision value is very far from the box’s node (considered as an outlier value), and 75% of precision values take a range (88–100%). Recall values are identical singular points and they are equal to 100% (i.e., minimum = Q1 = median = Q3 = maximum). For the Joomla repository, the maximum precision value is far from the box’s Joomla and 50% of precision values in a range (48–63%). As mentioned before, this degradation in precision values is due to that different vocabulary is used in the title and description of some PRs. All recall values take a range (70–100%) where (minimum = Q1 = 70%) and (Q3 = maximum = 100%). Finally, all other repositories are identical where their Boxplots are singular points and they are equal to 100% (i.e., minimum = Q1 = median = Q3 = maximum) for both precision and recall values.

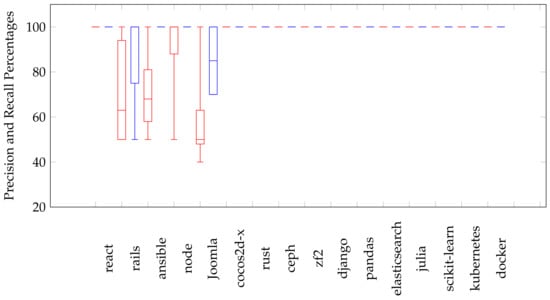
Figure 8. Precision and Recall values distribution of the identified clusters using AHC.

As a summary, to answer the first research question (RQ1), we can confidentially answer that the proposed approach is efficient to identify relevant clusters of similar PRs using the K-means algorithm and AHC algorithm. K-means algorithm is aware of the number of available reviewers while the AHC algorithm is unaware of this parameter but it considers similarity threshold as an alternative preference for repository owner. Both algorithms achieve high precision and recall values on average. This answer is based on the results displayed on Table 2, Table 3 and Table 4.

5.3.2. Saving Reviewing Efforts (RQ2)

The results displayed in Table 5 and Table 6 show the reviewing efforts could be saved by applying the K-means algorithm and AHC algorithm, respectively. These results are under column title SRE and calculated for the identified cluster that has the maximum size in each repository. It is noteworthy that SRE values depend on the size of identified clusters. When the size of these clusters increases, the SRE values increase, too. According to the results shown in Table 5, the K-means algorithm achieves a high range of SRE (67–91%). Furthermore, the results in Table 6 show that the AHC algorithm also achieves a high range of SRE (67–83%). The general observation regarding the reviewing efforts saved is satisfying in both algorithms. However, the range of SRE values achieved by K-means is better than the AHC algorithm. This is because SRE values are influenced by the size of identified clusters as the size of identified clusters using K-means is larger than the clusters identified by AHC algorithm.

Table 5. Statistical information of identified clusters using K-mean clustering with (NRs < #PRs).

Repository Name	#PRs	#ACs	#ICs	Cluster Size			SRE
				Min	Max	Avg
angular/angular.js	31	8	15	1	4	2.0	75%
twbs/bootstrap	47	14	16	1	11	2.9	91%
symfony/symfony	33	9	23	1	4	1.3	75%
symfony/symfony-docs	19	5	9	1	3	2.1	67%

Table 6. Statistical information of identified clusters using AHC with (NRs > #PRs).

Repository Name	#PRs	#ACs	#ICs	Cluster Size			SRE
				Min	Max	Avg
facebook/react	15	4	4	3	6	3.75	83%
rails/rails	25	8	6	3	4	3.6	75%
ansible/ansible	18	6	4	3	6	4.3	83%
nodejs/node	15	5	4	3	6	4.0	83%
joomla/joomla-cms	19	6	4	4	6	4.75	83%
cocos2d/cocos2d-x	3	1	1	3	3	3	67%
rust-lang/rust	9	3	3	3	3	3	67%
ceph/ceph	9	3	3	3	3	3	67%
zendframework/zf2	9	3	3	3	3	3	67%
django/django	3	1	1	3	3	3	67%
pydata/pandas	3	1	1	3	3	3	67%
elastic/elasticsearch	6	2	2	3	3	3	67%
JuliaLang/julia	3	1	1	3	3	3	67%
scikit-learn/scikit-learn	3	1	1	3	3	3	67%
kubernetes/kubernetes	13	4	4	3	4	3.25	75%
docker/docker	7	2	2	3	4	3.5	75%

As a summary, the answer to the research question (RQ2) is that the proposed approach is efficient in saving the reviewers’ efforts according to SRE measure. This answer is based on the experimental results shown in Table 5 and Table 6.

5.3.3. The Effectiveness of the Proposed Approach against the Existing Work (RQ3)

We organize existing works related to our proposal into two categories. The first category includes approaches that retrieve a ranked list of PRs for a given new PR [9,21] while the approaches of the second category assign a label (duplicated or not duplicated) for a given new PR using a ML algorithm [5,8]. The approaches of the first category struggle with the problem, on one hand, of how to adjust the threshold value such that these approaches only retrieve the duplicate or similar PRs and exclude others. On other hand, these approaches are applied to new PRs individually even though these new PRs are duplicated and submitted at the same time by different contributors, especially in large and popular repositories. Our proposal overcomes these problems by identifying similar and duplicate PRs as groups without the need for a threshold value. The main limitation of the second category’s approaches is the identification of duplicated PRs in pairs and thus these fail to detect the duplication in new PRs as groups. They label (duplicated or not duplicated) each new PR individually even though these PRs arrive simultaneously. Our proposal overcomes these approaches by identifying groups of similar PRs with three or more PRs.

Additionally, all the above-mentioned approaches rely on closed/merged PRs to detect if new PR is duplicated or not and ignore if new submitted group PRs are duplicated (open PRs). This causes to distribution a group of duplicated PRs to different reviewers in spite of all members of this group are duplicated. This limitation is overcome by our proposal through identifying a group of similar PRs in an open pool of PRs (new PRs).

5.4. Threats to Validity

The proposed approach is subjected to two following types of threats: internal and external threats.

5.4.1. Threats to Internal Validity

We identify the following issues as internal threats to the validity of our proposed approach:

-

Our research contribution in this article is to identify similar PRs clusters from a given GitHub repository. This contribution has been evaluated only using duplicate PRs clusters from different repositories. Indeed, in this subject, there are no benchmark or public case studies that provide clusters of similar PRs. However, we consider duplication as a special case of similarity (100% similarity).

-

Our identification process uses descriptive textual information to find similar PRs, so the proposed approach is sensitive to the vocabulary used to describe these PRs. Consequently, our proposal may succeed or fail depending on the vocabulary used. However, this threat is common among all works that use textual matching to find similarities between the artifacts of interest.

-

The proposed approach can be used only to identify similar PRs from open PRs.

5.4.2. Threats to External Validity

Regarding external validity, we have validated our proposed using only GitHub repositories. This could be a threat to generalize our approach to other social coding repositories. However, this set of considered repositories is popular and covers different programming languages, and thus it is enough to validate the proposed approach.

6. Conclusions and Future Work

In this article, we propose An automatic approach to cluster open similar PRs together of a given repository using two supervised and unsupervised ML algorithms considering the number of reviewers or repository’s owner preferences. These algorithms are K-means clustering and agglomeration hierarchical clustering. Such clustering helps to submit similar pull-requests to the same reviewer and thus saves reviewing time and effort. We first extract textual information from PRs to link similar PRs together. Then, the extracted information is used to find similarities among PRs. Finally, the textual similarity helps ML algorithms to group similar PRs together. To evaluate our proposed approach, we have run it on twenty popular repositories from a public dataset. The experimental results show that the proposed approach is efficient in identifying relevant clusters. K-Means algorithm achieves 94% and 91% average precision and recall values overall considered repositories, respectively, while agglomeration hierarchical clustering performs 93% and 98% average precision and recall values overall considered repositories, respectively. Moreover, the experimental results show that the proposed approach saves reviewing time and effort on average between (67% and 91%) by K-Means algorithm and between (67% and 83%) by agglomeration hierarchical clustering algorithm.

The proposed approach has been applied only on GitHub repositories but, to generalize the results, it should be applied on different repositories from different social coding platforms such as bitbucket and others. Therefore, in the future, we plan to run the proposed approach on a larger number of repositories from different social coding platforms. Furthermore, we will investigate other pull-request information or features which could improve the identification process, and therefore the experimental results. Additionally, we intend to investigate the results of using other NLP techniques such as word2vec and doc2vec, etc.