A Missing Data Compensation Method Using LSTM Estimates and Weights in AMI System
Abstract
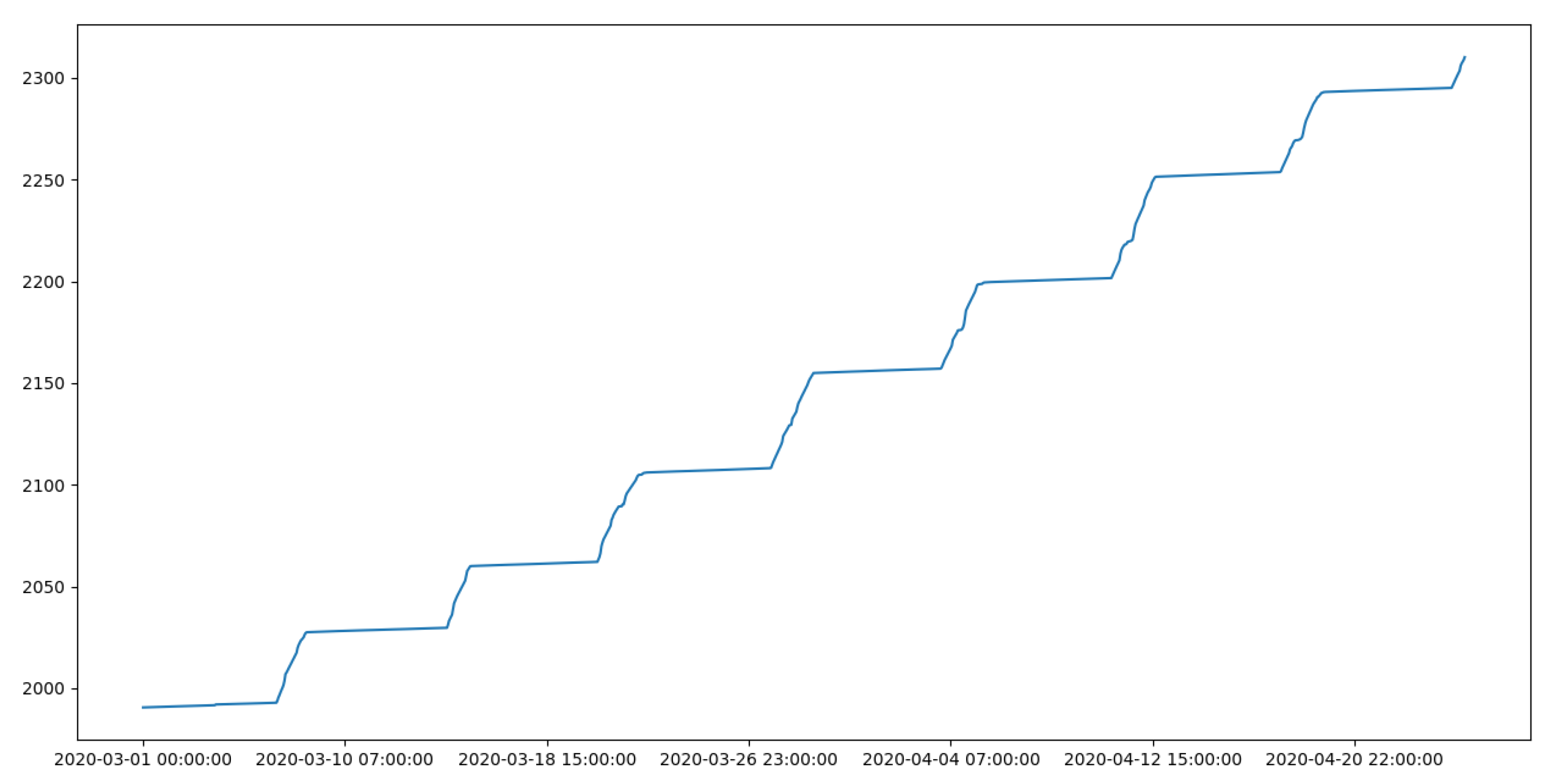
:1. Introduction
2. Related Work
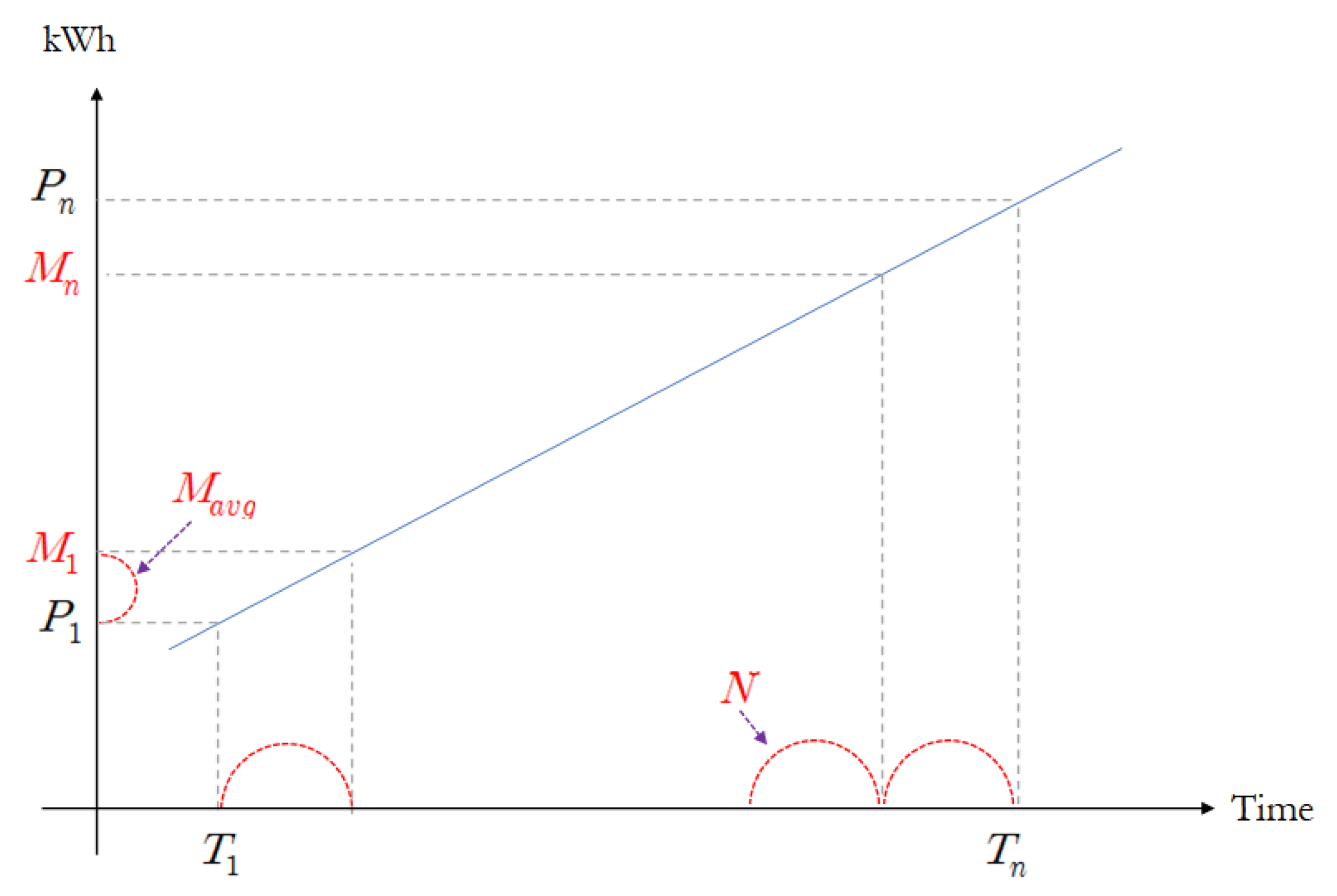
2.1. Linear Interpolation Method
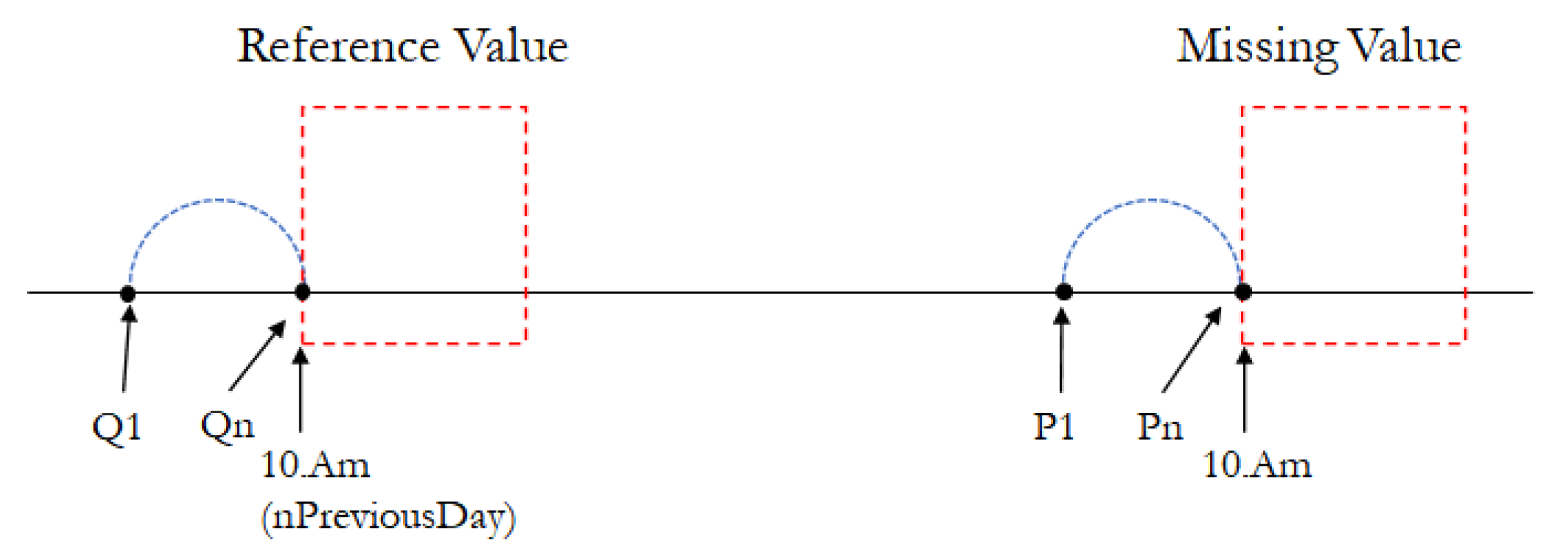
2.2. Similar-Past-Situation Substitution Method
2.3. ARIMA Estimation-Based Compensation Method
2.4. LSTM Estimation-Based Compensation Method
3. Comparative Experiments on Missing Data Compensation Methods
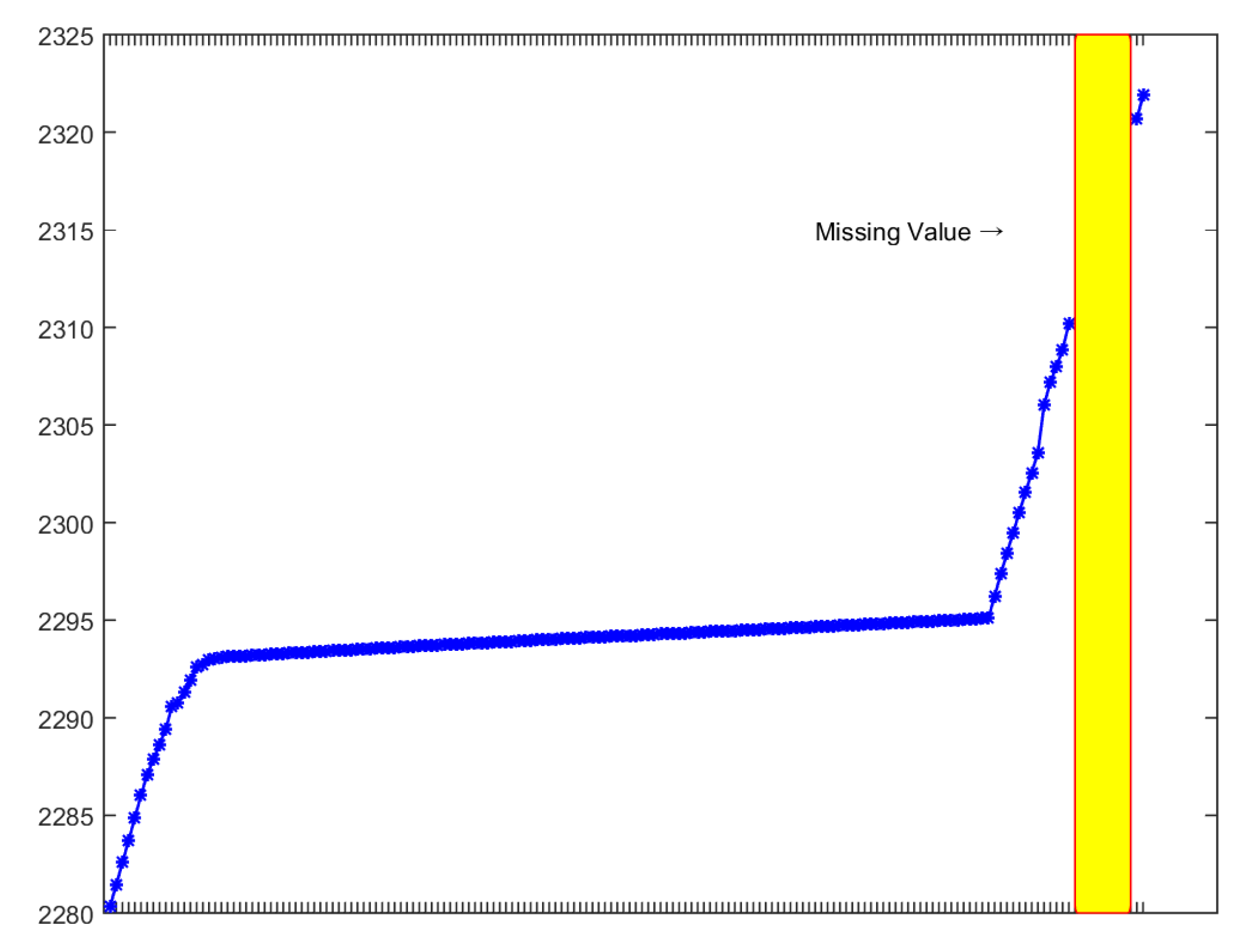
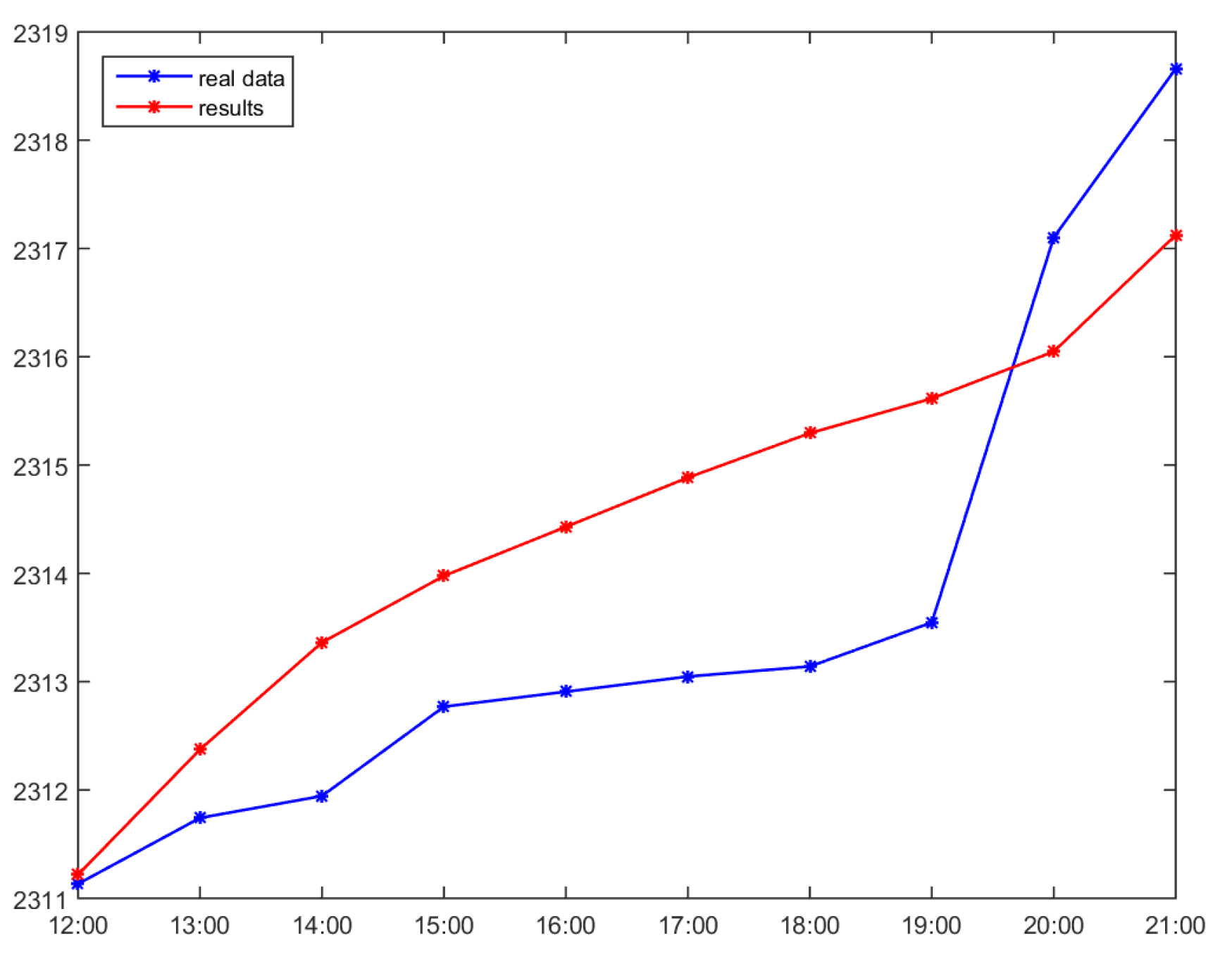
3.1. Linear Interpolation
3.2. Similar-Past-Situation Substitution
3.3. ARIMA Estimation-Based Compensation Method
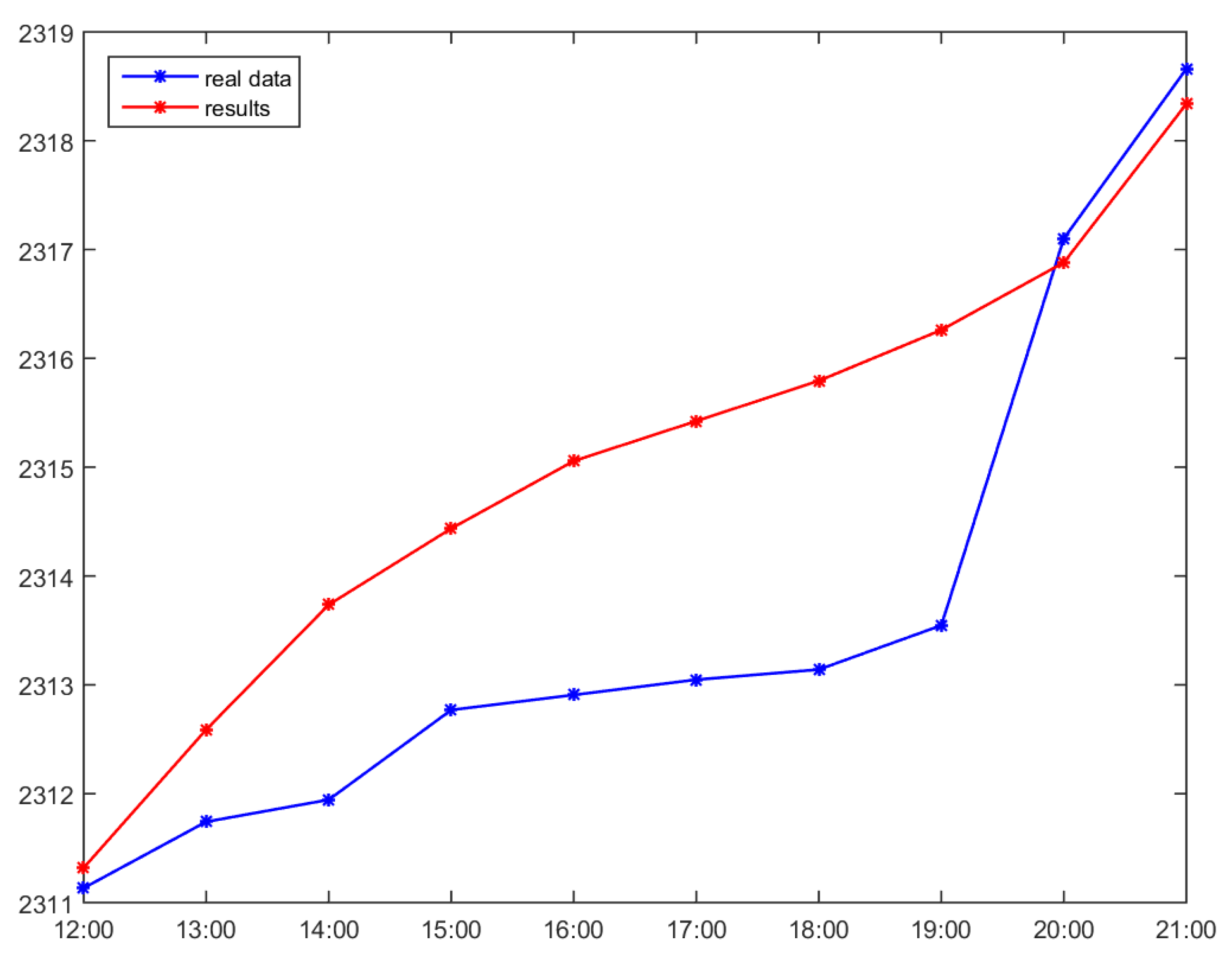
3.4. LSTM Estimation-Based Compensation Method
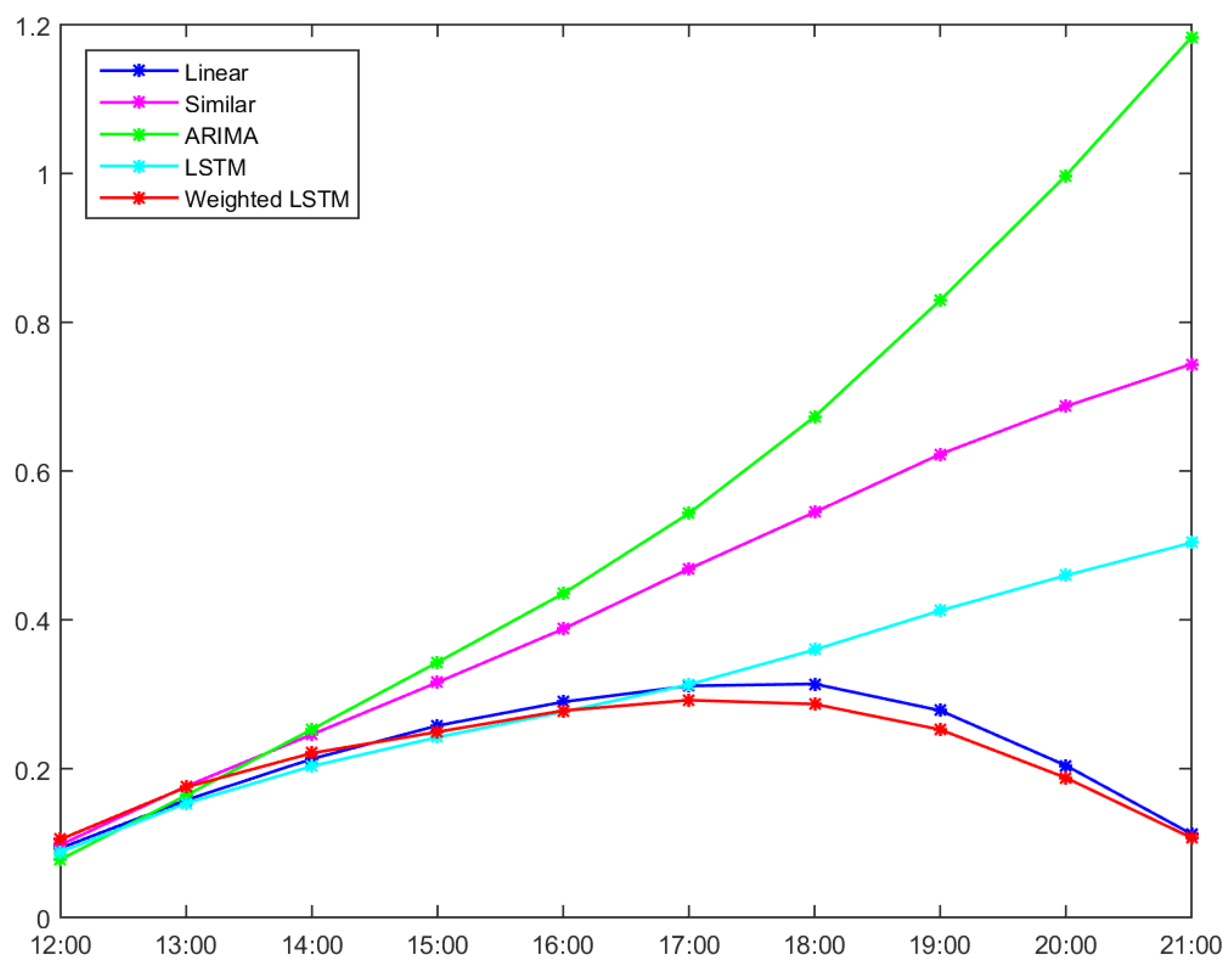
3.5. LSTM Estimate and Weight-Applied Compensation Method
| Algorithm 1 Weighted LSTM Processing |
| Input: MeterList |
| Output: ResultDataPool |
| Definition 1. : Rf—Fisrt real data(real data just before missing) |
| Rs—Second real data(first real data after missing termination) |
| for all attribute ∈ do |
| for all attribute ∈ do |
| end for |
| ClearTmpRet |
| end for |
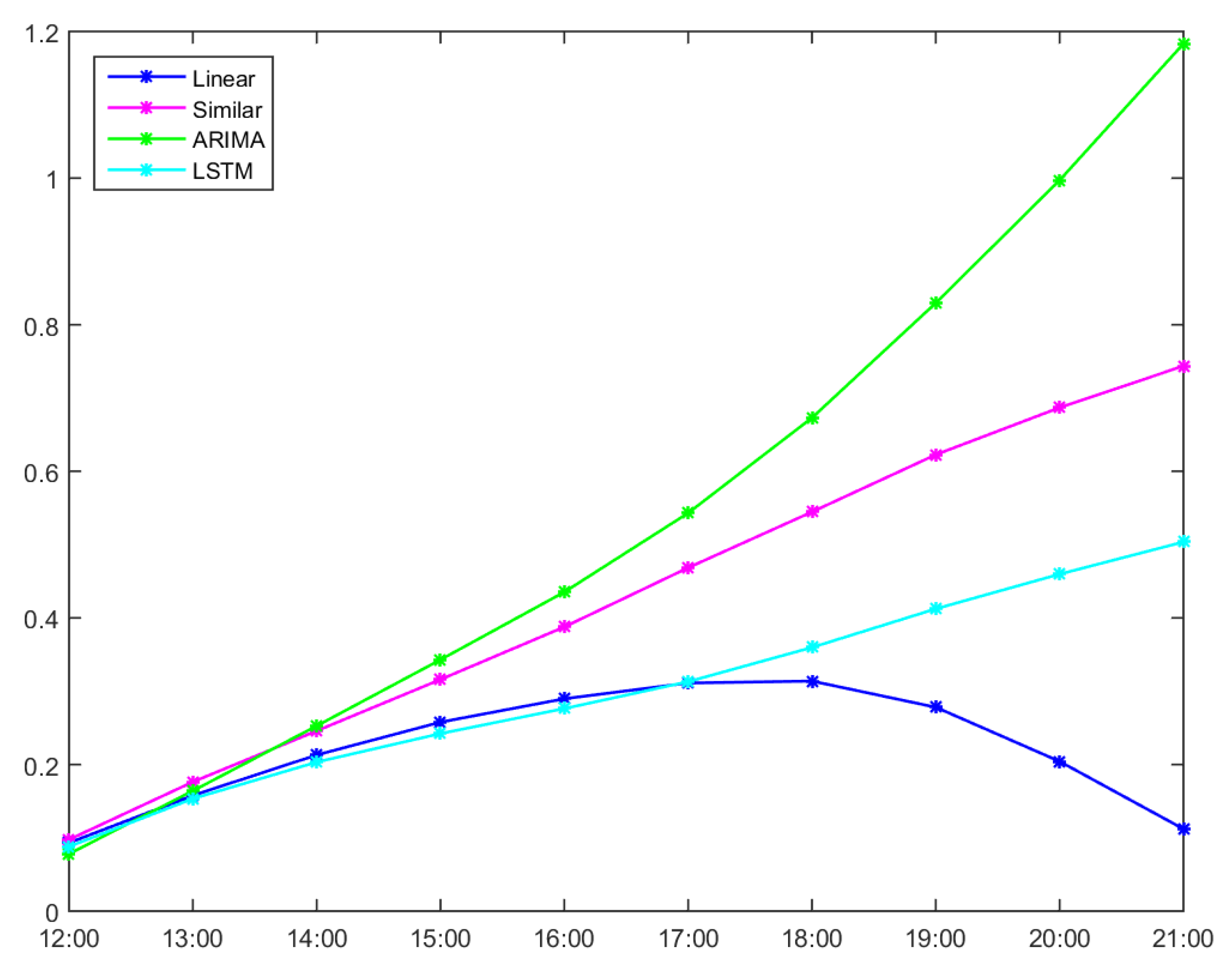
3.6. Experimental Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jung, J.; Seo, C. An Efficient Method for Meter Data Collection in AMI System. J. Korean Inst. Commun. Inf. Sci. 2018, 43, 1311–1320. [Google Scholar]
- Dusa, P.; Novac, C.; Purice, E.; Dodun, O.; Slătineanu, L. Configuration a Meter Data Management System using Axiomatic Design. Procedia CIRP 2015, 34, 174–179. [Google Scholar] [CrossRef] [Green Version]
- Kang, H.-J. A Study on the AMI Communication Method Combining High-Rate PLC of ISO/IEC 12139-1 and IEEE 802.15.4g Based Wi-SUN. Ph.D. Dissertation, Department of Electronic Communication Engineering Graduate School Chonnam National University. Gwangju, Korea, 2018. [Google Scholar]
- Kwon, H.R.; Hong, T.E.; Kim, P.K. Estimate method of missing data using Similarity in AMI system. Smart Media J. 2019, 8, 80–84. [Google Scholar] [CrossRef]
- Qian, X.; Yang, Y.; Li, C.; Tan, S.C. Economic Dispatch of DC Microgrids Under Real-Time Pricing Using Adaptive Differential Evolution Algorithm. In Proceedings of the 2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 29 November–2 December 2020. [Google Scholar]
- Song, H.; Yoon, Y.; Kwon, S. Optimal scheduling of critical peak pricing considering photovoltaic generation and electric vehicle load. In Proceedings of the 2019 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Seogwipo, Korea, 8–10 May 2019. [Google Scholar]
- Lv, H.; Wang, Y.; Dong, X.; Jiang, F.; Wang, C.; Zhang, Z. Optimization Scheduling of Integrated Energy System Considering Demand Response and Coupling Degree. In Proceedings of the 2021 IEEE/IAS 57th Industrial and Commercial Power Systems Technical Conference (I&CPS), Las Vegas, NV, USA, 27–30 April 2021. [Google Scholar]
- Choi, M.-S. Development and Performance Analysis of Hybrid Communication Technology for AdvancedMetering Infrastructure System. KIEE 2020, 69, 610–616. [Google Scholar] [CrossRef]
- Inga, E.; Hincapié, R.; Céspedes, S. Capacitated Multicommodity Flow Problem for Heterogeneous Smart Electricity Metering Communications Using Column Generation. Energies 2020, 13, 97. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Zhou, K.; Yang, S.; Wu, C. Data quality of electricity consumption data in a smart grid environment. Renew. Sustain. Energy Rev. 2017, 75, 98–105. [Google Scholar] [CrossRef]
- Choi, Y.J.; Kim, S.Y. Analysis on The Change of Power Consumption Pattern According to Single-Households. In Proceedings of the 2014 Conference on The Korean Institute of Electrical Engineers, Jeju, Korea, 15–19 June 2014; pp. 153–154. [Google Scholar]
- Lee, J.; Shin, J.; Joo, Y.; Noh, J.; Park, Y.; Jung, N. A VEE Algorithm Improvement Research for Improving Estimation Accuracy and Verification Responsibility of The AMI Meter Data. KEPCO J. Electr. Power Energy 2016, 2, 557–562. [Google Scholar] [CrossRef] [Green Version]
- Jang, M.; Nam, K.; Lee, Y. Analysis and Application of Power Consumption Patterns for Changing the Power Consumption Behaviors. J. Korea Inst. Inf. Commun. Eng. 2021, 25, 603–610. [Google Scholar]
- Kim, J.-O. A Study on the Prediction of Short Term Electric Power Load by Deep Learning System. Master’s Dissertation, Dankook University, Yongin-si, Korea, 2019. [Google Scholar]
- Ryu, S. Deep Learning for Electric Load Data Analytics. Master’s Dissertation, Sogang University, Seoul, Korea, 2020. [Google Scholar]
- Choi, H. Short-Term Load Forecasting Based on ResNet and LSTM. Master’s Dissertation, Sogang University, Seoul, Korea, 2018. [Google Scholar]
- Kim, D. Short-Term Load Forecasting Based on LSTM and CNN. Master’s Dissertation, Konkuk University, Seoul, Korea, 2019. [Google Scholar]
- Kwon, B.-S.; Park, R.-J.; Song, K.-B. Analysis of Short-Term Load Forecasting Accuracy Based on Various Normalization Methods. J. Korean Inst. Illum. Electr. Install. Eng. 2018, 32, 30–33. [Google Scholar]
- Koh, S. Outlier Detection and Imputation Method for Smart Meter Data Using Pattern Analysis. Master’s Dissertation, Korea University, Seoul, Korea, 2019. [Google Scholar]
- Timofey, S.; Antonio, N. Fraction-of- Time Density Estimation Based on Linear Interpolation of Time Series. In Proceedings of the 2021 Systems of Signals Generating and Processing in the Field of on Board Communications Signals Generating and Processing in the Field of on Board Communications, Moscow, Russia, 16–18 March 2021; pp. 1–4. [Google Scholar]
- Seo, S.-W.; Kim, D.-H.; Kim, S.J. A Study on the Linear Compensation Method of Ideal Surface Roughness to Actual Roughness in Milling. Korean Soc. Manuf. Process. Eng. 2016, 15, 15–20. [Google Scholar]
- Pejić, N.; Cvetanović, M.; Radivojević, Z. Estimating similarity between differently compiled procedures using neural networks. In Proceedings of the 2019 27th Telecommunications Forum (TELFOR), Serbia, Belgrade, 26–27 November 2019; pp. 26–27. [Google Scholar]
- Lee, S. Applying Different Similarity Measures based on Jaccard Index in Collaborative Filtering. J. Korea Soc. Comput. Inf. 2021, 26, 47–53. [Google Scholar]
- Behera, A.P.; Gaurisaria, M.K.; Rautaray, S.S.; Pandey, M. Predicting Future Call Volume Using ARIMA Models. In Proceedings of the 2021 5th International Conference on Intelligent Computing and Control Systems (ICICCS) Intelligent Computing and Control Systems (ICICCS), Madurai, India, 6–8 May 2021; pp. 1351–1354. [Google Scholar]
- Garlapati, A.; Krishna, D.R.; Garlapati, K.; Rahul, U.; Narayanan, G. Stock Price Prediction Using Facebook Prophet and Arima Models. In Proceedings of the 2021 6th International Conference for Convergence in Technology (I2CT) Convergence in Technology (I2CT), Maharashtra, India, 2–4 April 2021; pp. 1–7. [Google Scholar]
- Chang, H.; Park, D.; Lee, Y.; Yoon, B. Multiple time period imputation technique for multiple missing traffic variables: Nonparametric regression approach. Can. J. Civ. Eng. 2012, 39, 448–459. [Google Scholar] [CrossRef]
- Asif, M.T.; Mitrovic, N.; Dauwels, J.; Jaillet, P. Matrix and Tensor Based Methods for Missing Data Estimation in Large Traffic Networks. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1816–1825. [Google Scholar] [CrossRef]
- Shakir, M.; Marwala, T. Neural network based techniques for estimating missin data in databases. In Proceedings of the 16th Annual Symposium of the Recognition Association of South Africa, Langebaan, South Africa, 23–25 November 2005. [Google Scholar]
- Kwon, H.R.; Hong, T.E. Method of estimation of missing data in AMI system. In Proceedings of the 9th International Conference on Smart Media & Applications, Jeju Island, Korea, 17–19 September 2020. Paper ID-8. [Google Scholar]
- Huang, Z.; Zhu, T. Real-time data and energy management in microgrids. In Proceedings of the 2016 IEEE Real-Time Systems Symposium (RTSS), Porto, Portugal, 29 November–22 December 2016; pp. 79–88. [Google Scholar]
- Peppanen, J.; Zhang, X.; Grijalva, S.; Reno, M.J. Handling bad or missing smart meter data through advanced data imputation. In Proceedings of the 2016 IEEE Power &Energy Society, Innovative Smart Grid Technologies Conference (ISGT), Minneapolis, MN, USA, 6–9 September 2016; pp. 1–5. [Google Scholar]
- Yu, K.; Guo, G.-D.; Li, J.; Lin, S. Quantum Algorithms for Similarity Measurement Based on Euclidean Distance. Int. J. Theor. Phys. 2020, 59, 3134–3144. [Google Scholar] [CrossRef]
- Iglesias, F.; Kastner, W. Analysis of Similarity Measures in Times Series Clustering for the Discovery of Building Energy Patterns. Energies 2013, 2013, 579–597. [Google Scholar] [CrossRef] [Green Version]



| Year | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 |
|---|---|---|---|---|---|---|
| Outlook | 730 | 1000 | 1250 | 1500 | 1830 | 2250 |
| Performance | 250 | 435 | 520 | 680 | 980 | - |
| Time | Accumulated Usage | Interval Usage | Linear Usage | Estimated Usage | Absolute Error |
|---|---|---|---|---|---|
| 11:00 | 2310.19 | 1.351 | - | - | - |
| 12:00 | 2311.134 | 0.944 | 2311.1422 | 0.9522 | 0.0082 |
| 13:00 | 2311.743 | 0.609 | 2312.0944 | 0.9522 | 0.3514 |
| 14:00 | 2311.945 | 0.202 | 2313.0465 | 0.9522 | 1.1015 |
| 15:00 | 2312.77 | 0.825 | 2313.9987 | 0.9522 | 1.2287 |
| 16:00 | 2312.908 | 0.138 | 2314.9509 | 0.9522 | 2.0429 |
| 17:00 | 2313.048 | 0.14 | 2315.9031 | 0.9522 | 2.8551 |
| 18:00 | 2313.141 | 0.093 | 2316.8553 | 0.9522 | 3.7143 |
| 19:00 | 2313.547 | 0.406 | 2317.8075 | 0.9522 | 4.2605 |
| 20:00 | 2317.101 | 3.554 | 2318.7596 | 0.9522 | 1.6586 |
| 21:00 | 2318.66 | 1.559 | 2319.7118 | 0.9522 | 1.0518 |
| 22:00 | 2320.664 | 2.004 | - | - | - |
| Time | 4/17 | 4/18 | 4/19 | 4/20 | 4/21 | 4/22 | 4/23 | 4/24 |
|---|---|---|---|---|---|---|---|---|
| 2:00 | 1.048 | 1.095 | 1.139 | 0.019 | 0.019 | 0.018 | 0.01 | 0.011 |
| 3:00 | 1.041 | 1.104 | 1.117 | 0.019 | 0.01 | 0.011 | 0.018 | 0.017 |
| 4:00 | 1.021 | 1.071 | 1.173 | 0.019 | 0.018 | 0.018 | 0.012 | 0.018 |
| 5:00 | 1.012 | 1.069 | 1.14 | 0.019 | 0.018 | 0.01 | 0.016 | 0.01 |
| 6:00 | 1.011 | 1.087 | 1.075 | 0.018 | 0.016 | 0.017 | 0.018 | 0.018 |
| 7:00 | 2.46 | 1.936 | 0.767 | 0.019 | 0.012 | 0.018 | 0.01 | 0.01 |
| 8:00 | 1.153 | 0.748 | 0.79 | 0.01 | 0.018 | 0.01 | 0.018 | 0.018 |
| 9:00 | 0.837 | 0.737 | 0.762 | 0.018 | 0.014 | 0.018 | 0.01 | 0.018 |
| 10:00 | 0.829 | 1.401 | 1.183 | 0.019 | 0.015 | 0.011 | 0.018 | 0.01 |
| 11:00 | 1.351 | 0.828 | 0.146 | 0.018 | 0.018 | 0.018 | 0.01 | 0.018 |
| Sum Of Error | - | 2.417 | 4.201 | 11.585 | 11.605 | 11.614 | 11.623 | 11.615 |
| YMD | Time | Accumulated Usage | Interval Usage |
|---|---|---|---|
| 4/18 | 2:00 | 2258.726 | 1.095 |
| 4/18 | 3:00 | 2259.83 | 1.104 |
| 4/18 | 4:00 | 2260.901 | 1.071 |
| 4/18 | 5:00 | 2261.97 | 1.069 |
| 4/18 | 6:00 | 2263.057 | 1.087 |
| 4/18 | 7:00 | 2264.993 | 1.936 |
| 4/18 | 8:00 | 2265.741 | 0.748 |
| 4/18 | 9:00 | 2266.478 | 0.737 |
| 4/18 | 10:00 | 2267.879 | 1.401 |
| 4/18 | 11:00 | 2268.707 | 0.828 |
| 4/18 | 12:00 | 2269.295 | 0.588 |
| 4/18 | 13:00 | 2269.349 | 0.054 |
| 4/18 | 14:00 | 2269.392 | 0.043 |
| 4/18 | 15:00 | 2269.455 | 0.063 |
| 4/18 | 16:00 | 2269.63 | 0.175 |
| 4/18 | 17:00 | 2269.858 | 0.228 |
| 4/18 | 18:00 | 2270.308 | 0.45 |
| 4/18 | 19:00 | 2270.98 | 0.672 |
| 4/18 | 20:00 | 2272.995 | 2.015 |
| 4/18 | 21:00 | 2275.534 | 2.539 |
| Time | Accumulated Usage | Interval Usage | Similar Estimated | Similar Interval | Absolute Error |
|---|---|---|---|---|---|
| 12:00 | 2311.134 | 0.944 | 2310.778 | 0.588 | 0.356 |
| 13:00 | 2311.743 | 0.609 | 2310.832 | 0.054 | 0.911 |
| 14:00 | 2311.945 | 0.202 | 2310.875 | 0.043 | 1.07 |
| 15:00 | 2312.77 | 0.825 | 2310.938 | 0.063 | 1.832 |
| 16:00 | 2312.908 | 0.138 | 2311.113 | 0.175 | 1.795 |
| 17:00 | 2313.048 | 0.14 | 2311.341 | 0.228 | 1.707 |
| 18:00 | 2313.141 | 0.093 | 2311.791 | 0.45 | 1.35 |
| 19:00 | 2313.547 | 0.406 | 2312.463 | 0.672 | 1.084 |
| 20:00 | 2317.101 | 3.554 | 2314.478 | 2.015 | 2.623 |
| 21:00 | 2318.66 | 1.559 | 2317.017 | 2.539 | 1.643 |
| Time | Accumulated Usage | Interval Usage | ARIMA Estimated | ARIMA Interval | Absolute Error |
|---|---|---|---|---|---|
| 12:00 | 2311.134 | 0.944 | 2311.2877 | 0.1537 | 0.1537 |
| 13:00 | 2311.743 | 0.609 | 2312.3328 | 0.5898 | 0.5898 |
| 14:00 | 2311.945 | 0.202 | 2313.2851 | 1.3401 | 1.3401 |
| 15:00 | 2312.77 | 0.825 | 2314.1631 | 1.3931 | 1.3931 |
| 16:00 | 2312.908 | 0.138 | 2314.9699 | 2.0619 | 2.0619 |
| 17:00 | 2313.048 | 0.14 | 2315.7121 | 2.6641 | 2.6641 |
| 18:00 | 2313.141 | 0.093 | 2316.3946 | 3.2536 | 3.2536 |
| 19:00 | 2313.547 | 0.406 | 2317.0223 | 3.4753 | 3.4753 |
| 20:00 | 2317.101 | 3.554 | 2317.5995 | 0.4985 | 0.4985 |
| 21:00 | 2318.66 | 1.559 | 2318.1303 | 0.5297 | 0.5297 |
| Device | Model | Spec |
|---|---|---|
| OS | Windows 10 64 bit | - |
| CPU | Intel(R) Core(TM)i7-8500U@1.8 GHz | - |
| MEM | - | 8 GB |
| GPU | Intel(R) UHD Graphics 620 | - |
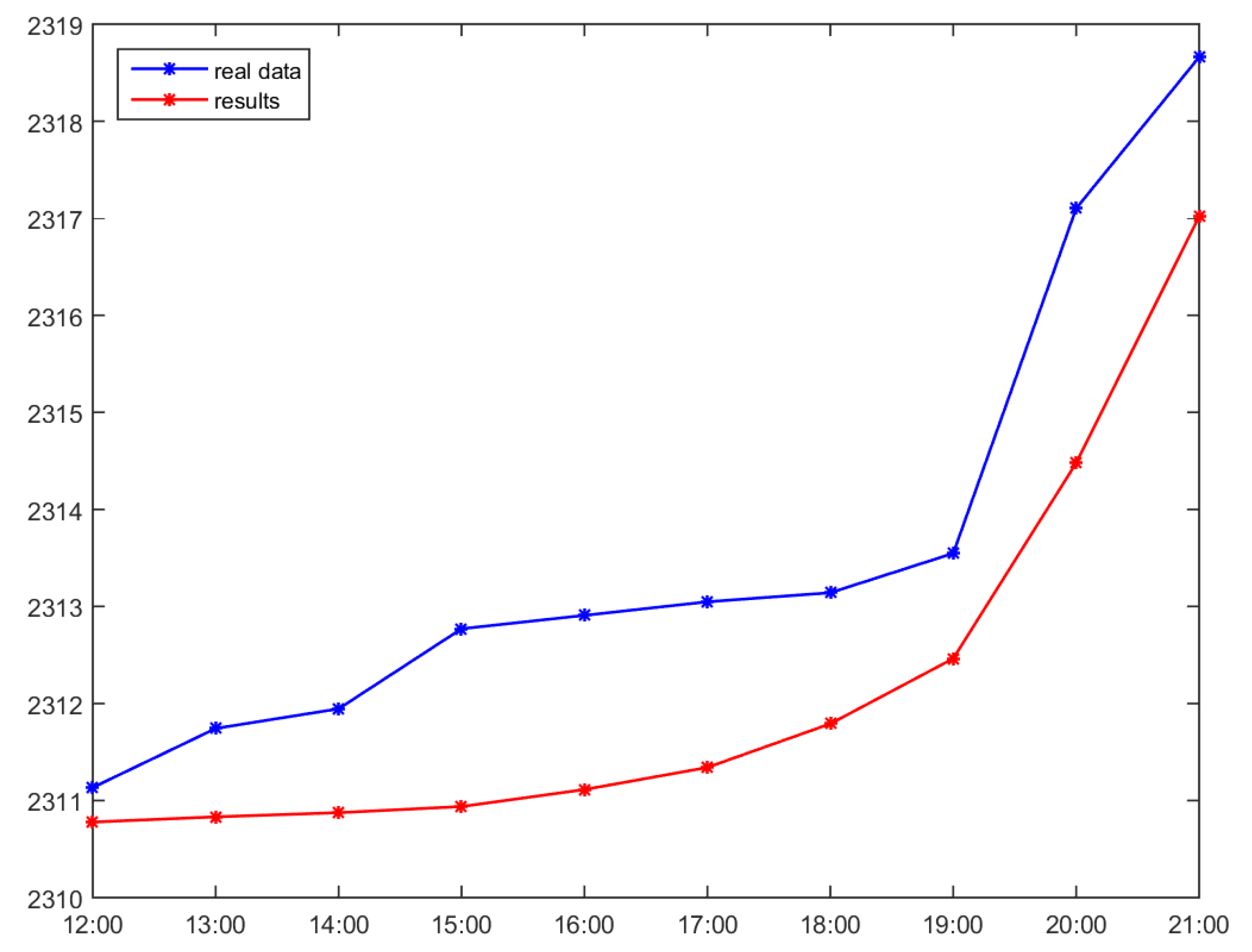
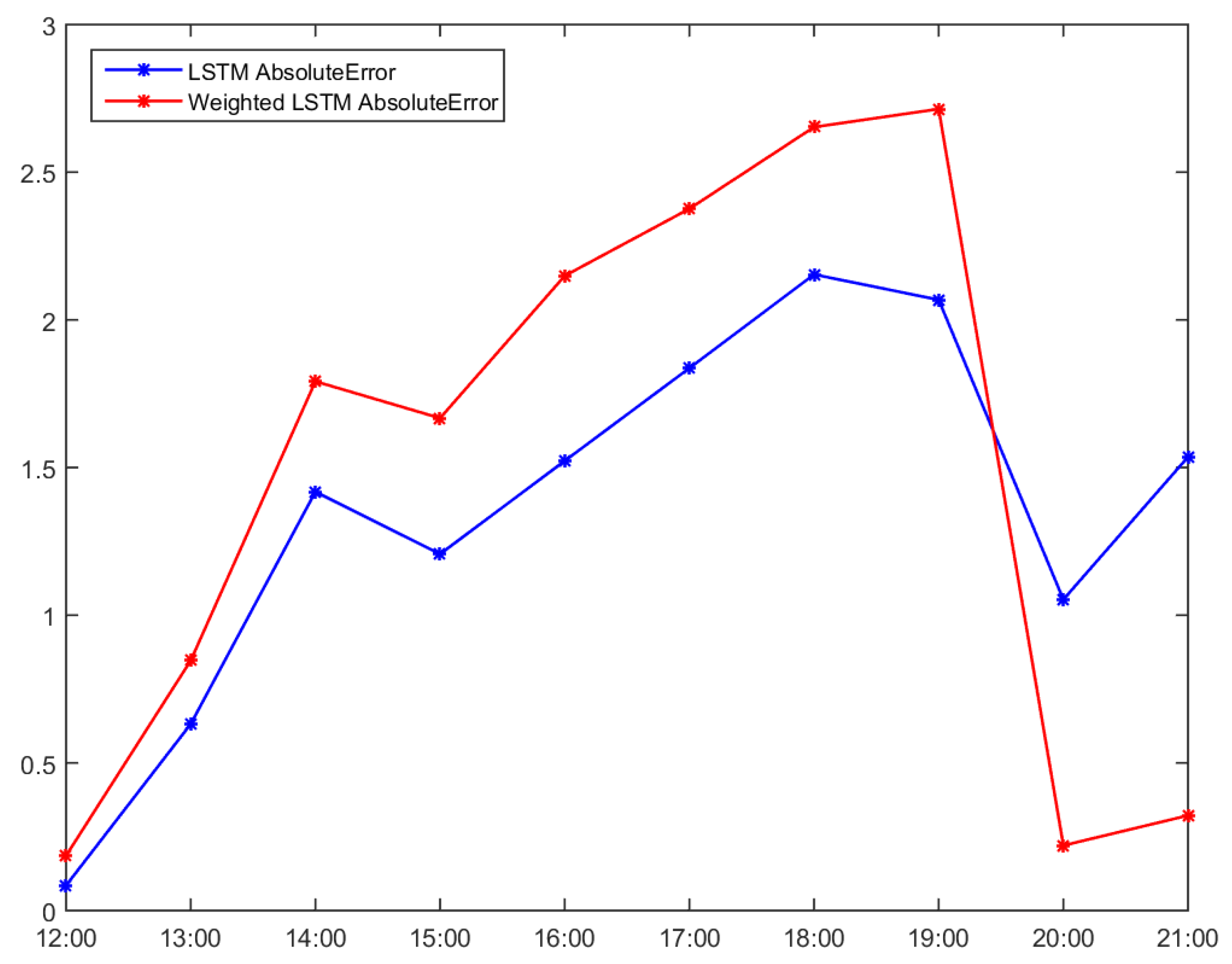
| Time | Accumulated Usage | Interval Usage | LSTM Estimated | LSTM Interval | Absolute Error |
|---|---|---|---|---|---|
| 12:00 | 2311.134 | 0.944 | 2311.219 | 0.085 | 0.085 |
| 13:00 | 2311.743 | 0.609 | 2312.3747 | 0.6317 | 0.6317 |
| 14:00 | 2311.945 | 0.202 | 2313.3628 | 1.4178 | 1.4178 |
| 15:00 | 2312.77 | 0.825 | 2313.9771 | 1.2071 | 1.2071 |
| 16:00 | 2312.908 | 0.138 | 2314.4305 | 1.5225 | 1.5225 |
| 17:00 | 2313.048 | 0.14 | 2314.8846 | 1.8366 | 1.8366 |
| 18:00 | 2313.141 | 0.093 | 2315.2946 | 2.1536 | 2.1536 |
| 19:00 | 2313.547 | 0.406 | 2315.6148 | 2.0678 | 2.0678 |
| 20:00 | 2317.101 | 3.554 | 2316.048 | 1.053 | 1.053 |
| 21:00 | 2318.66 | 1.559 | 2317.1243 | 1.5357 | 1.5357 |
| Time | Accumulated Usage | LSTM Estimated | LSTM TermRate | W.LSTM Usage | W.LSTM Estimated | Absolute Error |
|---|---|---|---|---|---|---|
| 11:00 | 2310.19 | - | - | - | - | - |
| 12:00 | 2311.134 | 0.8943 | 0.1079 | 1.1299 | 2311.3199 | 0.1859 |
| 13:00 | 2311.743 | 1.0049 | 0.1212 | 1.2697 | 2312.5896 | 0.8466 |
| 14:00 | 2311.945 | 0.9078 | 0.1095 | 1.147 | 2313.7365 | 1.7915 |
| 15:00 | 2312.77 | 0.5546 | 0.0669 | 0.7007 | 2314.4372 | 1.6672 |
| 16:00 | 2312.908 | 0.4906 | 0.0592 | 0.6199 | 2315.0571 | 2.1491 |
| 17:00 | 2313.048 | 0.2905 | 0.035 | 0.367 | 2315.4241 | 2.3761 |
| 18:00 | 2313.141 | 0.2925 | 0.0353 | 0.3696 | 2315.7937 | 2.6527 |
| 19:00 | 2313.547 | 0.3697 | 0.0446 | 0.4671 | 2316.2608 | 2.7138 |
| 20:00 | 2317.101 | 0.4906 | 0.0592 | 0.6199 | 2316.8807 | 0.2203 |
| 21:00 | 2318.66 | 1.1536 | 0.1392 | 1.4575 | 2318.3382 | 0.3218 |
| 22:00 | 2320.664 | 1.8408 | 0.2221 | 2.3258 | 2320.664 | 0 |
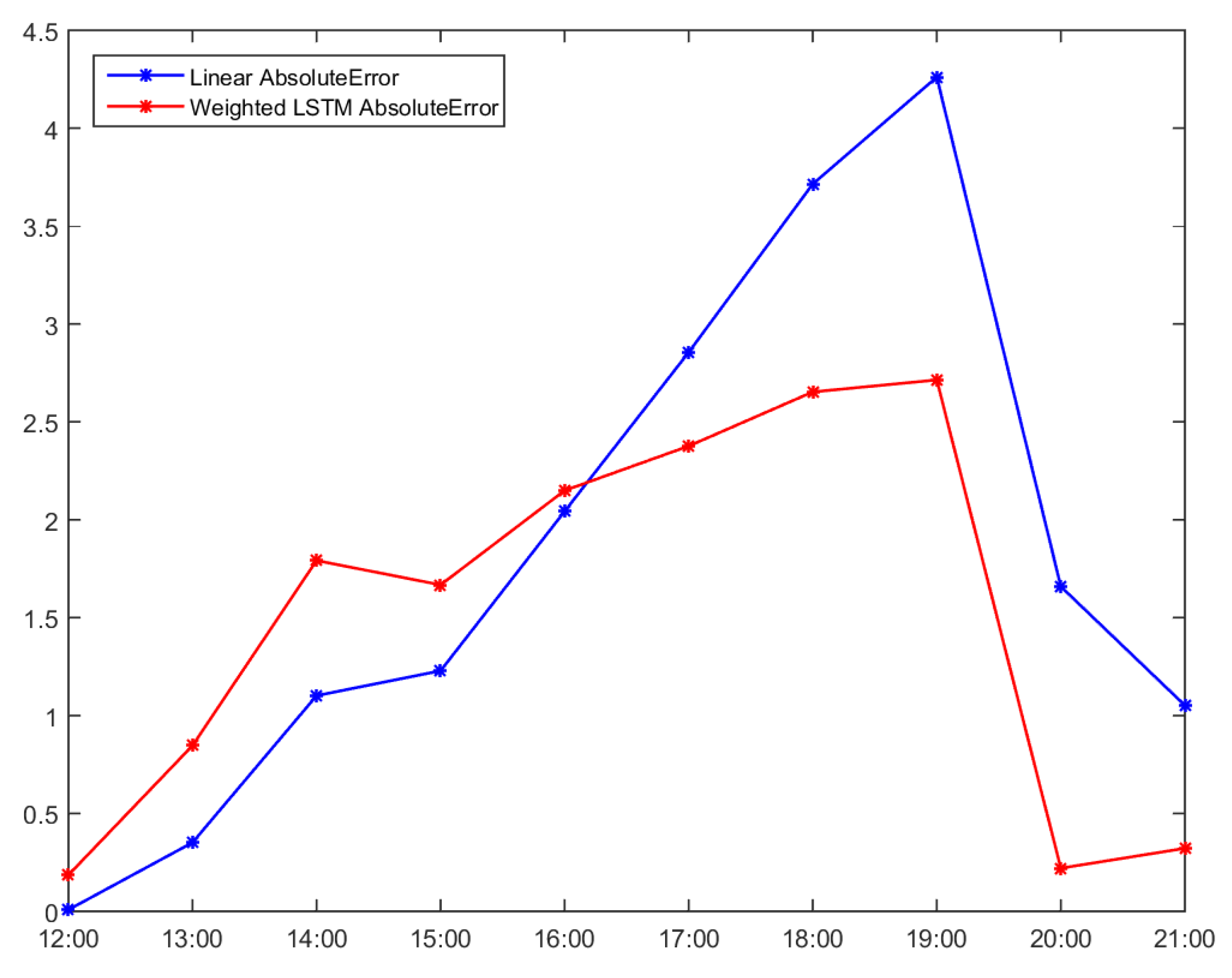
| Time | Linear | Similar | ARIMA | LSTM | Weight LSTM |
|---|---|---|---|---|---|
| 12:00 | 0.0932 | 0.0976 | 0.0781 | 0.088 | 0.105 |
| 13:00 | 0.1578 | 0.1763 | 0.1641 | 0.1534 | 0.1751 |
| 14:00 | 0.213 | 0.2459 | 0.2527 | 0.2033 | 0.2208 |
| 15:00 | 0.2578 | 0.316 | 0.343 | 0.2422 | 0.2494 |
| 16:00 | 0.2897 | 0.3877 | 0.4353 | 0.2763 | 0.2779 |
| 17:00 | 0.3112 | 0.4685 | 0.5431 | 0.313 | 0.292 |
| 18:00 | 0.3138 | 0.5446 | 0.673 | 0.3597 | 0.2867 |
| 19:00 | 0.2781 | 0.6227 | 0.8297 | 0.4124 | 0.2524 |
| 20:00 | 0.2042 | 0.6869 | 0.9971 | 0.4597 | 0.1877 |
| 21:00 | 0.1121 | 0.7437 | 1.1833 | 0.5036 | 0.1075 |
| SUM | 2.2309 | 4.2899 | 5.4994 | 3.0116 | 2.1545 |
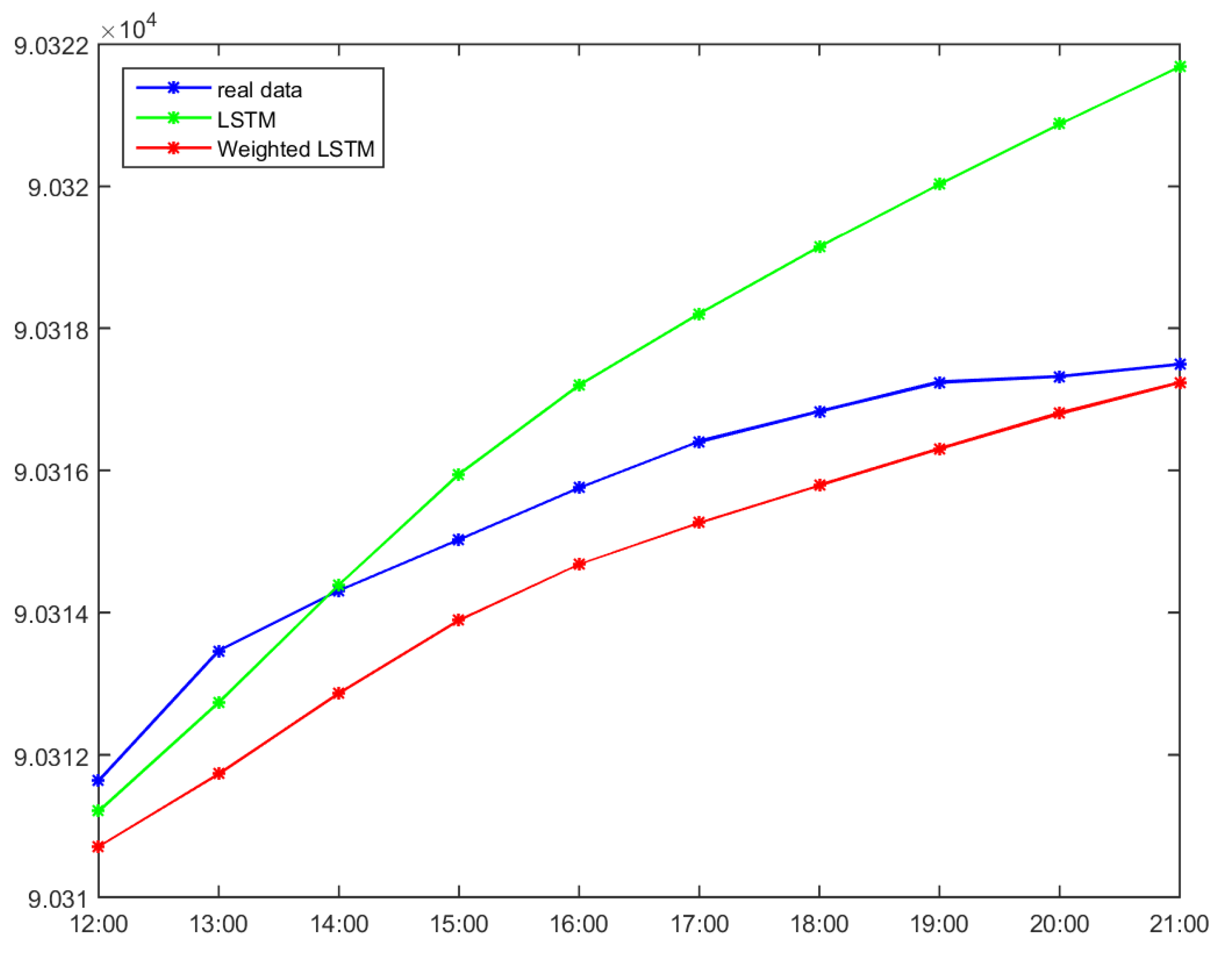
| YMD | Time | Accumulated Usage | LSTM Estimated | Weight LSTM |
|---|---|---|---|---|
| 4/25 | 12:00 | 90,311.64 | 90,311.213 | 90,310.7109 |
| 4/25 | 13:00 | 90,313.46 | 90,312.7315 | 90,311.7347 |
| 4/25 | 14:00 | 90,314.31 | 90,314.3932 | 90,312.8699 |
| 4/25 | 15:00 | 90,315.02 | 90,315.9478 | 90,313.8991 |
| 4/25 | 16:00 | 90,315.76 | 90,317.2015 | 90,314.6807 |
| 4/25 | 17:00 | 90,316.41 | 90,318.2029 | 90,315.266 |
| 4/25 | 18:00 | 90,316.83 | 90,319.1466 | 90,315.7897 |
| 4/25 | 19:00 | 90,317.24 | 90,320.0283 | 90,316.3056 |
| 4/25 | 20:00 | 90,317.32 | 90,320.8727 | 90,316.8031 |
| 4/25 | 21:00 | 90,317.49 | 90,321.6765 | 90,317.2351 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwon, H.-R.; Kim, P.-K. A Missing Data Compensation Method Using LSTM Estimates and Weights in AMI System. Information 2021, 12, 341. https://doi.org/10.3390/info12090341
Kwon H-R, Kim P-K. A Missing Data Compensation Method Using LSTM Estimates and Weights in AMI System. Information. 2021; 12(9):341. https://doi.org/10.3390/info12090341
Chicago/Turabian StyleKwon, Hyuk-Rok, and Pan-Koo Kim. 2021. "A Missing Data Compensation Method Using LSTM Estimates and Weights in AMI System" Information 12, no. 9: 341. https://doi.org/10.3390/info12090341
APA StyleKwon, H.-R., & Kim, P.-K. (2021). A Missing Data Compensation Method Using LSTM Estimates and Weights in AMI System. Information, 12(9), 341. https://doi.org/10.3390/info12090341






