Abstract
Presently, data that are collected from real systems and organized as information networks are universal. Mining hidden information from these data is generally helpful to understand and benefit the corresponding systems. The challenges of analyzing such data include high computational complexity and low parallelizability because of the nature of complicated interconnected structure of their nodes. Network representation learning, also called network embedding, provides a practical and promising way to solve these issues. One of the foremost requirements of network embedding is preserving network topology properties in learned low-dimension representations. Community structure is a prominent characteristic of complex networks and thus should be well maintained. However, the difficulty lies in the fact that the properties of community structure are multivariate and complicated; therefore, it is insufficient to model community structure using a predefined model, the way that is popular in most state-of-the-art network embedding algorithms explicitly considering community structure preservation. In this paper, we introduce a multi-process parallel framework for network embedding that is enhanced by found partial community information and can preserve community properties well. We also implement the framework and propose two node embedding methods that use game theory for detecting partial community information. A series of experiments are conducted to evaluate the performance of our methods and six state-of-the-art algorithms. The results demonstrate that our methods can effectively preserve community properties of networks in their low-dimension representations. Specifically, compared to the involved baselines, our algorithms behave the best and are the runners-up on networks with high overlapping diversity and density.
1. Introduction
With the advancement of data collecting and processing technologies, network structure data are universal and extensive. The reason for this lies in the fact that information network is a direct and natural way for organizing data that are from a wide diversity of real-world systems, such as social networks, citation networks, web networks, the Internet, and so forth. Mining useful hidden information from such networks is essential because it is helpful to understand and may benefit the corresponding applications by making good usage of the found information. For example, based on a community structure of an online social network being detected, a better recommendation in terms of friendship can be made due to the observation that users within then same community generally have similar roles or properties and may make friends with a higher probability. The efficiency of network data analyzing heavily relies on the way how a network is represented. Generally, a network can be denoted as a graph where is a node set that represents objects in a system, is an edge set that stands for connection relationships among these objects, and is the side information that associates with the nodes and edges, like node labels, edge weights, etc.. However, such a way of representation will induce high computational complexity and low parallelizability as analyzing due to the nature of complicated interconnected structure of graph nodes. It even may cause the analysis of large-scale networks being impossible in terms of computing time.
Recently, network representation learning (NRL), also called network embedding (NE), provides a practical and promising way to alleviate these issues, and has received a lot of research attention with several algorithms being developed [1,2,3,4,5,6]. Its basic idea is to learn latent, low-dimensional representations (usually continuous vectors) for network nodes, edges, or subgraphs with the property that preserves the network topology structure proximity and node and edge side information affinity. In a low-dimensional space, network analytic tasks, such as node classification, node clustering, link prediction, and so on, can be easily and efficiently carried out by applying a plenty of ready vector-based machine learning algorithms.
Community structure is a prominent mesoscopic topology property in complex networks, therefore it is necessary to preserve it in learned low-dimensional representations. Our previous work [7] has quantitatively shown the necessity and importance of incorporating community structure properties in network embedding. In that paper, we defined the concept of partial community structure and presented two algorithms using it to enhance node representation learning. The crucial point is how can we find an accurate community structure for a network. However, the method for finding a partial community structure [7] is executed directly on whole network, and thus is not easy to parallel program. In this paper, we design a multi-process parallel approach for partial community information extracting. We will mention other recently proposed network embedding algorithms that explicitly consider preserving community properties later in Section 2.
In summary, the main contributions of this paper are:
- (1)
- We introduced a multi-process parallel framework for network node representation learning enhanced by partial community structure information. The framework first extracts the ego-net of each node in a network, and then finds the partial community information for the center node on it. The information is then incorporated into collecting random walks that will be used to learn node representations. As a result, the community structure properties can be well preserved in learned low-dimension representations.
- (2)
- We proposed an improved game theory-based algorithm for partial community information extraction. A merging operation is added at the end of each game-playing iteration, to reduce community labels if it is possible and thus speed up the game convergence. A post-process operation from the viewpoint of a community is introduced as well, to mend the quality of the found information. The algorithm is employed in the proposed framework for partial community information finding on ego-nets. Though game theory-based algorithms are superior at overlapping community structure detecting, they are generally computational cost and thus cannot be used on large-scale networks. Our framework can avoid this drawback because an ego-net is usually much smaller in size than the whole network.
- (3)
- We implemented the framework to improve two popular node representation learning methods based on random walk, DeepWalk [8] and node2vec [9], and bring forth GameNE-DW (Game-based Network Embedding on DeepWalk) and GameNE-N2V (Game-based Network Embedding on Node2Vec).
- (4)
- We conducted a series of experiments on synthesized networks, of which their community structure properties can be controlled through model parameters, to evaluate the ability of community structure preservation of our algorithms. We also compare our methods against six state-of-the-art representation learning algorithms. The results demonstrate that GameNE-DW and GameNE-N2V are adept at preserving community structure properties, especially on networks with high overlapping diversity and density.
The structure of the rest paper is organized as follows: in Section 2, we mainly describe the algorithms that explicitly consider to preserve community property of networks in node representation learning, and game theory-based algorithms designed for community structure detecting; in Section 3, we briefly introduce the concepts of game theory for community detection; Section 4 details our multi-process parallel framework that uses game-playing to enhance network node representation learning; Section 5 gives out the experiment results that show the excellent ability of community structure preserving of our algorithms, especially on networks with high-density overlapping nodes and high-diversity overlapping memberships; at last, Section 6 discusses the pros and cons of our methods and Section 7 concludes the paper.
2. Related Work
2.1. DeepWalk and Node2vec
We first introduce DeepWalk and node2vec, two sequence-based network embedding approaches, on which our algorithms build.
DeepWalk by Perozzi et al. [8] is the first practical algorithm that can learn node representations for large-scale networks. It is inspired by the observation that the distribution of node pair appearance in random walks collected on a network within a given window is power-law, and such a distribution is considerably similar to the distribution of word co-occurrences in natural language corpus. DeepWalk learns network node representations by imitating word embedding: treats a node as a word and a short random walk as a special sentence and then solves node representations using the Skip-Gram optimizing model. Actually, DeepWalk tries to keep the likelihood of observed neighborhood samples.
Node2vec by Grover et al. [9] extends DeepWalk by designing a biased random walk with introducing two parameters: returning p and in-out q that control how fast the next walk explores or leaves the neighborhood of a starting node, respectively. As setting p and q as 1.0, node2vec becomes DeepWalk. Our algorithms control random walks further using partial community information of a network.
2.2. Network Embedding Preserving Community Structure
Noting the affect and importance of community structure on network analysis, recently a few studies have considered to preserve community features explicitly in node embedding [7,10,11,12,13,14,15,16,17,18,19]. In general, there are two ways to take community structure into consideration. The first is assuming the existence of a prior community model and introducing it in node embedding model, then jointly solving them to compute node representations and community representations (or a community structure) simultaneously. The other is finding some community structure information for networks first and then making good use of the information to enhance node representation learning. Most previous works fall into the first category in which detecting a high-quality community structure for a network is a hard problem to tackle.
Wang et al. [10] combined a non-negative matrix factorizing (NMF) model for node representations learning and a NMF model for community structure detecting, and proposed M-NMF (Modularized NMF). One of its drawbacks is it can only deal with disjoint community structure, which is usually not true for real networks. Benedek et al. [11] presented GEMSEC (Graph Embedding with Self-Clustering) that considered the two problems of node embedding and community detection at the same time by introducing a clustering optimizing term in the objective function, where a clustering means a community. Like Wang et al’s work, it only deals with disjoint communities. Similarly, NECS (Network Embedding with Community Structure information) by Li et al. [12] modeled community structure using a matrix and introduced a community optimizing term in its objective function. COSINE (COmmunity-preserving Social Network Embedding from Information diffusion cascades) proposed by Zhang et al. [13] employed the Gaussian Mixture Model to model communities in low-dimension space and learned node representations using information diffusion model. Cavallari et al. [14] introduced the ComE (Community Embedding) framework that integrated the three tasks of community detection, community embedding and node embedding as a closed loop procedure. It takes the Multivariate Gaussian Distribution as the model for community representations and supposes that node representations are generated from such community distributions. In contrast to aforementioned algorithms, the ComE supports overlapping community structure. CNRL (Community-enhanced Network Representation Learning) designed by Tu et al. [16] extends the idea of DeepWalk by modeling a community as a topic in natural language and hires the Gibbs Sampling of Latent Dirichlet Allocation to find community assignments for nodes. Jia et al. [17] proposed CommunityGAN (Community Generative Adversary Network) to learn node representations and detect overlapping communities simultaneously. It uses the generative and discriminative thinking. However, it requires the dimension of learned node representation must be same with the number of communities. Sun et al. [18] proposed vGraph for joint community detection and node representation learning. It assumes that each node can be represented as a mixture of communities and each community is defined as a multinomial distribution over nodes.
The forenamed algorithms, including M-NMF [10], GEMSEC [11], NECS [12], COSINE [13], ComE [14], CNRL [16], CommunityGAN [17] and vGraph [18] need to specify the number of communities as an input parameter, which is usually not known in practice and hard to estimate accurately, however. Cavallari et al. have improved their ComE to ComE+ [15] that can handle the issue of unknown number of communities through an inferring algorithm using Bayesian model. Another problem of the first-class algorithms is that the community structure properties of real networks are multivariate and complicated. High overlapping diversity, high overlapping density, wider ranging community size are just some examples. Therefore, a predefined model may be insufficient to capture community properties well.
CARE (Community Aware Random walk for network Embedding) proposed by Mohammad et al. [19] and our previous work PCGNE (Partial Community structure Guided Network Embedding) [7] belong to the second class. CARE first detects a community structure for a network using Louvain, a popular community detection method, and then uses the obtained communities to guide DeepWalk random walks. However, the aggressive way of using community information leads to its performance severely relaying on the accuracy of found communities. Up to now, detecting a high-quality community structure is not easy for large-scale networks. Our PCGNE was inspired by CARE, but used the information of partial community structure that was easier and more cost-effective to find for random walk guidance.
Though it is possible to implement a parallel version of the partial community structure finding algorithm used in PCGNE, the programming will not be easier. The algorithm needs to sit on a distributed graph processing platform Giraph++ [20], and deal with complicate inter-communication among processing computing servers. In this paper, we design a multi-process parallel framework for finding partial community information of each node in a network. We extract the 2-hop ego-net for each node and detect a community structure for it. Every and each detection is completely independent and thus can be executed parallel by multiple processes. On each ego-net, the detection is achieved using a game theory-based method that is superior at overlapping community structure finding.
2.3. Game Theory for Community Detection
The game theory is an abstract mathematical model that focus on decision-making scenarios. The formation of a community structure of a network also can be modeled as a game-playing. Several game-based approaches have been proposed to solve the problem of disjoint or overlapping community detection on social networks. Annapurna and Lakshmanan [21] did a survey work in this regard. In general, these algorithms can be categorized into three classes, the non-cooperative game-based, the cooperative game-based (also known as coalitional game-based), and the evolutionary game-based. In non-cooperative game-based methods, the game players are individual nodes that update their strategies (community labels) according to a defined personal utility function, while in cooperative game-based ones, the players can be viewed as communities, i.e., individuals update their strategies to improve the quality of related communities, measured by a community utility function. The evolutionary game-based approaches aim to find community structures of dynamic networks. During evolutionary game-playing, players can be added or removed as needed. Chen’s algorithm [22] is a non-cooperative game method for finding overlapping community structure and has a wide influence. It is the first game algorithm that models the dynamics of community formation of a network. Based on Chen’s algorithm, several extension and improvements have been made, as reported in this survey [21].
Except the adopted game theory class, the differences of game-based community detection methods mainly lie on the designed utility functions (especially gain functions) and player actions (individual or community). Neo-algorithms have been proposed by defining new utility functions and (or) actions. Mahboobeh et al. [23] presented an overlapping community structure detection algorithm, in which a new action attract was added and the local influence was used as profit (gain) function. The local influence of a node measures the influence from its local neighbors, i.e., adjacent and 2-hop neighbors. Sun et al. [24] proposed GExplorer for overlapping community structure detection as well. It investigates how similar vertices affect the formation of community game and introduces indirect impact from 2-hop neighbors in gain function. Zhou et al. [25] improved Chen’s algorithm by introducing node pair similarity in the gain function and designing two strategies to suggest candidate labels for players during game-playing. The before-mentioned three algorithms belong to the non-cooperative class. Konstantin et al. [26] employed the cooperative game theory to find disjoint community structure on social networks. They proposed two approaches that based on Myerson value and Hedonic game, respectively. Zhou et al. proposed cooperative game-based methods for identifying overlapping and hierarchical communities [27], and for detecting communities in multi-relational networks [28].
One main challenge of game theory-based algorithms is that they are usually computational cost to converge, therefore cannot be used on large-scale networks. Moscato et al. [29] further improved Zhou’s algorithm to reduce computational requirements through using a greedy approach and a gain function working only on neighbors of nodes.
In this paper, we improve Chen’s algorithm to find network community information, as it has the closest relationship with the community modularity definition. In addition, it explores more strategies for nodes than others during game-playing and thus may reveal a more accurate community structure. Since we play a game on 2-hop ego-net of each network node, of which the size is much smaller than that of the whole network, the issue of convergence time does not need to be considered any more.
3. Game Theory Preliminary
3.1. Basic Concepts
A game has several players (or agents) and each player is assumed to be rational or selfish. In non-cooperative game, players will make their own decisions to increase their own benefit. The key is that as one player selects its choice, the decision will influence its neighbors and trigger chain reactions, i.e., the influenced neighbor players may change their decisions to make their benefit maximize, and they will further influence their neighbors, and so on. At the moment no player can increase its benefit from changing its own decision, the game is said to reach an equilibrium, namely all players have made their best decisions.
In a non-cooperative community formation game, each and every node is a player, and its decision is to select the labels of communities in which it prefers to join. In formal, a node v keeps the labels of the communities it wants to join in, which is referred as the strategy of v, denoted as . Denote the set of all possible community labels as , the strategy of a node is a subset of and can be none, which means the node does not join in any community. Here K is polynomial in the number of nodes. For example, the maximum K can be the number of nodes, which means each node forms a singleton community. K can also be less than the number of nodes if some nodes have a same label for sure at start. Usually, as a community formation game reaches its equilibrium, the final community structure has much smaller number of communities than K.
The strategies of all players, denoted as where N is the number of nodes and () is the strategy of node , is called the strategy profile of a game.
The notations of community formation game are listed in Table 1.

Table 1.
Notations of Community Formation Game.
3.2. Utility Function for Community Detection
Each player makes its own decision to increase its own benefit that is measured by a utility function in a non-cooperative game. A utility function consists of two parts, the gain function and the loss function , and
In a community formation game, given , the set of strategies of players other than , the best response strategy of is :
If all players have their best strategies, the community formation game reaches a pure Nash equilibrium, at that no player can increase its own utility by changing its strategy unilaterally.
In this paper, we will use the utility function put forth by Chen et al. [22], of that the gain function, called the Personalized modularity function, is defined as (the symbols are revised as used in this paper):
where is the set of strategies of players other than and is the strategy of ; m is the number of network edges; is the component of the ith row and the jth column in the network adjacent matrix; is 1 if , otherwise 0; indicates the number of common labels that node and have; and () is the degree of (). The associate loss function is:
It has been proved that both the personalized modularity function and the loss function are locally linear functions with linear factor 1/2 and 1, respectively, and thus the community formation game is a potential game, and a Nash equilibrium is guaranteed to exist [22].
3.3. Local Equilibrium
However, computing the best strategy for a player might be NP-hard even in some simple cases. Therefore, it is unreasonable to assume that players always chose their best strategies. The local equilibrium, in which a player is only allowed to select a response strategy from a restricted strategy space that depends on the player’s current state, was proposed to replace the pure Nash equilibrium [22]. In particular, given the player ’s current strategy and a set of candidate labels , can only chose its local optimal response from the following strategies:
- a set of strategies formed by join action, i.e., ;
- a set of strategies built by switch action, i.e., ;
- a set of strategies created by leave action, i.e., .
The distinct joining community labels of ’s neighbors are appropriate for candidates.
4. The Algorithms
The framework of our partial community information enhanced network node embedding approach is shown in Algorithm 1. Figure 1 shows its conception structure. It consists of four steps: (1) extracting 2-hop ego-nets for all nodes of the analyzed network, of which the sizes are much smaller than that of the original network; (2) detecting a community structure using a game theory-based algorithm for each ego-net and extracting the partial community information of the center node for each ego-net; (3) collecting random walks that incorporate the found partial community information on the network; and (4) learning low-dimension node representations using the Word2Vec algorithm. Here, the hyper parameters stands for all parameters needed and will be introduced in following related algorithms. Please note that all the four steps can be executed in multi-process parallel manner easily.
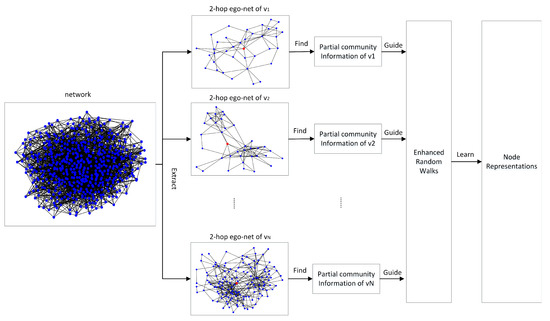
Figure 1.
The Conception Structure of GameNE.
Our overriding contributions lie in the first two steps. The third step is same as in our previous work [7]. In the last step, the framework directly calls the Word2Vec. We will explain the first three steps in detail one by one.
| Algorithm 1: GameNE |
| input: network G, hyper parameters |
| output: node representations |
| 1 extract the 2-hop ego-net for all nodes in G (call Algorithm 2); |
| 2 find the partial community information of the center node for all ego-nets (call Algorithm 3); |
| 3 collect random walks guided by the partial community information on G; |
| 4 learn node representations using Word2Vec |
4.1. Ego-Net Extracting
The parallel 2-hop ego-net extracting method is show in Algorithm 2.
| Algorithm 2: ExtractEgos |
 |
For each node, the method first extracts its 2-hop ego-net, which consists of the node itself, its 1-hop and 2-hop neighbors and the connecting edges among them. Then, it repeatedly drops leaf nodes that has only one edge connection to reduce later game-playing computational cost, because they have no contribution to the community game formation. In addition, side information including the center node of the ego-net, the degrees of ego-net nodes in the original network G and the total number of edges starting from ego-net nodes in G are recorded for using in later game-playing. At last, ego-nets and their side information of all nodes are returned for further use.
The extractions are parallel executed by multiple processes from a pool. Nodes should be randomly assigned to a process for handling to make the running time of each process be roughly equal, in that node degrees may change greatly.
4.2. Partial Community Structure Detecting
The non-cooperative game theory-based method that finds the partial community information for the center nodes of extracted ego-nets is depicted in Algorithm 3.
| Algorithm 3: GamePCS |
 |
For each ego-net, at the start, the strategy of each node is initialized as a unique label, i.e., each node forms a singular community. After that, nodes will play the community formation game through updating their strategies. Specifically, a node collects candidate labels from its direct neighbors, builds candidate strategies using the join, switch and leave actions, and then selects the best that brings out the maximum utility. If the best candidate strategy is better than the old one, the node replaces its old strategy with the best. Here in the gain function computation (3), the edge number m and the node degrees and are using the actual values in the original network (getting from the recorded side information during the ego-net extraction), but not the values in ego-net. By doing this way, we hope that the impacts of missing 2-above-hop nodes and edges can be alleviated and the found partial communities, especially for the center node, can be closer to that in the original network. The playing will stop if no node changes its strategy or if the playing iterations reach the set maximum. Please note that at the very beginning of each iteration, the playing order is randomly permuted to remove the effect of processing order. To speed up convergence, at the end of each playing iteration, the method merges small communities into a larger one that contains the smaller. This operation can reduce the number of community labels if mergence happens.
Then, a post-process procedure (Algorithm 4) is called to further improve the quality of the found community structure.
| Algorithm 4: PostProc |
 |
The post procedure achieves this from the viewpoint of a community. For each found community, it first repeatedly removes these nodes that have 0 or 1 edge connection with the community or of which their modularity contribution is negative. Such nodes may exist due to the sequential playing of nodes. Then, for these neighbors of the center node that have not joined in any community to which the center node belongs, the procedure tries to find if they should join in any one (a community the center node has joined in). The criterion is that the modularity contribution of the node (suppose the node is a member) is not less than a threshold, which is the minimum modularity contribution of neighbors of the center node to the community.
The modularity contribution of a node to a community is easy to compute. According to Newman’s modularity definition [30], the contribution of a community to the network modularity is:
where m is the number of network edges, is the component of the ith row and the jth column in the network adjacent matrix, and () is the degree of (). If node v is added to the community, the variation of the community modularity, namely the modularity contribution of the node, will be:
Finally, based on the found community structure, the partial community information of the center node is extracted. Here the information refers to the groups of direct neighbors of the center node: the group consisting of neighbors that share at least one community with the center node and the group of neighbors that do not.
Because the game-playing is a heuristic algorithm and unstable, i.e., the result of different runs on the same network can be variant, the formation game-playing is conducted several times and their results are combined by group union.
At last, the partial community information of all nodes is returned for random walk guidance in next step.
Similarly, the community information finding on ego-nets are parallel executed by processes from a pool. Ego-nets should be randomly assigned to a process for dealing with to make the running time of each process be roughly equal, in that the sizes of ego-nets may change dramatically.
4.3. Random Walks Incorporating Partial Community Information
With the found partial community information, random walks used for node representation learning are collected on the analyzed network as we do in our previous work [7]. Specifically, for a walk, the next step node selection is ruled as:
where the means DeepWalk or node2vec walk, i.e., randomly selecting a neighbor of the current node as the next walk in DeepWalk or choosing the next node with probabilities controlled by the parameters return p and in-out q. The incorporates partial community information, i.e., randomly selecting a neighbor that shares at least one community with the current node as the next walk. The random number r is uniformly drawn from range before each walk and is a designated threshold. By giving neighbors sharing communities a priority, which is adjusted by , the generated walks are likely trapped within communities; therefore, the community properties of the network can be implicitly preserved in walks, which will be used to learn node representations. We denote the methods using DeepWalk and node2vec walk as GameNE-DW and GameNE-N2V, respectively.
4.4. Time Complexity
The most time-consuming step in our GameNE framework is the partial community information extraction using game-playing. Its time complexity will dominate that of the whole algorithm. Here, we analyze the time complexity of this step. According to the analysis by Chen et al. [22], the worst time complexity to reach a local equilibrium on an ego-net is , where m is the edge number of the ego-net. Therefore, the upper-limit time complexity of our parallel partial community information extracting should be , where P is the number of processes used and is the maximum edge number of ego-nets.
5. Evaluation
We test the performance of community property preservation of our GameNE methods using the multi-label classification application. We compare them against six existing network embedding algorithms, which are DeepWalk [8], node2vec [9], LINE [31], GraRep [32], ComE [14] and CNRL [16]. DeepWalk and node2vec are the bases of our methods. ComE and CNRL are two algorithms that explicitly take network community structure into consideration during node representation learning. Both are based on DeepWalk and node2vec. For CNRL, we adopt the “Embedding-based assignment” strategy that use low-dimension representations of nodes and communities to estimate assignments of node to community due to its computing efficiency.
5.1. Network Data
Experiments are conducted on synthesized undirected and unweighted networks generated using LFR model [33], which is widely applied for evaluating the performance of community detection algorithms. In the model, community structure properties of network are controlled by several parameters, as shown in Table 2.

Table 2.
LFR parameter settings of synthesized networks.
Game theory are superior at overlapping community detection because it is nature that a player can join in multiple communities at the same time. In our experiment settings, we mainly change two overlapping node control parameters, the overlapping density and the overlapping diversity . The overlapping density specifies the number of overlapping nodes, while the overlapping diversity designates the number of community memberships of each overlapping node. We vary and to generate networks with high overlapping density and high overlapping diversity. Specifically, the is set as , and of total network nodes with and , and the is appointed to 3, 6, and 9 with and . The mixing ratio is a parameter that controls the fraction of edges connecting with nodes that are outside of a community to edges inside the community. The smaller the , the clearer the community structure. We set as 0.3 to obtain networks with some blur community structure. The overall model parameters of our experiments can be found in Table 2. Totally, we generate 6 networks for experiments. These networks are denoted by their specific parameter or . Please note that the parameters of the network % and are same, but they are two distinct networks.
We also rectify the community structures of these generated networks, because we find that there are portions of nodes violating the property of a strong community, i.e., a node has more connections within the belonging community but relatively less connections with the rest of the network. The operations of rectification are reported below:
- (1)
- a node leaves an enrolling community with which it has zero or one connection. The zero-connection node should leave the community for sure. The one connection joining comes up mainly on some high overlapping membership nodes. Their connection number to each joining community is one. Since one connection is a trivial structure, we believe the node should not belong to such a community.
- (2)
- a node joins in a not-enrolling community to which the connection number of the node is equal to or larger than a designated threshold, which here we take as the minimum number of connections the node with its already joining-in communities. Such a situation occurs mostly as the connection number of a new joining is 2.
Both the leaving and joining actions are executed repeatedly until no node changes its community enrollments, or up to a designated number of times. Leaving actions should be carried out first. These rectifications may change the overlapping memberships of some nodes. The distributions of amended community memberships (except one) of generated networks are shown in Figure 2. As can be seen, overlapping memberships spread in a wider range, compared with the original same one designated by for all overlapping nodes. The blue bar stands for the specified . Moreover, there are some nodes of which their communities become singleton, namely with just itself as member. All in all, the community structures of these networks become more complicated and are more likely as what should be in real networks.
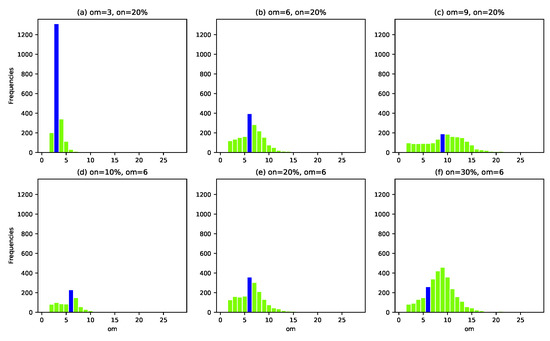
Figure 2.
Distributions of amended overlapping memberships of LFR synthesized networks.
5.2. Multi-Label Classification
We label nodes of the synthesized networks using their community identifications. Such a labeling mechanism makes the community structure of a network totally incorporated in its node labels, namely nodes in a community with density connections will have the same label. Therefore, we can use the multi-label classification to verify whether community structure properties are properly preserved in low-dimension node representations.
In experiments, we first learn the node representations for a network, then split its nodes to two parts, training part and testing part. The training part is used to train a classifier according to its node representations and labels, and then the classifier is hired to predict labels for the testing nodes. The classifier employed here is the libsvm [34], in which the linear kernel function is used, and other parameters are set as defaults.
The metrics for evaluating classification performance are Micro-F1 and Macro-F1. Micro-F1 is computed from each label prediction instance of each node, while Macro-F1 is the averaged F1 scores of each label prediction.
5.3. Experiment Settings
We run all involved algorithms on the rectified LFR networks to get their low-dimension node representations 10 times, and then use the multi-label classification to evaluate their performance in terms of preserving community structure properties. The Micro-F1 and Macro-F1 scores are averaged on the 10 results. Similar to evaluation using classification in previous works, we randomly sample 50% to 90% nodes as training nodes and leave the rest as testing nodes. In addition, we ensure that the same ratio of overlapping nodes is sampled but no singleton community node is chosen. Singleton nodes have no contribution to training because their labels are not needed for and have little impact on prediction, yet their labels cannot be correctly predicted if left as testing nodes since no other nearby nodes in embedding space have their label information.
Following previous works, the node embedding dimension is set as 128. For random walk-based approaches, the length of walk is 40 and the walk number starting from each node is 80. Both the context window size and the negative sample number in the Skip-Gram model are set as 5. For ComE and CNRL algorithms, the required community number is set as the actual number(excluding singleton communities). The two trade-off parameters of ComE, and , are set as 0.1 according to the analysis in that paper. The max transition probability order of GraRep is 4. For the parameter p and q of node2vec and algorithms based on it, as well as the walking within community threshold of our GameNE, we run the corresponding algorithm with each candidate parameter combination three times and select the one that results the maximum average Micro-F1.
5.4. Results of Different Overlapping Diversity
We first show the label prediction results of networks with changing. Remember that the actual overlapping memberships of these networks spread in a wide range after our adjustment, as shown in Figure 2.
Table 3 displays the scores of the network . LINE-1 uses only the first order similarity in LINE, while LINE-c employs both the first and second order similarities. The best score is shown in bold and the second best in bold and italic. As can be seen, from the Micro-F1 scores, GameNE-DW or GameNE-N2V is the best or the runner-up except while the training ratio is 70%, at which ComE is the best. GameNE methods improve their base approaches greatly. Examining other compared algorithms, ComE that explicitly considers preserving community structure is the third best and LINE-1 surprisingly is the fourth in general. However, the two CNRL algorithms that also explicitly take community structure preservation into consideration are even worse than their base approaches and are the worst among involved algorithms.

Table 3.
Micro- and Macro-F1 Scores of Multi-Label Classification, Network .
From the viewpoint of Macro scores, the phenomena are a little different. LINE-1 is the best, and our GameNE-N2V and GameNE-DW are the second and third best, respectively. ComE becomes the fourth. Macro-F1 is computed as the average F1 scores of each label prediction; therefore, the variation of F1 scores of some labels may induce a different rank.
Table 4 presents the scores of the network . As shown, GameNE-DW or GameNE-N2V is the best or the runner-up in both terms of Micro-F1 and Macro-F1. The following three in rank in general are node2vec, ComE and DeepWalk from Micro-F1, and ComE, LINE-1 and node2vec from Macro-F1. The results of the network are similar, as shown in Table 5.

Table 4.
Micro- and Macro-F1 Scores of Multi-Label Classification, Network .

Table 5.
Micro- and Macro-F1 Scores of Multi-Label Classification, Network .
In general, it can be concluded that our GameNE methods are superior at node representation learning for networks with high and various overlapping diversity.
5.5. Results of Different Overlapping Density
We also test the effects of overlapping node density on performance of our methods by changing . Table 6 shows the scores for the network . It can be seen that GraRep is the best while our GameNE-DW or GameNE-N2V is the runner-up in most cases. The two following regarding Micro-F1 are node2vec or DeepWalk, while Macro-F1 are ComE, node2vec or DeepWalk. The results suggest that GraRep is good at topology properties preserving for networks with simple overlapping community structure.

Table 6.
Micro- and Macro F1-Scores of Multi-Label Classification, Network .
As increases to 20%, the phenomena are similar to those of is 6. As shown in Table 7, GameNE-DW and GameNE-N2V are the best or the runner-up in both terms of Micro-F1 and Macro-F1. The following three are node2vec, ComE and DeepWalk with respect to Micro-F1 and ComE, LINE-1 and node2vec to Macro-F1.

Table 7.
Micro- and Macro F1-Scores of Multi-Label Classification, Network .
The label prediction results of the network are depicted in Table 8. Once more, GameNE-DW and GameNE-N2V are the best or the second regarding both Micro-F1 and Macro-F1. In general, the three following are ComE, node2vec and DeepWalk from Micro-F1, and LINE-1, ComE and node2vec from Macro-F1.

Table 8.
Micro- and Macro F1-Scores of Multi-Label Classification, Network .
In summary, from the experiment results above, the conclusion can be safely drawn that our GameNE methods can improve their bases, DeepWalk and node2vec, greatly and perform better than the compared baselines on networks with high overlapping diversity and density. The improvement rises from the fact that game theory-based algorithm can detect high-quality overlapping community structure information for networks. In addition, ComE that explicitly considers preserving community properties is the following best in most cases, and contrary to the intuition, LINE-1 that only takes the first order node pair similarity and thus is expected to be worse than LINE-c that takes both the first and the second order node similarities shows relatively good performance. We believe that the reason behind is the way the second order similarity is used in LINE-c, but not that the second order similarity is unimportant or unnecessary.
6. Discussion
Our framework provides a new way for community structure preservation in network representation learning. In contrast to the majority of previous works that generally make an assumption on community structure model and solve network node embedding and community embedding (or community detection) jointly, our framework (Algorithm 1) first finds partial community information of a network and then incorporates the information into the collected random walks, which will be used for representation learning of the network. A predefined model may not capture complicated properties of communities well. In addition, detecting a high-quality community structure is usually computation cost. Our framework sets no community model restriction and reduces the cost by finding just partial community information, which still can greatly improve the performance of node representation learning, as shown in Section 5.4 and Section 5.5.
The pivot of our framework is how can we find accurate community information to enhance random walks. In the implementation of this paper, we design a game theory-based algorithm to achieve this (Algorithm 3). The game methods are superior at overlapping community detecting; however, they cannot be used on large-scale networks due to computation cost as converging. We avoid this problem by finding partial community information for each node on its 2-hop ego-net (Algorithm 2), the size of which is generally dramatically smaller than that of the whole network. Moreover, the analyzing of ego-nets gives two chances for a node pair to find if they belong to a same community independently, and thus may bring out better partial community information. Other high-quality community structure detection algorithms, including other game theory-based ones, are worth to try as well to further improve the quality of found partial community information.
In the current framework implementation, we use a multi-process parallel manner to independently run many ego-net analyzing. Therefore, the running time will rest with how many processes can be actually parallel executed by the used server, which in turn mainly depends on the number of CPU cores of that server. We are planning to improve the framework to make it run in a distributed multi-process parallel manner, namely it can be executed on a server cluster, to further expands its scalability.
7. Conclusions
The preservation of network topology structure properties is a basic requirement in network representation learning. In this paper, we introduced a multi-process parallel framework for network node representation learning that can maintain community structure properties well. Ground on the framework, we implemented two methods, GameNE-DW and Game-N2V, found on random walks of DeepWalk and node2vec, respectively and use an improved game theory-based method for partial community information finding on ego-nets. A series of multi-label classification experiments have been conducted to evaluate the performance of community structure preserving for the proposed methods and six existing node embedding algorithms. The results showed that our GameNE methods are superior at learning node representations that can preserve community structure properties, especially on networks with high overlapping diversity and density.
Author Contributions
Conceptualization, H.S. and W.J.; methodology, H.S., J.L. and L.C.; software, G.L. and S.Z.; validation, Z.W. and S.M.; formal analysis, H.S. and W.J.; investigation, G.L.; data curation, S.Z.; writing—original draft preparation, H.S.; writing—review and editing, W.J., J.L. and L.C.; funding acquisition, H.S. and G.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the International Science and Technology Cooperation Project of Shaanxi Province, China, grant number 2019KW-008; and the Science and Technology Projects of Xi’an City, China, grant number 2019218114GXRC017CG018-GXYD17.9.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data and code presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy reasons.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, D.; Yin, J.; Zhu, X.; Zhang, C. Network representation learning: A survey. IEEE Trans. Big Data 2020, 6, 3–28. [Google Scholar] [CrossRef]
- Goyal, P.; Ferrara, E. Graph embedding techniques, applications, and performance: A survey. Knowl. Based Syst. 2018, 151, 78–94. [Google Scholar] [CrossRef]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Representation learning on graphs: Methods and applications. arXiv 2018, arXiv:1709.05584. [Google Scholar]
- Cai, H.; Zheng, V.W.; Chang, K.C.C. A comprehensive survey of graph embedding: Problems, techniques, and applications. IEEE Trans. Knowl. Data Eng. 2018, 30, 1616–1637. [Google Scholar] [CrossRef]
- Qi, J.; Liang, X.; Li, Z.; Chen, Y.; Xu, Y. Representation learning of large-scale complex information network: Concepts, methods and challenges. Chin. J. Comput. 2018, 41, 2394–2420. (In Chinese) [Google Scholar]
- Tu, C.; Yang, C.; Liu, Z.; Sun, M. Network representation learning: An overview. Sci. Sin. Inf. 2017, 47, 980–996. (In Chinese) [Google Scholar]
- Sun, H.; Jie, W.; Wang, Z.; Wang, H.; Ma, S. Network Representation Learning Guided by Partial Community Structure. IEEE Access 2020, 8, 46665–46681. [Google Scholar] [CrossRef]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. DeepWalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar] [CrossRef]
- Grover, A.; Leskovec, J. node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 855–864. [Google Scholar] [CrossRef]
- Wang, X.; Cui, P.; Wang, J.; Pei, J.; Zhu, W.; Yang, S. Community preserving network embedding. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 203–209. [Google Scholar]
- Rozemberczki, B.; Davies, R.; Sarkar, R.; Sutton, C. GEMSEC: Graph Embedding with Self Clustering. In Proceedings of the 2019 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, Vancouver, BC, Canada, 27–30 August 2019. [Google Scholar]
- Li, Y.; Wang, Y.; Zhang, T.; Zhang, J.; Chang, Y. Learning Network Embedding with Community Structural Information. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019. [Google Scholar] [CrossRef]
- Zhang, Y.; Lyu, T.; Zhang, Y. COSINE: Community-preserving social network embedding from information diffusion cascades. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; pp. 2620–2627. [Google Scholar]
- Cavallari, S.; Zheng, V.W.; Cai, H. Learning community embedding with community detection and node embedding on graphs. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, Singapore, 6–10 November 2017; pp. 377–386. [Google Scholar] [CrossRef]
- Cavallar, S.; Cambria, E.; Cai, H.; Chang, K.C.C.; Zheng, V.W. Embedding Both Finite and Infinite Communities on Graphs. IEEE Comput. Intell. Mag. 2019, 14, 39–50. [Google Scholar] [CrossRef]
- Tu, C.; Zeng, X.; Wang, H.; Zhang, Z.; Liu, Z.; Sun, M.; Zhang, B.; Lin, L. A unified framework for community detection and network representation learning. IEEE Trans. Knowl. Data Eng. 2019, 31, 1051–1065. [Google Scholar] [CrossRef]
- Jia, Y.; Zhang, Q.; Zhang, W.; Wang, X. CommunityGan: Community detection with generative adversarial nets. In Proceedings of the World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 784–794. [Google Scholar]
- Sun, F.Y.; Qu, M.; Hoffmann, J.; Huang, C.W.; Tang, J. vGraph: A Generative Model for Joint Community Detection and Node Representation Learning. In Advances in Neural Information Processing Systems (NeurIPS 2019); Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; Volume 32. [Google Scholar]
- Keikha, M.M.; Rahgozar, M.; Asadpour, M. Community aware random walk for network embedding. Knowl. Based Syst. 2018, 148, 47–54. [Google Scholar] [CrossRef]
- Tian, Y.; Balmin, A.; Corsten, S.A.; Tatikonda, S.; McPherson, J. From “Think Like a Vertex” to “Think Like a Graph”. In Proceedings of the 40th International Conference on Very Large Data Bases, Hangzhou, China, 1–5 September 2014; pp. 193–204. [Google Scholar] [CrossRef]
- Jonnalagadda, A.; Kuppusamy, L. A survey on game theoretic models for community detection in social networks. Soc. Netw. Anal. Min. 2016, 6, 1–24. [Google Scholar] [CrossRef]
- Chen, W.; Liu, Z.; Sun, X.; Wang, Y. A Game-Theoretic Framework to Identify Overlapping Communities in Social Networks. Data Min. Knowl. Discov. 2010, 21, 224–240. [Google Scholar] [CrossRef]
- Soleimanpour, M.; Hamze, A. A game-theoretic approach for locally detecting overlapping communities in social networks. In Proceedings of the Eighth International Conference on Information and Knowledge Technology, Hamedan, Iran, 7–8 September 2016; pp. 38–44. [Google Scholar]
- Sun, H.L.; Ch’Ng, E.; Yong, X.; Garibaldi, J.M.; See, S.; Chen, D.B. An improved game-theoretic approach to uncover overlapping communities. Int. J. Mod. Phys. C 2017, 28, 1750112. [Google Scholar] [CrossRef]
- Zhou, X.; Zhao, X.; Liu, Y.; Sun, G. A game theoretic algorithm to detect overlapping community structure in networks. Phys. Lett. A 2018, 382, 872–879. [Google Scholar] [CrossRef]
- Avrachenkov, K.E.; Kondratev, A.Y.; Mazalov, V.V. Cooperative Game Theory Approaches for Network Partitioning. In Proceedings of the 6th International Conference on Computational Social Networks, Hong Kong, China, 3–5 August 2017. [Google Scholar]
- Zhou, L.; Lü, K.; Yang, P.; Wang, L.; Kong, B. An Approach for Overlapping and Hierarchical Community Detection in Social Networks Based on Coalition Formation Game Theory. Expert Syst. Appl. 2015, 42, 9634–9646. [Google Scholar] [CrossRef]
- Zhou, L.; Yang, P.; Lü, K.; Zhang, Z.; Chen, H. A Coalition Formation Game Theory-Based Approach for Detecting Communities in Multi-relational Networks. In Proceedings of the 16th International conference on Web-Age Information Management, Qingdao, China, 8–10 June 2015; pp. 30–41. [Google Scholar]
- Moscato, V.; Picariello, A.; Sperlí, G. Community detection based on Game Theory. Eng. Appl. Artif. Intell. 2019, 85, 773–782. [Google Scholar] [CrossRef]
- Newman, M.E.J. Modularity and community structure in networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar] [CrossRef]
- Tang, J.; Qu, M.; Wang, M.; Zhang, M.; Yan, J.; Mei, Q. LINE: Large-scale information network embedding. In Proceedings of the 24th International World Wide Web Conference, Florence, Italy, 18–22 May 2015; pp. 1067–1077. [Google Scholar] [CrossRef]
- Cao, S.; Lu, W.; Xu, Q. GraRep: Learning graph representations with global structural information. In Proceedings of the 24th ACM International Conference on Information and Knowledge Management, Melbourne, Australia, 19–23 October 2015; pp. 891–900. [Google Scholar] [CrossRef]
- Lancichinetti, A.; Fortunato, S.; Radicchi, F. Benchmark graphs for testing community detection algorithms. Phy. Rev. E 2008, 78, 046110. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).